
Эконометрический подход к анализу графиков
Теория без фактов может быть пустой, но факты без теории бессмысленны.
К.Боулдинг
Введение
Часто
приходится слышать, что рынки изменчивы, что нет постоянства. Это обусловливает
невозможность прибыльно торговать на длинном промежутке времени. Так ли это? Давайте
попробуем подойти к этой проблеме с научной стороны. В качестве методов
исследования выберем эконометрические. Почему именно эти? Ну, во-первых, потому что MQL сообщество любит точность, которую нам беспристрастно обеспечат математика и статистика. А во-вторых, если не ошибаюсь, об этом ещё не писали.
Сразу оговорюсь, что в рамках одной статьи поставленную задачу - возможно ли прибыльно торговать на длинном промежутке времени - не решить. Сегодня я только опишу некоторые методы диагностики для выбранной модели, которые, надеюсь, окажутся полезными для будущего исследования.
Кроме того, я постараюсь, насколько это возможно, изложить временами сухой материал, включающий в себя формулы, теоремы, гипотезы, доступным, не птичьим языком. Однако, я ожидаю, что читатель будет знаком или ознакомится с базовыми статистическими понятиями, такими как: гипотеза, статистическая значимость, статистика (статистический критерий), дисперсия, распределение, вероятность, регрессия, автокорреляция и т.п.
1. Характеристики временного ряда
Очевидно, что объект анализа - ценовой ряд (его производные), который является по своей природе временным (time series).
Эконометристы изучают временной ряд с точки зрения частотных методов (спектральный анализ, вейвлетный анализ) и методов временной области (кросс-корреляционный анализ, автокорреляционный анализ). Читателю ранее была представлена статья "Строим анализатор спектра", которая касалась частотных методов. Теперь я предлагаю рассмотреть методы временной области, в частности, автокорреляционный анализ и анализ условной дисперсии.
Нелинейные модели описывают поведение ценовых временных рядов лучше, чем линейные модели. Поэтому в данной статье сосредоточим своё внимание на изучении нелинейных моделей.
Ценовым временным рядам присущи специфические особенности, учесть которые способны лишь определённые эконометрические модели. К таким особенностям прежде всего относят: «толстые хвосты», кластеризацию волатильности и эффекты рычага.
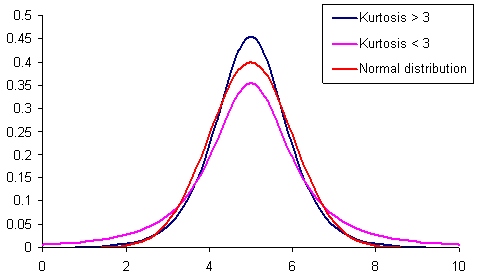
Рисунок 1. Распределения с разным куртосисом.
На Рис.1 представлены 3 распределения с различным куртосисом (островершинностью). Распределение, чья островершинность меньше аналогичной нормального распределения, чаще всего имеет «толстые хвосты». Оно отображено розовым цветом.
Распределение нам нужно для того, чтобы отобразить плотность вероятности случайной величины, которой мы считаем значения исследуемого ряда.
Под кластеризацией (от англ. cluster - пучок, скопление, концентрация) волатильности понимается следующее. За промежутком времени с высокой волатильностью следует такой же, а за промежутком с низкой - идентичный. Если вчера цены сильно колебались, то и сегодня, вероятнее всего, они будут колебаться так же сильно. В этом смысле, присутствует некоторая инерция волатильности. На Рис.2 показано, что волатильность имеет пучкообразную форму.
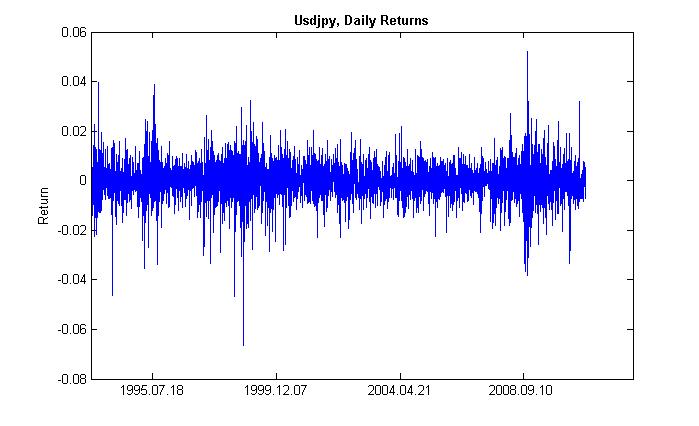
Рисунок 2. Волатильность дневных доходностей пары usdjpy, её кластеризация.
Эффект рычага состоит в том, что на падающем рынке волатильность выше, чем на растущем. Получается так потому, что при снижении цен акций увеличивается коэффициент рычага, зависящего от отношения заёмного и собственного капитала. Но скорее это явление касается фондового рынка, а не валютного. Далее этот эффект рассматриваться не будет.
2. GARCH-модель
Итак, наша основная цель - сделать прогноз валютного курса (цены) с помощью некоторой модели. Эконометристы используют математические модели, описывая те или иные явления, поддающиеся количественной оценке. Если говорить проще, то они подводят под явление какую-то формулу. И таким образом описывают это явление.
Ввиду того, что исследуемый временной ряд имеет свойства, указанные выше, оптимальной моделью, учитывающей эти свойства, можно назвать нелинейную модель. Одна из самых универсальных нелинейных моделей - это GARCH-модель. Чем она нам поможет? Она будет учитывать в своём теле (формуле) волатильность ряда, т.е. изменчивость дисперсии на различных интервалах наблюдения. Эконометристы называют это явление мудрёным словом гетероскедастичность (от греч. hetero - разный, skedasis - дисперсия).
Если мы непосредственно посмотрим на формулу, то увидим, что данная модель предполагает, что на текущую изменчивость дисперсии (σ2t) влияют как предыдущие изменения показателей (ϵ2t-i), так и предыдущие оценки дисперсии (т.н. «старые новости») (σ2t-i):
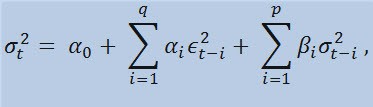
с ограничениями
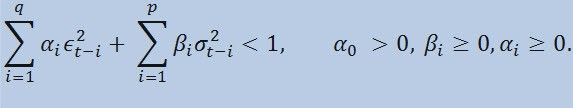
Где, ϵt - ненормированные инновации; α0 , βi , αi , q (порядок ARCH-членов ϵ2), p (порядок GARCH-членов σ2) - оцениваемые параметры и порядок моделей.
3. Индикатор доходностей
На самом деле оценивать мы будем не сам ценовой ряд, а ряд доходностей. Логарифм изменения цены (непрерывно начисляемая доходность) определяется как натуральный логарифм процентной доходности, а именно:
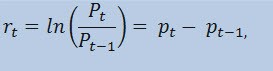
где,
- Pt - это значение ценового временного ряда в момент времени t;
- Pt-1 - это значение ценового временного ряда в момент времени t-1;
- pt = ln(Pt) - это натуральный логарифм Pt.
На практике, основная причина, по которой работа с доходностями активов является более предпочтительной, чем с непосредственными ценами активов, заключается в том, что доходности имеют более привлекательные статистические свойства.
Итак, давайте создадим для начала индикатор доходностей ReturnsIndicator.mq5, который в последующем нам очень пригодится. Тут я позволю себе сослаться на статью «Пользовательские индикаторы в MQL5 для начинающих», в которой доступно изложен алгоритм создания индикатора. Поэтому приведу только программный код, непосредственно реализующий указанную формулу. Думаю, что он очень простой, и пояснять ничего не нужно.
//+------------------------------------------------------------------+ //| Custom indicator iteration function | //+------------------------------------------------------------------+ int OnCalculate(const int rates_total, // размер массива price[] const int prev_calculated, // количество доступных баров на предыдущем вызове const int begin, // с какого индекса в массиве price[] начинаются достоверные данные const double& price[]) // массив, по которому и будет считаться индикатор { //--- int start; if(prev_calculated<2) start=1; // начнем заполнять ReturnsBuffer[] с 1-го индекса, а не с 0-го else start=prev_calculated-1; // установим start равным последнему индексу в массивах for(int i=start;i<rates_total;i++) { ReturnsBuffer[i]=MathLog(price[i]/price[i-1]); } //--- return value of prev_calculated for next call return(rates_total); } //+------------------------------------------------------------------+
Единственное, что хотелось бы отметить, по своей сущности ряд доходностей всегда меньше исходного ряда на 1 элемент. Поэтому массив доходностей мы будем рассчитывать со второго элемента, а первый всегда будет равен 0.
Итак, с помощью индикатора ReturnsIndicator мы получили тот производный временной
ряд, который станет объектом наших исследований.
4. Статистические тесты
Теперь настаёт очередь статистических тестов. Они проводятся для того, чтобы определить, есть ли во временном ряде какие-то признаки, подтверждающие целесообразность применения той или иной модели. В нашем случае такой моделью станет GARCH-модель.
С помощью Q-теста Льюнга-Бокса-Пирса проверим, случайны ли автокорреляции ряда или есть какая-то зависимость. Для этого нам придётся написать новую функцию. Тут под автокорреляцией мы понимаем корреляцию (вероятностную связь) между значениями одного и того же временного ряда X (t) в моменты времени t1 и t2. Если моменты времени t1 и t2 являются соседними (т.е. следуют друг за другом), то мы ищем связь членов ряда и передвинутых на одну единицу времени членов того же ряда: x1, x2, x3, ... и x1+1, x2+1, x3+1, ... Такое запаздывание передвинутых членов называется лагом (от англ. lag - отставание; задержка, запаздывание). Значение лага может быть любым положительным целым числом.
Тут я сделаю небольшое лирическое отступление и скажу вот о чём. Насколько я знаю, ни в языке С++, ни в MQL5 нет стандартных библиотек, охватывающих сложные и не очень статистические расчёты. Обычно такие расчеты производятся в специальных статистических пакетах. Лично для меня гораздо проще было бы воспользоваться такими пакетами, как например Matlab, STATISTICA 9 и подобными, чтобы решить поставленную задачу. Но я решил отказаться от использования внешних библиотек, с одной стороны, чтобы продемонстрировать, насколько сам язык MQL5 представляет собой мощный инструмент для расчётов, а с другой... я сам в процессе написания MQL кода многому научился.
Теперь нужно заметить следующее. Для проведения Q-теста потребуются комплексные числа. Поэтому я создал класс Complex. В идеале он конечно должен называться CComplex. Но я немного позволил себе расслабиться. Уверен, что читатель является подготовленным, и ему не нужно объяснять, что собой представляет комплексное число. Лично мне не очень понравились функции, рассчитывающие преобразования Фурье, которые появлялись и на сайте MQL5, и на сайте MQL4, где неявно фигурировали комплексные числа. Тем более, что ещё одно препятствие имело место - это невозможность, в частности, перегружать в MQL5 арифметические операторы. Пришлось искать другие подходы и обходить стандартную сишную нотацию. Класс комплексных чисел я представил примерно так:
class Complex { public: double re,im; //re -вещественная часть комплексного числа, im - мнимая public: void Complex(){}; //конструктор по умолчанию void setComplex(double rE,double iM){re=rE; im=iM;};//set-метод (1-й вариант) void setComplex(double rE){re=rE; im=0;}; //set-метод (2-й вариант) void ~Complex(){}; //деструктор void opEqual(const Complex &y){re=y.re;im=y.im;}; //operator= void opPlus(const Complex &x,const Complex &y); //operator+ void opPlusEq(const Complex &y); //operator+= void opMinus(const Complex &x,const Complex &y); //operator- void opMult(const Complex &x,const Complex &y); //operator* void opMultEq(const Complex &y); //operator*= (1-й вариант) void opMultEq(const double y); //operator*= (2-й вариант) void conjugate(const Complex &y); //сопряжение комплексных чисел double norm(); //нормализация };
То есть, например, операцию сложения двух комплексных чисел теперь можно провести с помощью метода opPlus, вычитания - opMinus и т.д. Если просто в коде написать c = a + b (где a, b, с - это комплексные числа), то компилятор взбунтуется. Но примет такое выражение: c.opPlus(a,b).
Пользователь по необходимости может расширить набор методов класса Complex. Например, можно добавить оператор деления.
Ещё мне понадобились вспомогательные функции, обрабатывающие массивы комплексных чисел. Поэтому я их вывел за рамки класса Complex, чтобы не зацикливать обработку элементов массива класса Complex, а работать с переданными по ссылке массивами напрямую. Всего таких функций три:
- getComplexArr (возвращает двумерный массив вещественных чисел из массива комплексных);
- setComplexArr (возвращает массив комплексных чисел из одномерного массива вещественных чисел);
- setComplexArr2 (возвращает массив комплексных чисел из двумерного массива вещественных чисел).
Нужно заметить, что эти функции возвращают массивы, переданные им по ссылке. Поэтому в их теле отсутствует оператор return. Но рассуждая логически, по-моему, можно говорить о возврате, несмотря на тип void.
Класс комплексных чисел и вспомогательных функций определён в заголовочном файле Complex_class.mqh.
Затем нам понадобятся при проведении теста автокорреляционная функция и функции преобразования Фурье. И здесь возникает необходимость в создании нового класса, который я назову CFFT. Он будет обрабатывать массивы комплексных чисел для Фурье-преобразований. Фурье-класс я представил примерно так:
class CFFT { public: Complex Input[]; //входной массив комплексных чисел Complex Output[]; //выходной массив комплексных чисел public: bool Forward(const uint N); //прямое преобразование Фурье bool InverseT(const uint N,const bool Scale=true); //обратное преобразование Фурье взвешенное bool InverseF(const uint N,const bool Scale=false); //обратное преобразование Фурье невзвешенное void setCFFT(Complex &data1[],Complex &data2[],const uint N); //set-метод (1-й вариант) void setCFFT(Complex &data1[],Complex &data2[]); //set-метод (2-й вариант) protected: void Rearrange(const uint N); // перегруппировка void Perform(const uint N,const bool Inverse); // реализация преобразования void Scale(const uint N); // взвешивание };
Нужно отметить, что все Фурье-преобразования проводятся с массивами, длина которых удовлетворяет условию 2^N (где N - это степень двойки). Как правило, длина массива не равна 2^N. Тогда длина массива увеличивается до такого значения 2^N, что 2^N >= n, где n - это длина массива. Добавленные элементы массива равны нулю. Такая обработка массива происходит в теле функции autocorr с помощью служебной функции nextpow2 и функции pow:
int nFFT=pow(2,nextpow2(ArraySize(res))+1); //степенной показатель двойки
Так, если мы имеем исходный массив, длина (n) которого равна 73585, то функция nextpow2 вернёт нам значение 17, где 2^17 = 131072. Т.е. возвращаемое значение больше n на pow(2, ceil(log(n)/log(2))). Потом мы вычислим значение nFFT: 2^(17+1) = 262144. Это будет длина служебного массива, элементы которого с 73585-го по 262143-ий будут равны нулю.
Фурье-класс определён в заголовочном файле FFT_class.mqh.
Снова в целях экономии пропущу описание реализаций класса CFFT. Интересующиеся смогут сами проверить их в прилагаемом включаемом файле. Давайте перейдём теперь непосредственно к автокорреляционной функции.
void autocorr(double &ACF[],double &res[],int nLags) //1-ый вариант функции /* Выборочная автокорреляционная функция (АКФ) для одномерного стохастического временного ряда ACF - выходной массив вычисленных значений автокорреляционной функции; res - массив наблюдений стохастического временного ряда; nLags - максимальное число лагов, для которых рассчитывается АКФ. */ { Complex Data1[],Data21[], //входные массивы комплексных чисел Data2[],Data22[], //выходные массивы комплексных чисел cData[]; //массив сопряжённых комплексных чисел double rA[][2]; //вспомогательный двумерный массив вещественных чисел int nFFT=pow(2,nextpow2(ArraySize(res))+1); //степенной показатель двойки ArrayResize(rA,nFFT);ArrayResize(Data1,nFFT); //подгонка размеров массивов ArrayResize(Data2,nFFT);ArrayResize(Data21,nFFT); ArrayResize(Data22,nFFT);ArrayResize(cData,nFFT); double rets1[]; //служебный массив для наблюдений ряда double m=mean(res); //среднее арифметическое массива res ArrayResize(rets1,nFFT); //подгонка размера массива for(int t=0;t<ArraySize(res);t++) //копируем исходный массив наблюдений // в служебный с поправкой на среднее rets1[t]=res[t]-m; setComplexArr(Data1,rets1); //задаём входной массив комплексных чисел CFFT F,F1; //инициализируем экземпляры класса CFFT F.setCFFT(Data1,Data2); //инициализируем данные-члены для экземпляра F F.Forward(nFFT); //проводим прямое преобразование Фурье for(int i=0;i<nFFT;i++) { Data21[i].opEqual(F.Output[i]);//присваиваем массиву Data21 значения массива F.Output; cData[i].conjugate(Data21[i]); //производим операцию сопряжения над массивом Data21 Data21[i].opMultEq(cData[i]); //произведение комплексного числа на сопряжённое ему //даёт комплексное число, имеющее ненулевой только действительную часть } F1.setCFFT(Data21,Data22); //инициализируем данные-члены для экземпляра F1 F1.InverseT(nFFT); //проводим обратное преобразование Фурье взвешенное getComplexArr(rA,F1.Output); //получаем результат в double формате после //обратного взвешенного преобразования Фурье for(int i=0;i<nLags+1;i++) { ACF[i]=rA[i][0]; //сохраним в выходной массив ACF вычисленные значения //автокорреляционной функции ACF[i]=ACF[i]/rA[0][0]; //нормализация относительно первого элемента } }
Итак, мы вычислили значения АКФ для заданного количества лагов. Теперь можно использовать автокорреляционную функцию для Q-теста. Сама функция теста будет выглядеть примерно так:
void lbqtest(bool &H[],double &rets[]) /* Функция, реализующая Q-тест Льюнга-Бокса-Пирса H - выходной массив логических значений, опровергающих или подтверждающих нулевую гипотезу на заданном лаге; rets - массив наблюдений стохастического временного ряда; */ { double lags[3]={10.0,15.0,20.0}; //заданные лаги int maxLags=20; //максимальное число лагов double ACF[]; ArrayResize(ACF,21); //пустой массив АКФ double acf[]; ArrayResize(acf,20); //дублёр массива АКФ autocorr(ACF,rets,maxLags); //вычисленный массив АКФ for(int i=0;i<20;i++) acf[i]=ACF[i+1]; //убираем первый элемент - единицу, заполняем //массив-дублёр double alpha[3]={0.05,0.05,0.05}; //массив уровней значимости теста /*Расчёт массива Q-статистик для заданных лагов согласно формуле: L |----| \ Q = T(T+2) || (rho(k)^2/(T-k)), / |----| k=1 где T - размер выборки, L - число лагов, rho(k) - значение АКФ на k-том лаге. */ double idx[]; ArrayResize(idx,maxLags); //вспомогательный массив индексов int len=ArraySize(rets); //длина массива наблюдений int arrLags[];ArrayResize(arrLags,maxLags); //вспомогательный массив лагов double stat[]; ArrayResize(stat,maxLags); //массив Q-статистик double sum[]; ArrayResize(sum,maxLags); //вспомогательный массив сумм double iACF[];ArrayResize(iACF,maxLags); //вспомогательный массив АКФ for(int i=0;i<maxLags;i++) { //заполним: arrLags[i]=i+1; //вспомогательный массив лагов idx[i]=len-arrLags[i]; //вспомогательный массив индексов iACF[i]=pow(acf[i],2)/idx[i]; //вспомогательный массив АКФ } cumsum(sum,iACF); //суммируем вспомогательный массив АКФ //нарастающим итогом for(int i=0;i<maxLags;i++) stat[i]=sum[i]*len*(len+2); //заполним массив Q-статистик double stat1[]; //дублёр массива Q-статистик ArrayResize(stat1,ArraySize(lags)); for(int i=0;i<ArraySize(lags);i++) stat1[i]=stat[lags[i]-1]; //заполним массив-дублёр для указанных лагов double pValue[ArraySize(lags)]; //массив p-значений for(int i=0;i<ArraySize(lags);i++) { pValue[i]=1-gammp(lags[i]/2,stat1[i]/2); //расчёт p-значений H[i]=alpha[i]>=pValue[i]; //оценка нулевой гипотезы } }
Итак, наша функция проводит Q-тест Льюнга-Бокса-Пирса и возвращает массив логических значений для заданных лагов. Тут нужно уточнить, что тест Льюинга-Бокса является так называемым portmanteau тестом (примерный перевод с англ. - объединённый тест).
Это означает, что проверяется некоторая группа лагов на наличие автокорреляции
вплоть до указанного лага. Обычно проверяют есть ли автокорреляция до 10-го, 15-го и 20-го лага включительно. Вывод о наличие автокорреляции во всём ряде делается по последнему значению элемента массива H, т.е. от первого лага до двадцатого.
Если элемент массива равен false, то нулевая гипотеза о том, что на предыдущих и заданном лаге не имеет место автокорреляция, не отвергается. Т.е. при значении false автокорреляции нет. В противном случае, тест указывает на наличие автокорреляции. Поэтому принимается альтернативная нулевой гипотеза о наличии автокорреляции при значении true.
Случается так, что автокорреляции в ряде доходностей не обнаруживается. Тогда для большей убедительности тестируют квадраты доходностей. Вывод о принятии или отвержении нулевой гипотезы делается так же, как и при тесте исходного ряда доходностей. Зачем берутся квадраты доходностей? - Таким образом мы искусственно увеличиваем возможную неслучайную автокорреляционную составляющую исследуемого ряда, которую потом и выявляем в рамках начальных значений доверительных пределов. Теоретически можно брать и кубы, и прочие степени доходностей. Но это уже излишняя статистическая нагрузка, при которой утрачивается смысл тестирования.
Можно заметить, что в конце тела функции Q-теста при расчёте р-значения (читается как пи-значения) появилась ещё одна функция gammp(x1/2,x2/2). Она позволяет вычислить неполную гамма-функцию для соответствующих элементов. Вообще-то нам была нужна изначально кумулятивная функция χ2-распределения (читается как хи-квадрат-распределения). Но именно она является частным случаем Гамма распределения.
В общем, для подтверждения того, что следует воспользоваться GARCH-моделью, достаточно получить положительное значение любого из лагов Q-теста. Кроме того, эконометристы проводят ещё такой тест, как ARCH-тест Энгля, проверяющий наличие условной гетероскедастичности. Но, полагаю, что нам вполне достаточно Q-теста для начала. Он является самым универсальным.
Теперь, когда у нас есть все необходимые функции для проведения указанного теста, нужно подумать о том, как вывести полученные результаты на экран. Для этого я написал ещё одну функцию lbqtestInfo, которая и выведет нам результаты эконометрического тестирования в форме окна сообщений, а диаграммы автокорреляций - прямо на график исследуемого инструмента.
Давайте посмотрим, что у нас вышло на конкретном примере. Первым инструментом для исследования я выбрал пару usdjpy. Сначала я открыл график пары в виде ломаной линии (по ценам закрытия) и загрузил пользовательский индикатор ReturnsIndicator для иллюстрации ряда доходностей. График максимально сжал, чтобы лучше видеть кластеризацию волатильности индикатора. Затем запустил на выполнение скрипт GarchTest. Возможно, что у нас с Вами разные разрешения мониторов, поэтому скрипт спросит Вас, какого размера диаграммы в пикселях Вы желаете получить. Мой стандарт 700*250.
Несколько примеров тестирования приведено на Рис.3.
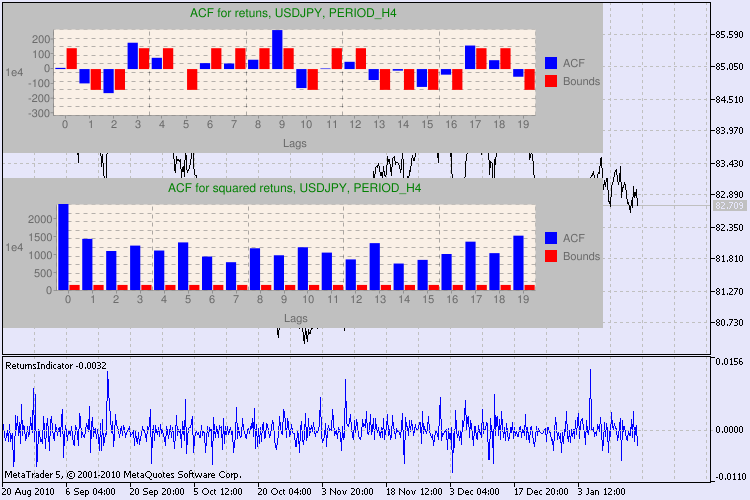
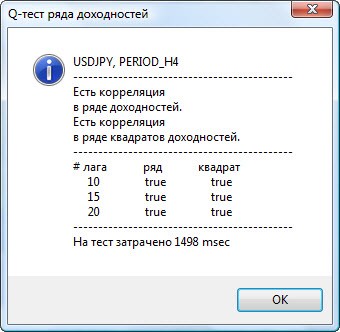
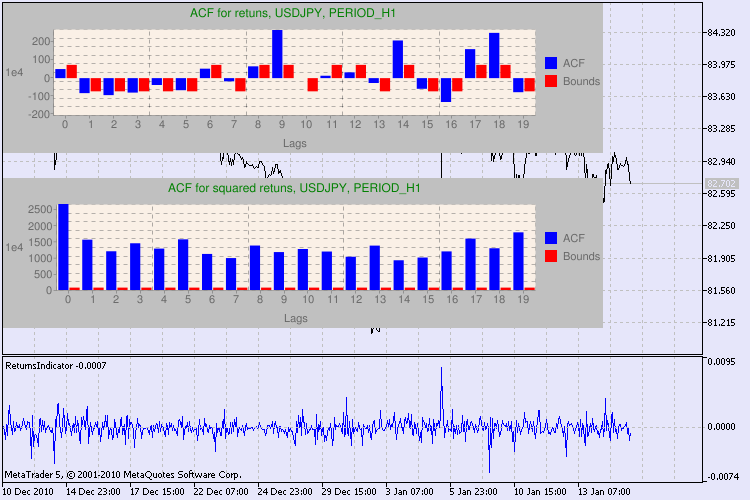
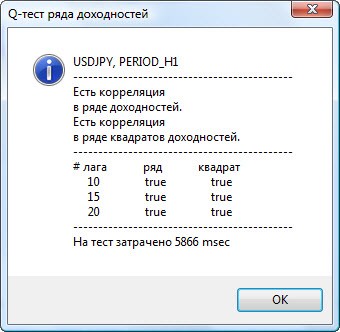
Рисунок 3. Результаты Q-теста и диаграммы автокорреляций для пары usdjpy для разных тайм-фреймов.
Да, я долго искал вариант отображения диаграммы на графике инструмента в MetaTrader 5. И самым оптимальным счёл - воспользоваться библиотекой для построения диаграмм средствами Google Chart API, о которой рассказано в одноимённой статье.
Как интерпретировать выведенную информацию? Давайте разберёмся. Вверху окна графика находится диаграмма автокорреляционной функции (АКФ) исходного ряда доходностей. На первом графике мы анализируем ряд пары usdjpy четырёхчасового тайм-фрейма. Видим, что некоторые значения АКФ (синие столбики) выходят за пределы (красные столбики). Т.е. на лицо небольшая автокорреляция в исходном ряде доходностей. Диаграмма ниже - это диаграмма автокорреляционной функции (АКФ) ряда квадратов доходностей для указанной пары. Там вообще всё ясно - полная победа синих столбиков. Диаграммы для часового тайм-фрейма анализируются аналогично.
Пару слов об описании осей диаграммы. С осью x всё ясно - на ней представлены индексы лагов. На оси y указано экспоненциальное значение, на которое было умножено исходное значение АКФ. Так, 1e4 означает, что исходное значение умножено на 1e4 (1e4=10000), а 1e2 - на 100 и т.д. Такое умножение было сделано для читабельности диаграммы.
Вверху диалогового окна отображено название пары или кросса и тайм-фрейм инструмента. Затем идут 2 предложения, которые указывают на наличие или отсутствие автокорреляция в исходном ряде доходностей и в ряде квадратов доходностей. Затем перечислен 10-ый, 15-ый и 20-ый лаг, значение автокорреляции в исходном ряде и в ряде квадратов. Тут для автокорреляции указано относительное значение в виде булевого флага при Q-тесте: есть ли автокорреляция на предыдущих и заданном лаге.
В итоге, если мы видим, что автокорреляция на предыдущих и заданном лаге присутствует, то флаг будет равен true, иначе - false. В первом случае наш ряд является "клиентом" для применения нелинейной GARCH-модели, а во втором - нужно использовать более простые аналитические модели. Внимательный читатель без труда заметит, что исходные ряды доходностей пары usdjpy незначительно коррелируют сами с собой, особенно старшего тайм-фрейма. Но ряды квадратов доходностей уже проявляют автокорреляцию.
Внизу окна указано время в мсек, затраченное на тестирование.
Всё тестирование мы проводили с помощью скрипта GarchTest.mq5.
Выводы
В своей статье я описал то, как эконометристы исследуют временные ряды, а точнее с чего они начинают свои исследования. При этом пришлось самому кодировать многие функции и некоторые типы данных (например комплексные числа). Возможно, что визуальная оценка исходного ряда даёт приблизительно похожий результат, что и оценка эконометрическая. Однако, мы условились, что при изучении проблемы будут использоваться точные методы. Так, опытный доктор может поставить диагноз больного без применения сложной техники и методологии. Но, как правило, он изучает недуг больного тщательно и скрупулёзно.
Что нам даёт описанный в статье подход? Применение нелинейной GARCH-модели позволяет, во-первых, формально представить исследуемый ряд с математической точки зрения, а во-вторых, создать прогноз на заданное количество шагов. Что поможет нам в дальнейшем симулировать поведение ряда в прогнозной области и протестировать любой из торговых экспертов на основании спрогнозированных данных.
Расположение файлов:
| # | File | Path |
|---|---|---|
| 1 | ReturnsIndicator.mq5 | %MetaTrader%\MQL5\Indicators |
| 2 | Complex_class.mqh | %MetaTrader%\MQL5\Include |
| 3 | FFT_class.mqh | %MetaTrader%\MQL5\Include |
| 4 | GarchTest.mq5 | %MetaTrader%\MQL5\Scripts |
Файлы и описание библиотеки google_charts.mqh и Libraries.rar можно скачать в указанной ранее статье.
Используемая литература:
- Analysis of Financial Time Series, Ruey S. Tsay, 2nd Edition, 2005. - 638 pp.
- Applied Econometric Time Series,Walter Enders, John Wiley & Sons, 2nd Edition, 1994. - 448 pp.
- Bollerslev, T., R. F. Engle, and D. B. Nelson. "ARCH Models." Handbook of Econometrics. Vol. 4, Chapter 49, Amsterdam: Elsevier Science B.V.
- Box, G. E. P., G. M. Jenkins, and G. C. Reinsel. Time Series Analysis: Forecasting and Control. 3rd ed. Upper Saddle River, NJ: Prentice-Hall, 1994.
- Numerical Recipes in C, The Art of Scientific Computing, 2nd Edition, W.H. Press, B.P. Flannery, S. A. Teukolsky, W. T. Vetterling, 1993. - 1020 pp.
- Голуб Дж., Ван Лоун Ч. Матричные вычисления: Пер. с англ. - М.: Мир, 1999. - 548 с., ил.
- Поршнев С.В. "Вычислительная математика. Курс лекций" C-Пб.: БХВ-Петербург, 2004. - 314 с.
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Графики и диаграммы в формате HTML
Графики и диаграммы в формате HTML
 Собери свой торговый советник в Мастере MQL5
Собери свой торговый советник в Мастере MQL5
 Подключение нейросетей от NeuroSolutions
Подключение нейросетей от NeuroSolutions
 Мастер MQL5: Как написать свой модуль управления капиталом и рисками
Мастер MQL5: Как написать свой модуль управления капиталом и рисками
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
Я не могу скомпилировать
GarchTest
GarchTest_html
Опубликована новая статья Эконометрический подход к анализу графиков:
Автор: Денис Кириченко
При попытке скомпилировать "garchtest.mq5" возникает ошибка.
'-' - ожидается целочисленное выражение garchtest.mq5 154 28
Но, исходя из вашего опыта, как вы думаете, имеет ли такой метод хорошую точность на практике?
Это была достойная статья. Мне очень понравилось. Я хочу предсказать, начнется ли тренд или нет на валютной паре на определенном временном интервале, скажем, H1. Для этого я сначала получаю доходность за временной интервал, скажем, за последние N "свечей H1", а затем использую Q-тест. Если Q-тест пройден, то я подгоняю параметры модели GARCH(1,1) к полученным доходностям из выбранного временного окна, а затем вычисляю ожидаемое значение прогнозируемой дисперсии для следующей свечи H1. Если оно выше определенного порога, то можно ожидать наступления тренда.
Но, исходя из вашего опыта, как вы думаете, имеет ли такой метод хорошую точность на практике?
Спасибо за ваше мнение. Модель не предсказывает тренд или флет. Она скорее позволяет определить границы будущей доходности. И вторая возможность - смоделировать будущие доходности (цены) в пределах утвержденных границ.
Спасибо, Денис, за ценный ответ. Итак, модель предсказывает "границы" будущих доходностей, а не их "знак". Можно ли как-то предсказать знак будущей доходности с помощью других дополнительных статистических моделей?