Análisis espectral singular unidimensional

Introducción

Los mercados financieros se caracterizan por su gran volatilidad y sus complejos procesos dinámicos, lo cual dificulta enormemente la previsión y la identificación de patrones. El análisis espectral singular (SSA) es un método eficaz de análisis de series temporales que permite representar la compleja estructura de una serie como una descomposición en componentes simples, como la tendencia, las fluctuaciones estacionales (periódicas) y el ruido. El método SSA, basado en el álgebra lineal, no requiere supuestos de estacionariedad, lo cual lo convierte en una herramienta versátil para investigar la estructura de las series temporales. 

Sin embargo, el uso extensivo de la teoría del álgebra vectorial y matricial en la bibliografía sobre el SSA crea un umbral de entrada bastante elevado, que puede dificultar la comprensión del tema a los lectores inexpertos e impedirles entender todos los entresijos y ventajas de este método de análisis. Este artículo pretende presentar de forma accesible y clara los fundamentos teóricos del SSA, pues sin su comprensión el método se convierte en una "caja negra", así como ofrecer una aplicación práctica de los conceptos descritos. 

Conviene aclarar que el término SSA debe entenderse como toda una familia de métodos de análisis, pero todos ellos se basan en la aplicación secuencial de cuatro pasos:

• la transformación de series temporales en una matriz de trayectorias (matriz de Hankel),
• la descomposición de la matriz de trayectorias en una suma de matrices elementales de rango uno,
• la agrupación de matrices elementales,
• la restauración (reconstrucción) de las series temporales.

Veamos cada uno de estos pasos con mayor detenimiento.

Construcción de la matriz de trayectorias

La idea básica consiste en transformar una serie temporal en una matriz que refleje su estructura en un espacio multidimensional. Esto se hace para revelar dependencias ocultas entre valores sucesivos de una serie. La matriz de trayectorias se construye del siguiente modo. Tomamos una muestra de serie temporal unidimensional de volumen N y la transformamos en un conjunto de K vectores (K= N — L + 1) realizando submuestras deslizantes de volumen L (longitud de la ventana). Los vectores resultantes de longitud L(x1,x2,...,xL},{x2,x3,...,xL+1}y etc.,), se ubican en columnas de matrices de trayectorias X.

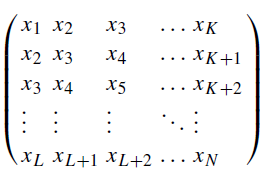
Figura 1 matriz de trayectorias X

Aquí, el parámetro L determina la profundidad del análisis, y suele ser igual a N/2.

Descomposición de una matriz de trayectorias en una suma de matrices de rango uno

Tras construir la matriz de trayectorias, se procede a su descomposición. Al usar la descomposición en valores singulares (SVD) de la matriz de trayectorias como tal descomposición, este método de análisis se denomina básico (Basic-SSA).

Mediante la descomposición en valores singulares, se obtienen las denominadas tripletas propias (√λi, Ui, Vi) donde

• σi = √λi — valores singulares iguales a la raíz de los valores propios de la matriz XX',
• Ui — vectores singulares izquierdos,
• Vi — vectores singulares derechos,
• i — número de valores singulares igual al rango de la matriz de trayectorias X.

Los números singulares σi muestran el peso de cada componente, en este caso, además, los valores grandes se corresponden con patrones importantes (tendencia, ciclos) y los pequeños con el ruido.

Así, usando la descomposición SVD, la matriz de trayectorias puede representarse como una suma de matrices elementales Xi de rango uno:

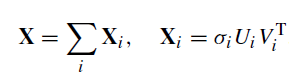
Las matrices de rango uno son los "ladrillos" a partir de los cuales se construyen matrices más complejas.

Vamos a explicar ahora el concepto de rango de matriz en el contexto del método SSA. El objetivo del SSA es extraer una señal determinista de una serie temporal. Las secuencias deterministas, como un exponente, un polinomio o una sinusoide, se caracterizan por poseer un rango finito. Esto se debe a que satisfacen las relaciones de recurrencia lineal (LRR) y sus matrices de trayectoria contienen un número finito de vectores independientes linealmente. Por ejemplo, la matriz de trayectorias de una secuencia exponencial tiene rango 1 (solo un vector linealmente independiente), una sinusoide tiene rango 2, un polinomio de grado (k) tiene rango k+1, etc.

Aquí tenemos el script Rank, que demuestra el concepto de rango de series deterministas:

//+------------------------------------------------------------------+
//|                                                         Rank.mq5 |
//|                                                           Eugene |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Eugene"
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs

input int         N  = 100;                // N - length of generated time series
input int         L  = 30;                 // L - window length
input int         T  = 22;                 // T - period length of sine function
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   matrix X=matrix::Zeros(L,N-L+1);
   vector x_exp= vector::Zeros(N);
   vector x_sinus= vector::Zeros(N);
   vector x_polynom= vector::Zeros(N);
   for(int t=0; t <N; t++)
     {
      x_exp[t] = MathPow(1.01,t);           // 1. Экспоненциальная последовательность: x_t = 1.01^t
      x_sinus[t] = MathSin(2*M_PI*t/T);     // 2. Синусоида: x_t = sin(2 * pi * t / T)
      x_polynom[t] =  1 + t+ MathPow(t,2);  // 3. Полином степени 2: x_t = 1 + t + t^2
     }
   trajectory_matrix(x_exp,L,X);
   Print("Rank Exponential sequence = ",Rank_SVD(X));
   trajectory_matrix(x_sinus,L,X);
   Print("Rank Sinus sequence = ",Rank_SVD(X));
   trajectory_matrix(x_polynom,L,X);
   Print("Rank Polynom sequence = ",Rank_SVD(X));
  }
//+------------------------------------------------------------------+
//| Траекторная матрица X                                            |
//+------------------------------------------------------------------+
void trajectory_matrix(vector & series,int window_length, matrix & X)
  {
   int N_ = (int)series.Size();
   int L_ = window_length;
   int K = N_ - L_ + 1;
   X=matrix::Zeros(L_,K);
   for(int i=0; i <L_;  i++)
     {
      for(int j=0; j <K;  j++)
        {
         X[i,j] = series[i+j];
        }
     }
  }
//+------------------------------------------------------------------+
//|Finds the rank of a matrix using SVD                              |
//+------------------------------------------------------------------+
int Rank_SVD(matrix & X)
  {
   vector sv;
   matrix U,V;
   double tol = 1e-8;  // Порог для ненулевых значений
   X.SingularValueDecompositionDC(SVDZ_N,sv,U,V);
   double threshold = tol * sv.Max();
   int rank=0;
   for(int i=0; i<(int)sv.Size(); i++)
     {
      if(sv[i] > threshold)
         rank++;
     }
   return rank;
  }
//+------------------------------------------------------------------+

Las series en tiempo real, como los precios de las acciones, no son secuencias de rango finito debido a la presencia de ruido, lo cual las convierte en series de rango completo = min(L, K). Sin embargo, si la serie es la suma de una señal determinista de rango finito y ruido, el método SSA es capaz de aislar aproximadamente esta señal. A continuación, la predicción se realiza solo para el componente determinista y se descarta el ruido. Para ello, la matriz de trayectorias (X) se descompone en matrices elementales de rango 1, a partir de las cuales se forman matrices más complejas correspondientes a la señal determinista útil. Esta es la idea clave del método SSA.

Agrupación

En el paso de la agrupación, las matrices elementales de rango uno se combinan en grupos que se interpretan como distintos componentes de la serie (tendencia, estacionalidad, ruido). Una de las formas más comunes es agrupar matrices basándose en la proximidad de los valores singulares de la matriz X. Tras definir m grupos no intersecantes I, la descomposición de la matriz de trayectorias X puede escribirse de la forma:

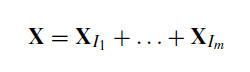
Por ejemplo:

• Itrend = {1} — para la tendencia,
• Iseasonal = {2,3} — para la estacionalidad,
• Inoise = {4....,i} — para el ruido,
  donde i = el número de valores singulares.

La representación gráfica de los vectores singulares izquierdos resulta útil para evaluar visualmente la presencia de una señal determinista. Por ejemplo, si una serie temporal contiene una tendencia, el vector singular correspondiente mostrará una trayectoria que cambia suavemente. Si existe un componente periódico, el par de vectores singulares (ya que la señal periódica tiene un rango de 2) se asemejará a sinusoides. Los vectores singulares, visualmente similares al ruido blanco gaussiano y vinculados a valores singulares pequeños, corresponden al componente de ruido. Estas propiedades nos permiten realizar la agrupación de componentes basándonos en el análisis visual de los vectores singulares.

Restauración (reconstrucción) de series temporales

El siguiente paso consiste en convertir cada matriz agrupada resultante en una nueva serie temporal de longitud N usando la promediación diagonal (diagonal averaging):

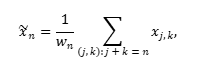
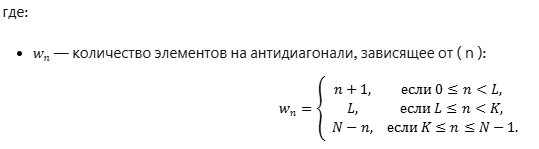
a, xj,k — elementos de la matriz agrupada (o elemental).

La serie temporal así reconstruida será responsable de la tendencia o del componente periódico. La suma de estas series supone un modelo no paramétrico de la serie temporal original que depende de la longitud de ventana L y de la forma de agrupar las matrices elementales. En este caso, la suma de todas las series reconstruidas (incluido el ruido) restablecerá por completo la serie temporal original.

Previsión

La predicción de los valores de la serie temporal gi para M pasos por delante en el método SSA se realiza a partir de la serie reconstruida mediante una fórmula de recurrencia lineal:

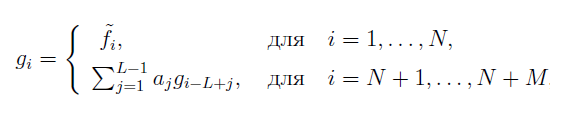
donde:

• aj  — coeficientes de la LRR (relación de recurrencia lineal),
• fi — valores de la serie reconstruida.

Vector de coeficientes aj se determina a partir de los vectores singulares Ui:

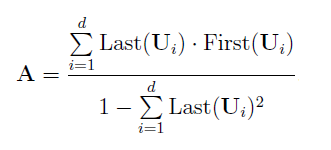
donde:

• First : las primeras 𝐿 − 1 coordenadas del vector singular Ui,
• Last : la última coordenada del vector singular Ui,
• 𝑑 — número de vectores singulares seleccionados que representan la señal útil.
  

Toeplitz-SSA

Existe otra opción de la SSA que difiere del planteamiento tradicional. A diferencia del SSA básico, que usa una matriz de trayectorias basada en una ventana deslizante de la serie temporal, el Toeplitz-SSA construye una matriz de autocovarianza con una estructura toeplitz (de ahí el nombre del método). A continuación, se realiza una descomposición SVD de la matriz de autocovarianza. El método de agrupación, la media diagonal, la determinación de los coeficientes LRR y la previsión se realizan exactamente igual que en el SSA básico.

Toeplitz-SSA resulta más adecuado para analizar series temporales estacionarias (ofrece un error de previsión menor que el de referencia). Sin embargo, para las series no estacionarias, el SSA clásico muestra mejores resultados. Como tenemos que tratar con procesos no estacionarios en los mercados de valores, en este artículo hemos decidido limitarnos únicamente al algoritmo básico.

Ejemplo de análisis Basic-SSA

Pasemos de la teoría a la aplicación práctica de los conceptos descritos en MQL5. Para ello, hemos preparado un script que genera cuatro series temporales sintéticas:

• seno + ruido blanco gaussiano,
• tendencia lineal + seno + ruido blanco gaussiano,
• paseo aleatorio gaussiano simétrico, ruido blanco gaussiano.
  

Estas series poseen las siguientes características:

• La primera serie es estacionaria, con un componente periódico,
• La segunda serie es no estacionaria, con una tendencia determinista y un componente periódico,
• La tercera es una serie no estacionaria con una tendencia estocástica,
• La cuarta es el ruido blanco estacionario.
  
  

Estos modelos abarcan parcialmente la gama de series temporales que se encuentran en los problemas del mundo real.

El script genera una serie sintética de nuestra elección e implementa secuencialmente los pasos que hemos discutido anteriormente, además de mostrar los siguientes gráficos en el monitor:

• los datos generados,
• los valores singulares relativos (la proporción de varianza de cada tripleta singular),
• los dos primeros vectores singulares,
• el diagrama de dispersión de los dos primeros vectores singulares,
• las series de datos + su reconstrucción + la previsión,
• la reconstrucción + la previsión mediante la función MQL5SingularSpectrumAnalysisForecast.
  
  

El gráfico de valores espectrales singulares relativos (la fracción del cuadrado del valor singular de la suma de cuadrados de todos los valores singularesσi^2/∑ σj^2 — Fig.2) nos permite determinar el tipo de componente que está presente en la serie temporal y seleccionar el número de tripletas singulares para la reconstrucción de la señal. Normalmente se seleccionan componentes hasta el punto de caída brusca (el llamado "codo" del gráfico).

Para el componente periódico, deben estar presentes dos valores singulares próximos. También puede darse una meseta seguida de un descenso. Esto indicará la presencia de varios componentes armónicos (sinusoides con distintas frecuencias) seguidos de ruido.

La suave disminución de los valores del espectro indica la ausencia de una señal determinista.

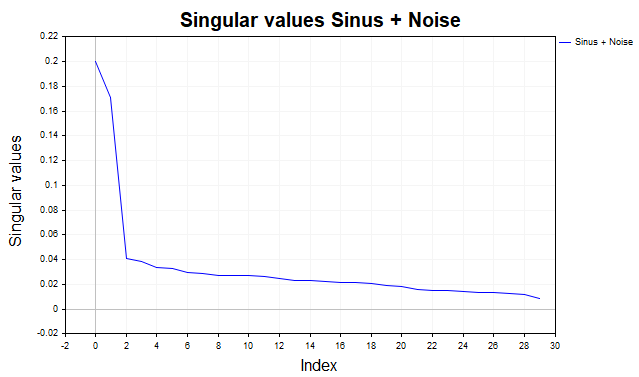
Fig.2 Espectro relativo, sinus+noise

Aquí cabe mencionar la desventaja del SSA, que es su incapacidad para distinguir entre una tendencia estocástica y una tendencia determinista. Por ejemplo, para una serie de paseo aleatorio, solo tendremos un componente expresado, que es el responsable de la tendencia. Pero todos sabemos que esta tendencia es aleatoria e impredecible. Especialmente para probar este caso, hemos incluido datos de paseo aleatorio.

Tras identificar varios valores singulares mayores, resulta útil estudiar los gráficos de los vectores singulares izquierdos correspondientes (fig.3). Para una señal periódica mezclada con ruido, los dos primeros vectores singulares asociados a los mayores valores singulares suelen tener una forma cercana a un seno o un coseno, lo cual refleja la naturaleza periódica de la señal.

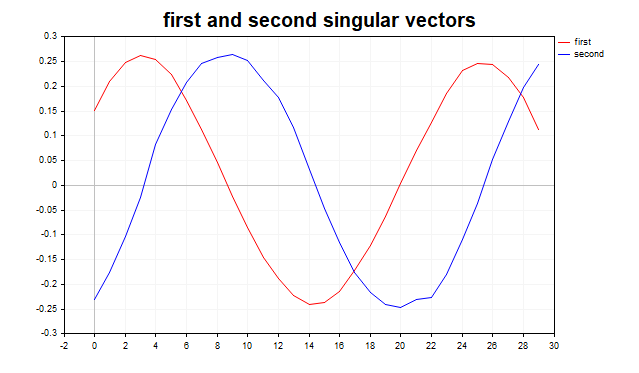
Fig.3 Primeros dos vectores singulares, sinus+noise

Además, podemos construir un gráfico de dispersión para un par de vectores singulares, en el que, por ejemplo, el primer vector singular (U1) se represente en el eje (x) y el segundo (U2) en el eje (y). (Fig.4)

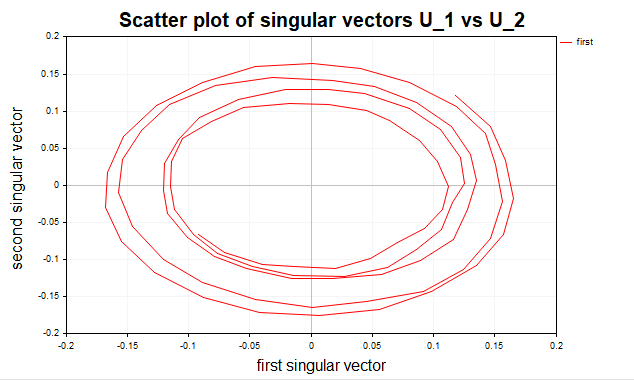
Fig.4 Diagrama de dispersión de los dos primeros vectores singulares, sinus+noise

Si los datos contienen componentes cíclicos, el diagrama de dispersión suele adoptar la forma de una elipse o un círculo, lo cual confirma la naturaleza sinusoidal de la señal. Esto se debe a que el par de vectores singulares del componente periódico se corresponde con los dos armónicos ortogonales (por ejemplo, seno y coseno). Si los puntos del diagrama de dispersión forman una nube caótica sin una estructura geométrica clara, esto indicará la ausencia de un componente periódico o determinista pronunciado.

La figura 5 muestra la serie sintética sinus+noise, su reconstrucción y la previsión para 100 pasos adelante. Detectar visualmente la presencia de una señal periódica en los datos de origen resulta difícil debido al fuerte ruido, pero el SSA destaca eficazmente el componente periódico. Obviamente, se trata de un ejemplo muy sencillo, y una imagen tan clara es poco frecuente en los datos financieros reales. No obstante, el SSA ofrece una excelente oportunidad para confirmar o refutar la hipótesis de la presencia de ciclos en los precios.

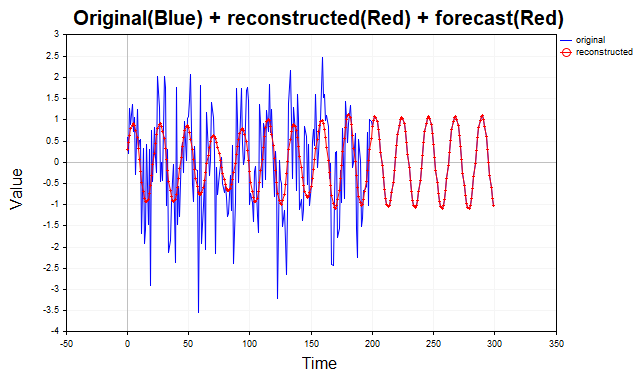
Fig.5 Previsión de series sinus+noise

Implementación de SSA en MQL5

Vamos a centrarnos en las implementaciones de SSA ya existentes en MQL5. La función SingularSpectrumAnalysisForecast de la sección Métodos matriciales y vectoriales\OpenBLAS se suministra con el terminal. A partir de la descripción de esta función, no me quedó demasiado claro qué tipo de SSA se implementa exactamente.

Al principio supuse que se trataba de una variante de Toeplitz-SSA basada en la descomposición de la matriz de autocovarianza. Pero como los resultados de la previsión y reconstrucción de la serie utilizando el script Basic-SSA y la función SingularSpectrumAnalysisForecast coinciden completamente, es probable que siga siendo la implementación del algoritmo básico. A modo de ejemplo, aquí tenemos un gráfico con la previsión de la serie trend+sinus+noise usando tres componentes principales (fig.6). La serie analizada consta de 200 valores, el pronóstico lo hacemos para 100 pasos adelante.

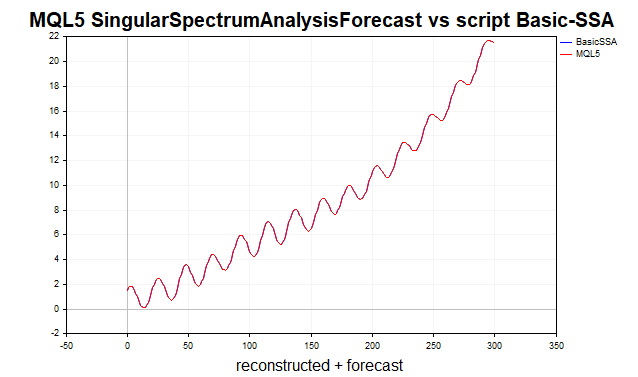
Fig.6 Reconstrucción MQL5 frente a BasicSSA y series de previsiones

Para descomponer la matriz de trayectorias utilicé la función SingularValueDecompositionDC de la misma sección de OpenBLAS, ya que los desarrolladores posicionan el algoritmo divide y vencerás (divide and conquer)^ como el más rápido entre otros algoritmos SVD. Resulta muy cómodo que esta función permita calcular tanto matrices completas como truncadas de vectores singulares.

Código del script Basic-SSA:

//+------------------------------------------------------------------+
//|                                                    Basic-SSA.mq5 |
//|                                                           Eugene |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Eugene"
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include <Math\Stat\Stat.mqh>
#include <Graphics\Graphic.mqh>

enum SimpleData
  {
   SinusPlusNoise,
   Trend_Sinus_Noise,
   RandomWalk,
   WhiteNoise,
  };

input int         L  = 30;                 // L - window length
input int         N  = 200;                // N - length of generated time series
input int         T  = 22;                 // T - period length of sine function
input int         fs = 100;                // fs - forecast horizon
input int         r_ = 2;                  // r - singular components
input SimpleData  sd = SinusPlusNoise;     // Data
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   int err;
   vector x = vector::Zeros(N); // time series
   double x_array[];
   double original_series[];
//------------1. Данные --------------------
//------------------ sinus + noise ---------
   if(sd == SinusPlusNoise)
     {
      for(int i=0; i <N;  i++)
        {
         x[i] = MathSin(2*M_PI*(i+1)/T) + MathRandomNormal(0,1,err);
        }
      VectortoArray(x,x_array);
      ArrayCopy(original_series,x_array,0,0,WHOLE_ARRAY);
      PlotGraphic(x_array,5,1);
     }
//------------------trend + sinus + noise ----
   if(sd == Trend_Sinus_Noise)
     {
      for(int i=0; i <N;  i++)
        {
         x[i] =  0.05 * i + MathSin(2*M_PI*(i+1)/T) + MathRandomNormal(0,1,err);
        }
      VectortoArray(x,x_array);
      ArrayCopy(original_series,x_array,0,0,WHOLE_ARRAY);
      PlotGraphic(x_array,5,1);
     }
//-------------- random walk -----------------
   if(sd == RandomWalk)
     {
      x[0]=100;
      for(int i=1; i <N;  i++)
        {
         x[i] = x[i-1] + MathRandomNormal(0,1,err);
        }
      VectortoArray(x,x_array);
      ArrayCopy(original_series,x_array,0,0,WHOLE_ARRAY);
      PlotGraphic(x_array,5,1);
     }
//-------------- white noise -----------------
   if(sd == WhiteNoise)
     {
      for(int i=0; i <N;  i++)
        {
         x[i] = MathRandomNormal(0,1,err);
        }
      VectortoArray(x,x_array);
      ArrayCopy(original_series,x_array,0,0,WHOLE_ARRAY);
      PlotGraphic(x_array,5,1); // график белого шума
     }
//------------2. Траекторная матрица -------------------
   matrix X;
   trajectory_matrix(x,L,X);
//-------------3. Cингулярное разложение (SVD) ----
   matrix U, V;
   vector singular_values;
   X.SingularValueDecompositionDC(SVDZ_A,singular_values,U,V);
   V = V.Transpose();
   double total_variance;
   vector powv = singular_values*singular_values;
   total_variance = powv.Sum();
   VectortoArray(powv/total_variance,x_array);
   PlotGraphic(x_array,5,2); // График  сингулярного спектра
   double x_1[],x_2[];
   VectortoArray(U.Col(0),x_1);
   VectortoArray(U.Col(1),x_2);
   PlotGraphic(x_1,x_2,5,3); // график первых двух сингулярных векторов
   PlotGraphic(x_1,x_2,5,4); // диаграмма рассеяния первых двух сингулярных векторов
//---------- 4. Реконструкция временного ряда----
   int K = N - L + 1;
   matrix X_i = matrix::Zeros(L,K);
   matrix Ui = matrix::Zeros(L,1);
   matrix Vi = matrix::Zeros(1,K);
   vector x_tilde;
   vector recon_series = vector::Zeros(N);
   for(int i=0; i<r_;i++)
     {
      Ui.Col(U.Col(i),0);
      Vi.Row(V.Col(i),0);
      X_i = (Ui.MatMul(Vi))*singular_values[i];  // матрицы ранга один
      diagonal_averaging(X_i,x_tilde);
      recon_series = recon_series + x_tilde;     // реконструированный ряд
     }
   double recon[];
   VectortoArray(recon_series,recon);

//------------5. Вектор коэффициентов LRR   --------------------
   matrix U_r = U;
   U_r.Resize(L,r_);              // r левых сингулярных векторов
   vector a = vector::Zeros(L-1); // вектор а коэффициентов LRR
   double denom =0;
   vector u_k;
   double last;
   for(int k=0; k<r_;k++)
     {
      u_k = U_r.Col(k);           //  k-ый сингулярный вектор
      last = u_k[L-1];
      u_k.Resize(L-1);
      a = a + last*u_k;
      denom = denom + MathPow(last,2);
     }
   denom = 1 - denom;
   a = a/denom;                   // вектор а коэффициентов LRR

//----------------- 6. Прогноз с использованием LRR-коэффициентов -----------
   int forecast_steps = fs;
   double forecast[];
   ArrayResize(forecast,forecast_steps);
   double fi[];
   ArrayCopy(fi,recon,0,N-L+1,L-1);
   for(int i=0;i<forecast_steps;i++)
     {
      double sum = 0.0;
      for(int j = 0; j < L-1; j++)
        {
         sum += a[j] * fi[j];
        }
      forecast[i]= sum;  // Прогноз
      // Обновляем fi
      ArrayCopy(fi, fi, 0, 1, ArraySize(fi)-1); // Сдвигаем влево
      fi[L-2] = forecast[i];                    // Добавляем новое значение
     }

   double originalplusforecast[];
   ArrayResize(originalplusforecast,N+forecast_steps);
   ArrayCopy(originalplusforecast,original_series,0,0,WHOLE_ARRAY);
   ArrayCopy(originalplusforecast,forecast,N,0,WHOLE_ARRAY);

   double reconstructedplusforecast[];
   ArrayResize(reconstructedplusforecast,N+forecast_steps);
   ArrayCopy(reconstructedplusforecast,recon,0,0,WHOLE_ARRAY);
   ArrayCopy(reconstructedplusforecast,forecast,N,0,WHOLE_ARRAY);
   PlotGraphic(originalplusforecast,reconstructedplusforecast,15,5);

//----реконструированные данные и прогноз по функции SingularSpectrumAnalysisForecast
   vector MQLreconforecast;
   x.SingularSpectrumAnalysisForecast(L,r_,forecast_steps,MQLreconforecast);
   double MQL_RF[];
   VectortoArray(MQLreconforecast,MQL_RF);
   PlotGraphic(reconstructedplusforecast,MQL_RF,10,6);
  }

//+------------------------------------------------------------------+
//| Plot Graphic                                                     |
//+------------------------------------------------------------------+
void PlotGraphic(double &data[], int sec, int n_graph)
  {
   ChartSetInteger(0,CHART_SHOW,false);
   CGraphic graphic;
   ulong width = ChartGetInteger(0,CHART_WIDTH_IN_PIXELS);
   ulong height = ChartGetInteger(0,CHART_HEIGHT_IN_PIXELS);

   if(ObjectFind(0,"Graphic")<0)
      graphic.Create(0,"Graphic",0,0,0,int(width),int(height));
   else
      graphic.Attach(0,"Graphic");

   string st;
   if(sd == SinusPlusNoise)
     {
      st = "Sinus + Noise";
     }
   if(sd == Trend_Sinus_Noise)
     {
      st = "Trend + Sinus + Noise";
     }
   if(sd == RandomWalk)
     {
      st = "Random Walk";
     }
   if(sd == WhiteNoise)
     {
      st = "White Noise ";
     }

   if(n_graph==1) // график данных
     {
      CCurve *curve = graphic.CurveAdd(data,ColorToARGB(clrRed,255),CURVE_LINES,st);
      graphic.XAxis().Name("Series " + st);
      graphic.BackgroundMain(st);
     }
   if(n_graph==2) // график сингулярных значений (relative_variance = sigma_i^2/Sum Sigma_j^2)
     {
      CCurve *curve = graphic.CurveAdd(data,ColorToARGB(clrBlue,255),CURVE_LINES,st);
      graphic.XAxis().Name("Index ");
      graphic.YAxis().Name("Singular values ");
      graphic.BackgroundMain("Singular values " + st);
     }
   graphic.XAxis().NameSize(18);
   graphic.YAxis().NameSize(18);
   graphic.BackgroundMainColor(ColorToARGB(clrBlack,255));
   graphic.BackgroundMainSize(24);
   graphic.CurvePlotAll();
   graphic.Update();
   Sleep(sec*1000);
   ChartSetInteger(0,CHART_SHOW,true);
   graphic.Destroy();
   ChartRedraw(0);
  }

//+------------------------------------------------------------------+
//| Plot Graphic                                                     |
//+------------------------------------------------------------------+
void PlotGraphic(double &data1[],double &data2[], int sec,int n_graph)
  {
   ChartSetInteger(0,CHART_SHOW,false);
   CGraphic graphic;
   ulong width = ChartGetInteger(0,CHART_WIDTH_IN_PIXELS);
   ulong height = ChartGetInteger(0,CHART_HEIGHT_IN_PIXELS);

   if(ObjectFind(0,"Graphic")<0)
      graphic.Create(0,"Graphic",0,0,0,int(width),int(height));
   else
      graphic.Attach(0,"Graphic");

   if(n_graph==3)
     {
      CCurve *curve =  graphic.CurveAdd(data1,ColorToARGB(clrRed,255),CURVE_LINES,"first");
      CCurve *curve1 = graphic.CurveAdd(data2,ColorToARGB(clrBlue,255),CURVE_LINES,"second");
      graphic.XAxis().Name(" ");
      graphic.BackgroundMain("first and second singular vectors");
     }
   if(n_graph==4) // scatter plot of singular vectors
     {
      CCurve *curve =  graphic.CurveAdd(data1,data2,ColorToARGB(clrRed,255),CURVE_LINES,"first");
      graphic.XAxis().Name("first singular vector");
      graphic.YAxis().Name("second singular vector");
      graphic.BackgroundMain("Scatter plot of singular vectors U_1 vs U_2");
     }

   if(n_graph==5) // график данных плюс прогноз
     {
      CCurve *curve = graphic.CurveAdd(data1,ColorToARGB(clrBlue,255),CURVE_LINES,"original");
      CCurve *curve1 = graphic.CurveAdd(data2,ColorToARGB(clrRed,255),CURVE_POINTS_AND_LINES,"reconstructed");
      graphic.XAxis().Name("Time ");
      graphic.YAxis().Name("Value ");
      graphic.BackgroundMain("Original(Blue) + reconstructed(Red) + forecast(Red) ");
      curve1.PointsSize(3);
     }

// график сравнения прогноза функции MQL5 SingularSpectrumAnalysisForecast с прогнозом Basic-SSA
   if(n_graph==6)
     {
      CCurve *curve = graphic.CurveAdd(data1,ColorToARGB(clrBlue,255),CURVE_LINES,"BasicSSA");
      CCurve *curve1 = graphic.CurveAdd(data2,ColorToARGB(clrRed,255),CURVE_LINES,"MQL5");
      graphic.XAxis().Name("reconstructed + forecast ");
      graphic.BackgroundMain(" MQL5 SingularSpectrumAnalysisForecast vs script Basic-SSA ");
      curve1.PointsSize(3);
     }
   graphic.XAxis().NameSize(18);
   graphic.YAxis().NameSize(18);
   graphic.BackgroundMainColor(ColorToARGB(clrBlack,255));
   graphic.BackgroundMainSize(24);
   graphic.CurvePlotAll();
   graphic.Update();
   Sleep(sec*1000);
   ChartSetInteger(0,CHART_SHOW,true);
   graphic.Destroy();
   ChartRedraw(0);
  }

//+------------------------------------------------------------------+
//| Копируем вектор в массив                                         |
//+------------------------------------------------------------------+
void VectortoArray(vector &v, double &array[])
  {
   int v_size = (int)v.Size();
   ArrayResize(array,v_size);
   for(int i=0; i<v_size; i++)
     {
      array[i]   =  v[i];
     }
  }
//+------------------------------------------------------------------+
//| Траекторная матрица X                                            |
//+------------------------------------------------------------------+
void trajectory_matrix(vector & series,int window_length, matrix & X)
  {
   int N_ = (int)series.Size();
   int L_ = window_length;
   int K = N_ - L_ + 1;
   X=matrix::Zeros(L_,K);
   for(int i=0; i <L_;  i++)
     {
      for(int j=0; j <K;  j++)
        {
         X[i,j] = series[i+j];
        }
     }
  }
//+-------------------------------------------------------------------+
//| Диагональное усреднение матрицы                                   |
//| Вход: Xi - матрица L x K (элементарная матрица i-ой компоненты)   |
//| Выход: x_tilde - восстановленный временной ряд                    |
//+-------------------------------------------------------------------+
void diagonal_averaging(matrix &Xi,vector &x_tilde)
  {
   int L_ = (int)Xi.Rows();
   int K  = (int)Xi.Cols();
   int N_ = L_ + K - 1; // Длина исходного временного ряда

   x_tilde = vector::Zeros(N_);
   double total; // Сумма элементов на антидиагонали
   int w_n;      // Количество элементов на антидиагонали
   int k;
   for(int n=0; n < N_; n++)
     {
      total = 0;
      w_n = 0;
      for(int j=0; j <L_; j++)
        {
         k = n - j ; // Индекс столбца: n = j + k ---> k = n - j
         if(k >= 0 && k < K) // Проверка, что индекс в пределах матрицы
           {
            total = total + Xi[j, k];
            w_n = w_n + 1;
           }
        }
      x_tilde[n] = total / w_n; // Усреднение
     }
  }
//+------------------------------------------------------------------+

Conclusión

En este artículo, hemos analizado los fundamentos del análisis espectral singular (SSA), una técnica que utiliza la descomposición de valores singulares (SVD) de una matriz de trayectorias para identificar estructuras ocultas en los datos. Asimismo, hemos demostrado cómo el SSA divide eficazmente las series temporales en componentes interpretables -tendencia, estacionalidad y ruido-, facilitando su reconstrucción y predicción.

Sin embargo, el método tiene limitaciones, en particular la incapacidad de distinguir de forma fiable entre tendencias deterministas y estocásticas, como el paseo aleatorio gaussiano. Al mismo tiempo, cabe señalar que el SSA no se impone la tarea de realizar una clasificación estadística estricta de las tendencias; su fuerza reside en la descomposición flexible y la extracción de estructuras de datos, que afronta con éxito.

La aplicación del SSA no se limita al análisis de series temporales univariantes. El método permite trabajar con datos multivariantes, y puede usarse para construir un indicador de detección de puntos de cambio para detectar cambios repentinos en el comportamiento de los instrumentos financieros. Estas direcciones son prometedoras para futuras investigaciones, ya que una comprensión precisa de la naturaleza de los datos resulta fundamental para encontrar patrones de mercado.