
Aplicação de métodos de ensemble para tarefas de classificação em MQL5
Introdução
No artigo anterior, exploramos métodos de combinação de modelos voltados para previsões numéricas. Este artigo complementa aquele estudo, focando nos métodos de ensemble desenvolvidos especificamente para tarefas de classificação. Além disso, consideraremos estratégias para o uso de classificadores que geram rankings de classe em uma escala ordinal. A aplicação de técnicas numéricas de combinação pode ser apropriada para resolver tarefas de classificação em alguns casos, especialmente quando os modelos se baseiam em saídas numéricas. No entanto, muitos classificadores seguem uma abordagem menos flexível, produzindo apenas decisões discretas de classe. Além disso, os classificadores baseados em métodos numéricos frequentemente apresentam previsões instáveis, o que destaca a necessidade de se desenvolverem métodos de combinação especializados.
Os classificadores em ensemble discutidos neste artigo funcionam com base em determinadas suposições sobre seus modelos componentes. Primeiramente, supõe-se que esses modelos são treinados em dados com classes-alvo mutuamente exclusivas e exaustivas, de modo que cada exemplo pertença apenas a uma classe. Quando a opção "nenhum dos anteriores" é necessária, ela deve ser tratada como uma classe separada ou gerenciada por meio de métodos numéricos de combinação com um limiar de pertencimento definido. Além disso, quando um vetor de entrada com preditores é fornecido, espera-se que os modelos componentes produzam N saídas, onde N representa o número de classes. Essas saídas podem ser valores de probabilidade ou classificações de confiança, que indicam a probabilidade de pertencimento a cada classe. Também podem ser decisões binárias, quando uma saída é igual a 1.0 (true) e as demais a 0.0 (false), ou ainda saídas inteiras de 1 a N, refletindo a probabilidade relativa de pertencimento a cada classe.
Alguns dos métodos de ensemble que analisaremos apresentam vantagens significativas quando utilizam classificadores componentes capazes de produzir saídas ranqueadas. Modelos que conseguem estimar com precisão as probabilidades de pertencimento às classes costumam ser altamente valorizados, mas existe um risco considerável em interpretar suas saídas como probabilidades quando, na verdade, elas não o são. Quando há incerteza sobre o que exatamente as saídas de um modelo representam, pode ser útil convertê-las em rankings. A utilidade das informações baseadas em rankings aumenta à medida que o número de classes cresce. Em classificações binárias, os rankings não acrescentam informação adicional e seu valor em tarefas de três classes é relativamente limitado. No entanto, em cenários com um grande número de classes, a capacidade de interpretar alternativas secundárias de escolha do modelo se torna extremamente valiosa, especialmente quando as previsões individuais estão associadas a um alto grau de incerteza. As máquinas de vetores de suporte (SVM), por exemplo, podem ser aprimoradas para fornecer não apenas classificações binárias, mas também as distâncias entre as fronteiras de decisão de cada classe, oferecendo informações mais detalhadas sobre a confiabilidade das previsões.
Os rankings também auxiliam na solução de um desafio essencial no uso de métodos ensemble: a normalização das saídas de diferentes modelos de classificação. Considere dois modelos que analisam movimentos de mercado: um deles é especializado em flutuações de curto prazo em mercados de alta liquidez, enquanto o outro trabalha com tendências de longo prazo, que se estendem por semanas ou meses. O foco mais amplo do segundo modelo pode introduzir ruído nas previsões de curto prazo. Converter a confiabilidade das decisões de classe em rankings ajuda a minimizar esse problema, garantindo que informações valiosas de curto prazo não sejam ofuscadas por sinais de tendência de longo prazo. Essa abordagem resulta em previsões de ensemble mais equilibradas e eficazes.
Objetivos alternativos na combinação de classificadores
O principal objetivo da utilização de classificadores em ensemble é, normalmente, melhorar a precisão da classificação. No entanto, nem sempre esse é o caso, pois, em algumas tarefas, pode ser útil ir além desse objetivo específico. Além da precisão básica, é possível adotar critérios de sucesso mais complexos para lidar com cenários em que a decisão inicial esteja incorreta. Dessa forma, as abordagens de classificação podem buscar dois objetivos distintos, porém complementares; cada um deles pode servir como uma métrica de desempenho para estratégias de combinação de classes:
- Redução do conjunto de classes: esse enfoque tem como objetivo identificar o menor subconjunto possível entre as classes originais que ainda mantenha alta probabilidade de conter a classe verdadeira. Nesse caso, o ranqueamento interno dentro do subconjunto é secundário em relação à garantia de que ele seja, ao mesmo tempo, compacto e tenha alta probabilidade de conter a classificação correta.
- Ordenação das classes: esse método concentra-se em ranquear as probabilidades de pertencimento às classes, de modo que a classe verdadeira esteja posicionada o mais alto possível no ranking. Em vez de utilizar limiares fixos de ranking, a eficácia é avaliada pela distância média entre a classe verdadeira e a posição mais alta no ranking.
Em determinados cenários, priorizar uma abordagem em relação à outra pode oferecer vantagens significativas, mesmo quando essa prioridade não é explicitamente exigida. Escolher o objetivo mais relevante e adotar os critérios de erro correspondentes muitas vezes fornece métricas de desempenho mais confiáveis do que confiar exclusivamente na precisão da classificação. Além disso, essas duas metas não precisam ser mutuamente exclusivas. Uma abordagem híbrida pode ser extremamente eficaz: primeiro, aplique um método de combinação voltado à redução do conjunto de classes, com o objetivo de identificar um pequeno subconjunto de classes com alta probabilidade de conter a classe verdadeira. Em seguida, use um segundo método para ranquear as classes dentro desse subconjunto refinado. A classe com o ranking mais alto, resultante desse processo em duas etapas, torna-se a decisão final, beneficiada tanto pela eficácia da redução do conjunto quanto pela precisão promovida pela ordenação. Essa estratégia de dois objetivos pode oferecer uma técnica de classificação mais robusta do que os métodos tradicionais de previsão por classe única, especialmente em cenários complexos, nos quais há grande variação no nível de certeza da classificação. Diante do exposto, iniciaremos nossa investigação sobre classificadores em ensemble.
Ensembles baseados na regra da maioria
A regra da maioria é uma abordagem simples e intuitiva para a classificação ensemble, derivada do princípio de votação conhecido por todos. Esse método consiste em escolher a classe que recebe a maioria dos votos dos modelos componentes. Essa abordagem direta é útil em cenários nos quais os modelos só podem emitir decisões discretas de classe, o que a torna uma escolha ideal para sistemas com modelos de sofisticação limitada. A formulação matemática formal da regra da maioria é apresentada na equação a seguir.
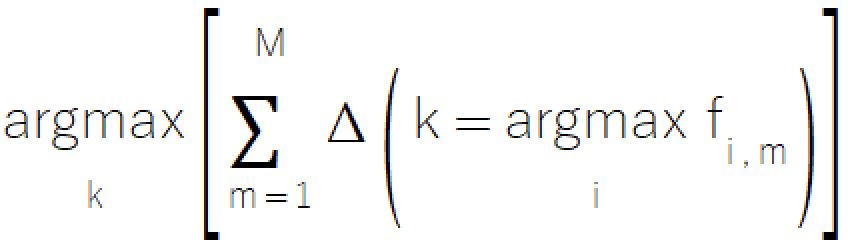
A regra da maioria é implementada no arquivo ensemble.mqh, onde a classe CMajority gerencia sua funcionalidade principal por meio do método classify().
//+------------------------------------------------------------------+ //| Compute the winner via simple majority | //+------------------------------------------------------------------+ class CMajority { private: ulong m_outputs; ulong m_inputs; vector m_output; matrix m_out; public: CMajority(void); ~CMajority(void); ulong classify(vector &inputs, IClassify* &models[]); };
Esse método recebe como entrada um vetor de preditores e um array de modelos componentes, representado sob a forma de ponteiros IClassify. A interface IClassify padroniza a manipulação dos modelos essencialmente da mesma maneira que a interface IModel, descrita no artigo anterior.
//+------------------------------------------------------------------+ //| IClassify interface defining methods for manipulation of | //|classification algorithms | //+------------------------------------------------------------------+ interface IClassify { //train a model bool train(matrix &predictors,matrix&targets); //make a prediction with a trained model vector classify(vector &predictors); //get number of inputs for a model ulong getNumInputs(void); //get number of class outputs for a model ulong getNumOutputs(void); };
A função classify() retorna um número inteiro que representa a classe selecionada, assumindo valores de zero até o total de classes menos um. A classe retornada é aquela que recebe o maior número de "votos" dos modelos componentes. Embora a implementação da regra da maioria pareça bastante simples à primeira vista, há uma questão importante a ser considerada em sua aplicação prática: o que acontece quando duas ou mais classes recebem o mesmo número de votos? Em um contexto democrático, essa situação resultaria em uma nova rodada de votação, mas isso não é viável aqui. Para resolver o problema dos empates, o método introduz pequenas variações no processo de contagem de votos de cada classe durante a comparação. Essa técnica garante que classes com o mesmo número de votos tenham a mesma probabilidade de serem escolhidas, preservando a integridade do método e evitando qualquer viés sistemático.
//+------------------------------------------------------------------+ //| ensemble classification | //+------------------------------------------------------------------+ ulong CMajority::classify(vector &inputs,IClassify *&models[]) { double best, sum, temp; ulong ibest; best =0; ibest = 0; CHighQualityRandStateShell state; CHighQualityRand::HQRndRandomize(state.GetInnerObj()); m_output = vector::Zeros(models[0].getNumOutputs()); for(uint i = 0; i<models.Size(); i++) { vector classification = models[i].classify(inputs); m_output[classification.ArgMax()] += 1.0; } sum = 0.0; for(ulong i=0 ; i<m_output.Size() ; i++) { temp = m_output[i] + 0.999 * CAlglib::HQRndUniformR(state); if((i == 0) || (temp > best)) { best = temp ; ibest = i ; } sum += m_output[i] ; } if(sum>0.0) m_output/=sum; return ibest; }
Apesar de sua utilidade, a regra da maioria apresenta algumas limitações que devem ser levadas em consideração:
- Esse método considera apenas a escolha principal de cada modelo, podendo assim descartar informações valiosas contidas em posições inferiores no ranking. Embora a aplicação de uma média aritmética simples das saídas por classe possa parecer uma solução, esse procedimento apresenta dificuldades adicionais relacionadas ao ruído e à escala.
- Em cenários com muitas classes, o mecanismo de votação simples pode deixar de capturar relações sutis entre as diferentes opções de classe.
- Essa abordagem trata todos os modelos componentes como iguais, sem levar em conta as diferenças de desempenho ou confiabilidade de cada um em diferentes contextos.
O próximo método que discutiremos é outro sistema baseado em "votos", que busca compensar algumas limitações da regra da maioria, introduzindo certos refinamentos adicionais.
Método da contagem de Borda
O método de contagem de Borda calcula um ranking para cada classe, agregando, entre todos os modelos, o número de classes com posição inferior à da classe analisada em cada avaliação realizada pelo modelo. Esse método encontra um equilíbrio ideal entre moderar escolhas de baixa posição e transformá-las em informação útil, oferecendo uma alternativa mais robusta em comparação com mecanismos de votação simples. Em um sistema com "m" modelos e "k" classes, o intervalo de rankings possíveis é rigidamente definido: a classe consistentemente classificada como a última por todos os modelos recebe zero pontos de Borda, enquanto a classe que obtém o maior ranking em todos eles atinge o valor máximo de pontos de Borda, igual a m(k-1).

Esse método representa um avanço significativo em relação aos métodos de votação simples, pois oferece capacidades aprimoradas para identificar e explorar todo o espectro de previsões feitas pelos modelos, mantendo, ao mesmo tempo, a eficiência computacional. Embora o método lide de maneira eficaz com empates entre posições individuais atribuídas pelos modelos, é importante dedicar atenção aos empates nos cálculos finais de Borda entre diferentes modelos. Para tarefas de classificação binária, o método de contagem de Borda é funcionalmente equivalente à regra da maioria. Portanto, suas vantagens explícitas se manifestam principalmente em cenários com três classes ou mais. A eficácia do método decorre de sua abordagem baseada em ordenação, que garante um processamento otimizado das classes produzidas, preservando suas associações indexadas corretas.A classe que obtém o maior ranking em todos os modelos atinge o valor máximo de pontos de Borda, igual a m(k-1).
A implementação da contagem de Borda compartilha semelhanças estruturais com a metodologia utilizada na regra da maioria, mas oferece eficiência computacional adicional. O processo é conduzido pela classe CBorda, no arquivo ensemble.mqh, e não requer uma fase prévia de treinamento.
//+------------------------------------------------------------------+ //| Compute the winner via Borda count | //+------------------------------------------------------------------+ class CBorda { private: ulong m_outputs; ulong m_inputs; vector m_output; matrix m_out; long m_indices[]; public: CBorda(void); ~CBorda(void); ulong classify(vector& inputs, IClassify* &models[]); };
O procedimento de classificação começa com a inicialização de um vetor de saídas destinado a armazenar os valores acumulados de Borda. Em seguida, todos os modelos componentes avaliam o vetor de entrada fornecido. É criado um array de índices para rastrear as relações entre as classes. As saídas de classificação de cada modelo são então ordenadas em ordem crescente. Por fim, os valores de Borda são sistematicamente acumulados com base nos rankings ordenados.
//+------------------------------------------------------------------+ //| ensemble classification | //+------------------------------------------------------------------+ ulong CBorda::classify(vector &inputs,IClassify *&models[]) { double best=0, sum, temp; ulong ibest=0; CHighQualityRandStateShell state; CHighQualityRand::HQRndRandomize(state.GetInnerObj()); if(m_indices.Size()) ArrayFree(m_indices); m_output = vector::Zeros(models[0].getNumOutputs()); if(ArrayResize(m_indices, int(m_output.Size()))<0) { Print(__FUNCTION__, " ", __LINE__, " array resize error ", GetLastError()); return ULONG_MAX; } for(uint i = 0; i<models.Size(); i++) { vector classification = models[i].classify(inputs); for(long j = 0; j<long(classification.Size()); j++) m_indices[j] = j; if(!classification.Size()) { Print(__FUNCTION__," ", __LINE__," empty vector "); return ULONG_MAX; } qsortdsi(0,classification.Size()-1,classification,m_indices); for(ulong k =0; k<classification.Size(); k++) m_output[m_indices[k]] += double(k); } sum = 0.0; for(ulong i=0 ; i<m_output.Size() ; i++) { temp = m_output[i] + 0.999 * CAlglib::HQRndUniformR(state); if((i == 0) || (temp > best)) { best = temp ; ibest = i ; } sum += m_output[i] ; } if(sum>0.0) m_output/=sum; return ibest; }
Nas próximas partes, analisaremos ensembles que incorporam grande parte (se não toda) da informação gerada pelos modelos componentes durante a definição da decisão final das classes.
Média das saídas dos modelos componentes
Quando os modelos componentes geram saídas com valores relativos significativos e comparáveis entre si, a introdução dessas medidas numéricas aumenta consideravelmente a eficiência do ensemble. Enquanto os métodos da regra da maioria e da contagem de Borda desconsideram uma parte substancial das informações disponíveis, a média das saídas dos modelos componentes representa uma abordagem mais abrangente para aproveitar os dados. O método calcula a média das saídas para cada classe com base nas respostas de todos os modelos componentes. Desde que o número de modelos permaneça constante, essa abordagem é matematicamente equivalente à soma das saídas. Essa técnica trata cada modelo de classificação como um preditor numérico e os combina por meio de uma média simples. A decisão final de classificação é determinada ao se identificar a classe com a maior saída agregada.
A média em tarefas de previsão numérica difere significativamente da média em tarefas de classificação. Em previsões numéricas, os modelos componentes geralmente compartilham o mesmo objetivo de aprendizado, assegurando, assim, uniformidade nas saídas. No entanto, em tarefas de classificação, quando apenas os rankings das saídas individuais são relevantes, as saídas resultantes podem se tornar incomparáveis de maneira não intencional. Às vezes, o resultado dessa falta de coerência é uma combinação que, na prática, se comporta mais como uma média ponderada implícita do que como uma média aritmética real. Em outras situações, determinados modelos podem exercer uma influência desproporcional sobre a soma final, comprometendo a eficácia do ensemble. Desse modo, para preservar a integridade do metamodelo, é essencial verificar a consistência das saídas entre todos os modelos componentes.
A suposição de que as saídas dos modelos componentes representam, essencialmente, probabilidades levou ao desenvolvimento de métodos alternativos de combinação, semelhantes, em termos conceituais, à média. Um desses métodos é a regra da multiplicação. Ela substitui a soma das saídas dos modelos pelo seu produto. Entretanto, essa abordagem demonstra extrema sensibilidade até mesmo às menores violações das suposições probabilísticas. A subestimação significativa da probabilidade de uma classe por parte de um único modelo pode eliminar irreversivelmente essa classe dos resultados, pois a multiplicação por valores próximos de zero gera resultados desprezíveis, independentemente dos demais fatores. Essa sensibilidade acentuada torna a regra da multiplicação impraticável na maioria dos cenários, apesar de sua elegância teórica. Esse exemplo serve como um alerta de que mesmo métodos matematicamente impecáveis podem causar problemas quando aplicados na prática.
A implementação da regra da média é apresentada na classe CAvgClass, cuja estrutura é semelhante à da classe CMajority.
//+------------------------------------------------------------------+ //| full resolution' version of majority rule. | //+------------------------------------------------------------------+ class CAvgClass { private: ulong m_outputs; ulong m_inputs; vector m_output; public: CAvgClass(void); ~CAvgClass(void); ulong classify(vector &inputs, IClassify* &models[]); };
Durante o processo de classificação, o método classify() coleta as previsões de todos os modelos componentes e acumula suas respectivas saídas. A classe final é determinada com base no maior valor agregado do ranking.
//+------------------------------------------------------------------+ //| make classification with consensus model | //+------------------------------------------------------------------+ ulong CAvgClass::classify(vector &inputs, IClassify* &models[]) { m_output=vector::Zeros(models[0].getNumOutputs()); vector model_classification; for(uint i =0 ; i<models.Size(); i++) { model_classification = models[i].classify(inputs); m_output+=model_classification; } double sum = m_output.Sum(); ulong min = m_output.ArgMax(); m_output/=sum; return min; }
Mediana
Embora o uso da média aproveite de forma abrangente todas as informações disponíveis, há o risco de uma maior sensibilidade a valores atípicos, o que pode comprometer a eficiência do ensemble. A mediana surge como uma alternativa útil, pois, embora reduza ligeiramente o aproveitamento total da informação, fornece uma medida confiável do centro da distribuição e mantém a resistência a valores extremos. O método ensemble baseado na mediana, implementado pela classe CMedian no arquivo ensemble.mqh, oferece uma abordagem direta e eficaz para a classificação em ensemble. Essa implementação lida com os desafios relacionados à presença de previsões extremas e à preservação da ordem significativa entre as classes. O problema dos valores atípicos é resolvido por meio de uma transformação baseada em rankings. As saídas de cada modelo componente são classificadas de forma independente e, em seguida, calcula-se a média desses rankings para cada classe. Essa abordagem reduz eficazmente o impacto de previsões extremas, ao mesmo tempo em que preserva as relações hierárquicas mais importantes entre as previsões de classe.
A abordagem pela mediana aumenta a estabilidade em casos de previsões extremas. Ela mantém sua eficácia ao lidar com distribuições assimétricas ou enviesadas, alcançando um equilíbrio entre o uso da informação disponível e o controle de valores atípicos. Ao aplicar a regra da mediana, recomenda-se avaliar cuidadosamente os requisitos específicos do cenário de uso. Quando há alta probabilidade de previsões extremas ou a estabilidade das previsões é especialmente importante, o método da mediana oferece o equilíbrio ideal entre confiabilidade e desempenho.
//+------------------------------------------------------------------+ //| median of predications | //+------------------------------------------------------------------+ class CMedian { private: ulong m_outputs; ulong m_inputs; vector m_output; matrix m_out; public: CMedian(void); ~CMedian(void); ulong classify(vector &inputs, IClassify* &models[]); }; //+------------------------------------------------------------------+ //| constructor | //+------------------------------------------------------------------+ CMedian::CMedian(void) { } //+------------------------------------------------------------------+ //| destructor | //+------------------------------------------------------------------+ CMedian::~CMedian(void) { } //+------------------------------------------------------------------+ //| consensus classification | //+------------------------------------------------------------------+ ulong CMedian::classify(vector &inputs,IClassify *&models[]) { m_out = matrix::Zeros(models[0].getNumOutputs(),models.Size()); vector model_classification; for(uint i = 0; i<models.Size(); i++) { model_classification = models[i].classify(inputs); if(!m_out.Col(model_classification,i)) { Print(__FUNCTION__, " ", __LINE__, " failed row insertion ", GetLastError()); return ULONG_MAX; } } m_output = vector::Zeros(models[0].getNumOutputs()); for(ulong i = 0; i<m_output.Size(); i++) { vector row = m_out.Row(i); if(!row.Size()) { Print(__FUNCTION__," ", __LINE__," empty vector "); return ULONG_MAX; } qsortd(0,row.Size()-1,row); m_output[i] = row.Median(); } double sum = m_output.Sum(); ulong mx = m_output.ArgMax(); if(sum>0.0) m_output/=sum; return mx; }
Classificadores ensemble MaxMax e MaxMin
Às vezes, em alguns ensembles de modelos componentes, certos modelos podem apresentar especialização em subconjuntos específicos do conjunto total de classes. Quando operam em suas respectivas áreas de especialização, esses modelos geram saídas com alto grau de confiabilidade, ao mesmo tempo em que produzem valores moderados e menos significativos para classes fora de sua zona de expertise. A regra MaxMax oferece uma solução para esse tipo de cenário ao avaliar cada classe com base em seu maior valor entre todos os modelos. Essa abordagem prioriza previsões altamente confiáveis, ignorando saídas moderadas que podem ser potencialmente menos informativas. No entanto, é importante lembrar que esse método não é adequado para cenários em que as previsões secundárias têm valor analítico significativo.
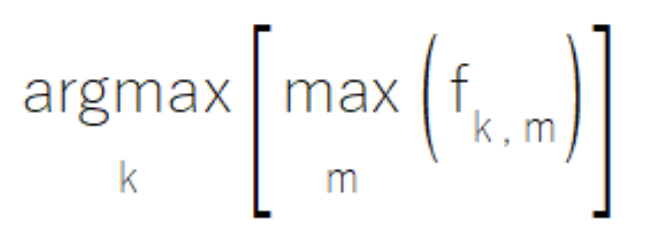
A regra MaxMax é implementada na classe CMaxmax no arquivo ensemble.mqh e fornece uma estrutura completa para lidar com os padrões de especialização dos modelos.
//+------------------------------------------------------------------+ //|Compute the maximum of the predictions | //+------------------------------------------------------------------+ class CMaxMax { private: ulong m_outputs; ulong m_inputs; vector m_output; matrix m_out; public: CMaxMax(void); ~CMaxMax(void); ulong classify(vector &inputs, IClassify* &models[]); }; //+------------------------------------------------------------------+ //| constructor | //+------------------------------------------------------------------+ CMaxMax::CMaxMax(void) { } //+------------------------------------------------------------------+ //| destructor | //+------------------------------------------------------------------+ CMaxMax::~CMaxMax(void) { } //+------------------------------------------------------------------+ //| ensemble classification | //+------------------------------------------------------------------+ ulong CMaxMax::classify(vector &inputs,IClassify *&models[]) { double sum; ulong ibest; m_output = vector::Zeros(models[0].getNumOutputs()); for(uint i = 0; i<models.Size(); i++) { vector classification = models[i].classify(inputs); for(ulong j = 0; j<classification.Size(); j++) { if(classification[j] > m_output[j]) m_output[j] = classification[j]; } } ibest = m_output.ArgMax(); sum = m_output.Sum(); if(sum>0.0) m_output/=sum; return ibest; }
Por outro lado, alguns sistemas ensemble utilizam modelos particularmente eficazes em excluir classes, em vez de identificá-las. Nesses casos, quando uma instância pertence a uma classe específica, pelo menos um dos modelos do ensemble gera uma saída significativamente baixa para cada classe incorreta, eliminando-as de fato da consideração.
A regra MaxMin aplica essa lógica, avaliando a pertinência a uma classe com base no menor valor de saída entre todos os modelos para cada classe.
Essa abordagem, implementada na classe CMaxmin no arquivo ensemble.mqh, fornece um mecanismo que aproveita a capacidade de certos modelos de realizar exclusões.
//+------------------------------------------------------------------+ //| Compute the minimum of the predictions | //+------------------------------------------------------------------+ class CMaxMin { private: ulong m_outputs; ulong m_inputs; vector m_output; matrix m_out; public: CMaxMin(void); ~CMaxMin(void); ulong classify(vector &inputs, IClassify* &models[]); }; //+------------------------------------------------------------------+ //| constructor | //+------------------------------------------------------------------+ CMaxMin::CMaxMin(void) { } //+------------------------------------------------------------------+ //| destructor | //+------------------------------------------------------------------+ CMaxMin::~CMaxMin(void) { } //+------------------------------------------------------------------+ //| ensemble classification | //+------------------------------------------------------------------+ ulong CMaxMin::classify(vector &inputs,IClassify *&models[]) { double sum; ulong ibest; for(uint i = 0; i<models.Size(); i++) { vector classification = models[i].classify(inputs); if(i == 0) m_output = classification; else { for(ulong j = 0; j<classification.Size(); j++) if(classification[j] < m_output[j]) m_output[j] = classification[j]; } } ibest = m_output.ArgMax(); sum = m_output.Sum(); if(sum>0.0) m_output/=sum; return ibest; }
Ao implementar um dos métodos (MaxMax ou MaxMin), o desenvolvedor deve avaliar cuidadosamente as características do seu ensemble de modelos. Para o método MaxMax, por exemplo, é essencial garantir que os modelos apresentem padrões claros de especialização. É particularmente importante verificar se os valores de saída moderados representam mais ruído do que informações secundárias valiosas e garantir que o ensemble ofereça cobertura completa de todas as classes relevantes. Ao adotar o método MaxMin, é necessário assegurar que o ensemble como um todo consiga lidar com todos os cenários potenciais de classificação incorreta e identificar eventuais lacunas na cobertura por exclusão.
Método das interseções
O método das interseções é uma abordagem especializada para combinar classificadores, focada principalmente em reduzir o conjunto de classes, em vez de realizar tarefas gerais de classificação. Sua aplicação direta é amplamente reconhecida como limitada, e ele é descrito aqui como um precursor conceitual fundamental para métodos mais robustos, especialmente o de união. Essa abordagem exige que os modelos componentes gerem rankings por classe para cada amostra de entrada, do mais ao menos provável. Muitos classificadores atendem a esse requisito, e a ordenação das saídas do tipo real frequentemente melhora o desempenho ao filtrar o ruído de maneira eficaz, preservando, ao mesmo tempo, informações valiosas. Na fase de treinamento, o método identifica o número mínimo de saídas com o ranking mais alto que cada modelo componente pode manter, garantindo a inclusão consistente da classe verdadeira em todo o conjunto de dados de treinamento. Para novas amostras, a decisão combinada consiste em um subconjunto mínimo que contenha a classe verdadeira, determinado pelo cruzamento dos subconjuntos mínimos gerados por todos os modelos componentes.
Considere um exemplo prático com múltiplas classes e quatro modelos. A análise de cinco amostras do conjunto de treinamento revela padrões de ranking distintos entre os modelos para a classe verdadeira.
| Amostra | Modelo 1 | Modelo 2 | Modelo 3 | Modelo 4 |
|---|---|---|---|---|
| 1 | 3 | 21 | 4 | 5 |
| 2 | 8 | 4 | 8 | 9 |
| 3 | 1 | 17 | 12 | 3 |
| 4 | 7 | 16 | 2 | 8 |
| 5 | 7 | 8 | 6 | 1 |
| Máximo | 8 | 21 | 12 | 9 |
A tabela mostra que a classe verdadeira na segunda amostra recebeu o oitavo ranking do primeiro modelo, o quarto do segundo e o nono do quarto modelo. A última linha da tabela mostra os rankings máximos em cada uma das colunas: 8, 21, 12 e 9, respectivamente. Ao avaliar amostras desconhecidas, o ensemble seleciona as classes com os rankings mais altos de cada modelo com base nesses limites e realiza a interseção dessas classes, gerando o subconjunto final de classes comuns a todos os conjuntos de treinamento.
A classe CIntersection implementa o método das interseções e possui um procedimento de treinamento dedicado por meio da função fit(). Essa função analisa os dados de treinamento para determinar os piores rankings de cada modelo, rastreando o número mínimo de classes com os rankings mais altos necessário para garantir a inclusão estável das classificações corretas.
//+------------------------------------------------------------------+ //| Use intersection rule to compute minimal class set | //+------------------------------------------------------------------+ class CIntersection { private: ulong m_nout; long m_indices[]; vector m_ranks; vector m_output; public: CIntersection(void); ~CIntersection(void); ulong classify(vector &inputs, IClassify* &models[]); bool fit(matrix &inputs, matrix &targets, IClassify* &models[]); vector proba(void) { return m_output;} };
A chamada do método classify() da classe CIntersection realiza uma avaliação sequencial de todos os modelos componentes com base nos dados de entrada. Para cada modelo, seu vetor de saída é ordenado, e os índices do vetor ordenado são usados para calcular a interseção das classes que pertencem ao subconjunto de rankings mais altos de cada modelo.
//+------------------------------------------------------------------+ //| fit an ensemble model | //+------------------------------------------------------------------+ bool CIntersection::fit(matrix &inputs,matrix &targets,IClassify *&models[]) { m_nout = targets.Cols(); m_output = vector::Ones(m_nout); m_ranks = vector::Zeros(models.Size()); double best = 0.0; ulong nbad; if(ArrayResize(m_indices,int(m_nout))<0) { Print(__FUNCTION__, " ", __LINE__, " array resize error ", GetLastError()); return false; } ulong k; for(ulong i = 0; i<inputs.Rows(); i++) { vector trow = targets.Row(i); vector inrow = inputs.Row(i); k = trow.ArgMax(); best = trow[k]; for(uint j = 0; j<models.Size(); j++) { vector classification = models[j].classify(inrow); best = classification[k]; nbad = 1; for(ulong ii = 0; ii<m_nout; ii++) { if(ii == k) continue; if(classification[ii] >= best) ++nbad; } if(nbad > ulong(m_ranks[j])) m_ranks[j] = double(nbad); } } return true; } //+------------------------------------------------------------------+ //| ensemble classification | //+------------------------------------------------------------------+ ulong CIntersection::classify(vector &inputs,IClassify *&models[]) { for(long j =0; j<long(m_nout); j++) m_indices[j] = j; for(uint i =0; i<models.Size(); i++) { vector classification = models[i].classify(inputs); ArraySort(m_indices); qsortdsi(0,classification.Size()-1,classification,m_indices); for(ulong j = 0; j<m_nout-ulong(m_ranks[i]); j++) { m_output[m_indices[j]] = 0.0; } } ulong n=0; double cut = 0.5; for(ulong i = 0; i<m_nout; i++) { if(m_output[i] > cut) ++n; } return n; }
Apesar de sua elegância teórica, o método das interseções apresenta algumas limitações significativas. Embora ele garanta a inclusão das classes verdadeiras do conjunto de treinamento, essa vantagem é restringida por limitações inerentes ao próprio método. Ele também pode gerar subconjuntos vazios de classes para amostras fora do conjunto de treinamento, especialmente quando os subconjuntos de maior ranking de diferentes modelos não compartilham elementos em comum. O mais crítico, porém, é o fato de que o método se baseia na análise dos piores desempenhos, o que frequentemente resulta em subconjuntos de classes excessivamente amplos, afetando negativamente tanto a eficiência quanto a eficácia do método.
O método das interseções pode ser útil em contextos específicos nos quais todos os modelos componentes apresentam desempenho estável em todo o conjunto de classes. No entanto, sua sensibilidade ao fraco desempenho de modelos fora de suas áreas de especialização frequentemente limita sua utilidade prática, especialmente em aplicações que dependem de modelos especializados para diferentes subconjuntos de classes. Em última análise, o valor principal desse método reside mais em sua contribuição conceitual para abordagens mais robustas, como o método de união, do que em sua aplicação direta na maioria das tarefas de classificação.
Regra de união
A regra de união representa um aprimoramento estratégico do método das interseções, solucionando sua principal limitação: a dependência excessiva da análise dos piores desempenhos. Essa modificação se mostra particularmente eficaz ao combinar modelos especializados com diferentes áreas de expertise, deslocando o foco da análise de cenários desfavoráveis para a análise de cenários favoráveis. O processo inicial segue o mesmo princípio do método das interseções: analisar amostras do conjunto de treinamento para obter os rankings da classe verdadeira a partir dos modelos componentes. No entanto, a regra de união se diferencia ao identificar e rastrear os modelos com melhor desempenho para cada amostra, em vez de monitorar os casos de pior eficácia. Em seguida, o método avalia os menos favoráveis dentre esses melhores desempenhos dentro do conjunto de dados de treinamento. Para a classificação de amostras desconhecidas, o sistema gera um subconjunto combinado de classes por meio da união dos subconjuntos ótimos de cada um dos modelos componentes. Considere o mesmo conjunto de dados do exemplo anterior, agora complementado com colunas adicionais para rastrear o desempenho, identificadas pelo prefixo "Perf".
| Amostra | Modelo 1 | Modelo 2 | Modelo 3 | Modelo 4 | Perf_Model 1 | Perf_Model 2 | Perf_Model 3 | Perf_Model 4 |
|---|---|---|---|---|---|---|---|---|
| 1 | 3 | 21 | 4 | 5 | 3 | 0 | 0 | 0 |
| 2 | 8 | 4 | 8 | 9 | 0 | 4 | 0 | 0 |
| 3 | 1 | 17 | 12 | 3 | 1 | 0 | 0 | 0 |
| 4 | 7 | 16 | 2 | 8 | 0 | 0 | 2 | 0 |
| 5 | 7 | 8 | 6 | 1 | 0 | 0 | 0 | 1 |
| Máximo | 3 | 4 | 2 | 1 |
Nas colunas adicionais, são registrados os casos em que cada modelo demonstra desempenho superior, e a linha inferior indica os valores máximos observados nesses melhores cenários.
A regra de união apresenta várias vantagens claras em relação ao método das interseções. Ela elimina a possibilidade de subconjuntos vazios, pois ao menos um modelo sempre apresentará um desempenho ideal de maneira consistente para qualquer amostra fornecida. O método também gerencia de maneira eficaz os modelos especializados, desconsiderando desempenhos fracos fora de suas áreas de expertise durante o treinamento, o que permite que esses modelos especialistas assumam o controle. Por fim, a regra de união fornece um mecanismo natural para identificar e potencialmente excluir modelos com desempenho consistentemente baixo, identificados por colunas de zeros na matriz de rastreamento.
A implementação do método de união é estruturalmente muito semelhante ao método das interseções, utilizando o container m_ranks para monitorar os valores máximos nas colunas de rastreamento de desempenho.
//+------------------------------------------------------------------+ //| Use union rule to compute minimal class set | //+------------------------------------------------------------------+ class CUnion { private: ulong m_nout; long m_indices[]; vector m_ranks; vector m_output; public: CUnion(void); ~CUnion(void); ulong classify(vector &inputs, IClassify* &models[]); bool fit(matrix &inputs, matrix &targets, IClassify* &models[]); vector proba(void) { return m_output;} };
No entanto, as diferenças principais estão no tratamento dos rankings das classes e na inicialização dos indicadores. Durante o treinamento, o sistema monitora os rankings mínimos de todos os modelos para cada amostra, atualizando os valores máximos de m_ranks sempre que necessário.
//+------------------------------------------------------------------+ //| fit an ensemble model | //+------------------------------------------------------------------+ bool CUnion::fit(matrix &inputs,matrix &targets,IClassify *&models[]) { m_nout = targets.Cols(); m_output = vector::Zeros(m_nout); m_ranks = vector::Zeros(models.Size()); double best = 0.0; ulong nbad; if(ArrayResize(m_indices,int(m_nout))<0) { Print(__FUNCTION__, " ", __LINE__, " array resize error ", GetLastError()); return false; } ulong k, ibestrank=0, bestrank=0; for(ulong i = 0; i<inputs.Rows(); i++) { vector trow = targets.Row(i); vector inrow = inputs.Row(i); k = trow.ArgMax(); for(uint j = 0; j<models.Size(); j++) { vector classification = models[j].classify(inrow); best = classification[k]; nbad = 1; for(ulong ii = 0; ii<m_nout; ii++) { if(ii == k) continue; if(classification[ii] >= best) ++nbad; } if(j == 0 || nbad < bestrank) { bestrank = nbad; ibestrank = j; } } if(bestrank > ulong(m_ranks[ibestrank])) m_ranks[ibestrank] = double(bestrank); } return true; }
A fase de classificação inclui progressivamente as classes que atendem a critérios específicos de desempenho.
//+------------------------------------------------------------------+ //| ensemble classification | //+------------------------------------------------------------------+ ulong CUnion::classify(vector &inputs,IClassify *&models[]) { for(long j =0; j<long(m_nout); j++) m_indices[j] = j; for(uint i =0; i<models.Size(); i++) { vector classification = models[i].classify(inputs); ArraySort(m_indices); qsortdsi(0,classification.Size()-1,classification,m_indices); for(ulong j =(m_nout-ulong(m_ranks[i])); j<m_nout; j++) { m_output[m_indices[j]] = 1.0; } } ulong n=0; double cut = 0.5; for(ulong i = 0; i<m_nout; i++) { if(m_output[i] > cut) ++n; } return n; }
Apesar de a regra de união mitigar eficazmente muitas limitações do método das interseções, ela ainda é vulnerável à presença de valores atípicos quando todos os modelos componentes geram rankings baixos. Esse cenário, embora desafiador, geralmente é raro em aplicações bem projetadas e pode ser minimizado com um bom sistema de arquitetura e seleção de modelos. A eficácia do método é especialmente evidente em ambientes com modelos especializados, nos quais cada modelo componente tem bom desempenho em determinadas áreas, mas pode ser menos eficaz em outras. Essa característica o torna particularmente valioso para tarefas complexas de classificação que exigem expertise diversificada.
Combinações de classificadores baseadas em regressão logística
Entre todos os classificadores ensemble discutidos até o momento, o método de contagem de Borda se destaca como uma solução de eficácia universal para a combinação de classificadores com desempenho semelhante, ou seja, ele assume que todos os modelos possuem capacidade preditiva equivalente. No entanto, quando os modelos apresentam diferenças significativas em termos de desempenho, pode ser desejável aplicar pesos diferenciados com base nos indicadores de eficácia de cada modelo. A regressão logística se apresenta como um aprimoramento avançado para o nosso método de combinação ponderada.
A implementação da regressão logística para a combinação de classificadores baseia-se nos princípios da regressão linear comum, mas é projetada para lidar com problemas específicos de classificação. Em vez de prever diretamente valores em um modo contínuo, a regressão logística calcula a probabilidade de pertencimento às classes, oferecendo uma abordagem mais refinada para tarefas de classificação. O processo começa com a conversão dos dados brutos de treinamento para um formato compatível com regressão. Considere um sistema com três classes e quatro modelos, que gera as seguintes saídas:
| Modelo 1 | Modelo 2 | Modelo 3 | Modelo 4 | |
|---|---|---|---|---|
| 1 | 0.7 | 0.1 | 0.8 | 0.4 |
| 2 | 0.8 | 0.3 | 0.9 | 0.3 |
| 3 | 0.2 | 0.2 | 0.7 | 0.2 |
Esses dados geram três novas amostras de treinamento para regressão para cada amostra original, onde o valor da variável alvo será 1.0 para a classe correta e 0.0 para as classes incorretas. Os preditores utilizam rankings proporcionais em vez das saídas brutas, o que melhora a estabilidade das soluções numéricas.
A classe CLogitReg, localizada no arquivo ensemble.mqh, gerencia a implementação do método de combinação ponderada para ensembles de classificadores.
//+------------------------------------------------------------------+ //| Use logistic regression to find best class | //| This uses one common weight vector for all classes. | //+------------------------------------------------------------------+ class ClogitReg { private: ulong m_nout; long m_indices[]; matrix m_ranks; vector m_output; vector m_targs; matrix m_input; logistic::Clogit *m_logit; public: ClogitReg(void); ~ClogitReg(void); ulong classify(vector &inputs, IClassify* &models[]); bool fit(matrix &inputs, matrix &targets, IClassify* &models[]); vector proba(void) { return m_output;} };
O método fit() cria o conjunto de dados de treinamento para regressão por meio do processamento sistemático de cada amostra individual. Primeiro, é identificada a classe verdadeira para cada uma das amostras de treinamento. Em seguida, os resultados das avaliações de cada modelo componente são coletados em uma matriz m_ranks. Essa matriz é processada para gerar as variáveis dependentes e independentes para a tarefa de regressão, que é então resolvida usando o objeto m_logit.
//+------------------------------------------------------------------+ //| fit an ensemble model | //+------------------------------------------------------------------+ bool ClogitReg::fit(matrix &inputs,matrix &targets,IClassify *&models[]) { m_nout = targets.Cols(); m_input = matrix::Zeros(inputs.Rows(),models.Size()); m_targs = vector::Zeros(inputs.Rows()); m_output = vector::Zeros(m_nout); m_ranks = matrix::Zeros(models.Size(),m_nout); double best = 0.0; ulong nbelow; if(ArrayResize(m_indices,int(m_nout))<0) { Print(__FUNCTION__, " ", __LINE__, " array resize error ", GetLastError()); return false; } ulong k; if(CheckPointer(m_logit) == POINTER_DYNAMIC) delete m_logit; m_logit = new logistic::Clogit(); for(ulong i = 0; i<inputs.Rows(); i++) { vector trow = targets.Row(i); vector inrow = inputs.Row(i); k = trow.ArgMax(); best = trow[k]; for(uint j = 0; j<models.Size(); j++) { vector classification = models[j].classify(inrow); if(!m_ranks.Row(classification,j)) { Print(__FUNCTION__, " ", __LINE__, " failed row insertion ", GetLastError()); return false; } } for(ulong j = 0; j<m_nout; j++) { for(uint jj =0; jj<models.Size(); jj++) { nbelow = 0; best = m_ranks[jj][j]; for(ulong ii =0; ii<m_nout; ii++) { if(m_ranks[jj][ii]<best) ++nbelow; } m_input[i][jj] = double(nbelow)/double(m_nout); } m_targs[i] = (j == k)? 1.0:0.0; } } return m_logit.fit(m_input,m_targs); }
Essa implementação representa uma abordagem mais sofisticada para a combinação de classificadores, sendo particularmente valiosa em cenários nos quais os modelos componentes apresentam níveis variados de desempenho para diferentes tarefas de classificação.
O processo de classificação ponderada é construído com base no método da contagem de Borda, utilizando valores de peso específicos para os modelos. O algoritmo começa com a inicialização dos vetores de acumulação e o processamento das amostras desconhecidas por cada modelo componente. Os pesos ideais, calculados pelo objeto m_logit, são aplicados para ajustar as contribuições dos classificadores componentes. A classe final é determinada como o índice correspondente ao maior valor de m_output.
//+------------------------------------------------------------------+ //| classify with ensemble model | //+------------------------------------------------------------------+ ulong ClogitReg::classify(vector &inputs,IClassify *&models[]) { double temp; for(uint i =0; i<models.Size(); i++) { vector classification = models[i].classify(inputs); for(long j =0; j<long(classification.Size()); j++) m_indices[j] = j; if(!classification.Size()) { Print(__FUNCTION__," ", __LINE__," empty vector "); return ULONG_MAX; } qsortdsi(0,classification.Size()-1,classification,m_indices); temp = m_logit.coeffAt(i); for(ulong j = 0 ; j<m_nout; j++) { m_output[m_indices[j]] += j * temp; } } double sum = m_output.Sum(); ulong ibest = m_output.ArgMax(); double best = m_output[ibest]; if(sum>0.0) m_output/=sum; return ibest; }
Nesta implementação, dá-se ênfase ao uso de pesos universais devido à sua alta estabilidade e ao baixo risco de sobreajuste. No entanto, pesos específicos por classe continuam sendo uma opção válida para cenários com grandes volumes de dados de treinamento. O método que utiliza pesos específicos por classe será abordado na próxima seção. Por ora, vamos focar em como os pesos ideais são determinados, em especial no modelo de regressão logística.
O conceito central da regressão logística é a transformação logística, ou logit, apresentada a seguir.
Essa função mapeia um domínio ilimitado para o intervalo [0, 1]. Quando x na equação acima é fortemente negativo, o resultado tende a zero. Por outro lado, à medida que x aumenta, o valor da função se aproxima de um. Quando x = 0, a função retorna um valor exatamente no meio entre os dois extremos. Permitir que x represente a variável predita no modelo de regressão significa que, com x menor que zero, existe uma chance de 50% de que a amostra pertença a uma determinada classe. À medida que o valor de x aumenta a partir de zero, a probabilidade percentual desse pertencimento cresce proporcionalmente. Da mesma forma, conforme x diminui em relação a zero, essa probabilidade decresce.
Uma forma alternativa de expressar a probabilidade é por meio dos coeficientes de chance. Formalmente, esses são chamados de razão de chances, que corresponde à probabilidade de ocorrência de um evento dividida pela probabilidade de ele não ocorrer. Se expressarmos e^x na transformação logit como f(x), obtemos a seguinte equação.
Se removermos as exponenciais dessa equação aplicando logaritmos em ambos os lados, e assumirmos que x é a variável predita na tarefa de regressão, obtemos a equação mostrada a seguir.
Essa expressão, mencionada no contexto de ensembles de classificadores, afirma que, para cada amostra no conjunto de dados de treinamento, uma combinação linear dos preditores dos classificadores componentes representa o logaritmo da razão de chances para o respectivo rótulo de classe. Os pesos ideais, w, podem ser obtidos por meio da estimativa de máxima verossimilhança ou pela minimização de uma função objetivo. Os detalhes sobre como isso é feito não são abordados neste artigo.
Inicialmente, encontrar uma implementação completa de regressão logística na linguagem MQL5 revelou-se uma tarefa difícil. A biblioteca Alglib, portada para MQL5, contém ferramentas específicas para regressão logística, mas o autor não conseguiu fazê-las compilar com sucesso. Além disso, não há exemplos de uso dessas ferramentas nos programas de demonstração da Alglib que ilustrem seu funcionamento. Ainda assim, a biblioteca Alglib foi útil para a implementação da classe Clogit, definida no arquivo logistic.mqh. Esse arquivo contém a definição da classe CFg, que implementa a interface CNDimensional_Grad.
//+------------------------------------------------------------------+ //| function and gradient calculation object | //+------------------------------------------------------------------+ class CFg:public CNDimensional_Grad { private: matrix m_preds; vector m_targs; ulong m_nclasses,m_samples,m_features; double loss_gradient(matrix &coef,double &gradients[]); void weight_intercept_raw(matrix &coef,matrix &x, matrix &wghts,vector &intcept,matrix &rpreds); void weight_intercept(matrix &coef,matrix &wghts,vector &intcept); double l2_penalty(matrix &wghts,double strenth); void sum_exp_minus_max(ulong index,matrix &rp,vector &pr); void closs_grad_halfbinmial(double y_true,double raw, double &inout_1,double &intout_2); public: //--- constructor, destructor CFg(matrix &predictors,vector &targets, ulong num_classes) { m_preds = predictors; vector classes = np::unique(targets); np::sort(classes); vector checkclasses = np::arange(classes.Size()); if(checkclasses.Compare(classes,1.e-1)) { double classv[]; np::vecAsArray(classes,classv); m_targs = targets; for(ulong i = 0; i<targets.Size(); i++) m_targs[i] = double(ArrayBsearch(classv,m_targs[i])); } else m_targs = targets; m_nclasses = num_classes; m_features = m_preds.Cols(); m_samples = m_preds.Rows(); } ~CFg(void) {} virtual void Grad(double &x[],double &func,double &grad[],CObject &obj); virtual void Grad(CRowDouble &x,double &func,CRowDouble &grad,CObject &obj); }; //+------------------------------------------------------------------+ //| this function is not used | //+------------------------------------------------------------------+ void CFg::Grad(double &x[],double &func,double &grad[],CObject &obj) { matrix coefficients; arrayToMatrix(x,coefficients,m_nclasses>2?m_nclasses:m_nclasses-1,m_features+1); func=loss_gradient(coefficients,grad); return; } //+------------------------------------------------------------------+ //| get function value and gradients | //+------------------------------------------------------------------+ void CFg::Grad(CRowDouble &x,double &func,CRowDouble &grad,CObject &obj) { double xarray[],garray[]; x.ToArray(xarray); Grad(xarray,func,garray,obj); grad = garray; return; } //+------------------------------------------------------------------+ //| loss gradient | //+------------------------------------------------------------------+ double CFg::loss_gradient(matrix &coef,double &gradients[]) { matrix weights; vector intercept; vector losses; matrix gradpointwise; matrix rawpredictions; matrix gradient; double loss; double l2reg; //calculate weights intercept and raw predictions weight_intercept_raw(coef,m_preds,weights,intercept,rawpredictions); gradpointwise = matrix::Zeros(m_samples,rawpredictions.Cols()); losses = vector::Zeros(m_samples); double sw_sum = double(m_samples); //loss gradient calculations if(m_nclasses>2) { double max_value, sum_exps; vector p(rawpredictions.Cols()+2); //--- for(ulong i = 0; i< m_samples; i++) { sum_exp_minus_max(i,rawpredictions,p); max_value = p[rawpredictions.Cols()]; sum_exps = p[rawpredictions.Cols()+1]; losses[i] = log(sum_exps) + max_value; //--- for(ulong k = 0; k<rawpredictions.Cols(); k++) { if(ulong(m_targs[i]) == k) losses[i] -= rawpredictions[i][k]; p[k]/=sum_exps; gradpointwise[i][k] = p[k] - double(int(ulong(m_targs[i])==k)); } } } else { for(ulong i = 0; i<m_samples; i++) { closs_grad_halfbinmial(m_targs[i],rawpredictions[i][0],losses[i],gradpointwise[i][0]); } } //--- loss = losses.Sum()/sw_sum; l2reg = 1.0 / (1.0 * sw_sum); loss += l2_penalty(weights,l2reg); gradpointwise/=sw_sum; //--- if(m_nclasses>2) { gradient = gradpointwise.Transpose().MatMul(m_preds) + l2reg*weights; gradient.Resize(gradient.Rows(),gradient.Cols()+1); vector gpsum = gradpointwise.Sum(0); gradient.Col(gpsum,m_features); } else { gradient = m_preds.Transpose().MatMul(gradpointwise) + l2reg*weights.Transpose(); gradient.Resize(gradient.Rows()+1,gradient.Cols()); vector gpsum = gradpointwise.Sum(0); gradient.Row(gpsum,m_features); } //--- matrixToArray(gradient,gradients); //--- return loss; } //+------------------------------------------------------------------+ //| weight intercept raw preds | //+------------------------------------------------------------------+ void CFg::weight_intercept_raw(matrix &coef,matrix &x,matrix &wghts,vector &intcept,matrix &rpreds) { weight_intercept(coef,wghts,intcept); matrix intceptmat = np::vectorAsRowMatrix(intcept,x.Rows()); rpreds = (x.MatMul(wghts.Transpose()))+intceptmat; } //+------------------------------------------------------------------+ //| weight intercept | //+------------------------------------------------------------------+ void CFg::weight_intercept(matrix &coef,matrix &wghts,vector &intcept) { intcept = coef.Col(m_features); wghts = np::sliceMatrixCols(coef,0,m_features); } //+------------------------------------------------------------------+ //| sum exp minus max | //+------------------------------------------------------------------+ void CFg::sum_exp_minus_max(ulong index,matrix &rp,vector &pr) { double mv = rp[index][0]; double s_exps = 0.0; for(ulong k = 1; k<rp.Cols(); k++) { if(mv<rp[index][k]) mv=rp[index][k]; } for(ulong k = 0; k<rp.Cols(); k++) { pr[k] = exp(rp[index][k] - mv); s_exps += pr[k]; } pr[rp.Cols()] = mv; pr[rp.Cols()+1] = s_exps; } //+------------------------------------------------------------------+ //| l2 penalty | //+------------------------------------------------------------------+ double CFg::l2_penalty(matrix &wghts,double strenth) { double norm2_v; if(wghts.Rows()==1) { matrix nmat = (wghts).MatMul(wghts.Transpose()); norm2_v = nmat[0][0]; } else norm2_v = wghts.Norm(MATRIX_NORM_FROBENIUS); return 0.5*strenth*norm2_v; } //+------------------------------------------------------------------+ //| closs_grad_half_binomial | //+------------------------------------------------------------------+ void CFg::closs_grad_halfbinmial(double y_true,double raw, double &inout_1,double &inout_2) { if(raw <= -37.0) { inout_2 = exp(raw); inout_1 = inout_2 - y_true * raw; inout_2 -= y_true; } else if(raw <= -2.0) { inout_2 = exp(raw); inout_1 = log1p(inout_2) - y_true * raw; inout_2 = ((1.0 - y_true) * inout_2 - y_true) / (1.0 + inout_2); } else if(raw <= 18.0) { inout_2 = exp(-raw); // log1p(exp(x)) = log(1 + exp(x)) = x + log1p(exp(-x)) inout_1 = log1p(inout_2) + (1.0 - y_true) * raw; inout_2 = ((1.0 - y_true) - y_true * inout_2) / (1.0 + inout_2); } else { inout_2 = exp(-raw); inout_1 = inout_2 + (1.0 - y_true) * raw; inout_2 = ((1.0 - y_true) - y_true * inout_2) / (1.0 + inout_2); } }
Isso é necessário para o procedimento de minimização da função LBFGS. A classe Clogit contém os métodos já conhecidos para treinamento e geração de saídas.
//+------------------------------------------------------------------+ //| logistic regression implementation | //+------------------------------------------------------------------+ class Clogit { public: Clogit(void); ~Clogit(void); bool fit(matrix &predictors, vector &targets); double predict(vector &preds); vector proba(vector &preds); matrix probas(matrix &preds); double coeffAt(ulong index); private: ulong m_nsamples; ulong m_nfeatures; bool m_trained; matrix m_train_preds; vector m_train_targs; matrix m_coefs; vector m_bias; vector m_classes; double m_xin[]; CFg *m_gradfunc; CObject m_dummy; vector predictProba(double &in); }; //+------------------------------------------------------------------+ //| constructor | //+------------------------------------------------------------------+ Clogit::Clogit(void) { } //+------------------------------------------------------------------+ //| destructor | //+------------------------------------------------------------------+ Clogit::~Clogit(void) { if(CheckPointer(m_gradfunc) == POINTER_DYNAMIC) delete m_gradfunc; } //+------------------------------------------------------------------+ //| fit a model to a dataset | //+------------------------------------------------------------------+ bool Clogit::fit(matrix &predictors, vector &targets) { m_trained = false; m_classes = np::unique(targets); np::sort(m_classes); if(predictors.Rows()!=targets.Size() || m_classes.Size()<2) { Print(__FUNCTION__," ",__LINE__," invalid inputs "); return m_trained; } m_train_preds = predictors; m_train_targs = targets; m_nfeatures = m_train_preds.Cols(); m_nsamples = m_train_preds.Rows(); m_coefs = matrix::Zeros(m_classes.Size()>2?m_classes.Size():m_classes.Size()-1,m_nfeatures+1); matrixToArray(m_coefs,m_xin); m_gradfunc = new CFg(m_train_preds,m_train_targs,m_classes.Size()); //--- CMinLBFGSStateShell state; CMinLBFGSReportShell rep; CNDimensional_Rep frep; //--- CAlglib::MinLBFGSCreate(m_xin.Size(),m_xin.Size()>=5?5:m_xin.Size(),m_xin,state); //--- CAlglib::MinLBFGSOptimize(state,m_gradfunc,frep,true,m_dummy); //--- CAlglib::MinLBFGSResults(state,m_xin,rep); //--- if(rep.GetTerminationType()>0) { m_trained = true; arrayToMatrix(m_xin,m_coefs,m_classes.Size()>2?m_classes.Size():m_classes.Size()-1,m_nfeatures+1); m_bias = m_coefs.Col(m_nfeatures); m_coefs = np::sliceMatrixCols(m_coefs,0,m_nfeatures); } else Print(__FUNCTION__," ", __LINE__, " failed to train the model ", rep.GetTerminationType()); delete m_gradfunc; return m_trained; } //+------------------------------------------------------------------+ //| get probability for single sample | //+------------------------------------------------------------------+ vector Clogit::proba(vector &preds) { vector predicted; if(!m_trained) { Print(__FUNCTION__," ", __LINE__," no trained model available "); predicted.Fill(EMPTY_VALUE); return predicted; } predicted = ((preds.MatMul(m_coefs.Transpose()))); predicted += m_bias; if(predicted.Size()>1) { if(!predicted.Activation(predicted,AF_SOFTMAX)) { Print(__FUNCTION__," ", __LINE__," errror ", GetLastError()); predicted.Fill(EMPTY_VALUE); return predicted; } } else { predicted = predictProba(predicted[0]); } return predicted; } //+------------------------------------------------------------------+ //| get probability for binary classification | //+------------------------------------------------------------------+ vector Clogit::predictProba(double &in) { vector out(2); double n = 1.0/(1.0+exp(-1.0*in)); out[0] = 1.0 - n; out[1] = n; return out; } //+------------------------------------------------------------------+ //| get probabilities for multiple samples | //+------------------------------------------------------------------+ matrix Clogit::probas(matrix &preds) { matrix output(preds.Rows(),m_classes.Size()); vector rowin,rowout; for(ulong i = 0; i<preds.Rows(); i++) { rowin = preds.Row(i); rowout = proba(rowin); if(rowout.Max() == EMPTY_VALUE || !output.Row(rowout,i)) { Print(__LINE__," probas error ", GetLastError()); output.Fill(EMPTY_VALUE); break; } } return output; } //+------------------------------------------------------------------+ //| get probability for single sample | //+------------------------------------------------------------------+ double Clogit::predict(vector &preds) { vector prob = proba(preds); if(prob.Max() == EMPTY_VALUE) { Print(__LINE__," predict error "); return EMPTY_VALUE; } return m_classes[prob.ArgMax()]; } //+------------------------------------------------------------------+ //| get model coefficient at specific index | //+------------------------------------------------------------------+ double Clogit::coeffAt(ulong index) { if(index<(m_coefs.Rows())) { return (m_coefs.Row(index)).Sum(); } else { return 0.0; } } } //+------------------------------------------------------------------+
Combinações em ensemble baseadas em regressão logística com pesos específicos por classe
A abordagem descrita na seção anterior, com um único conjunto de pesos, oferece estabilidade e eficiência, mas é limitada no sentido de não explorar plenamente a especialização dos modelos. Se determinados modelos apresentam melhor desempenho para classes específicas, seja por design do desenvolvedor ou como resultado de um desenvolvimento natural, a implementação de conjuntos de pesos separados para cada classe pode permitir o aproveitamento mais eficaz dessas vantagens. A transição para conjuntos de pesos específicos por classe torna o processo de otimização significativamente mais complexo. Em vez de otimizar um único conjunto de pesos, o ensemble precisa gerenciar K conjuntos (um para cada classe), cada um contendo M parâmetros, resultando em um total de K*M parâmetros. Esse aumento no número de parâmetros exige atenção cuidadosa aos requisitos de dados e aos riscos envolvidos na implementação.
A aplicação confiável de conjuntos de pesos separados exige uma quantidade substancial de dados de treinamento para manter a validade estatística. Como orientação geral, deve-se garantir que cada classe disponha de pelo menos dez vezes mais amostras de treinamento do que o número de modelos. Mesmo com volume suficiente de dados, essa abordagem deve ser implementada com cautela e apenas quando houver sinais claros de especialização relevante dos modelos para classes específicas.
A classe CLogitRegSep gerencia a implementação dos conjuntos separados de pesos, diferenciando-se da CLogitReg por alocar instâncias distintas da classe Clogit para cada classe. O processo de treinamento distribui as amostras de regressão entre conjuntos de dados de treinamento específicos por classe, em vez de combiná-las em um único conjunto.
//+------------------------------------------------------------------+ //| Use logistic regression to find best class. | //| This uses separate weight vectors for each class. | //+------------------------------------------------------------------+ class ClogitRegSep { private: ulong m_nout; long m_indices[]; matrix m_ranks; vector m_output; vector m_targs[]; matrix m_input[]; logistic::Clogit *m_logit[]; public: ClogitRegSep(void); ~ClogitRegSep(void); ulong classify(vector &inputs, IClassify* &models[]); bool fit(matrix &inputs, matrix &targets, IClassify* &models[]); vector proba(void) { return m_output;} };
A classificação de casos desconhecidos segue o mesmo algoritmo usado na abordagem com um conjunto único de pesos, com uma diferença essencial: os pesos específicos por classe são aplicados nos cálculos da contagem de Borda. Essa especialização permite ao sistema utilizar de forma mais eficaz a expertise dos modelos em relação a determinadas classes.
//+------------------------------------------------------------------+ //| classify with ensemble model | //+------------------------------------------------------------------+ ulong ClogitRegSep::classify(vector &inputs,IClassify *&models[]) { double temp; for(uint i =0; i<models.Size(); i++) { vector classification = models[i].classify(inputs); for(long j =0; j<long(classification.Size()); j++) m_indices[j] = j; if(!classification.Size()) { Print(__FUNCTION__," ", __LINE__," empty vector "); return ULONG_MAX; } qsortdsi(0,classification.Size()-1,classification,m_indices); for(ulong j = 0 ; j<m_nout; j++) { temp = m_logit[j].coeffAt(i); m_output[m_indices[j]] += j * temp; } } double sum = m_output.Sum(); ulong ibest = m_output.ArgMax(); double best = m_output[ibest]; if(sum>0.0) m_output/=sum; return ibest; }
Na implementação de conjuntos de pesos separados, são necessárias rotinas rigorosas de verificação. O especialista deve monitorar a distribuição dos pesos em busca de valores extremos sem justificativa, assegurando que qualquer desproporção esteja alinhada com características conhecidas do modelo. Devem ser aplicadas medidas de proteção para evitar instabilidades no processo de regressão. Todas essas práticas podem ser implementadas com eficácia mediante a adoção de protocolos de teste abrangentes.
O sucesso na implementação de conjuntos de pesos específicos por classe depende de uma atenção cuidadosa a diversos fatores críticos: garantir volume suficiente de dados de treinamento para cada classe, verificar se os padrões de especialização justificam o uso de pesos distintos, monitorar a estabilidade dos pesos e confirmar melhorias na acurácia da classificação em comparação com abordagens baseadas em um único conjunto de pesos. Embora essa implementação avançada de regressão logística ofereça capacidades ampliadas para classificação, ela exige uma gestão atenta para lidar com os desafios aumentados de complexidade e para minimizar os riscos potenciais.
Ensembles que utilizam precisão local
Para explorar ainda mais as vantagens das diferentes modelos, podemos considerar a precisão local de cada uma no espaço dos preditores. Às vezes, os classificadores componentes apresentam desempenho superior em regiões específicas do espaço de preditores. Essa especialização surge quando os modelos obtêm melhores resultados sob determinadas condições das variáveis preditoras: por exemplo, um modelo pode ter desempenho ideal com valores baixos de uma variável, enquanto outro opera melhor com valores mais altos. Esses padrões de especialização, sejam eles planejados intencionalmente ou surgidos de forma natural, podem melhorar substancialmente a precisão da classificação quando corretamente aplicados.
A implementação segue uma abordagem direta, porém eficaz. Ao avaliar uma amostra desconhecida, o sistema coleta as classificações de todos os modelos componentes e seleciona aquele considerado mais confiável para aquela amostra específica. O ensemble avalia a confiabilidade do modelo com base em um método proposto no trabalho intitulado "Combinação de múltiplos classificadores com base em estimativas de precisão local", dos autores Woods, Kegelmeyer e Bowyer. Essa abordagem é composta por diversas etapas bem definidas:
- Cálculo das distâncias euclidianas entre a amostra desconhecida e todas as amostras de treinamento.
- Identificação de uma quantidade predefinida de amostras de treinamento mais próximas para análise comparativa.
- Avaliação do desempenho de cada modelo especificamente sobre essas amostras vizinhas, com foco especial nos casos em que o modelo atribui a mesma classe que foi prevista para a amostra de teste.
- Cálculo do critério de desempenho com base na proporção de classificações corretas entre as amostras para as quais o modelo previu a mesma classe tanto para a amostra de teste quanto para as vizinhas.
Considere um cenário em que são analisadas as dez amostras mais próximas. Após a identificação dessas amostras por meio do cálculo das distâncias euclidianas, o ensemble entrega a amostra de teste a um modelo, que a classifica como pertencente à classe 3. Em seguida, o sistema avalia o desempenho do modelo sobre as dez amostras de treinamento mais próximas. Se o modelo classificar seis dessas amostras como classe 3, e quatro dessas seis classificações forem corretas, o modelo recebe um critério de desempenho igual a 0,67 (4/6). Esse processo de avaliação é repetido para todos os modelos componentes, e o modelo com a maior pontuação final determina a classificação definitiva. Essa abordagem garante que a decisão de classificação utilize o modelo mais confiável para o contexto específico de cada amostra.
Para resolver o problema de "empates", escolhemos o modelo com maior grau de certeza, que é calculado como a razão entre sua maior saída e a soma de todas as saídas. A definição do tamanho desse subconjunto local é essencial, pois quanto menor for o subconjunto, maior será sua sensibilidade às variações locais; quanto maior, mais robusto será, mas a avaliação pode deixar de ser verdadeiramente "local". A validação cruzada pode ajudar a definir o tamanho ideal do subconjunto, sendo que normalmente se dá preferência a tamanhos menores para melhor desempenho em casos de empate. Ao aplicar essa abordagem, o ensemble utiliza com eficiência a especialização dos modelos em áreas específicas, mantendo ao mesmo tempo a eficiência computacional. O método permite que o ensemble se adapte dinamicamente a diferentes regiões do espaço dos preditores, e também é possível implementar um critério de confiabilidade para fornecer uma métrica transparente na escolha dos modelos.
A classe ClocalAcc, localizada no arquivo ensemble.mqh, foi desenvolvida para determinar a classe mais provável com base na precisão local utilizando um ensemble de classificadores.
//+------------------------------------------------------------------+ //| Use local accuracy to choose the best model | //+------------------------------------------------------------------+ class ClocalAcc { private: ulong m_knn; ulong m_nout; long m_indices[]; matrix m_ranks; vector m_output; vector m_targs; matrix m_input; vector m_dist; matrix m_trnx; matrix m_trncls; vector m_trntrue; ulong m_classprep; bool m_crossvalidate; public: ClocalAcc(void); ~ClocalAcc(void); ulong classify(vector &inputs, IClassify* &models[]); bool fit(matrix &inputs, matrix &targets, IClassify* &models[], bool crossvalidate = false); vector proba(void) { return m_output;} };
O método fit() treina o objeto ClocalAcc. Ele recebe os dados de entrada (inputs), os valores-alvo (targets), um array de modelos classificadores (models) e um parâmetro opcional para validação cruzada (crossvalidate). Durante o treinamento, fit() calcula a distância entre cada ponto dos dados de entrada e todos os demais pontos do conjunto de dados. Em seguida, ele identifica os k vizinhos mais próximos para cada ponto, sendo k determinado por validação cruzada se crossvalidate for igual a true. Para cada amostra vizinha, o método avalia o desempenho de cada classificador no ensemble.
//+------------------------------------------------------------------+ //| fit an ensemble model | //+------------------------------------------------------------------+ bool ClocalAcc::fit(matrix &inputs,matrix &targets,IClassify *&models[], bool crossvalidate = false) { m_crossvalidate = crossvalidate; m_nout = targets.Cols(); m_input = matrix::Zeros(inputs.Rows(),models.Size()); m_targs = vector::Zeros(inputs.Rows()); m_output = vector::Zeros(m_nout); m_ranks = matrix::Zeros(models.Size(),m_nout); m_dist = vector::Zeros(inputs.Rows()); m_trnx = matrix::Zeros(inputs.Rows(),inputs.Cols()); m_trncls = matrix::Zeros(inputs.Rows(),models.Size()); m_trntrue = vector::Zeros(inputs.Rows()); double best = 0.0; if(ArrayResize(m_indices,int(inputs.Rows()))<0) { Print(__FUNCTION__, " ", __LINE__, " array resize error ", GetLastError()); return false; } ulong k, knn_min,knn_max,knn_best=0,true_class, ibest=0; for(ulong i = 0; i<inputs.Rows(); i++) { np::matrixCopyRows(m_trnx,inputs,i,i+1,1); vector trow = targets.Row(i); vector inrow = inputs.Row(i); k = trow.ArgMax(); best = trow[k]; m_trntrue[i] = double(k); for(uint j=0; j<models.Size(); j++) { vector classification = models[j].classify(inrow); ibest = classification.ArgMax(); best = classification[ibest]; m_trncls[i][j] = double(ibest); } } m_classprep = 1; if(!m_crossvalidate) { m_knn=3; return true; } else { ulong ncases = inputs.Rows(); if(inputs.Rows()<20) { m_knn=3; return true; } knn_min = 3; knn_max = 10; vector testcase(inputs.Cols()) ; vector clswork(m_nout) ; vector knn_counts(knn_max - knn_min + 1) ; for(ulong i = knn_min; i<=knn_max; i++) knn_counts[i-knn_min] = 0; --ncases; for(ulong i = 0; i<=ncases; i++) { testcase = m_trnx.Row(i); true_class = ulong(m_trntrue[i]); if(i<ncases) { if(!m_trnx.SwapRows(ncases,i)) { Print(__FUNCTION__, " ", __LINE__, " failed row swap ", GetLastError()); return false; } m_trntrue[i] = m_trntrue[ncases]; double temp; for(uint j = 0; j<models.Size(); j++) { temp = m_trncls[i][j]; m_trncls[i][j] = m_trncls[ncases][j]; m_trncls[ncases][j] = temp; } } m_classprep = 1; for(ulong knn = knn_min; knn<knn_max; knn++) { ulong iclass = classify(testcase,models); if(iclass == true_class) { ++knn_counts[knn-knn_min]; } m_classprep=0; } if(i<ncases) { if(!m_trnx.SwapRows(i,ncases) || !m_trnx.Row(testcase,i)) { Print(__FUNCTION__, " ", __LINE__, " error ", GetLastError()); return false; } m_trntrue[ncases] = m_trntrue[i]; m_trntrue[i] = double(true_class); double temp; for(uint j = 0; j<models.Size(); j++) { temp = m_trncls[i][j]; m_trncls[i][j] = m_trncls[ncases][j]; m_trncls[ncases][j] = temp; } } } ++ncases; for(ulong knn = knn_min; knn<=knn_max; knn++) { if((knn==knn_min) || (ulong(knn_counts[knn-knn_min])>ibest)) { ibest = ulong(knn_counts[knn-knn_min]); knn_best = knn; } } m_knn = knn_best; m_classprep = 1; } return true; }
O método classify() prevê o rótulo de classe para um vetor de entrada fornecido. Ele calcula as distâncias entre o vetor de entrada e todos os pontos do conjunto de dados de treinamento e determina os k vizinhos mais próximos. O método então mede a precisão de cada classificador do ensemble com base nessas amostras vizinhas. O classificador com maior precisão em relação aos vizinhos mais próximos é selecionado, e o rótulo de classe previsto por ele é retornado.
//+------------------------------------------------------------------+ //| classify with an ensemble model | //+------------------------------------------------------------------+ ulong ClocalAcc::classify(vector &inputs,IClassify *&models[]) { double dist=0, diff=0, best=0, crit=0, bestcrit=0, conf=0, bestconf=0, sum ; ulong k, ibest, numer, denom, bestmodel=0, bestchoice=0 ; if(m_classprep) { for(ulong i = 0; i<m_input.Rows(); i++) { m_indices[i] = long(i); dist = 0.0; for(ulong j = 0; j<m_trnx.Cols(); j++) { diff = inputs[j] - m_trnx[i][j]; dist+= diff*diff; } m_dist[i] = dist; } if(!m_dist.Size()) { Print(__FUNCTION__," ", __LINE__," empty vector "); return ULONG_MAX; } qsortdsi(0, m_dist.Size()-1, m_dist,m_indices); } for(uint i = 0; i<models.Size(); i++) { vector vec = models[i].classify(inputs); sum = vec.Sum(); ibest = vec.ArgMax(); best = vec[ibest]; conf = best/sum; denom = numer = 0; for(ulong ii = 0; ii<m_knn; ii++) { k = m_indices[ii]; if(ulong(m_trncls[k][i]) == ibest) { ++denom; if(ibest == ulong(m_trntrue[k])) ++numer; } } if(denom > 0) crit = double(numer)/double(denom); else crit = 0.0; if((i == 0) || (crit > bestcrit)) { bestcrit = crit; bestmodel = ulong(i); bestchoice = ibest; bestconf = conf; m_output = vec; } else if(fabs(crit-bestcrit)<1.e-10) { if(conf > bestconf) { bestcrit= crit; bestmodel = ulong(i); bestchoice = ibest; bestconf = conf; m_output = vec; } } } sum = m_output.Sum(); if(sum>0) m_output/=sum; return bestchoice; }
Ensembles combinados por meio do integral fuzzy
A lógica fuzzy é um ramo da matemática que lida com graus de verdade em vez de valores absolutos como "verdadeiro" ou "falso". No contexto da combinação de classificadores, a lógica fuzzy pode ser usada para integrar as saídas de vários modelos levando em consideração a confiabilidade de cada um deles. O integral fuzzy, originalmente proposto por Sugeno (1977), utiliza uma medida fuzzy que atribui valores a subconjuntos de um universo. Essa medida segue certas propriedades, incluindo condições de fronteira, monotonicidade e continuidade. Sugeno complementou esse conceito com a medida fuzzy λ, que inclui um coeficiente adicional para combinar medidas de conjuntos disjuntos.
O próprio integral fuzzy é calculado com base em uma fórmula específica que usa uma função de pertinência e a medida fuzzy. Embora o cálculo possa ser feito por força bruta, existe um método mais eficiente para conjuntos finitos que utiliza um processo recursivo. O valor de λ é determinado de forma que a medida final seja igual a um. No contexto da combinação de classificadores, o integral fuzzy pode ser aplicado tratando cada classificador como um elemento do universo com seus próprios valores de confiabilidade e pertinência. O integral fuzzy é então calculado para cada classe, e a classe com o maior valor do integral é selecionada. Esse método combina de maneira eficaz as saídas de múltiplos classificadores, considerando a confiabilidade individual de cada um.
A classe CFuzzyInt implementa o método do integral fuzzy para combinação de classificadores.
//+------------------------------------------------------------------+ //| Use fuzzy integral to combine decisions | //+------------------------------------------------------------------+ class CFuzzyInt { private: ulong m_nout; vector m_output; long m_indices[]; matrix m_sort; vector m_g; double m_lambda; double recurse(double x); public: CFuzzyInt(void); ~CFuzzyInt(void); bool fit(matrix &predictors, matrix &targets, IClassify* &models[]); ulong classify(vector &inputs, IClassify* &models[]); vector proba(void) { return m_output;} };
A base desse método é a função recurse(), que calcula iterativamente a medida fuzzy. O parâmetro-chave λ é determinado encontrando-se um valor que garanta que a medida fuzzy de todos os modelos converja para a unidade. Começamos com um valor inicial e o ajustamos gradualmente até que a medida fuzzy de todos os modelos atinja exatamente o valor um. Normalmente, esse valor adequado de λ é inicialmente delimitado por um intervalo, e depois é refinado por meio de uma busca mais precisa utilizando o método da bisseção.
//+------------------------------------------------------------------+ //| recurse | //+------------------------------------------------------------------+ double CFuzzyInt::recurse(double x) { double val ; val = m_g[0] ; for(ulong i=1 ; i<m_g.Size() ; i++) val += m_g[i] + x * m_g[i] * val ; return val - 1.0 ; }
Para avaliar a confiabilidade de cada modelo, medimos sua acurácia sobre o conjunto de dados de treinamento. Em seguida, ajustamos essa acurácia subtraindo a taxa de acerto esperada por puro acaso e escalonando o resultado para um valor entre zero e um. Existem métodos mais sofisticados para avaliar a confiabilidade dos modelos, mas este é utilizado por sua simplicidade.
//+------------------------------------------------------------------+ //| fit ensemble model | //+------------------------------------------------------------------+ bool CFuzzyInt::fit(matrix &predictors,matrix &targets,IClassify *&models[]) { m_nout = targets.Cols(); m_output = vector::Zeros(m_nout); m_sort = matrix::Zeros(models.Size(), m_nout); m_g = vector::Zeros(models.Size()); if(ArrayResize(m_indices,int(models.Size()))<0) { Print(__FUNCTION__, " ", __LINE__, " array resize error ", GetLastError()); return false; } ulong k=0, iclass =0 ; double best=0, xlo=0, xhi=0, y=0, ylo=0, yhi=0, step=0 ; for(ulong i = 0; i<predictors.Rows(); i++) { vector trow = targets.Row(i); vector inrow = predictors.Row(i); k = trow.ArgMax(); best = trow[k]; for(uint ii = 0; ii< models.Size(); ii++) { vector vec = models[ii].classify(inrow); iclass = vec.ArgMax(); best = vec[iclass]; if(iclass == k) m_g[ii] += 1.0; } } for(uint i = 0; i<models.Size(); i++) { m_g[i] /= double(predictors.Rows()) ; m_g[i] = (m_g[i] - 1.0 / m_nout) / (1.0 - 1.0 / m_nout) ; if(m_g[i] > 1.0) m_g[i] = 1.0 ; if(m_g[i] < 0.0) m_g[i] = 0.0 ; } xlo = m_lambda = -1.0 ; ylo = recurse(xlo) ; if(ylo >= 0.0) // Theoretically should never exceed zero return true; // But allow for pathological numerical problems step = 1.0 ; for(;;) { xhi = xlo + step ; yhi = recurse(xhi) ; if(yhi >= 0.0) // If we have just bracketed the root break ; // We can quit the search if(xhi > 1.e5) // In the unlikely case of extremely poor models { m_lambda = xhi ; // Fudge a value return true ; // And quit } step *= 2.0 ; // Keep increasing the step size to avoid many tries xlo = xhi ; // Move onward ylo = yhi ; } for(;;) { m_lambda = 0.5 * (xlo + xhi) ; y = recurse(m_lambda) ; // Evaluate the function here if(fabs(y) < 1.e-8) // Primary convergence criterion break ; if(xhi - xlo < 1.e-10 * (m_lambda + 1.1)) // Backup criterion break ; if(y > 0.0) { xhi = m_lambda ; yhi = y ; } else { xlo = m_lambda ; ylo = y ; } } return true; }
Durante o processo de classificação, é selecionada a classe com o maior valor de integral fuzzy. O integral fuzzy para cada classe é calculado iterativamente, comparando a saída do modelo com a medida fuzzy obtida recursivamente e selecionando o menor valor em cada etapa. O valor final do integral fuzzy para uma classe representa a confiabilidade combinada dos modelos para aquela classe.
//+------------------------------------------------------------------+ //| classify with ensemble | //+------------------------------------------------------------------+ ulong CFuzzyInt::classify(vector &inputs,IClassify *&models[]) { ulong k, iclass; double sum, gsum, minval, maxmin, best ; for(uint i = 0; i<models.Size(); i++) { vector vec = models[i].classify(inputs); sum = vec.Sum(); vec/=sum; if(!m_sort.Row(vec,i)) { Print(__FUNCTION__, " ", __LINE__, " row insertion error ", GetLastError()); return false; } } for(ulong i = 0; i<m_nout; i++) { for(uint ii =0; ii<models.Size(); ii++) m_indices[ii] = long(ii); vector vec = m_sort.Col(i); if(!vec.Size()) { Print(__FUNCTION__," ", __LINE__," empty vector "); return ULONG_MAX; } qsortdsi(0,long(vec.Size()-1), vec, m_indices); maxmin = gsum = 0.0; for(int j = int(models.Size()-1); j>=0; j--) { k = m_indices[j]; if(k>=vec.Size()) { Print(__FUNCTION__," ",__LINE__, " out of range ", k); } gsum += m_g[k] + m_lambda * m_g[k] * gsum; if(gsum<vec[k]) minval = gsum; else minval = vec[k]; if(minval > maxmin) maxmin = minval; } m_output[i] = maxmin; } iclass = m_output.ArgMax(); best = m_output[iclass]; return iclass; }
Combinação par-a-par
A combinação par-a-par é uma abordagem única para classificação multiclasse que explora eficientemente as capacidades de classificadores binários especializados. Ela combina um conjunto de K(K−1)/2 classificadores binários (onde K é o número de classes), cada um projetado para distinguir entre uma par de classes específicas. Imagine que temos um conjunto de dados com três classes como objetivo. Para compará-las, criaremos um conjunto de 3*(3−1)/2 = 3 modelos. Cada modelo é projetado para tomar decisões apenas entre duas classes. As classes são rotuladas como A, B e C. Os três modelos terão a seguinte configuração:
- Modelo 1: toma decisões entre a classe A e a classe B.
- Modelo 2: toma decisões entre a classe A e a classe C.
- Modelo 3: toma decisões entre a classe B e a classe C.
Os dados de treinamento devem ser particionados para conter apenas amostras relevantes para as tarefas de classificação atribuídas a cada um dos modelos. As previsões feitas por esses modelos gerarão um conjunto de probabilidades que podem ser organizadas em uma matriz de tamanho K por K. Abaixo é apresentado um exemplo hipotético dessa matriz.
| A | B | C | |
| A | ---- | 0.2 | 0.7 |
| B | 0.8 | ---- | 0.4 |
| C | 0.3 | 0.6 | ---- |
Nesta matriz, o modelo que faz distinção entre as classes A e B atribui a probabilidade de 0,2 para que a amostra pertença à classe A. Os elementos da diagonal que começa no canto superior direito da matriz representam o conjunto completo de probabilidades calculadas para as decisões entre pares de classes, já que a matriz é simétrica. Após obter as saídas dos modelos, o objetivo passa a ser calcular a probabilidade de que uma amostra fora da amostragem pertença a uma determinada classe. Isso significa que é necessário encontrar um conjunto de probabilidades cujo padrão de distribuição coincida ou, pelo menos, se aproxime ao máximo da distribuição observada nas probabilidades dos pares. Para processar essas estimativas iniciais de probabilidade, é utilizado um método iterativo, sem a necessidade de aplicar um procedimento de minimização de função.
Esse processo iterativo refina progressivamente as probabilidades iniciais de pertencimento a cada classe, ajustando-as para que se alinhem melhor com os prognósticos fornecidos pelos classificadores de pares. Na essência, isso se assemelha ao processo de completar um mapa até que ele reflita com precisão a realidade. Começamos com um esboço grosseiro e vamos fazendo pequenos ajustes com base em novas informações, até alcançarmos um mapa preciso. Essa abordagem iterativa é eficiente e normalmente conduz a uma solução rapidamente.
O algoritmo de combinação par-a-par é implementado na classe CPairWise.
//+------------------------------------------------------------------+ //| Use pairwise coupling to combine decisions | //+------------------------------------------------------------------+ class CPairWise { private: ulong m_nout; ulong m_npairs; vector m_output; vector m_rij; vector m_uij; public: CPairWise(void); ~CPairWise(void); ulong classify(ulong numclasses,vector &inputs,IClassify *&models[],ulong &samplesPerModel[]); vector proba(void) { return m_output;} };
Os principais cálculos são realizados no método classify(), que aplica um processo estruturado para estimar as probabilidades de classe com base nas saídas dos classificadores por pares. O método começa avaliando todos os modelos de pares para a amostra de teste fornecida. Cada modelo corresponde a uma combinação específica de duas classes e gera uma saída que representa a probabilidade de que a amostra de teste pertença a uma das duas classes envolvidas.
//+------------------------------------------------------------------+ //| classify using ensemble model | //+------------------------------------------------------------------+ ulong CPairWise::classify(ulong numclasses,vector &inputs,IClassify *&models[],ulong &samplesPerModel[]) { m_nout=numclasses; m_npairs = m_nout*(m_nout-1)/2; m_output = vector::Zeros(m_nout); m_rij = vector::Zeros(m_npairs); m_uij = vector::Zeros(m_npairs); long k; ulong iclass=0 ; double rr, best=0, numer, denom, sum, delta, oldval ; for(ulong i = 0; i<m_npairs; i++) { vector vec = models[i].classify(inputs); rr = vec[0]; if(vec[0]> 0.999999) vec[0] = 0.999999 ; if(vec[0] < 0.000001) vec[0] = 0.000001 ; m_rij[i] = vec[0] ; } k = 0 ; for(ulong i=0 ; i<m_nout-1 ; i++) { for(ulong j=i+1 ; j<m_nout ; j++) { rr = m_rij[k++] ; m_output[i] += rr ; m_output[j] += 1.0 - rr ; } } for(ulong i=0 ; i<m_nout ; i++) m_output[i] /= double(m_npairs) ; k = 0 ; for(ulong i=0 ; i<m_nout-1 ; i++) { for(ulong j=i+1 ; j<m_nout ; j++) m_uij[k++] = m_output[i] / (m_output[i] + m_output[j]) ; } for(int iter=0 ; iter<10000 ; iter++) { delta = 0.0 ; for(ulong i=0 ; i<m_nout ; i++) { numer = denom = 0.0 ; for(ulong j=0 ; j<m_nout ; j++) { if(i < j) { k = (long(i) * (2 * long(m_nout) - long(i) - 3) - 2) / 2 + long(j) ; numer += samplesPerModel[k] * m_rij[k] ; denom += samplesPerModel[k] * m_uij[k] ; } else if(i > j) { k = (long(j) * (2 * long(m_nout) - long(j) - 3) - 2) / 2 + long(i) ; //Print(__FUNCTION__," ",__LINE__," k ", k); numer += samplesPerModel[k] * (1.0 - m_rij[k]) ; denom += samplesPerModel[k] * (1.0 - m_uij[k]) ; } } oldval = m_output[i] ; m_output[i] *= numer / denom ; sum = 0.0 ; for(ulong j=0 ; j<m_nout ; j++) sum += m_output[j] ; for(ulong j=0 ; j<m_nout ; j++) m_output[j] /= sum ; if(fabs(m_output[i]-oldval) > delta) delta = fabs(m_output[i]-oldval) ; k = 0 ; for(ulong i=0 ; i<m_nout-1 ; i++) { for(ulong j=i+1 ; j<m_nout ; j++) m_uij[k++] = m_output[i] / (m_output[i] + m_output[j]) ; } } if(delta < 1.e-6) break ; } return m_output.ArgMax() ; }
Uma vez obtidas as saídas iniciais (as probabilidades), elas são utilizadas como estimativas de partida para a probabilidade de pertencimento a cada classe. Em seguida, o método refina essas estimativas de forma iterativa para aumentar a precisão. A etapa final, após o ajuste das probabilidades, é a identificação da classe com a maior probabilidade. A classe com a probabilidade mais alta é considerada a mais plausível para a amostra de teste em questão, e o método classify() retorna seu índice.
Considerações finais: Comparação dos métodos de combinação
O script ClassificationEnsemble_Demo.mq5 foi desenvolvido para comparar a eficácia dos algoritmos de ensemble discutidos neste artigo em diferentes cenários. Ao executar diversas replicações de Monte Carlo, o script avalia o desempenho de cada um dos métodos ensemble sob variadas condições. Ele permite ao usuário especificar a quantidade de amostras de treinamento a ser utilizada em cada execução, possibilitando testes com conjuntos de dados de diferentes tamanhos, desde pequenos até grandes volumes. Também é possível ajustar o número de classes, o que permite testar a escalabilidade dos métodos ensemble à medida que a complexidade da tarefa aumenta. O número de classificadores base (modelos) utilizados no ensemble também pode ser alterado, permitindo avaliar como os algoritmos se comportam em diferentes níveis de complexidade.
Os usuários podem especificar o número de replicações de Monte Carlo por cenário, com o objetivo de medir a estabilidade e a precisão dos algoritmos ensemble. A métrica utilizada para avaliar a eficácia é a taxa de erro de classificação fora da amostra, o que garante que os modelos sejam testados com dados desconhecidos, simulando condições reais de classificação. Quando quatro ou mais modelos são utilizados, um deles é intencionalmente tornado inútil (por exemplo, gerando previsões aleatórias ou constantes). Isso permite testar a robustez dos algoritmos ensemble e avaliar sua capacidade de lidar com modelos irrelevantes ou não informativos.
Se cinco ou mais modelos forem utilizados, o quinto modelo é configurado para, ocasionalmente, gerar previsões extremas ou caóticas, simulando cenários do mundo real em que uma das modelos pode se comportar de forma instável ou apresentar ruído. Esse recurso permite avaliar como os métodos ensemble lidam com modelos pouco confiáveis, e se conseguem manter a qualidade da classificação ao ajustar corretamente o peso ou reduzir a influência desses modelos problemáticos. O coeficiente de complexidade da classificação determina o spread entre as classes, o qual controla o grau de dificuldade da tarefa para os modelos componentes. Quanto maior esse spread, mais fácil distinguir as classes; quanto menor, mais difícil a tarefa. Esse recurso possibilita testar o desempenho dos métodos ensemble em diferentes níveis de dificuldade, avaliando sua capacidade de manter a precisão mesmo em cenários mais exigentes.
//+------------------------------------------------------------------+ //| ClassificationEnsemble_Demo.mq5 | //| Copyright 2024, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2024, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #property script_show_inputs #include<ensemble.mqh> #include<multilayerperceptron.mqh> //--- input parameters input int NumSamples=10; input int NumClasses=3; input int NumModels=3; input int NumReplications=1000; input double ClassificationDifficultyFactor=0.0; //+------------------------------------------------------------------+ //| normal(rngstate) | //+------------------------------------------------------------------+ double normal(CHighQualityRandStateShell &state) { return CAlglib::HQRndNormal(state); } //+------------------------------------------------------------------+ //| unifrand(rngstate) | //+------------------------------------------------------------------+ double unifrand(CHighQualityRandStateShell &state) { return CAlglib::HQRndUniformR(state); } //+------------------------------------------------------------------+ //|Multilayer perceptron | //+------------------------------------------------------------------+ class CMLPC:public ensemble::IClassify { private: CMlp *m_mlfn; double m_learningrate; double m_tolerance; double m_alfa; double m_beyta; uint m_epochs; ulong m_in,m_out; ulong m_hl1,m_hl2; public: CMLPC(ulong ins, ulong outs,ulong numhl1,ulong numhl2); ~CMLPC(void); void setParams(double alpha_, double beta_,double learning_rate, double tolerance, uint num_epochs); bool train(matrix &predictors,matrix&targets); vector classify(vector &predictors); ulong getNumInputs(void) { return m_in;} ulong getNumOutputs(void) { return m_out;} }; //+------------------------------------------------------------------+ //| constructor | //+------------------------------------------------------------------+ CMLPC::CMLPC(ulong ins, ulong outs,ulong numhl1,ulong numhl2) { m_in = ins; m_out = outs; m_alfa = 0.3; m_beyta = 0.01; m_learningrate=0.001; m_tolerance=1.e-8; m_epochs= 1000; m_hl1 = numhl1; m_hl2 = numhl2; m_mlfn = new CMlp(); } //+------------------------------------------------------------------+ //| destructor | //+------------------------------------------------------------------+ CMLPC::~CMLPC(void) { if(CheckPointer(m_mlfn) == POINTER_DYNAMIC) delete m_mlfn; } //+------------------------------------------------------------------+ //| set other hyperparameters of the i_model | //+------------------------------------------------------------------+ void CMLPC::setParams(double alpha_, double beta_,double learning_rate, double tolerance, uint num_epochs) { m_alfa = alpha_; m_beyta = beta_; m_learningrate=learning_rate; m_tolerance=tolerance; m_epochs= num_epochs; } //+------------------------------------------------------------------+ //| fit a i_model to the data | //+------------------------------------------------------------------+ bool CMLPC::train(matrix &predictors,matrix &targets) { if(m_in != predictors.Cols() || m_out != targets.Cols()) { Print(__FUNCTION__, " failed training due to invalid training data"); return false; } return m_mlfn.fit(predictors,targets,m_alfa,m_beyta,m_hl1,m_hl2,m_epochs,m_learningrate,m_tolerance); } //+------------------------------------------------------------------+ //| make a prediction with the trained i_model | //+------------------------------------------------------------------+ vector CMLPC::classify(vector &predictors) { return m_mlfn.predict(predictors); } //+------------------------------------------------------------------+ //| clean up dynamic array pointers | //+------------------------------------------------------------------+ void cleanup(ensemble::IClassify* &array[]) { for(uint i = 0; i<array.Size(); i++) if(CheckPointer(array[i])==POINTER_DYNAMIC) delete array[i]; } //+------------------------------------------------------------------+ //| global variables | //+------------------------------------------------------------------+ int nreplications, nsamps,nmodels, divisor, nreps_done ; int n_classes, nnn, n_pairs, nh_g ; ulong ntrain_pair[]; matrix xdata, xbad_data, xtainted_data, test[],x_targ,xbad_targ,xwild_targ; vector inputdata; double cd_factor, err_score, err_score_1, err_score_2, err_score_3 ; vector classification_err_raw, output_vector; double classification_err_average ; double classification_err_median ; double classification_err_maxmax ; double classification_err_maxmin ; double classification_err_intersection_1 ; double classification_err_intersection_2 ; double classification_err_intersection_3 ; double classification_err_union_1 ; double classification_err_union_2 ; double classification_err_union_3 ; double classification_err_majority ; double classification_err_borda ; double classification_err_logit ; double classification_err_logitsep ; double classification_err_localacc ; double classification_err_fuzzyint ; double classification_err_pairwise ; //+------------------------------------------------------------------+ //| ensemble i_model objects | //+------------------------------------------------------------------+ ensemble::CAvgClass average_ensemble ; ensemble::CMedian median_ensemble ; ensemble::CMaxMax maxmax_ensemble ; ensemble::CMaxMin maxmin_ensemble ; ensemble::CIntersection intersection_ensemble ; ensemble::CUnion union_rule ; ensemble::CMajority majority_ensemble ; ensemble::CBorda borda_ensemble ; ensemble::ClogitReg logit_ensemble ; ensemble::ClogitRegSep logitsep_ensemble ; ensemble::ClocalAcc localacc_ensemble ; ensemble::CFuzzyInt fuzzyint_ensemble ; ensemble::CPairWise pairwise_ensemble ; int n_hid = 4 ; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { CHighQualityRandStateShell rngstate; CHighQualityRand::HQRndRandomize(rngstate.GetInnerObj()); //--- nsamps = NumSamples ; n_classes = NumClasses ; nmodels = NumModels ; nreplications = NumReplications ; cd_factor = ClassificationDifficultyFactor ; if((nsamps <= 3) || (n_classes <= 1) || (nmodels <= 0) || (nreplications <= 0) || (cd_factor < 0.0)) { Alert(" Invalid inputs "); return; } divisor = 1 ; ensemble::IClassify* models[]; ensemble::IClassify* model_pairs[]; /* Allocate memory and initialize */ n_pairs = n_classes * (n_classes-1) / 2 ; if(ArrayResize(models,nmodels)<0 || ArrayResize(model_pairs,n_pairs)<0 || ArrayResize(test,10)<0 || ArrayResize(ntrain_pair,n_pairs)<0) { Print(" Array resize errors ", GetLastError()); cleanup(models); cleanup(model_pairs); return; } ArrayInitialize(ntrain_pair,0); for(int i=0 ; i<nmodels ; i++) models[i] = new CMLPC(2,ulong(n_classes),4,0) ; xdata = matrix::Zeros(nsamps,(2+n_classes)); xbad_data = matrix::Zeros(nsamps,(2+n_classes)); xtainted_data = matrix::Zeros(nsamps,(2+n_classes)); inputdata = vector::Zeros(3); for(uint i = 0; i<test.Size(); i++) test[i] = matrix::Zeros(nsamps,(2+n_classes)); classification_err_raw = vector::Zeros(nmodels); classification_err_average = 0.0 ; classification_err_median = 0.0 ; classification_err_maxmax = 0.0 ; classification_err_maxmin = 0.0 ; classification_err_intersection_1 = 0.0 ; classification_err_intersection_2 = 0.0 ; classification_err_intersection_3 = 0.0 ; classification_err_union_1 = 0.0 ; classification_err_union_2 = 0.0 ; classification_err_union_3 = 0.0 ; classification_err_majority = 0.0 ; classification_err_borda = 0.0 ; classification_err_logit = 0.0 ; classification_err_logitsep = 0.0 ; classification_err_localacc = 0.0 ; classification_err_fuzzyint = 0.0 ; classification_err_pairwise = 0.0 ; for(int i_rep=0 ; i_rep<nreplications ; i_rep++) { nreps_done = i_rep + 1 ; if(i_rep>0) xdata.Fill(0.0); //--- for(int i=0, z=0; i<nsamps ; i++) { xdata[i][0] = normal(rngstate) ; xdata[i][1] = normal(rngstate) ; if(i < n_classes) z = i ; else z = (int)(unifrand(rngstate) * n_classes) ; if(z >= n_classes) z = n_classes - 1 ; xdata[i][2+z] = 1.0 ; xdata[i][0] += double(z) * cd_factor ; xdata[i][1] -= double(z) * cd_factor ; } if(nmodels >= 4) { xbad_data = xdata; matrix arm = np::sliceMatrixCols(xbad_data,2); for(int i = 0; i<nsamps; i++) for(int z = 0; z<n_classes; z++) arm[i][z] = (unifrand(rngstate)<(1.0/double(n_classes)))?1.0:0.0; np::matrixCopy(xbad_data,arm,0,xbad_data.Rows(),1,2); } if(nmodels >= 5) { xtainted_data = xdata; matrix arm = np::sliceMatrixCols(xtainted_data,2); for(int i = 0; i<nsamps; i++) for(int z = 0; z<n_classes; z++) if(unifrand(rngstate)<0.1) arm[i][z] = xdata[i][2+z] * 1000.0 - 500.0 ; np::matrixCopy(xtainted_data,arm,0,xtainted_data.Rows(),1,2); } for(int i=0 ; i<10 ; i++) // Build a test dataset { if(i_rep>0) test[i].Fill(0.0); for(int j=0,z=0; j<nsamps; j++) { test[i][j][0] = normal(rngstate) ; test[i][j][1] = normal(rngstate) ; z = (int)(unifrand(rngstate) * n_classes) ; if(z >= n_classes) z = n_classes - 1 ; test[i][j][2+z] = 1.0 ; test[i][j][0] += double(z) * cd_factor ; test[i][j][1] -= double(z) * cd_factor ; } } for(int i_model=0 ; i_model<nmodels ; i_model++) { matrix preds,targs; if(i_model == 3) { targs = np::sliceMatrixCols(xbad_data,2); preds = np::sliceMatrixCols(xbad_data,0,2); } else if(i_model == 4) { targs = np::sliceMatrixCols(xtainted_data,2); preds = np::sliceMatrixCols(xtainted_data,0,2); } else { targs = np::sliceMatrixCols(xdata,2); preds = np::sliceMatrixCols(xdata,0,2); } if(!models[i_model].train(preds,targs)) { Print(" failed to train i_model at shift ", i_model); cleanup(model_pairs); cleanup(models); return; } err_score = 0.0 ; for(int i=0 ; i<10 ; i++) { vector testvec,testin,testtarg; for(int j=0; j<nsamps; j++) { testvec = test[i].Row(j); testtarg = np::sliceVector(testvec,2); testin = np::sliceVector(testvec,0,2); output_vector = models[i_model].classify(testin) ; if(output_vector.ArgMax() != testtarg.ArgMax()) err_score += 1.0 ; } } classification_err_raw[i_model] += err_score / (10 * nsamps) ; } int i_model = 0; for(int i=0 ; i<n_classes-1 ; i++) { for(int j=i+1 ; j<n_classes ; j++) { ntrain_pair[i_model] = 0 ; for(int z=0 ; z<nsamps ; z++) { if((xdata[z][2+i]> 0.5) || (xdata[z][2+j] > 0.5)) ++ntrain_pair[i_model] ; } nh_g = (n_hid < int(ntrain_pair[i_model]) - 1) ? n_hid : int(ntrain_pair[i_model]) - 1; model_pairs[i_model] = new CMLPC(2, 1, ulong(nh_g+1),0) ; matrix training; matrix preds,targs; ulong msize=0; for(int z=0 ; z<nsamps ; z++) { inputdata[0] = xdata[z][0] ; inputdata[1] = xdata[z][1] ; if(xdata[z][2+i]> 0.5) inputdata[2] = 1.0 ; else if(xdata[z][2+j] > 0.5) inputdata[2] = 0.0 ; else continue ; training.Resize(msize+1,inputdata.Size()); training.Row(inputdata,msize++); } preds = np::sliceMatrixCols(training,0,2); targs = np::sliceMatrixCols(training,2); model_pairs[i_model].train(preds,targs); ++i_model ; } } err_score = 0.0 ; for(int i=0 ; i<10 ; i++) { for(int z=0;z<nsamps;z++) { vector row = test[i].Row(z); vector rowtest = np::sliceVector(row,0,2); vector rowtarg = np::sliceVector(row,2); if(average_ensemble.classify(rowtest,models) != rowtarg.ArgMax()) err_score += 1.0 ; } } classification_err_average += err_score / (10 * nsamps) ; /* median_ensemble */ err_score = 0.0 ; for(int i=0 ; i<10 ; i++) { for(int z=0;z<nsamps;z++) { vector row = test[i].Row(z); vector rowtest = np::sliceVector(row,0,2); vector rowtarg = np::sliceVector(row,2); if(median_ensemble.classify(rowtest,models) != rowtarg.ArgMax()) err_score += 1.0 ; } } classification_err_median += err_score / (10 * nsamps) ; /* maxmax_ensemble */ err_score = 0.0 ; for(int i=0 ; i<10 ; i++) { for(int z=0;z<nsamps;z++) { vector row = test[i].Row(z); vector rowtest = np::sliceVector(row,0,2); vector rowtarg = np::sliceVector(row,2); if(maxmax_ensemble.classify(rowtest,models) != rowtarg.ArgMax()) err_score += 1.0 ; } } classification_err_maxmax += err_score / (10 * nsamps) ; err_score = 0.0 ; for(int i=0 ; i<10 ; i++) { for(int z=0;z<nsamps;z++) { vector row = test[i].Row(z); vector rowtest = np::sliceVector(row,0,2); vector rowtarg = np::sliceVector(row,2); if(maxmin_ensemble.classify(rowtest,models) != rowtarg.ArgMax()) // If predicted class not true class err_score += 1.0 ; // Count this misclassification } } classification_err_maxmin += err_score / (10 * nsamps) ; matrix preds,targs; err_score_1 = err_score_2 = err_score_3 = 0.0 ; preds = np::sliceMatrixCols(xdata,0,2); targs = np::sliceMatrixCols(xdata,2); intersection_ensemble.fit(preds,targs,models); for(int i=0 ; i<10 ; i++) { for(int z=0;z<nsamps;z++) { vector row = test[i].Row(z); vector rowtest = np::sliceVector(row,0,2); vector rowtarg = np::sliceVector(row,2); ulong class_ = intersection_ensemble.classify(rowtest,models) ; output_vector = intersection_ensemble.proba(); if(output_vector[rowtarg.ArgMax()] < 0.5) { err_score_1 += 1.0 ; err_score_2 += 1.0 ; err_score_3 += 1.0 ; } else { if(class_ > 3) err_score_3 += 1.0 ; if(class_ > 2) err_score_2 += 1.0 ; if(class_ > 1) err_score_1 += 1.0 ; } } } classification_err_intersection_1 += err_score_1 / (10 * nsamps) ; classification_err_intersection_2 += err_score_2 / (10 * nsamps) ; classification_err_intersection_3 += err_score_3 / (10 * nsamps) ; union_rule.fit(preds,targs,models); err_score_1 = err_score_2 = err_score_3 = 0.0 ; for(int i=0 ; i<10 ; i++) { for(int z=0;z<nsamps;z++) { vector row = test[i].Row(z); vector rowtest = np::sliceVector(row,0,2); vector rowtarg = np::sliceVector(row,2); ulong clss = union_rule.classify(rowtest,models) ; output_vector = union_rule.proba(); if(output_vector[rowtarg.ArgMax()] < 0.5) { err_score_1 += 1.0 ; err_score_2 += 1.0 ; err_score_3 += 1.0 ; } else { if(clss > 3) err_score_3 += 1.0 ; if(clss > 2) err_score_2 += 1.0 ; if(clss > 1) err_score_1 += 1.0 ; } } } classification_err_union_1 += err_score_1 / (10 * nsamps) ; classification_err_union_2 += err_score_2 / (10 * nsamps) ; classification_err_union_3 += err_score_3 / (10 * nsamps) ; err_score = 0.0 ; for(int i=0 ; i<10 ; i++) { for(int z=0;z<nsamps;z++) { vector row = test[i].Row(z); vector rowtest = np::sliceVector(row,0,2); vector rowtarg = np::sliceVector(row,2); if(majority_ensemble.classify(rowtest,models) != rowtarg.ArgMax()) err_score += 1.0 ; } } classification_err_majority += err_score / (10 * nsamps) ; err_score = 0.0 ; for(int i=0 ; i<10 ; i++) { for(int z=0;z<nsamps;z++) { vector row = test[i].Row(z); vector rowtest = np::sliceVector(row,0,2); vector rowtarg = np::sliceVector(row,2); if(borda_ensemble.classify(rowtest,models) != rowtarg.ArgMax()) err_score += 1.0 ; } } classification_err_borda += err_score / (10 * nsamps) ; err_score = 0.0 ; logit_ensemble.fit(preds,targs,models); for(int i=0 ; i<10 ; i++) { for(int z=0;z<nsamps;z++) { vector row = test[i].Row(z); vector rowtest = np::sliceVector(row,0,2); vector rowtarg = np::sliceVector(row,2); if(logit_ensemble.classify(rowtest,models) != rowtarg.ArgMax()) err_score += 1.0 ; } } classification_err_logit += err_score / (10 * nsamps) ; err_score = 0.0 ; logitsep_ensemble.fit(preds,targs,models); for(int i=0 ; i<10 ; i++) { for(int z=0;z<nsamps;z++) { vector row = test[i].Row(z); vector rowtest = np::sliceVector(row,0,2); vector rowtarg = np::sliceVector(row,2); if(logitsep_ensemble.classify(rowtest,models) != rowtarg.ArgMax()) err_score += 1.0 ; } } classification_err_logitsep += err_score / (10 * nsamps) ; err_score = 0.0 ; localacc_ensemble.fit(preds,targs,models); for(int i=0 ; i<10 ; i++) { for(int z=0;z<nsamps;z++) { vector row = test[i].Row(z); vector rowtest = np::sliceVector(row,0,2); vector rowtarg = np::sliceVector(row,2); if(localacc_ensemble.classify(rowtest,models) != rowtarg.ArgMax()) err_score += 1.0 ; } } classification_err_localacc += err_score / (10 * nsamps) ; err_score = 0.0 ; fuzzyint_ensemble.fit(preds,targs,models); for(int i=0 ; i<10 ; i++) { for(int z=0;z<nsamps;z++) { vector row = test[i].Row(z); vector rowtest = np::sliceVector(row,0,2); vector rowtarg = np::sliceVector(row,2); if(fuzzyint_ensemble.classify(rowtest,models) != rowtarg.ArgMax()) err_score += 1.0 ; } } classification_err_fuzzyint += err_score / (10 * nsamps) ; err_score = 0.0 ; for(int i=0 ; i<10 ; i++) { for(int z=0;z<nsamps;z++) { vector row = test[i].Row(z); vector rowtest = np::sliceVector(row,0,2); vector rowtarg = np::sliceVector(row,2); if(pairwise_ensemble.classify(ulong(n_classes),rowtest,model_pairs,ntrain_pair) != rowtarg.ArgMax()) err_score += 1.0 ; } } classification_err_pairwise += err_score / (10 * nsamps) ; cleanup(model_pairs); } err_score = 0.0 ; PrintFormat("Test Config: Classification Difficulty - %8.8lf\nNumber of classes - %5d\nNumber of component models - %5d\n Sample Size - %5d", ClassificationDifficultyFactor,NumClasses,NumModels,NumSamples); PrintFormat("%5d Replications:", nreps_done) ; for(int i_model=0 ; i_model<nmodels ; i_model++) { PrintFormat(" %.8lf", classification_err_raw[i_model] / nreps_done) ; err_score += classification_err_raw[i_model] / nreps_done ; } PrintFormat(" Mean raw error = %8.8lf", err_score / nmodels) ; PrintFormat(" average_ensemble error = %8.8lf", classification_err_average / nreps_done) ; PrintFormat(" median_ensemble error = %8.8lf", classification_err_median / nreps_done) ; PrintFormat(" maxmax_ensemble error = %8.8lf", classification_err_maxmax / nreps_done) ; PrintFormat(" maxmin_ensemble error = %8.8lf", classification_err_maxmin / nreps_done) ; PrintFormat(" majority_ensemble error = %8.8lf", classification_err_majority / nreps_done) ; PrintFormat(" borda_ensemble error = %8.8lf", classification_err_borda / nreps_done) ; PrintFormat(" logit_ensemble error = %8.8lf", classification_err_logit / nreps_done) ; PrintFormat(" logitsep_ensemble error = %8.8lf", classification_err_logitsep / nreps_done) ; PrintFormat(" localacc_ensemble error = %8.8lf", classification_err_localacc / nreps_done) ; PrintFormat(" fuzzyint_ensemble error = %8.8lf", classification_err_fuzzyint / nreps_done) ; PrintFormat(" pairwise_ensemble error = %8.8lf", classification_err_pairwise / nreps_done) ; PrintFormat(" intersection_ensemble error 1 = %8.8lf", classification_err_intersection_1 / nreps_done) ; PrintFormat(" intersection_ensemble error 2 = %8.8lf", classification_err_intersection_2 / nreps_done) ; PrintFormat(" intersection_ensemble error 3 = %8.8lf", classification_err_intersection_3 / nreps_done) ; PrintFormat(" Union error 1 = %8.8lf", classification_err_union_1 / nreps_done) ; PrintFormat(" Union error 2 = %8.8lf", classification_err_union_2 / nreps_done) ; PrintFormat(" Union error 3 = %8.8lf", classification_err_union_3 / nreps_done) ; cleanup(models); } //+------------------------------------------------------------------+
Abaixo são apresentados exemplos de resultados obtidos após a execução do script. Esses resultados foram gerados para uma tarefa de classificação com complexidade máxima definida.
ClassificationDifficultyFactor=0.0 DM 0 05:40:06.441 ClassificationEnsemble_Demo (BTCUSD,D1) Test Config: Classification Difficulty - 0.00000000 RP 0 05:40:06.441 ClassificationEnsemble_Demo (BTCUSD,D1) Number of classes - 3 QI 0 05:40:06.441 ClassificationEnsemble_Demo (BTCUSD,D1) Number of component models - 3 EK 0 05:40:06.441 ClassificationEnsemble_Demo (BTCUSD,D1) Sample Size - 10 MN 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) 1000 Replications: CF 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) 0.66554000 HI 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) 0.66706000 DP 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) 0.66849000 II 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) Mean raw error = 0.66703000 JS 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) average_ensemble error = 0.66612000 HR 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) median_ensemble error = 0.66837000 QF 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) maxmax_ensemble error = 0.66704000 MD 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) maxmin_ensemble error = 0.66586000 GI 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) majority_ensemble error = 0.66772000 HR 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) borda_ensemble error = 0.66747000 MO 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) logit_ensemble error = 0.66556000 MP 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) logitsep_ensemble error = 0.66570000 JD 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) localacc_ensemble error = 0.66578000 OJ 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) fuzzyint_ensemble error = 0.66503000 KO 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) pairwise_ensemble error = 0.66799000 GS 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) intersection_ensemble error 1 = 0.96686000 DP 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) intersection_ensemble error 2 = 0.95847000 QE 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) intersection_ensemble error 3 = 0.95447000 OI 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) Union error 1 = 0.99852000 DM 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) Union error 2 = 0.97931000 JR 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) Union error 3 = 0.01186000
Em seguida, são apresentados os resultados de um teste realizado com complexidade de classificação intermediária.
LF 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) Test Config: Classification Difficulty - 1.00000000 IG 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) Number of classes - 3 JP 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) Number of component models - 3 FQ 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) Sample Size - 10 KH 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) 1000 Replications: NO 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) 0.46236000 QF 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) 0.45818000 II 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) 0.45779000 FR 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) Mean raw error = 0.45944333 DI 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) average_ensemble error = 0.44881000 PH 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) median_ensemble error = 0.45564000 JO 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) maxmax_ensemble error = 0.46763000 GS 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) maxmin_ensemble error = 0.44935000 GP 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) majority_ensemble error = 0.45573000 PI 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) borda_ensemble error = 0.45593000 DF 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) logit_ensemble error = 0.46353000 FO 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) logitsep_ensemble error = 0.46726000 ER 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) localacc_ensemble error = 0.46096000 KP 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) fuzzyint_ensemble error = 0.45098000 OD 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) pairwise_ensemble error = 0.66485000 IJ 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) intersection_ensemble error 1 = 0.93533000 RO 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) intersection_ensemble error 2 = 0.92527000 OL 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) intersection_ensemble error 3 = 0.92527000 OR 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) Union error 1 = 0.99674000 KG 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) Union error 2 = 0.97231000 NK 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) Union error 3 = 0.00877000
O último conjunto demonstra os resultados de um teste realizado em condições de complexidade relativamente baixa.
PL 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) Test Config: Classification Difficulty - 10.00000000 CN 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) Number of classes - 3 PK 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) Number of component models - 3 LH 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) Sample Size - 10 EQ 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) 1000 Replications: MD 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) 0.02905000 LO 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) 0.02861000 CF 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) 0.02879000 IK 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) Mean raw error = 0.02881667 RN 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) average_ensemble error = 0.02263000 PQ 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) median_ensemble error = 0.02956000 QD 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) maxmax_ensemble error = 0.03426000 KJ 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) maxmin_ensemble error = 0.02263000 IO 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) majority_ensemble error = 0.02956000 HP 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) borda_ensemble error = 0.02956000 KM 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) logit_ensemble error = 0.03171000 OE 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) logitsep_ensemble error = 0.04840000 GK 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) localacc_ensemble error = 0.03398000 FO 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) fuzzyint_ensemble error = 0.02263000 QM 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) pairwise_ensemble error = 0.65277000 CQ 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) intersection_ensemble error 1 = 0.96303000 DF 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) intersection_ensemble error 2 = 0.96167000 IK 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) intersection_ensemble error 3 = 0.96167000 IK 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) Union error 1 = 0.98620000 CP 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) Union error 2 = 0.95624000 LD 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) Union error 3 = 0.00000000
Todo o código utilizado neste artigo está anexado a ele. A tabela abaixo apresenta a descrição de todos os arquivos-fonte.
| Nome do arquivo | Descrição do arquivo |
|---|---|
| MQL5/include/np.mqh | Conjunto de funções utilitárias para operações com vetores e matrizes |
| MQL5/include/nom2ord.mqh | Este arquivo contém classes para codificação de dados categóricos |
| MQL5/include/multilayerperceptron.mqh | Contém a definição da classe CMlp, que representa uma rede neural de propagação direta |
| MQL5/include/logistic.mqh | Contém a definição da classe Clogit, que implementa a regressão logística |
| MQL5/include/ensemble.mqh | Contém definições de várias implementações de metamodelos |
| MQL5/scripts/ClassificationEnsemble_Demo.mq5 | Este script compara a eficácia dos classificadores ensemble definidos no arquivo ensemble.mqh |
| MQL5/scripts/PairWise_Ensemble_Demo.mq5 | Script de demonstração mostrando como aplicar a classe CPairWise para combinação par-a-par |
Traduzido do Inglês pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/en/articles/16838
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 Dominando registros de log (Parte 2): Formatação dos logs
Dominando registros de log (Parte 2): Formatação dos logs
 Construa EAs auto-otimizáveis em MQL5 (Parte 3): Acompanhamento dinâmico de tendência e retorno à média
Construa EAs auto-otimizáveis em MQL5 (Parte 3): Acompanhamento dinâmico de tendência e retorno à média
 Recursos do Assistente MQL5 que você precisa conhecer (Parte 52): Oscilador Accelerator
Recursos do Assistente MQL5 que você precisa conhecer (Parte 52): Oscilador Accelerator
 Simplificando a negociação com base em notícias (Parte 6): Executando trades (III)
Simplificando a negociação com base em notícias (Parte 6): Executando trades (III)
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso