Modelos ocultos de Markov para previsão de volatilidade com consideração de tendência

Introdução

Os modelos ocultos de Markov(HMM) são uma poderosa ferramenta estatística que permite identificar estados ocultos do mercado com base na análise de movimentos observáveis dos preços. No trading, os HMM permitem melhorar a previsão da volatilidade e são aplicados no desenvolvimento de estratégias de tendência, modelando as mudanças nos regimes de mercado.

Neste artigo, apresentaremos um processo passo a passo para o desenvolvimento de uma estratégia de seguimento de tendência que utiliza HMM como filtro para previsão de volatilidade. O processo inclui o desenvolvimento de uma estratégia básica em MQL5 utilizando o MetaTrader 5, a obtenção dos dados e o treinamento do HMM em Python, além da integração dos modelos de volta ao MetaTrader 5, onde testaremos a estratégia com dados históricos.

Motivação

No livro "Análise Técnica Baseada em Evidências" Dave Aronson propõe que os traders desenvolvam suas estratégias utilizando métodos científicos. Esse processo começa com a formulação de uma hipótese baseada na intuição subjacente à ideia, seguida de testes rigorosos para evitar viés de sobreajuste aos dados. Neste artigo, adotaremos uma abordagem semelhante. Primeiro, vamos entender o que é um modelo oculto de Markov e por que ele pode ser útil no desenvolvimento da nossa estratégia.

Um modelo oculto de Markov (HMM) é um modelo de aprendizado de máquina não supervisionado que representa sistemas em que o estado subjacente está oculto, mas pode ser inferido com base em eventos ou dados observáveis. Ele se baseia na suposição de Markov, segundo a qual o estado futuro do sistema depende apenas de seu estado atual, e não de estados passados. No HMM, o sistema é modelado como um conjunto de estados discretos, sendo que cada estado tem uma determinada probabilidade de transição para outro. Essas transições são descritas por um conjunto de probabilidades conhecidas como probabilidades de transição. Os dados observáveis (como preços de ativos ou retornos de mercado) são gerados pelo sistema, mas os próprios estados não podem ser observados diretamente, daí o termo "oculto".

Aqui estão seus componentes:

1. Os estados são condições ou regimes não observáveis do sistema. Nos mercados financeiros, esses estados podem representar diferentes condições de mercado, como um mercado de alta, um mercado de baixa ou períodos de alta e baixa volatilidade. Esses estados evoluem com base em determinadas regras probabilísticas.

2. As probabilidades de transição determinam a chance de mudança de um estado para outro. O estado do sistema no momento t depende apenas do estado no momento t-1, o que corresponde à propriedade de Markov. Para quantificar essas probabilidades, utilizam-se matrizes de transição.

3. As probabilidades de observação descrevem a chance de observar um determinado fragmento de dados (por exemplo, o preço de uma ação ou o retorno) considerando o estado subjacente. Cada estado possui uma distribuição de probabilidade que define a chance de observar certas condições de mercado ou movimentos de preço naquele estado.

4. As probabilidades iniciais representam a chance de o sistema começar em um determinado estado, fornecendo o ponto de partida para a análise do modelo.

Considerando esses componentes, o modelo utiliza inferência bayesiana para determinar a sequência mais provável de estados ocultos ao longo do tempo com base nos dados observáveis. Isso geralmente é feito com algoritmos como o algoritmo Forward-Backward ou o algoritmo de Viterbi, que estimam a probabilidade dos dados observados levando em conta a sequência de estados ocultos.

No trading, a volatilidade é um fator essencial que influencia os preços dos ativos e a dinâmica do mercado. Os HMM podem ser particularmente eficazes na previsão da volatilidade, pois identificam regimes de mercado subjacentes que não são diretamente observáveis, mas exercem forte influência sobre o comportamento do mercado.

1. Identificação de regimes de mercado. Ao dividir as condições de mercado em estados separados (como alta volatilidade ou baixa volatilidade), os HMM podem capturar mudanças nos regimes de mercado. Isso permite que os traders compreendam quando o mercado provavelmente passará por períodos de alta volatilidade ou por condições estáveis, o que pode se refletir diretamente nos preços dos ativos.

2. Agrupamento de volatilidade. Os mercados financeiros exibem o fenômeno de agrupamento de volatilidade, em que períodos de alta volatilidade tendem a ser seguidos por novos períodos de alta volatilidade, enquanto períodos de baixa volatilidade costumam ser seguidos por baixa volatilidade. Os HMM podem modelar essa característica atribuindo altas probabilidades de permanência nos estados de alta ou baixa volatilidade por longos períodos, oferecendo previsões mais precisas dos movimentos futuros do mercado.

3. Previsão de volatilidade. Ao observar as transições entre diferentes estados de mercado, os HMM podem fornecer dados preditivos sobre a volatilidade futura. Por exemplo, se o modelo identificar que o mercado se encontra em um estado de alta volatilidade, os traders podem esperar flutuações de preços mais expressivas e ajustar suas estratégias de forma correspondente. Além disso, se o mercado entrar em um estado de baixa volatilidade, o modelo pode ajudar os traders a ajustar seu nível de risco ou adaptar suas estratégias de negociação.

4. Adaptabilidade. Os HMM atualizam continuamente suas distribuições de probabilidade e transições entre estados com base em novos dados, o que lhes permite adaptar-se às mudanças nas condições do mercado. Essa capacidade de adaptação em tempo real oferece aos traders uma vantagem na previsão de alterações de volatilidade e na correção dinâmica de suas estratégias.

De acordo com estudos de diversos pesquisadores, partimos da hipótese de que, em condições de alta volatilidade, nossa estratégia de seguimento de tendência tende a funcionar melhor, já que movimentos de mercado mais expressivos levam à formação de tendências. Planejamos usar modelos ocultos de Markov (HMM) para agrupar a volatilidade e identificar estados de alta e baixa volatilidade. Em seguida, treinaremos o modelo para prever se o próximo estado de volatilidade será alto ou baixo. Se o sinal da estratégia ocorrer em um momento em que o modelo prevê um estado de alta volatilidade, entraremos na operação; caso contrário, permaneceremos fora do mercado.

Estratégia principal

A estratégia de seguimento de tendência que usaremos é a mesma que implementei em meu artigo anterior sobre aprendizado de máquina. A lógica principal envolve duas médias móveis: uma rápida e outra lenta. O sinal de entrada é gerado quando as duas médias móveis se cruzam, e a direção da negociação segue a média móvel rápida, daí o termo "seguimento de tendência". O sinal de saída ocorre quando o preço cruza a média móvel lenta, o que proporciona mais espaço para trailing stops. O código completo é o seguinte:

#include <Trade/Trade.mqh>
//XAU - 1h.
CTrade trade;

input ENUM_TIMEFRAMES TF = PERIOD_CURRENT;
input ENUM_MA_METHOD MaMethod = MODE_SMA;
input ENUM_APPLIED_PRICE MaAppPrice = PRICE_CLOSE;
input int MaPeriodsFast = 15;
input int MaPeriodsSlow = 25;
input int MaPeriods = 200;
input double lott = 0.01;
ulong buypos = 0, sellpos = 0;
input int Magic = 0;
int barsTotal = 0;
int handleMaFast;
int handleMaSlow;
int handleMa;

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
   trade.SetExpertMagicNumber(Magic);
   handleMaFast =iMA(_Symbol,TF,MaPeriodsFast,0,MaMethod,MaAppPrice);
   handleMaSlow =iMA(_Symbol,TF,MaPeriodsSlow,0,MaMethod,MaAppPrice);  
   handleMa = iMA(_Symbol,TF,MaPeriods,0,MaMethod,MaAppPrice); 
   return(INIT_SUCCEEDED);
  }

//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {

  }  

//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
  int bars = iBars(_Symbol,PERIOD_CURRENT);
  //Beware, the last element of the buffer list is the most recent data, not [0]
  if (barsTotal!= bars){
     barsTotal = bars;
     double maFast[];
     double maSlow[];
     double ma[];
     CopyBuffer(handleMaFast,BASE_LINE,1,2,maFast);
     CopyBuffer(handleMaSlow,BASE_LINE,1,2,maSlow);
     CopyBuffer(handleMa,0,1,1,ma);
     double bid = SymbolInfoDouble(_Symbol, SYMBOL_BID);
     double ask = SymbolInfoDouble(_Symbol, SYMBOL_ASK);
     double lastClose = iClose(_Symbol, PERIOD_CURRENT, 1);
     //The order below matters
     if(buypos>0&& lastClose<maSlow[1]) trade.PositionClose(buypos);
     if(sellpos>0 &&lastClose>maSlow[1])trade.PositionClose(sellpos);   
     if (maFast[1]>maSlow[1]&&maFast[0]<maSlow[0]&&buypos ==sellpos)executeBuy(); 
     if(maFast[1]<maSlow[1]&&maFast[0]>maSlow[0]&&sellpos ==buypos) executeSell();
     if(buypos>0&&(!PositionSelectByTicket(buypos)|| PositionGetInteger(POSITION_MAGIC) != Magic)){
      buypos = 0;
      }
     if(sellpos>0&&(!PositionSelectByTicket(sellpos)|| PositionGetInteger(POSITION_MAGIC) != Magic)){
      sellpos = 0;
      }
    }
 }

//+------------------------------------------------------------------+
//| Expert trade transaction handling function                       |
//+------------------------------------------------------------------+
void OnTradeTransaction(const MqlTradeTransaction& trans, const MqlTradeRequest& request, const MqlTradeResult& result) {
    if (trans.type == TRADE_TRANSACTION_ORDER_ADD) {
        COrderInfo order;
        if (order.Select(trans.order)) {
            if (order.Magic() == Magic) {
                if (order.OrderType() == ORDER_TYPE_BUY) {
                    buypos = order.Ticket();
                } else if (order.OrderType() == ORDER_TYPE_SELL) {
                    sellpos = order.Ticket();
                }
            }
        }
    }
}

//+------------------------------------------------------------------+
//| Execute sell trade function                                      |
//+------------------------------------------------------------------+
void executeSell() {      
       double bid = SymbolInfoDouble(_Symbol, SYMBOL_BID);
       bid = NormalizeDouble(bid,_Digits);
       trade.Sell(lott,_Symbol,bid);  
       sellpos = trade.ResultOrder();  
       }   

//+------------------------------------------------------------------+
//| Execute buy trade function                                       |
//+------------------------------------------------------------------+
void executeBuy() {
       double ask = SymbolInfoDouble(_Symbol, SYMBOL_ASK);
       ask = NormalizeDouble(ask,_Digits);
       trade.Buy(lott,_Symbol,ask);
       buypos = trade.ResultOrder();
}

Não entrarei em detalhes sobre a verificação ou as considerações na escolha da estratégia principal. Informações mais detalhadas podem ser encontradas em meu artigo anterior sobre aprendizado de máquina, cujo link está disponível aqui.

Obtenção de dados

Neste artigo, definiremos dois estados: alta volatilidade e baixa volatilidade, representados respectivamente pelos números 1 e 0. A volatilidade será determinada como o desvio padrão do retorno das últimas 50 velas da seguinte forma:

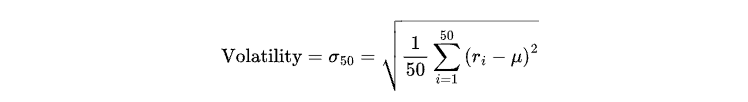
Onde:

• ri representa o retorno da i-ésima vela (calculado como a variação percentual do preço entre dois fechamentos consecutivos).

• μ é o retorno médio das últimas 50 velas fechadas, definido da seguinte maneira:

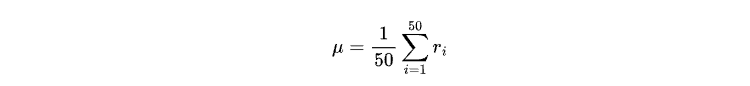
Para o treinamento do modelo, precisaremos apenas dos dados de preço de fechamento e do tempo. Embora seja possível obter dados diretamente do terminal MetaTrader 5, grande parte dos dados fornecidos pelo terminal é limitada a dados de ticks reais. Para obter dados OHLC de períodos mais longos do seu broker, podemos criar um EA coletor de OHLC (OHLC getter) para essa finalidade.

#include <FileCSV.mqh>

int barsTotal = 0;
CFileCSV csvFile;

input string fileName = "Name.csv";
string headers[] = {
    "time",
    "close"
};

string data[100000][2];
int indexx = 0;
vector xx;

input bool SaveData = true;

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {//Initialize model
   return(INIT_SUCCEEDED);
  }

//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
   if (!SaveData) return;
   if(csvFile.Open(fileName, FILE_WRITE|FILE_ANSI))
     {
      //Write the header
      csvFile.WriteHeader(headers);
      //Write data rows
      csvFile.WriteLine(data);
      //Close the file
      csvFile.Close();
     }
   else
     {
      Print("File opening error!");
     }

  }
  
//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
  int bars = iBars(_Symbol,PERIOD_CURRENT);
  
  if (barsTotal!= bars){
     barsTotal = bars;
   data[indexx][0] =(string)TimeTradeServer() ;
   data[indexx][1] = DoubleToString(iClose(_Symbol,PERIOD_CURRENT,1), 8); 
   indexx++;
   }
 }

Esse código lê e grava dados financeiros (tempo e preço de fechamento) em um arquivo CSV. A cada tick, ele verifica se o número de barras mudou. Caso positivo, o código atualiza o array de dados com o horário atual do servidor e o preço de fechamento do símbolo. Quando o script é desinicializado, ele grava os dados coletados no arquivo CSV, incluindo cabeçalhos e linhas de dados. Para o processamento de arquivos, utiliza a classeCFileCSV.

Execute esse EA no testador de estratégias, usando o período e o timeframe desejados, e o arquivo CSV será salvo no diretório /Tester/Agent-sth000.

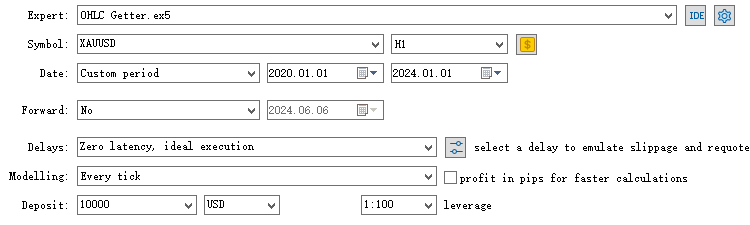
Para o treinamento, utilizaremos dados de 1º de janeiro de 2020 a 1º de janeiro de 2024. Os dados de 1º de janeiro de 2024 a 1º de janeiro de 2025 serão usados para teste fora da amostra.

Modelos de treinamento

Agora, abra qualquer editor Python e certifique-se de ter instalado as bibliotecas necessárias com o comando pip, conforme descrito nesta seção.

O arquivo CSV inicialmente contém apenas uma coluna, na qual os valores de tempo e fechamento estão combinados e separados por ponto e vírgula. Para facilitar o armazenamento, esses valores são mantidos como strings. Para processá-los, primeiro lemos o arquivo CSV da seguinte maneira, separando as duas colunas e convertendo os valores de string para os tipos datetime e float.

import pandas as pd
data = pd.read_csv("XAU_test.csv",sep=";")
data = data.dropna()
data["close"] = data["close"].astype(float)
data['time'] = pd.to_datetime(data['time'])
data.set_index('time', inplace=True)

A volatilidade pode ser facilmente calculada com esta linha:

data['volatility'] = data['returns'].rolling(window=50).std()

Em seguida, visualizamos a distribuição da volatilidade para entender melhor suas características. Neste caso, fica evidente que ela segue aproximadamente uma distribuição normal.

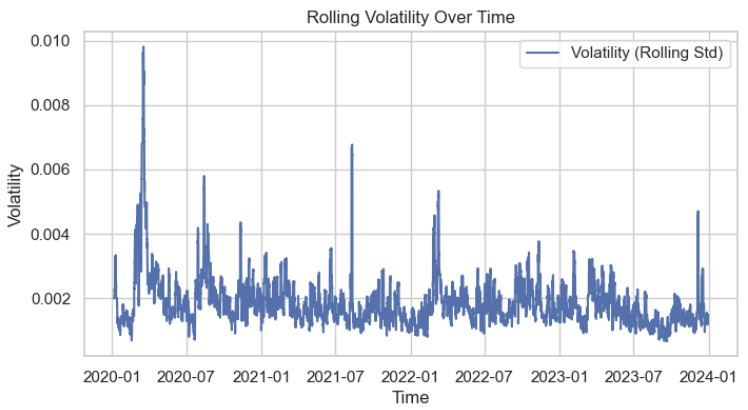
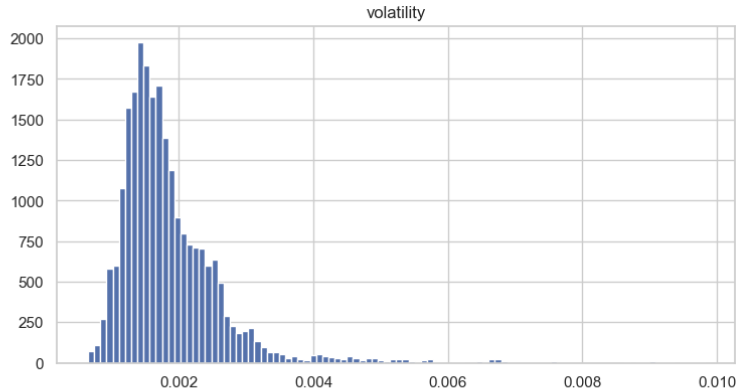
Usamos o teste ampliado de Dickey-Fuller para confirmar que os dados de volatilidade são estacionários. Muito provavelmente, o teste apresentará o seguinte resultado:

Augmented Dickey-Fuller Test: Volatility
ADF Statistic: -13.120552520156329
p-value: 1.5664189630119278e-24
# Lags Used: 46
Number of Observations Used: 23516
=> The series is likely stationary.

Embora os modelos ocultos de Markov (HMM) não sejam estritamente necessários para dados estacionários devido ao seu comportamento de atualização progressiva, a presença de dados estacionários facilita bastante o processo de agrupamento e aumenta a precisão do modelo.

Apesar de os dados de volatilidade provavelmente serem estacionários e próximos de uma distribuição normal, ainda assim desejamos normalizá-los para uma distribuição normal padrão, de modo que o intervalo de valores se torne mais controlável.

Em estatística, esse processo é chamado de "escalonamento", no qual qualquer variável aleatória normalmente distribuída x pode ser transformada em uma distribuição normal padrão N(0,1) por meio da seguinte operação:

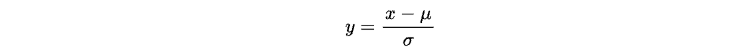
Aqui, μ representa o valor médio e σ o desvio padrão de x.

É importante lembrar que, mais adiante, ao reintegrarmos o modelo no editor do MetaTrader 5, precisaremos realizar as mesmas operações de normalização. Por isso, também será necessário salvar o valor médio e o desvio padrão.

from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaled_volatility = scaler.fit_transform(data[['volatility']])
scaled_volatility = scaled_volatility.reshape(-1, 1)
scaler_mean = scaler.mean_[0]  # Mean of the volatility feature
scaler_std = scaler.scale_[0]  # Standard deviation of the volatility feature

Em seguida, treinamos o modelo com os dados de volatilidade escalonados da seguinte forma:

from hmmlearn import hmm
import numpy as np
# Define the number of hidden states
n_states = 2
# Initialize the Gaussian HMM
model = hmm.GaussianHMM(n_components=n_states, covariance_type="full", n_iter=100, random_state=42, verbose = True)
# Fit the model to the scaled volatility data
model.fit(scaled_volatility)

Ao prever os estados ocultos para cada ponto dos dados de treinamento, a distribuição dos agrupamentos se mostra bastante coerente, apresentando apenas pequenas imprecisões.

# Predict the hidden states
hidden_states = model.predict(scaled_volatility)

# Add the hidden states to your dataframe
data['hidden_state'] = hidden_states
plt.figure(figsize=(14, 6))
for state in range(n_states):
    state_mask = data['hidden_state'] == state
    plt.plot(data.index[state_mask], data['volatility'][state_mask], 'o', label=f'State {state}')
plt.title('Hidden States and Rolling Volatility')
plt.xlabel('Time')
plt.ylabel('Volatility')
plt.legend()
plt.show()

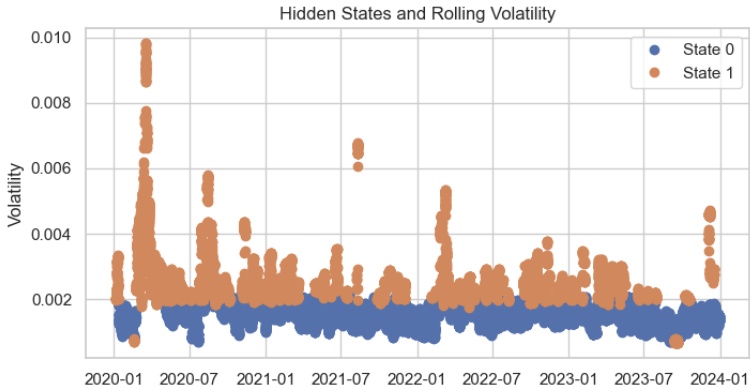
Por fim, formatamos a saída desejada na linguagem MQL5 e a salvamos em um arquivo de cabeçalho JSON, o que simplifica o processo de copiar e colar os valores correspondentes da matriz no editor do MetaTrader 5.

import json

# Your HMM model parameters
transition_matrix = model.transmat_
means = model.means_
covars = model.covars_

# Construct the data in the required format
data = {
    "A": [
        [transition_matrix[0, 0], transition_matrix[0, 1]],
        [transition_matrix[1, 0], transition_matrix[1, 1]]
    ],
    "mu": [means[0, 0], means[1, 0]],
    "sigma_sq": [covars[0, 0], covars[1, 0]],
    "scaler_mean": scaler_mean,
    "scaler_std": scaler_std
}

# Create the output content in the desired format
output_str = """
const double A[2][2] = { 
    {%.16f, %.16f}, 
    {%.16f, %.16f}
};
const double mu[2] = {%.16f, %.16f};
const double sigma_sq[2] = {%.16f, %.16f};
const double scaler_mean = %.16f;
const double scaler_std = %.16f;
""" % (
    data["A"][0][0], data["A"][0][1], data["A"][1][0], data["A"][1][1],
    data["mu"][0], data["mu"][1],
    data["sigma_sq"][0], data["sigma_sq"][1],
    data["scaler_mean"], data["scaler_std"]
)

# Write to a file
with open('model_parameters.h', 'w') as f:
    f.write(output_str)

print("Parameters saved to model_parameters.h")

O arquivo resultante deve ter aproximadamente a seguinte aparência:

const double A[2][2] = { 
    {0.9941485184089348, 0.0058514815910651}, 
    {0.0123877225858242, 0.9876122774141759}
};
const double mu[2] = {-0.4677410059727503, 0.9797900996225393};
const double sigma_sq[2] = {0.1073520489683212, 1.4515804806463273};
const double scaler_mean = 0.0018685496675093;
const double scaler_std = 0.0008350190448735;

Esses valores precisam ser inseridos no código do nosso EA como variáveis globais.

Integração

Agora retornamos ao editor de código do MetaTrader 5 e aprimoramos o código-fonte da nossa estratégia.

Primeiro, precisamos criar funções para o cálculo da volatilidade móvel, que será atualizada continuamente.

//+------------------------------------------------------------------+
//| Get volatility Function                                          |
//+------------------------------------------------------------------+
void GetVolatility(){
// Step 1: Get the last two close prices to compute the latest percent change
        double close_prices[2];
        int copied = CopyClose(_Symbol, PERIOD_CURRENT, 1, 2, close_prices);
        if(copied != 2){
            Print("Failed to copy close prices. Copied: ", copied);
            return;
        }
        
        // Step 2: Compute the latest percent change
        double latest_close = close_prices[0];
        double previous_close = close_prices[1];
        double percent_change = 0.0;
        if(previous_close != 0){
            percent_change = (latest_close - previous_close) / previous_close;
        }
        else{
            Print("Previous close price is zero. Percent change set to 0.");
        }
        
        // Step 3: Update the percent_changes buffer
        percent_changes[percent_change_index] = percent_change;
        percent_change_index++;
        if(percent_change_index >= 50){
            percent_change_index = 0;
            percent_change_filled = true;
        }
        
        // Step 4: Once the buffer is filled, compute the rolling std dev
        if(percent_change_filled){
            double current_stddev = ComputeStdDev(percent_changes, 50);
            // Step 5: Scale the std dev
            double scaled_stddev = (current_stddev - scaler_mean) / scaler_std;
            
            // Step 6: Update the volatility array (ring buffer for Viterbi)
            // Shift the volatility array to make room for the new std dev
            for(int i = 0; i < 49; i++){
                volatility[i] = volatility[i+1];
            }
            volatility[49] = scaled_stddev; // Insert the latest std dev
       }
}

//+------------------------------------------------------------------+
//| Compute Standard Deviation Function                              |
//+------------------------------------------------------------------+
double ComputeStdDev(double &data[], int size)
{
    if(size <= 1)
        return 0.0;
    
    double sum = 0.0;
    double sum_sq = 0.0;
    for(int i = 0; i < size; i++)
    {
        sum += data[i];
        sum_sq += data[i] * data[i];
    }
    double mean = sum / size;
    double variance = (sum_sq - (sum * sum) / size) / (size - 1);
    return MathSqrt(variance);
}

• A função GetVolatility() calcula e acompanha a volatilidade móvel ao longo do tempo, usando o desvio padrão escalonado das variações percentuais de preço.
• A função auxiliar ComputeDtsDev() serve para calcular o desvio padrão de um determinado conjunto de dados.

Depois, escrevemos duas funções que calculam o estado oculto atual com base em nossas matrizes e na volatilidade móvel corrente.

//+------------------------------------------------------------------+
//| Viterbi Algorithm Implementation in MQL5                         |
//+------------------------------------------------------------------+
int Viterbi(double &obs[], int &states[])
{
    // Initialize dynamic programming tables
    double T1[2][50];
    int T2[2][50];

    // Initialize first column
    for(int s = 0; s < 2; s++)
    {
         double emission_prob = (1.0 / MathSqrt(2 * M_PI * sigma_sq[s])) * MathExp(-MathPow(obs[0] - mu[s], 2) / (2 * sigma_sq[s])) + 1e-10;

        T1[s][0] = MathLog(pi[s]) + MathLog(emission_prob);
        T2[s][0] = 0;
    }

    // Fill the tables
    for(int t = 1; t < 50; t++)
    {
        for(int s = 0; s < 2; s++)
        {
            double max_prob = -DBL_MAX; // Initialize to negative infinity
            int max_state = 0;
            for(int s_prev = 0; s_prev < 2; s_prev++)
            {
                double transition_prob = A[s_prev][s];
                if(transition_prob <= 0) transition_prob = 1e-10; // Prevent log(0)
                double prob = T1[s_prev][t-1] + MathLog(transition_prob);
                if(prob > max_prob)
                {
                    max_prob = prob;
                    max_state = s_prev;
                }
            }
            // Calculate emission probability with epsilon
            double emission_prob = (1.0 / MathSqrt(2 * M_PI * sigma_sq[s])) * MathExp(-MathPow(obs[t] - mu[s], 2) / (2 * sigma_sq[s])) + 1e-10;
            T1[s][t] = max_prob + MathLog(emission_prob);
            T2[s][t] = max_state;
        }
    }

    // Backtrack to find the optimal state sequence
    // Find the state with the highest probability in the last column
    double max_final_prob = -DBL_MAX;
    int last_state = 0;
    for(int s = 0; s < 2; s++)
    {
        if(T1[s][49] > max_final_prob)
        {
            max_final_prob = T1[s][49];
            last_state = s;
        }
    }    
    // Initialize the states array
    ArrayResize(states, 50);
    states[49] = last_state;
    // Backtrack
    for(int t = 48; t >= 0; t--)
    {
        states[t] = T2[states[t+1]][t+1];
    }
    return 0; // Success
}

//+------------------------------------------------------------------+
//| Predict Current Hidden State                                     |
//+------------------------------------------------------------------+
int PredictCurrentState(double &obs[])
{   
    // Define states array
    int states[50];
    
    // Apply Viterbi
    int ret = Viterbi(obs, states);
    if(ret != 0)
        return -1; // Error
    
    // Return the most probable current state
    return states[49];
}

A função Viterbi() implementa o algoritmo de Viterbi, um método de programação dinâmica que encontra a sequência mais provável de estados ocultos em um modelo oculto de Markov (HMM) com base nos dados observados (obs[]).

1. Inicialização:

• Tabelas de programação dinâmica:

  • T1[s][t] representa a probabilidade logarítmica da sequência mais provável de estados que termina no estado s no instante de tempo t.
  • T2[s][t] é a tabela de ponteiros que armazena o estado que maximizou a probabilidade de transição para o estado s no instante de tempo t.

• Primeiro passo temporal (t = 0):

  • Calcule as probabilidades iniciais usando as probabilidades a priori de cada estado (π[s]) e as probabilidades de ocorrência do primeiro valor observado (obs[0]).

2. Cálculo recursivo:

Para cada passo temporal t de 1 a 49:

1. Para cada estado s:

   Calcule a probabilidade máxima de transição de qualquer estado anterior s_prev para s utilizando a seguinte equação:

   

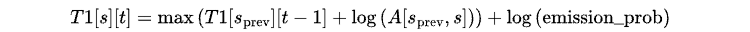
   Aqui, a probabilidade de transição A[s_prev, s] é convertida para o espaço logarítmico para evitar estouro numérico.

2. Armazene o estado s_prev que maximizou a probabilidade em T2[s][t].

3. Propagação reversa para extrair o caminho ótimo:

1. Comece com o estado que possui a maior probabilidade no último passo temporal (t = 49).
2. Percorra T2 para reconstruir a sequência mais provável de estados, armazenando o resultado em states[].

O resultado final é o array states[], que contém a sequência mais provável de estados.

A função PredictCurrentState() usa a função Viterbi() para prever o estado oculto atual com base nas observações.

1. Na inicialização, ela define o array states[50] para armazenar o resultado retornado pela função Viterbi().
2. Em seguida, passa a sequência de observações obs[] para a função Viterbi(), a fim de calcular a sequência mais provável de estados ocultos.
3. Por fim, retorna o estado no último passo temporal (states[49]), que representa o estado oculto atual mais provável.

Se a matemática por trás disso parecer confusa, recomendo fortemente consultar ilustrações mais intuitivas disponíveis na internet. Aqui, tentarei explicar brevemente o que está sendo feito.

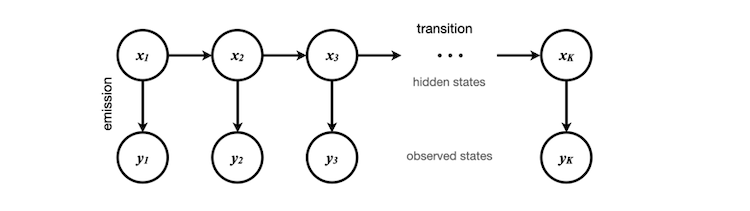
Os estados observáveis são os dados de volatilidade escalonados, que podemos obter e armazenar no array obs[], contendo, neste caso, 50 elementos. Esses elementos correspondem a y1, y2, ... y50 no diagrama. Os estados ocultos correspondentes podem ser 0 ou 1, representando as condições abstratas da volatilidade atual (alta ou baixa).

Esses estados ocultos são determinados por meio do agrupamento realizado no processo de treinamento do modelo, que executamos anteriormente em Python. É importante observar que o código em Python não sabe exatamente o que cada número representa — ele apenas sabe como agrupar os dados e identificar os padrões das propriedades de transição entre os estados.

Inicialmente, atribuímos aleatoriamente o estado x1, presumindo que cada estado tem peso igual. Caso não queiramos fazer essa suposição, podemos calcular a distribuição estacionária do estado inicial usando nossos dados de treinamento, que será o vetor próprio da matriz de transição. Para simplificar, assumimos que o vetor da distribuição estacionária é [0,5, 0,5].

Ao treinar o modelo oculto de Markov, obtemos a probabilidade de transição para outro estado oculto e a probabilidade de ocorrência de outra observação. Utilizando o teorema de Bayes, podemos calcular a probabilidade de todos os caminhos possíveis para cada cadeia de Markov e determinar o caminho mais provável. Isso nos permite encontrar o resultado mais provável para x50, o estado oculto final na sequência.

Por fim, ajustamos a lógica original da função OnTick(), calculando os estados ocultos para cada fechamento e adicionando um critério de entrada segundo o qual o estado oculto deve ser igual a 1.

//+------------------------------------------------------------------+
//| Check Volatility is filled Function                              |
//+------------------------------------------------------------------+
bool IsVolatilityFilled(){
     bool volatility_filled = true;
     for(int i = 0; i < 50; i++){
         if(volatility[i] == 0){
             volatility_filled = false;
             break;
         }
     }
     if(!volatility_filled){
         Print("Volatility buffer not yet filled.");
         return false;
     }
     else return true;
}  

//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
  int bars = iBars(_Symbol,PERIOD_CURRENT);
  if (barsTotal!= bars){
     barsTotal = bars;
     double maFast[];
     double maSlow[];
     double ma[];  
     
     GetVolatility();
     if(!IsVolatilityFilled()) return;
     int currentState = PredictCurrentState(volatility);
     
     CopyBuffer(handleMaFast,BASE_LINE,1,2,maFast);
     CopyBuffer(handleMaSlow,BASE_LINE,1,2,maSlow);
     CopyBuffer(handleMa,0,1,1,ma);

     double bid = SymbolInfoDouble(_Symbol, SYMBOL_BID);
     double ask = SymbolInfoDouble(_Symbol, SYMBOL_ASK);
     double lastClose = iClose(_Symbol, PERIOD_CURRENT, 1);
     //The order below matters
     if(buypos>0&& lastClose<maSlow[1]) trade.PositionClose(buypos);
     if(sellpos>0 &&lastClose>maSlow[1])trade.PositionClose(sellpos);        
     if (maFast[1]>maSlow[1]&&maFast[0]<maSlow[0]&&buypos ==sellpos&&currentState==1)executeBuy(); 
     if(maFast[1]<maSlow[1]&&maFast[0]>maSlow[0]&&sellpos ==buypos&&currentState==1) executeSell();
     
     if(buypos>0&&(!PositionSelectByTicket(buypos)|| PositionGetInteger(POSITION_MAGIC) != Magic)){
      buypos = 0;
      }
     if(sellpos>0&&(!PositionSelectByTicket(sellpos)|| PositionGetInteger(POSITION_MAGIC) != Magic)){
      sellpos = 0;
      }
    }
 }

Testes com dados históricos

Treinamos o modelo usando dados de 1º de janeiro de 2020 a 1º de janeiro de 2024. Agora queremos testar os resultados para o período de 1º de janeiro de 2024 a 1º de janeiro de 2025 no par XAUUSD, em um timeframe de 1 hora.

Primeiro, comparamos o desempenho com o indicador básico, que representa o resultado sem a integração do HMM.

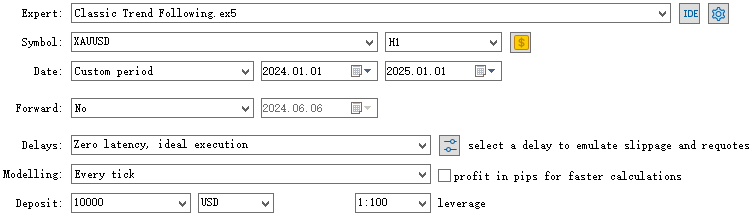
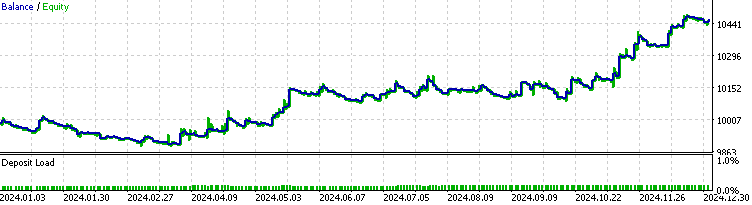
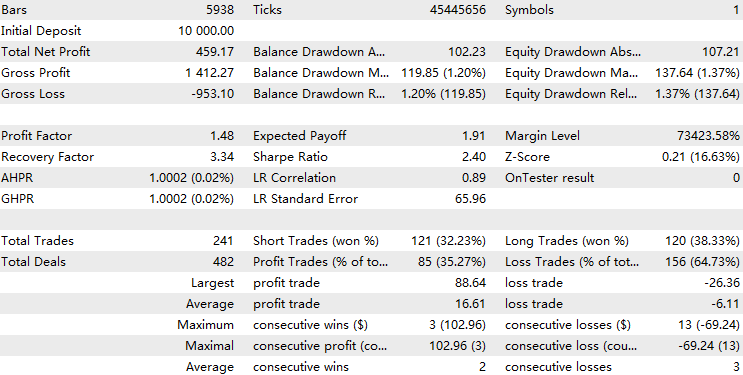
Agora testamos nosso EA com o filtro do modelo HMM implementado nos dados históricos.

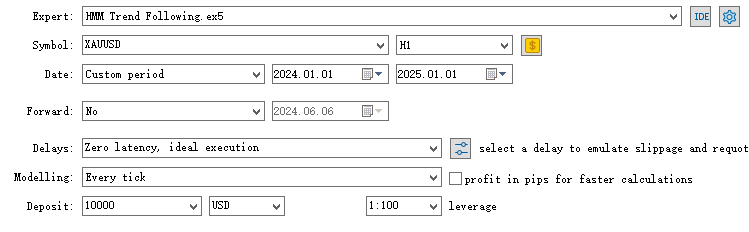
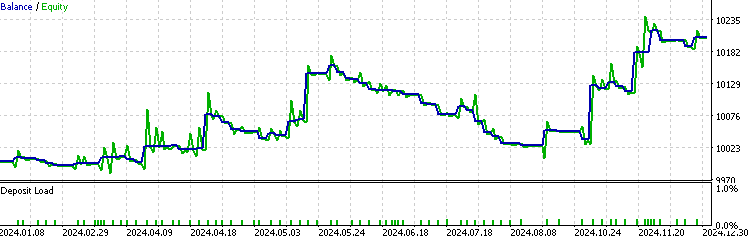
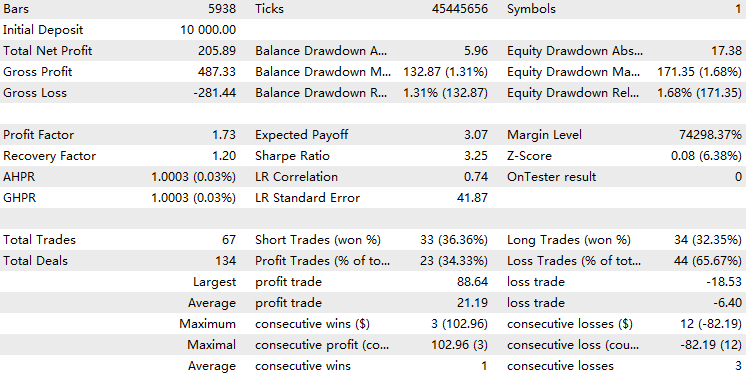
Observamos que o EA com a implementação do HMM filtrou cerca de 70% de todas as operações. Ele superou o nível base com um fator de lucro de 1,73 (contra 1,48 no caso base), além de apresentar um coeficiente de Sharpe mais elevado. Isso indica que o modelo HMM treinado demonstra um certo grau de previsibilidade.

Se realizarmos um teste deslizante com dados históricos — repetindo o procedimento de treinamento de 4 anos e teste de 1 ano, começando em 2004 — e compilarmos todos os resultados em uma única curva de capital, obteremos o seguinte resultado:

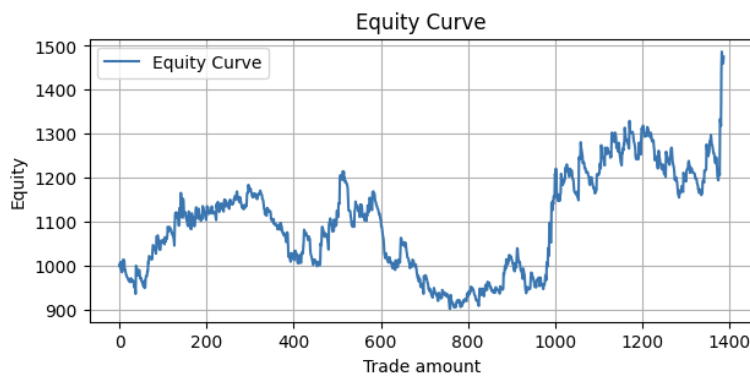
Indicadores:

Profit Factor: 1.10
Maximum Drawdown: -313.17
Average Win: 11.41
Average Loss: -5.01
Win Rate: 32.56%

Os resultados são positivos, embora ainda exista potencial para melhorias adicionais.

Discussão dos resultados

No cenário atual do trading, dominado por métodos de aprendizado de máquina, há um debate constante sobre se devemos utilizar modelos mais complexos, como redes neurais recorrentes (RNN), ou permanecer com modelos mais simples, como os modelos ocultos de Markov (HMM).

Vantagens:

1. Simplicidade. É mais simples de implementar e interpretar em comparação com modelos complexos, como as RNN, que introduzem ambiguidade quanto ao significado de cada parâmetro e operação.
2. Menor exigência de dados. Requer um número menor de amostras de treinamento para estimar os parâmetros do modelo e também menos poder computacional.
3. Menor número de parâmetros. É mais resistente a problemas de sobreajuste.

Desvantagens:

1. Complexidade limitada. Pode não capturar padrões complexos em dados voláteis que as RNN são capazes de modelar.
2. Suposição do processo de Markov. Parte do princípio de que as transições de volatilidade não possuem memória, o que pode não refletir com precisão a realidade dos mercados.
3. Risco de sobreajuste. Apesar de sua simplicidade, se forem definidos estados demais, o HMM ainda estará sujeito ao problema de sobreajuste.

Uma abordagem popular no aprendizado de máquina é prever a volatilidade, e não os preços, pois pesquisadores demonstraram que as previsões de volatilidade tendem a ser mais confiáveis. No entanto, uma limitação do método apresentado neste artigo é que as observações obtidas para cada nova barra (a volatilidade móvel de 50 períodos) e os estados ocultos definidos (estados de alta e baixa volatilidade) são, em certa medida, correlacionados, o que reduz a confiabilidade das previsões. Isso indica que resultados semelhantes poderiam ser alcançados simplesmente utilizando os próprios dados de observação como filtros.

Para aprofundar o desenvolvimento, recomendo aos leitores que explorem outras definições de estados ocultos e também experimentem utilizar mais de dois estados, a fim de aprimorar a confiabilidade do modelo e sua capacidade preditiva.

Considerações finais

Neste artigo, explicamos inicialmente a motivação para o uso dos HMM como preditores de estados de volatilidade em estratégias de seguimento de tendência e apresentamos os principais conceitos por trás desses modelos. Em seguida, percorremos todo o processo de desenvolvimento da estratégia, que incluiu a criação de uma estratégia básica em MQL5 usando o MetaTrader 5, a obtenção de dados e o treinamento do HMM em Python, seguido da integração dos modelos de volta ao MetaTrader 5. Posteriormente, realizamos testes com dados históricos e analisamos os resultados, explicando de forma resumida a lógica matemática dos HMM por meio de um diagrama. Por fim, compartilhei algumas considerações sobre a estratégia e apontei possíveis caminhos para o aprimoramento futuro dessa abordagem.

Tabela de arquivos

Nome do arquivo	Uso
HMM Test.mq5	Implementação do EA de negociação
Classic Trend Following.mq5	EA da estratégia básica
OHLC Getter.mq5	EA para extração de dados
FileCSV.mqh	Arquivo incluído para armazenamento de dados em formato CSV
rollingBacktest.ipynb	Usado para o treinamento do modelo e obtenção das matrizes