トレンドフォロー型ボラティリティ予測のための隠れマルコフモデル

はじめに

隠れマルコフモデル(HMM)は、観測可能な価格変動を分析することで、市場の潜在的な状態を特定する強力な統計手法です。取引においては、市場レジームの変化をモデル化・予測することで、ボラティリティの予測精度を高め、トレンドフォロー戦略の構築に役立ちます。 

本記事では、HMMをボラティリティのフィルターとして活用し、トレンドフォロー戦略を開発するための一連の手順を紹介します。まず、MetaTrader 5上でMQL5を用いてバックボーン戦略を構築し、その後、市場データを取得してPythonでHMMを学習させます。そして、学習済みモデルをMetaTrader 5に統合し、最終的に過去のデータを用いたバックテストによって戦略の有効性を検証します。

動機

Dave Aronsonの著書『Evidence-Based Technical Analysis Dave Aronson』では、トレーダーは科学的手法に基づいて戦略を開発すべきだと提唱されています。このプロセスは、アイデアに基づいた直感から仮説を立て、それを厳密に検証してデータスヌーピング・バイアス（データの偏り）を避けることから始まります。本記事では、私たちもこのアプローチを採用します。まずは、隠れマルコフモデル(HMM)とは何か、そしてそれが戦略開発にどのように役立つのかを理解する必要があります。

隠れマルコフモデル(HMM)は、内部状態が直接観測できないシステムを、観測可能なデータから推定するための教師なし機械学習モデルです。これは「マルコフ仮定」、すなわち「将来の状態は現在の状態のみに依存し、過去の状態には依存しない」という前提に基づいています。HMMでは、システムを複数の離散的な状態としてモデル化し、それぞれの状態間を確率的に遷移します。これらの遷移は、遷移確率と呼ばれる一連の確率によって制御されます。観測されるデータ（例えば資産価格やリターン）はその背後にある状態から生成されますが、状態自体は観測できないため「隠れた」モデルと呼ばれます。

HMMの主な構成要素は次のとおりです。

1. 状態：観測できないシステムの状態（レジーム）で、金融市場においては、異なる市場レジーム（強気相場、弱気相場、高ボラティリティ期、低ボラティリティ期など）を表します。これらの状態は確率的に変化していきます。

2. 遷移確率：ある状態から別の状態へ移行する確率を定義します。時刻tにおける状態は、直前の時刻t-1の状態にのみ依存します。この確率は遷移行列によって表されます。

3. 排出確率：ある状態にあるときに特定の観測データ（株価やリターンなど）が現れる確率を示します。各状態には固有の確率分布があり、それに基づいてデータが生成されます。

4. 初期確率：システムが各状態でスタートする確率を表し、モデルの初期設定として重要です。

これらの構成要素に基づき、HMMはベイズ推論を用いて、観測されたデータからもっとも可能性の高い隠れ状態の時系列を推定します。これは通常、「Forward-Backwardアルゴリズム」や「ビタビアルゴリズム」などを使用して計算されます。これらのアルゴリズムは、隠れ状態の列が与えられたときに観測されたデータが出現する確率（尤度）を推定するために使用されます。

取引において、ボラティリティは資産価格や市場の動向に大きな影響を与える重要な要素です。HMMは、直接観測できないが市場行動に影響を与えるレジームを特定することで、ボラティリティ予測において非常に効果を発揮します。

1. 市場レジームの特定：HMMを使うことで、市場を高ボラティリティ・低ボラティリティなどの明確な状態に分類し、市場の構造変化を捉えることができます。これにより、価格変動の大きい時期や安定した時期を事前に把握することが可能になります。

2. ボラティリティのクラスタリング：金融市場では、ボラティリティが「クラスタ」を形成する傾向があります。つまり、高ボラティリティの時期が続きやすく、低ボラティリティの時期も同様に継続しやすい傾向です。HMMはこれを反映し、状態が長期間持続する確率を学習できるため、より正確な将来予測が可能となります。

3. ボラティリティ予測：異なる市場状態間の遷移を観察することで、HMMは将来のボラティリティに関する有益な洞察を提供します。たとえば、モデルが現在市場が高ボラティリティ状態にあると判断した場合、トレーダーは大きな価格変動を見込んだ戦略を採用できます。逆に、低ボラティリティへの移行が予測される場合には、リスク管理や戦略の調整が可能となります。

4. 適応性：HMMは新たなデータを取り込むことで、状態遷移や確率分布を継続的に更新できます。これにより、市場の変化に即座に対応でき、トレーダーは常に最新の市場環境に基づいた意思決定が可能になります。

数多くの研究でも示されている通り、私たちの仮説は「ボラティリティが高いときほど、価格変動が大きくなりトレンドが形成されやすくなるため、トレンドフォロー戦略のパフォーマンスが向上する」というものです。私たちはHMMを用いてボラティリティをクラスタ化し、「高ボラティリティ状態」と「低ボラティリティ状態」を定義します。そして、次の状態が高ボラティリティになるか低ボラティリティになるかを予測するモデルを学習させます。戦略のシグナルが発生した時にモデルが高ボラティリティ状態を予測していれば取引をおこない、そうでない場合は市場に参加しません。

バックボーン戦略

本記事で使用するトレンドフォロー戦略は、以前の機械学習に関する記事で実装したものと同じです。基本的なロジックは、2本の移動平均線（短期と長期）に基づいています。これら2本の移動平均線がクロスしたときに売買シグナルが発生し、短期移動平均線の方向に従って取引をおこないます。そのため、「トレンドフォロー戦略」と呼ばれます。決済シグナルは、価格が長期移動平均線をクロスしたときに発生します。これにより、トレーリングストップにある程度の余裕を持たせることができます。以下に、戦略の完全なコードを示します。

#include <Trade/Trade.mqh>
//XAU - 1h.
CTrade trade;

input ENUM_TIMEFRAMES TF = PERIOD_CURRENT;
input ENUM_MA_METHOD MaMethod = MODE_SMA;
input ENUM_APPLIED_PRICE MaAppPrice = PRICE_CLOSE;
input int MaPeriodsFast = 15;
input int MaPeriodsSlow = 25;
input int MaPeriods = 200;
input double lott = 0.01;
ulong buypos = 0, sellpos = 0;
input int Magic = 0;
int barsTotal = 0;
int handleMaFast;
int handleMaSlow;
int handleMa;

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
   trade.SetExpertMagicNumber(Magic);
   handleMaFast =iMA(_Symbol,TF,MaPeriodsFast,0,MaMethod,MaAppPrice);
   handleMaSlow =iMA(_Symbol,TF,MaPeriodsSlow,0,MaMethod,MaAppPrice);  
   handleMa = iMA(_Symbol,TF,MaPeriods,0,MaMethod,MaAppPrice); 
   return(INIT_SUCCEEDED);
  }

//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {

  }  

//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
  int bars = iBars(_Symbol,PERIOD_CURRENT);
  //Beware, the last element of the buffer list is the most recent data, not [0]
  if (barsTotal!= bars){
     barsTotal = bars;
     double maFast[];
     double maSlow[];
     double ma[];
     CopyBuffer(handleMaFast,BASE_LINE,1,2,maFast);
     CopyBuffer(handleMaSlow,BASE_LINE,1,2,maSlow);
     CopyBuffer(handleMa,0,1,1,ma);
     double bid = SymbolInfoDouble(_Symbol, SYMBOL_BID);
     double ask = SymbolInfoDouble(_Symbol, SYMBOL_ASK);
     double lastClose = iClose(_Symbol, PERIOD_CURRENT, 1);
     //The order below matters
     if(buypos>0&& lastClose<maSlow[1]) trade.PositionClose(buypos);
     if(sellpos>0 &&lastClose>maSlow[1])trade.PositionClose(sellpos);   
     if (maFast[1]>maSlow[1]&&maFast[0]<maSlow[0]&&buypos ==sellpos)executeBuy(); 
     if(maFast[1]<maSlow[1]&&maFast[0]>maSlow[0]&&sellpos ==buypos) executeSell();
     if(buypos>0&&(!PositionSelectByTicket(buypos)|| PositionGetInteger(POSITION_MAGIC) != Magic)){
      buypos = 0;
      }
     if(sellpos>0&&(!PositionSelectByTicket(sellpos)|| PositionGetInteger(POSITION_MAGIC) != Magic)){
      sellpos = 0;
      }
    }
 }

//+------------------------------------------------------------------+
//| Expert trade transaction handling function                       |
//+------------------------------------------------------------------+
void OnTradeTransaction(const MqlTradeTransaction& trans, const MqlTradeRequest& request, const MqlTradeResult& result) {
    if (trans.type == TRADE_TRANSACTION_ORDER_ADD) {
        COrderInfo order;
        if (order.Select(trans.order)) {
            if (order.Magic() == Magic) {
                if (order.OrderType() == ORDER_TYPE_BUY) {
                    buypos = order.Ticket();
                } else if (order.OrderType() == ORDER_TYPE_SELL) {
                    sellpos = order.Ticket();
                }
            }
        }
    }
}

//+------------------------------------------------------------------+
//| Execute sell trade function                                      |
//+------------------------------------------------------------------+
void executeSell() {      
       double bid = SymbolInfoDouble(_Symbol, SYMBOL_BID);
       bid = NormalizeDouble(bid,_Digits);
       trade.Sell(lott,_Symbol,bid);  
       sellpos = trade.ResultOrder();  
       }   

//+------------------------------------------------------------------+
//| Execute buy trade function                                       |
//+------------------------------------------------------------------+
void executeBuy() {
       double ask = SymbolInfoDouble(_Symbol, SYMBOL_ASK);
       ask = NormalizeDouble(ask,_Digits);
       trade.Buy(lott,_Symbol,ask);
       buypos = trade.ResultOrder();
}

バックボーン戦略の検証や選定に関する詳細な説明は、ここでは省略します。より詳しく知りたい方は、こちらにリンクした以前の機械学習に関する記事をご参照ください。

データの取得

本記事では、ボラティリティの状態を「高ボラティリティ」と「低ボラティリティ」の2つに定義し、それぞれ1と0で表します。ボラティリティは、直近50本のローソク足におけるリターンの標準偏差として以下のように定義します。

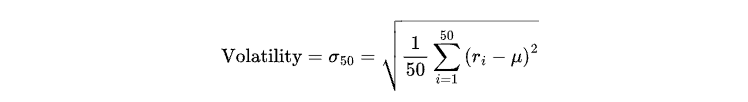
ここで

• riは、i番目のローソク足のリターン（連続するクローズ価格間の変化率）を表します。

• μは、直近50本のローソク足の平均リターンであり、以下の式で求められます。

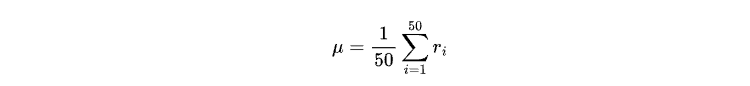
モデルを学習させる際に必要なデータは、終値と日時のみです。MetaTrader 5端末からデータを直接取得することも可能ですが、端末で提供されるデータは主に実ティックデータに限られています。より長期間のOHLCデータ（始値、高値、安値、終値）をブローカーから取得するには、専用のOHLC取得用EAを作成して対応することができます。

#include <FileCSV.mqh>

int barsTotal = 0;
CFileCSV csvFile;

input string fileName = "Name.csv";
string headers[] = {
    "time",
    "close"
};

string data[100000][2];
int indexx = 0;
vector xx;

input bool SaveData = true;

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {//Initialize model
   return(INIT_SUCCEEDED);
  }

//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
   if (!SaveData) return;
   if(csvFile.Open(fileName, FILE_WRITE|FILE_ANSI))
     {
      //Write the header
      csvFile.WriteHeader(headers);
      //Write data rows
      csvFile.WriteLine(data);
      //Close the file
      csvFile.Close();
     }
   else
     {
      Print("File opening error!");
     }

  }
  
//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
  int bars = iBars(_Symbol,PERIOD_CURRENT);
  
  if (barsTotal!= bars){
     barsTotal = bars;
   data[indexx][0] =(string)TimeTradeServer() ;
   data[indexx][1] = DoubleToString(iClose(_Symbol,PERIOD_CURRENT,1), 8); 
   indexx++;
   }
 }

このコードは、金融データ（時刻と終値）をCSVファイルに読み書きします。ティックごとにバーの本数が変化しているかを確認し、変化があれば現在のサーバー時刻と銘柄の終値をデータ配列に追加します。スクリプトが初期化解除されると、収集したデータがヘッダーとデータ行を含むCSVファイルとして書き出されます。ファイル処理にはCFileCSVクラスが使用されています。

このエキスパートアドバイザーを、希望する時間足と期間でストラテジーテスター上で実行すると、CSVファイルが/Tester/Agent-sth000ディレクトリに保存されます。

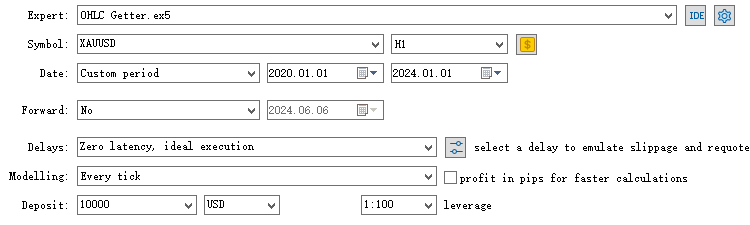
学習には2020年1月1日から2024年1月1日までのインサンプルデータを使用し、2024年1月1日から2025年1月1日までのデータをアウトオブサンプルのテストに使用します。

モデルの学習

まず、任意のPythonエディタを開き、本節で必要に応じて紹介するライブラリをpipでインストールしてください。

CSVファイルには当初、時間と終値が混在しており、セミコロンで区切られた1列だけが存在します。値は保存効率を考慮して文字列として格納されています。このデータを処理するために、まずCSVファイルを読み込み、2つの列に分割し、時間をdatetime型に、終値をfloat型に変換します。

import pandas as pd
data = pd.read_csv("XAU_test.csv",sep=";")
data = data.dropna()
data["close"] = data["close"].astype(float)
data['time'] = pd.to_datetime(data['time'])
data.set_index('time', inplace=True)

ボラティリティは次の1行で簡単に計算できます。

data['volatility'] = data['returns'].rolling(window=50).std()

次に、ボラティリティの分布を可視化して、その特徴をよりよく理解します。分布はおおよそ正規分布に従っていることがはっきりと確認できます。

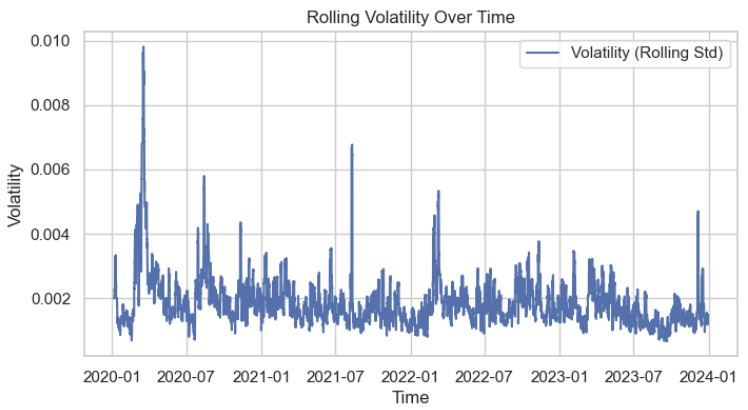
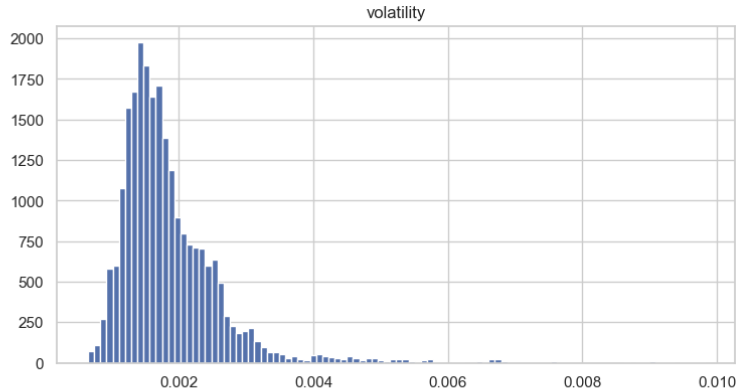
ボラティリティデータが定常過程であることを検証するために、拡張ディッキー–フラー検定(ADF: Augmented Dickey-Fuller)を使用します。検定結果はおそらく以下のようになるでしょう。

Augmented Dickey-Fuller Test: Volatility
ADF Statistic: -13.120552520156329
p-value: 1.5664189630119278e-24
# Lags Used: 46
Number of Observations Used: 23516
=> The series is likely stationary.

隠れマルコフモデル(HMM)はローリング更新の性質上、必ずしも定常データに限定されるわけではありませんが、定常データがあることでクラスタリングの過程が大幅に改善され、モデルの精度向上に寄与します。

ボラティリティデータは定常であり、かつ正規分布に近いと考えられますが、扱いやすい範囲にするために標準正規分布へ正規化をおこないます。 

統計学ではこの処理を「スケーリング」と呼び、正規分布に従うランダム変数xは以下の式で標準正規分布N(0,1) に変換できます。

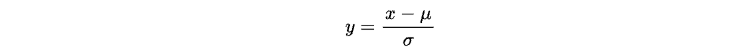
ここで、μはxの平均値、σは標準偏差を表します。

また、後でMetaTrader 5のエディターに統合する際に、同じ正規化処理をおこなう必要があるため、平均値と標準偏差を保存しておくことが重要です。

from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaled_volatility = scaler.fit_transform(data[['volatility']])
scaled_volatility = scaled_volatility.reshape(-1, 1)
scaler_mean = scaler.mean_[0]  # Mean of the volatility feature
scaler_std = scaler.scale_[0]  # Standard deviation of the volatility feature

次に、以下のようにスケーリングされたボラティリティデータでモデルを学習させます。

from hmmlearn import hmm
import numpy as np
# Define the number of hidden states
n_states = 2
# Initialize the Gaussian HMM
model = hmm.GaussianHMM(n_components=n_states, covariance_type="full", n_iter=100, random_state=42, verbose = True)
# Fit the model to the scaled volatility data
model.fit(scaled_volatility)

各学習データポイントに対して隠れ状態を予測したところ、クラスタの分布は非常に妥当であり、わずかな誤差しか見られませんでした。

# Predict the hidden states
hidden_states = model.predict(scaled_volatility)

# Add the hidden states to your dataframe
data['hidden_state'] = hidden_states
plt.figure(figsize=(14, 6))
for state in range(n_states):
    state_mask = data['hidden_state'] == state
    plt.plot(data.index[state_mask], data['volatility'][state_mask], 'o', label=f'State {state}')
plt.title('Hidden States and Rolling Volatility')
plt.xlabel('Time')
plt.ylabel('Volatility')
plt.legend()
plt.show()

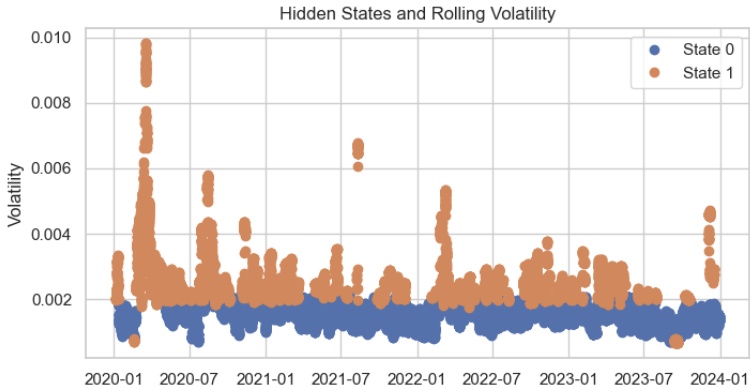
最後に、目的の出力をMQL5の形式に整形し、JSON形式のヘッダーファイルとして保存します。これにより、対応する行列の値をMetaTrader 5エディターに簡単にコピー＆ペーストできるようになります。

import json

# Your HMM model parameters
transition_matrix = model.transmat_
means = model.means_
covars = model.covars_

# Construct the data in the required format
data = {
    "A": [
        [transition_matrix[0, 0], transition_matrix[0, 1]],
        [transition_matrix[1, 0], transition_matrix[1, 1]]
    ],
    "mu": [means[0, 0], means[1, 0]],
    "sigma_sq": [covars[0, 0], covars[1, 0]],
    "scaler_mean": scaler_mean,
    "scaler_std": scaler_std
}

# Create the output content in the desired format
output_str = """
const double A[2][2] = { 
    {%.16f, %.16f}, 
    {%.16f, %.16f}
};
const double mu[2] = {%.16f, %.16f};
const double sigma_sq[2] = {%.16f, %.16f};
const double scaler_mean = %.16f;
const double scaler_std = %.16f;
""" % (
    data["A"][0][0], data["A"][0][1], data["A"][1][0], data["A"][1][1],
    data["mu"][0], data["mu"][1],
    data["sigma_sq"][0], data["sigma_sq"][1],
    data["scaler_mean"], data["scaler_std"]
)

# Write to a file
with open('model_parameters.h', 'w') as f:
    f.write(output_str)

print("Parameters saved to model_parameters.h")

結果のファイルは次のようになります。

const double A[2][2] = { 
    {0.9941485184089348, 0.0058514815910651}, 
    {0.0123877225858242, 0.9876122774141759}
};
const double mu[2] = {-0.4677410059727503, 0.9797900996225393};
const double sigma_sq[2] = {0.1073520489683212, 1.4515804806463273};
const double scaler_mean = 0.0018685496675093;
const double scaler_std = 0.0008350190448735;

これらをグローバル変数としてEAのコードに貼り付ける必要があります。

統合

それでは、MetaTrader 5のコードエディターに戻り、もともとの戦略コードの上に機能を追加していきましょう。

まずは、ローリングで更新され続けるボラティリティを計算する関数を作成する必要があります。

//+------------------------------------------------------------------+
//| Get volatility Function                                          |
//+------------------------------------------------------------------+
void GetVolatility(){
// Step 1: Get the last two close prices to compute the latest percent change
        double close_prices[2];
        int copied = CopyClose(_Symbol, PERIOD_CURRENT, 1, 2, close_prices);
        if(copied != 2){
            Print("Failed to copy close prices. Copied: ", copied);
            return;
        }
        
        // Step 2: Compute the latest percent change
        double latest_close = close_prices[0];
        double previous_close = close_prices[1];
        double percent_change = 0.0;
        if(previous_close != 0){
            percent_change = (latest_close - previous_close) / previous_close;
        }
        else{
            Print("Previous close price is zero. Percent change set to 0.");
        }
        
        // Step 3: Update the percent_changes buffer
        percent_changes[percent_change_index] = percent_change;
        percent_change_index++;
        if(percent_change_index >= 50){
            percent_change_index = 0;
            percent_change_filled = true;
        }
        
        // Step 4: Once the buffer is filled, compute the rolling std dev
        if(percent_change_filled){
            double current_stddev = ComputeStdDev(percent_changes, 50);
            // Step 5: Scale the std dev
            double scaled_stddev = (current_stddev - scaler_mean) / scaler_std;
            
            // Step 6: Update the volatility array (ring buffer for Viterbi)
            // Shift the volatility array to make room for the new std dev
            for(int i = 0; i < 49; i++){
                volatility[i] = volatility[i+1];
            }
            volatility[49] = scaled_stddev; // Insert the latest std dev
       }
}

//+------------------------------------------------------------------+
//| Compute Standard Deviation Function                              |
//+------------------------------------------------------------------+
double ComputeStdDev(double &data[], int size)
{
    if(size <= 1)
        return 0.0;
    
    double sum = 0.0;
    double sum_sq = 0.0;
    for(int i = 0; i < size; i++)
    {
        sum += data[i];
        sum_sq += data[i] * data[i];
    }
    double mean = sum / size;
    double variance = (sum_sq - (sum * sum) / size) / (size - 1);
    return MathSqrt(variance);
}

• GetVolatility()は、価格変動率のスケールされた標準偏差を用いて、時間とともにローリングボラティリティを計算・追跡します。
• ComputeDtsDev()は、指定されたデータ配列の標準偏差を計算するための補助関数です。 

その後、事前に定義した行列と現在のローリングボラティリティに基づいて、現在の隠れ状態を算出する2つの関数を作成します。

//+------------------------------------------------------------------+
//| Viterbi Algorithm Implementation in MQL5                         |
//+------------------------------------------------------------------+
int Viterbi(double &obs[], int &states[])
{
    // Initialize dynamic programming tables
    double T1[2][50];
    int T2[2][50];

    // Initialize first column
    for(int s = 0; s < 2; s++)
    {
         double emission_prob = (1.0 / MathSqrt(2 * M_PI * sigma_sq[s])) * MathExp(-MathPow(obs[0] - mu[s], 2) / (2 * sigma_sq[s])) + 1e-10;

        T1[s][0] = MathLog(pi[s]) + MathLog(emission_prob);
        T2[s][0] = 0;
    }

    // Fill the tables
    for(int t = 1; t < 50; t++)
    {
        for(int s = 0; s < 2; s++)
        {
            double max_prob = -DBL_MAX; // Initialize to negative infinity
            int max_state = 0;
            for(int s_prev = 0; s_prev < 2; s_prev++)
            {
                double transition_prob = A[s_prev][s];
                if(transition_prob <= 0) transition_prob = 1e-10; // Prevent log(0)
                double prob = T1[s_prev][t-1] + MathLog(transition_prob);
                if(prob > max_prob)
                {
                    max_prob = prob;
                    max_state = s_prev;
                }
            }
            // Calculate emission probability with epsilon
            double emission_prob = (1.0 / MathSqrt(2 * M_PI * sigma_sq[s])) * MathExp(-MathPow(obs[t] - mu[s], 2) / (2 * sigma_sq[s])) + 1e-10;
            T1[s][t] = max_prob + MathLog(emission_prob);
            T2[s][t] = max_state;
        }
    }

    // Backtrack to find the optimal state sequence
    // Find the state with the highest probability in the last column
    double max_final_prob = -DBL_MAX;
    int last_state = 0;
    for(int s = 0; s < 2; s++)
    {
        if(T1[s][49] > max_final_prob)
        {
            max_final_prob = T1[s][49];
            last_state = s;
        }
    }    
    // Initialize the states array
    ArrayResize(states, 50);
    states[49] = last_state;
    // Backtrack
    for(int t = 48; t >= 0; t--)
    {
        states[t] = T2[states[t+1]][t+1];
    }
    return 0; // Success
}

//+------------------------------------------------------------------+
//| Predict Current Hidden State                                     |
//+------------------------------------------------------------------+
int PredictCurrentState(double &obs[])
{   
    // Define states array
    int states[50];
    
    // Apply Viterbi
    int ret = Viterbi(obs, states);
    if(ret != 0)
        return -1; // Error
    
    // Return the most probable current state
    return states[49];
}

Viterbi()関数は、観測データ (obs[])が与えられたときに、隠れマルコフモデル(HMM)における最も確からしい隠れ状態の系列を求めるための動的計画法「ビタビアルゴリズム」を実装したものです。

1. 初期化

• 動的計画法テーブル

  • T1[s][t] :時刻tに状態sで終わる、最も確からしい状態系列の対数確率
  • T2[s][t]：時刻tに状態sに遷移する確率を最大化した前の状態s_prevを格納するポインタテーブル

• 最初の時間ステップ(t=0)

  • 各状態sに対して、事前確率(π[s])と最初の観測値(obs[0])に対する出力確率を用いて初期確率を計算します。

2. 再帰的計算

1から49までの各時間ステップtについて：

1. 各状態sについて：

   任意の前の状態s_prevから状態sに遷移する確率のうち、最大のものを次の式で計算します。               

   

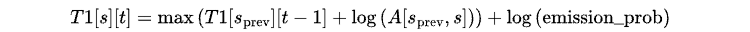
   ここで、遷移確率A[s_prev, s]は、数値のアンダーフローを防ぐために対数空間に変換されます。

2. 最大化された確率を与えた状態s_prevをT2[s][t]に保存します。

3. 最適経路のバックトラッキング

1. 最終時刻(t = 49)における最大確率を持つ状態からスタートします。
2. T2テーブルを逆にたどることで、最も確からしい状態系列をstates[]に復元します。

最終的な出力は、最も確からしい状態系列を格納したstates[]です。

PredictCurrentState関数は、観測データに基づいて現在の隠れ状態を予測するためにViterbi関数を利用します。

1. 初期化として、Viterbi()からの結果を格納するためにstates[50]配列を定義します。
2. 次に、観測系列obs[]をViterbi関数に渡し、最も確からしい隠れ状態系列を計算します。
3. 最後に、最終時刻(states[49])の状態を返します。これは、現在の最も確からしい隠れ状態を表します。

もしこの背後にある数学が分かりづらい場合は、インターネット上でより直感的な図解を探してみることを強くお勧めします。ここで、私たちが何をしているのかを簡単に説明してみたいと思います。

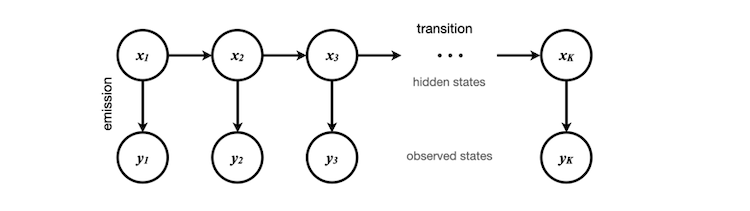
観測された状態はスケーリング済みのボラティリティデータであり、これを obs[]配列に格納します。この配列には50個の要素が含まれており、それぞれが図中の y1, y2, ..., y50 に対応します。対応する隠れ状態は0または1のいずれかで、現在のボラティリティが「高い」か「低い」かという抽象的な状態を表します。

これらの隠れ状態は、先に Python で実施したモデル学習プロセス中にクラスタリングによって決定されたものです。ここで重要なのは、Pythonのコード自体は各数値が「高ボラティリティ」や「低ボラティリティ」といった意味を直接理解しているわけではなく、あくまでデータのクラスタ化と状態間の遷移特性の識別に基づいて分類しているという点です。

初期状態x1に対しては、各状態の出現確率が等しい（均等に分布している）と仮定し、ランダムに状態を割り当てます。この仮定を避けたい場合は、学習データから遷移行列の固有ベクトルを用いて定常分布を計算することも可能です。今回は簡便のため、定常分布ベクトルを [0.5, 0.5] と仮定します。

HMM（隠れマルコフモデル）の学習を通じて、隠れ状態間の遷移確率と各隠れ状態から観測される出力（スケーリングされたボラティリティ）に対応する出力確率の情報が得られます。これらをもとにベイズの定理を使えば、すべての可能な状態遷移パスの確率を計算でき、最も確からしいパスを選定することができます。これにより、最終的な隠れ状態 x50（つまり現在のボラティリティの状態）が最も高い確率でどれであるかを推定できるのです。

最後に、元のOnTick()関数のロジックに手を加え、各終値に対応する隠れ状態を計算します。そして、「隠れ状態が1であること」を新たなエントリー条件として追加します。

//+------------------------------------------------------------------+
//| Check Volatility is filled Function                              |
//+------------------------------------------------------------------+
bool IsVolatilityFilled(){
     bool volatility_filled = true;
     for(int i = 0; i < 50; i++){
         if(volatility[i] == 0){
             volatility_filled = false;
             break;
         }
     }
     if(!volatility_filled){
         Print("Volatility buffer not yet filled.");
         return false;
     }
     else return true;
}  

//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
  int bars = iBars(_Symbol,PERIOD_CURRENT);
  if (barsTotal!= bars){
     barsTotal = bars;
     double maFast[];
     double maSlow[];
     double ma[];  
     
     GetVolatility();
     if(!IsVolatilityFilled()) return;
     int currentState = PredictCurrentState(volatility);
     
     CopyBuffer(handleMaFast,BASE_LINE,1,2,maFast);
     CopyBuffer(handleMaSlow,BASE_LINE,1,2,maSlow);
     CopyBuffer(handleMa,0,1,1,ma);

     double bid = SymbolInfoDouble(_Symbol, SYMBOL_BID);
     double ask = SymbolInfoDouble(_Symbol, SYMBOL_ASK);
     double lastClose = iClose(_Symbol, PERIOD_CURRENT, 1);
     //The order below matters
     if(buypos>0&& lastClose<maSlow[1]) trade.PositionClose(buypos);
     if(sellpos>0 &&lastClose>maSlow[1])trade.PositionClose(sellpos);        
     if (maFast[1]>maSlow[1]&&maFast[0]<maSlow[0]&&buypos ==sellpos&&currentState==1)executeBuy(); 
     if(maFast[1]<maSlow[1]&&maFast[0]>maSlow[0]&&sellpos ==buypos&&currentState==1) executeSell();
     
     if(buypos>0&&(!PositionSelectByTicket(buypos)|| PositionGetInteger(POSITION_MAGIC) != Magic)){
      buypos = 0;
      }
     if(sellpos>0&&(!PositionSelectByTicket(sellpos)|| PositionGetInteger(POSITION_MAGIC) != Magic)){
      sellpos = 0;
      }
    }
 }

バックテスト

2020年1月1日から2024年1月1日までのインサンプルデータを使ってモデルを学習させました。次に、2024年1月1日から2025年1月1日までの期間において、XAUUSDの1時間足チャートで結果をテストしたいと考えます。

まずは、HMMを統合しない状態での結果（ベースライン）と比較して、パフォーマンスを評価します。

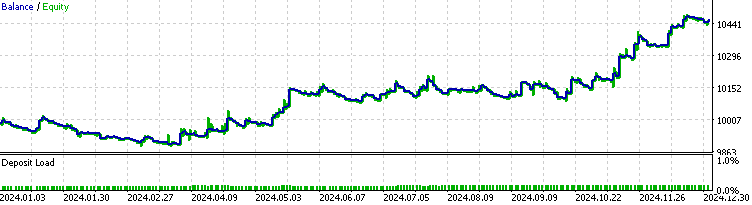
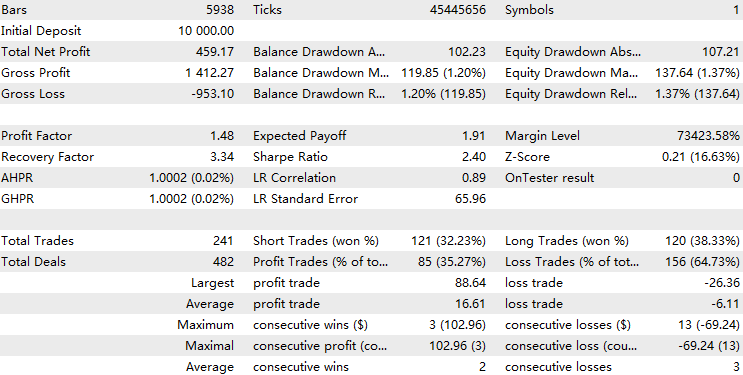
ここで、HMMモデルフィルターを実装したEAのバックテストを実行します。

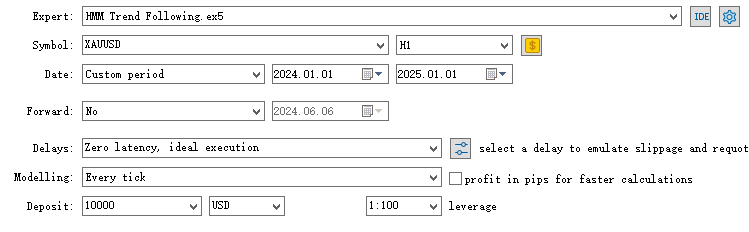
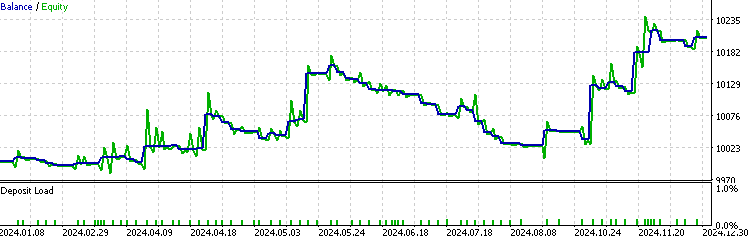
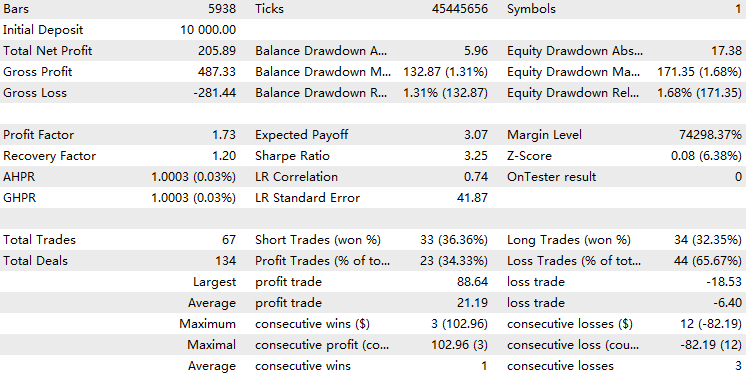
HMMを実装したEAは、全体の取引のおよそ70%をフィルタリングしていることが分かります。ベースラインと比較して優れた成績を示しており、プロフィットファクターはベースラインの1.48に対して1.73、シャープレシオもより高くなっています。これは、学習したHMMモデルがある程度の予測能力を持っていることを示唆しています。

次に、2004年から開始して、4年間のトレーニングと1年間のテストという手順を繰り返しながらローリングバックテストをおこない、そのすべての結果を1つのエクイティカーブにまとめると、次のような結果が得られます。

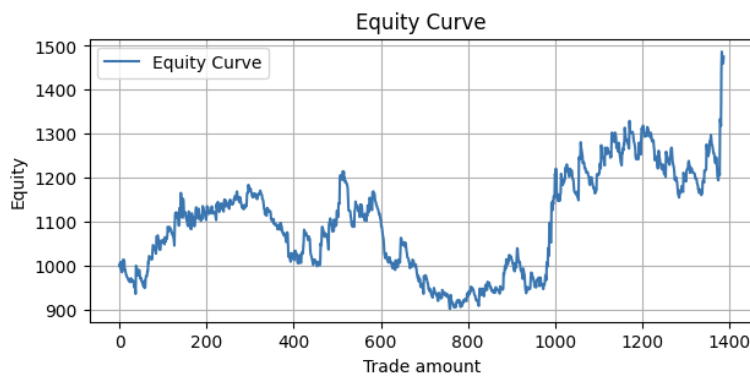
メトリクス：

Profit Factor: 1.10
Maximum Drawdown: -313.17
Average Win: 11.41
Average Loss: -5.01
Win Rate: 32.56%

収益性はかなり高いですが、改善の余地はあります。

考察

現在の取引の世界では、機械学習手法が主流となっており、再帰型ニューラルネットワーク(RNN)のようなより複雑なモデルを使うべきか、それとも隠れマルコフモデル(HMM)のようなシンプルなモデルにとどめるべきかという議論が続いています。

長所

1. シンプルさ：RNNのような複雑なモデルと比べて、実装が簡単で、各パラメータや処理内容の意味も理解しやすい。
2. 少ないデータ要件：モデルのパラメータ推定に必要な学習データが少なく、計算資源の消費も少ない。
3. 少ないパラメータ：過剰適合のに対して比較的耐性がある。

短所

1. 複雑さの限界：RNNのように複雑なパターンや非線形性を捉える能力には劣る可能性がある。
2. マルコフ過程の仮定：状態遷移が記憶を持たない（マルコフ性）と仮定しているが、実際の市場ではこの仮定が成り立たない場合がある。
3. 過剰適合のリスク：シンプルなモデルであっても、状態数を増やしすぎると過学習のリスクは残る。

機械学習を使ったアプローチでは、価格そのものよりもボラティリティを予測する手法が一般的です。これは、ボラティリティの方が予測しやすいとする学術的な知見に基づいています。ただし、本記事で紹介した手法には限界もあります。それは、各バーで取得する観測データ（50期間のローリング標準偏差によるボラティリティ）と、定義された隠れ状態（高/低ボラティリティ）がある程度相関しているため、予測としての意義がやや薄れるという点です。つまり、観測データだけをフィルターとして使っても、似たような結果が得られた可能性があるのです。

将来的な改良としては、隠れ状態の定義を見直すことや、2つ以上の状態を導入してモデルの堅牢性や予測精度を向上させることを検討すると良いでしょう。

結論

この記事では、まずトレンドフォロー戦略におけるボラティリティ状態予測器として隠れマルコフモデル(HMM)を利用する動機を説明し、HMMの基本的な概念を紹介しました。次に、MetaTrader 5を使ってMQL5でバックボーン戦略を開発し、データを取得、PythonでHMMを学習し、その後モデルをMetaTrader 5に統合するという戦略開発の全工程を解説しました。続いてバックテストをおこない、パフォーマンスを分析し、図を用いてHMMの背後にある数学的なロジックについて簡潔に説明しました。最後に、この戦略に対する私の考察と、このフレームワークを基にした将来の発展への期待を共有しました。

ファイルテーブル

ファイル名	使用法
HMM Test.mq5	取引EAの実装
ClassicTrendFollowing.mq5	ベースライン戦略EA
OHLC Getter.mq5	データを取得するためのEA
FileCSV.mqh	CSV形式でデータを保存するためのインクルードファイル
rollingBacktest.ipynb	モデルの学習と行列の取得