Hidden Markov Modelle für trendfolgende Volatilitätsprognosen

Einführung

Das Hidden Markov Model (HMM) ist ein leistungsstarkes statistisches Instrumente, das durch die Analyse beobachtbarer Kursbewegungen die zugrunde liegenden Marktzustände identifiziert. Im Handel verbessern HMM die Volatilitätsprognose und liefern Informationen für Trendfolgestrategien, indem sie Marktverschiebungen modellieren und antizipieren. 

In diesem Artikel stellen wir das vollständige Verfahren zur Entwicklung einer Trendfolgestrategie vor, die HMM zur Prognose der Volatilität als Filter einsetzt. Der Prozess umfasst die Entwicklung einer Backbone-Strategie in MQL5 unter Verwendung von MetaTrader 5, das Abrufen von Daten und das Trainieren der HMM in Python und die Integration der Modelle zurück in MetaTrader 5, wo wir die Strategie durch Backtesting validieren werden.

Motivation

In dem Buch „Evidence-Based Technical Analysis“ schlägt Dave Aronson vor, dass Händler ihre Strategien mit wissenschaftlichen Methoden entwickeln. Dieser Prozess beginnt mit der Aufstellung einer Hypothese auf der Grundlage der Intuition, die hinter der Idee steht, und deren strikter Überprüfung, um eine Verzerrung durch Datenschnüffelei zu vermeiden. In diesem Artikel werden wir versuchen, das Gleiche zu tun. Zunächst müssen wir versuchen zu verstehen, was ein Hidden Markov Modell ist und warum es uns bei der Entwicklung unserer Strategie helfen kann.

Ein Hidden Markov Model (HMM) ist ein unüberwachtes, maschinelles Lernmodell, das Systeme darstellt, bei denen der zugrunde liegende Zustand verborgen ist, aber durch beobachtbare Ereignisse oder Daten abgeleitet werden kann. Es basiert auf der Markov-Annahme, die besagt, dass der künftige Zustand des Systems nur von seinem gegenwärtigen Zustand und nicht von seinen vergangenen Zuständen abhängt. In einem HMM wird das System als eine Reihe von diskreten Zuständen modelliert, wobei jeder Zustand eine bestimmte Wahrscheinlichkeit für den Übergang in einen anderen Zustand hat. Diese Übergänge werden durch eine Reihe von Wahrscheinlichkeiten bestimmt, die als Übergangswahrscheinlichkeiten bezeichnet werden. Die beobachteten Daten (z. B. Vermögenspreise oder Marktrenditen) werden vom System erzeugt, aber die Zustände selbst sind nicht direkt beobachtbar, daher der Begriff „hidden“ (verborgen).

Dies sind seine Bestandteile:

1. Zustände: Dies sind die nicht beobachtbaren Bedingungen oder Zustände des Systems. Auf den Finanzmärkten können diese Zustände verschiedene Marktbedingungen repräsentieren, wie z. B. ein Auf- oder Abwärtstrend oder Zeiten hoher und niedriger Volatilität. Diese Zustände entwickeln sich auf der Grundlage bestimmter probabilistischer Regeln.

2. Übergangswahrscheinlichkeiten: Diese bestimmen die Wahrscheinlichkeit, von einem Zustand in einen anderen zu wechseln. Der Zustand des Systems zum Zeitpunkt t hängt nur von dem Zustand zum Zeitpunkt t-1 ab, was der Markov-Eigenschaft entspricht. Um diese Wahrscheinlichkeiten zu quantifizieren, werden Übergangsmatrizen verwendet.

3. Emissionswahrscheinlichkeiten: Diese beschreiben die Wahrscheinlichkeit der Beobachtung eines bestimmten Datenteils (z. B. eines Aktienkurses oder einer Rendite) in Abhängigkeit vom zugrunde liegenden Zustand. Jeder Zustand hat eine Wahrscheinlichkeitsverteilung, die die Wahrscheinlichkeit der Beobachtung bestimmter Marktbedingungen oder Preisbewegungen in diesem Zustand vorgibt.

4. Anfangswahrscheinlichkeiten: Diese stellen die Wahrscheinlichkeit dar, dass sich das System in einem bestimmten Zustand befindet und bilden den Ausgangspunkt für die Analyse des Modells.

Ausgehend von diesen Komponenten nutzt das Modell die Bayes'sche Inferenz, um auf der Grundlage der beobachteten Daten die wahrscheinlichste Abfolge der verborgenen Zustände im Zeitverlauf abzuleiten. Dies geschieht in der Regel durch Algorithmen wie den Vorwärts-Rückwärts-Algorithmus oder den Viterbi-Algorithmus, die die Wahrscheinlichkeit der beobachteten Daten in Abhängigkeit von der Abfolge der verborgenen Zustände schätzen.

Beim Handel ist die Volatilität ein wichtiger Faktor, der die Preise von Vermögenswerten und die Marktdynamik beeinflusst. HMM können bei der Prognose von Volatilität besonders effektiv sein, indem sie zugrunde liegende Marktregimes identifizieren, die nicht direkt beobachtbar sind, aber das Marktverhalten erheblich beeinflussen.

1. Identifizierung von Marktregimen: Durch die Unterteilung der Marktbedingungen in verschiedene Zustände (z. B. hohe oder niedrige Volatilität) können HMM die Verschiebungen in den Marktregimen erfassen. Auf diese Weise können Händler erkennen, wann der Markt wahrscheinlich Zeiten hoher Volatilität oder stabiler Bedingungen erleben wird, was sich direkt auf die Preise von Vermögenswerten auswirken kann.

2. Clustering der Volatilität: Die Finanzmärkte weisen ein Volatilitätscluster auf, d. h. auf Zeiten hoher Volatilität folgt häufig eine hohe Volatilität und auf Zeiten niedriger Volatilität folgt eine niedrige Volatilität. HMM können diese Eigenschaft modellieren, indem sie hohe Wahrscheinlichkeiten für das Verbleiben in Zuständen mit hoher oder niedriger Volatilität für längere Zeiträume zuweisen und so genauere Prognosen über zukünftige Marktbewegungen liefern.

3. Volatilitätsprognose: Durch die Beobachtung der Übergänge zwischen verschiedenen Marktzuständen können HMM Prognosen über die zukünftige Volatilität treffen. Wenn das Modell beispielsweise erkennt, dass sich der Markt in einem Zustand hoher Volatilität befindet, können die Händler größere Kursbewegungen vorhersehen und ihre Strategien entsprechend anpassen. Wenn sich der Markt auf eine niedrige Volatilität zubewegt, kann das Modell den Händlern helfen, ihr Risikoengagement anzupassen oder ihre Handelsstrategien zu ändern.

4. Anpassungsfähigkeit: HMM aktualisieren kontinuierlich ihre Wahrscheinlichkeitsverteilungen und Zustandsübergänge auf der Grundlage neuer Daten, wodurch sie an veränderte Marktbedingungen angepasst werden können. Diese Fähigkeit zur Anpassung in Echtzeit verschafft den Händlern einen Vorteil bei der Antizipation von Volatilitätsverschiebungen und der dynamischen Anpassung ihrer Strategien.

Wie von zahlreichen Wissenschaftlern untersucht, lautet unsere Hypothese, dass unsere Trendfolgestrategie bei hoher Volatilität tendenziell besser abschneidet, weil eine größere Marktbewegung den Kurs dazu bringt, einen Trend zu bilden. Wir planen den Einsatz von Hidden Markov Modellen (HMM), um die Volatilität zu clustern und Zustände hoher und niedriger Volatilität zu definieren. Dann wird ein Modell trainiert, das vorhersagt, ob die nächste Volatilität hoch oder niedrig sein wird. Wenn ein Strategiesignal auftritt, während das Modell eine hohe Volatilität vorhersagt, gehen wir ein Geschäft ein; andernfalls bleiben wir dem Markt fern.

Backbone-Strategie

Die Trendfolgestrategie, die wir verwenden werden, ist dieselbe, die ich in meinem vorherigen Artikel über maschinelles Lernen implementiert habe. Die grundlegende Logik beinhaltet zwei gleitende Durchschnitte: einen schnellen und einen langsamen. Ein Handelssignal wird generiert, wenn sich die beiden MAs kreuzen und die Handelsrichtung dem schnellen gleitenden Durchschnitt folgt, daher der Begriff „trendfolgend“. Das Ausstiegssignal tritt ein, wenn der Kurs den langsamen gleitenden Durchschnitt überschreitet, was mehr Spielraum für Trailing-Stops bietet. Der vollständige Code lautet wie folgt:

#include <Trade/Trade.mqh>
//XAU - 1h.
CTrade trade;

input ENUM_TIMEFRAMES TF = PERIOD_CURRENT;
input ENUM_MA_METHOD MaMethod = MODE_SMA;
input ENUM_APPLIED_PRICE MaAppPrice = PRICE_CLOSE;
input int MaPeriodsFast = 15;
input int MaPeriodsSlow = 25;
input int MaPeriods = 200;
input double lott = 0.01;
ulong buypos = 0, sellpos = 0;
input int Magic = 0;
int barsTotal = 0;
int handleMaFast;
int handleMaSlow;
int handleMa;

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
   trade.SetExpertMagicNumber(Magic);
   handleMaFast =iMA(_Symbol,TF,MaPeriodsFast,0,MaMethod,MaAppPrice);
   handleMaSlow =iMA(_Symbol,TF,MaPeriodsSlow,0,MaMethod,MaAppPrice);  
   handleMa = iMA(_Symbol,TF,MaPeriods,0,MaMethod,MaAppPrice); 
   return(INIT_SUCCEEDED);
  }

//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {

  }  

//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
  int bars = iBars(_Symbol,PERIOD_CURRENT);
  //Beware, the last element of the buffer list is the most recent data, not [0]
  if (barsTotal!= bars){
     barsTotal = bars;
     double maFast[];
     double maSlow[];
     double ma[];
     CopyBuffer(handleMaFast,BASE_LINE,1,2,maFast);
     CopyBuffer(handleMaSlow,BASE_LINE,1,2,maSlow);
     CopyBuffer(handleMa,0,1,1,ma);
     double bid = SymbolInfoDouble(_Symbol, SYMBOL_BID);
     double ask = SymbolInfoDouble(_Symbol, SYMBOL_ASK);
     double lastClose = iClose(_Symbol, PERIOD_CURRENT, 1);
     //The order below matters
     if(buypos>0&& lastClose<maSlow[1]) trade.PositionClose(buypos);
     if(sellpos>0 &&lastClose>maSlow[1])trade.PositionClose(sellpos);   
     if (maFast[1]>maSlow[1]&&maFast[0]<maSlow[0]&&buypos ==sellpos)executeBuy(); 
     if(maFast[1]<maSlow[1]&&maFast[0]>maSlow[0]&&sellpos ==buypos) executeSell();
     if(buypos>0&&(!PositionSelectByTicket(buypos)|| PositionGetInteger(POSITION_MAGIC) != Magic)){
      buypos = 0;
      }
     if(sellpos>0&&(!PositionSelectByTicket(sellpos)|| PositionGetInteger(POSITION_MAGIC) != Magic)){
      sellpos = 0;
      }
    }
 }

//+------------------------------------------------------------------+
//| Expert trade transaction handling function                       |
//+------------------------------------------------------------------+
void OnTradeTransaction(const MqlTradeTransaction& trans, const MqlTradeRequest& request, const MqlTradeResult& result) {
    if (trans.type == TRADE_TRANSACTION_ORDER_ADD) {
        COrderInfo order;
        if (order.Select(trans.order)) {
            if (order.Magic() == Magic) {
                if (order.OrderType() == ORDER_TYPE_BUY) {
                    buypos = order.Ticket();
                } else if (order.OrderType() == ORDER_TYPE_SELL) {
                    sellpos = order.Ticket();
                }
            }
        }
    }
}

//+------------------------------------------------------------------+
//| Execute sell trade function                                      |
//+------------------------------------------------------------------+
void executeSell() {      
       double bid = SymbolInfoDouble(_Symbol, SYMBOL_BID);
       bid = NormalizeDouble(bid,_Digits);
       trade.Sell(lott,_Symbol,bid);  
       sellpos = trade.ResultOrder();  
       }   

//+------------------------------------------------------------------+
//| Execute buy trade function                                       |
//+------------------------------------------------------------------+
void executeBuy() {
       double ask = SymbolInfoDouble(_Symbol, SYMBOL_ASK);
       ask = NormalizeDouble(ask,_Digits);
       trade.Buy(lott,_Symbol,ask);
       buypos = trade.ResultOrder();
}

Ich werde nicht weiter auf die Validierung und die Vorschläge zur Auswahl Ihrer Backbone-Strategie eingehen. Weitere Einzelheiten finden Sie in meinem früheren Artikel über maschinelles Lernen, der hier verlinkt ist.

Abrufen von Daten

In diesem Artikel werden wir zwei Zustände definieren: hohe Volatilität und niedrige Volatilität, dargestellt durch 1 bzw. 0. Die Volatilität wird als Standardabweichung der Renditen der letzten 50 Kerzen wie folgt definiert:

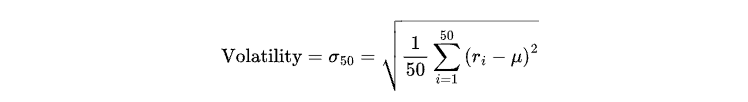
wobei:

• ri steht für die Rendite der i-ten Kerze (berechnet als prozentuale Kursveränderung zwischen aufeinanderfolgenden geschlossenen Kerzen).

• μ ist die mittlere Rendite der letzten 50 geschlossenen Kerzen, gegeben durch:

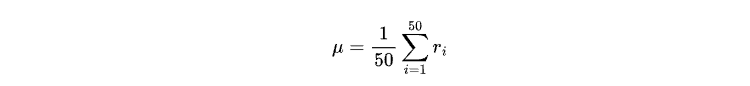
Für das Training des Modells benötigen wir nur die Schlusskursdaten und die Datumsangabe. Obwohl es möglich ist, Daten direkt vom MetaTrader 5-Terminal abzurufen, beschränken sich die meisten der vom Terminal bereitgestellten Daten auf echte Tick-Daten. Um längerfristige OHLC-Daten von unserem Broker zu erhalten, können wir einen Expert Advisor erstellen, der die Aufgabe übernimmt, OHLC herunterzuladen.

#include <FileCSV.mqh>

int barsTotal = 0;
CFileCSV csvFile;

input string fileName = "Name.csv";
string headers[] = {
    "time",
    "close"
};

string data[100000][2];
int indexx = 0;
vector xx;

input bool SaveData = true;

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {//Initialize model
   return(INIT_SUCCEEDED);
  }

//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
   if (!SaveData) return;
   if(csvFile.Open(fileName, FILE_WRITE|FILE_ANSI))
     {
      //Write the header
      csvFile.WriteHeader(headers);
      //Write data rows
      csvFile.WriteLine(data);
      //Close the file
      csvFile.Close();
     }
   else
     {
      Print("File opening error!");
     }

  }
  
//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
  int bars = iBars(_Symbol,PERIOD_CURRENT);
  
  if (barsTotal!= bars){
     barsTotal = bars;
   data[indexx][0] =(string)TimeTradeServer() ;
   data[indexx][1] = DoubleToString(iClose(_Symbol,PERIOD_CURRENT,1), 8); 
   indexx++;
   }
 }

Dieser Code liest und schreibt Finanzdaten (Zeit und Schlusskurs) in eine CSV-Datei. Bei jedem Tick wird geprüft, ob sich die Anzahl der Balken geändert hat. Ist dies der Fall, wird das Datenfeld mit der aktuellen Serverzeit und dem Schlusskurs des Symbols aktualisiert. Wenn das Skript deinitialisiert wird, schreibt es die gesammelten Daten in eine CSV-Datei, einschließlich Kopfzeilen und Datenzeilen. Es verwendet die Klasse CFileCSV für die Dateiverarbeitung.

Führen Sie diesen Expert Advisor im Strategietester mit dem gewünschten Zeitrahmen und Zeitraum aus, und es wird eine CSV-Datei im Verzeichnis /Tester/Agent-sth000 gespeichert.

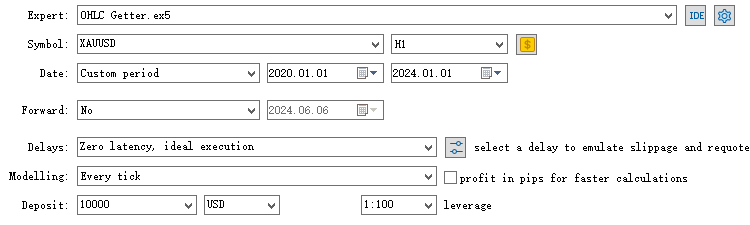
Wir werden die Daten der Stichprobe vom 1. Januar 2020 bis zum 1. Januar 2024 für die Ausbildung verwenden. Die Daten vom 1. Januar 2024 bis zum 1. Januar 2025 werden für Out-of-Sample-Tests verwendet.

Ausbildungsmodelle

Öffnen Sie nun einen beliebigen Python-Editor und stellen Sie sicher, dass Sie die erforderlichen Bibliotheken mit pip installieren, wie in diesem Abschnitt gefordert.

Die CSV-Datei enthält zunächst nur eine Spalte, in der Zeit- und Abschlusswerte gemischt und durch ein Semikolon getrennt sind. Die Werte werden zur besseren Aufbewahrung als Zeichenketten gespeichert. Dazu lesen wir die CSV-Datei zunächst wie folgt, um die beiden Spalten zu trennen und die Zeichenketten in die Typen Datetime und Float umzuwandeln.

import pandas as pd
data = pd.read_csv("XAU_test.csv",sep=";")
data = data.dropna()
data["close"] = data["close"].astype(float)
data['time'] = pd.to_datetime(data['time'])
data.set_index('time', inplace=True)

Die Volatilität kann mit dieser Zeile leicht berechnet werden:

data['volatility'] = data['returns'].rolling(window=50).std()

Als Nächstes wird die Volatilitätsverteilung visualisiert, um ihre Merkmale besser zu verstehen. Es ist deutlich zu erkennen, dass sie annähernd einer Normalverteilung folgt.

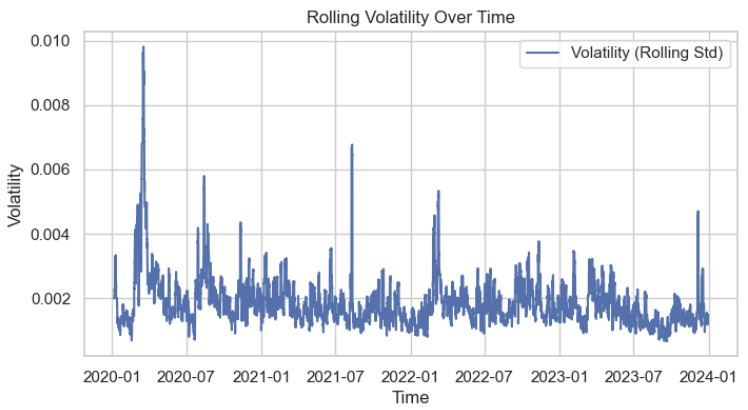
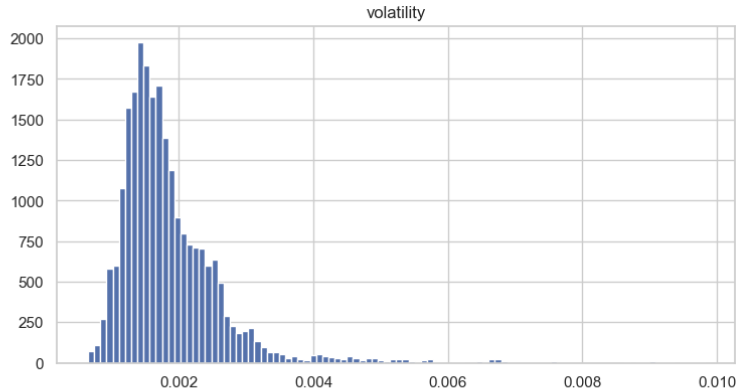
Wir verwenden den Test von Augmented Dickey-Fuller (ADF), um zu überprüfen, ob die Volatilitätsdaten stationär sind. Der Test sollte höchstwahrscheinlich das folgende Ergebnis liefern:

Augmented Dickey-Fuller Test: Volatility
ADF Statistic: -13.120552520156329
p-value: 1.5664189630119278e-24
# Lags Used: 46
Number of Observations Used: 23516
=> The series is likely stationary.

Obwohl Hidden Markov Modelle (HMM) aufgrund ihres rollierenden Aktualisierungsverhaltens für stationäre Daten nicht unbedingt erforderlich sind, sind stationäre Daten für den Clustering-Prozess von großem Nutzen und verbessern die Modellgenauigkeit.

Obwohl die Volatilitätsdaten wahrscheinlich stationär und normalverteilt sind, wollen wir sie dennoch auf eine Standardnormalverteilung normalisieren, damit der Bereich überschaubarer wird. 

In der Statistik wird dieser Vorgang als „Skalierung“ bezeichnet, wobei jede normalverteilte Zufallsvariable x durch die folgende Operation in eine Standardnormalverteilung N(0,1) transformiert werden kann:

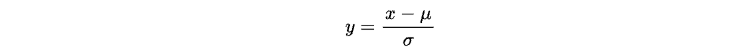
Dabei steht μ für den Mittelwert und σ für die Standardabweichung von x.

Denken Sie daran, dass wir später, wenn wir uns wieder in den MetaTrader 5-Editor integrieren, dieselben Normalisierungsoperationen durchführen müssen. Aus diesem Grund müssen wir auch den Mittelwert und die Standardabweichung speichern.

from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaled_volatility = scaler.fit_transform(data[['volatility']])
scaled_volatility = scaled_volatility.reshape(-1, 1)
scaler_mean = scaler.mean_[0]  # Mean of the volatility feature
scaler_std = scaler.scale_[0]  # Standard deviation of the volatility feature

Anschließend trainieren wir das Modell anhand der skalierten Volatilitätsdaten wie folgt:

from hmmlearn import hmm
import numpy as np
# Define the number of hidden states
n_states = 2
# Initialize the Gaussian HMM
model = hmm.GaussianHMM(n_components=n_states, covariance_type="full", n_iter=100, random_state=42, verbose = True)
# Fit the model to the scaled volatility data
model.fit(scaled_volatility)

Bei der Prognose der versteckten Zustände für jeden Trainingsdatenpunkt erscheint die Clusterverteilung recht vernünftig, mit nur geringen Fehlern.

# Predict the hidden states
hidden_states = model.predict(scaled_volatility)

# Add the hidden states to your dataframe
data['hidden_state'] = hidden_states
plt.figure(figsize=(14, 6))
for state in range(n_states):
    state_mask = data['hidden_state'] == state
    plt.plot(data.index[state_mask], data['volatility'][state_mask], 'o', label=f'State {state}')
plt.title('Hidden States and Rolling Volatility')
plt.xlabel('Time')
plt.ylabel('Volatility')
plt.legend()
plt.show()

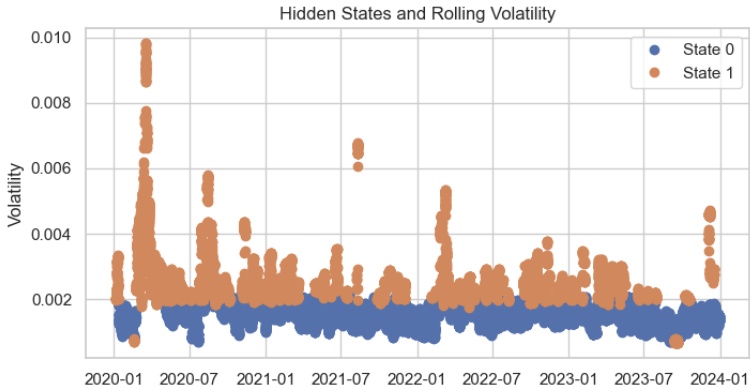
Schließlich formatieren wir die gewünschte Ausgabe in MQL5-Sprache und speichern sie in einer JSON-Header-Datei, was das Kopieren und Einfügen der entsprechenden Matrixwerte in den MetaTrader 5-Editor erleichtert.

import json

# Your HMM model parameters
transition_matrix = model.transmat_
means = model.means_
covars = model.covars_

# Construct the data in the required format
data = {
    "A": [
        [transition_matrix[0, 0], transition_matrix[0, 1]],
        [transition_matrix[1, 0], transition_matrix[1, 1]]
    ],
    "mu": [means[0, 0], means[1, 0]],
    "sigma_sq": [covars[0, 0], covars[1, 0]],
    "scaler_mean": scaler_mean,
    "scaler_std": scaler_std
}

# Create the output content in the desired format
output_str = """
const double A[2][2] = { 
    {%.16f, %.16f}, 
    {%.16f, %.16f}
};
const double mu[2] = {%.16f, %.16f};
const double sigma_sq[2] = {%.16f, %.16f};
const double scaler_mean = %.16f;
const double scaler_std = %.16f;
""" % (
    data["A"][0][0], data["A"][0][1], data["A"][1][0], data["A"][1][1],
    data["mu"][0], data["mu"][1],
    data["sigma_sq"][0], data["sigma_sq"][1],
    data["scaler_mean"], data["scaler_std"]
)

# Write to a file
with open('model_parameters.h', 'w') as f:
    f.write(output_str)

print("Parameters saved to model_parameters.h")

Die resultierende Datei sollte in etwa so aussehen:

const double A[2][2] = { 
    {0.9941485184089348, 0.0058514815910651}, 
    {0.0123877225858242, 0.9876122774141759}
};
const double mu[2] = {-0.4677410059727503, 0.9797900996225393};
const double sigma_sq[2] = {0.1073520489683212, 1.4515804806463273};
const double scaler_mean = 0.0018685496675093;
const double scaler_std = 0.0008350190448735;

Wir sollten sie als globale Variablen in den Code unseres EAs einfügen.

Integration

Kehren wir nun zum MetaTrader 5 Code-Editor zurück und bauen auf unserem ursprünglichen Strategiecode auf.

Zunächst müssen wir Funktionen zur Berechnung der rollierenden Volatilität erstellen, die ständig aktualisiert wird.

//+------------------------------------------------------------------+
//| Get volatility Function                                          |
//+------------------------------------------------------------------+
void GetVolatility(){
// Step 1: Get the last two close prices to compute the latest percent change
        double close_prices[2];
        int copied = CopyClose(_Symbol, PERIOD_CURRENT, 1, 2, close_prices);
        if(copied != 2){
            Print("Failed to copy close prices. Copied: ", copied);
            return;
        }
        
        // Step 2: Compute the latest percent change
        double latest_close = close_prices[0];
        double previous_close = close_prices[1];
        double percent_change = 0.0;
        if(previous_close != 0){
            percent_change = (latest_close - previous_close) / previous_close;
        }
        else{
            Print("Previous close price is zero. Percent change set to 0.");
        }
        
        // Step 3: Update the percent_changes buffer
        percent_changes[percent_change_index] = percent_change;
        percent_change_index++;
        if(percent_change_index >= 50){
            percent_change_index = 0;
            percent_change_filled = true;
        }
        
        // Step 4: Once the buffer is filled, compute the rolling std dev
        if(percent_change_filled){
            double current_stddev = ComputeStdDev(percent_changes, 50);
            // Step 5: Scale the std dev
            double scaled_stddev = (current_stddev - scaler_mean) / scaler_std;
            
            // Step 6: Update the volatility array (ring buffer for Viterbi)
            // Shift the volatility array to make room for the new std dev
            for(int i = 0; i < 49; i++){
                volatility[i] = volatility[i+1];
            }
            volatility[49] = scaled_stddev; // Insert the latest std dev
       }
}

//+------------------------------------------------------------------+
//| Compute Standard Deviation Function                              |
//+------------------------------------------------------------------+
double ComputeStdDev(double &data[], int size)
{
    if(size <= 1)
        return 0.0;
    
    double sum = 0.0;
    double sum_sq = 0.0;
    for(int i = 0; i < size; i++)
    {
        sum += data[i];
        sum_sq += data[i] * data[i];
    }
    double mean = sum / size;
    double variance = (sum_sq - (sum * sum) / size) / (size - 1);
    return MathSqrt(variance);
}

• GetVolatility() berechnet und verfolgt die rollierende Volatilität im Zeitverlauf unter Verwendung der skalierten Standardabweichung der prozentualen Kursänderungen.
• ComputeDtsDev() dient als Hilfsfunktion zur Berechnung der Standardabweichung eines gegebenen Datenfeldes. 

Dann schreiben wir zwei Funktionen, die den aktuellen verborgenen Zustand auf der Grundlage unserer Matrizen und der aktuellen rollierenden Volatilität berechnen.

//+------------------------------------------------------------------+
//| Viterbi Algorithm Implementation in MQL5                         |
//+------------------------------------------------------------------+
int Viterbi(double &obs[], int &states[])
{
    // Initialize dynamic programming tables
    double T1[2][50];
    int T2[2][50];

    // Initialize first column
    for(int s = 0; s < 2; s++)
    {
         double emission_prob = (1.0 / MathSqrt(2 * M_PI * sigma_sq[s])) * MathExp(-MathPow(obs[0] - mu[s], 2) / (2 * sigma_sq[s])) + 1e-10;

        T1[s][0] = MathLog(pi[s]) + MathLog(emission_prob);
        T2[s][0] = 0;
    }

    // Fill the tables
    for(int t = 1; t < 50; t++)
    {
        for(int s = 0; s < 2; s++)
        {
            double max_prob = -DBL_MAX; // Initialize to negative infinity
            int max_state = 0;
            for(int s_prev = 0; s_prev < 2; s_prev++)
            {
                double transition_prob = A[s_prev][s];
                if(transition_prob <= 0) transition_prob = 1e-10; // Prevent log(0)
                double prob = T1[s_prev][t-1] + MathLog(transition_prob);
                if(prob > max_prob)
                {
                    max_prob = prob;
                    max_state = s_prev;
                }
            }
            // Calculate emission probability with epsilon
            double emission_prob = (1.0 / MathSqrt(2 * M_PI * sigma_sq[s])) * MathExp(-MathPow(obs[t] - mu[s], 2) / (2 * sigma_sq[s])) + 1e-10;
            T1[s][t] = max_prob + MathLog(emission_prob);
            T2[s][t] = max_state;
        }
    }

    // Backtrack to find the optimal state sequence
    // Find the state with the highest probability in the last column
    double max_final_prob = -DBL_MAX;
    int last_state = 0;
    for(int s = 0; s < 2; s++)
    {
        if(T1[s][49] > max_final_prob)
        {
            max_final_prob = T1[s][49];
            last_state = s;
        }
    }    
    // Initialize the states array
    ArrayResize(states, 50);
    states[49] = last_state;
    // Backtrack
    for(int t = 48; t >= 0; t--)
    {
        states[t] = T2[states[t+1]][t+1];
    }
    return 0; // Success
}

//+------------------------------------------------------------------+
//| Predict Current Hidden State                                     |
//+------------------------------------------------------------------+
int PredictCurrentState(double &obs[])
{   
    // Define states array
    int states[50];
    
    // Apply Viterbi
    int ret = Viterbi(obs, states);
    if(ret != 0)
        return -1; // Error
    
    // Return the most probable current state
    return states[49];
}

Die Funktion Viterbi() implementiert den Viterbi-Algorithmus, eine Methode der dynamischen Programmierung zum Auffinden der wahrscheinlichsten Abfolge von verborgenen Zuständen in einem Hidden Markov Model (HMM) unter Berücksichtigung der beobachteten Daten (obs[]).

1. Initialisierung:

• Dynamische Programmiertabellen:

  • T1[s][t] : Log-Wahrscheinlichkeit der wahrscheinlichsten Zustandsfolge, die zum Zeitpunkt t im Zustand s endet.
  • T2[s][t] : Zeigertabelle, die den Zustand speichert, der die Wahrscheinlichkeit des Übergangs zum Zustand s zum Zeitpunkt t maximiert.

• Erster Zeitschritt (t = 0):

  • Berechnen der Anfangswahrscheinlichkeiten unter Verwendung der Vorwahrscheinlichkeiten für jeden Zustand (π[s]) und der Emissionswahrscheinlichkeiten für die erste Beobachtung (obs[0]).

2. Rekursive Berechnung:

Für jeden Zeitschritt t von 1 bis 49 :

1. Für jeden Zustand s:

   Berechnen der maximale Wahrscheinlichkeit des Übergangs von einem beliebigen vorherigen Zustand s_prev zu s anhand der folgenden Gleichung:               

   

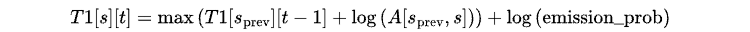
   Hier wird die Übergangswahrscheinlichkeit A[s_prev, s] in den log-Raum umgewandelt, um einen numerischen Unterlauf zu vermeiden.

2. Speichern des Zustands s_prev, der die Wahrscheinlichkeit in T2[s][t] maximiert hat.

3. Backtracking, um den optimalen Pfad zu finden:

1. Beginnen mit dem Zustand, der beim letzten Zeitschritt (t = 49) die höchste Wahrscheinlichkeit hatte.
2. Rückverfolgung durch T2, um die wahrscheinlichste Abfolge von Zuständen zu rekonstruieren und das Ergebnis in states[] zu speichern.

Die endgültige Ausgabe ist states[], die die wahrscheinlichste Zustandsfolge enthält.

Die Funktion PredictCurrentState() verwendet die Funktion Viterbi(), um den aktuellen verborgenen Zustand auf der Grundlage von Beobachtungen vorherzusagen.

1. Zur Initialisierung wird ein Array states[50] definiert, um das Ergebnis von Viterbi() zu speichern.
2. Dann übergibt sie die Beobachtungssequenz obs[] an die Funktion Viterbi(), um die wahrscheinlichste Sequenz der verborgenen Zustände zu berechnen.
3. Schließlich wird der Zustand im letzten Zeitschritt (states[49]) zurückgegeben, der den wahrscheinlichsten aktuellen verborgenen Zustand darstellt.

Wenn Sie die Mathematik dahinter verwirrt, empfehle ich Ihnen, sich im Internet einige intuitivere Illustrationen anzusehen. Ich werde hier versuchen, kurz zu erklären, was wir tun.

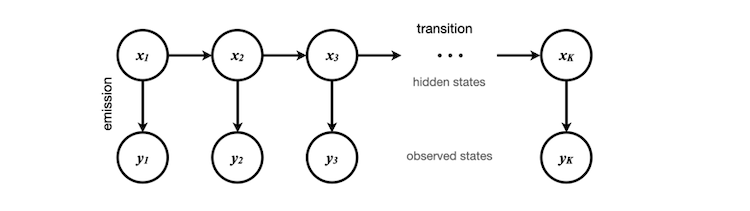
Die beobachteten Zustände sind die skalierten Volatilitätsdaten, die wir erhalten und in dem Array obs[] speichern können, das in diesem Fall 50 Elemente enthält. Diese Elemente entsprechen y1, y2, ... y50 im Diagramm. Die entsprechenden verborgenen Zustände können entweder 0 oder 1 sein und stellen die abstrakten Bedingungen der aktuellen Volatilität (hoch oder niedrig) dar.

Diese versteckten Zustände werden während des Modelltrainings, das wir zuvor in Python durchgeführt haben, durch Clustering bestimmt. Es ist wichtig zu wissen, dass der Python-Code nicht genau weiß, wofür die einzelnen Zahlen stehen - er weiß nur, wie man die Daten clustert und die Merkmale der Übergänge zwischen den Zuständen identifiziert.

Zu Beginn weisen wir x1 nach dem Zufallsprinzip einen Zustand zu, wobei wir davon ausgehen, dass jeder Zustand das gleiche Gewicht hat. Wenn wir diese Annahme nicht treffen wollen, könnten wir die stationäre Verteilung des Ausgangszustands anhand unserer Trainingsdaten berechnen, die der Eigenvektor der Übergangsmatrix wäre. Der Einfachheit halber nehmen wir an, dass der Vektor der stationären Verteilung [0,5, 0,5] ist.

Durch das Training des Hidden Markov Modells erhalten wir die Wahrscheinlichkeit des Übergangs in einen anderen versteckten Zustand und die Wahrscheinlichkeit, eine andere Beobachtung zu senden. Mit Hilfe des Satzes von Bayes können wir die Wahrscheinlichkeit aller möglichen Pfade für jede Markov-Kette berechnen und den wahrscheinlichsten Pfad bestimmen. Auf diese Weise lässt sich das wahrscheinlichste Ergebnis für x50, den letzten verborgenen Zustand in der Sequenz, ermitteln.

Schließlich passen wir die ursprüngliche Logik in OnTick() an, indem wir die versteckten Zustände für jeden Abschluss berechnen und ein Eingabekriterium hinzufügen, dass der versteckte Zustand gleich 1 sein muss.

//+------------------------------------------------------------------+
//| Check Volatility is filled Function                              |
//+------------------------------------------------------------------+
bool IsVolatilityFilled(){
     bool volatility_filled = true;
     for(int i = 0; i < 50; i++){
         if(volatility[i] == 0){
             volatility_filled = false;
             break;
         }
     }
     if(!volatility_filled){
         Print("Volatility buffer not yet filled.");
         return false;
     }
     else return true;
}  

//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
  int bars = iBars(_Symbol,PERIOD_CURRENT);
  if (barsTotal!= bars){
     barsTotal = bars;
     double maFast[];
     double maSlow[];
     double ma[];  
     
     GetVolatility();
     if(!IsVolatilityFilled()) return;
     int currentState = PredictCurrentState(volatility);
     
     CopyBuffer(handleMaFast,BASE_LINE,1,2,maFast);
     CopyBuffer(handleMaSlow,BASE_LINE,1,2,maSlow);
     CopyBuffer(handleMa,0,1,1,ma);

     double bid = SymbolInfoDouble(_Symbol, SYMBOL_BID);
     double ask = SymbolInfoDouble(_Symbol, SYMBOL_ASK);
     double lastClose = iClose(_Symbol, PERIOD_CURRENT, 1);
     //The order below matters
     if(buypos>0&& lastClose<maSlow[1]) trade.PositionClose(buypos);
     if(sellpos>0 &&lastClose>maSlow[1])trade.PositionClose(sellpos);        
     if (maFast[1]>maSlow[1]&&maFast[0]<maSlow[0]&&buypos ==sellpos&&currentState==1)executeBuy(); 
     if(maFast[1]<maSlow[1]&&maFast[0]>maSlow[0]&&sellpos ==buypos&&currentState==1) executeSell();
     
     if(buypos>0&&(!PositionSelectByTicket(buypos)|| PositionGetInteger(POSITION_MAGIC) != Magic)){
      buypos = 0;
      }
     if(sellpos>0&&(!PositionSelectByTicket(sellpos)|| PositionGetInteger(POSITION_MAGIC) != Magic)){
      sellpos = 0;
      }
    }
 }

Backtest

Wir haben das Modell anhand der Daten der Stichprobe vom 1. Januar 2020 bis zum 1. Januar 2024 trainiert. Nun wollen wir die Ergebnisse für den Zeitraum vom 1. Januar 2024 bis zum 1. Januar 2025 für den XAUUSD im 1-Stunden-Zeitrahmen testen.

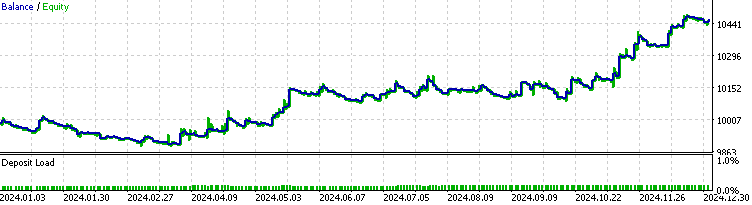
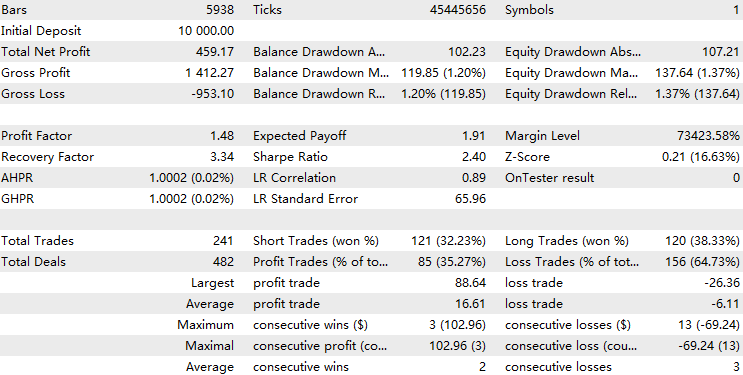
Zunächst wird die Leistung mit der Basislinie verglichen, d. h. mit dem Ergebnis ohne Integration des HMM.

Nun führen wir einen Backtest des EA mit dem implementierten HMM-Modellfilter durch.

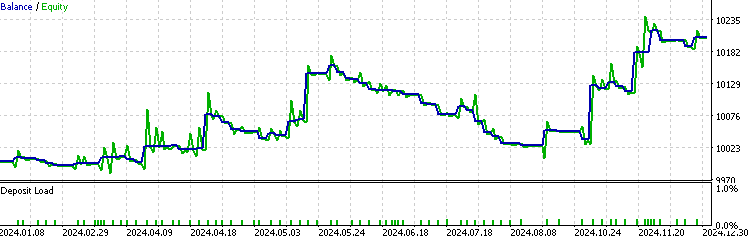
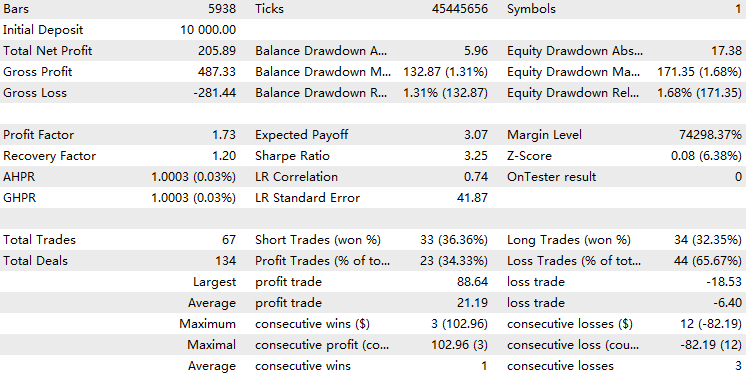
Wir können sehen, dass der EA mit der HMM-Implementierung etwa 70 % der gesamten Handelsgeschäfte herausgefiltert hat. Mit einem Gewinnfaktor von 1,73 gegenüber 1,48 übertrifft er die Baseline und weist eine bessere Sharpe Ratio auf. Dies deutet darauf hin, dass das von uns trainierte HMM-Modell über einen gewissen Grad an Vorhersagbarkeit verfügt.

Wenn wir einen rollierenden Backtest durchführen, bei dem wir dieses 4-Jahres-Trainings- und 1-Jahres-Testverfahren ab 2004 wiederholen, und alle Ergebnisse in einer Kapitalkurve zusammenfassen, erhalten wir folgendes Ergebnis:

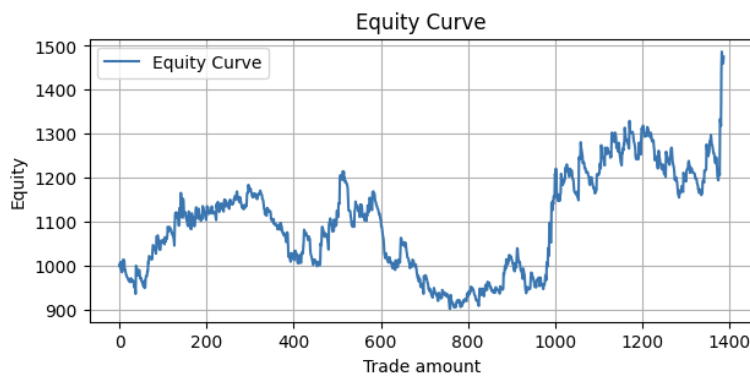
Metrics:

Profit Factor: 1.10
Maximum Drawdown: -313.17
Average Win: 11.41
Average Loss: -5.01
Win Rate: 32.56%

Dies ist recht rentabel, aber es gibt noch Raum für Verbesserungen.

Überlegungen

In der heutigen Handelswelt, die von Methoden des maschinellen Lernens beherrscht wird, gibt es eine ständige Debatte darüber, ob komplexere Modelle wie rekurrente neuronale Netze (RNN) oder einfachere Modelle wie Hidden Markov Modelle (HMM) verwendet werden sollen.

Vorteile:

1. Einfachheit: Einfacher zu implementieren und zu interpretieren im Vergleich zu komplexen Modellen wie RNN, bei denen nicht klar ist, was die einzelnen Parameter und Operationen bedeuten.
2. Weniger Daten erforderlich: Erfordert weniger Trainingsbeispiele zur Schätzung von Modellparametern und benötigt weniger Rechenleistung.
3. Weniger Parameter: Widerstandsfähiger gegen Überanpassungsprobleme.

Nachteile

1. Begrenzte Komplexität: Sie können komplizierte Muster in flüchtigen Daten, die RNNs modellieren können, nicht erfassen.
2. Annahme eines Markov-Prozesses: Es wird davon ausgegangen, dass die Volatilitätsübergänge gedächtnislos sind, was in realen Märkten möglicherweise nicht der Fall ist.
3. Risiko der Überanpassung: Trotz seiner Einfachheit würde das HMM bei zu vielen Zuständen zu einer Überanpassung neigen.

Ein beliebter Ansatz ist die Prognose der Volatilität und nicht der Preise mit Hilfe von Methoden des maschinellen Lernens, da Wissenschaftler festgestellt haben, dass Volatilitätsprognosen zuverlässiger sind. Eine Einschränkung des in diesem Artikel vorgestellten Ansatzes besteht jedoch darin, dass die Beobachtungen, die wir bei jedem neuen Balken abrufen (rollierende 50-Perioden-Durchschnittsvolatilität), und die von uns definierten verborgenen Zustände (hohe/niedrige Volatilitätszustände) in gewissem Maße korreliert sind, was zu einer geringeren Prognosekraft führt. Dies deutet darauf hin, dass man ähnliche Ergebnisse hätte erzielen können, wenn man einfach die Beobachtungsdaten als Filter verwendet hätte.

Für die zukünftige Entwicklung möchte ich die Leser ermutigen, andere Definitionen für verborgene Zustände zu erforschen und mit mehr als zwei Zuständen zu experimentieren, um die Robustheit und Prognosekraft des Modells zu verbessern.

Schlussfolgerung

In diesem Artikel haben wir zunächst die Motivation für den Einsatz von HMM als Volatilitätsprognose für eine Trendfolgestrategie erläutert und gleichzeitig das Grundkonzept von HMM vorgestellt. Als Nächstes haben wir den gesamten Strategieentwicklungsprozess durchlaufen, einschließlich der Entwicklung einer Backbone-Strategie in MQL5 unter Verwendung von MetaTrader 5, dem Abrufen von Daten und dem Training der HMM in Python, gefolgt von der Integration der Modelle zurück in MetaTrader 5. Anschließend führten wir einen Backtest durch und analysierten seine Leistung, wobei wir die mathematische Logik hinter HMM anhand eines Diagramms kurz erläuterten. Abschließend teilte ich meine Überlegungen zur Strategie mit und äußerte meine Hoffnungen für die künftige Entwicklung auf der Grundlage dieses Rahmens.

Datei-Tabelle

Datei Name	Verwendung
HMM Test.mq5	Die Implementierung des Handels-EAs
Classic Trend Following.mq5	Der ES der Basisstrategie
OHLC Getter.mq5	Der EA zum Abrufen von Daten
FileCSV.mqh	Die Include-Datei zum Speichern von Daten in CSV
rollingBacktest.ipynb	Für das Training des Modells und die Erstellung der Matrizen