Modelos ocultos de Markov para la predicción de la volatilidad siguiendo tendencias

Introducción

Los modelos ocultos de Markov (HMM) son potentes herramientas estadísticas que identifican los estados subyacentes del mercado mediante el análisis de los movimientos observables de los precios. En el ámbito bursátil, los HMM mejoran la predicción de la volatilidad y proporcionan información para las estrategias de seguimiento de tendencias mediante la modelización y la anticipación de los cambios en los regímenes de mercado. 

En este artículo, presentaremos el procedimiento completo para desarrollar una estrategia de seguimiento de tendencias que utiliza HMM para predecir la volatilidad como filtro. El proceso implica desarrollar una estrategia central en MQL5 utilizando MetaTrader 5, obtener datos y entrenar los HMM en Python, e integrar los modelos nuevamente en MetaTrader 5, donde validaremos la estrategia mediante pruebas retrospectivas.

Motivación

En el libro Evidence-Based Technical Analysis (Análisis técnico basado en la evidencia), Dave Aronson sugiere que los operadores desarrollen sus estrategias utilizando métodos científicos. Este proceso comienza con la formulación de una hipótesis basada en la intuición que subyace a la idea y su rigurosa comprobación para evitar el sesgo de espionaje de datos. En este artículo, intentaremos hacer lo mismo. En primer lugar, debemos intentar comprender qué es el modelo oculto de Markov y por qué podría beneficiarnos en el desarrollo de nuestra estrategia.

Un modelo oculto de Markov (HMM) es un modelo de aprendizaje automático no supervisado que representa sistemas en los que el estado subyacente está oculto, pero puede inferirse a través de eventos o datos observables. Se basa en la hipótesis de Markov, que postula que el estado futuro del sistema depende únicamente de su estado actual y no de sus estados pasados. En un HMM, el sistema se modela como un conjunto de estados discretos, y cada estado tiene una probabilidad determinada de pasar a otro estado. Estas transiciones se rigen por un conjunto de probabilidades conocidas como probabilidades de transición. Los datos observados (como los precios de los activos o los rendimientos del mercado) son generados por el sistema, pero los estados en sí mismos no son directamente observables, de ahí el término «ocultos».

Estos son sus componentes:

1. Estados: Son las condiciones o regímenes no observables del sistema. En los mercados financieros, estos estados pueden representar diferentes condiciones del mercado, como un mercado alcista, un mercado bajista o períodos de alta y baja volatilidad. Estos estados evolucionan basándose en ciertas reglas probabilísticas.

2. Probabilidades de transición: Definen la probabilidad de pasar de un estado a otro. El estado del sistema en el momento t solo depende del estado en el momento t-1, adhiriéndose a la propiedad de Markov. Las matrices de transición se utilizan para cuantificar estas probabilidades.

3. Probabilidades de emisión: Describen la probabilidad de observar un dato concreto (por ejemplo, el precio de una acción o su rendimiento) dado el estado subyacente. Cada estado tiene una distribución de probabilidad que determina la probabilidad de observar determinadas condiciones de mercado o movimientos de precios cuando se encuentra en ese estado.

4. Probabilidades iniciales: Representan la probabilidad de que el sistema comience en un estado concreto, lo que proporciona el punto de partida para el análisis del modelo.

Dados estos componentes, el modelo utiliza la inferencia bayesiana para inferir la secuencia más probable de estados ocultos a lo largo del tiempo basándose en los datos observados. Esto se suele hacer mediante algoritmos como el algoritmo adelante-atrás o el algoritmo de Viterbi, que estiman la probabilidad de los datos observados dada la secuencia de estados ocultos.

En el comercio, la volatilidad es un factor clave que influye en los precios de los activos y la dinámica del mercado. Los HMM pueden ser especialmente eficaces para predecir la volatilidad, ya que identifican los regímenes subyacentes del mercado que no son directamente observables, pero que influyen significativamente en el comportamiento del mercado.

1. Identificación de regímenes de mercado: Al segmentar las condiciones del mercado en estados distintos (como alta volatilidad o baja volatilidad), los HMM pueden captar los cambios en los regímenes de mercado. Esto permite a los operadores comprender cuándo es probable que el mercado experimente períodos de alta volatilidad o condiciones estables, lo que puede afectar directamente a los precios de los activos.

2. Agrupación de la volatilidad: Los mercados financieros muestran una agrupación de la volatilidad, en la que los periodos de alta volatilidad suelen ir seguidos de alta volatilidad, y los periodos de baja volatilidad van seguidos de baja volatilidad. Los HMM pueden modelar esta característica asignando altas probabilidades de permanecer en estados de alta volatilidad o baja volatilidad durante períodos prolongados, lo que proporciona predicciones más precisas de los movimientos futuros del mercado.

3. Previsión de la volatilidad: Al observar las transiciones entre diferentes estados del mercado, los HMM pueden proporcionar información predictiva sobre la volatilidad futura. Por ejemplo, si el modelo identifica que el mercado se encuentra en un estado de alta volatilidad, los operadores pueden anticipar movimientos de precios más amplios y ajustar sus estrategias en consecuencia. Además, si el mercado está pasando a un estado de baja volatilidad, el modelo puede ayudar a los operadores a ajustar su exposición al riesgo o adaptar sus estrategias de negociación.

4. Adaptabilidad: Los HMM actualizan continuamente sus distribuciones de probabilidad y transiciones de estado basándose en nuevos datos, lo que los hace adaptables a las condiciones cambiantes del mercado. Esta capacidad de ajustarse en tiempo real ofrece a los operadores una ventaja a la hora de anticipar cambios en la volatilidad y ajustar sus estrategias de forma dinámica.

Según los estudios realizados por numerosos académicos, nuestra hipótesis es que, en condiciones de alta volatilidad, nuestra estrategia de seguimiento de tendencias tiende a obtener mejores resultados, ya que un mayor movimiento del mercado impulsa al precio a formar una tendencia. Tenemos previsto utilizar modelos ocultos de Markov (HMM) para agrupar la volatilidad y definir estados de volatilidad alta y baja. A continuación, entrenaremos un modelo para predecir si el próximo estado de volatilidad será alto o bajo. Si se produce una señal estratégica mientras el modelo predice un estado de alta volatilidad, entraremos en una operación; de lo contrario, nos mantendremos al margen del mercado.

Estrategia fundamental

La estrategia de seguimiento de tendencias que utilizaremos es la misma que implementé en mi artículo anterior sobre aprendizaje automático. La lógica básica implica dos medias móviles: una rápida y otra lenta. Se genera una señal de operación cuando las dos medias móviles se cruzan, y la dirección de la operación sigue la media móvil rápida, de ahí el término «seguimiento de tendencias». La señal de salida se produce cuando el precio cruza la media móvil lenta, lo que deja más margen para los stops dinámicos. El código completo es el siguiente:

#include <Trade/Trade.mqh>
//XAU - 1h.
CTrade trade;

input ENUM_TIMEFRAMES TF = PERIOD_CURRENT;
input ENUM_MA_METHOD MaMethod = MODE_SMA;
input ENUM_APPLIED_PRICE MaAppPrice = PRICE_CLOSE;
input int MaPeriodsFast = 15;
input int MaPeriodsSlow = 25;
input int MaPeriods = 200;
input double lott = 0.01;
ulong buypos = 0, sellpos = 0;
input int Magic = 0;
int barsTotal = 0;
int handleMaFast;
int handleMaSlow;
int handleMa;

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
   trade.SetExpertMagicNumber(Magic);
   handleMaFast =iMA(_Symbol,TF,MaPeriodsFast,0,MaMethod,MaAppPrice);
   handleMaSlow =iMA(_Symbol,TF,MaPeriodsSlow,0,MaMethod,MaAppPrice);  
   handleMa = iMA(_Symbol,TF,MaPeriods,0,MaMethod,MaAppPrice); 
   return(INIT_SUCCEEDED);
  }

//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {

  }  

//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
  int bars = iBars(_Symbol,PERIOD_CURRENT);
  //Beware, the last element of the buffer list is the most recent data, not [0]
  if (barsTotal!= bars){
     barsTotal = bars;
     double maFast[];
     double maSlow[];
     double ma[];
     CopyBuffer(handleMaFast,BASE_LINE,1,2,maFast);
     CopyBuffer(handleMaSlow,BASE_LINE,1,2,maSlow);
     CopyBuffer(handleMa,0,1,1,ma);
     double bid = SymbolInfoDouble(_Symbol, SYMBOL_BID);
     double ask = SymbolInfoDouble(_Symbol, SYMBOL_ASK);
     double lastClose = iClose(_Symbol, PERIOD_CURRENT, 1);
     //The order below matters
     if(buypos>0&& lastClose<maSlow[1]) trade.PositionClose(buypos);
     if(sellpos>0 &&lastClose>maSlow[1])trade.PositionClose(sellpos);   
     if (maFast[1]>maSlow[1]&&maFast[0]<maSlow[0]&&buypos ==sellpos)executeBuy(); 
     if(maFast[1]<maSlow[1]&&maFast[0]>maSlow[0]&&sellpos ==buypos) executeSell();
     if(buypos>0&&(!PositionSelectByTicket(buypos)|| PositionGetInteger(POSITION_MAGIC) != Magic)){
      buypos = 0;
      }
     if(sellpos>0&&(!PositionSelectByTicket(sellpos)|| PositionGetInteger(POSITION_MAGIC) != Magic)){
      sellpos = 0;
      }
    }
 }

//+------------------------------------------------------------------+
//| Expert trade transaction handling function                       |
//+------------------------------------------------------------------+
void OnTradeTransaction(const MqlTradeTransaction& trans, const MqlTradeRequest& request, const MqlTradeResult& result) {
    if (trans.type == TRADE_TRANSACTION_ORDER_ADD) {
        COrderInfo order;
        if (order.Select(trans.order)) {
            if (order.Magic() == Magic) {
                if (order.OrderType() == ORDER_TYPE_BUY) {
                    buypos = order.Ticket();
                } else if (order.OrderType() == ORDER_TYPE_SELL) {
                    sellpos = order.Ticket();
                }
            }
        }
    }
}

//+------------------------------------------------------------------+
//| Execute sell trade function                                      |
//+------------------------------------------------------------------+
void executeSell() {      
       double bid = SymbolInfoDouble(_Symbol, SYMBOL_BID);
       bid = NormalizeDouble(bid,_Digits);
       trade.Sell(lott,_Symbol,bid);  
       sellpos = trade.ResultOrder();  
       }   

//+------------------------------------------------------------------+
//| Execute buy trade function                                       |
//+------------------------------------------------------------------+
void executeBuy() {
       double ask = SymbolInfoDouble(_Symbol, SYMBOL_ASK);
       ask = NormalizeDouble(ask,_Digits);
       trade.Buy(lott,_Symbol,ask);
       buypos = trade.ResultOrder();
}

No voy a entrar en más detalles sobre la validación y las sugerencias para seleccionar su estrategia principal. Para más detalles, consulte mi artículo anterior sobre aprendizaje automático, cuyo enlace se encuentra aquí.

Obtención de datos

En este artículo, definiremos dos estados: alta volatilidad y baja volatilidad, representados por 1 y 0, respectivamente. La volatilidad se definirá como la desviación estándar de los rendimientos durante las últimas 50 velas, de la siguiente manera:

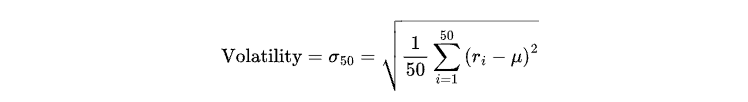
Donde:

• "ri" representa el rendimiento de la vela i-ésima (calculado como el cambio porcentual en el precio entre velas cerradas consecutivas).

• "μ" es el rendimiento medio de las últimas 50 velas cerradas, dado por:

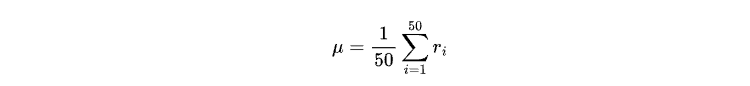
Para entrenar el modelo, solo necesitaremos los datos del precio de cierre y la fecha y hora. Aunque es posible obtener datos directamente desde el terminal MetaTrader 5, la mayor parte de los datos proporcionados por el terminal se limitan a datos de ticks reales. Para obtener datos OHLC de períodos más largos de su corredor, podemos crear un Asesor Experto en obtención de OHLC para manejar esta tarea.

#include <FileCSV.mqh>

int barsTotal = 0;
CFileCSV csvFile;

input string fileName = "Name.csv";
string headers[] = {
    "time",
    "close"
};

string data[100000][2];
int indexx = 0;
vector xx;

input bool SaveData = true;

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {//Initialize model
   return(INIT_SUCCEEDED);
  }

//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
   if (!SaveData) return;
   if(csvFile.Open(fileName, FILE_WRITE|FILE_ANSI))
     {
      //Write the header
      csvFile.WriteHeader(headers);
      //Write data rows
      csvFile.WriteLine(data);
      //Close the file
      csvFile.Close();
     }
   else
     {
      Print("File opening error!");
     }

  }
  
//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
  int bars = iBars(_Symbol,PERIOD_CURRENT);
  
  if (barsTotal!= bars){
     barsTotal = bars;
   data[indexx][0] =(string)TimeTradeServer() ;
   data[indexx][1] = DoubleToString(iClose(_Symbol,PERIOD_CURRENT,1), 8); 
   indexx++;
   }
 }

Este código lee y escribe datos financieros (hora y precio de cierre) en un archivo CSV. En cada tick, comprueba si ha cambiado el número de barras. Si es así, actualiza la matriz de datos con la hora actual del servidor y el precio de cierre del símbolo. Cuando se desinicializa el script, escribe los datos recopilados en un archivo CSV, incluidos los encabezados y las filas de datos. Utiliza la clase CFileCSV para el manejo de archivos.

Ejecute este Asesor Experto en el probador de estrategias utilizando el marco temporal y el período deseados, y se guardará un archivo CSV en el directorio /Tester/Agent-sth000.

Utilizaremos datos de la muestra comprendidos entre el 1 de enero de 2020 y el 1 de enero de 2024 para el entrenamiento. Los datos del 1 de enero de 2024 al 1 de enero de 2025 se utilizarán para las pruebas fuera de la muestra.

Modelos de entrenamiento

Ahora, abre cualquier editor de Python y asegúrate de instalar las librerías necesarias utilizando pip según se requiera a lo largo de esta sección.

El archivo CSV contiene inicialmente solo una columna, en la que se mezclan los valores de tiempo y cierre, separados por un punto y coma. Los valores se almacenan como cadenas para un mejor almacenamiento. Para procesar esto, primero leemos el archivo CSV de la siguiente manera para separar las dos columnas y convertir los valores de cadenas en tipos datetime y float.

import pandas as pd
data = pd.read_csv("XAU_test.csv",sep=";")
data = data.dropna()
data["close"] = data["close"].astype(float)
data['time'] = pd.to_datetime(data['time'])
data.set_index('time', inplace=True)

La volatilidad se puede calcular fácilmente con esta línea:

data['volatility'] = data['returns'].rolling(window=50).std()

A continuación, visualizamos la distribución de la volatilidad para comprender mejor sus características. Podemos ver claramente que sigue aproximadamente una distribución normal.

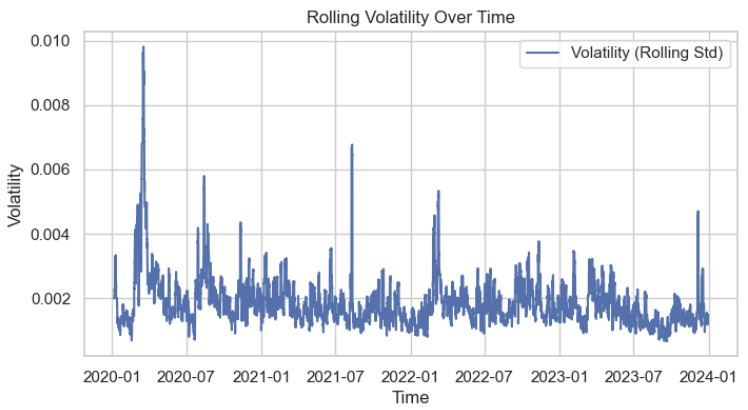
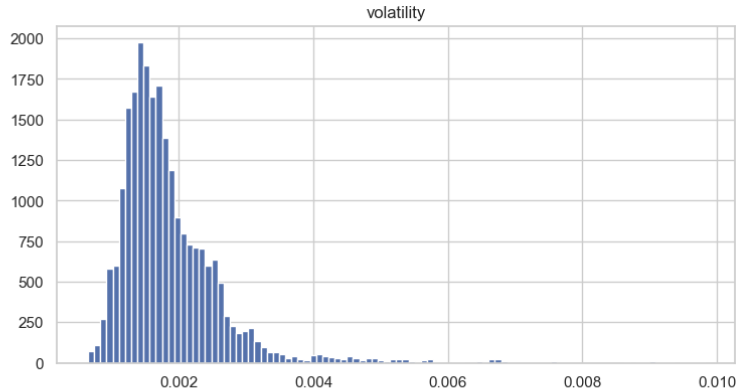
Utilizamos la prueba de Dickey-Fuller aumentada (Augmented Dickey-Fuller, ADF) para validar que los datos de volatilidad son estacionarios. Lo más probable es que la prueba arroje el siguiente resultado:

Augmented Dickey-Fuller Test: Volatility
ADF Statistic: -13.120552520156329
p-value: 1.5664189630119278e-24
# Lags Used: 46
Number of Observations Used: 23516
=> The series is likely stationary.

Aunque los modelos ocultos de Markov (HMM) no son estrictamente necesarios para los datos estacionarios debido a su comportamiento de actualización continua, disponer de datos estacionarios beneficia significativamente al proceso de agrupamiento y mejora la precisión del modelo.

A pesar de que los datos de volatilidad probablemente sean estacionarios y sigan una distribución normal, queremos normalizarlos a una distribución normal estándar para que el rango sea más manejable. 

En estadística, este proceso se denomina «escalado», en el que cualquier variable aleatoria x distribuida normalmente puede transformarse en una distribución normal estándar N(0,1) mediante la siguiente operación:

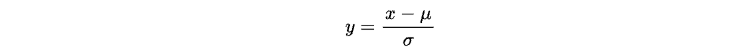
Aquí, μ representa la media y σ representa la desviación estándar de x.

Tenga en cuenta que más adelante, al volver a integrarlo en el editor MetaTrader 5, tendremos que realizar las mismas operaciones de normalización. Por eso también necesitamos almacenar la media y la desviación estándar.

from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaled_volatility = scaler.fit_transform(data[['volatility']])
scaled_volatility = scaled_volatility.reshape(-1, 1)
scaler_mean = scaler.mean_[0]  # Mean of the volatility feature
scaler_std = scaler.scale_[0]  # Standard deviation of the volatility feature

A continuación, entrenamos el modelo con los datos de volatilidad escalados de la siguiente manera:

from hmmlearn import hmm
import numpy as np
# Define the number of hidden states
n_states = 2
# Initialize the Gaussian HMM
model = hmm.GaussianHMM(n_components=n_states, covariance_type="full", n_iter=100, random_state=42, verbose = True)
# Fit the model to the scaled volatility data
model.fit(scaled_volatility)

Al predecir los estados ocultos para cada punto de datos de entrenamiento, la distribución de los clústeres parece bastante razonable, con solo errores menores.

# Predict the hidden states
hidden_states = model.predict(scaled_volatility)

# Add the hidden states to your dataframe
data['hidden_state'] = hidden_states
plt.figure(figsize=(14, 6))
for state in range(n_states):
    state_mask = data['hidden_state'] == state
    plt.plot(data.index[state_mask], data['volatility'][state_mask], 'o', label=f'State {state}')
plt.title('Hidden States and Rolling Volatility')
plt.xlabel('Time')
plt.ylabel('Volatility')
plt.legend()
plt.show()

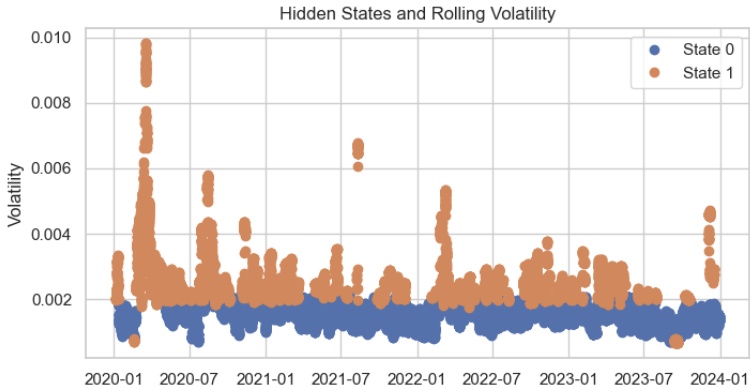
Por último, formateamos el resultado deseado en lenguaje MQL5 y lo guardamos en un archivo de encabezado JSON, lo que facilita copiar y pegar los valores de la matriz correspondientes en el editor de MetaTrader 5.

import json

# Your HMM model parameters
transition_matrix = model.transmat_
means = model.means_
covars = model.covars_

# Construct the data in the required format
data = {
    "A": [
        [transition_matrix[0, 0], transition_matrix[0, 1]],
        [transition_matrix[1, 0], transition_matrix[1, 1]]
    ],
    "mu": [means[0, 0], means[1, 0]],
    "sigma_sq": [covars[0, 0], covars[1, 0]],
    "scaler_mean": scaler_mean,
    "scaler_std": scaler_std
}

# Create the output content in the desired format
output_str = """
const double A[2][2] = { 
    {%.16f, %.16f}, 
    {%.16f, %.16f}
};
const double mu[2] = {%.16f, %.16f};
const double sigma_sq[2] = {%.16f, %.16f};
const double scaler_mean = %.16f;
const double scaler_std = %.16f;
""" % (
    data["A"][0][0], data["A"][0][1], data["A"][1][0], data["A"][1][1],
    data["mu"][0], data["mu"][1],
    data["sigma_sq"][0], data["sigma_sq"][1],
    data["scaler_mean"], data["scaler_std"]
)

# Write to a file
with open('model_parameters.h', 'w') as f:
    f.write(output_str)

print("Parameters saved to model_parameters.h")

El archivo resultante debería tener un aspecto similar al siguiente:

const double A[2][2] = { 
    {0.9941485184089348, 0.0058514815910651}, 
    {0.0123877225858242, 0.9876122774141759}
};
const double mu[2] = {-0.4677410059727503, 0.9797900996225393};
const double sigma_sq[2] = {0.1073520489683212, 1.4515804806463273};
const double scaler_mean = 0.0018685496675093;
const double scaler_std = 0.0008350190448735;

Debemos pegarlos en el código de nuestro EA como variables globales.

Integración

Ahora, regresemos al editor de código de MetaTrader 5 y construyamos sobre nuestro código de estrategia original.

Primero necesitamos crear funciones para calcular la volatilidad continua que se actualiza constantemente.

//+------------------------------------------------------------------+
//| Get volatility Function                                          |
//+------------------------------------------------------------------+
void GetVolatility(){
// Step 1: Get the last two close prices to compute the latest percent change
        double close_prices[2];
        int copied = CopyClose(_Symbol, PERIOD_CURRENT, 1, 2, close_prices);
        if(copied != 2){
            Print("Failed to copy close prices. Copied: ", copied);
            return;
        }
        
        // Step 2: Compute the latest percent change
        double latest_close = close_prices[0];
        double previous_close = close_prices[1];
        double percent_change = 0.0;
        if(previous_close != 0){
            percent_change = (latest_close - previous_close) / previous_close;
        }
        else{
            Print("Previous close price is zero. Percent change set to 0.");
        }
        
        // Step 3: Update the percent_changes buffer
        percent_changes[percent_change_index] = percent_change;
        percent_change_index++;
        if(percent_change_index >= 50){
            percent_change_index = 0;
            percent_change_filled = true;
        }
        
        // Step 4: Once the buffer is filled, compute the rolling std dev
        if(percent_change_filled){
            double current_stddev = ComputeStdDev(percent_changes, 50);
            // Step 5: Scale the std dev
            double scaled_stddev = (current_stddev - scaler_mean) / scaler_std;
            
            // Step 6: Update the volatility array (ring buffer for Viterbi)
            // Shift the volatility array to make room for the new std dev
            for(int i = 0; i < 49; i++){
                volatility[i] = volatility[i+1];
            }
            volatility[49] = scaled_stddev; // Insert the latest std dev
       }
}

//+------------------------------------------------------------------+
//| Compute Standard Deviation Function                              |
//+------------------------------------------------------------------+
double ComputeStdDev(double &data[], int size)
{
    if(size <= 1)
        return 0.0;
    
    double sum = 0.0;
    double sum_sq = 0.0;
    for(int i = 0; i < size; i++)
    {
        sum += data[i];
        sum_sq += data[i] * data[i];
    }
    double mean = sum / size;
    double variance = (sum_sq - (sum * sum) / size) / (size - 1);
    return MathSqrt(variance);
}

• GetVolatility() calcula y realiza un seguimiento de la volatilidad móvil a lo largo del tiempo utilizando la desviación estándar escalada de los cambios porcentuales en los precios.
• ComputeDtsDev() sirve como función auxiliar para calcular la desviación estándar de una matriz de datos determinada. 

A continuación, escribimos dos funciones que calculan el estado oculto actual basándose en nuestras matrices y la volatilidad actual.

//+------------------------------------------------------------------+
//| Viterbi Algorithm Implementation in MQL5                         |
//+------------------------------------------------------------------+
int Viterbi(double &obs[], int &states[])
{
    // Initialize dynamic programming tables
    double T1[2][50];
    int T2[2][50];

    // Initialize first column
    for(int s = 0; s < 2; s++)
    {
         double emission_prob = (1.0 / MathSqrt(2 * M_PI * sigma_sq[s])) * MathExp(-MathPow(obs[0] - mu[s], 2) / (2 * sigma_sq[s])) + 1e-10;

        T1[s][0] = MathLog(pi[s]) + MathLog(emission_prob);
        T2[s][0] = 0;
    }

    // Fill the tables
    for(int t = 1; t < 50; t++)
    {
        for(int s = 0; s < 2; s++)
        {
            double max_prob = -DBL_MAX; // Initialize to negative infinity
            int max_state = 0;
            for(int s_prev = 0; s_prev < 2; s_prev++)
            {
                double transition_prob = A[s_prev][s];
                if(transition_prob <= 0) transition_prob = 1e-10; // Prevent log(0)
                double prob = T1[s_prev][t-1] + MathLog(transition_prob);
                if(prob > max_prob)
                {
                    max_prob = prob;
                    max_state = s_prev;
                }
            }
            // Calculate emission probability with epsilon
            double emission_prob = (1.0 / MathSqrt(2 * M_PI * sigma_sq[s])) * MathExp(-MathPow(obs[t] - mu[s], 2) / (2 * sigma_sq[s])) + 1e-10;
            T1[s][t] = max_prob + MathLog(emission_prob);
            T2[s][t] = max_state;
        }
    }

    // Backtrack to find the optimal state sequence
    // Find the state with the highest probability in the last column
    double max_final_prob = -DBL_MAX;
    int last_state = 0;
    for(int s = 0; s < 2; s++)
    {
        if(T1[s][49] > max_final_prob)
        {
            max_final_prob = T1[s][49];
            last_state = s;
        }
    }    
    // Initialize the states array
    ArrayResize(states, 50);
    states[49] = last_state;
    // Backtrack
    for(int t = 48; t >= 0; t--)
    {
        states[t] = T2[states[t+1]][t+1];
    }
    return 0; // Success
}

//+------------------------------------------------------------------+
//| Predict Current Hidden State                                     |
//+------------------------------------------------------------------+
int PredictCurrentState(double &obs[])
{   
    // Define states array
    int states[50];
    
    // Apply Viterbi
    int ret = Viterbi(obs, states);
    if(ret != 0)
        return -1; // Error
    
    // Return the most probable current state
    return states[49];
}

La función Viterbi() implementa el algoritmo de Viterbi, un método de programación dinámica para encontrar la secuencia más probable de estados ocultos en un modelo oculto de Markov (HMM) a partir de los datos observados (obs[]).

1. Inicialización:

• Tablas de programación dinámica:

  • T1[s][t] : Probabilidad logarítmica de la secuencia de estados más probable que termina en el estado s en el momento t.
  • T2[s][t] : Tabla de punteros que almacena el estado que maximizó la probabilidad de transición al estado s en el momento t.

• Primer paso (t = 0):

  • Calcula las probabilidades iniciales utilizando las probabilidades a priori de cada estado (π[s]) y las probabilidades de emisión para la primera observación (obs[0]).

2. Cálculo recursivo:

Para cada intervalo de tiempo t de 1 a 49:

1. Para cada estado s:

   Calcula la probabilidad máxima de transición desde cualquier estado anterior s_prev a s utilizando la siguiente ecuación:               

   

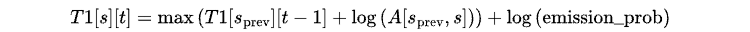
   Aquí, la probabilidad de transición A[s_prev, s] se convierte al espacio logarítmico para evitar el desbordamiento numérico.

2. Almacena el estado s_prev que maximizó la probabilidad en T2[s][t].

3. Retroceso para recuperar la ruta óptima:

1. Comience por el estado con mayor probabilidad en el último intervalo de tiempo (t = 49).
2. Rastrear a través de T2 para reconstruir la secuencia más probable de estados, almacenando el resultado en states[].

El resultado final es states[], que contiene la secuencia de estados más probable.

La función PredictCurrentState() utiliza la función Viterbi() para predecir el estado oculto actual basándose en observaciones.

1. Para la inicialización, define una matriz states[50] para almacenar el resultado de Viterbi().
2. A continuación, pasa la secuencia de observación obs[] a la función Viterbi() para calcular la secuencia más probable de estados ocultos.
3. Por último, devuelve el estado en el último intervalo de tiempo (estados[49]), que representa el estado oculto actual más probable.

Si te confunde la matemática detrás de esto, te recomiendo que busques ilustraciones más intuitivas en Internet. Aquí, intentaré explicar brevemente lo que estamos haciendo.

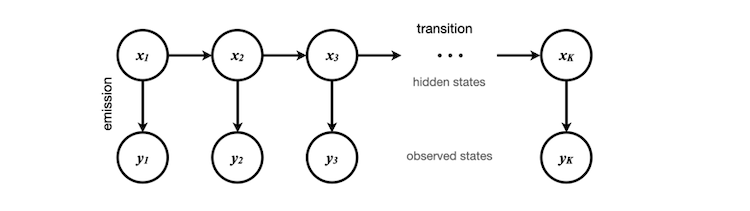
Los estados observados son los datos de volatilidad escalados, que podemos obtener y almacenar en la matriz obs[], que en este caso contiene 50 elementos. Estos elementos corresponden a y1, y2, ... y50 en el diagrama. Los estados ocultos correspondientes pueden ser 0 o 1, lo que representa las condiciones abstractas de la volatilidad actual (alta o baja).

Estos estados ocultos se determinan a través de la agrupación en clústeres durante el proceso de entrenamiento del modelo que realizamos anteriormente en Python. Es importante tener en cuenta que el código Python no sabe exactamente qué representa cada número; solo sabe cómo agrupar los datos e identificar las características de las propiedades de transición entre estados.

Inicialmente, asignamos aleatoriamente un estado a x1, asumiendo que cada estado tiene un peso igual. Si no queremos hacer esta suposición, podríamos calcular la distribución estacionaria del estado inicial utilizando nuestros datos de entrenamiento, que sería el vector propio de la matriz de transición. Para simplificar, suponemos que el vector de distribución estacionaria es [0.5, 0.5].

Mediante el entrenamiento del modelo oculto de Markov, obtenemos la probabilidad de transición a un estado oculto diferente y la probabilidad de emitir una observación diferente. Utilizando el teorema de Bayes, podemos calcular la probabilidad de todas las rutas posibles para cada cadena de Markov y determinar la ruta más probable. Esto nos permite encontrar el resultado más probable para x50, el estado oculto final de la secuencia.

Por último, ajustamos la lógica original de OnTick() calculando los estados ocultos para cada cierre y añadiendo un criterio de entrada según el cual el estado oculto debe ser igual a 1.

//+------------------------------------------------------------------+
//| Check Volatility is filled Function                              |
//+------------------------------------------------------------------+
bool IsVolatilityFilled(){
     bool volatility_filled = true;
     for(int i = 0; i < 50; i++){
         if(volatility[i] == 0){
             volatility_filled = false;
             break;
         }
     }
     if(!volatility_filled){
         Print("Volatility buffer not yet filled.");
         return false;
     }
     else return true;
}  

//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
  int bars = iBars(_Symbol,PERIOD_CURRENT);
  if (barsTotal!= bars){
     barsTotal = bars;
     double maFast[];
     double maSlow[];
     double ma[];  
     
     GetVolatility();
     if(!IsVolatilityFilled()) return;
     int currentState = PredictCurrentState(volatility);
     
     CopyBuffer(handleMaFast,BASE_LINE,1,2,maFast);
     CopyBuffer(handleMaSlow,BASE_LINE,1,2,maSlow);
     CopyBuffer(handleMa,0,1,1,ma);

     double bid = SymbolInfoDouble(_Symbol, SYMBOL_BID);
     double ask = SymbolInfoDouble(_Symbol, SYMBOL_ASK);
     double lastClose = iClose(_Symbol, PERIOD_CURRENT, 1);
     //The order below matters
     if(buypos>0&& lastClose<maSlow[1]) trade.PositionClose(buypos);
     if(sellpos>0 &&lastClose>maSlow[1])trade.PositionClose(sellpos);        
     if (maFast[1]>maSlow[1]&&maFast[0]<maSlow[0]&&buypos ==sellpos&&currentState==1)executeBuy(); 
     if(maFast[1]<maSlow[1]&&maFast[0]>maSlow[0]&&sellpos ==buypos&&currentState==1) executeSell();
     
     if(buypos>0&&(!PositionSelectByTicket(buypos)|| PositionGetInteger(POSITION_MAGIC) != Magic)){
      buypos = 0;
      }
     if(sellpos>0&&(!PositionSelectByTicket(sellpos)|| PositionGetInteger(POSITION_MAGIC) != Magic)){
      sellpos = 0;
      }
    }
 }

Prueba retrospectiva

Entrenamos el modelo utilizando datos de la muestra del 1 de enero de 2020 al 1 de enero de 2024. Ahora, queremos comprobar los resultados para el periodo comprendido entre el 1 de enero de 2024 y el 1 de enero de 2025, en XAUUSD en el marco temporal de 1 hora.

En primer lugar, compararemos el rendimiento con la línea de base, que es el resultado sin integrar el HMM.

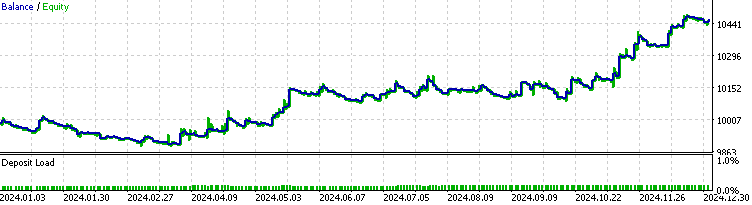
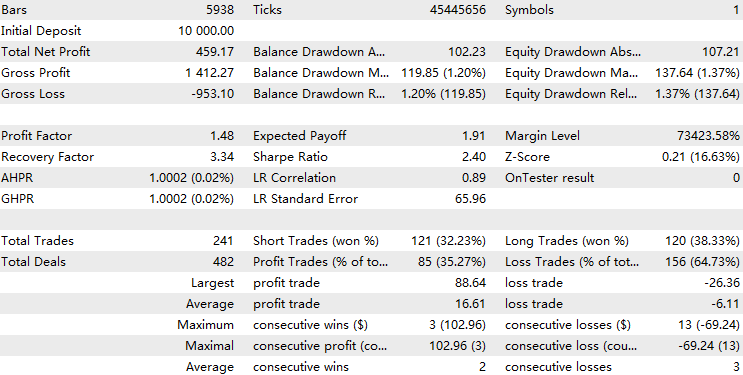
Ahora realizamos una prueba retrospectiva del EA con el filtro del modelo HMM implementado.

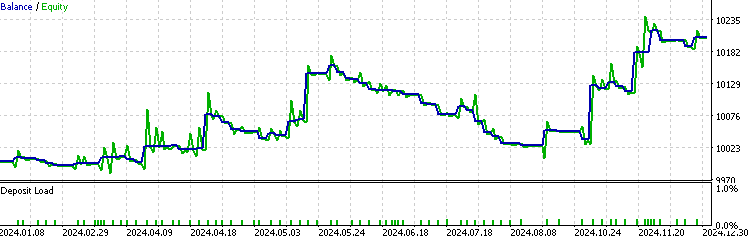
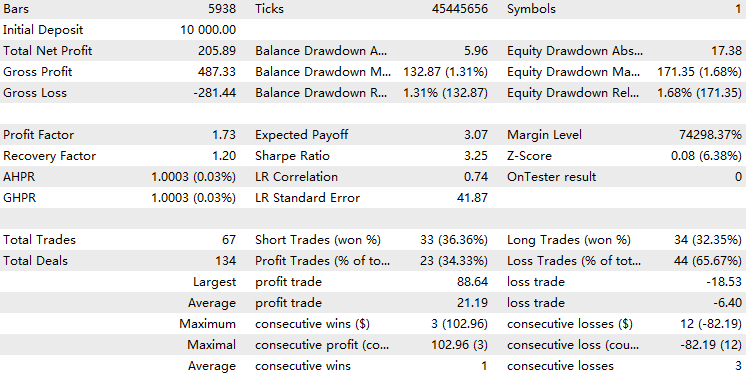
Podemos ver que el EA con la implementación HMM filtró alrededor del 70 % del total de operaciones. Supera al índice de referencia, con un factor de beneficio de 1.73 frente al 1.48 del índice de referencia, así como un ratio de Sharpe más alto. Esto sugiere que el modelo HMM que hemos entrenado muestra cierto nivel de predictibilidad.

Si realizamos una prueba retrospectiva continua, en la que repetimos este procedimiento de entrenamiento de 4 años y prueba de 1 año a partir de 2004, y recopilamos todos los resultados en una curva de capital, obtendremos un resultado como este:

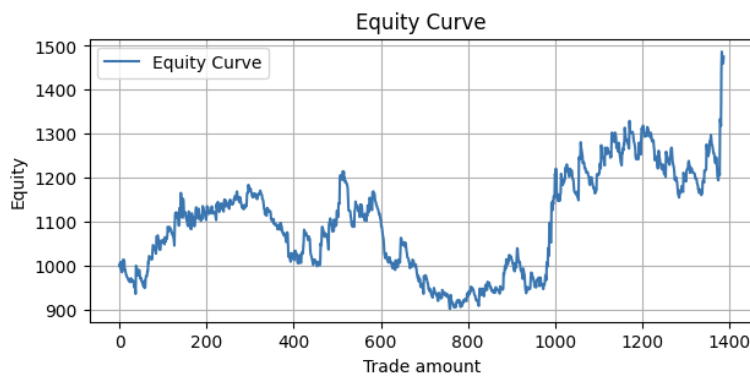
Métrica:

Profit Factor: 1.10
Maximum Drawdown: -313.17
Average Win: 11.41
Average Loss: -5.01
Win Rate: 32.56%

Esto es bastante rentable y tiene margen de mejora.

Reflexiones

En el mundo actual del comercio, dominado por los métodos de aprendizaje automático, existe un debate continuo sobre si es mejor utilizar modelos más complejos, como las redes neuronales recurrentes (Recurrent Neural Networks, RNN), o seguir con modelos más sencillos, como los modelos ocultos de Markov (Hidden Markov Models, HMM).

Ventajas:

1. Simplicidad: Más fácil de implementar e interpretar en comparación con modelos complejos como RNN, que introducen ambigüedad sobre lo que representa cada parámetro y operación.
2. Menores requisitos de datos: Requiere menos muestras de entrenamiento para estimar los parámetros del modelo y menos potencia de cálculo.
3. Menos parámetros: Más resistente a los problemas de sobreajuste.

Contras:

1. Complejidad limitada: Puede no captar patrones intrincados en datos volátiles que las RNN pueden modelar.
2. Supuesto del proceso de Markov: Supone que las transiciones de volatilidad son sin memoria, lo que puede no ser válido en los mercados reales.
3. Riesgo de sobreajuste: A pesar de su simplicidad, si hay demasiados estados involucrados, el HMM seguiría siendo propenso al sobreajuste.

Es un enfoque popular predecir la volatilidad en lugar de los precios utilizando métodos de aprendizaje automático, ya que los académicos han descubierto que las predicciones de volatilidad son más fiables. Sin embargo, una limitación del enfoque presentado en este artículo es que las observaciones que obtenemos en cada nueva barra (volatilidad media móvil de 50 períodos) y los estados ocultos que definimos (estados de volatilidad alta/baja) están algo correlacionados, lo que reduce la significación de la predicción. Esto sugiere que se podrían haber obtenido resultados similares simplemente utilizando los datos de observación como filtros.

Para el desarrollo futuro, animo a los lectores a explorar otras definiciones de estados ocultos, así como a experimentar con más de dos estados para mejorar la solidez y la capacidad de predicción del modelo.

Conclusión

En este artículo, primero explicamos la motivación para utilizar los HMM como predictores del estado de volatilidad para una estrategia de seguimiento de tendencias, al tiempo que presentamos el concepto básico de los HMM. A continuación, repasamos todo el proceso de desarrollo de la estrategia, que incluyó el desarrollo de una estrategia básica en MQL5 utilizando MetaTrader 5, la obtención de datos y el entrenamiento de los HMM en Python, seguido de la integración de los modelos de nuevo en MetaTrader 5. Posteriormente, realizamos una prueba retrospectiva y analizamos su rendimiento, explicando brevemente la lógica matemática detrás de los HMM mediante un diagrama. Por último, compartí mis reflexiones sobre la estrategia, junto con mis aspiraciones para el desarrollo futuro sobre la base de este marco.

Tabla de archivos

Nombre del archivo	Uso
HMM Test.mq5	La implementación del EA comercial.
Classic Trend Following.mq5	La estrategia de base del EA.
OHLC Getter.mq5	El EA para obtener datos.
FileCSV.mqh	El archivo de inclusión para almacenar datos en CSV.
rollingBacktest.ipynb	Para entrenar el modelo y obtener matrices.