Portfolio Risk Model using Kelly Criterion and Monte Carlo Simulation
Introdução
Por décadas, traders vêm usando a fórmula do Critério de Kelly para determinar a proporção ideal de capital a alocar em um investimento ou aposta, a fim de maximizar o crescimento no longo prazo enquanto minimizam o risco de ruína. No entanto, seguir cegamente o Critério de Kelly utilizando o resultado de um único backtest costuma ser perigoso para traders individuais, pois, na negociação ao vivo, a vantagem de trading diminui com o tempo, e o desempenho passado não é garantia de resultado futuro. Neste artigo, apresentarei uma abordagem realista para aplicar o Critério de Kelly para alocação de risco de um ou mais EAs no MetaTrader 5, incorporando resultados de simulação de Monte Carlo provenientes do Python.
A Teoria do Modelo de Espaço de Alavancagem para Trading
O Modelo de Espaço de Alavancagem para Trading (LSTM) é uma estrutura teórica utilizada principalmente no contexto dos mercados financeiros e da gestão de ativos. Ela integra o conceito de alavancagem, que se refere ao uso de fundos emprestados para amplificar os retornos potenciais, com uma abordagem mais dinâmica e orientada ao espaço para modelar o comportamento do mercado.
O LSTM utiliza o critério de Kelly para calcular o percentual do portfólio a ser arriscado por operação para uma única estratégia é
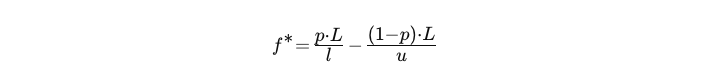
- L: fator de alavancagem
- p: probabilidade de sucesso
- u: razão de ganho alavancado
- l: razão de perda alavancada
Dado um resultado de backtest, podemos obter o valor da variável pelas fórmulas a seguir.

Vamos supor que você está operando com alavancagem de 2:1. Assuma o seguinte:
- A probabilidade de uma operação bem-sucedida (p) = 0,6 (60% de chance de ganhar).
- O retorno esperado (u) = 0,1 (10% de ganho sem alavancagem, então alavancado 2:1 = 20% de ganho).
- A perda esperada (l) = 0,05 (5% de perda sem alavancagem, então alavancado 2:1 = 10% de perda).
Substitua na fórmula de Kelly:
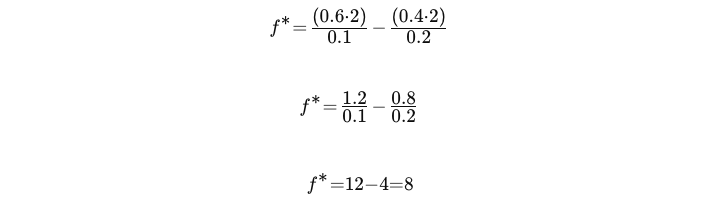
Portanto, a fração ótima do seu capital a ser arriscada nessa operação seria 8% do seu capital total.
Após aplicar esta fórmula em um dos seus próprios EAs, acredito que você inevitavelmente sentirá um certo desconforto ao ver quanto risco deveria assumir por operação. De fato, esta fórmula assume que seus resultados futuros serão tão bons quanto seu backtest, o que é irrealista. É por isso que, no setor, normalmente se aplica o Kelly fracionado ao risco, ou seja, divide-se o valor por algum número inteiro para diminuir o risco e deixar margem para adversidades futuras.
Agora temos que responder: qual fração deve ser escolhida para que os traders se sintam confortáveis ao arriscar, enquanto ainda maximizam o retorno esperado por operação?
No livro The Leverage Space Trading Model de Ralph Vince, concluiu-se, através de um processo de otimização estocástica, que a função de expectativa de retorno é convexa, independentemente da dimensão. Isso significa que o retorno esperado ótimo possui uma única solução, e a expectativa diminui continuamente à medida que o valor de f* se afasta da solução ótima.
Isso implica que, como a negociação ao vivo não é tão ideal quanto o backtest, esperamos que o verdadeiro f* que maximiza nosso retorno seja menor do que o f* calculado pela fórmula de Kelly. Portanto, tudo o que precisamos fazer é aumentar nosso risco alocado até o nível máximo que conseguimos tolerar, garantindo que ainda seja menor que o risco de Kelly.
Normalmente, o nível de tolerância de um trader é medido pelo rebaixamento máximo (maximum drawdown) que ele pode suportar. Assumirei que um nível de tolerância razoável é um drawdown máximo de 30% para o restante do artigo.
Aplicando risco alavancado no MQL5
Para aplicar risco alavancado no MQL5, primeiro declaramos a porcentagem de risco como uma variável global. Neste caso, arriscamos 2% por operação.
input double risk = 2.0;
Em seguida, escreveremos uma função para calcular o volume do lote com base no stop loss na unidade de preço atual. Por exemplo, se o stop loss for definido em um preço de 0, os pontos de stop loss corresponderão diretamente ao preço atual, e o resultado da operação refletirá exatamente o movimento do ativo subjacente.
//+------------------------------------------------------------------+ //| Calculate the corresponding lot size given the risk | //+------------------------------------------------------------------+ double calclots(double slpoints) { double riskAmount = AccountInfoDouble(ACCOUNT_BALANCE) * risk / 100; double ticksize = SymbolInfoDouble(_Symbol, SYMBOL_TRADE_TICK_SIZE); double tickvalue = SymbolInfoDouble(_Symbol, SYMBOL_TRADE_TICK_VALUE); double lotstep = SymbolInfoDouble(_Symbol, SYMBOL_VOLUME_STEP); double moneyperlotstep = slpoints / ticksize * tickvalue * lotstep; double lots = MathFloor(riskAmount / moneyperlotstep) * lotstep; lots = MathMin(lots, SymbolInfoDouble(_Symbol, SYMBOL_VOLUME_MAX)); lots = MathMax(lots, SymbolInfoDouble(_Symbol, SYMBOL_VOLUME_MIN)); return lots; }
O código acima primeiro determina o valor do risco multiplicando o saldo da conta pela porcentagem de risco.
Depois, ele recupera o tamanho do tick, o valor do tick e o passo do lote do símbolo, e calcula o valor monetário de cada passo de lote com base na distância do stop loss.
O tamanho do lote é determinado dividindo o valor do risco pelo dinheiro por passo de lote e arredondando para o passo de lote mais próximo.
Por fim, garante que o tamanho do lote calculado esteja dentro dos limites mínimos e máximos permitidos para o símbolo antes de retornar o resultado.
Observe que nem toda estratégia de negociação envolve stop loss e take profit fixos. Mas, no espaço de negociação alavancada, assumimos que estamos usando um ponto de stop loss fixo porque, no Critério de Kelly, precisamos saber quanto queremos arriscar antes de executar uma operação.
Chamamos essa função logo antes de fazer qualquer execução. Um exemplo seria assim.
//+------------------------------------------------------------------+ //| Execute buy trade function | //+------------------------------------------------------------------+ void executeBuy(double price) { double sl = price- slp*_Point; sl = NormalizeDouble(sl, _Digits); double lots = lotpoint; if (risk > 0) lots = calclots(slp*_Point); trade.BuyStop(lots,price,_Symbol,sl,0,ORDER_TIME_DAY,1); buypos = trade.ResultOrder(); }Normalmente, para um EA consistentemente lucrativo, seu resultado de backtest deve se parecer com uma função exponencial como esta:
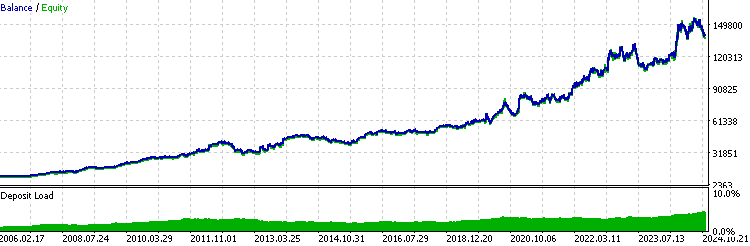
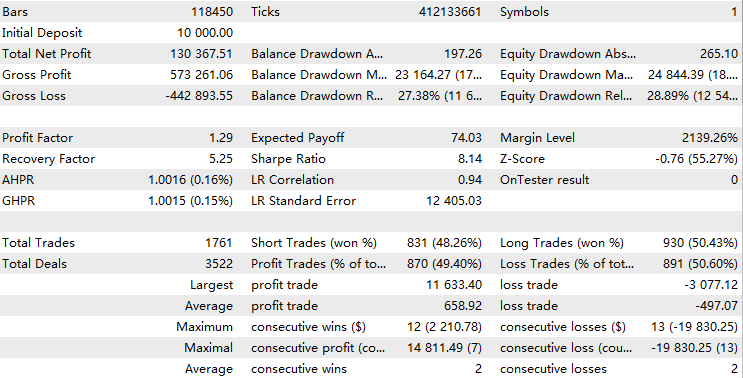
Aqui estão algumas coisas das quais se deve estar ciente ao analisar estatísticas de backtest ao utilizar este modelo de negociação alavancada:
- Se o seu Expert Advisor é consistentemente lucrativo, os resultados recentes terão um impacto maior no desempenho geral do backtest do que os anteriores. Essencialmente, você está atribuindo mais peso à importância do desempenho recente.
- A LR-Correlação não é útil porque o gráfico será uma curva exponencial.
- O índice de Sharpe se torna irrealista porque assume uma relação linear entre risco e retorno. A alavancagem amplifica tanto os retornos potenciais quanto os riscos, levando a métricas distorcidas de desempenho ajustado ao risco.
Se você ainda quiser avaliar as métricas acima, simplesmente fixe o tamanho do lote e faça outro teste.
Simulação de Monte Carlo do Drawdown Máximo
Vemos uma curva de patrimônio como uma série de variações percentuais no saldo da nossa conta, e o drawdown máximo pode ser visto como o segmento dessa série com o menor percentual acumulado. Um único backtest representa apenas uma possível organização dessa série, tornando sua robustez estatística limitada. O objetivo desta seção é entender os possíveis drawdowns que podemos enfrentar e selecionar o percentil 95 como nossa referência para tolerância máxima.
A simulação de Monte Carlo pode ser usada para simular uma possível curva de patrimônio de diversas formas:
-
Amostragem Aleatória dos Retornos: Gerando retornos aleatórios com base no desempenho histórico ou distribuições estatísticas assumidas (por exemplo, normal), você simula curvas de patrimônio potenciais ao compor os retornos ao longo do tempo.
-
Bootstrapping: Reamostrando os retornos históricos com reposição para criar múltiplos caminhos simulados de patrimônio, que refletem a variabilidade observada no desempenho passado.
-
Embaralhamento: Embaralhando aleatoriamente a ordem dos retornos históricos e usando a série embaralhada para gerar diferentes caminhos de patrimônio, permitindo um conjunto diversificado de cenários.
-
Ajustes de Risco/Retorno: Modificando os parâmetros de entrada (por exemplo, volatilidade ou limites de drawdown) com base em critérios de risco especificados para gerar curvas de patrimônio realistas sob diferentes condições de mercado.
Neste artigo, vamos focar no método de embaralhamento.
Primeiramente, obtemos o relatório de operações do backtest clicando com o botão direito assim.
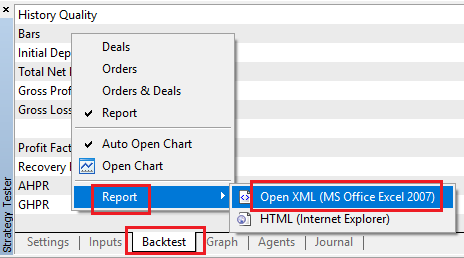
Depois, abrimos o Python e extraímos as linhas úteis que possuem saldo da conta e lucro/prejuízo de cada operação com este código.
import pandas as pd # Replace 'your_file.xlsx' with the path to your file input_file = 'DBG-XAU.xlsx' # Load the Excel file and skip the first {skiprows} rows data = pd.read_excel(input_file, skiprows=10757) # Select the 'profit' column (assumed to be 'Unnamed: 10') and filter rows as per your instructions profit_data = data[['Profit','Balance']][1:-1] profit_data = profit_data[profit_data.index % 2 == 0] # Filter for rows with odd indices profit_data = profit_data.reset_index(drop=True) # Reset index # Convert to float, then apply the condition to set values to 1 if > 0, otherwise to 0 profit_data = profit_data.apply(pd.to_numeric, errors='coerce').fillna(0) # Convert to float, replacing NaN with 0 # Save the processed data to a new CSV file with index output_csv_path = 'processed-DBG-XAU.csv' profit_data.to_csv(output_csv_path, index=True, header=['profit_loss','account_balance']) print(f"Processed data saved to {output_csv_path}")
As linhas a serem ignoradas são basicamente as linhas acima deste índice -1.
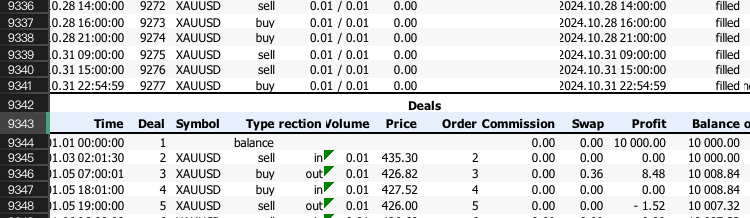
Em seguida, precisamos converter o lucro em variação percentual para cada operação, a fim de garantir que a série embaralhada resulte no mesmo saldo final. Isso é feito deslocando a coluna de saldo da conta em uma linha e calculando o lucro ou prejuízo como uma porcentagem do saldo antes de cada operação.
initial_balance = account_balance.iloc[0] - profit_loss.iloc[0] # Calculate the account balance before each trade account_balance_before_trade = account_balance.shift(1) account_balance_before_trade.iloc[0] = initial_balance # Compute the percentage change made to the account balance for each trade percentage_change = profit_loss / account_balance_before_trade # Fill any NaN values that might have occurred percentage_change.fillna(0, inplace=True)
Por fim, simulamos 1000 séries aleatórias e plotamos as 10 principais com maior drawdown máximo. Observe que o patrimônio final deve terminar igual para todas, por conta da Propriedade Comutativa da Multiplicação. Multiplicar a série de variações percentuais resultará no mesmo valor, independentemente da ordem em que os valores foram embaralhados.
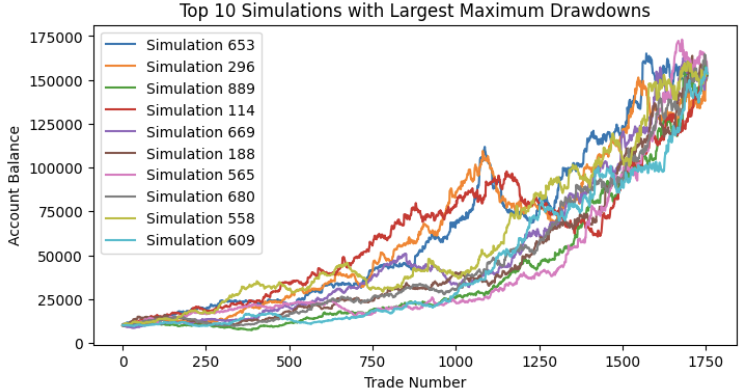
A distribuição do drawdown máximo deve ser semelhante a uma distribuição normal, e podemos ver aqui que o percentil de 95% (cerca de dois desvios padrão) está em aproximadamente 30% de drawdown máximo.
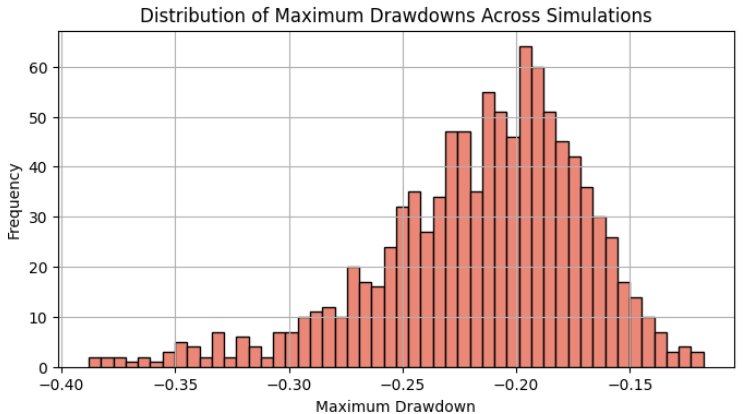
O drawdown máximo do nosso backtest inicial foi de apenas 17%, que é menor que a média dessa distribuição. Se tivéssemos considerado esse valor como o drawdown máximo esperado, teríamos aumentado nosso risco por um fator de 2 em comparação ao risco que estamos dispostos a assumir agora, após obter os resultados da simulação de Monte Carlo. Escolhemos o percentil de 95% porque é um resultado geral que estudiosos consideram próximo do desempenho em operações ao vivo. Tivemos sorte aqui porque o percentil de 95% está alinhado com nossa tolerância máxima de 30%, definida no início. Isso significa que, se estivermos operando este único EA em nosso portfólio, um risco de 2% por operação irá maximizar nosso lucro mantendo-nos bem dentro da nossa tolerância máxima. Se o resultado for diferente, devemos repetir o procedimento acima até encontrar a solução ideal.
Critério de Kelly para Otimização de Portfólio
Se estivermos rodando múltiplos EAs em uma única conta, primeiro precisamos concluir o procedimento acima para cada EA a fim de determinar seu risco ideal. Depois, aplicamos esse risco ao capital alocado para cada EA dentro do portfólio total. Do ponto de vista da conta inteira, o valor de risco para cada EA será o risco original multiplicado pela fração alocada.
A fração de alocação de Kelly para cada EA é determinada por suas correlações de retorno com outros EAs e pelo desempenho geral do backtest. Nosso objetivo principal é garantir que os EAs compensem os drawdowns uns dos outros tanto quanto possível, resultando em uma curva de patrimônio mais suave para o portfólio inteiro. É importante observar que adicionar mais EAs e estratégias só aumenta a diversidade do portfólio se eles forem descorrelacionados; caso contrário, pode aumentar o risco total, como se estivesse amplificando o risco de um único EA.
Especificamente, calculamos a fração de alocação de Kelly para cada estratégia com base nos retornos esperados e na matriz de covariância dos retornos, usando as seguintes fórmulas:
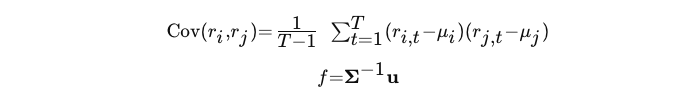
- r: o retorno do EAi ou EAj no tempo t
- μ: o retorno médio do EAi ou EAj
- f: alocação de Kelly para cada EA
- <i0>f</i0>: alocação de Kelly para cada EA
- u: o vetor de retorno esperado para cada EA
Para extrair os valores das variáveis mencionadas acima, devemos realizar um backtest para cada estratégia e armazenar a série de retornos percentuais de cada estratégia em um único dataframe. Em seguida, com base na frequência de todos os EAs, selecionamos o intervalo de tempo apropriado para registro, pois a covariância é calculada com base nas correlações dos retornos dentro do mesmo período. Realizamos tais operações com este código em Python:
# Read returns for each strategy for file in strategy_files: try: data = pd.read_csv(file, index_col='Time') # Ensure 'Time' is parsed correctly as datetime data.index = pd.to_datetime(data.index, errors='coerce') # Drop rows where 'Time' or 'return' is invalid data.dropna(subset=['return'], inplace=True) # Aggregate duplicate time indices by mean (or could use 'sum', but here mean can ignore the trade frequency significance) data = data.groupby(data.index).agg({'return': 'mean'}) # Append results returns_list.append(data['return']) strategy_names.append(file) except Exception as e: print(f"Error processing {file}: {e}") continue # Check if any data was successfully loaded if not returns_list: print("No valid data found in files.") return # Combine returns into a single DataFrame, aligning by date returns_df = pd.concat(returns_list, axis=1, keys=strategy_names) # Uncomment the below line if u wanna drop rows with missing values across strategies #returns_df.dropna(inplace=True) #Uncomment the below line if u wanna just fill unaligned rows with 0( I think this is best for backtest that may have years differences) returns_df.fillna(0, inplace=True)
Garanta que todos os resultados de backtest comecem e terminem no mesmo momento. Além disso, selecione um intervalo de tempo adequado para agregar os resultados, de modo que nenhum intervalo tenha um número excessivo de operações, nem algum intervalo sem nenhuma operação. Se os intervalos de tempo forem muito espaçados, pode haver pontos de dados insuficientes dentro das mesmas faixas de tempo para calcular a covariância de forma precisa. No nosso caso, selecionamos um intervalo de um mês e usamos o retorno médio de cada mês como a característica de retorno.
Agora fazemos os cálculos:
# Calculate expected returns (mean returns) expected_returns = returns_df.mean() # Calculate the covariance matrix of returns cov_matrix = returns_df.cov() # Compute the inverse of the covariance matrix try: inv_cov_matrix = np.linalg.inv(cov_matrix.values) except np.linalg.LinAlgError: # Use pseudo-inverse if covariance matrix is singular inv_cov_matrix = np.linalg.pinv(cov_matrix.values) # Calculate Kelly optimal fractions kelly_fractions = inv_cov_matrix @ expected_returns.values kelly_fractions = kelly_fractions / np.sum(kelly_fractions)
No final, será gerado algo assim:
Strategy Kelly Fraction 0 A1-DBG-XAU.csv 0.211095 1 A1-DBG-SP.csv 0.682924 2 A1-DBG-EU.csv 0.105981
Podemos implementar esse risco diretamente em nosso código original em MQL5, porque o cálculo inicial de risco já foi baseado no saldo total da conta. À medida que o saldo da conta muda, o capital alocado será recalculado automaticamente e aplicado à próxima operação.
double riskAmount = AccountInfoDouble(ACCOUNT_BALANCE) * risk / 100;
Por exemplo, para aplicar a Fração de Kelly calculada ao nosso EA de exemplo, basta modificar esta parte do código original, e a tarefa está concluída.
input double risk = 2.0*0.211095;
Estou plenamente ciente de que poderíamos, alternativamente, recalcular o risco com base na mudança de capital alocado para cada EA, mas calcular com base no portfólio inteiro é preferível pelos seguintes motivos:
- Acompanhar a mudança de diferentes capitais alocados é, na minha opinião, inviável. Pode ser necessário abrir várias contas ou escrever um programa para atualizar as mudanças após cada operação.
- O Critério de Kelly é usado para maximizar o crescimento de longo prazo de todo o portfólio. O desempenho de EAs individuais afeta o risco dos outros EAs, facilitando assim o crescimento eficiente de um pequeno portfólio à medida que ele aumenta de escala.
- Se basearmos o risco na mudança de capital alocado para cada EA, os EAs com melhor desempenho verão um aumento no capital alocado ao longo do tempo, levando a uma maior exposição ao risco para esses EAs. Isso prejudica nossa intenção inicial de calcular a alocação de risco com base nas correlações.
No entanto, nossa abordagem possui certas limitações:
- O risco de cada EA oscila com o desempenho geral do portfólio, dificultando o acompanhamento do desempenho individual dos EAs. O portfólio inteiro pode ser visto como um índice como o S&P 500. Para avaliar o desempenho individual, seria necessário calcular a variação percentual em vez do lucro absoluto.
- Nosso cálculo de alocação de risco não leva em conta a frequência de operações de cada EA. Isso significa que, se os EAs da mesma conta tiverem frequências de operação significativamente diferentes, pode haver uma exposição desigual ao risco, apesar da alocação.
De modo geral, considerando o potencial de maximizar o crescimento para traders individuais, essa abordagem vale a pena ser adotada.
Conclusão
Neste artigo, introduzimos o Critério de Kelly no contexto do Modelo de Espaço de Alavancagem e sua aplicação ao trading. Em seguida, fornecemos o código de implementação em MQL5. Após isso, usamos simulação de Monte Carlo para determinar o drawdown máximo ideal a ser considerado com base em um único backtest, que então foi aplicado para avaliar o risco de EAs individuais. Por fim, apresentamos uma abordagem para alocação de capital para cada EA com base no desempenho do backtest e nas correlações.
Tabela de Arquivos
| Nome | Uso |
|---|---|
| KellyMultiFactors.ipynb | Calcule as Frações de Kelly para alocação de capital |
| MonteCarloDrawdown.ipynb | Realize Simulações de Monte Carlo |
Traduzido do Inglês pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/en/articles/16500
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 Métodos de conjunto para aprimorar previsões numéricas em MQL5
Métodos de conjunto para aprimorar previsões numéricas em MQL5
 Simulação de mercado: Position View (XVI)
Simulação de mercado: Position View (XVI)
 Do básico ao intermediário: Filas, Listas e Árvores (VI)
Do básico ao intermediário: Filas, Listas e Árvores (VI)
 Do básico ao intermediário: Classes (III)
Do básico ao intermediário: Classes (III)
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
Existe o testador para simular negociações no passado, então você pode processar os relatórios do testador em vez de on-line.
Isso é impressionante, bom trabalho!
Obrigado