MQL5とPythonで自己最適化エキスパートアドバイザーを構築する（第5回）：深層マルコフモデル

MetaTrader 5 — 例 | 16 12月 2024, 16:11

221

こちらにリンクされているマルコフ連鎖に関する前回の議論では、遷移行列を使用して市場の確率的動作を理解する方法を説明しました。遷移マトリックスには多くの情報がまとめられており、いつ売買すべきかを教えてくれただけでなく、市場に強いトレンドがあるか、それともほとんどが平均回帰傾向にあるかも示されていました。今回の記事では、システム状態の定義を、最初の説明で使用した移動平均から相対力インジケーター(RSI)に変更します。

ほとんどの人がRSIを使用して取引する方法を教わるとき、RSIが30に達したら買い、70に達したら売るように言われます。コミュニティのメンバーの中には、これがすべての市場において最善の決定であるかどうか疑問に思う人もいるかもしれません。すべての市場で同じように取引することはできないことは誰もが知っています。この記事では、最適な取引ルールをアルゴリズム的に学習するために独自のマルコフ連鎖を構築する方法を説明します。それだけでなく、私たちが学習するルールは、取引を予定している市場から収集したデータに合わせて動的に調整されます。

取引戦略の概要

RSIは、極端な価格レベルを識別するためにテクニカルアナリストによって広く使用されています。通常、市場価格は平均値に戻る傾向があります。したがって、価格アナリストは、証券が極端なRSIレベルで推移していることを発見すると、通常は支配的なトレンドに逆らって賭けることになります。この戦略は少しずつ変更され、さまざまなバージョンに生まれ変わりましたが、すべて1つのソースから派生したものです。この戦略の欠点は、ある市場で強いRSIレベルと見なされるものが、必ずしもすべての市場で強いRSIレベルであるとは限らないことです。

この点を説明するために、下の図1は、2つの異なる市場でRSI値の標準偏差がどのように変化するかを示しています。青い線はXPDUSD市場におけるRSIの平均標準偏差を表し、オレンジ色の線はNZDJPY市場を表します。経験豊富なトレーダーなら誰でも、貴金属市場が著しく変動しやすいことは広く知られています。したがって、2つの市場間のRSIレベルの変化には明らかな相違が見られます。NZDUSDペアなどの通貨ペアのRSIの高値は、XPDUSDなどのより変動の大きい金融商品を取引する場合、通常の市場ノイズとみなされる場合があります。

各市場がRSIインジケーターに対して独自の関心レベルを持つ可能性があることがすぐに明らかになります。言い換えれば、RSIインジケーターを使用する場合、取引を開始する最適なレベルは、取引される銘柄によって異なります。したがって、どのRSIレベルで売買すべきかをアルゴリズム的に学習するにはどうすればよいでしょうか。遷移マトリックスを使用すると、念頭にある任意の銘柄に対してこの質問に答えることができます。

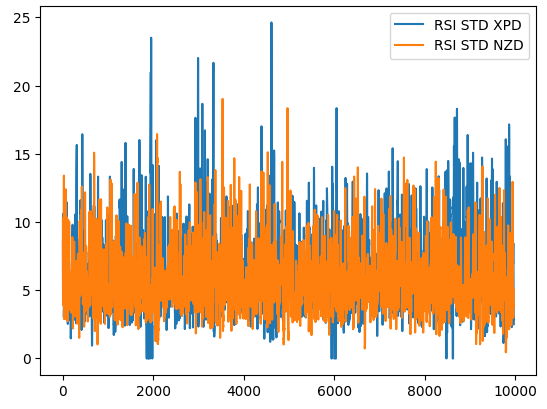
図1：XPDUSD市場におけるRSIインジケーターのローリングボラティリティ（青）、NZDUSD市場におけるRSIインジケーターのローリングボラティリティ（橙）

方法論の概要

保有するデータから戦略を学習するために、まずPython用のMetaTrader 5ライブラリを使用して300,000行のM1データを収集しました。データにラベルを付け、それを訓練用とテスト用に分割しました。訓練セットでは、RSIの読み取り値を0～10、11～20、91～100まで直線的に10個のビンにグループ化しました。 RSIの各グループを通過する際に、価格が将来どのように変動するかを記録しました。訓練データによると、価格がRSIの41～50ゾーンを通過すると価格レベルが上昇する傾向が最も強く、61～70ゾーンを通過すると価格レベルが下落する傾向が最も強いことがわかりました。

この推定遷移行列を使用して、事前分布から常に最も可能性の高い結果を選択する貪欲モデルを構築しました。私たちのシンプルなモデルは、テストセットで52%の精度を達成しました。このアプローチのもう1つの利点は相互運用性であり、モデルがどのように決定を下しているかを簡単に理解できます。さらに、重要な業界で使用されているAIモデルは説明可能であることが一般的になり、この確率モデルファミリではコンプライアンスの問題は発生しないので安心できます。

次に、私たちの関心はモデルの精度だけにあるわけではありません。むしろ、私たちは訓練セットで特定した10個のゾーンの個々の精度レベルに重点を置きました。訓練セット内で最も高い分布を示した2つのゾーンは、どちらも検証セットでは信頼できるとは証明されませんでした。データの検証セットでは、11〜20の範囲で購入し、71〜80の範囲で売却した場合に最高の精度が得られました。それぞれのゾーンからの精度レベルは51.4%と75.8%でした。これらのゾーンは、NZDJPYペアの買いポジションと売りポジションを開くための最適なゾーンとして選択されました。

最後に、分析結果をPythonで実装したMQL5エキスパートアドバイザー(EA)の構築に着手しました。さらに、アプリケーションにポジションをクローズする2つの方法を実装しました。RSIがポジションを減少させるゾーンを超えたときにポジションをクローズするか、価格が移動平均を超えたときにいつでもポジションをクローズするかをユーザーに決定させました。

データの取得とクリーニング

では、必要なライブラリをインポートして始めましょう。

#Let's get started
import MetaTrader5       as mt5
import pandas            as pd
import numpy             as np
import seaborn           as sns
import matplotlib.pyplot as plt
import pandas_ta         as ta

端末にアクセスできるかどうかを確認します。

mt5.initialize()

True

いくつかのグローバル変数を定義します。

#Fetch market data
SYMBOL    = "NZDJPY"
TIMEFRAME = mt5.TIMEFRAME_M1

端末からデータをコピーしましょう。

data = pd.DataFrame(mt5.copy_rates_from_pos(SYMBOL,TIMEFRAME,0,300000))

時間形式を秒から変換します。

data["time"]  = pd.to_datetime(data["time"],unit='s')

RSIを計算します。

data.ta.rsi(length=20,append=True)

どのくらい先の将来を予測すべきかを定義します。

#Define the look ahead
look_ahead = 20

データにラベルを付けます。

#Label the data
data["Target"] = np.nan

data.loc[data["close"] > data["close"].shift(-20),"Target"] = -1
data.loc[data["close"] < data["close"].shift(-20),"Target"] = 1

データから欠落している行をすべて削除します。

data.dropna(inplace=True)
data.reset_index(inplace=True,drop=True)

RSI値の10グループを表すベクトルを作成します。

#Create a dataframe 
rsi_matrix = pd.DataFrame(columns=["0-10","11-20","21-30","31-40","41-50","51-60","61-70","71-80","81-90","91-100"],index=[0])

これまでのデータは次のようになります。

data

図2：データフレーム内のいくつかの列

RSI行列をすべて0に初期化します。

#Initialize the rsi matrix to 0
for i in np.arange(0,9):
    rsi_matrix.iloc[0,i] = 0

データをパーティションに分割します。

#Split the data into train and test sets
train = data.loc[:(data.shape[0]//2),:]
test  = data.loc[(data.shape[0]//2):,:]

ここで、訓練データセットを調べて、各RSIの読み取り値と、それに対応する将来の価格レベルの変化を観察します。RSIの値が11で、価格レベルが将来20ステップ上昇した場合、RSIマトリックスの対応する11～20列を1つ増やします。さらに、価格レベルが下がるたびに、列にペナルティが課され、1ずつ減少します。直感的に、最終的には、正の値を持つ列は、価格レベルの上昇に先行する傾向のあるRSIレベルに対応し、負の値を持つ列の場合はその逆が当てはまることがすぐにわかります。

for i in np.arange(0,train.shape[0]):
    #Fill in the rsi matrix, what happened in the future when we saw RSI readings below 10?
    if((train.loc[i,"RSI_20"] <= 10)):
        rsi_matrix.iloc[0,0] = rsi_matrix.iloc[0,0] + train.loc[i,"Target"]
    #What tends to happen in the future, after seeing RSI readings between 11 and 20?
    if((train.loc[i,"RSI_20"] > 10) & (train.loc[i,"RSI_20"] <= 20)):
        rsi_matrix.iloc[0,1] = rsi_matrix.iloc[0,1] + train.loc[i,"Target"]
    #What tends to happen in the future, after seeing RSI readings between 21 and 30?
    if((train.loc[i,"RSI_20"] > 20) & (train.loc[i,"RSI_20"] <= 30)):
        rsi_matrix.iloc[0,2] = rsi_matrix.iloc[0,2] + train.loc[i,"Target"]
    #What tends to happen in the future, after seeing RSI readings between 31 and 40?
    if((train.loc[i,"RSI_20"] > 30) & (train.loc[i,"RSI_20"] <= 40)):
        rsi_matrix.iloc[0,3] = rsi_matrix.iloc[0,3] + train.loc[i,"Target"]
    #What tends to happen in the future, after seeing RSI readings between 41 and 50?
    if((train.loc[i,"RSI_20"] > 40) & (train.loc[i,"RSI_20"] <= 50)):
        rsi_matrix.iloc[0,4] = rsi_matrix.iloc[0,4] + train.loc[i,"Target"]
    #What tends to happen in the future, after seeing RSI readings between 51 and 60?
    if((train.loc[i,"RSI_20"] > 50) & (train.loc[i,"RSI_20"] <= 60)):
        rsi_matrix.iloc[0,5] = rsi_matrix.iloc[0,5] + train.loc[i,"Target"]
    #What tends to happen in the future, after seeing RSI readings between 61 and 70?
    if((train.loc[i,"RSI_20"] > 60) & (train.loc[i,"RSI_20"] <= 70)):
        rsi_matrix.iloc[0,6] = rsi_matrix.iloc[0,6] + train.loc[i,"Target"]
    #What tends to happen in the future, after seeing RSI readings between 71 and 80?
    if((train.loc[i,"RSI_20"] > 70) & (train.loc[i,"RSI_20"] <= 80)):
        rsi_matrix.iloc[0,7] = rsi_matrix.iloc[0,7] + train.loc[i,"Target"]
    #What tends to happen in the future, after seeing RSI readings between 81 and 90?
    if((train.loc[i,"RSI_20"] > 80) & (train.loc[i,"RSI_20"] <= 90)):
        rsi_matrix.iloc[0,8] = rsi_matrix.iloc[0,8] + train.loc[i,"Target"]
    #What tends to happen in the future, after seeing RSI readings between 91 and 100?
    if((train.loc[i,"RSI_20"] > 90) & (train.loc[i,"RSI_20"] <= 100)):
        rsi_matrix.iloc[0,9] = rsi_matrix.iloc[0,9] + train.loc[i,"Target"]

これは訓練セット内のカウントの分布です。ここで最初の問題に遭遇しました。91～100ゾーンに訓練観測がないということです。したがって、隣接するゾーンはすべて価格レベルの低下をもたらしたため、ゾーンに任意の負の値を割り当てることにすることにしました。

rsi_matrix

0-10	11-20	21-30	31-40	41-50	51-60	61-70	71-80	81-90	91-100
4.0	47.0	221.0	1171.0	3786.0	945.0	-1159.0	-35.0	-3.0	NaN

この分布を視覚化することができます。価格はほとんどの時間を31～70ゾーンで過ごしているようです。これはRSIの中央部分に相当します。先ほど述べたように、価格は41～50の領域では非常に強気で、61～70の領域では弱気のように見えました。ただし、この関係は検証データでは当てはまらなかったため、これらは訓練データの単なるアーティファクトであると思われます。

sns.barplot(rsi_matrix)

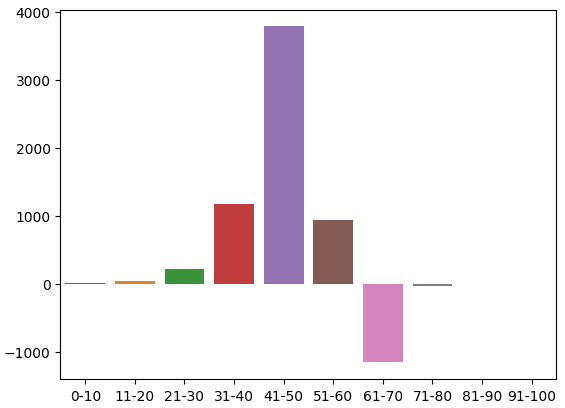
図3：RSIゾーンの観測された効果の分布

図4：これまでの変革を視覚的に表現

ここで、検証データでモデルの精度を評価します。まず、訓練データのインデックスをリセットします。

test.reset_index(inplace=True,drop=True)

モデルの予測用の列を作成します。

test["Predictions"]  = np.nan

モデルの予測を入力してください。

for i in np.arange(0,test.shape[0]):
    #Fill in the predictions
    if((test.loc[i,"RSI_20"] <= 10)):
        test.loc[i,"Predictions"] = 1
    
    if((test.loc[i,"RSI_20"] > 10) & (test.loc[i,"RSI_20"] <= 20)):
        test.loc[i,"Predictions"] = 1
    
    if((test.loc[i,"RSI_20"] > 20) & (test.loc[i,"RSI_20"] <= 30)):
        test.loc[i,"Predictions"] = 1
        
    if((test.loc[i,"RSI_20"] > 30) & (test.loc[i,"RSI_20"] <= 40)):
        test.loc[i,"Predictions"] = 1

    if((test.loc[i,"RSI_20"] > 40) & (test.loc[i,"RSI_20"] <= 50)):
        test.loc[i,"Predictions"] = 1

    if((test.loc[i,"RSI_20"] > 50) & (test.loc[i,"RSI_20"] <= 60)):
        test.loc[i,"Predictions"] = 1

    if((test.loc[i,"RSI_20"] > 60) & (test.loc[i,"RSI_20"] <= 70)):
        test.loc[i,"Predictions"] = -1

    if((test.loc[i,"RSI_20"] > 70) & (test.loc[i,"RSI_20"] <= 80)):
        test.loc[i,"Predictions"] = -1

    if((test.loc[i,"RSI_20"] > 80) & (test.loc[i,"RSI_20"] <= 90)):
        test.loc[i,"Predictions"] = -1

    if((test.loc[i,"RSI_20"] > 90) & (test.loc[i,"RSI_20"] <= 100)):
        test.loc[i,"Predictions"] = -1

null値がないことを確認します。

test.loc[:,"Predictions"].isna().any()

False

pandasを使用して、モデルの予測とターゲットの関係を説明しましょう。最も一般的なエントリはTrueです。これは良いインジケーターです。

(test["Target"] == test["Predictions"]).describe()

count     148636
unique         2
top         True
freq       77409
dtype: object

モデルがどれだけ正確であるかを推定してみましょう。

#Our estimation of the model's accuracy
((test["Target"] == test["Predictions"]).describe().freq / (test["Target"] == test["Predictions"]).shape[0])

0.5207957695309346

10個のRSIゾーンそれぞれの精度に興味があります。

val_err = []

各ゾーンでの精度を記録します。

val_err.append(test.loc[(test["RSI_20"] < 10) & (test["Predictions"] == test["Target"])].shape[0] / test.loc[test["RSI_20"] < 10].shape[0])
val_err.append(test.loc[((test["RSI_20"] <= 20) & (test["RSI_20"] > 10)) & (test["Predictions"] == test["Target"])].shape[0] / test.loc[((test["RSI_20"] <= 20) & (test["RSI_20"] > 10))].shape[0])
val_err.append(test.loc[((test["RSI_20"] <= 30) & (test["RSI_20"] > 20)) & (test["Predictions"] == test["Target"])].shape[0] / test.loc[((test["RSI_20"] <= 30) & (test["RSI_20"] > 20))].shape[0])
val_err.append(test.loc[((test["RSI_20"] <= 40) & (test["RSI_20"] > 30)) & (test["Predictions"] == test["Target"])].shape[0] / test.loc[((test["RSI_20"] <= 40) & (test["RSI_20"] > 30))].shape[0])
val_err.append(test.loc[((test["RSI_20"] <= 50) & (test["RSI_20"] > 40)) & (test["Predictions"] == test["Target"])].shape[0] / test.loc[((test["RSI_20"] <= 50) & (test["RSI_20"] > 40))].shape[0])
val_err.append(test.loc[((test["RSI_20"] <= 60) & (test["RSI_20"] > 50)) & (test["Predictions"] == test["Target"])].shape[0] / test.loc[((test["RSI_20"] <= 60) & (test["RSI_20"] > 50))].shape[0])
val_err.append(test.loc[((test["RSI_20"] <= 70) & (test["RSI_20"] > 60)) & (test["Predictions"] == test["Target"])].shape[0] / test.loc[((test["RSI_20"] <= 70) & (test["RSI_20"] > 60))].shape[0])
val_err.append(test.loc[((test["RSI_20"] <= 80) & (test["RSI_20"] > 70)) & (test["Predictions"] == test["Target"])].shape[0] / test.loc[((test["RSI_20"] <= 80) & (test["RSI_20"] > 70))].shape[0])
val_err.append(test.loc[((test["RSI_20"] <= 90) & (test["RSI_20"] > 80)) & (test["Predictions"] == test["Target"])].shape[0] / test.loc[((test["RSI_20"] <= 90) & (test["RSI_20"] > 80))].shape[0])
val_err.append(test.loc[((test["RSI_20"] <= 100) & (test["RSI_20"] > 90)) & (test["Predictions"] == test["Target"])].shape[0] / test.loc[((test["RSI_20"] <= 100) & (test["RSI_20"] > 90))].shape[0])

精度をプロットします。赤い線は50%のカットオフポイントです。この線より下のRSIゾーンは信頼できない可能性があります。最後のゾーンのスコアが完璧な1であることがはっきりとわかります。ただし、これは、私たちが持っていた100,000分を超える訓練データで一度も発生しなかった、欠落している91～100ゾーンに対応することを思い出してください。したがって、このゾーンはおそらくめったに見られず、取引要件には最適ではありません。11～20ゾーンの精度レベルは75%で、強気ゾーンの中では最高です。71-80ゾーンについても同様で、すべての弱気ゾーンの中で最も高い精度を示しました。

plt.plot(val_err)
plt.plot(fifty,'r')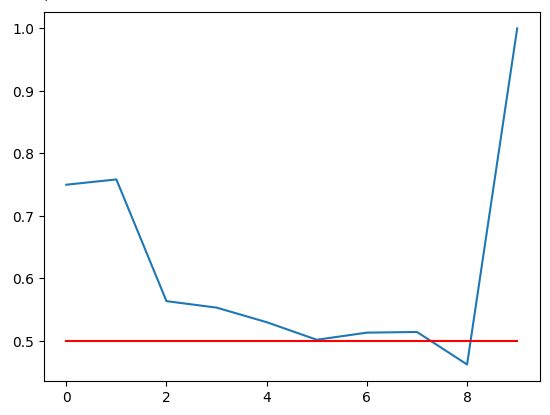

図5：検証精度の視覚化

さまざまなRSIゾーンでの検証精度です。91～100の範囲で100%の精度が得られたことに注意してください。訓練セットは約100,000行でしたが、そのゾーンではRSIの読み取り値は観測されなかったことを思い出してください。したがって、価格がそれらの極値に達することはめったになく、その結果は私たちにとって最適な決定ではない可能性があると結論付けることができます。

0-10	11-20	21-30	31-40	41-50	51-60	61-70	71-80	81-90	91-100
0.75	0.75	0.56	0.55	0.53	0.50	0.51	0.51	0.46	1.0

深層マルコフモデルの構築

これまでのところ、過去のデータ分布から学習するモデルのみを構築しました。より柔軟な学習者を積み重ねてこの戦略を強化し、マルコフモデルを使用する最適な戦略を学習することは可能でしょうか。ディープニューラルネットワークを訓練し、マルコフモデルによる予測を入力として与えて、観測された価格レベルの変化をターゲットにします。このタスクを効果的に達成するには、訓練セットを2つに分割する必要があります。訓練セットの最初の半分だけを使用して、新しいマルコフモデルを適合させます。私たちのニューラルネットワークは、前半の訓練セットに対するマルコフモデルの予測と、それに応じた価格レベルの変化に適合します。

ニューラルネットワークと単純なマルコフモデルの両方が、OHLC市場の相場から直接価格レベルの変化を学習しようとする同一のニューラルネットワークよりも優れたパフォーマンスを発揮することがわかりました。これらの結論は、訓練手順で使用されていなかったテストデータから導き出されました。驚くべきことに、ディープニューラルネットワークとシンプルマルコフモデルは同等のパフォーマンスを発揮しました。つまり、マルコフモデルによって設定されたベンチマークを上回るために、さらなる努力が必要であるとみなすことができます。

必要なライブラリをインポートすることから始めましょう。

#Let us now try find a machine learning model to learn how to optimally use our transition matrix
from sklearn.neural_network import MLPClassifier
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split,TimeSeriesSplit

ここで、訓練データに対して訓練とテストの分割を実行する必要があります。

#Now let us partition our train set into 2 halves 
train , train_val = train_test_split(train,shuffle=False,test_size=0.5)

新しい列車セットにマルコフモデルを適合させます。

#Now let us recalculate our transition matrix, based on the first half of the training set
rsi_matrix.iloc[0,0] = train.loc[(train["RSI_20"] < 10) & (train["Target"] == 1)].shape[0] / train.loc[(train["RSI_20"] < 10)].shape[0]
rsi_matrix.iloc[0,1] = train.loc[((train["RSI_20"] > 10) & (train["RSI_20"] <=20)) & (train["Target"] == 1)].shape[0] / train.loc[((train["RSI_20"] > 10) & (train["RSI_20"] <=20))].shape[0]
rsi_matrix.iloc[0,2] = train.loc[((train["RSI_20"] > 20) & (train["RSI_20"] <=30)) & (train["Target"] == 1)].shape[0] / train.loc[((train["RSI_20"] > 20) & (train["RSI_20"] <=30))].shape[0]
rsi_matrix.iloc[0,3] = train.loc[((train["RSI_20"] > 30) & (train["RSI_20"] <=40)) & (train["Target"] == 1)].shape[0] / train.loc[((train["RSI_20"] > 30) & (train["RSI_20"] <=40))].shape[0]
rsi_matrix.iloc[0,4] = train.loc[((train["RSI_20"] > 40) & (train["RSI_20"] <=50)) & (train["Target"] == 1)].shape[0] / train.loc[((train["RSI_20"] > 40) & (train["RSI_20"] <=50))].shape[0]
rsi_matrix.iloc[0,5] = train.loc[((train["RSI_20"] > 50) & (train["RSI_20"] <=60)) & (train["Target"] == 1)].shape[0] / train.loc[((train["RSI_20"] > 50) & (train["RSI_20"] <=60))].shape[0]
rsi_matrix.iloc[0,6] = train.loc[((train["RSI_20"] > 60) & (train["RSI_20"] <=70)) & (train["Target"] == 1)].shape[0] / train.loc[((train["RSI_20"] > 60) & (train["RSI_20"] <=70))].shape[0]
rsi_matrix.iloc[0,7] = train.loc[((train["RSI_20"] > 70) & (train["RSI_20"] <=80)) & (train["Target"] == 1)].shape[0] / train.loc[((train["RSI_20"] > 70) & (train["RSI_20"] <=80))].shape[0]
rsi_matrix.iloc[0,8] = train.loc[((train["RSI_20"] > 80) & (train["RSI_20"] <=90)) & (train["Target"] == 1)].shape[0] / train.loc[((train["RSI_20"] > 80) & (train["RSI_20"] <=90))].shape[0]

rsi_matrix

0-10	11-20	21-30	31-40	41-50	51-60	61-70	71-80	81-90	91-100
1.0	0.655172	0.541701	0.536398	0.53243	0.516551	0.460306	0.491154	0.395349	0

この確率分布を視覚化することができます。これらの量は、価格が10個のRSIゾーンのそれぞれを通過した後、20分後に価格レベルが上昇する確率を表していることを思い出してください。赤い線は50%レベルを表します。50%レベルを超えるすべてのゾーンは強気であり、それ以下のすべてのゾーンは弱気です。訓練データの前半を考慮すると、これが真実であると想定できます。

#From the training set, it appears that RSI readings above 61 are bearish and RSI readings below 61 are bullish
plt.plot(rsi_matrix.iloc[0,:])
plt.plot(fifty,'r')

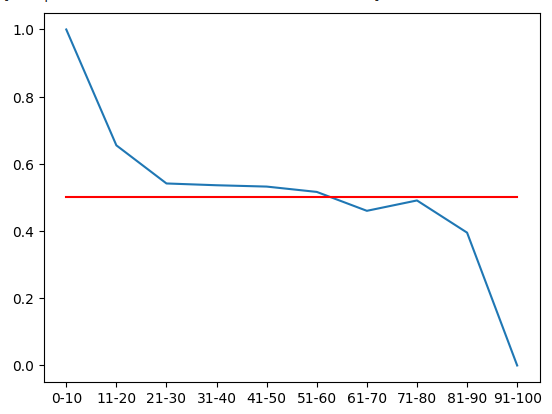
図6：訓練セットの前半から、61未満のゾーンはすべて強気で、61を超えるゾーンは弱気であることがわかります。

マルコフモデルによっておこなわれた新しい予測を記録します。

#Let's now store our model's predictions
train["Predictions"] = -1
train.loc[train["RSI_20"] < 61,"Predictions"] = 1

train_val["Predictions"] = -1
train_val.loc[train_val["RSI_20"] < 61,"Predictions"] = 1

test["Predictions"] = -1
test.loc[test["RSI_20"] < 61,"Predictions"] = 1

ニューラルネットワークを使い始める前に、原則として、標準化とスケーリングをおこなうと役立ちます。さらに、RSIは0～100の固定スケールですが、価格の読み取りには制限がありません。このような場合には標準化が必要になります。

#Let's Standardize and scale our data
from sklearn.preprocessing import RobustScaler

入力とターゲットを定義します。

ohlc_predictors = ["open","high","low","close","tick_volume","spread","RSI_20"]
transition_matrix = ["Predictions"]
all_predictors = ohlc_predictors + transition_matrix
target = ["Target"]

データをスケーリングします。

scaler = RobustScaler()
scaler =  scaler.fit(train.loc[:,predictors])
train_scaled = pd.DataFrame(scaler.transform(train.loc[:,predictors]),columns=predictors)
train_val_scaled = pd.DataFrame(scaler.transform(train_val.loc[:,predictors]),columns=predictors)
test_scaled = pd.DataFrame(scaler.transform(test.loc[:,predictors]),columns=predictors)

精度を保存するためのデータフレームを作成します。

#Create a dataframe to store our cv error on the training set, validation training set and the test set
train_err     = pd.DataFrame(columns=["Transition Matrix","Deep Markov Model","OHLC Model","All Model"],index=np.arange(0,5)) 
train_val_err = pd.DataFrame(columns=["Transition Matrix","Deep Markov Model","OHLC Model","All Model"],index=[0]) 
test_err      = pd.DataFrame(columns=["Transition Matrix","Deep Markov Model","OHLC Model","All Model"],index=[0])

時系列分割オブジェクトを定義します。

#Create a time series split object
tscv = TimeSeriesSplit(n_splits = 5,gap=look_ahead)

モデルを相互検証します。

model = MLPClassifier(hidden_layer_sizes=(20,10))
for i , (train_index,test_index) in enumerate(tscv.split(train_scaled)):
    #Fit the model
    model.fit(train.loc[train_index,transition_matrix],train.loc[train_index,"Target"])
    #Record its accuracy
    train_err.iloc[i,1] = accuracy_score(train.loc[test_index,"Target"],model.predict(train.loc[test_index,transition_matrix]))

#Record our accuracy levels on the validation training set
train_val_err.iloc[0,1] = accuracy_score(train_val.loc[:,"Target"],model.predict(train_val.loc[:,transition_matrix]))

#Record our accuracy levels on the test set
test_err.iloc[0,1] = accuracy_score(test.loc[:,"Target"],model.predict(test.loc[:,transition_matrix]))

#Our accuracy levels on the training set
train_err

ここで、訓練セットの検証半分でモデルの精度を観察してみましょう。

train_val_err.iloc[0,0] = train_val.loc[train_val["Predictions"] == train_val["Target"]].shape[0] / train_val.shape[0]
train_val_err

遷移マトリックス	深層マルコフモデル	OHLCモデル	全モデル
0.52309	0.52309	0.507306	0.517291

ここで最も重要なこととして、テストデータセットの精度を確認しましょう。2つの表からわかるように、ハイブリッド深層マルコフモデルは、シンプルマルコフモデルを上回ることができませんでした。私にとっては、これは驚きでした。これは、ディープニューラルネットワークを訓練する手順が最適ではなかったことを意味している可能性がありますが、代わりに、候補となる機械学習モデルのより広範なプールを常に検索することができます。結果におけるもう1つの興味深い特徴は、すべてのデータを使用したモデルが最高のパフォーマンスを発揮しなかったことです。

良いニュースは、市場相場から直接価格を予測することで、ベンチマークセットを上回るパフォーマンスを達成できたことです。マルコフモデルの単純なヒューリスティックは、ニューラルネットワークが低レベルの市場構造を迅速に学習するのに役立つようです。

test_err.iloc[0,0] = test.loc[test["Predictions"] == test["Target"]].shape[0] / test.shape[0]
test_err

遷移マトリックス	深層マルコフモデル	OHLCモデル	全モデル
0.519322	0.519322	0.497127	0.496724

MQL5での実装

RSIベースのEAを実装するには、まず必要なライブラリをインポートすることから始めます。

//+------------------------------------------------------------------+
//|                                                     Auto RSI.mq5 |
//|                                        Gamuchirai Zororo Ndawana |
//|                          https://www.mql5.com/ja/gamuchiraindawa |
//+------------------------------------------------------------------+
#property copyright "Gamuchirai Zororo Ndawana"
#property link      "https://www.mql5.com/ja/gamuchiraindawa"
#property version   "1.00"

//+------------------------------------------------------------------+
//| Libraries                                                        |
//+------------------------------------------------------------------+
#include <Trade\Trade.mqh>
CTrade Trade;

次に、グローバル変数を定義します。

//+------------------------------------------------------------------+
//| Global variables                                                 |
//+------------------------------------------------------------------+
int rsi_handler;
double rsi_buffer[];
int ma_handler;
int system_state;
double ma_buffer[];
double bid,ask;

//--- Custom enumeration
enum close_conditions
  {
   MA_Close  = 0,
   RSI_Close
  };

ユーザーからの入力を取得します。

//+------------------------------------------------------------------+
//| Inputs                                                           |
//+------------------------------------------------------------------+
input group "Technical Indicators"
input int rsi_period = 20; //RSI Period
input int ma_period = 20; //MA Period

input group "Money Management"
input double trading_volume = 0.3; //Lot size

input group "Trading Rules"
input close_conditions user_close = RSI_Close; //How should we close the positions?

EAが初めてロードされるたびに、インジケーターをロードして検証しましょう。

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//--- Load the indicator
   rsi_handler = iRSI(_Symbol,PERIOD_M1,rsi_period,PRICE_CLOSE);
   ma_handler = iMA(_Symbol,PERIOD_M1,ma_period,0,MODE_EMA,PRICE_CLOSE);

//--- Validate our technical indicators
   if(rsi_handler == INVALID_HANDLE || ma_handler == INVALID_HANDLE)
     {
      //--- We failed to load the rsi
      Comment("Failed to load the RSI Indicator");
      return(INIT_FAILED);
     }

//---
   return(INIT_SUCCEEDED);
  }

アプリケーションが使用されていない場合は、インジケーターを解放します。

//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//--- Release our technical indicators
   IndicatorRelease(rsi_handler);
   IndicatorRelease(ma_handler);
  }

最後に、ポジションがないので、モデルの取引ルールに従います。それ以外の場合、ポジションが開いている場合は、取引を終了する方法についてはユーザーの指示に従います。

//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
//--- Update market and technical data
   update();

//--- Check if we have any open positions
   if(PositionsTotal() == 0)
     {
      check_setup();
     }

   if(PositionsTotal() > 0)
     {
      manage_setup();
     }
  }
//+------------------------------------------------------------------+

次の関数は、ユーザーがRSIから学習した取引ルールを使用するか、単純移動平均を使用するかに応じて、ポジションをクローズします。移動平均線の使用を希望する場合は、価格が移動平均線を越えるたびにポジションをクローズするだけです。

//+------------------------------------------------------------------+
//| Manage our open setups                                           |
//+------------------------------------------------------------------+
void manage_setup(void)
  {
   if(user_close == RSI_Close)
     {
      if((system_state == 1) && ((rsi_buffer[0] > 71) && (rsi_buffer[80] <= 80)))
        {
         PositionSelect(Symbol());
         Trade.PositionClose(PositionGetTicket(0));
         return;
        }

      if((system_state == -1) && ((rsi_buffer[0] > 11) && (rsi_buffer[80] <= 20)))
        {
         PositionSelect(Symbol());
         Trade.PositionClose(PositionGetTicket(0));
         return;
        }
     }


   else
      if(user_close == MA_Close)
        {
         if((iClose(_Symbol,PERIOD_CURRENT,0) > ma_buffer[0]) && (system_state == -1))
           {
            PositionSelect(Symbol());
            Trade.PositionClose(PositionGetTicket(0));
            return;
           }

         if((iClose(_Symbol,PERIOD_CURRENT,0) < ma_buffer[0]) && (system_state == 1))
           {
            PositionSelect(Symbol());
            Trade.PositionClose(PositionGetTicket(0));
            return;
           }
        }
  }

次の関数は、有効なセットアップがあるかどうかを確認します。つまり、価格が利益が出るゾーンに入った場合です。さらに、ユーザーがポジションをクローズするために移動平均を使用するように指定した場合、ポジションを開くかどうかを決定する前に、価格が移動平均の右側になるまで待機します。

//+------------------------------------------------------------------+
//| Find if we have any setups to trade                              |
//+------------------------------------------------------------------+
void check_setup(void)
  {

   if(user_close == RSI_Close)
     {
      if((rsi_buffer[0] > 71) && (rsi_buffer[0] <= 80))
        {
         Trade.Sell(trading_volume,_Symbol,bid,0,0,"Auto RSI");
         system_state = -1;
        }

      if((rsi_buffer[0] > 11) && (rsi_buffer[0] <= 20))
        {
         Trade.Buy(trading_volume,_Symbol,ask,0,0,"Auto RSI");
         system_state = 1;
        }
     }

   if(user_close == MA_Close)
     {
      if(((rsi_buffer[0] > 71) && (rsi_buffer[0] <= 80)) && (iClose(_Symbol,PERIOD_CURRENT,0) < ma_buffer[0]))
        {
         Trade.Sell(trading_volume,_Symbol,bid,0,0,"Auto RSI");
         system_state = -1;
        }

      if(((rsi_buffer[0] > 11) && (rsi_buffer[0] <= 20)) && (iClose(_Symbol,PERIOD_CURRENT,0) > ma_buffer[0]))
        {
         Trade.Buy(trading_volume,_Symbol,ask,0,0,"Auto RSI");
         system_state = 1;
        }
     }
  }

以下の関数により、テクニカルデータと市場データが更新されます。

//+------------------------------------------------------------------+
//| Fetch market quotes and technical data                           |
//+------------------------------------------------------------------+
void update(void)
  {
   bid = SymbolInfoDouble(_Symbol,SYMBOL_BID);
   ask = SymbolInfoDouble(_Symbol,SYMBOL_ASK);

   CopyBuffer(rsi_handler,0,0,1,rsi_buffer);
   CopyBuffer(ma_handler,0,0,1,ma_buffer);
  }
//+------------------------------------------------------------------+

図7：EA

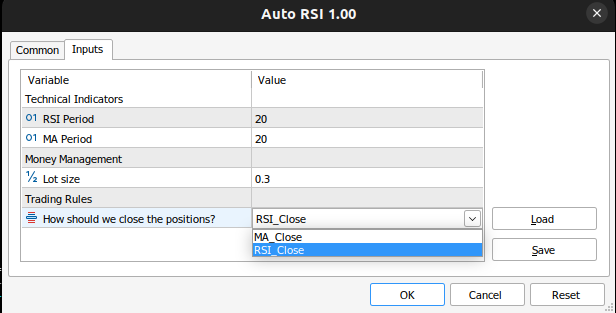
図8：EAアプリケーション

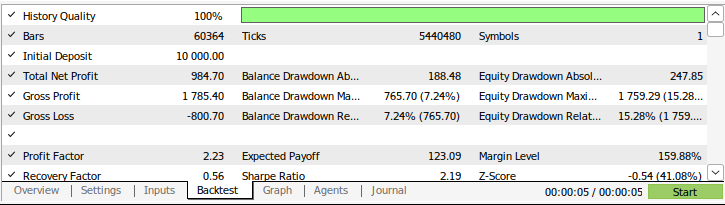
図9：戦略のバックテスト結果

結論

この記事では、単純な確率モデルの威力を実証しました。驚いたことに、シンプルマルコフモデルの間違いから学習しようとしても、そのモデルを上回ることはできませんでした。しかし、本連載を注意深く読んでいる方は、私たちが今正しい方向に向かっているという私の見解に賛同していただけると思います。私たちは、価格そのものをモデル化するのと同じくらい有益であるという制約の下で、価格そのものよりもモデル化しやすい一連のアルゴリズムをゆっくりと蓄積しています。次回のディスカッションでは、単純なマルコフモデルを上回るパフォーマンスを得るために必要な理由について学びたいと思います。

MetaQuotes Ltdにより英語から翻訳されました。
元の記事: https://www.mql5.com/en/articles/16030

添付されたファイル |

ZIPをダウンロード

RSI_Self_Optimizer.ipynb (131.78 KB)

Auto_RSI.mq5 (6.11 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動

ボリンジャーバンドを活用したピラニア戦略に基づくMQL5エキスパートアドバイザーの作成

この記事では、ボリンジャーバンドを利用したピラニア戦略に基づいてMQL5でエキスパートアドバイザー(EA)を作成し、取引の有効性を高めます。この戦略の重要な原則、コーディングの実装、テストと最適化の方法について説明します。この知識によって、取引シナリオにEAを効果的に導入することが可能になります。

知っておくべきMQL5ウィザードのテクニック（第41回）：DQN (Deep-Q-Network)

DQN (Deep-Q-Network)は強化学習アルゴリズムであり、機械学習モジュールの学習プロセスにおいて、次のQ値と理想的な行動を予測する際にニューラルネットワークを関与させます。別の強化学習アルゴリズムであるQ学習についてはすでに検討しました。そこでこの記事では、強化学習で訓練されたMLPが、カスタムシグナルクラス内でどのように使用できるかを示すもう1つの例を紹介します。

Connexusにおけるヘッダ（第3部）：リクエスト用HTTPヘッダの使い方をマスターする

Connexusライブラリの開発を続けます。この章では、HTTPプロトコルにおけるヘッダの概念を探求し、ヘッダとは何か、何のためにあるのか、リクエストでどのように使うのかを説明します。APIとの通信で使用される主なヘッダを取り上げ、ライブラリでの設定方法の実践例を紹介します。

古典的な戦略を再構築する（第9回）：多時間枠分析(II)

本日のディスカッションでは、AIモデルがどの時間枠で最高のパフォーマンスを発揮するかを明らかにするため、多時間枠分析の戦略を検討します。この分析により、EURUSDペアにおいて月次および時間足の時間枠が比較的誤差の少ないモデルを生成することが分かりました。この結果を活用し、月次時間枠でAIによる予測を行い、時間枠で取引を実行するアルゴリズムを作成しました。