Selbstoptimierender Expert Advisor mit MQL5 und Python (Teil V): Tiefe Markov-Modelle
172
0
In unserer früheren Diskussion über Markov-Ketten, die hier verlinkt ist, haben wir gezeigt, wie man eine Übergangsmatrix verwendet, um das probabilistische Verhalten des Marktes zu verstehen. Unsere Übergangsmatrix hat viele Informationen für uns zusammengefasst. Sie gab uns nicht nur Hinweise darauf, wann wir kaufen und verkaufen sollten, sondern informierte uns auch darüber, ob unser Markt starke Trends aufwies oder ob es sich eher um eine mittlere Umkehrung handelte. In der heutigen Diskussion werden wir unsere Definition des Systemzustands von den gleitenden Durchschnitten, die wir in unserer ersten Diskussion verwendet haben, auf den Relative Strength Indicator (RSI) Indikator ändern.
Wenn den meisten Menschen beigebracht wird, wie man mit dem RSI handelt, wird ihnen gesagt, sie sollen kaufen, wenn der RSI 30 erreicht, und verkaufen, wenn er 70 erreicht. Einige Mitglieder der Gemeinschaft mögen sich fragen, ob dies die beste Entscheidung für alle Märkte ist. Wir alle wissen, dass man nicht einfach alle Märkte auf die gleiche Weise handeln kann. Dieser Artikel zeigt Ihnen, wie Sie Ihre eigenen Markov-Ketten erstellen können, um algorithmisch optimale Handelsregeln zu lernen. Und nicht nur das: Die Regeln, die wir lernen, passen sich dynamisch an die Daten an, die Sie auf dem Markt sammeln, auf dem Sie handeln wollen.
Überblick über die Handelsstrategie
Der RSI wird von technischen Analysten häufig verwendet, um extreme Kursniveaus zu erkennen. Normalerweise tendieren die Marktpreise dazu, zu ihren Durchschnittswerten zurückzukehren. Wenn Kursanalysten also feststellen, dass sich ein Wertpapier in extremen RSI-Niveaus bewegt, würden sie normalerweise gegen den vorherrschenden Trend wetten. Diese Strategie wurde leicht abgewandelt in viele verschiedene Versionen, die alle aus einer Quelle stammen. Der Nachteil dieser Strategie besteht darin, dass ein starkes RSI-Niveau, das auf einem Markt als stark angesehen werden kann, nicht notwendigerweise ein starkes RSI-Niveau für alle Märkte darstellt.
Zur Veranschaulichung dieses Punktes zeigt die folgende Abbildung 1, wie sich die Standardabweichung des RSI-Wertes auf 2 verschiedenen Märkten entwickelt. Die blaue Linie stellt die durchschnittliche Standardabweichung des RSI im XPDUSD-Markt dar, während die orange Linie den NZDJPY-Markt repräsentiert. Es ist allen erfahrenen Händlern bekannt, dass der Edelmetallmarkt sehr volatil ist. Daher können wir eine deutliche Diskrepanz zwischen den Veränderungen der RSI-Werte zwischen den beiden Märkten erkennen. Was bei einem Währungspaar wie dem NZDUSD als hoher RSI-Wert angesehen werden kann, kann beim Handel mit einem volatileren Instrument wie dem XPDUSD als gewöhnliches Marktrauschen betrachtet werden.
Es wird schnell klar, dass für jeden Markt der RSI-Indikator seine eigene Bedeutung haben könnte. Mit anderen Worten: Wenn wir den RSI-Indikator verwenden, hängt das optimale Niveau für den Einstieg in einen Handel von dem gehandelten Symbol ab. Wie können wir also algorithmisch lernen, auf welchem RSI-Level wir kaufen oder verkaufen sollten? Wir können unsere Übergangsmatrix verwenden, um diese Frage für jedes beliebige Symbol zu beantworten, das uns vorschwebt.
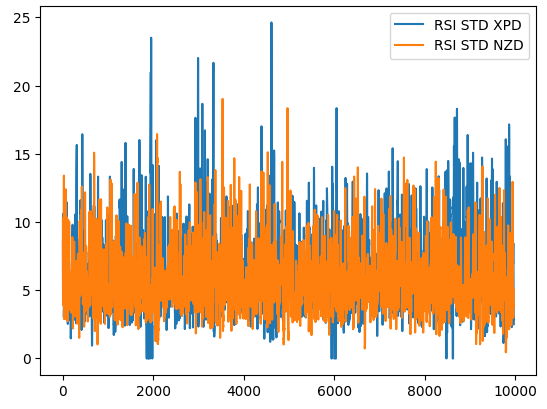
Abb. 1: Die rollende Volatilität des RSI-Indikators auf dem XPDUSD-Markt in blau und dem NZDUSD-Markt in orange
Überblick über die Methodik
Um mit unserer Strategie aus den uns zur Verfügung stehenden Daten zu lernen, haben wir zunächst 300 000 Zeilen von M1-Daten mit Hilfe der MetaTrader 5-Bibliothek für Python gesammelt. Wir haben die Daten gekennzeichnet und sie dann in Trainings- und Testdaten aufgeteilt. In der Trainingsgruppe haben wir die RSI-Werte in 10 Bins eingeteilt, von 0-10, 11-20, linear bis 91-100. Wir haben aufgezeichnet, wie sich der Preis in der Zukunft verhalten hat, als er jede Gruppe auf dem RSI durchlief. Die Trainingsdaten zeigten, dass die Preisniveaus die höchste Tendenz zur Aufwertung hatten, wenn der Preis die 41-50-Zone des RSI passierte, und die höchste Tendenz zur Abwertung in der 61-70-Zone.
Anhand dieser geschätzten Übergangsmatrix haben wir ein gieriges Modell erstellt, das immer das wahrscheinlichste Ergebnis aus den vorherigen Verteilungen auswählt. Unser einfaches Modell erreichte eine Genauigkeit von 52 % bei der Testmenge. Ein weiterer Vorteil dieses Ansatzes ist seine Interoperabilität: Wir können leicht nachvollziehen, wie unser Modell seine Entscheidungen trifft. Darüber hinaus ist es heute üblich, dass KI-Modelle, die in wichtigen Branchen eingesetzt werden, erklärbar sind, und Sie können sicher sein, dass diese Familie probabilistischer Modelle keine Probleme mit der Einhaltung von Vorschriften verursachen wird.
Unser Interesse galt aber nicht nur der Genauigkeit des Modells. Vielmehr haben wir in die individuellen Genauigkeitsstufen der 10 Zonen investiert, die wir in unserem Trainingssatz identifiziert haben. Keine der beiden Zonen, die in unserem Trainingsset die höchsten Verteilungen aufwiesen, erwies sich in der Validierungsmenge als zuverlässig. Bei der Validierung der Daten erzielten wir die höchste Genauigkeit, wenn wir im Bereich 11-20 kauften und im Bereich 71-80 verkauften. Die Trefferquote lag bei 51,4 % und 75,8 % in den jeweiligen Zonen. Wir haben diese Zonen als unsere optimalen Zonen für die Eröffnung von Kauf- und Verkaufspositionen für das NZDJPY-Paar ausgewählt.
Schließlich haben wir uns daran gemacht, einen MQL5 Expert Advisor zu erstellen, der die Ergebnisse unserer Analyse in Python umsetzt. Außerdem haben wir in unserer Anwendung 2 Möglichkeiten zum Schließen von Positionen implementiert. Wir haben dem Nutzer die Wahl gelassen, entweder Positionen zu schließen, wenn der RSI in eine Zone übergeht, die unsere offenen Positionen verringert, oder alternativ Positionen zu schließen, wenn der Preis den gleitenden Durchschnitt überquert.
Abrufen und Bereinigen der Daten
Fangen wir an und importieren die benötigten Bibliotheken.
#Let's get started import MetaTrader5 as mt5 import pandas as pd import numpy as np import seaborn as sns import matplotlib.pyplot as plt import pandas_ta as ta
Prüfen wir, ob das Terminal erreicht werden kann.
mt5.initialize()
Wir definieren ein paar globale Variablen,
#Fetch market data SYMBOL = "NZDJPY" TIMEFRAME = mt5.TIMEFRAME_M1
kopieren die Daten von unserem Terminal,
data = pd.DataFrame(mt5.copy_rates_from_pos(SYMBOL,TIMEFRAME,0,300000))
konvertieren das Zeitformat von Sekunden,
data["time"] = pd.to_datetime(data["time"],unit='s')
berechnen den RSI,
data.ta.rsi(length=20,append=True) legen fest, wie weit wir in die Zukunft vorausschauen sollen,
#Define the look ahead look_ahead = 20
kennzeichnen die Daten,
#Label the data data["Target"] = np.nan data.loc[data["close"] > data["close"].shift(-20),"Target"] = -1 data.loc[data["close"] < data["close"].shift(-20),"Target"] = 1
entfernen alle fehlenden Zeilen aus den Daten und
data.dropna(inplace=True) data.reset_index(inplace=True,drop=True)
erstellen einen Vektor zur Darstellung der 10 Gruppen von RSI-Werten.
#Create a dataframe rsi_matrix = pd.DataFrame(columns=["0-10","11-20","21-30","31-40","41-50","51-60","61-70","71-80","81-90","91-100"],index=[0])
So sehen unsere Daten bis jetzt aus.
data
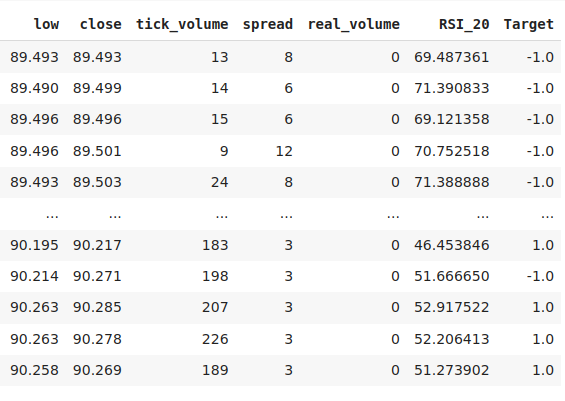
Abb. 2: Einige der Spalten in unserem Datenrahmen
Initialisierung der RSI-Matrix mit 0.
#Initialize the rsi matrix to 0 for i in np.arange(0,9): rsi_matrix.iloc[0,i] = 0
Teilen wir die Daten auf.
#Split the data into train and test sets train = data.loc[:(data.shape[0]//2),:] test = data.loc[(data.shape[0]//2):,:]
Wir werden nun den Trainingsdatensatz durchgehen und jeden RSI-Wert und die entsprechende künftige Veränderung des Preisniveaus beobachten. Wenn der RSI-Wert 11 beträgt und die Kurse in der Zukunft um 20 Stufen steigen, erhöhen wir die entsprechende Spalte 11-20 in unserer RSI-Matrix um eins. Außerdem wird die Spalte jedes Mal, wenn das Preisniveau sinkt, bestraft und um eins verringert. Intuitiv versteht man schnell, dass jede Spalte mit einem positiven Wert einem RSI-Niveau entspricht, das eine Tendenz zu steigenden Kursniveaus hat, und das Gegenteil gilt für Spalten mit negativen Werten.
for i in np.arange(0,train.shape[0]): #Fill in the rsi matrix, what happened in the future when we saw RSI readings below 10? if((train.loc[i,"RSI_20"] <= 10)): rsi_matrix.iloc[0,0] = rsi_matrix.iloc[0,0] + train.loc[i,"Target"] #What tends to happen in the future, after seeing RSI readings between 11 and 20? if((train.loc[i,"RSI_20"] > 10) & (train.loc[i,"RSI_20"] <= 20)): rsi_matrix.iloc[0,1] = rsi_matrix.iloc[0,1] + train.loc[i,"Target"] #What tends to happen in the future, after seeing RSI readings between 21 and 30? if((train.loc[i,"RSI_20"] > 20) & (train.loc[i,"RSI_20"] <= 30)): rsi_matrix.iloc[0,2] = rsi_matrix.iloc[0,2] + train.loc[i,"Target"] #What tends to happen in the future, after seeing RSI readings between 31 and 40? if((train.loc[i,"RSI_20"] > 30) & (train.loc[i,"RSI_20"] <= 40)): rsi_matrix.iloc[0,3] = rsi_matrix.iloc[0,3] + train.loc[i,"Target"] #What tends to happen in the future, after seeing RSI readings between 41 and 50? if((train.loc[i,"RSI_20"] > 40) & (train.loc[i,"RSI_20"] <= 50)): rsi_matrix.iloc[0,4] = rsi_matrix.iloc[0,4] + train.loc[i,"Target"] #What tends to happen in the future, after seeing RSI readings between 51 and 60? if((train.loc[i,"RSI_20"] > 50) & (train.loc[i,"RSI_20"] <= 60)): rsi_matrix.iloc[0,5] = rsi_matrix.iloc[0,5] + train.loc[i,"Target"] #What tends to happen in the future, after seeing RSI readings between 61 and 70? if((train.loc[i,"RSI_20"] > 60) & (train.loc[i,"RSI_20"] <= 70)): rsi_matrix.iloc[0,6] = rsi_matrix.iloc[0,6] + train.loc[i,"Target"] #What tends to happen in the future, after seeing RSI readings between 71 and 80? if((train.loc[i,"RSI_20"] > 70) & (train.loc[i,"RSI_20"] <= 80)): rsi_matrix.iloc[0,7] = rsi_matrix.iloc[0,7] + train.loc[i,"Target"] #What tends to happen in the future, after seeing RSI readings between 81 and 90? if((train.loc[i,"RSI_20"] > 80) & (train.loc[i,"RSI_20"] <= 90)): rsi_matrix.iloc[0,8] = rsi_matrix.iloc[0,8] + train.loc[i,"Target"] #What tends to happen in the future, after seeing RSI readings between 91 and 100? if((train.loc[i,"RSI_20"] > 90) & (train.loc[i,"RSI_20"] <= 100)): rsi_matrix.iloc[0,9] = rsi_matrix.iloc[0,9] + train.loc[i,"Target"]
Dies ist die Verteilung der Zählungen in der Trainingsmenge. Wir sind bei unserem ersten Problem angelangt: Es gab keine Ausbildungsbeobachtungen im Bereich 91-100. Daher habe ich beschlossen, davon auszugehen, dass wir der Zone einen willkürlichen negativen Wert zuweisen, da die benachbarten Zonen alle zu fallenden Kursniveaus führten.
rsi_matrix
| 0-10 | 11-20 | 21-30 | 31-40 | 41-50 | 51-60 | 61-70 | 71-80 | 81-90 | 91-100 |
|---|---|---|---|---|---|---|---|---|---|
| 4.0 | 47.0 | 221.0 | 1171.0 | 3786.0 | 945.0 | -1159.0 | -35.0 | -3.0 | NaN |
Wir können diese Verteilung visualisieren. Es scheint, dass sich der Preis die meiste Zeit im Bereich von 31-70 bewegt. Dies entspricht dem mittleren Teil des RSI. Wie wir bereits erwähnt haben, scheinen die Kurse im Bereich von 41-50 stark zu steigen und im Bereich von 61-70 zu fallen. Dabei handelte es sich jedoch offenbar nur um Artefakte der Trainingsdaten, da diese Beziehung bei den Validierungsdaten nicht zutraf.
sns.barplot(rsi_matrix)
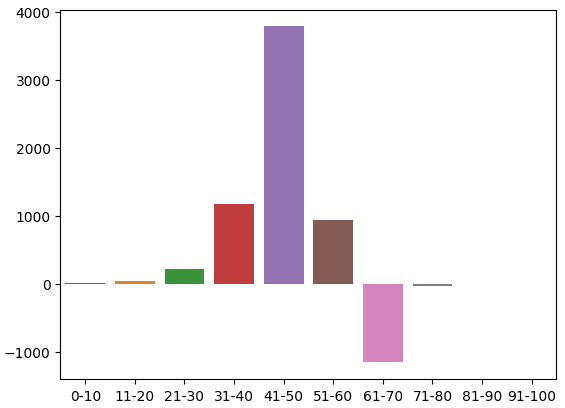
Abb. 3: Die Verteilung der beobachteten Auswirkungen der RSI-Zonen
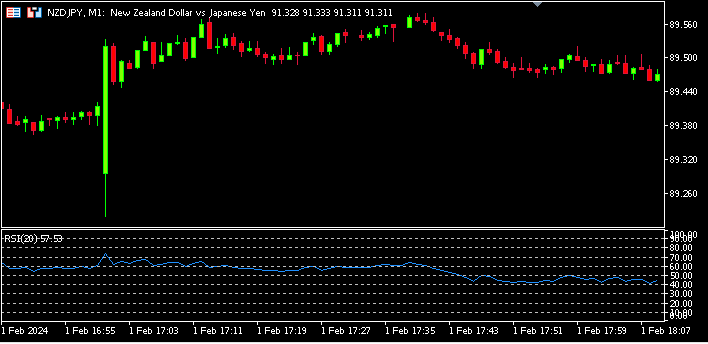
Abb. 4: Eine visuelle Darstellung unserer bisherigen Transformationen
Nun werden wir die Genauigkeit unseres Modells anhand von Validierungsdaten bewerten. Setzen wir zunächst den Index der Trainingsdaten zurück,
test.reset_index(inplace=True,drop=True)
erstellen eine Spalte für die Vorhersagen unseres Modells,
test["Predictions"] = np.nan tragen die Vorhersagen unseres Modells ein und
for i in np.arange(0,test.shape[0]): #Fill in the predictions if((test.loc[i,"RSI_20"] <= 10)): test.loc[i,"Predictions"] = 1 if((test.loc[i,"RSI_20"] > 10) & (test.loc[i,"RSI_20"] <= 20)): test.loc[i,"Predictions"] = 1 if((test.loc[i,"RSI_20"] > 20) & (test.loc[i,"RSI_20"] <= 30)): test.loc[i,"Predictions"] = 1 if((test.loc[i,"RSI_20"] > 30) & (test.loc[i,"RSI_20"] <= 40)): test.loc[i,"Predictions"] = 1 if((test.loc[i,"RSI_20"] > 40) & (test.loc[i,"RSI_20"] <= 50)): test.loc[i,"Predictions"] = 1 if((test.loc[i,"RSI_20"] > 50) & (test.loc[i,"RSI_20"] <= 60)): test.loc[i,"Predictions"] = 1 if((test.loc[i,"RSI_20"] > 60) & (test.loc[i,"RSI_20"] <= 70)): test.loc[i,"Predictions"] = -1 if((test.loc[i,"RSI_20"] > 70) & (test.loc[i,"RSI_20"] <= 80)): test.loc[i,"Predictions"] = -1 if((test.loc[i,"RSI_20"] > 80) & (test.loc[i,"RSI_20"] <= 90)): test.loc[i,"Predictions"] = -1 if((test.loc[i,"RSI_20"] > 90) & (test.loc[i,"RSI_20"] <= 100)): test.loc[i,"Predictions"] = -1
prüfen, dass es keine Nullwerte gibt.
test.loc[:,"Predictions"].isna().any() Beschreiben wir die Beziehung zwischen den Vorhersagen unseres Modells und dem Ziel, indem wir Pandas verwenden. Der häufigste Eintrag ist True, das ist ein guter Indikator.
(test["Target"] == test["Predictions"]).describe()
unique 2
top True
freq 77409
dtype: object
Schätzen wir, wie genau unser Modell ist.
#Our estimation of the model's accuracy ((test["Target"] == test["Predictions"]).describe().freq / (test["Target"] == test["Predictions"]).shape[0])
Wir interessieren uns für die Genauigkeit jeder der 10 RSI-Zonen.
val_err = []
Erfassen wir unsere Genauigkeit in jeder Zone.
val_err.append(test.loc[(test["RSI_20"] < 10) & (test["Predictions"] == test["Target"])].shape[0] / test.loc[test["RSI_20"] < 10].shape[0]) val_err.append(test.loc[((test["RSI_20"] <= 20) & (test["RSI_20"] > 10)) & (test["Predictions"] == test["Target"])].shape[0] / test.loc[((test["RSI_20"] <= 20) & (test["RSI_20"] > 10))].shape[0]) val_err.append(test.loc[((test["RSI_20"] <= 30) & (test["RSI_20"] > 20)) & (test["Predictions"] == test["Target"])].shape[0] / test.loc[((test["RSI_20"] <= 30) & (test["RSI_20"] > 20))].shape[0]) val_err.append(test.loc[((test["RSI_20"] <= 40) & (test["RSI_20"] > 30)) & (test["Predictions"] == test["Target"])].shape[0] / test.loc[((test["RSI_20"] <= 40) & (test["RSI_20"] > 30))].shape[0]) val_err.append(test.loc[((test["RSI_20"] <= 50) & (test["RSI_20"] > 40)) & (test["Predictions"] == test["Target"])].shape[0] / test.loc[((test["RSI_20"] <= 50) & (test["RSI_20"] > 40))].shape[0]) val_err.append(test.loc[((test["RSI_20"] <= 60) & (test["RSI_20"] > 50)) & (test["Predictions"] == test["Target"])].shape[0] / test.loc[((test["RSI_20"] <= 60) & (test["RSI_20"] > 50))].shape[0]) val_err.append(test.loc[((test["RSI_20"] <= 70) & (test["RSI_20"] > 60)) & (test["Predictions"] == test["Target"])].shape[0] / test.loc[((test["RSI_20"] <= 70) & (test["RSI_20"] > 60))].shape[0]) val_err.append(test.loc[((test["RSI_20"] <= 80) & (test["RSI_20"] > 70)) & (test["Predictions"] == test["Target"])].shape[0] / test.loc[((test["RSI_20"] <= 80) & (test["RSI_20"] > 70))].shape[0]) val_err.append(test.loc[((test["RSI_20"] <= 90) & (test["RSI_20"] > 80)) & (test["Predictions"] == test["Target"])].shape[0] / test.loc[((test["RSI_20"] <= 90) & (test["RSI_20"] > 80))].shape[0]) val_err.append(test.loc[((test["RSI_20"] <= 100) & (test["RSI_20"] > 90)) & (test["Predictions"] == test["Target"])].shape[0] / test.loc[((test["RSI_20"] <= 100) & (test["RSI_20"] > 90))].shape[0])
Zeichnen wir unsere Genauigkeit. Die rote Linie ist unsere 50%-Grenze. Jede RSI-Zone unterhalb dieser Linie ist möglicherweise nicht zuverlässig. Es ist deutlich zu erkennen, dass die letzte Zone eine perfekte Punktzahl von 1 hat. Es sei jedoch daran erinnert, dass dies der fehlenden Zone 91-100 entspricht, die in den mehr als 100 000 Minuten Trainingsdaten, die wir hatten, nicht ein einziges Mal vorkam. Daher ist diese Zone wahrscheinlich selten zu sehen und für unsere Handelsanforderungen nicht optimal. Die Zone 11-20 weist eine Genauigkeit von 75 % auf und ist damit die höchste unserer Aufwärts-Zonen. Das Gleiche gilt für die Zone 71-80, die die höchste Genauigkeit unter allen Abwärts-Zonen aufwies.
plt.plot(val_err)
plt.plot(fifty,'r')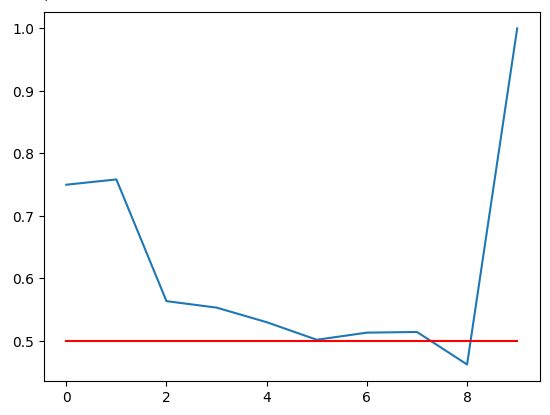 
FIg 5: Visualisierung unserer Validierungsgenauigkeit
Unsere Validierungsgenauigkeit in den verschiedenen RSI-Zonen. Beachten Sie, dass wir eine 100%ige Genauigkeit im Bereich 91-100 erreicht haben. Es sei daran erinnert, dass unser Trainingsset etwa 100 000 Zeilen umfasste, wir aber keine RSI-Werte in diesem Bereich beobachtet haben. Daraus können wir schließen, dass die Preise selten diese Extreme erreichen, sodass das Ergebnis für uns keine optimale Entscheidung sein kann.
| 0-10 | 11-20 | 21-30 | 31-40 | 41-50 | 51-60 | 61-70 | 71-80 | 81-90 | 91-100 |
|---|---|---|---|---|---|---|---|---|---|
| 0.75 | 0.75 | 0.56 | 0.55 | 0.53 | 0.50 | 0.51 | 0.51 | 0.46 | 1.0 |
Aufbau unseres tiefen Markov-Modells
Bislang haben wir nur ein Modell entwickelt, das aus der Verteilung der Daten in der Vergangenheit lernt. Wäre es möglich, diese Strategie zu verbessern, indem wir einen flexibleren Lerner einsetzen, um eine optimale Strategie für die Verwendung unseres Markov-Modells zu erlernen? Wir trainieren ein tiefes neuronales Netz und geben ihm die Vorhersagen des Markov-Modells als Eingaben, und die beobachteten Veränderungen der Preisniveaus werden das Ziel sein. Um diese Aufgabe effektiv zu bewältigen, müssen wir unsere Trainingsmenge in zwei Hälften unterteilen. Wir werden unser neues Markov-Modell nur mit der ersten Hälfte des Trainingssatzes anpassen. Unser neuronales Netz wird auf die Vorhersagen des Markov-Modells für die erste Hälfte des Trainingssatzes und die entsprechenden Änderungen des Preisniveaus angepasst.
Wir haben festgestellt, dass sowohl unser neuronales Netz als auch unser einfaches Markov-Modell besser abschneiden als ein identisches neuronales Netz, das versucht, Änderungen der Preisniveaus direkt aus den OHLC-Marktnotierungen zu lernen. Diese Schlussfolgerungen wurden aus unseren Testdaten gezogen, die nicht für das Trainingsverfahren verwendet worden waren. Erstaunlich ist, dass unser Deep Neural Network und unser Simple Markov Model gleich gut abschneiden. Dies kann daher als Aufforderung zu größeren Anstrengungen gesehen werden, um die vom Markov-Modell gesetzte Benchmark zu übertreffen.
Beginnen wir damit, die benötigten Bibliotheken zu importieren.
#Let us now try find a machine learning model to learn how to optimally use our transition matrix from sklearn.neural_network import MLPClassifier from sklearn.metrics import accuracy_score from sklearn.model_selection import train_test_split,TimeSeriesSplit
Nun müssen wir mit unseren Trainingsdaten eine Aufteilung in Training und Test durchführen.
#Now let us partition our train set into 2 halves train , train_val = train_test_split(train,shuffle=False,test_size=0.5)
Passen wir das Markov-Modell an die neue Trainingseinstellungen an.
#Now let us recalculate our transition matrix, based on the first half of the training set rsi_matrix.iloc[0,0] = train.loc[(train["RSI_20"] < 10) & (train["Target"] == 1)].shape[0] / train.loc[(train["RSI_20"] < 10)].shape[0] rsi_matrix.iloc[0,1] = train.loc[((train["RSI_20"] > 10) & (train["RSI_20"] <=20)) & (train["Target"] == 1)].shape[0] / train.loc[((train["RSI_20"] > 10) & (train["RSI_20"] <=20))].shape[0] rsi_matrix.iloc[0,2] = train.loc[((train["RSI_20"] > 20) & (train["RSI_20"] <=30)) & (train["Target"] == 1)].shape[0] / train.loc[((train["RSI_20"] > 20) & (train["RSI_20"] <=30))].shape[0] rsi_matrix.iloc[0,3] = train.loc[((train["RSI_20"] > 30) & (train["RSI_20"] <=40)) & (train["Target"] == 1)].shape[0] / train.loc[((train["RSI_20"] > 30) & (train["RSI_20"] <=40))].shape[0] rsi_matrix.iloc[0,4] = train.loc[((train["RSI_20"] > 40) & (train["RSI_20"] <=50)) & (train["Target"] == 1)].shape[0] / train.loc[((train["RSI_20"] > 40) & (train["RSI_20"] <=50))].shape[0] rsi_matrix.iloc[0,5] = train.loc[((train["RSI_20"] > 50) & (train["RSI_20"] <=60)) & (train["Target"] == 1)].shape[0] / train.loc[((train["RSI_20"] > 50) & (train["RSI_20"] <=60))].shape[0] rsi_matrix.iloc[0,6] = train.loc[((train["RSI_20"] > 60) & (train["RSI_20"] <=70)) & (train["Target"] == 1)].shape[0] / train.loc[((train["RSI_20"] > 60) & (train["RSI_20"] <=70))].shape[0] rsi_matrix.iloc[0,7] = train.loc[((train["RSI_20"] > 70) & (train["RSI_20"] <=80)) & (train["Target"] == 1)].shape[0] / train.loc[((train["RSI_20"] > 70) & (train["RSI_20"] <=80))].shape[0] rsi_matrix.iloc[0,8] = train.loc[((train["RSI_20"] > 80) & (train["RSI_20"] <=90)) & (train["Target"] == 1)].shape[0] / train.loc[((train["RSI_20"] > 80) & (train["RSI_20"] <=90))].shape[0] rsi_matrix
| 0-10 | 11-20 | 21-30 | 31-40 | 41-50 | 51-60 | 61-70 | 71-80 | 81-90 | 91-100 |
|---|---|---|---|---|---|---|---|---|---|
| 1.0 | 0.655172 | 0.541701 | 0.536398 | 0.53243 | 0.516551 | 0.460306 | 0.491154 | 0.395349 | 0 |
Wir können diese Wahrscheinlichkeitsverteilung visualisieren. Diese Mengen stellen die Wahrscheinlichkeit dar, dass die Preise 20 Minuten in der Zukunft steigen, nachdem der Preis jede der 10 RSI-Zonen durchlaufen hat. Die rote Linie stellt die 50%-Marke dar. Alle Zonen oberhalb der 50 %-Marke tendieren aufwärts, und alle Zonen darunter fallen. Davon können wir ausgehen, wenn wir die erste Hälfte der Trainingsdaten betrachten.
#From the training set, it appears that RSI readings above 61 are bearish and RSI readings below 61 are bullish plt.plot(rsi_matrix.iloc[0,:]) plt.plot(fifty,'r')
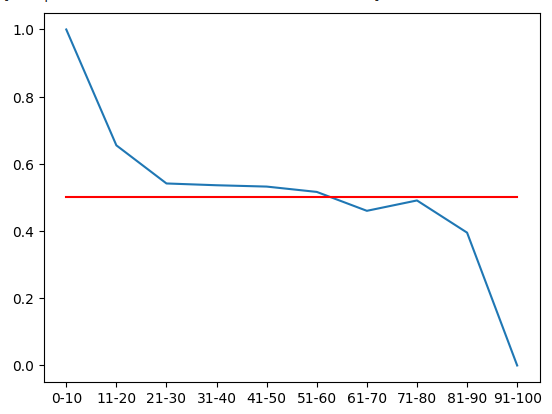
Abb. 6: Aus der ersten Hälfte des Trainingsdatensatzes geht hervor, dass alle Zonen unterhalb von 61 aufwärts und oberhalb von 61 abwärts tendieren.
Aufzeichnung der neuen Vorhersagen des Markov-Modells.
#Let's now store our model's predictions train["Predictions"] = -1 train.loc[train["RSI_20"] < 61,"Predictions"] = 1 train_val["Predictions"] = -1 train_val.loc[train_val["RSI_20"] < 61,"Predictions"] = 1 test["Predictions"] = -1 test.loc[test["RSI_20"] < 61,"Predictions"] = 1
Bevor wir mit dem Einsatz neuronaler Netze beginnen können, hilft als Faustregel die Standardisierung und Skalierung. Außerdem liegt unser RSI auf einer festen Skala von 0-100, während unsere Kurswerte unbegrenzt sind. In solchen Fällen ist eine Standardisierung notwendig.
#Let's Standardize and scale our data from sklearn.preprocessing import RobustScaler
Definieren wir unseren Input und unser Ziel.
ohlc_predictors = ["open","high","low","close","tick_volume","spread","RSI_20"] transition_matrix = ["Predictions"] all_predictors = ohlc_predictors + transition_matrix target = ["Target"]
Skalieren wir die Daten,
scaler = RobustScaler() scaler = scaler.fit(train.loc[:,predictors]) train_scaled = pd.DataFrame(scaler.transform(train.loc[:,predictors]),columns=predictors) train_val_scaled = pd.DataFrame(scaler.transform(train_val.loc[:,predictors]),columns=predictors) test_scaled = pd.DataFrame(scaler.transform(test.loc[:,predictors]),columns=predictors)
erstellen den Datenrahmen, um unsere Genauigkeit zu speichern und
#Create a dataframe to store our cv error on the training set, validation training set and the test set train_err = pd.DataFrame(columns=["Transition Matrix","Deep Markov Model","OHLC Model","All Model"],index=np.arange(0,5)) train_val_err = pd.DataFrame(columns=["Transition Matrix","Deep Markov Model","OHLC Model","All Model"],index=[0]) test_err = pd.DataFrame(columns=["Transition Matrix","Deep Markov Model","OHLC Model","All Model"],index=[0])
definieren das Objekt für die Aufteilung der Zeitserie.
#Create a time series split object tscv = TimeSeriesSplit(n_splits = 5,gap=look_ahead)
Kreuzvalidierung der Modelle.
model = MLPClassifier(hidden_layer_sizes=(20,10)) for i , (train_index,test_index) in enumerate(tscv.split(train_scaled)): #Fit the model model.fit(train.loc[train_index,transition_matrix],train.loc[train_index,"Target"]) #Record its accuracy train_err.iloc[i,1] = accuracy_score(train.loc[test_index,"Target"],model.predict(train.loc[test_index,transition_matrix])) #Record our accuracy levels on the validation training set train_val_err.iloc[0,1] = accuracy_score(train_val.loc[:,"Target"],model.predict(train_val.loc[:,transition_matrix])) #Record our accuracy levels on the test set test_err.iloc[0,1] = accuracy_score(test.loc[:,"Target"],model.predict(test.loc[:,transition_matrix])) #Our accuracy levels on the training set train_err
Betrachten wir nun die Genauigkeit unseres Modells in der Validierungshälfte der Trainingsmenge.
train_val_err.iloc[0,0] = train_val.loc[train_val["Predictions"] == train_val["Target"]].shape[0] / train_val.shape[0] train_val_err
| Übergangsmatrix | Tiefes Markov-Modell | OHLC-Modell | Alle Modelle |
|---|---|---|---|
| 0.52309 | 0.52309 | 0.507306 | 0.517291 |
Das Wichtigste ist nun, dass wir unsere Genauigkeit im Testdatensatz sehen. Wie wir aus den beiden Tabellen ersehen können, hat unser hybrides Deep Markov Model unser einfaches Markov Model nicht übertroffen. Das hat mich sehr überrascht. Es könnte bedeuten, dass unser Verfahren zum Trainieren des tiefen neuronalen Netzes nicht optimal war. Alternativ dazu können wir jederzeit einen breiteren Pool von Kandidaten für maschinelles Lernen durchsuchen. Ein weiteres interessantes Merkmal unserer Ergebnisse ist, dass das Modell, das alle Daten verwendet hat, nicht am besten abgeschnitten hat.
Die gute Nachricht ist, dass es uns gelungen ist, die Benchmark zu übertreffen, die wir bei dem Versuch, den Preis direkt aus den Marktnotierungen vorherzusagen, gesetzt haben. Es scheint, dass die einfachen Heuristiken des Markov-Modells dem neuronalen Netz dabei helfen, die Marktstruktur auf der unteren Ebene schnell zu lernen.
test_err.iloc[0,0] = test.loc[test["Predictions"] == test["Target"]].shape[0] / test.shape[0] test_err
| Übergangsmatrix | Tiefes Markov-Modell | OHLC-Modell | Alle Modelle |
|---|---|---|---|
| 0.519322 | 0.519322 | 0.497127 | 0.496724 |
Implementierung in MQL5
Um unseren RSI-basierten Expert Advisor zu implementieren, müssen wir zunächst die benötigten Bibliotheken einbinden.
//+------------------------------------------------------------------+ //| Auto RSI.mq5 | //| Gamuchirai Zororo Ndawana | //| https://www.mql5.com/en/gamuchiraindawa | //+------------------------------------------------------------------+ #property copyright "Gamuchirai Zororo Ndawana" #property link "https://www.mql5.com/en/gamuchiraindawa" #property version "1.00" //+------------------------------------------------------------------+ //| Libraries | //+------------------------------------------------------------------+ #include <Trade\Trade.mqh> CTrade Trade;
Definieren wir nun unsere globalen Variablen.
//+------------------------------------------------------------------+ //| Global variables | //+------------------------------------------------------------------+ int rsi_handler; double rsi_buffer[]; int ma_handler; int system_state; double ma_buffer[]; double bid,ask; //--- Custom enumeration enum close_conditions { MA_Close = 0, RSI_Close };
Wir müssen Eingaben von unserem Nutzer erhalten.
//+------------------------------------------------------------------+ //| Inputs | //+------------------------------------------------------------------+ input group "Technical Indicators" input int rsi_period = 20; //RSI Period input int ma_period = 20; //MA Period input group "Money Management" input double trading_volume = 0.3; //Lot size input group "Trading Rules" input close_conditions user_close = RSI_Close; //How should we close the positions?
Wenn unser Expert Advisor zum ersten Mal geladen wird, sollten wir die Indikatoren laden und sie validieren.
//+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- Load the indicator rsi_handler = iRSI(_Symbol,PERIOD_M1,rsi_period,PRICE_CLOSE); ma_handler = iMA(_Symbol,PERIOD_M1,ma_period,0,MODE_EMA,PRICE_CLOSE); //--- Validate our technical indicators if(rsi_handler == INVALID_HANDLE || ma_handler == INVALID_HANDLE) { //--- We failed to load the rsi Comment("Failed to load the RSI Indicator"); return(INIT_FAILED); } //--- return(INIT_SUCCEEDED); }
Wenn unsere Anwendung nicht in Gebrauch ist, geben wir die Indikatoren frei.
//+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- Release our technical indicators IndicatorRelease(rsi_handler); IndicatorRelease(ma_handler); }
Schließlich haben wir keine offenen Positionen, sondern folgen den Handelsregeln unseres Modells. Andernfalls, wenn wir eine offene Position haben, befolgen wir die Anweisungen des Nutzers, wie wir die Handelsgeschäfte schließen.
//+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { //--- Update market and technical data update(); //--- Check if we have any open positions if(PositionsTotal() == 0) { check_setup(); } if(PositionsTotal() > 0) { manage_setup(); } } //+------------------------------------------------------------------+
Die folgende Funktion schließt unsere Positionen, je nachdem, ob der Nutzer möchte, dass wir die Handelsregeln verwenden, die wir aus dem RSI oder dem einfachen gleitenden Durchschnitt gelernt haben. Wenn wir den gleitenden Durchschnitt verwenden wollen, schließen wir unsere Positionen einfach, sobald der Kurs den gleitenden Durchschnitt überschreitet.
//+------------------------------------------------------------------+ //| Manage our open setups | //+------------------------------------------------------------------+ void manage_setup(void) { if(user_close == RSI_Close) { if((system_state == 1) && ((rsi_buffer[0] > 71) && (rsi_buffer[80] <= 80))) { PositionSelect(Symbol()); Trade.PositionClose(PositionGetTicket(0)); return; } if((system_state == -1) && ((rsi_buffer[0] > 11) && (rsi_buffer[80] <= 20))) { PositionSelect(Symbol()); Trade.PositionClose(PositionGetTicket(0)); return; } } else if(user_close == MA_Close) { if((iClose(_Symbol,PERIOD_CURRENT,0) > ma_buffer[0]) && (system_state == -1)) { PositionSelect(Symbol()); Trade.PositionClose(PositionGetTicket(0)); return; } if((iClose(_Symbol,PERIOD_CURRENT,0) < ma_buffer[0]) && (system_state == 1)) { PositionSelect(Symbol()); Trade.PositionClose(PositionGetTicket(0)); return; } } }
Mit der folgenden Funktion wird geprüft, ob gültige Einstellungen vorhanden sind. Das heißt, wenn der Preis eine unserer profitablen Zonen erreicht hat. Wenn der Nutzer außerdem festgelegt hat, dass wir den gleitenden Durchschnitt zum Schließen unserer Positionen verwenden sollen, warten wir zunächst, bis der Kurs auf der rechten Seite des gleitenden Durchschnitts liegt, bevor wir entscheiden, ob wir eine Position eröffnen sollen.
//+------------------------------------------------------------------+ //| Find if we have any setups to trade | //+------------------------------------------------------------------+ void check_setup(void) { if(user_close == RSI_Close) { if((rsi_buffer[0] > 71) && (rsi_buffer[0] <= 80)) { Trade.Sell(trading_volume,_Symbol,bid,0,0,"Auto RSI"); system_state = -1; } if((rsi_buffer[0] > 11) && (rsi_buffer[0] <= 20)) { Trade.Buy(trading_volume,_Symbol,ask,0,0,"Auto RSI"); system_state = 1; } } if(user_close == MA_Close) { if(((rsi_buffer[0] > 71) && (rsi_buffer[0] <= 80)) && (iClose(_Symbol,PERIOD_CURRENT,0) < ma_buffer[0])) { Trade.Sell(trading_volume,_Symbol,bid,0,0,"Auto RSI"); system_state = -1; } if(((rsi_buffer[0] > 11) && (rsi_buffer[0] <= 20)) && (iClose(_Symbol,PERIOD_CURRENT,0) > ma_buffer[0])) { Trade.Buy(trading_volume,_Symbol,ask,0,0,"Auto RSI"); system_state = 1; } } }
Mit dieser Funktion werden unsere technischen Daten und Marktdaten aktualisiert.
//+------------------------------------------------------------------+ //| Fetch market quotes and technical data | //+------------------------------------------------------------------+ void update(void) { bid = SymbolInfoDouble(_Symbol,SYMBOL_BID); ask = SymbolInfoDouble(_Symbol,SYMBOL_ASK); CopyBuffer(rsi_handler,0,0,1,rsi_buffer); CopyBuffer(ma_handler,0,0,1,ma_buffer); } //+------------------------------------------------------------------+
Abb. 7: Unser Expert Advisor
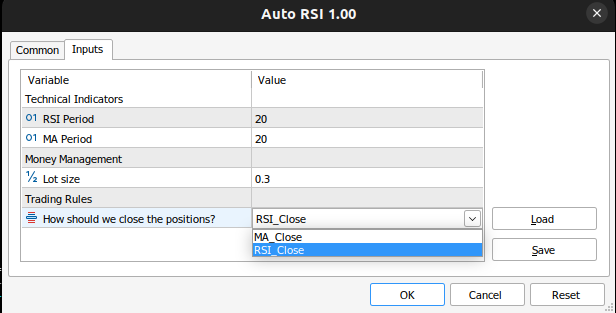
Abb. 8: Die Eingaben unseres Expert Advisors
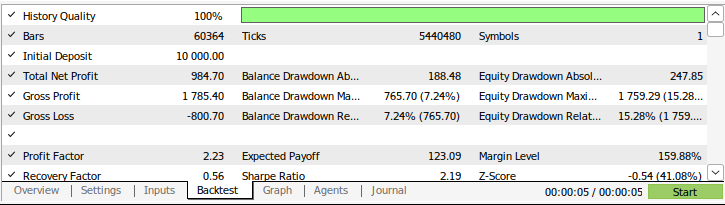
Abb. 9: Die Ergebnisse des Backtestings unserer Strategie
Schlussfolgerung
In diesem Artikel haben wir die Leistungsfähigkeit von einfachen probabilistischen Modellen demonstriert. Zu unserer Überraschung konnten wir das einfache Markov-Modell nicht übertreffen, indem wir versuchten, aus dessen Fehlern zu lernen. Wenn Sie jedoch diese Artikelserie aufmerksam verfolgt haben, werden Sie wahrscheinlich meine Ansicht teilen, dass wir uns jetzt in die richtige Richtung bewegen. Wir bauen langsam eine Reihe von Algorithmen auf, die einfacher zu modellieren sind als der Preis selbst, und zwar unter der Bedingung, dass sie genauso informativ sind wie die Modellierung des Preises selbst. In unseren nächsten Diskussionen werden wir versuchen herauszufinden, warum es notwendig ist, das einfache Markov-Modell zu übertreffen.
Übersetzt aus dem Englischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/en/articles/16030
MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 42): ADX-Oszillator
Erstellen eines MQL5 Expert Advisors basierend auf der PIRANHA Strategie unter Verwendung von Bollinger Bändern
Ordinale Kodierung für Nominalvariablen
Der Header im Connexus (Teil 3): Die Verwendung von HTTP-Headern für Anfragen beherrschen
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.