Самооптимизирующийся советник на языках MQL5 и Python (Часть V): Глубокие марковские модели

MetaTrader 5 — Примеры | 9 мая 2025, 07:19

573

В нашем предыдущем обсуждении цепей Маркова мы продемонстрировали, как использовать матрицу перехода для понимания вероятностного поведения рынка. Наша матрица перехода обобщила для нас большой объем информации. Она не только подсказывал нам, когда покупать и продавать, но и сообщала, наблюдаются ли на нашем рынке сильные тренды или он в основном возвращается к среднему значению. В этой системе мы изменим наше определение состояния системы, заменив скользящие средние, которые мы использовали в нашем первом обсуждении, на индикатор относительной силы (RSI).

Когда большинство людей обучают торговле с использованием RSI, им говорят покупать, когда RSI достигает 30, и продавать, когда он достигает 70. Некоторые члены сообщества могут усомниться в том, что это лучшее решение для всех рынков. Мы все знаем, что невозможно торговать на всех рынках одинаково. В этой статье будет показано, как можно построить собственные цепи Маркова для алгоритмического изучения оптимальных правил торговли. Более того, правила, которые мы изучим, динамически подстраиваются под данные, собираемые на рынке, на котором вы хотите торговать.

Обзор торговой стратегии

RSI широко используется техническими аналитиками для определения экстремальных уровней цен. Как правило, рыночные цены имеют тенденцию возвращаться к своим средним значениям. Поэтому всякий раз, когда ценовые аналитики обнаруживают, что актив колеблется на экстремальных уровнях RSI, они обычно делают ставку против доминирующего тренда. Эта стратегия существует во множестве различных версий, которые все происходят из одного источника. Недостатком этой стратегии является то, что то, что можно считать сильным уровнем RSI на одном рынке, не обязательно является сильным уровнем RSI для остальных рынков.

Для иллюстрации на рисунке 1 ниже показано, как меняется стандартное отклонение значения RSI на двух разных рынках. Синяя линия представляет среднее стандартное отклонение RSI на рынке XPDUSD, а оранжевая линия представляет рынок NZDJPY. Всем опытным трейдерам хорошо известно, что рынок драгоценных металлов весьма волатилен. Таким образом, мы можем наблюдать явное несоответствие между изменениями уровней RSI на двух рынках. То, что можно считать высоким значением RSI для валютной пары, например, пары NZDUSD, может считаться обычным рыночным шумом при торговле более волатильным инструментом, например, XPDUSD.

Вскоре становится очевидным, что каждый рынок может иметь свой собственный уникальный интерпретируемый уровень индикатора RSI. Другими словами, когда мы используем индикатор RSI, оптимальный уровень для входа в сделку зависит от торгуемого символа. Итак, как мы можем алгоритмически узнать, на каком уровне RSI нам следует покупать или продавать? Мы можем использовать нашу матрицу перехода, чтобы ответить на этот вопрос применительно к любому символу.

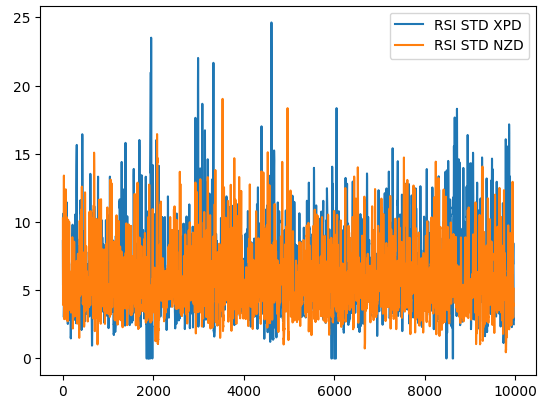
Рис. 1. Скользящая волатильность RSI на XPDUSD (синий цвет) и NZDUSD (оранжевый)

Обзор методологии

Чтобы изучить нашу стратегию на основе имеющихся данных, мы сначала собрали 300 000 строк данных M1 с помощью библиотеки MetaTrader 5 для Python. Мы маркировали данные, а затем разделили их на обучающую и тестовую части. На обучающем наборе мы сгруппировали показания RSI в 10 ячеек, от 0-10, 11-20, линейно до 91-100. Мы записали, как цена вела себя в будущем, проходя через каждую группу на RSI. Обучающие данные показали, что уровни цен имели наибольшую тенденцию к росту всякий раз, когда цена проходила через зону 41-50 RSI, и наибольшую тенденцию к снижению - при движении через зону 61-70.

Мы использовали эту предполагаемую матрицу перехода для построения жадной модели, которая всегда выбирает наиболее вероятный результат из предыдущих распределений. Наша простая модель показала точность 52% на тестовом наборе. Еще одним преимуществом этого подхода является его совместимость: мы можем легко понять, как наша модель принимает решения. Более того, сейчас стало обычным явлением, когда модели ИИ, используемые в важных отраслях, можно объяснить, и вы можете быть уверены, что это семейство вероятностных моделей не вызовет у вас проблем с соответствием.

Нас интересовала не только точность модели. Скорее, мы были сосредоточены на индивидуальных уровнях точности 10 зон, которые мы определили в нашем обучающем наборе. Ни одна из двух зон, имевших самые высокие распределения в нашем обучающем наборе, не оказалась надежной в проверочном наборе. При проверке набора данных мы получили самую высокую точность, когда покупали в диапазоне 11–20 и продавали в диапазоне 71–80. Уровни точности в соответствующих зонах составили 51,4% и 75,8%. Мы выбрали эти зоны в качестве оптимальных зон для открытия позиций на покупку и продажу по паре NZDJPY.

Наконец, мы приступили к созданию советника MQL5, реализовавшего результаты нашего анализа на Python. Кроме того, в нашем приложении мы реализовали 2 способа закрытия позиций. Мы предоставили пользователю возможность либо закрыть позиции, когда RSI пересечет зону, которая уменьшит наши открытые позиции, либо они могут закрывать позиции всякий раз, когда цена пересекает скользящую среднюю.

Извлечение и очистка данных

Прежде всего импортируем необходимые нам библиотеки.

#Let's get started
import MetaTrader5       as mt5
import pandas            as pd
import numpy             as np
import seaborn           as sns
import matplotlib.pyplot as plt
import pandas_ta         as ta

Проверим, можно ли добраться до терминала.

mt5.initialize()

True

Определим несколько глобальных переменных.

#Fetch market data
SYMBOL    = "NZDJPY"
TIMEFRAME = mt5.TIMEFRAME_M1

Скопируем данные из нашего терминала.

data = pd.DataFrame(mt5.copy_rates_from_pos(SYMBOL,TIMEFRAME,0,300000))

Преобразуем формат времени из секунд.

data["time"]  = pd.to_datetime(data["time"],unit='s')

Рассчитаем RSI.

data.ta.rsi(length=20,append=True)

Определим период в будущем, на который следует делать прогнозы.

#Define the look ahead
look_ahead = 20

Маркируем данные.

#Label the data
data["Target"] = np.nan

data.loc[data["close"] > data["close"].shift(-20),"Target"] = -1
data.loc[data["close"] < data["close"].shift(-20),"Target"] = 1

Удалим все отсутствующие строки из данных.

data.dropna(inplace=True)
data.reset_index(inplace=True,drop=True)

Создадим вектор для представления 10 групп значений RSI.

#Create a dataframe 
rsi_matrix = pd.DataFrame(columns=["0-10","11-20","21-30","31-40","41-50","51-60","61-70","71-80","81-90","91-100"],index=[0])

Вот как выглядят наши данные на данный момент.

data

Рис. 2. Некоторые столбцы в нашем фрейме данных

Инициализируем матрицу RSI нулями.

#Initialize the rsi matrix to 0
for i in np.arange(0,9):
    rsi_matrix.iloc[0,i] = 0

Разделим данные.

#Split the data into train and test sets
train = data.loc[:(data.shape[0]//2),:]
test  = data.loc[(data.shape[0]//2):,:]

Теперь мы рассмотрим обучающий набор данных и проследим за каждым показанием RSI и соответствующим будущим изменением уровней цен. Если значение RSI составило 11, а уровень цен вырос на 20 пунктов в будущем периоде, мы увеличим соответствующий столбец 11–20 в нашей матрице RSI на единицу. Более того, каждый раз, когда уровень цен падает, мы штрафуем столбец и уменьшаем его на единицу. Интуитивно мы быстро понимаем, что в конце концов любой столбец с положительным значением соответствует уровню RSI, который имел тенденцию предшествовать повышению ценовых уровней. Обратное верно для столбцов, которые будут иметь отрицательные значения.

for i in np.arange(0,train.shape[0]):
    #Fill in the rsi matrix, what happened in the future when we saw RSI readings below 10?
    if((train.loc[i,"RSI_20"] <= 10)):
        rsi_matrix.iloc[0,0] = rsi_matrix.iloc[0,0] + train.loc[i,"Target"]
    #What tends to happen in the future, after seeing RSI readings between 11 and 20?
    if((train.loc[i,"RSI_20"] > 10) & (train.loc[i,"RSI_20"] <= 20)):
        rsi_matrix.iloc[0,1] = rsi_matrix.iloc[0,1] + train.loc[i,"Target"]
    #What tends to happen in the future, after seeing RSI readings between 21 and 30?
    if((train.loc[i,"RSI_20"] > 20) & (train.loc[i,"RSI_20"] <= 30)):
        rsi_matrix.iloc[0,2] = rsi_matrix.iloc[0,2] + train.loc[i,"Target"]
    #What tends to happen in the future, after seeing RSI readings between 31 and 40?
    if((train.loc[i,"RSI_20"] > 30) & (train.loc[i,"RSI_20"] <= 40)):
        rsi_matrix.iloc[0,3] = rsi_matrix.iloc[0,3] + train.loc[i,"Target"]
    #What tends to happen in the future, after seeing RSI readings between 41 and 50?
    if((train.loc[i,"RSI_20"] > 40) & (train.loc[i,"RSI_20"] <= 50)):
        rsi_matrix.iloc[0,4] = rsi_matrix.iloc[0,4] + train.loc[i,"Target"]
    #What tends to happen in the future, after seeing RSI readings between 51 and 60?
    if((train.loc[i,"RSI_20"] > 50) & (train.loc[i,"RSI_20"] <= 60)):
        rsi_matrix.iloc[0,5] = rsi_matrix.iloc[0,5] + train.loc[i,"Target"]
    #What tends to happen in the future, after seeing RSI readings between 61 and 70?
    if((train.loc[i,"RSI_20"] > 60) & (train.loc[i,"RSI_20"] <= 70)):
        rsi_matrix.iloc[0,6] = rsi_matrix.iloc[0,6] + train.loc[i,"Target"]
    #What tends to happen in the future, after seeing RSI readings between 71 and 80?
    if((train.loc[i,"RSI_20"] > 70) & (train.loc[i,"RSI_20"] <= 80)):
        rsi_matrix.iloc[0,7] = rsi_matrix.iloc[0,7] + train.loc[i,"Target"]
    #What tends to happen in the future, after seeing RSI readings between 81 and 90?
    if((train.loc[i,"RSI_20"] > 80) & (train.loc[i,"RSI_20"] <= 90)):
        rsi_matrix.iloc[0,8] = rsi_matrix.iloc[0,8] + train.loc[i,"Target"]
    #What tends to happen in the future, after seeing RSI readings between 91 and 100?
    if((train.loc[i,"RSI_20"] > 90) & (train.loc[i,"RSI_20"] <= 100)):
        rsi_matrix.iloc[0,9] = rsi_matrix.iloc[0,9] + train.loc[i,"Target"]

Это распределение значений в обучающем наборе. Мы подошли к нашей первой проблеме: в зоне 91-100 не было обучающих наблюдений. Поэтому я предположил, что поскольку все соседние зоны привели к падению уровня цен, мы присвоим зоне произвольное отрицательное значение.

rsi_matrix

0-10	11-20	21-30	31-40	41-50	51-60	61-70	71-80	81-90	91-100
4.0	47.0	221.0	1171.0	3786.0	945.0	-1159.0	-35.0	-3.0	NaN

Мы можем визуализировать это распределение. Похоже, что большую часть времени цена проводит в зоне 31-70. Это соответствует средней части RSI. Как мы уже упоминали ранее, цена выглядела очень оптимистичной в районе 41-50 и пессимистичной в районе 61-70. Однако, по-видимому, это были всего лишь артефакты обучающих данных, поскольку эта взаимосвязь не сохранялась на проверочных данных.

sns.barplot(rsi_matrix)

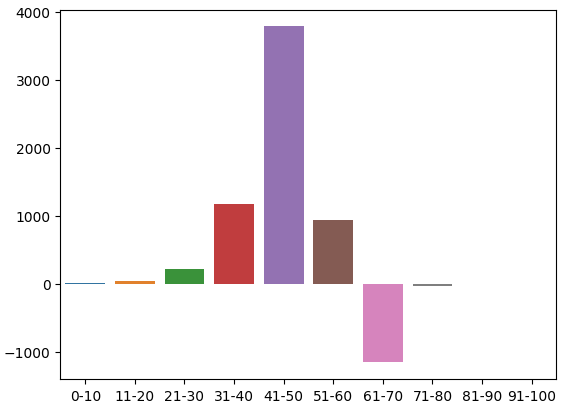
Рис. 3. Распределение наблюдаемых эффектов зон RSI

Рис. 4. Визуальное представление наших преобразований на данный момент

Теперь оценим точность нашей модели на проверочных данных. Сначала сбросим индекс обучающих данных.

test.reset_index(inplace=True,drop=True)

Создадим столбец для прогнозов нашей модели.

test["Predictions"]  = np.nan

Введите прогнозы нашей модели.

for i in np.arange(0,test.shape[0]):
    #Fill in the predictions
    if((test.loc[i,"RSI_20"] <= 10)):
        test.loc[i,"Predictions"] = 1
    
    if((test.loc[i,"RSI_20"] > 10) & (test.loc[i,"RSI_20"] <= 20)):
        test.loc[i,"Predictions"] = 1
    
    if((test.loc[i,"RSI_20"] > 20) & (test.loc[i,"RSI_20"] <= 30)):
        test.loc[i,"Predictions"] = 1
        
    if((test.loc[i,"RSI_20"] > 30) & (test.loc[i,"RSI_20"] <= 40)):
        test.loc[i,"Predictions"] = 1

    if((test.loc[i,"RSI_20"] > 40) & (test.loc[i,"RSI_20"] <= 50)):
        test.loc[i,"Predictions"] = 1

    if((test.loc[i,"RSI_20"] > 50) & (test.loc[i,"RSI_20"] <= 60)):
        test.loc[i,"Predictions"] = 1

    if((test.loc[i,"RSI_20"] > 60) & (test.loc[i,"RSI_20"] <= 70)):
        test.loc[i,"Predictions"] = -1

    if((test.loc[i,"RSI_20"] > 70) & (test.loc[i,"RSI_20"] <= 80)):
        test.loc[i,"Predictions"] = -1

    if((test.loc[i,"RSI_20"] > 80) & (test.loc[i,"RSI_20"] <= 90)):
        test.loc[i,"Predictions"] = -1

    if((test.loc[i,"RSI_20"] > 90) & (test.loc[i,"RSI_20"] <= 100)):
        test.loc[i,"Predictions"] = -1

Убедимся, что у нас нет нулевых значений.

test.loc[:,"Predictions"].isna().any()

False

Опишем связь между прогнозами нашей модели и целью, используя pandas. Наиболее распространенное значение — True. Это хороший показатель.

(test["Target"] == test["Predictions"]).describe()

count     148636
unique         2
top         True
freq       77409
dtype: object

Давайте оценим, насколько точна наша модель.

#Our estimation of the model's accuracy
((test["Target"] == test["Predictions"]).describe().freq / (test["Target"] == test["Predictions"]).shape[0])

0.5207957695309346

Нас интересует точность каждой из 10 зон RSI.

val_err = []

Запишем нашу точность в каждой зоне.

val_err.append(test.loc[(test["RSI_20"] < 10) & (test["Predictions"] == test["Target"])].shape[0] / test.loc[test["RSI_20"] < 10].shape[0])
val_err.append(test.loc[((test["RSI_20"] <= 20) & (test["RSI_20"] > 10)) & (test["Predictions"] == test["Target"])].shape[0] / test.loc[((test["RSI_20"] <= 20) & (test["RSI_20"] > 10))].shape[0])
val_err.append(test.loc[((test["RSI_20"] <= 30) & (test["RSI_20"] > 20)) & (test["Predictions"] == test["Target"])].shape[0] / test.loc[((test["RSI_20"] <= 30) & (test["RSI_20"] > 20))].shape[0])
val_err.append(test.loc[((test["RSI_20"] <= 40) & (test["RSI_20"] > 30)) & (test["Predictions"] == test["Target"])].shape[0] / test.loc[((test["RSI_20"] <= 40) & (test["RSI_20"] > 30))].shape[0])
val_err.append(test.loc[((test["RSI_20"] <= 50) & (test["RSI_20"] > 40)) & (test["Predictions"] == test["Target"])].shape[0] / test.loc[((test["RSI_20"] <= 50) & (test["RSI_20"] > 40))].shape[0])
val_err.append(test.loc[((test["RSI_20"] <= 60) & (test["RSI_20"] > 50)) & (test["Predictions"] == test["Target"])].shape[0] / test.loc[((test["RSI_20"] <= 60) & (test["RSI_20"] > 50))].shape[0])
val_err.append(test.loc[((test["RSI_20"] <= 70) & (test["RSI_20"] > 60)) & (test["Predictions"] == test["Target"])].shape[0] / test.loc[((test["RSI_20"] <= 70) & (test["RSI_20"] > 60))].shape[0])
val_err.append(test.loc[((test["RSI_20"] <= 80) & (test["RSI_20"] > 70)) & (test["Predictions"] == test["Target"])].shape[0] / test.loc[((test["RSI_20"] <= 80) & (test["RSI_20"] > 70))].shape[0])
val_err.append(test.loc[((test["RSI_20"] <= 90) & (test["RSI_20"] > 80)) & (test["Predictions"] == test["Target"])].shape[0] / test.loc[((test["RSI_20"] <= 90) & (test["RSI_20"] > 80))].shape[0])
val_err.append(test.loc[((test["RSI_20"] <= 100) & (test["RSI_20"] > 90)) & (test["Predictions"] == test["Target"])].shape[0] / test.loc[((test["RSI_20"] <= 100) & (test["RSI_20"] > 90))].shape[0])

Отобразим наше значение точности. Красная линия — это наша 50%-ная точка отсечения, любая зона RSI ниже этой линии может быть ненадежной. Мы можем ясно видеть, что последняя зона имеет наивысшую оценку — 1. Однако следует помнить, что это соответствует отсутствующей зоне 91–100, которая не встречалась ни разу за более чем 100 000 минут имеющихся у нас данных обучения. Поэтому эта зона, вероятно, встречается редко и не является оптимальной для наших торговых потребностей. Зона 11-20 имеет уровень точности 75%, что является самым высоким показателем среди наших бычьих зон. То же самое относится и к зоне 71-80, она имела самую высокую точность среди всех медвежьих зон.

plt.plot(val_err)
plt.plot(fifty,'r')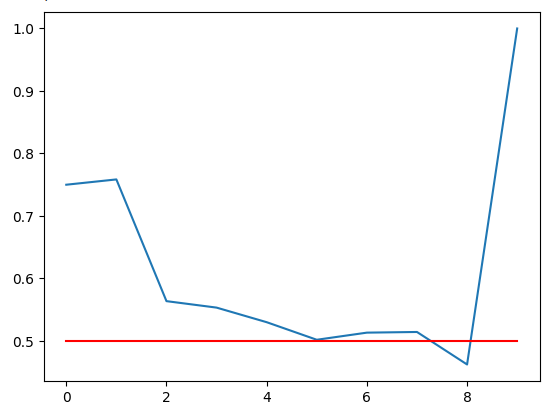

Рис. 5. Визуализация точности нашей проверки

Точность нашей проверки в различных зонах RSI. Обратите внимание, что мы получили 100% точность в диапазоне 91–100. Напомним, что наш обучающий набор состоял примерно из 100 000 строк, но мы не наблюдали никаких показаний RSI в этой зоне. Таким образом, мы можем сделать вывод, что цена редко достигает таких крайних значений, поэтому такой результат может не быть для нас оптимальным решением.

0-10	11-20	21-30	31-40	41-50	51-60	61-70	71-80	81-90	91-100
0.75	0.75	0.56	0.55	0.53	0.50	0.51	0.51	0.46	1.0

Построение глубокой марковской модели

До сих пор мы строили только модель, которая обучается на прошлом распределении данных. Возможно ли нам улучшить эту стратегию, добавив более гибкого обучающегося, чтобы изучить оптимальную стратегию использования нашей Марковской модели? Давайте обучим глубокую нейронную сеть и дадим ей в качестве входных данных прогнозы, сделанные моделью Маркова, а целью будут наблюдаемые изменения уровней цен. Чтобы эффективно выполнить эту задачу, нам необходимо разделить наш тренировочный набор на две половины. Мы подгоним нашу новую марковскую модель, используя только первую половину обучающего набора. Наша нейронная сеть будет подстроена под прогнозы Марковской модели на первой половине обучающего набора и соответствующие изменения уровней цен.

Мы заметили, что и наша нейронная сеть, и наша простая марковская модель превзошли идентичную нейронную сеть, пытающуюся изучить изменения уровней цен непосредственно на основе рыночных котировок OHLC. Эти выводы были сделаны на основе наших тестовых данных, которые не использовались в процедуре обучения. Удивительно, но наша глубокая нейронная сеть и наша простая марковская модель показали одинаковые результаты. Возможно, это говорит о необходимости приложить больше усилий, чтобы превзойти эталон, установленный моделью Маркова.

Начнем с импорта необходимых нам библиотек.

#Let us now try find a machine learning model to learn how to optimally use our transition matrix
from sklearn.neural_network import MLPClassifier
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split,TimeSeriesSplit

Теперь нам нужно выполнить разделение данных на обучающие и тестовые.

#Now let us partition our train set into 2 halves 
train , train_val = train_test_split(train,shuffle=False,test_size=0.5)

Приспособим марковскую модель к новому обучающему набору.

#Now let us recalculate our transition matrix, based on the first half of the training set
rsi_matrix.iloc[0,0] = train.loc[(train["RSI_20"] < 10) & (train["Target"] == 1)].shape[0] / train.loc[(train["RSI_20"] < 10)].shape[0]
rsi_matrix.iloc[0,1] = train.loc[((train["RSI_20"] > 10) & (train["RSI_20"] <=20)) & (train["Target"] == 1)].shape[0] / train.loc[((train["RSI_20"] > 10) & (train["RSI_20"] <=20))].shape[0]
rsi_matrix.iloc[0,2] = train.loc[((train["RSI_20"] > 20) & (train["RSI_20"] <=30)) & (train["Target"] == 1)].shape[0] / train.loc[((train["RSI_20"] > 20) & (train["RSI_20"] <=30))].shape[0]
rsi_matrix.iloc[0,3] = train.loc[((train["RSI_20"] > 30) & (train["RSI_20"] <=40)) & (train["Target"] == 1)].shape[0] / train.loc[((train["RSI_20"] > 30) & (train["RSI_20"] <=40))].shape[0]
rsi_matrix.iloc[0,4] = train.loc[((train["RSI_20"] > 40) & (train["RSI_20"] <=50)) & (train["Target"] == 1)].shape[0] / train.loc[((train["RSI_20"] > 40) & (train["RSI_20"] <=50))].shape[0]
rsi_matrix.iloc[0,5] = train.loc[((train["RSI_20"] > 50) & (train["RSI_20"] <=60)) & (train["Target"] == 1)].shape[0] / train.loc[((train["RSI_20"] > 50) & (train["RSI_20"] <=60))].shape[0]
rsi_matrix.iloc[0,6] = train.loc[((train["RSI_20"] > 60) & (train["RSI_20"] <=70)) & (train["Target"] == 1)].shape[0] / train.loc[((train["RSI_20"] > 60) & (train["RSI_20"] <=70))].shape[0]
rsi_matrix.iloc[0,7] = train.loc[((train["RSI_20"] > 70) & (train["RSI_20"] <=80)) & (train["Target"] == 1)].shape[0] / train.loc[((train["RSI_20"] > 70) & (train["RSI_20"] <=80))].shape[0]
rsi_matrix.iloc[0,8] = train.loc[((train["RSI_20"] > 80) & (train["RSI_20"] <=90)) & (train["Target"] == 1)].shape[0] / train.loc[((train["RSI_20"] > 80) & (train["RSI_20"] <=90))].shape[0]

rsi_matrix

0-10	11-20	21-30	31-40	41-50	51-60	61-70	71-80	81-90	91-100
1.0	0.655172	0.541701	0.536398	0.53243	0.516551	0.460306	0.491154	0.395349	0

Мы можем визуализировать это распределение вероятностей. Напомним, что эти величины отражают вероятность роста ценовых уровней через 20 минут в будущем после того, как цена пройдет через каждую из 10 зон RSI. Красная линия представляет уровень 50%. Все зоны выше уровня 50% являются бычьими, а все зоны ниже — медвежьими. Мы можем считать этот вывод достаточно точным, учитывая первую половину обучающих данных.

#From the training set, it appears that RSI readings above 61 are bearish and RSI readings below 61 are bullish
plt.plot(rsi_matrix.iloc[0,:])
plt.plot(fifty,'r')

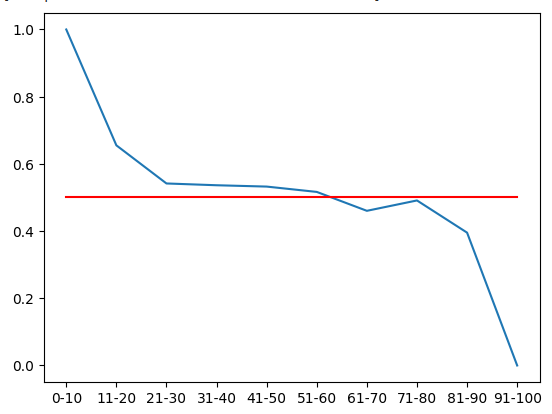
Рис. 6. Из первой половины обучающего набора следует, что все зоны ниже 61 являются бычьими, а выше 61 — медвежьими

Запись новых прогнозов, сделанных моделью Маркова.

#Let's now store our model's predictions
train["Predictions"] = -1
train.loc[train["RSI_20"] < 61,"Predictions"] = 1

train_val["Predictions"] = -1
train_val.loc[train_val["RSI_20"] < 61,"Predictions"] = 1

test["Predictions"] = -1
test.loc[test["RSI_20"] < 61,"Predictions"] = 1

Прежде чем начать использовать нейронные сети, как правило, полезно провести стандартизацию и масштабирование. Более того, наш RSI имеет фиксированную шкалу от 0 до 100, в то время как наши ценовые показания не имеют границ. В таких случаях необходима стандартизация.

#Let's Standardize and scale our data
from sklearn.preprocessing import RobustScaler

Определим наши входные параметры и цель.

ohlc_predictors = ["open","high","low","close","tick_volume","spread","RSI_20"]
transition_matrix = ["Predictions"]
all_predictors = ohlc_predictors + transition_matrix
target = ["Target"]

Масштабируем данные.

scaler = RobustScaler()
scaler =  scaler.fit(train.loc[:,predictors])
train_scaled = pd.DataFrame(scaler.transform(train.loc[:,predictors]),columns=predictors)
train_val_scaled = pd.DataFrame(scaler.transform(train_val.loc[:,predictors]),columns=predictors)
test_scaled = pd.DataFrame(scaler.transform(test.loc[:,predictors]),columns=predictors)

Создадим фреймы данных для хранения значения точности.

#Create a dataframe to store our cv error on the training set, validation training set and the test set
train_err     = pd.DataFrame(columns=["Transition Matrix","Deep Markov Model","OHLC Model","All Model"],index=np.arange(0,5)) 
train_val_err = pd.DataFrame(columns=["Transition Matrix","Deep Markov Model","OHLC Model","All Model"],index=[0]) 
test_err      = pd.DataFrame(columns=["Transition Matrix","Deep Markov Model","OHLC Model","All Model"],index=[0])

Определим объект разделения временного ряда.

#Create a time series split object
tscv = TimeSeriesSplit(n_splits = 5,gap=look_ahead)

Проведем перекрестную проверку моделей.

model = MLPClassifier(hidden_layer_sizes=(20,10))
for i , (train_index,test_index) in enumerate(tscv.split(train_scaled)):
    #Fit the model
    model.fit(train.loc[train_index,transition_matrix],train.loc[train_index,"Target"])
    #Record its accuracy
    train_err.iloc[i,1] = accuracy_score(train.loc[test_index,"Target"],model.predict(train.loc[test_index,transition_matrix]))

#Record our accuracy levels on the validation training set
train_val_err.iloc[0,1] = accuracy_score(train_val.loc[:,"Target"],model.predict(train_val.loc[:,transition_matrix]))

#Record our accuracy levels on the test set
test_err.iloc[0,1] = accuracy_score(test.loc[:,"Target"],model.predict(test.loc[:,transition_matrix]))

#Our accuracy levels on the training set
train_err

Посмотрим на точность нашей модели на проверочной половине обучающего набора.

train_val_err.iloc[0,0] = train_val.loc[train_val["Predictions"] == train_val["Target"]].shape[0] / train_val.shape[0]
train_val_err

Матрица перехода	Глубокая марковская модель	Модель OHLC	Все модели
0.52309	0.52309	0.507306	0.517291

Проверим нашу точность на тестовом наборе данных. Как видно из двух таблиц, наша гибридная глубокая марковская модель не смогла превзойти нашу простую марковскую модель. Меня это удивило. Это может означать, что наша процедура обучения глубокой нейронной сети не была оптимальной, или же мы всегда можем выполнить поиск среди более широкого пула возможных моделей машинного обучения. Модель, которая использовала все данные, не показала наилучших результатов.

Хорошей новостью является то, что нам удалось превзойти установленный эталон, попытавшись спрогнозировать цену непосредственно на основе рыночных котировок. Похоже, что простая эвристика Марковской модели помогает нейронной сети быстро изучить структуру рынка более низкого уровня.

test_err.iloc[0,0] = test.loc[test["Predictions"] == test["Target"]].shape[0] / test.shape[0]
test_err

Матрица перехода	Глубокая марковская модель	Модель OHLC	Все модели
0.519322	0.519322	0.497127	0.496724

Реализация средствами MQL5

Чтобы реализовать наш советник на основе RSI, мы начнем с импорта необходимых библиотек.

//+------------------------------------------------------------------+
//|                                                     Auto RSI.mq5 |
//|                                        Gamuchirai Zororo Ndawana |
//|                          https://www.mql5.com/en/gamuchiraindawa |
//+------------------------------------------------------------------+
#property copyright "Gamuchirai Zororo Ndawana"
#property link      "https://www.mql5.com/en/gamuchiraindawa"
#property version   "1.00"

//+------------------------------------------------------------------+
//| Libraries                                                        |
//+------------------------------------------------------------------+
#include <Trade\Trade.mqh>
CTrade Trade;

Определим наши глобальные переменные.

//+------------------------------------------------------------------+
//| Global variables                                                 |
//+------------------------------------------------------------------+
int rsi_handler;
double rsi_buffer[];
int ma_handler;
int system_state;
double ma_buffer[];
double bid,ask;

//--- Custom enumeration
enum close_conditions
  {
   MA_Close  = 0,
   RSI_Close
  };

Нам необходимо получить данные от нашего пользователя.

//+------------------------------------------------------------------+
//| Inputs                                                           |
//+------------------------------------------------------------------+
input group "Technical Indicators"
input int rsi_period = 20; //RSI Period
input int ma_period = 20; //MA Period

input group "Money Management"
input double trading_volume = 0.3; //Lot size

input group "Trading Rules"
input close_conditions user_close = RSI_Close; //How should we close the positions?

При первой загрузке нашего эксперта давайте загрузим индикаторы и проверим их.

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//--- Load the indicator
   rsi_handler = iRSI(_Symbol,PERIOD_M1,rsi_period,PRICE_CLOSE);
   ma_handler = iMA(_Symbol,PERIOD_M1,ma_period,0,MODE_EMA,PRICE_CLOSE);

//--- Validate our technical indicators
   if(rsi_handler == INVALID_HANDLE || ma_handler == INVALID_HANDLE)
     {
      //--- We failed to load the rsi
      Comment("Failed to load the RSI Indicator");
      return(INIT_FAILED);
     }

//---
   return(INIT_SUCCEEDED);
  }

Если приложение не используется, удаляем индикаторы.

//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//--- Release our technical indicators
   IndicatorRelease(rsi_handler);
   IndicatorRelease(ma_handler);
  }

Наконец, у нас нет открытых позиций, используем торговые правила нашей модели. В противном случае, если у нас есть открытая позиция, следуйте инструкциям пользователя о том, как закрыть сделки.

//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
//--- Update market and technical data
   update();

//--- Check if we have any open positions
   if(PositionsTotal() == 0)
     {
      check_setup();
     }

   if(PositionsTotal() > 0)
     {
      manage_setup();
     }
  }
//+------------------------------------------------------------------+

Следующая функция закроет наши позиции в зависимости от того, хочет ли пользователь, чтобы мы применяли правила торговли, которым мы научились из RSI, или простую скользящую среднюю. Если пользователь хочет, чтобы мы использовали скользящую среднюю, мы просто закрываем свои позиции всякий раз, когда цена пересекает скользящую среднюю.

//+------------------------------------------------------------------+
//| Manage our open setups                                           |
//+------------------------------------------------------------------+
void manage_setup(void)
  {
   if(user_close == RSI_Close)
     {
      if((system_state == 1) && ((rsi_buffer[0] > 71) && (rsi_buffer[80] <= 80)))
        {
         PositionSelect(Symbol());
         Trade.PositionClose(PositionGetTicket(0));
         return;
        }

      if((system_state == -1) && ((rsi_buffer[0] > 11) && (rsi_buffer[80] <= 20)))
        {
         PositionSelect(Symbol());
         Trade.PositionClose(PositionGetTicket(0));
         return;
        }
     }


   else
      if(user_close == MA_Close)
        {
         if((iClose(_Symbol,PERIOD_CURRENT,0) > ma_buffer[0]) && (system_state == -1))
           {
            PositionSelect(Symbol());
            Trade.PositionClose(PositionGetTicket(0));
            return;
           }

         if((iClose(_Symbol,PERIOD_CURRENT,0) < ma_buffer[0]) && (system_state == 1))
           {
            PositionSelect(Symbol());
            Trade.PositionClose(PositionGetTicket(0));
            return;
           }
        }
  }

Следующая функция проверит, есть ли у нас допустимые настройки. То есть вошла ли цена в любую из наших прибыльных зон. Более того, если пользователь указал, что для закрытия позиций следует использовать скользящую среднюю, то мы сначала дождемся, пока цена окажется на правой стороне скользящей средней, прежде чем решим, следует ли открывать позицию.

//+------------------------------------------------------------------+
//| Find if we have any setups to trade                              |
//+------------------------------------------------------------------+
void check_setup(void)
  {

   if(user_close == RSI_Close)
     {
      if((rsi_buffer[0] > 71) && (rsi_buffer[0] <= 80))
        {
         Trade.Sell(trading_volume,_Symbol,bid,0,0,"Auto RSI");
         system_state = -1;
        }

      if((rsi_buffer[0] > 11) && (rsi_buffer[0] <= 20))
        {
         Trade.Buy(trading_volume,_Symbol,ask,0,0,"Auto RSI");
         system_state = 1;
        }
     }

   if(user_close == MA_Close)
     {
      if(((rsi_buffer[0] > 71) && (rsi_buffer[0] <= 80)) && (iClose(_Symbol,PERIOD_CURRENT,0) < ma_buffer[0]))
        {
         Trade.Sell(trading_volume,_Symbol,bid,0,0,"Auto RSI");
         system_state = -1;
        }

      if(((rsi_buffer[0] > 11) && (rsi_buffer[0] <= 20)) && (iClose(_Symbol,PERIOD_CURRENT,0) > ma_buffer[0]))
        {
         Trade.Buy(trading_volume,_Symbol,ask,0,0,"Auto RSI");
         system_state = 1;
        }
     }
  }

Эта функция обновит наши технические и рыночные данные.

//+------------------------------------------------------------------+
//| Fetch market quotes and technical data                           |
//+------------------------------------------------------------------+
void update(void)
  {
   bid = SymbolInfoDouble(_Symbol,SYMBOL_BID);
   ask = SymbolInfoDouble(_Symbol,SYMBOL_ASK);

   CopyBuffer(rsi_handler,0,0,1,rsi_buffer);
   CopyBuffer(ma_handler,0,0,1,ma_buffer);
  }
//+------------------------------------------------------------------+

Рис. 7. Наш советник

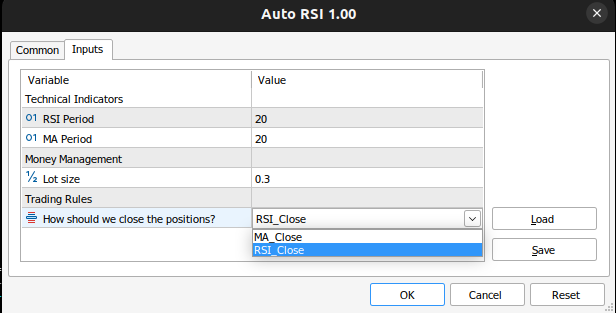
Рис. 8. Входные параметры советника

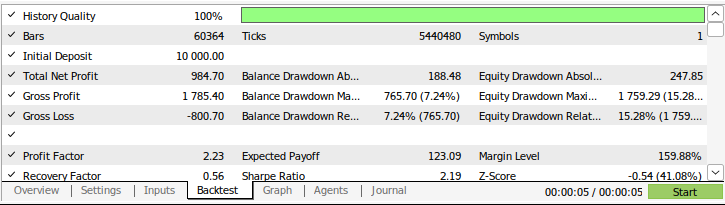
Рис. 9. Результаты тестирования нашей стратегии на истории

Заключение

В этой статье мы продемонстрировали мощь простых вероятностных моделей. К нашему удивлению, мы не смогли превзойти простую марковскую модель, пытаясь учиться на ее ошибках. Однако если вы внимательно следили за этой серией статей, то вы, вероятно, разделяете мою точку зрения о том, что сейчас мы движемся в правильном направлении. Мы постепенно накапливаем набор алгоритмов, которые легче моделировать, чем саму цену, при этом их информативность должна быть такой же, как и при моделировании самой цены. Присоединяйтесь к нам в следующих статьях, где мы попытаемся узнать, почему необходимо превзойти простую модель Маркова.

Перевод с английского произведен MetaQuotes Ltd.
Оригинальная статья: https://www.mql5.com/en/articles/16030

Прикрепленные файлы |

Загрузить ZIP

RSI_Self_Optimizer.ipynb (131.78 KB)

Auto_RSI.mq5 (6.11 KB)

Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.

Другие статьи автора

Последние комментарии | Перейти к обсуждению на форуме трейдеров (2)

linfo2 | 8 окт. 2024 в 20:51

Спасибо за ваши усилия, это полезно иметь видео, а также. пожалуйста, обратите внимание, что ваша ссылка на предыдущую статью приходит с 404 для меня

Gamuchirai Zororo Ndawana | 9 окт. 2024 в 09:18

linfo2 #:
Спасибо за ваши усилия, это полезно иметь видео также. пожалуйста, обратите внимание, что ваша ссылка на предыдущую статью приходит с 404 для меня

Привет, Нил, я рад, что видео было полезным, я сделаю все возможное, чтобы продолжать прикреплять видео.

Извините за мертвую ссылку, она проскользнула мимо меня, моя ошибка.

Количественный анализ трендов: Собираем статистику на Python

Что такое количественный анализ трендов на рынке Форекс. Собираем статистику по трендам, их величине и распределению по валютной паре EURUSD. Как количественный анализ трендов поможет создать прибыльный торговый советник.

Применение Conditional LSTM и индикатора VAM в автоматической торговле

В настоящей статье рассматривается разработка советника (EA) для автоматической торговли, сочетающего в себе технический анализ с прогнозами с помощью глубокого обучения.

Создание торговой панели администратора на MQL5 (Часть III): Расширение встроенных классов для управления темами (II)

Мы расширим существующую библиотеку Dialog, включив в нее логику управления темами. Кроме того, мы интегрируем методы переключения тем в классы CDialog, CEdit и CButton, используемые в нашем проекте панели администратора.

Компонент View для таблиц в парадигме MVC на MQL5: Базовый графический элемент

В статье рассматривается процесс разработки базового графического элемента для компонента View в рамках реализации таблиц в парадигме MVC (Model-View-Controller) на языке MQL5. Это первая статья, посвященная компоненту View, и третья в серии статей о создании таблиц для клиентского терминала MetaTrader 5.