
Redes neurais de maneira fácil (Parte 82): modelos de equações diferenciais ordinárias (NeuralODE)
Introdução
Apresento a você uma nova família de modelos baseados em equações diferenciais ordinárias (EDOs). Em vez de especificar uma sequência discreta de camadas ocultas, esses modelos parametrizam a derivada do estado oculto por meio de uma rede neural. Os resultados do modelo são calculados utilizando uma "caixa preta" — o solucionador de equações diferenciais. Esses modelos, que possuem profundidade contínua, utilizam uma quantidade constante de memória e adaptam sua estratégia de estimativa para cada sinal de entrada. Modelos como esses foram introduzidos pela primeira vez no artigo "Neural Ordinary Differential Equations". Nele, os autores demonstram a capacidade de escalar a retropropagação do erro utilizando qualquer solucionador de EDO sem acesso às suas operações internas, permitindo o treinamento de ponta a ponta de EDOs dentro de modelos maiores.
1. Descrição do algoritmo
A principal dificuldade técnica ao treinar modelos de equações diferenciais ordinárias está em realizar a diferenciação reversa durante a propagação do erro mediante um solucionador de EDO. Aplicar diferenciação utilizando operações de propagação para frente é simples, mas consome muita memória e pode introduzir erros numéricos adicionais.
Os autores do método propõem tratar o solucionador de EDO como uma caixa preta e calcular os gradientes utilizando o método de sensibilidade adjunta. Essa abordagem permite calcular gradientes resolvendo uma segunda EDO estendida de trás para frente, sendo aplicável a todos os solucionadores de EDO. Ela escala linearmente com o tamanho do problema e tem baixo consumo de memória, além de controlar explicitamente o erro numérico.
Vamos considerar a otimização de uma função escalar de perda L(), cujos dados de entrada são os resultados do solucionador de EDO:
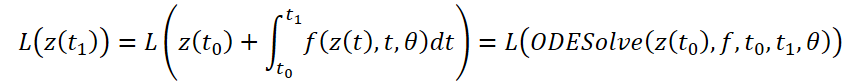
Para otimizar o erro L, precisamos dos gradientes em relação a θ. O primeiro passo do algoritmo, conforme proposto pelos autores, é determinar como o gradiente do erro depende do estado oculto z(t) em cada momento a(t)=∂L/∂z(t). Sua dinâmica é definida por outra EDO, que pode ser considerada análoga à regra:
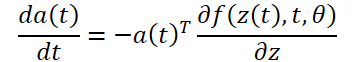
Podemos calcular ∂L/∂z(t) usando mais uma chamada ao solucionador de EDO. Este solucionador deve operar no sentido inverso, começando com o valor inicial ∂L/∂z(t1). Uma das dificuldades está no fato de que, para resolver essa EDO, é necessário conhecer os valores de z(t) ao longo de toda a trajetória. No entanto, podemos simplesmente enumerar z(t) de trás para frente, começando pelo seu valor final z(t1).
O cálculo dos gradientes em relação aos parâmetros θ requer a definição de um terceiro integral, que depende tanto de z(t) quanto de a(t):
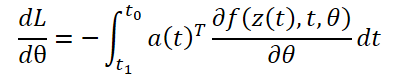
Todos os integrais para resolver 𝐳, 𝐚 e ∂L/∂θ podem ser calculados em uma única chamada ao solucionador de EDO, que combina o estado original, o adjunto e outras derivadas parciais em um único vetor. Abaixo está o algoritmo para construir a dinâmica necessária e chamar o solucionador de EDO para calcular todos os gradientes simultaneamente.

A maioria dos solucionadores de EDO permite calcular o estado z(t) várias vezes. Quando as perdas dependem desses estados intermediários, a derivada do modo reverso precisa ser dividida em uma sequência de soluções separadas, uma para cada par consecutivo de valores de saída. A cada observação, o adjunto deve ser ajustado na direção da derivada parcial correspondente ∂L/∂z(t).
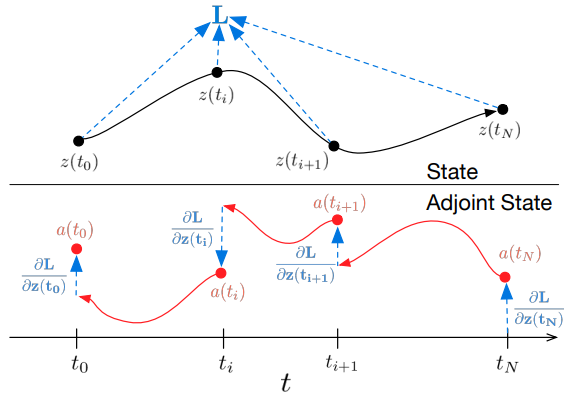
Os solucionadores de EDO podem garantir aproximadamente que os resultados obtidos estão dentro de uma tolerância definida em relação à solução real. Alterar essa tolerância modifica o comportamento do modelo. O tempo gasto na execução direta é proporcional ao número de cálculos da função, portanto, ajustar a tolerância nos oferece um equilíbrio entre precisão e custo computacional. É possível treinar com alta precisão, mas durante a operação mudar para uma precisão mais baixa.
2. Implementação usando MQL5
Para implementar as abordagens propostas, criaremos uma nova classe CNeuronNODEOCL, que herdará a funcionalidade básica da nossa camada totalmente conectada CNeuronBaseOCL. Abaixo está a estrutura da nova classe. Nela, além do conjunto básico de métodos, são adicionados alguns métodos e objetos específicos, cujo funcionamento será explorado durante a implementação.
class CNeuronNODEOCL : public CNeuronBaseOCL { protected: uint iDimension; uint iVariables; uint iLenth; int iBuffersK[]; int iInputsK[]; int iMeadl[]; CBufferFloat cAlpha; CBufferFloat cTemp; CCollection cBeta; CBufferFloat cSolution; CCollection cWeights; //--- virtual bool CalculateKBuffer(int k); virtual bool CalculateInputK(CBufferFloat* inputs, int k); virtual bool CalculateOutput(CBufferFloat* inputs); virtual bool feedForward(CNeuronBaseOCL *NeuronOCL); //--- virtual bool CalculateOutputGradient(CBufferFloat* inputs); virtual bool CalculateInputKGradient(CBufferFloat* inputs, int k); virtual bool CalculateKBufferGradient(int k); virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL); public: CNeuronNODEOCL(void) {}; ~CNeuronNODEOCL(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint dimension, uint variables, uint lenth, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual bool calcInputGradients(CNeuronBaseOCL *prevLayer); //--- virtual int Type(void) const { return defNeuronNODEOCL; } //--- methods for working with files virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); virtual void SetOpenCL(COpenCLMy *obj); };
Antes de tudo, é importante mencionar que, para possibilitar o trabalho com sequências de vários estados do ambiente, descritos por embeddings de várias características, criamos um objeto capaz de trabalhar com dados de entrada representados em 3 dimensões:
- iDimension — o tamanho do vetor de embedding de uma característica em um estado específico do ambiente;
- iVariables — o número de características que descrevem um estado do ambiente;
- iLenth — o número de estados do sistema que serão analisados.
A função de EDO em nosso caso será representada por duas camadas totalmente conectadas com a função de ativação ReLU entre elas. No entanto, assumimos que a dinâmica de cada característica individual pode ser diferente. Portanto, para cada característica, teremos matrizes de pesos próprias. Essa abordagem não nos permite usar camadas convolucionais como internas, como foi feito anteriormente. Por isso, na nossa nova classe, vamos decompor as camadas internas da função EDO. Declararemos buffers de dados que compõem as camadas internas. Em seguida, criaremos kernels e métodos para implementar os processos.
2.1 Kernel de propagação da função
Ao construir o kernel de propagação da função EDO, partimos das seguintes restrições:
- Cada estado do ambiente é descrito por um número fixo e igual de características;
- Todas as características têm o mesmo tamanho fixo de embedding.
Considerando essas restrições, criamos o kernel FeedForwardNODEF no lado do programa OpenCL. Nos parâmetros do nosso kernel, passaremos ponteiros para 3 buffers de dados e 3 variáveis. O kernel será executado em um espaço de tarefas tridimensional.
__kernel void FeedForwardNODEF(__global float *matrix_w, ///<[in] Weights matrix __global float *matrix_i, ///<[in] Inputs tensor __global float *matrix_o, ///<[out] Output tensor int dimension, ///< input dimension float step, ///< h int activation ///< Activation type (#ENUM_ACTIVATION) ) { int d = get_global_id(0); int dimension_out = get_global_size(0); int v = get_global_id(1); int variables = get_global_size(1); int i = get_global_id(2); int lenth = get_global_size(2);
No corpo do kernel, primeiro identificamos o fluxo atual em todas as 3 dimensões do espaço de tarefas. Depois, determinamos os deslocamentos nos buffers de dados até os dados que estão sendo analisados.
int shift = variables * i + v; int input_shift = shift * dimension; int output_shift = shift * dimension_out + d; int weight_shift = (v * dimension_out + d) * (dimension + 2);
Após a preparação, em um ciclo, calculamos os valores do resultado atual multiplicando o vetor de dados de entrada pelo vetor correspondente de coeficientes de pesos.
float sum = matrix_w[dimension + 1 + weight_shift] + matrix_w[dimension + weight_shift] * step; for(int w = 0; w < dimension; w++) sum += matrix_w[w + weight_shift] * matrix_i[input_shift + w];
Aqui é importante destacar que a função de EDO depende não apenas do estado do ambiente, mas também da marca temporal. Neste caso, a marca temporal é única para todo o estado do ambiente. E para evitar duplicá-la em função do número de características e do comprimento da sequência, não a incluímos no tensor de dados de entrada, mas simplesmente passamos o parâmetro step no kernel.
Em seguida, precisamos apenas passar o valor obtido pela função de ativação e salvar o resultado no elemento correspondente do buffer.
if(isnan(sum)) sum = 0; switch(activation) { case 0: sum = tanh(sum); break; case 1: sum = 1 / (1 + exp(-clamp(sum, -20.0f, 20.0f))); break; case 2: if(sum < 0) sum *= 0.01f; break; default: break; } matrix_o[output_shift] = sum; }
2.2 Kernel de propagação reversa da função
Após implementar o kernel de propagação da função, imediatamente criamos, no lado do programa OpenCL, a funcionalidade reversa — o kernel de distribuição do gradiente de erro HiddenGradientNODEF.
__kernel void HiddenGradientNODEF(__global float *matrix_w, ///<[in] Weights matrix __global float *matrix_g, ///<[in] Gradient tensor __global float *matrix_i, ///<[in] Inputs tensor __global float *matrix_ig, ///<[out] Inputs Gradient tensor int dimension_out, ///< output dimension int activation ///< Input Activation type (#ENUM_ACTIVATION) ) { int d = get_global_id(0); int dimension = get_global_size(0); int v = get_global_id(1); int variables = get_global_size(1); int i = get_global_id(2); int lenth = get_global_size(2);
Planejamos executar esse kernel também em um espaço tridimensional de tarefas, cuja identificação do fluxo ocorre no corpo do kernel. Nesse ponto, determinamos os deslocamentos nos buffers de dados até os elementos em análise.
int shift = variables * i + v; int input_shift = shift * dimension + d; int output_shift = shift * dimension_out; int weight_step = (dimension + 2); int weight_shift = (v * dimension_out) * weight_step + d;
Em seguida, somamos o gradiente de erro para o elemento analisado dos dados de entrada.
float sum = 0; for(int k = 0; k < dimension_out; k ++) sum += matrix_g[output_shift + k] * matrix_w[weight_shift + k * weight_step]; if(isnan(sum)) sum = 0;
Aqui vale a pena observar que a marca temporal, essencialmente, é uma constante para um estado específico. Portanto, não distribuímos o gradiente de erro para ela.
Corrigimos a soma obtida pela derivada da função de ativação e salvamos o valor resultante no elemento correspondente do buffer de dados.
float out = matrix_i[input_shift]; switch(activation) { case 0: out = clamp(out, -1.0f, 1.0f); sum = clamp(sum + out, -1.0f, 1.0f) - out; sum = sum * max(1 - pow(out, 2), 1.0e-4f); break; case 1: out = clamp(out, 0.0f, 1.0f); sum = clamp(sum + out, 0.0f, 1.0f) - out; sum = sum * max(out * (1 - out), 1.0e-4f); break; case 2: if(out < 0) sum *= 0.01f; break; default: break; } //--- matrix_ig[input_shift] = sum; }
2.3 Solucionador de EDO
Concluímos a primeira etapa do trabalho. Agora, vamos examinar o solucionador de EDO. Para sua implementação, escolhi o método Dormand-Prince de quinta ordem.
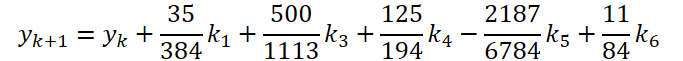
onde
![]()
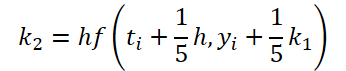
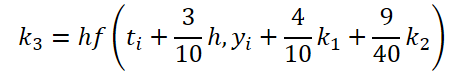
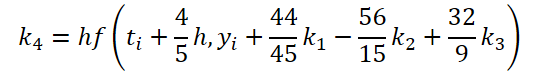
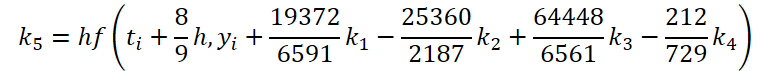
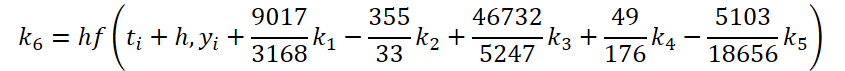
É fácil perceber que a função de solução e correção dos dados de entrada para calcular os coeficientes k1..k6 difere apenas nos coeficientes numéricos. Como os coeficientes ki ausentes podem ser adicionados multiplicando-os por zero, o que não afetará o resultado, unificamos o processo criando um único kernel FeedForwardNODEInpK no lado do programa OpenCL. Nos parâmetros do kernel, passamos os ponteiros para os buffers de dados de entrada e todos os coeficientes ki. Os multiplicadores necessários serão especificados no buffer matrix_beta.
__kernel void FeedForwardNODEInpK(__global float *matrix_i, ///<[in] Inputs tensor __global float *matrix_k1, ///<[in] K1 tensor __global float *matrix_k2, ///<[in] K2 tensor __global float *matrix_k3, ///<[in] K3 tensor __global float *matrix_k4, ///<[in] K4 tensor __global float *matrix_k5, ///<[in] K5 tensor __global float *matrix_k6, ///<[in] K6 tenтor __global float *matrix_beta, ///<[in] beta tensor __global float *matrix_o ///<[out] Output tensor ) { int i = get_global_id(0);
O kernel será executado em um espaço unidimensional de tarefas, com cálculo paralelo dos valores para cada elemento do buffer de resultados.
Após a identificação do fluxo, somaremos em um ciclo os produtos das multiplicações.
float sum = matrix_i[i]; for(int b = 0; b < 6; b++) { float beta = matrix_beta[b]; if(beta == 0.0f || isnan(beta)) continue; //--- float val = 0.0f; switch(b) { case 0: val = matrix_k1[i]; break; case 1: val = matrix_k2[i]; break; case 2: val = matrix_k3[i]; break; case 3: val = matrix_k4[i]; break; case 4: val = matrix_k5[i]; break; case 5: val = matrix_k6[i]; break; } if(val == 0.0f || isnan(val)) continue; //--- sum += val * beta; }
O valor obtido será salvo no elemento correspondente do buffer de resultados.
matrix_o[i] = sum; }
Para a propagação reversa, criaremos o kernel HiddenGradientNODEInpK, no qual distribuiremos o gradiente de erro nos buffers de dados correspondentes, considerando os mesmos coeficientes Beta.
__kernel void HiddenGradientNODEInpK(__global float *matrix_ig, ///<[in] Inputs tensor __global float *matrix_k1g, ///<[in] K1 tensor __global float *matrix_k2g, ///<[in] K2 tensor __global float *matrix_k3g, ///<[in] K3 tensor __global float *matrix_k4g, ///<[in] K4 tensor __global float *matrix_k5g, ///<[in] K5 tensor __global float *matrix_k6g, ///<[in] K6 tensor __global float *matrix_beta, ///<[in] beta tensor __global float *matrix_og ///<[out] Output tensor ) { int i = get_global_id(0); //--- float grad = matrix_og[i]; matrix_ig[i] = grad; for(int b = 0; b < 6; b++) { float beta = matrix_beta[b]; if(isnan(beta)) beta = 0.0f; //--- float val = beta * grad; if(isnan(val)) val = 0.0f; switch(b) { case 0: matrix_k1g[i] = val; break; case 1: matrix_k2g[i] = val; break; case 2: matrix_k3g[i] = val; break; case 3: matrix_k4g[i] = val; break; case 4: matrix_k5g[i] = val; break; case 5: matrix_k6g[i] = val; break; } } }
Observe que escrevemos valores nulos nos buffers de dados. Isso é necessário para evitar a contabilização dupla dos valores previamente salvos.
2.4 Kernel de Atualização de Pesos
Para finalizar o trabalho no lado do programa OpenCL, criaremos imediatamente o kernel de atualização dos coeficientes de peso da função de EDO. Como pode ser visto nas fórmulas apresentadas anteriormente, a função de EDO será usada para determinar todos os coeficientes ki. Consequentemente, ao ajustar os coeficientes de peso, precisamos reunir o gradiente de erro de todas as operações. Nenhum dos kernels de atualização de pesos que criamos anteriormente trabalhou com essa quantidade de buffers de gradientes. Portanto, precisamos criar um novo kernel. Para simplificar o experimento, criaremos apenas o kernel NODEF_UpdateWeightsAdam para atualizar os parâmetros usando o método Adam, que utilizo com mais frequência.
__kernel void NODEF_UpdateWeightsAdam(__global float *matrix_w, ///<[in,out] Weights matrix __global const float *matrix_gk1, ///<[in] Tensor of gradients at k1 __global const float *matrix_gk2, ///<[in] Tensor of gradients at k2 __global const float *matrix_gk3, ///<[in] Tensor of gradients at k3 __global const float *matrix_gk4, ///<[in] Tensor of gradients at k4 __global const float *matrix_gk5, ///<[in] Tensor of gradients at k5 __global const float *matrix_gk6, ///<[in] Tensor of gradients at k6 __global const float *matrix_ik1, ///<[in] Inputs tensor __global const float *matrix_ik2, ///<[in] Inputs tensor __global const float *matrix_ik3, ///<[in] Inputs tensor __global const float *matrix_ik4, ///<[in] Inputs tensor __global const float *matrix_ik5, ///<[in] Inputs tensor __global const float *matrix_ik6, ///<[in] Inputs tensor __global float *matrix_m, ///<[in,out] Matrix of first momentum __global float *matrix_v, ///<[in,out] Matrix of seconfd momentum __global const float *alpha, ///< h const int lenth, ///< Number of inputs const float l, ///< Learning rates const float b1, ///< First momentum multiplier const float b2 ///< Second momentum multiplier ) { const int d_in = get_global_id(0); const int dimension_in = get_global_size(0); const int d_out = get_global_id(1); const int dimension_out = get_global_size(1); const int v = get_global_id(2); const int variables = get_global_id(2);
Como já mencionado anteriormente, os parâmetros do kernel incluem ponteiros para uma quantidade considerável de buffers de dados globais. A estes, somam-se os parâmetros padrão do método de otimização utilizado.
Planejamos executar o kernel em um espaço tridimensional de tarefas, que considera a dimensionalidade dos vetores de embeddings dos dados de entrada e dos resultados, assim como o número de características analisadas. No corpo do kernel, identificamos o fluxo no espaço de tarefas em todas as três dimensões. Em seguida, determinamos os deslocamentos nos buffers de dados.
const int weight_shift = (v * dimension_out + d_out) * dimension_in; const int input_step = variables * (dimension_in - 2); const int input_shift = v * (dimension_in - 2) + d_in; const int output_step = variables * dimension_out; const int output_shift = v * dimension_out + d_out;
Em seguida, em um ciclo, reunimos o gradiente de erro para todos os estados do ambiente.
float weight = matrix_w[weight_shift]; float g = 0; for(int i = 0; i < lenth; i++) { int shift_g = i * output_step + output_shift; int shift_i = i * input_step + input_shift; switch(dimension_in - d_in) { case 1: g += matrix_gk1[shift_g] + matrix_gk2[shift_g] + matrix_gk3[shift_g] + matrix_gk4[shift_g] + matrix_gk5[shift_g] + matrix_gk6[shift_g]; break; case 2: g += matrix_gk1[shift_g] * alpha[0] + matrix_gk2[shift_g] * alpha[1] + matrix_gk3[shift_g] * alpha[2] + matrix_gk4[shift_g] * alpha[3] + matrix_gk5[shift_g] * alpha[4] + matrix_gk6[shift_g] * alpha[5]; break; default: g += matrix_gk1[shift_g] * matrix_ik1[shift_i] + matrix_gk2[shift_g] * matrix_ik2[shift_i] + matrix_gk3[shift_g] * matrix_ik3[shift_i] + matrix_gk4[shift_g] * matrix_ik4[shift_i] + matrix_gk5[shift_g] * matrix_ik5[shift_i] + matrix_gk6[shift_g] * matrix_ik6[shift_i]; break; } }
Depois, ajustamos os pesos conforme o algoritmo já implementado.
float mt = b1 * matrix_m[weight_shift] + (1 - b1) * g; float vt = b2 * matrix_v[weight_shift] + (1 - b2) * pow(g, 2); float delta = l * (mt / (sqrt(vt) + 1.0e-37f) - (l1 * sign(weight) + l2 * weight));
No final do kernel, salvamos os resultados e os valores auxiliares nos elementos correspondentes dos buffers de dados.
if(delta * g > 0) matrix_w[weight_shift] = clamp(matrix_w[weight_shift] + delta, -MAX_WEIGHT, MAX_WEIGHT); matrix_m[weight_shift] = mt; matrix_v[weight_shift] = vt; }
Com isso, concluímos o trabalho no lado do programa OpenCL e voltamos à implementação da nossa classe CNeuronNODEOCL.
2.5 Método de inicialização da classe CNeuronNODEOCL
A inicialização do nosso objeto de classe é realizada no método CNeuronNODEOCL::Init. Nos parâmetros do método, como de costume, passaremos os principais parâmetros da arquitetura do objeto.
bool CNeuronNODEOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint dimension, uint variables, uint lenth, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, dimension * variables * lenth, optimization_type, batch)) return false;
No corpo do método, a primeira coisa que fazemos é chamar o método equivalente da classe pai, onde é realizado o controle dos parâmetros recebidos e a inicialização dos objetos herdados. Podemos verificar o resultado geral das operações no corpo da classe pai por meio do valor lógico retornado.
Em seguida, armazenamos os parâmetros da arquitetura do objeto em variáveis locais da classe.
iDimension = dimension; iVariables = variables; iLenth = lenth;
Declaramos variáveis auxiliares e atribuímos os valores necessários a elas.
uint mult = 2; uint weights = (iDimension + 2) * iDimension * iVariables;
Agora, vejamos os buffers dos coeficientes ki e dos dados corrigidos usados para seu cálculo. Não é difícil perceber que os valores nesses buffers de dados são mantidos da passagem direta até a reversa. Durante a próxima passagem direta, os valores são sobrescritos. Portanto, para economizar recursos, não criaremos esses buffers na memória principal do programa. Eles serão criados apenas no lado do contexto OpenCL. Na classe, criamos apenas arrays para armazenar os ponteiros para eles. Em cada array, criamos três vezes mais elementos do que os coeficientes (k) utilizados. Isso é necessário para coletar os gradientes de erro.
if(ArrayResize(iBuffersK, 18) < 18) return false; if(ArrayResize(iInputsK, 18) < 18) return false;
Fazemos o mesmo com os valores intermediários dos cálculos, com o tamanho do array sendo menor.
if(ArrayResize(iMeadl, 12) < 12) return false;
Para melhorar a legibilidade do código, criaremos os buffers em um ciclo.
for(uint i = 0; i < 18; i++) { iBuffersK[i] = OpenCL.AddBuffer(sizeof(float) * Output.Total(), CL_MEM_READ_WRITE); if(iBuffersK[i] < 0) return false; iInputsK[i] = OpenCL.AddBuffer(sizeof(float) * Output.Total(), CL_MEM_READ_WRITE); if(iInputsK[i] < 0) return false; if(i > 11) continue; //--- Initilize Meadl Output and Gradient buffers iMeadl[i] = OpenCL.AddBuffer(sizeof(float) * Output.Total(), CL_MEM_READ_WRITE); if(iMeadl[i] < 0) return false; }
Na etapa seguinte, criamos as matrizes de coeficientes de peso da função EDO e os momentos correspondentes. Como já foi mencionado anteriormente, utilizaremos 2 camadas.
//--- Initilize Weights for(int i = 0; i < 2; i++) { temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.Reserve(weights)) return false; float k = (float)(1 / sqrt(iDimension + 2)); for(uint w = 0; w < weights; w++) { if(!temp.Add((GenerateWeight() - 0.5f)* k)) return false; } if(!temp.BufferCreate(OpenCL)) return false; if(!cWeights.Add(temp)) return false;
for(uint d = 0; d < 2; d++) { temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(weights, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!cWeights.Add(temp)) return false; } }
Em seguida, criaremos os buffers dos multiplicadores constantes:
- Passo de tempo Alpha
{
float temp_ar[] = {0, 0.2f, 0.3f, 0.8f, 8.0f / 9, 1, 1};
if(!cAlpha.AssignArray(temp_ar))
return false;
if(!cAlpha.BufferCreate(OpenCL))
return false;
}
- Correções dos dados de entrada
//--- Beta K1 { float temp_ar[] = {0, 0, 0, 0, 0, 0}; temp = new CBufferFloat(); if(!temp || !temp.AssignArray(temp_ar)) { delete temp; return false; } if(!temp.BufferCreate(OpenCL)) { delete temp; return false; } if(!cBeta.Add(temp)) { delete temp; return false; } }
//--- Beta K2 { float temp_ar[] = {0.2f, 0, 0, 0, 0, 0}; temp = new CBufferFloat(); if(!temp || !temp.AssignArray(temp_ar)) { delete temp; return false; } if(!temp.BufferCreate(OpenCL)) { delete temp; return false; } if(!cBeta.Add(temp)) { delete temp; return false; } }
//--- Beta K3 { float temp_ar[] = {3.0f / 40, 9.0f / 40, 0, 0, 0, 0}; temp = new CBufferFloat(); if(!temp || !temp.AssignArray(temp_ar)) { delete temp; return false; } if(!temp.BufferCreate(OpenCL)) { delete temp; return false; } if(!cBeta.Add(temp)) { delete temp; return false; } }
//--- Beta K4 { float temp_ar[] = {44.0f / 44, -56.0f / 15, 32.0f / 9, 0, 0, 0}; temp = new CBufferFloat(); if(!temp || !temp.AssignArray(temp_ar)) { delete temp; return false; } if(!temp.BufferCreate(OpenCL)) { delete temp; return false; } if(!cBeta.Add(temp)) { delete temp; return false; } }
//--- Beta K5 { float temp_ar[] = {19372.0f / 6561, -25360 / 2187.0f, 64448 / 6561.0f, -212.0f / 729, 0, 0}; temp = new CBufferFloat(); if(!temp || !temp.AssignArray(temp_ar)) { delete temp; return false; } if(!temp.BufferCreate(OpenCL)) { delete temp; return false; } if(!cBeta.Add(temp)) { delete temp; return false; } }
//--- Beta K6 { float temp_ar[] = {9017 / 3168.0f, -355 / 33.0f, 46732 / 5247.0f, 49.0f / 176, -5103.0f / 18656, 0}; temp = new CBufferFloat(); if(!temp || !temp.AssignArray(temp_ar)) { delete temp; return false; } if(!temp.BufferCreate(OpenCL)) { delete temp; return false; } if(!cBeta.Add(temp)) { delete temp; return false; } }
- Soluções das EDOs
{
float temp_ar[] = {35.0f / 384, 0, 500.0f / 1113, 125.0f / 192, -2187.0f / 6784, 11.0f / 84};
if(!cSolution.AssignArray(temp_ar))
return false;
if(!cSolution.BufferCreate(OpenCL))
return false;
}
No final do método de inicialização, adicionaremos um buffer local para armazenar valores intermediários.
if(!cTemp.BufferInit(Output.Total(), 0) || !cTemp.BufferCreate(OpenCL)) return false; //--- return true; }
2.6 Configuração da propagação para frente
Após a inicialização do objeto da classe, passamos para o desenvolvimento do algoritmo de propagação. Aqui é importante lembrar que, anteriormente, criamos 2 kernels no lado do programa OpenCL para configurar a propagação para frente. Portanto, precisamos criar métodos para chamá-los. Começaremos com um método relativamente simples, o CalculateInputK, que prepara os dados de entrada para o cálculo dos coeficientes k.
bool CNeuronNODEOCL::CalculateInputK(CBufferFloat* inputs, int k) { if(k < 0) return false; if(iInputsK.Size()/3 <= uint(k)) return false;
Nos parâmetros do método, recebemos um ponteiro para o buffer de dados de entrada, obtido da camada anterior, e o índice do coeficiente a ser calculado. No corpo do método, verificamos se o índice do coeficiente corresponde à nossa arquitetura.
Após passar no bloco de verificação, lidamos com o caso específico para k1.
![]()
Neste caso, não chamamos a execução do kernel, mas simplesmente copiamos o ponteiro para o buffer de dados de entrada.
if(k == 0) { if(iInputsK[k] != inputs.GetIndex()) { OpenCL.BufferFree(iInputsK[k]); iInputsK[k] = inputs.GetIndex(); } return true; }
De forma geral, chamaremos o kernel FeedForwardNODEInpK e gravaremos os dados de entrada corrigidos no buffer correspondente. Para isso, primeiro definimos o espaço de tarefas. Neste caso, unidimensional.
uint global_work_offset[1] = {0}; uint global_work_size[1] = {Neurons()};
Passamos os ponteiros dos buffers como parâmetros do kernel.
ResetLastError(); if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardNODEInpK, def_k_ffdopriInp_matrix_i, inputs.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardNODEInpK, def_k_ffdopriInp_matrix_k1, iBuffersK[0])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardNODEInpK, def_k_ffdopriInp_matrix_k2, iBuffersK[1])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardNODEInpK, def_k_ffdopriInp_matrix_k3, iBuffersK[2])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardNODEInpK, def_k_ffdopriInp_matrix_k4, iBuffersK[3])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardNODEInpK, def_k_ffdopriInp_matrix_k5, iBuffersK[4])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardNODEInpK, def_k_ffdopriInp_matrix_k6, iBuffersK[5])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardNODEInpK, def_k_ffdopriInp_matrix_beta, ((CBufferFloat *)cBeta.At(k)).GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardNODEInpK, def_k_ffdopriInp_matrix_o, iInputsK[k])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
E colocamos o kernel na fila de execução.
if(!OpenCL.Execute(def_k_FeedForwardNODEInpK, 1, global_work_offset, global_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; } //--- return true; }
Após a correção dos dados de entrada, precisamos calcular os valores dos coeficientes. Esse processo é realizado no método CalculateKBuffer. Como o método trabalha apenas com objetos internos, para realizar as operações basta indicar o índice do coeficiente necessário nos parâmetros do método.
bool CNeuronNODEOCL::CalculateKBuffer(int k) { if(k < 0) return false; if(iInputsK.Size()/3 <= uint(k)) return false;
No corpo do método, verificamos se o índice recebido é compatível com a arquitetura da classe.
Depois, definimos o espaço tridimensional de tarefas.
uint global_work_offset[3] = {0, 0, 0}; uint global_work_size[3] = {iDimension, iVariables, iLenth};
Em seguida, passamos os parâmetros ao kernel para a execução da primeira camada. Aqui, utilizamos LReLU para introduzir a não linearidade.
if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardNODEF, def_k_ffdoprif_matrix_i, iInputsK[k])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardNODEF, def_k_ffdoprif_matrix_w, ((CBufferFloat*)cWeights.At(0)).GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardNODEF, def_k_ffdoprif_matrix_o, iMeadl[k * 2])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_FeedForwardNODEF, def_k_ffdoprif_dimension, int(iDimension))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_FeedForwardNODEF, def_k_ffdoprif_step, float(cAlpha.At(k)))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_FeedForwardNODEF, def_k_ffdoprif_activation, int(LReLU))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
E colocamos o kernel na fila de execução.
if(!OpenCL.Execute(def_k_FeedForwardNODEF, 3, global_work_offset, global_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; }
O próximo passo é realizar a propagação pela segunda camada. O espaço de tarefas permanece o mesmo. Por isso, não alteramos os arrays correspondentes. Precisamos novamente passar os parâmetros ao kernel. Aqui, alteramos os buffers de dados de entrada, os coeficientes de peso e os resultados.
if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardNODEF, def_k_ffdoprif_matrix_i, iMeadl[k * 2])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardNODEF, def_k_ffdoprif_matrix_w, ((CBufferFloat*)cWeights.At(3)).GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardNODEF, def_k_ffdoprif_matrix_o, iBuffersK[k])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
Além disso, não utilizamos a função de ativação.
if(!OpenCL.SetArgument(def_k_FeedForwardNODEF, def_k_ffdoprif_activation, int(None))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
Os demais parâmetros permanecem inalterados.
if(!OpenCL.SetArgument(def_k_FeedForwardNODEF, def_k_ffdoprif_dimension, int(iDimension))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_FeedForwardNODEF, def_k_ffdoprif_step, cAlpha.At(k))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
E enviamos o kernel para a fila de execução.
if(!OpenCL.Execute(def_k_FeedForwardNODEF, 3, global_work_offset, global_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; } //-- return true; }
Depois de calcular todos os coeficientes k, podemos determinar o resultado da solução da EDO. Na prática, utilizaremos o kernel FeedForwardNODEInpK para esse fim, cuja chamada já foi implementada no método CalculateInputK. No entanto, neste caso, precisamos alterar os buffers de dados utilizados. Por isso, reescreveremos o algoritmo no método CalculateOutput.
bool CNeuronNODEOCL::CalculateOutput(CBufferFloat* inputs) { //--- uint global_work_offset[1] = {0}; uint global_work_size[1] = {Neurons()};
Nos parâmetros deste método, recebemos apenas um ponteiro para o buffer de dados de entrada. No corpo do método, imediatamente definimos o espaço unidimensional de tarefas. Em seguida, passamos os ponteiros dos buffers de dados de entrada como parâmetros do kernel.
ResetLastError(); if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardNODEInpK, def_k_ffdopriInp_matrix_i, inputs.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardNODEInpK, def_k_ffdopriInp_matrix_k1, iBuffersK[0])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardNODEInpK, def_k_ffdopriInp_matrix_k2, iBuffersK[1])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardNODEInpK, def_k_ffdopriInp_matrix_k3, iBuffersK[2])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardNODEInpK, def_k_ffdopriInp_matrix_k4, iBuffersK[3])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardNODEInpK, def_k_ffdopriInp_matrix_k5, iBuffersK[4])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardNODEInpK, def_k_ffdopriInp_matrix_k6, iBuffersK[5])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
Como multiplicadores, indicaremos o buffer de coeficientes da solução de EDO.
if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardNODEInpK, def_k_ffdopriInp_matrix_beta, cSolution.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
E os resultados serão gravados no buffer de resultados da nossa classe.
if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardNODEInpK, def_k_ffdopriInp_matrix_o, Output.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
E colocamos o kernel na fila de execução.
if(!OpenCL.Execute(def_k_FeedForwardNODEInpK, 1, global_work_offset, global_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; }
Os valores obtidos serão somados aos dados de entrada e normalizados.
if(!SumAndNormilize(Output, inputs, Output, iDimension, true, 0, 0, 0, 1)) return false; //--- return true; }
Anteriormente, preparamos métodos para chamar os kernels que realizam o processo de propagação para frente. Agora, resta apenas estabelecer o algoritmo no método de alto nível CNeuronNODEOCL::feedForward.
bool CNeuronNODEOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { for(int k = 0; k < 6; k++) { if(!CalculateInputK(NeuronOCL.getOutput(), k)) return false; if(!CalculateKBuffer(k)) return false; } //--- return CalculateOutput(NeuronOCL.getOutput()); }
Nos parâmetros, o método recebe um ponteiro para o objeto da camada anterior. No corpo do método, fazemos um loop, no qual corrigimos sequencialmente os dados de entrada e calculamos todos os coeficientes k. Durante cada iteração, monitoramos o processo de execução das operações. E, após calcular com sucesso os coeficientes necessários, chamamos o método de solução da EDO. Graças ao extenso trabalho preparatório, o algoritmo de alto nível do método ficou bastante conciso.
2.7 Preparação da propagação reversa
O algoritmo de propagação para frente garante o processo de utilização do modelo. No entanto, o treinamento do modelo é inseparável do processo de propagação reversa. É nesse estágio que os parâmetros de aprendizado são ajustados para minimizar o erro do modelo.
Assim como fizemos com os kernels de propagação para frente, no lado do programa OpenCL criamos dois kernels de propagação reversa. E agora, no lado do programa principal, precisamos criar métodos para chamar esses kernels de propagação reversa. E como estamos organizando a propagação reversa, a execução dos métodos será realizada na sequência da propagação reversa.
Ao receber o gradiente de erro da próxima camada, distribuímos o gradiente recebido entre a camada de dados de entrada e os coeficientes k. Esse processo é feito no método CalculateOutputGradient, que chama o kernel HiddenGradientNODEInpK.
bool CNeuronNODEOCL::CalculateOutputGradient(CBufferFloat *inputs) { //--- uint global_work_offset[1] = {0}; uint global_work_size[1] = {Neurons()};
Nos parâmetros do método, recebemos um ponteiro para o buffer de gradientes de erro da camada anterior. No corpo do método, geramos o processo de chamada do kernel do programa OpenCL. Primeiro, definimos o espaço unidimensional de tarefas. Em seguida, passamos os ponteiros dos buffers de dados como parâmetros do kernel.
Vale destacar que os parâmetros do kernel HiddenGradientNODEInpK são idênticos aos do kernel FeedForwardNODEInpK. A única diferença é que, na propagação para frente, foram utilizados os buffers de dados de entrada e os coeficientes k. Enquanto na propagação reversa, são utilizados os buffers dos gradientes correspondentes. Por essa razão, não redefini as constantes dos buffers do kernel, mas reutilizei as constantes da propagação para frente.
if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientNODEInpK, def_k_ffdopriInp_matrix_i, inputs.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientNODEInpK, def_k_ffdopriInp_matrix_k1, iBuffersK[6])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientNODEInpK, def_k_ffdopriInp_matrix_k2, iBuffersK[7])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientNODEInpK, def_k_ffdopriInp_matrix_k3, iBuffersK[8])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientNODEInpK, def_k_ffdopriInp_matrix_k4, iBuffersK[9])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientNODEInpK, def_k_ffdopriInp_matrix_k5, iBuffersK[10])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientNODEInpK, def_k_ffdopriInp_matrix_k6, iBuffersK[11])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientNODEInpK, def_k_ffdopriInp_matrix_beta, cSolution.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientNODEInpK, def_k_ffdopriInp_matrix_o, Gradient.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
Outro ponto importante é que, para gravar os coeficientes k, utilizamos buffers com índices no intervalo [0, 5]. Neste caso, para gravar os gradientes de erro, utilizamos buffers com índices no intervalo [6, 11].
Após transmitir com sucesso todos os parâmetros ao kernel, colocamos o kernel na fila de execução.
if(!OpenCL.Execute(def_k_HiddenGradientNODEInpK, 1, global_work_offset, global_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; } //--- return true; }
Agora, vamos considerar o método CalculateInputKGradient, que chama o mesmo kernel. No entanto, há nuances na construção do algoritmo que gostaria de destacar.
Primeiro, é claro, os parâmetros do método. Aqui, é adicionado o índice do coeficiente k.
bool CNeuronNODEOCL::CalculateInputKGradient(CBufferFloat *inputs, int k) { //--- uint global_work_offset[1] = {0}; uint global_work_size[1] = {Neurons()};
No corpo do método, definimos o mesmo espaço unidimensional de tarefas. Em seguida, passamos os parâmetros para o kernel.
ResetLastError(); if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientNODEInpK, def_k_ffdopriInp_matrix_i, inputs.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
Desta vez, para armazenar os gradientes de erro dos coeficientes k, utilizamos buffers com índices no intervalo [12, 17]. Isso é necessário para acumular os gradientes de erro para cada coeficiente.
if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientNODEInpK, def_k_ffdopriInp_matrix_k1, iBuffersK[12])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientNODEInpK, def_k_ffdopriInp_matrix_k2, iBuffersK[13])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientNODEInpK, def_k_ffdopriInp_matrix_k3, iBuffersK[14])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientNODEInpK, def_k_ffdopriInp_matrix_k4, iBuffersK[15])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientNODEInpK, def_k_ffdopriInp_matrix_k5, iBuffersK[16])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientNODEInpK, def_k_ffdopriInp_matrix_k6, iBuffersK[17])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
Além disso, utilizamos os multiplicadores do array cBeta.
if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientNODEInpK, def_k_ffdopriInp_matrix_beta, ((CBufferFloat *)cBeta.At(k)).GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientNODEInpK, def_k_ffdopriInp_matrix_o, iInputsK[k + 6])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
Após transmitir com sucesso todos os parâmetros necessários ao kernel, colocamos o kernel na fila de execução.
if(!OpenCL.Execute(def_k_HiddenGradientNODEInpK, 1, global_work_offset, global_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; }
Em seguida, precisamos somar o gradiente de erro atual com o acumulado anteriormente para o coeficiente k correspondente. Para isso, fazemos um ciclo reverso, no qual somamos gradualmente os gradientes de erro, começando pelo coeficiente k em análise até o menor índice.
for(int i = k - 1; i >= 0; i--) { float mult = 1.0f / (i == (k - 1) ? 6 - k : 1); uint global_work_offset[1] = {0}; uint global_work_size[1] = {iLenth * iVariables}; if(!OpenCL.SetArgumentBuffer(def_k_MatrixSum, def_k_sum_matrix1, iBuffersK[k + 6])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_MatrixSum, def_k_sum_matrix2, iBuffersK[k + 12])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_MatrixSum, def_k_sum_matrix_out, iBuffersK[k + 6])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_MatrixSum, def_k_sum_dimension, iDimension)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_MatrixSum, def_k_sum_shift_in1, 0)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_MatrixSum, def_k_sum_shift_in2, 0)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_MatrixSum, def_k_sum_shift_out, 0)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_MatrixSum, def_k_sum_multiplyer, mult)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.Execute(def_k_MatrixSum, 1, global_work_offset, global_work_size)) { string error; CLGetInfoString(OpenCL.GetContext(), CL_ERROR_DESCRIPTION, error); printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; } } //--- return true; }
Vale destacar que somamos apenas os gradientes de erro para os coeficientes k com índices menores que o atual. Isso ocorre porque o multiplicador ß para os coeficientes com índices maiores é evidentemente igual a "0". Esses coeficientes são calculados após o coeficiente atual e não participam da sua determinação. Consequentemente, o gradiente de erro deles será nulo. Além disso, para um treinamento mais estável, fazemos a média dos gradientes de erro acumulados.
O último kernel envolvido na distribuição do gradiente de erro é o kernel de distribuição do gradiente de erro através da camada interna da função EDO HiddenGradientNODEF. Ele é chamado no método CalculateKBufferGradient. Nos parâmetros, o método recebe apenas o índice do coeficiente k para o qual o gradiente está sendo distribuído.
bool CNeuronNODEOCL::CalculateKBufferGradient(int k) { if(k < 0) return false; if(iInputsK.Size()/3 <= uint(k)) return false;
No corpo do método, verificamos se o índice recebido é compatível com a arquitetura do objeto. Em seguida, definimos o espaço tridimensional de tarefas.
uint global_work_offset[3] = {0, 0, 0}; uint global_work_size[3] = {iDimension, iVariables, iLenth};
E passamos os parâmetros para o kernel. Como estamos distribuindo o gradiente de erro no contexto da propagação reversa, começamos especificando os buffers das duas camadas da função.
ResetLastError(); if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientNODEF, def_k_hddoprif_matrix_i, iMeadl[k * 2])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientNODEF, def_k_hddoprif_matrix_ig, iMeadl[k * 2 + 1])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientNODEF, def_k_hddoprif_matrix_w, ((CBufferFloat*)cWeights.At(3)).GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientNODEF, def_k_hddoprif_matrix_g, iBuffersK[k + 6])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_HiddenGradientNODEF, def_k_hddoprif_dimension_out, int(iDimension))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_HiddenGradientNODEF, def_k_hddoprif_activation, int(LReLU))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
E colocamos o kernel na fila de execução.
if(!OpenCL.Execute(def_k_HiddenGradientNODEF, 3, global_work_offset, global_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; }
O próximo passo, mantendo os arrays que definem o espaço de tarefas inalterados, é passar os dados da primeira camada da função como parâmetros para o kernel.
if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientNODEF, def_k_hddoprif_matrix_i, iInputsK[k])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientNODEF, def_k_hddoprif_matrix_ig, iInputsK[k + 12])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientNODEF, def_k_hddoprif_matrix_w, ((CBufferFloat*)cWeights.At(0)).GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientNODEF, def_k_hddoprif_matrix_g, iMeadl[k * 2 + 1])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_HiddenGradientNODEF, def_k_hddoprif_dimension_out, int(iDimension))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_HiddenGradientNODEF, def_k_hddoprif_activation, int(None))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
E, por fim, executamos o kernel.
if(!OpenCL.Execute(def_k_HiddenGradientNODEF, 3, global_work_offset, global_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; } //-- return true; }
Acima, criamos os métodos para chamar os kernels de distribuição do gradiente de erro entre os objetos da camada. No entanto, neste estado, são apenas fragmentos de código que ainda não formam um algoritmo coeso. Precisamos agora unificá-los em um único algoritmo. Escrevemos o algoritmo geral de distribuição do gradiente de erro dentro da nossa classe usando o método calcInputGradients.
bool CNeuronNODEOCL::calcInputGradients(CNeuronBaseOCL *prevLayer) { if(!CalculateOutputGradient(prevLayer.getGradient())) return false; for(int k = 5; k >= 0; k--) { if(!CalculateKBufferGradient(k)) return false; if(!CalculateInputKGradient(GetPointer(cTemp), k)) return false; if(!SumAndNormilize(prevLayer.getGradient(), GetPointer(cTemp), prevLayer.getOutput(), iDimension, false, 0, 0, 0, 1.0f / (k == 0 ? 6 : 1))) return false; } //--- return true; }
Nos parâmetros, o método recebe um ponteiro para o objeto da camada anterior, para o qual precisamos passar o gradiente de erro. Na primeira etapa, distribuímos o gradiente de erro recebido da camada subsequente entre a camada anterior e os coeficientes k segundo os multiplicadores da solução EDO. Como você deve lembrar, esse processo foi implementado no método CalculateOutputGradient.
Depois, configuramos o ciclo reverso de distribuição dos gradientes através da função EDO ao calcular os coeficientes correspondentes. Primeiro, passamos o gradiente de erro pelas duas camadas no método CalculateKBufferGradient. Em seguida, distribuímos o gradiente de erro obtido entre os respectivos k coeficientes e os dados de entrada no método CalculateInputKGradient. No entanto, em vez de usar o buffer de gradientes de erro da camada anterior, armazenamos os dados em um buffer temporário. Depois, somamos o gradiente obtido ao acumulado anteriormente no buffer de gradientes da camada anterior usando o método SumAndNormalize. Durante a última iteração, fazemos a média do gradiente de erro acumulado.
Neste estágio, distribuímos completamente o gradiente de erro entre todos os objetos que influenciam o resultado, de acordo com sua contribuição. Agora, só resta atualizar os parâmetros do modelo. Anteriormente, para realizar essa função, criamos o kernel NODEF_UpdateWeightsAdam. Agora, precisamos implementar a chamada desse kernel no programa principal. Essa funcionalidade é realizada no método updateInputWeights.
bool CNeuronNODEOCL::updateInputWeights(CNeuronBaseOCL *NeuronOCL) { uint global_work_offset[3] = {0, 0, 0}; uint global_work_size[3] = {iDimension + 2, iDimension, iVariables};
Nos parâmetros, o método recebe um ponteiro para o objeto da camada neural anterior, que neste caso é nominal e necessário apenas para o processo de virtualização dos métodos.
De fato, durante a propagação para frente e reversa, utilizamos os dados da camada anterior. E, para atualizar os parâmetros da primeira camada da função EDO, esses dados serão necessários. No entanto, a situação é tal que o ponteiro para o buffer de resultados da camada anterior na propagação para frente foi salvo no array iInputsK com o índice "0". É esse ponteiro que utilizaremos na nossa implementação.
No corpo do método, primeiro definimos o espaço tridimensional de tarefas. Em seguida, passamos os parâmetros necessários para o kernel. Inicialmente, atualizaremos os parâmetros da primeira camada.
if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_matrix_ik1, iInputsK[0])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_matrix_gk1, iMeadl[1])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_matrix_ik2, iInputsK[1])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_matrix_gk2, iMeadl[3])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_matrix_ik3, iInputsK[2])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_matrix_gk3, iMeadl[5])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_matrix_ik4, iInputsK[3])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_matrix_gk4, iMeadl[7])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_matrix_ik5, iInputsK[4])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_matrix_gk5, iMeadl[9])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_matrix_ik6, iInputsK[5])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_matrix_gk6, iMeadl[11])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_matrix_w, ((CBufferFloat*)cWeights.At(0)).GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_matrix_m, ((CBufferFloat*)cWeights.At(1)).GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_matrix_v, ((CBufferFloat*)cWeights.At(2)).GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_alpha, cAlpha.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_lenth, int(iLenth))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
if(!OpenCL.SetArgument(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_l, lr)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_b1, b1)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_b2, b2)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
E colocamos o kernel na fila de execução.
if(!OpenCL.Execute(def_k_NODEF_UpdateWeightsAdam, 3, global_work_offset, global_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; }
Depois, repetiremos as operações para organizar o processo de atualização dos parâmetros da segunda camada.
if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_matrix_ik1, iMeadl[0])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_matrix_gk1, iBuffersK[6])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_matrix_ik2, iMeadl[2])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_matrix_gk2, iBuffersK[7])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_matrix_ik3, iMeadl[4])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_matrix_gk3, iBuffersK[8])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_matrix_ik4, iMeadl[6])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_matrix_gk4, iBuffersK[9])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_matrix_ik5, iMeadl[8])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_matrix_gk5, iBuffersK[10])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_matrix_ik6, iMeadl[10])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_matrix_gk6, iBuffersK[11])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_matrix_w, ((CBufferFloat*)cWeights.At(3)).GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_matrix_m, ((CBufferFloat*)cWeights.At(4)).GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_matrix_v, ((CBufferFloat*)cWeights.At(5)).GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_alpha, cAlpha.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_lenth, int(iLenth))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_l, lr)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_b1, b1)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_b2, b2)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.Execute(def_k_NODEF_UpdateWeightsAdam, 3, global_work_offset, global_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; } //-- return true; }
2.8 Métodos de manipulação de arquivos
Acima, discutimos os métodos que lidam com o processo principal na classe. No entanto, gostaria de dizer algumas palavras sobre os métodos de manipulação de arquivos. Se analisarmos cuidadosamente a estrutura dos objetos internos da classe, podemos identificar que a única coleção a ser salva é a cWeights, que contém os coeficientes de peso e os momentos de sua correção. Além disso, precisamos salvar três parâmetros que definem a arquitetura da classe. Faremos isso no método Save.
bool CNeuronNODEOCL::Save(const int file_handle) { if(!CNeuronBaseOCL::Save(file_handle)) return false; if(!cWeights.Save(file_handle)) return false; if(FileWriteInteger(file_handle, int(iDimension), INT_VALUE) < INT_VALUE || FileWriteInteger(file_handle, int(iVariables), INT_VALUE) < INT_VALUE || FileWriteInteger(file_handle, int(iLenth), INT_VALUE) < INT_VALUE) return false; //--- return true; }
Nos parâmetros, o método recebe um handle do arquivo para salvar os dados. E, logo no início do corpo do método, chamamos o método homônimo da classe pai. Em seguida, salvamos a coleção e as constantes.
O método de salvamento da classe é bastante conciso e permite economizar espaço em disco. No entanto, essa economia tem um custo no método de carregamento dos dados.
bool CNeuronNODEOCL::Load(const int file_handle) { if(!CNeuronBaseOCL::Load(file_handle)) return false; if(!cWeights.Load(file_handle)) return false; cWeights.SetOpenCL(OpenCL); //--- iDimension = (int)FileReadInteger(file_handle); iVariables = (int)FileReadInteger(file_handle); iLenth = (int)FileReadInteger(file_handle);
Aqui, primeiro carregamos os dados salvos. Em seguida, criamos os objetos faltantes segundo os parâmetros da arquitetura carregados.
//--- CBufferFloat *temp = NULL; for(uint i = 0; i < 18; i++) { OpenCL.BufferFree(iBuffersK[i]); OpenCL.BufferFree(iInputsK[i]); //--- iBuffersK[i] = OpenCL.AddBuffer(sizeof(float) * Output.Total(), CL_MEM_READ_WRITE); if(iBuffersK[i] < 0) return false; iInputsK[i] = OpenCL.AddBuffer(sizeof(float) * Output.Total(), CL_MEM_READ_WRITE); if(iBuffersK[i] < 0) return false; if(i > 11) continue; //--- Initilize Output and Gradient buffers OpenCL.BufferFree(iMeadl[i]); iMeadl[i] = OpenCL.AddBuffer(sizeof(float) * Output.Total(), CL_MEM_READ_WRITE); if(iMeadl[i] < 0) return false; } //--- cTemp.BufferFree(); if(!cTemp.BufferInit(Output.Total(), 0) || !cTemp.BufferCreate(OpenCL)) return false; //--- return true; }
Com isso, concluímos a análise dos métodos da nossa nova classe CNeuronNODEOCL. O código completo da classe criada e de seus métodos, assim como de todos os programas utilizados na preparação deste artigo, está disponível no anexo.
2.9 Arquitetura dos modelos treináveis
Acima, criamos uma nova classe de camada neural baseada na solução de EDO CNeuronNODEOCL. O objeto desta classe será adicionado à arquitetura do Codificador, criado na artigo anterior.
Como sempre, a arquitetura dos modelos é especificada no método CreateDescriptions, no qual são passados ponteiros para três arrays dinâmicos que indicam a arquitetura dos modelos a serem criados.
bool CreateDescriptions(CArrayObj *encoder, CArrayObj *actor, CArrayObj *critic) { //--- CLayerDescription *descr; //--- if(!encoder) { encoder = new CArrayObj(); if(!encoder) return false; } if(!actor) { actor = new CArrayObj(); if(!actor) return false; } if(!critic) { critic = new CArrayObj(); if(!critic) return false; }
No corpo do método, verificamos os ponteiros recebidos e, se necessário, criamos novos objetos para os arrays.
Na entrada do modelo Codificador, alimentamos os dados "brutos" que descrevem o estado do ambiente.
//--- Encoder encoder.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Esses dados passam por um processamento inicial na camada de normalização em lotes.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = MathMax(1000, GPTBars); descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Em seguida, geramos os embeddings dos estados recebidos usando a camada de Embedding e uma camada convolucional subsequente.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronEmbeddingOCL; { int temp[] = {prev_count}; ArrayCopy(descr.windows, temp); } prev_count = descr.count = GPTBars; int prev_wout = descr.window_out = EmbeddingSize / 2; if(!encoder.Add(descr)) { delete descr; return false; } //--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConvOCL; descr.count = prev_count; descr.step = descr.window = prev_wout; prev_wout = descr.window_out = EmbeddingSize; if(!encoder.Add(descr)) { delete descr; return false; }
Os embeddings gerados são complementados com codificação posicional.
//--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronPEOCL; descr.count = prev_count; descr.window = prev_wout; if(!encoder.Add(descr)) { delete descr; return false; }
Depois, utilizamos uma camada complexa de análise de dados considerando o contexto.
//--- layer 5 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronCCMROCL; descr.count = prev_count; descr.window = prev_wout; descr.window_out = EmbeddingSize; if(!encoder.Add(descr)) { delete descr; return false; }
Até esse ponto, replicamos completamente o modelo apresentado na artigo anterior. No entanto, agora adicionamos duas camadas da nova classe.
//--- layer 6 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronNODEOCL; descr.count = prev_count; descr.window = EmbeddingSize/4; descr.step = 4; if(!encoder.Add(descr)) { delete descr; return false; } //--- layer 7 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronNODEOCL; descr.count = prev_count; descr.window = EmbeddingSize/4; descr.step = 4; if(!encoder.Add(descr)) { delete descr; return false; }
Os modelos do Ator e do Crítico foram completamente transferidos do artigo anterior sem alterações. Portanto, não entraremos em detalhes sobre eles agora.
A adição das novas camadas não afeta os processos de interação com o ambiente nem o treinamento dos modelos. Consequentemente, todos os EAs foram transferidos sem alterações. O código completo de todos os programas utilizados na preparação da artigo pode ser encontrado no anexo. Agora, passamos para a próxima etapa — o teste do trabalho realizado.
3. Testes
Acima, nos familiarizamos com a nova família de modelos de equações diferenciais ordinárias. E, com base nas abordagens propostas, implementamos no MQL5 uma nova classe CNeuronNODEOCL para preparar a camada neural em nossos modelos. Agora, passamos para a terceira etapa do nosso trabalho: o treinamento e o teste dos modelos com dados reais no testador de estratégias do MetaTrader 5.
Assim como com os modelos criados anteriormente, o treinamento e o teste foram realizados com dados históricos do par EURUSD no timeframe H1. Realizamos o treinamento offline dos modelos. Para isso, coletamos um conjunto de treinamento de 500 trajetórias distintas com dados históricos dos primeiros sete meses de 2023. Vale mencionar que a maioria das trajetórias foi coletada por meio de passagens aleatórias, resultando em uma proporção relativamente pequena de passagens lucrativas. Para equilibrar a rentabilidade média das passagens durante o treinamento, utilizamos amostragem das trajetórias com priorização de acordo com seu resultado. Isso atribui maior peso às passagens lucrativas, aumentando também a probabilidade de serem escolhidas. O teste dos modelos treinados foi realizado no testador de estratégias com dados históricos de agosto de 2023, mantendo o mesmo instrumento e timeframe.
Essa abordagem permite avaliar o desempenho do modelo treinado em novos dados (não incluídos no conjunto de treinamento) enquanto preserva ao máximo as características estatísticas dos conjuntos de treinamento e teste.
Os resultados dos testes demonstraram a viabilidade da abordagem para o treinamento de estratégias que geram lucro tanto no período de treinamento quanto no período de teste. As capturas de tela dos testes são apresentadas abaixo.
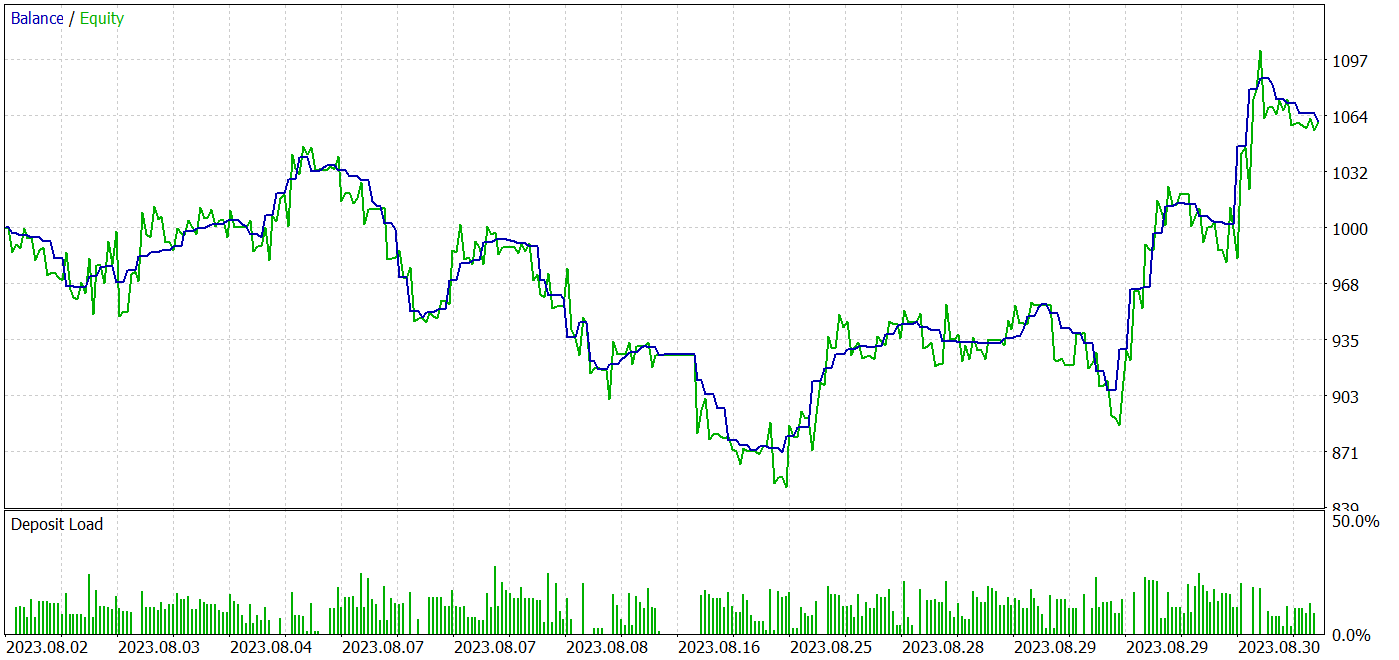
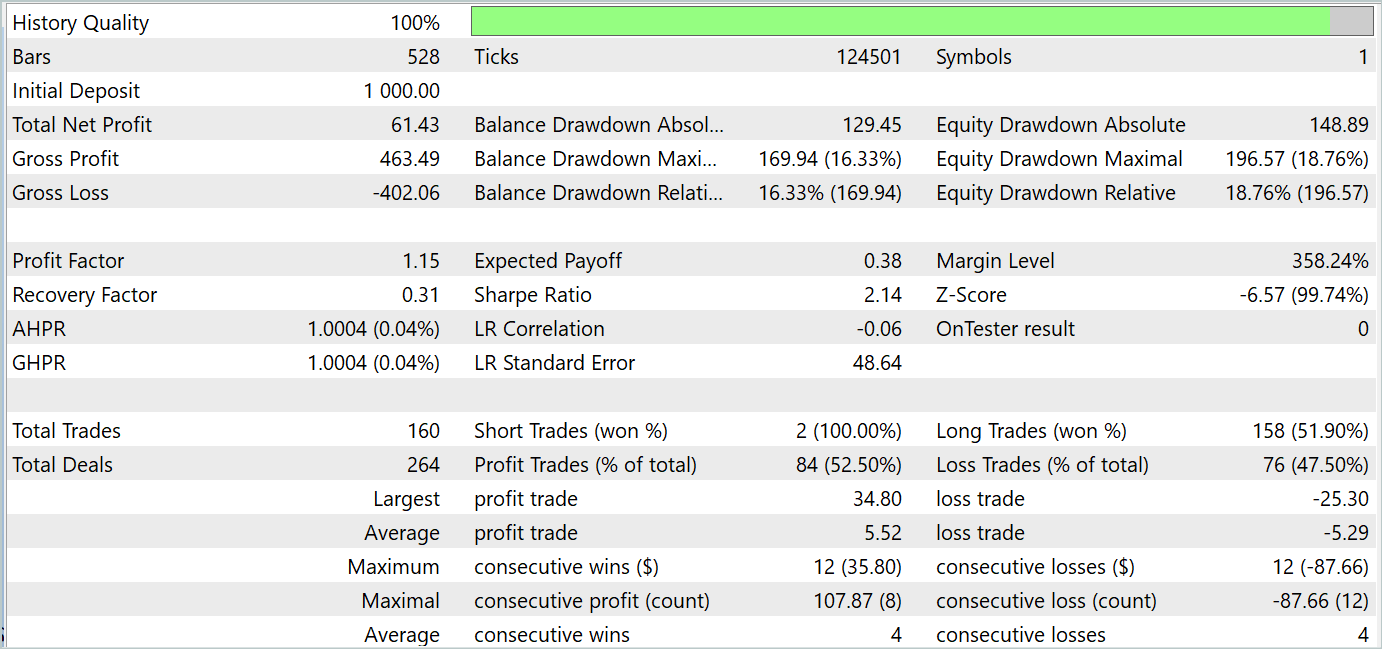
Com base nos resultados dos testes realizados em agosto de 2023, o modelo treinado efetuou 160 operações, das quais 84 foram lucrativas. O que corresponde a 52,5%. Pode-se dizer que o equilíbrio entre as operações inclinou-se ligeiramente a favor do lucro. A operação média lucrativa foi pouco mais de 4% superior à média das operações com perda. A sequência média de operações lucrativas foi equivalente à sequência média de operações com perda. A maior sequência lucrativa em termos de número de operações foi igual à maior sequência de perdas sob esse critério. No entanto, a maior operação lucrativa e a maior sequência lucrativa em termos de valor superaram as correspondentes sequências de perdas. Como resultado, durante o período de teste, o modelo apresentou um fator de lucro de 1,15 com um índice de Sharpe de 2,14.
Considerações finais
Neste artigo, exploramos uma nova classe de modelos baseados em equações diferenciais ordinárias (EDOs — ODEs). O uso de ODEs como componentes em modelos de aprendizado de máquina oferece várias vantagens e potenciais. Eles permitem modelar processos dinâmicos e mudanças nos dados, o que é especialmente importante para tarefas relacionadas a séries temporais, dinâmica de sistemas e previsão. As ODEs neurais podem ser integradas com sucesso em diversas arquiteturas de redes neurais, incluindo modelos profundos e recorrentes, ampliando assim o escopo de aplicação desses métodos.
Na parte prática do nosso artigo, implementamos as abordagens propostas usando MQL5. Treinamos e testamos o modelo com dados reais no testador de estratégias do MetaTrader 5. Os resultados dos testes apresentados acima permitem avaliar a eficácia das abordagens propostas para resolver nossas tarefas.
No entanto, é importante lembrar que todos os programas apresentados neste artigo são de caráter informativo e destinam-se apenas à demonstração e verificação das abordagens propostas.
Referências
Programas Utilizados no Artigo
| # | Nome | Tipo | Descrição |
|---|---|---|---|
| 1 | Research.mq5 | EA | EA para coleta de exemplos |
| 2 | ResearchRealORL.mq5 | EA | EA para coleta de exemplos usando o método Real-ORL |
| 3 | Study.mq5 | EA | EA para treinamento de modelos |
| 4 | Test.mq5 | EA | EA para teste do modelo |
| 5 | Trajectory.mqh | Biblioteca de classes | Estrutura de descrição do estado do sistema |
| 6 | NeuroNet.mqh | Biblioteca de classes | Biblioteca de classes para criação de redes neurais |
| 7 | NeuroNet.cl | Biblioteca | Biblioteca de código para o programa OpenCL |
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/14569
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 Filtragem de Sazonalidade e Período de Tempo para Modelos de Deep Learning ONNX com Python para EA
Filtragem de Sazonalidade e Período de Tempo para Modelos de Deep Learning ONNX com Python para EA
 Hibridização de algoritmos populacionais. Estruturas sequenciais e paralelas
Hibridização de algoritmos populacionais. Estruturas sequenciais e paralelas
 Desenvolvendo um sistema de Replay (Parte 61): Dando play no serviço (II)
Desenvolvendo um sistema de Replay (Parte 61): Dando play no serviço (II)
 Do básico ao intermediário: Passagem por valor ou por referência
Do básico ao intermediário: Passagem por valor ou por referência
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso