
Neural networks made easy (Part 82): Ordinary Differential Equation models (NeuralODE)
Introduction
Let's get acquainted with a new model family: Ordinary Differential Equations. Instead of specifying a discrete sequence of hidden layers, they parameterize the derivative of the hidden state using a neural network. The results of the model are calculated using a "black box", that is, the Differential Equation Solver. These continuous-depth models use a constant amount of memory and adapt their estimation strategy to each input signal. Such models were first introduced in the paper "Neural Ordinary Differential Equations". In this paper, the authors of the method demonstrate the ability to scale backpropagation using any Ordinary Differential Equation (ODE) solver without access to its internal operations. This enables end-to-end training of ODEs within larger models.
1. Algorithm
The main technical challenge in training ordinary differential equation models is to perform inverse mode differentiation of error propagation using an ODE solver. Differentiation using feed-forward operations is simple, but requires large amounts of memory and introduces additional numerical error.
The authors of the method propose to treat the ODE solver as a black box and calculate gradients using the conjugate sensitivity method. With this approach, we can compute gradients by solving a second extended ODE backwards in time. This is applicable to all ODE solvers. It scales linearly with task size and has low memory consumption. Furthermore, it clearly controls the numerical error.
Let's consider optimizing the scalar loss function L(), the input data of which are the results of the ODE solver:
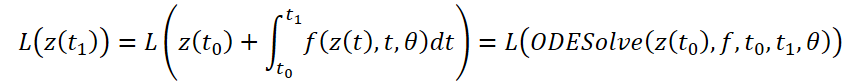
To optimize the L error, we need gradients along θ. The first step of the algorithm proposed by the authors of the method is to determine how the error gradient depends on the hidden state z(t) at every moment a(t)=∂L/∂z(t). Its dynamics are given by another ODE, which can be considered as an analogue of the rule:
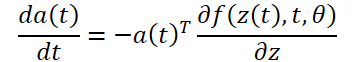
We can compute ∂L/∂z(t) using another call to the ODE solver. This solver must work backwards, starting from the initial value ∂L/∂z(t1). One of the difficulties is that to solve this ODE, we need to know the values of z(t) along the entire trajectory. However, we can simply list z(t) back in time, starting from its final value z(t1).
To compute gradients by θ parameters, we need to determine the third integral, which depends on both z(t) and a(t):
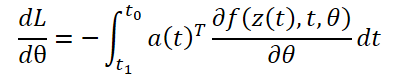
All integrals for solving 𝐳, 𝐚 and ∂L/∂θ can be computed in a single call of an ODE solver that combines the original state, conjugate, and other partial derivatives into a single vector. Below is an algorithm for constructing the necessary dynamics and calling an ODE solver to compute all gradients simultaneously.

Most ODE solvers have the ability to compute the z(t) state repeatedly. When losses depend on these intermediate states, the inverse mode derivative must be broken down into a sequence of separate solutions, one between each successive pair of output values. For each observation, the conjugate must be adjusted in the direction of the corresponding partial derivative ∂L/∂z(t).
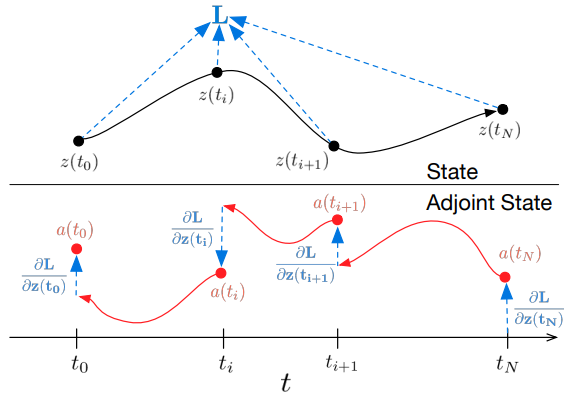
ODE solvers can approximately guarantee that the results obtained are within a given tolerance of the true solution. Changing the tolerance changes the behavior of the model. The time spent on a direct call is proportional to the number of function evaluations, so adjusting the tolerance gives us a trade-off between accuracy and computational cost. You can train with high accuracy but switch to lower accuracy during operation.
2. Implementing in MQL5
To implement the proposed approaches, we will create a new class CNeuronNODEOCL, which will inherit the basic functionality from our fully connected layer CNeuronBaseOCL. Below is the structure of the new class. In addition to the basic set of methods, the structure has several specific methods and objects. We will consider their functionality during the implementation process.
class CNeuronNODEOCL : public CNeuronBaseOCL { protected: uint iDimension; uint iVariables; uint iLenth; int iBuffersK[]; int iInputsK[]; int iMeadl[]; CBufferFloat cAlpha; CBufferFloat cTemp; CCollection cBeta; CBufferFloat cSolution; CCollection cWeights; //--- virtual bool CalculateKBuffer(int k); virtual bool CalculateInputK(CBufferFloat* inputs, int k); virtual bool CalculateOutput(CBufferFloat* inputs); virtual bool feedForward(CNeuronBaseOCL *NeuronOCL); //--- virtual bool CalculateOutputGradient(CBufferFloat* inputs); virtual bool CalculateInputKGradient(CBufferFloat* inputs, int k); virtual bool CalculateKBufferGradient(int k); virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL); public: CNeuronNODEOCL(void) {}; ~CNeuronNODEOCL(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint dimension, uint variables, uint lenth, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual bool calcInputGradients(CNeuronBaseOCL *prevLayer); //--- virtual int Type(void) const { return defNeuronNODEOCL; } //--- methods for working with files virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); virtual void SetOpenCL(COpenCLMy *obj); };
Please note that in order to be able to work with sequences of several environmental states, described by embeddings of several features, we create an object that can work with initial data presented in 3 dimensions:
- iDimension: the size of the embedding vector of one feature in a separate environmental state
- iVariables: the number of features describing one state of the environment
- iLenth: the number of analyzed system states
The ODE function in our case will be represented by 2 fully connected layers with the ReLU activation function between them. However, we admit that the dynamics of each individual feature may differ. Therefore, for each attribute, we will provide our own weight matrices. This approach does not allow us to use convolutional layers as internal ones, as was done previously. Therefore, in our new class, we decompose the inner layers of the ODE function. We will declare the data buffers that make up the internal data layers. Then we will create kernels and methods for implementing processes.
2.1 Feed-forward kernel
When constructing the feed-forward kernel for the ODE function, we proceed from the following restrictions:
- Each state of the environment is described by the same fixed number of features.
- All features have the same fixed embedding size.
Taking into account these restrictions, we create the FeedForwardNODEF kernel on the OpenCL program side. In the parameters of our kernel, we will pass pointers to 3 data buffers and 3 variables. The kernel will be launched in a 3-dimensional task space.
__kernel void FeedForwardNODEF(__global float *matrix_w, ///<[in] Weights matrix __global float *matrix_i, ///<[in] Inputs tensor __global float *matrix_o, ///<[out] Output tensor int dimension, ///< input dimension float step, ///< h int activation ///< Activation type (#ENUM_ACTIVATION) ) { int d = get_global_id(0); int dimension_out = get_global_size(0); int v = get_global_id(1); int variables = get_global_size(1); int i = get_global_id(2); int lenth = get_global_size(2);
In the kernel body, we first identify the current thread across all 3 dimensions of the task space. Then we will determine the shift in the data buffers to the analyzed data.
int shift = variables * i + v; int input_shift = shift * dimension; int output_shift = shift * dimension_out + d; int weight_shift = (v * dimension_out + d) * (dimension + 2);
After the preparatory work, we calculate the values of the current result in a loop, by multiplying the vector of initial data by the corresponding vector of weights.
float sum = matrix_w[dimension + 1 + weight_shift] + matrix_w[dimension + weight_shift] * step; for(int w = 0; w < dimension; w++) sum += matrix_w[w + weight_shift] * matrix_i[input_shift + w];
It should be noted here that the ODE function depends not only on the state of the environment, but also on the timestamp. In this case, there is one timestamp for the entire environmental state. To eliminate its duplication in terms of the number of features and sequence length, we did not add a timestamp to the source data tensor but simply passed it to the kernel as the step parameter.
Next, we just need to propagate the resulting value through the activation function and save the result into the corresponding buffer element.
if(isnan(sum)) sum = 0; switch(activation) { case 0: sum = tanh(sum); break; case 1: sum = 1 / (1 + exp(-clamp(sum, -20.0f, 20.0f))); break; case 2: if(sum < 0) sum *= 0.01f; break; default: break; } matrix_o[output_shift] = sum; }
2.2 Backpropagation kernel
After implementing the feed-forward kernel, we will create the reverse functionality on the OpenCL side of the program, the error gradient distribution kernel HiddenGradientNODEF.
__kernel void HiddenGradientNODEF(__global float *matrix_w, ///<[in] Weights matrix __global float *matrix_g, ///<[in] Gradient tensor __global float *matrix_i, ///<[in] Inputs tensor __global float *matrix_ig, ///<[out] Inputs Gradient tensor int dimension_out, ///< output dimension int activation ///< Input Activation type (#ENUM_ACTIVATION) ) { int d = get_global_id(0); int dimension = get_global_size(0); int v = get_global_id(1); int variables = get_global_size(1); int i = get_global_id(2); int lenth = get_global_size(2);
This kernel will also be launched in a 3-dimensional task space, and we identify the thread in the body of the kernel. We also determine the shifts in the data buffers to the analyzed elements.
int shift = variables * i + v; int input_shift = shift * dimension + d; int output_shift = shift * dimension_out; int weight_step = (dimension + 2); int weight_shift = (v * dimension_out) * weight_step + d;
Then we sum up the error gradient for the analyzed source data element.
float sum = 0; for(int k = 0; k < dimension_out; k ++) sum += matrix_g[output_shift + k] * matrix_w[weight_shift + k * weight_step]; if(isnan(sum)) sum = 0;
Please note that the timestamp is essentially a constant for a separate state. Therefore, we do not propagate the error gradient to it.
We adjust the resulting amount by the derivative of the activation function and save the resulting value into the corresponding element of the data buffer.
float out = matrix_i[input_shift]; switch(activation) { case 0: out = clamp(out, -1.0f, 1.0f); sum = clamp(sum + out, -1.0f, 1.0f) - out; sum = sum * max(1 - pow(out, 2), 1.0e-4f); break; case 1: out = clamp(out, 0.0f, 1.0f); sum = clamp(sum + out, 0.0f, 1.0f) - out; sum = sum * max(out * (1 - out), 1.0e-4f); break; case 2: if(out < 0) sum *= 0.01f; break; default: break; } //--- matrix_ig[input_shift] = sum; }
2.3 ODE solver
We have completed the first stage of work. Now let's look at the ODE solver side. For my implementation, I chose the 5th order Dorman-Prince method.
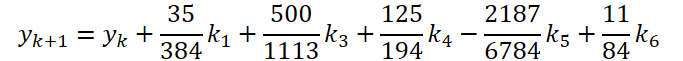
where
![]()
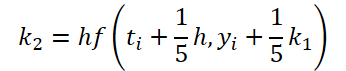
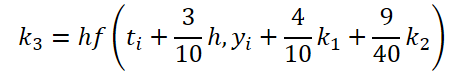
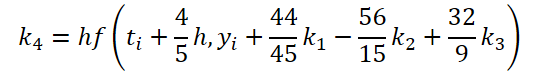
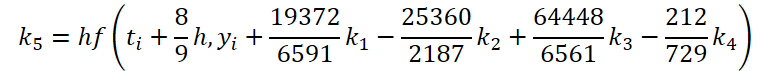
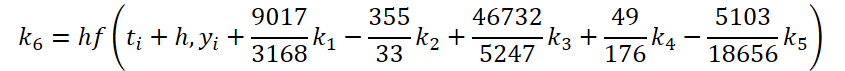
As you can see, the function of solving and adjusting the initial data for calculating the coefficients k1..k6 differ only in numerical coefficients. We can add the missing coefficients ki multiplied by 0, which will not affect the result. Therefore, to unify the process, we will create one FeedForwardNODEInpK kernel on the OpenCL side of the program. In the kernel parameters, we pass pointers to the buffers of the source data and all coefficients ki. We indicate the required multipliers in the matrix_beta buffer.
__kernel void FeedForwardNODEInpK(__global float *matrix_i, ///<[in] Inputs tensor __global float *matrix_k1, ///<[in] K1 tensor __global float *matrix_k2, ///<[in] K2 tensor __global float *matrix_k3, ///<[in] K3 tensor __global float *matrix_k4, ///<[in] K4 tensor __global float *matrix_k5, ///<[in] K5 tensor __global float *matrix_k6, ///<[in] K6 tenтor __global float *matrix_beta, ///<[in] beta tensor __global float *matrix_o ///<[out] Output tensor ) { int i = get_global_id(0);
We will run the kernel in a one-dimensional task space and will compute values for each individual value of the results buffer.
After identifying the flow, we will collect the sum of the products in a loop.
float sum = matrix_i[i]; for(int b = 0; b < 6; b++) { float beta = matrix_beta[b]; if(beta == 0.0f || isnan(beta)) continue; //--- float val = 0.0f; switch(b) { case 0: val = matrix_k1[i]; break; case 1: val = matrix_k2[i]; break; case 2: val = matrix_k3[i]; break; case 3: val = matrix_k4[i]; break; case 4: val = matrix_k5[i]; break; case 5: val = matrix_k6[i]; break; } if(val == 0.0f || isnan(val)) continue; //--- sum += val * beta; }
The resulting value is saved in the corresponding element of the results buffer.
matrix_o[i] = sum; }
For the backpropagation method, we create the HiddenGradientNODEInpK kernel, in which we propagate the error gradient into the corresponding data buffers, taking into account the same Beta coefficients.
__kernel void HiddenGradientNODEInpK(__global float *matrix_ig, ///<[in] Inputs tensor __global float *matrix_k1g, ///<[in] K1 tensor __global float *matrix_k2g, ///<[in] K2 tensor __global float *matrix_k3g, ///<[in] K3 tensor __global float *matrix_k4g, ///<[in] K4 tensor __global float *matrix_k5g, ///<[in] K5 tensor __global float *matrix_k6g, ///<[in] K6 tensor __global float *matrix_beta, ///<[in] beta tensor __global float *matrix_og ///<[out] Output tensor ) { int i = get_global_id(0); //--- float grad = matrix_og[i]; matrix_ig[i] = grad; for(int b = 0; b < 6; b++) { float beta = matrix_beta[b]; if(isnan(beta)) beta = 0.0f; //--- float val = beta * grad; if(isnan(val)) val = 0.0f; switch(b) { case 0: matrix_k1g[i] = val; break; case 1: matrix_k2g[i] = val; break; case 2: matrix_k3g[i] = val; break; case 3: matrix_k4g[i] = val; break; case 4: matrix_k5g[i] = val; break; case 5: matrix_k6g[i] = val; break; } } }
Please note that we also write zero values to the data buffers. This is necessary to avoid double counting of previously saved values.
2.4 Weight update kernel
To complete the OpenCL program side, we will create a kernel for updating the weights of the ODE function. As you can see from the formulas presented above, the ODE function will be used to determine all ki coefficients Therefore, when adjusting the weights, we must collect the error gradient from all operations. None of the weight updating kernels we have created previously worked with so many gradient buffers. So, we have to create a new kernel. To simplify the experiment, we will only create the NODEF_UpdateWeightsAdam kernel to update parameters using the Adam method, which is what I use most often.
__kernel void NODEF_UpdateWeightsAdam(__global float *matrix_w, ///<[in,out] Weights matrix __global const float *matrix_gk1, ///<[in] Tensor of gradients at k1 __global const float *matrix_gk2, ///<[in] Tensor of gradients at k2 __global const float *matrix_gk3, ///<[in] Tensor of gradients at k3 __global const float *matrix_gk4, ///<[in] Tensor of gradients at k4 __global const float *matrix_gk5, ///<[in] Tensor of gradients at k5 __global const float *matrix_gk6, ///<[in] Tensor of gradients at k6 __global const float *matrix_ik1, ///<[in] Inputs tensor __global const float *matrix_ik2, ///<[in] Inputs tensor __global const float *matrix_ik3, ///<[in] Inputs tensor __global const float *matrix_ik4, ///<[in] Inputs tensor __global const float *matrix_ik5, ///<[in] Inputs tensor __global const float *matrix_ik6, ///<[in] Inputs tensor __global float *matrix_m, ///<[in,out] Matrix of first momentum __global float *matrix_v, ///<[in,out] Matrix of seconfd momentum __global const float *alpha, ///< h const int lenth, ///< Number of inputs const float l, ///< Learning rates const float b1, ///< First momentum multiplier const float b2 ///< Second momentum multiplier ) { const int d_in = get_global_id(0); const int dimension_in = get_global_size(0); const int d_out = get_global_id(1); const int dimension_out = get_global_size(1); const int v = get_global_id(2); const int variables = get_global_id(2);
As noted above, kernel parameters pass pointers to a large number of global data buffers. Standard parameters of the selected optimization method are added to them.
We will run the kernel in a 3-dimensional task space, which takes into account the dimension of the embedding vectors of the source data and results, as well as the number of analyzed features. In the kernel body, we identify the flow in the task space along all 3 dimensions. Then we determine the offsets in the data buffers.
const int weight_shift = (v * dimension_out + d_out) * dimension_in; const int input_step = variables * (dimension_in - 2); const int input_shift = v * (dimension_in - 2) + d_in; const int output_step = variables * dimension_out; const int output_shift = v * dimension_out + d_out;
Next, in a loop, we collect the error gradient across all environmental states.
float weight = matrix_w[weight_shift]; float g = 0; for(int i = 0; i < lenth; i++) { int shift_g = i * output_step + output_shift; int shift_i = i * input_step + input_shift; switch(dimension_in - d_in) { case 1: g += matrix_gk1[shift_g] + matrix_gk2[shift_g] + matrix_gk3[shift_g] + matrix_gk4[shift_g] + matrix_gk5[shift_g] + matrix_gk6[shift_g]; break; case 2: g += matrix_gk1[shift_g] * alpha[0] + matrix_gk2[shift_g] * alpha[1] + matrix_gk3[shift_g] * alpha[2] + matrix_gk4[shift_g] * alpha[3] + matrix_gk5[shift_g] * alpha[4] + matrix_gk6[shift_g] * alpha[5]; break; default: g += matrix_gk1[shift_g] * matrix_ik1[shift_i] + matrix_gk2[shift_g] * matrix_ik2[shift_i] + matrix_gk3[shift_g] * matrix_ik3[shift_i] + matrix_gk4[shift_g] * matrix_ik4[shift_i] + matrix_gk5[shift_g] * matrix_ik5[shift_i] + matrix_gk6[shift_g] * matrix_ik6[shift_i]; break; } }
And then we adjust the weights according to the familiar algorithm.
float mt = b1 * matrix_m[weight_shift] + (1 - b1) * g; float vt = b2 * matrix_v[weight_shift] + (1 - b2) * pow(g, 2); float delta = l * (mt / (sqrt(vt) + 1.0e-37f) - (l1 * sign(weight) + l2 * weight));
At the end of the kernel, we save the result and auxiliary values into the corresponding elements of the data buffers.
if(delta * g > 0) matrix_w[weight_shift] = clamp(matrix_w[weight_shift] + delta, -MAX_WEIGHT, MAX_WEIGHT); matrix_m[weight_shift] = mt; matrix_v[weight_shift] = vt; }
This completes the OpenCL program side. Let's get back to the implementation of our CNeuronNODEOCL class.
2.5 CNeuronNODEOCL class initialization method
Initialization of our class object is performed in the CNeuronNODEOCL::Init method. In the method parameters, as usual, we will pass the main parameters of the object's architecture.
bool CNeuronNODEOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint dimension, uint variables, uint lenth, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, dimension * variables * lenth, optimization_type, batch)) return false;
In the body of the method, we first call the relevant method of the parent class, which controls the received parameters and initializes inherited objects. We can find out the generalized result of performing operations in the body of the parent class by the returned logical value.
Next, we save the resulting object architecture parameters into local class variables.
iDimension = dimension; iVariables = variables; iLenth = lenth;
Declare auxiliary variables and assign them the necessary values.
uint mult = 2; uint weights = (iDimension + 2) * iDimension * iVariables;
Now let's look at buffers of ki coefficient and adjusted initial data for their calculation. As you can guess, the values in these data buffers are saved from the feed-forward pass to the backpropagation pass. During the next feed-forward pass, the values are overwritten. Therefore, to save resources, we do not create these buffers in the main program memory. We create them only on the OpenCL side of the context. In the class, we only create arrays to store pointers to them. In each array, we create 3 times more elements than k coefficients are used. This is necessary to collect error gradients.
if(ArrayResize(iBuffersK, 18) < 18) return false; if(ArrayResize(iInputsK, 18) < 18) return false;
We do the same with intermediate calculation values. However, the array size is smaller.
if(ArrayResize(iMeadl, 12) < 12) return false;
In order to increase the readability of the code, we will create buffers in a loop.
for(uint i = 0; i < 18; i++) { iBuffersK[i] = OpenCL.AddBuffer(sizeof(float) * Output.Total(), CL_MEM_READ_WRITE); if(iBuffersK[i] < 0) return false; iInputsK[i] = OpenCL.AddBuffer(sizeof(float) * Output.Total(), CL_MEM_READ_WRITE); if(iInputsK[i] < 0) return false; if(i > 11) continue; //--- Initilize Meadl Output and Gradient buffers iMeadl[i] = OpenCL.AddBuffer(sizeof(float) * Output.Total(), CL_MEM_READ_WRITE); if(iMeadl[i] < 0) return false; }
The next step is to create matrices of weight coefficients of the ODE function model and moments to them. As mentioned above, we will use 2 layers.
//--- Initilize Weights for(int i = 0; i < 2; i++) { temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.Reserve(weights)) return false; float k = (float)(1 / sqrt(iDimension + 2)); for(uint w = 0; w < weights; w++) { if(!temp.Add((GenerateWeight() - 0.5f)* k)) return false; } if(!temp.BufferCreate(OpenCL)) return false; if(!cWeights.Add(temp)) return false;
for(uint d = 0; d < 2; d++) { temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(weights, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!cWeights.Add(temp)) return false; } }
Next we create constant multiplier buffers:
- Alpha time step
{
float temp_ar[] = {0, 0.2f, 0.3f, 0.8f, 8.0f / 9, 1, 1};
if(!cAlpha.AssignArray(temp_ar))
return false;
if(!cAlpha.BufferCreate(OpenCL))
return false;
}
- Source data adjustments
//--- Beta K1 { float temp_ar[] = {0, 0, 0, 0, 0, 0}; temp = new CBufferFloat(); if(!temp || !temp.AssignArray(temp_ar)) { delete temp; return false; } if(!temp.BufferCreate(OpenCL)) { delete temp; return false; } if(!cBeta.Add(temp)) { delete temp; return false; } }
//--- Beta K2 { float temp_ar[] = {0.2f, 0, 0, 0, 0, 0}; temp = new CBufferFloat(); if(!temp || !temp.AssignArray(temp_ar)) { delete temp; return false; } if(!temp.BufferCreate(OpenCL)) { delete temp; return false; } if(!cBeta.Add(temp)) { delete temp; return false; } }
//--- Beta K3 { float temp_ar[] = {3.0f / 40, 9.0f / 40, 0, 0, 0, 0}; temp = new CBufferFloat(); if(!temp || !temp.AssignArray(temp_ar)) { delete temp; return false; } if(!temp.BufferCreate(OpenCL)) { delete temp; return false; } if(!cBeta.Add(temp)) { delete temp; return false; } }
//--- Beta K4 { float temp_ar[] = {44.0f / 44, -56.0f / 15, 32.0f / 9, 0, 0, 0}; temp = new CBufferFloat(); if(!temp || !temp.AssignArray(temp_ar)) { delete temp; return false; } if(!temp.BufferCreate(OpenCL)) { delete temp; return false; } if(!cBeta.Add(temp)) { delete temp; return false; } }
//--- Beta K5 { float temp_ar[] = {19372.0f / 6561, -25360 / 2187.0f, 64448 / 6561.0f, -212.0f / 729, 0, 0}; temp = new CBufferFloat(); if(!temp || !temp.AssignArray(temp_ar)) { delete temp; return false; } if(!temp.BufferCreate(OpenCL)) { delete temp; return false; } if(!cBeta.Add(temp)) { delete temp; return false; } }
//--- Beta K6 { float temp_ar[] = {9017 / 3168.0f, -355 / 33.0f, 46732 / 5247.0f, 49.0f / 176, -5103.0f / 18656, 0}; temp = new CBufferFloat(); if(!temp || !temp.AssignArray(temp_ar)) { delete temp; return false; } if(!temp.BufferCreate(OpenCL)) { delete temp; return false; } if(!cBeta.Add(temp)) { delete temp; return false; } }
- ODE solutions
{
float temp_ar[] = {35.0f / 384, 0, 500.0f / 1113, 125.0f / 192, -2187.0f / 6784, 11.0f / 84};
if(!cSolution.AssignArray(temp_ar))
return false;
if(!cSolution.BufferCreate(OpenCL))
return false;
}
At the end of the initialization method, we add a local buffer for recording intermediate values.
if(!cTemp.BufferInit(Output.Total(), 0) || !cTemp.BufferCreate(OpenCL)) return false; //--- return true; }
2.6 Organizing the feed-forward pass
After initializing the class object, we move on to organizing the feed-forward algorithm. Above, we created 2 kernels on the OpenCL program side to organize the feed-forward pass. Therefore, we have to create methods to call them. We'll start with a fairly simple method CalculateInputK which prepares initial data for computing k coefficients
bool CNeuronNODEOCL::CalculateInputK(CBufferFloat* inputs, int k) { if(k < 0) return false; if(iInputsK.Size()/3 <= uint(k)) return false;
In the method parameters, we receive a pointer to the buffer of source data obtained from the previous layer and the index of the coefficient to be computed. In the body of the method, we check whether the specified coefficient index corresponds to our architecture.
After successfully passing the control block, we consider the special case for k1.
![]()
In this case, we do not call kernel execution but simply copy the pointer to the source data buffer.
if(k == 0) { if(iInputsK[k] != inputs.GetIndex()) { OpenCL.BufferFree(iInputsK[k]); iInputsK[k] = inputs.GetIndex(); } return true; }
In the general case, we call the FeedForwardNODEInpK kernel and write the adjusted source data to the appropriate buffer. To do this, we first define a task space. In this case, it is a one-dimensional space.
uint global_work_offset[1] = {0}; uint global_work_size[1] = {Neurons()};
Let's pass buffer pointers to the kernel parameters.
ResetLastError(); if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardNODEInpK, def_k_ffdopriInp_matrix_i, inputs.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardNODEInpK, def_k_ffdopriInp_matrix_k1, iBuffersK[0])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardNODEInpK, def_k_ffdopriInp_matrix_k2, iBuffersK[1])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardNODEInpK, def_k_ffdopriInp_matrix_k3, iBuffersK[2])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardNODEInpK, def_k_ffdopriInp_matrix_k4, iBuffersK[3])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardNODEInpK, def_k_ffdopriInp_matrix_k5, iBuffersK[4])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardNODEInpK, def_k_ffdopriInp_matrix_k6, iBuffersK[5])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardNODEInpK, def_k_ffdopriInp_matrix_beta, ((CBufferFloat *)cBeta.At(k)).GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardNODEInpK, def_k_ffdopriInp_matrix_o, iInputsK[k])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
Put the kernel in the execution queue.
if(!OpenCL.Execute(def_k_FeedForwardNODEInpK, 1, global_work_offset, global_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; } //--- return true; }
After adjusting the source data, we compute the value of the coefficients. This process is organized in the CalculateKBuffer method. Since the method works only with internal objects, you only need to specify the index of the required coefficient in the method parameters to perform operations.
bool CNeuronNODEOCL::CalculateKBuffer(int k) { if(k < 0) return false; if(iInputsK.Size()/3 <= uint(k)) return false;
In the body of the method, we check if the resulting index matches the class architecture.
Next, we define a 3-dimensional problem space.
uint global_work_offset[3] = {0, 0, 0}; uint global_work_size[3] = {iDimension, iVariables, iLenth};
We then pass parameters to the kernel to pass the first layer. Here we use LReLU to create nonlinearity.
if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardNODEF, def_k_ffdoprif_matrix_i, iInputsK[k])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardNODEF, def_k_ffdoprif_matrix_w, ((CBufferFloat*)cWeights.At(0)).GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardNODEF, def_k_ffdoprif_matrix_o, iMeadl[k * 2])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_FeedForwardNODEF, def_k_ffdoprif_dimension, int(iDimension))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_FeedForwardNODEF, def_k_ffdoprif_step, float(cAlpha.At(k)))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_FeedForwardNODEF, def_k_ffdoprif_activation, int(LReLU))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
Put the kernel into the execution queue.
if(!OpenCL.Execute(def_k_FeedForwardNODEF, 3, global_work_offset, global_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; }
The next step is to run a feed-forward pass of the second layer. The task space remains the same. Therefore, we do not modify the corresponding arrays. We need to re-pass the parameters to the kernel. This time we change the source data, weight and result buffers.
if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardNODEF, def_k_ffdoprif_matrix_i, iMeadl[k * 2])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardNODEF, def_k_ffdoprif_matrix_w, ((CBufferFloat*)cWeights.At(3)).GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardNODEF, def_k_ffdoprif_matrix_o, iBuffersK[k])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
We also do not use the activation function.
if(!OpenCL.SetArgument(def_k_FeedForwardNODEF, def_k_ffdoprif_activation, int(None))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
Other parameters do not change.
if(!OpenCL.SetArgument(def_k_FeedForwardNODEF, def_k_ffdoprif_dimension, int(iDimension))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_FeedForwardNODEF, def_k_ffdoprif_step, cAlpha.At(k))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
Send the kernel to the execution queue.
if(!OpenCL.Execute(def_k_FeedForwardNODEF, 3, global_work_offset, global_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; } //-- return true; }
After computing all k coefficients, we can determine the ODE solving result. In practice, for these purposes we will use the FeedForwardNODEInpK kernel. Its call has already been implemented in the CalculateInputK method. But in this case, we have to change the data buffers used. Therefore, we will rewrite the algorithm in the CalculateOutput method.
bool CNeuronNODEOCL::CalculateOutput(CBufferFloat* inputs) { //--- uint global_work_offset[1] = {0}; uint global_work_size[1] = {Neurons()};
In the parameters of this method, we receive only a pointer to the source data buffer. In the method body, we immediately define a one-dimensional problem space. Then we pass pointers to the source data buffers to the kernel parameters.
ResetLastError(); if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardNODEInpK, def_k_ffdopriInp_matrix_i, inputs.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardNODEInpK, def_k_ffdopriInp_matrix_k1, iBuffersK[0])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardNODEInpK, def_k_ffdopriInp_matrix_k2, iBuffersK[1])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardNODEInpK, def_k_ffdopriInp_matrix_k3, iBuffersK[2])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardNODEInpK, def_k_ffdopriInp_matrix_k4, iBuffersK[3])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardNODEInpK, def_k_ffdopriInp_matrix_k5, iBuffersK[4])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardNODEInpK, def_k_ffdopriInp_matrix_k6, iBuffersK[5])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
For the multipliers, we indicate a buffer of ODE solving coefficients.
if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardNODEInpK, def_k_ffdopriInp_matrix_beta, cSolution.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
We write the results into the results buffer of our class.
if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardNODEInpK, def_k_ffdopriInp_matrix_o, Output.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
Put the kernel in the execution queue.
if(!OpenCL.Execute(def_k_FeedForwardNODEInpK, 1, global_work_offset, global_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; }
We combine the obtained values with the source data and normalize it.
if(!SumAndNormilize(Output, inputs, Output, iDimension, true, 0, 0, 0, 1)) return false; //--- return true; }
We have prepared methods for calling kernels to organize the feed-forward pass process. Now we just need to formalize the algorithm in the top-level method CNeuronNODEOCL::feedForward.
bool CNeuronNODEOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { for(int k = 0; k < 6; k++) { if(!CalculateInputK(NeuronOCL.getOutput(), k)) return false; if(!CalculateKBuffer(k)) return false; } //--- return CalculateOutput(NeuronOCL.getOutput()); }
In the parameters, the method receives a pointer to the object of the previous layer. In the body of the method, we organize a loop in which we sequentially adjust the source data and compute all k coefficients At each iteration, we control the process of performing operations. After successfully computing the necessary coefficients, we call the ODE solving method. We have done a lot of preparatory work, and thus the algorithm of the top-level method turned out to be quite concise.
2.7 Organizing the backpropagation pass
The feed-forward algorithm provides the process of operating the model. However, model training is inseparable from the backpropagation process. During this process, the trained parameters are adjusted in order to minimize the error of the model.
Similar to feed-forward kernels, we have created 2 backpropagation kernels on the OpenCL program side. Now, on the side of the main program, we have to create methods for calling the backpropagation kernels. Since we are implementing a backward process, we work with methods in the sequence of the backpropagation pass.
After receiving the error gradient from the next layer, we distribute the resulting gradient between the source data layer and k coefficients. This process is implemented in the CalculateOutputGradient method which calls the HiddenGradientNODEInpK kernel.
bool CNeuronNODEOCL::CalculateOutputGradient(CBufferFloat *inputs) { //--- uint global_work_offset[1] = {0}; uint global_work_size[1] = {Neurons()};
In the method parameters, we receive a pointer to the error gradient buffer of the previous layer. In the body of the method, we organize the process of calling the OpenCL program kernel. First, we define a one-dimensional task space. Then we pass pointers to data buffers and kernel parameters.
Please note that the HiddenGradientNODEInpK kernel parameters completely replicate the FeedForwardNODEInpK kernel parameters. The only difference is that the feed-forward pass used buffers of the source data and k coefficients. The backpropagation pass uses buffers of the corresponding gradients. For this reason, I did not redefine the kernel buffer constants, but used the feed-forward pass constants.
if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientNODEInpK, def_k_ffdopriInp_matrix_i, inputs.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientNODEInpK, def_k_ffdopriInp_matrix_k1, iBuffersK[6])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientNODEInpK, def_k_ffdopriInp_matrix_k2, iBuffersK[7])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientNODEInpK, def_k_ffdopriInp_matrix_k3, iBuffersK[8])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientNODEInpK, def_k_ffdopriInp_matrix_k4, iBuffersK[9])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientNODEInpK, def_k_ffdopriInp_matrix_k5, iBuffersK[10])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientNODEInpK, def_k_ffdopriInp_matrix_k6, iBuffersK[11])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientNODEInpK, def_k_ffdopriInp_matrix_beta, cSolution.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientNODEInpK, def_k_ffdopriInp_matrix_o, Gradient.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
Also pay attention to the following thing. To record k coefficients, we used buffers with the corresponding index in the range [0, 5]. In this case, we use buffers with an index in the range [6, 11] to record error gradients.
After successfully passing all the parameters to the kernel, we put it in the execution queue.
if(!OpenCL.Execute(def_k_HiddenGradientNODEInpK, 1, global_work_offset, global_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; } //--- return true; }
Next, let's consider the CalculateInputKGradient method, which calls the same kernel. The construction of the algorithm has some nuances which we should pay special attention to.
The first is, of course, the method parameters. The index of the k coefficient is added here.
bool CNeuronNODEOCL::CalculateInputKGradient(CBufferFloat *inputs, int k) { //--- uint global_work_offset[1] = {0}; uint global_work_size[1] = {Neurons()};
In the body of the method, we define the same one-dimensional task space. Then we pass the parameters to the kernel.
ResetLastError(); if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientNODEInpK, def_k_ffdopriInp_matrix_i, inputs.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
However, this time, to write the error gradients of the k coefficients, we use buffers with an index in the range [12, 17]. This is due to the need to accumulate error gradients for each coefficient.
if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientNODEInpK, def_k_ffdopriInp_matrix_k1, iBuffersK[12])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientNODEInpK, def_k_ffdopriInp_matrix_k2, iBuffersK[13])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientNODEInpK, def_k_ffdopriInp_matrix_k3, iBuffersK[14])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientNODEInpK, def_k_ffdopriInp_matrix_k4, iBuffersK[15])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientNODEInpK, def_k_ffdopriInp_matrix_k5, iBuffersK[16])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientNODEInpK, def_k_ffdopriInp_matrix_k6, iBuffersK[17])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
In addition, we use multipliers from the cBeta array.
if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientNODEInpK, def_k_ffdopriInp_matrix_beta, ((CBufferFloat *)cBeta.At(k)).GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientNODEInpK, def_k_ffdopriInp_matrix_o, iInputsK[k + 6])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
After successfully passing all the parameters necessary to the kernel, we put it in the execution queue.
if(!OpenCL.Execute(def_k_HiddenGradientNODEInpK, 1, global_work_offset, global_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; }
Next, we need to sum up the current error gradient with the previously accumulated error gradient for the corresponding k coefficient. To do this, we organize a backward loop in which we sequentially add error gradients starting from the analyzed k coefficient to the minimum.
for(int i = k - 1; i >= 0; i--) { float mult = 1.0f / (i == (k - 1) ? 6 - k : 1); uint global_work_offset[1] = {0}; uint global_work_size[1] = {iLenth * iVariables}; if(!OpenCL.SetArgumentBuffer(def_k_MatrixSum, def_k_sum_matrix1, iBuffersK[k + 6])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_MatrixSum, def_k_sum_matrix2, iBuffersK[k + 12])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_MatrixSum, def_k_sum_matrix_out, iBuffersK[k + 6])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_MatrixSum, def_k_sum_dimension, iDimension)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_MatrixSum, def_k_sum_shift_in1, 0)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_MatrixSum, def_k_sum_shift_in2, 0)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_MatrixSum, def_k_sum_shift_out, 0)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_MatrixSum, def_k_sum_multiplyer, mult)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.Execute(def_k_MatrixSum, 1, global_work_offset, global_work_size)) { string error; CLGetInfoString(OpenCL.GetContext(), CL_ERROR_DESCRIPTION, error); printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; } } //--- return true; }
Note that we only sum the error gradients for k coefficients with an index less than the current one. This is due to the fact that the ß multiplier for coefficients with a larger index is obviously equal to 0. Because such coefficients are computed after the current one and do not participate in its determination. Accordingly, their error gradient is zero. In addition, for more stable training, we average the accumulated error gradients.
The last kernel that participates in the error gradient propagation is the kernel that propagates of the error gradient through the inner layer of the ODE function HiddenGradientNODEF. It is called in the CalculateKBufferGradient method. In parameters, the method receives only the index of the k coefficient for which the gradient is distributed.
bool CNeuronNODEOCL::CalculateKBufferGradient(int k) { if(k < 0) return false; if(iInputsK.Size()/3 <= uint(k)) return false;
In the body of the method, we check if the resulting index complies with the object's architecture. Then we define a 3-dimensional problem space.
uint global_work_offset[3] = {0, 0, 0}; uint global_work_size[3] = {iDimension, iVariables, iLenth};
Implement the transfer of parameters to the kernel. Since we are distributing the error gradient within the backpropagation pass, we first specify the buffers of layer 2 of the function.
ResetLastError(); if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientNODEF, def_k_hddoprif_matrix_i, iMeadl[k * 2])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientNODEF, def_k_hddoprif_matrix_ig, iMeadl[k * 2 + 1])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientNODEF, def_k_hddoprif_matrix_w, ((CBufferFloat*)cWeights.At(3)).GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientNODEF, def_k_hddoprif_matrix_g, iBuffersK[k + 6])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_HiddenGradientNODEF, def_k_hddoprif_dimension_out, int(iDimension))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_HiddenGradientNODEF, def_k_hddoprif_activation, int(LReLU))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
Put the kernel into the execution queue.
if(!OpenCL.Execute(def_k_HiddenGradientNODEF, 3, global_work_offset, global_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; }
In the next step, if the arrays defining the task space remain unchanged, we transfer the data of the 1st layer of the function to the kernel parameters.
if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientNODEF, def_k_hddoprif_matrix_i, iInputsK[k])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientNODEF, def_k_hddoprif_matrix_ig, iInputsK[k + 12])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientNODEF, def_k_hddoprif_matrix_w, ((CBufferFloat*)cWeights.At(0)).GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_HiddenGradientNODEF, def_k_hddoprif_matrix_g, iMeadl[k * 2 + 1])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_HiddenGradientNODEF, def_k_hddoprif_dimension_out, int(iDimension))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_HiddenGradientNODEF, def_k_hddoprif_activation, int(None))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
Call kernel execution.
if(!OpenCL.Execute(def_k_HiddenGradientNODEF, 3, global_work_offset, global_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; } //-- return true; }
We have created methods for calling kernels for distributing the error gradient between layer objects. But in this state, these are only scattered pieces of the program that do not form a single algorithm. We have to combine them into a single whole. We organize the general algorithm for distributing the error gradient within our class using the calcInputGradients method.
bool CNeuronNODEOCL::calcInputGradients(CNeuronBaseOCL *prevLayer) { if(!CalculateOutputGradient(prevLayer.getGradient())) return false; for(int k = 5; k >= 0; k--) { if(!CalculateKBufferGradient(k)) return false; if(!CalculateInputKGradient(GetPointer(cTemp), k)) return false; if(!SumAndNormilize(prevLayer.getGradient(), GetPointer(cTemp), prevLayer.getOutput(), iDimension, false, 0, 0, 0, 1.0f / (k == 0 ? 6 : 1))) return false; } //--- return true; }
In the parameters, the method receives a pointer to the object of the previous layer, to which we need to pass the error gradient. At the first stage, we distribute the error gradient obtained from the subsequent layer between the previous layer and k coefficients according to the factors of the ODE solution. As you remember, we implemented this process in the CalculateOutputGradient method.
We then run a backward loop to propagate gradients through the ODE function when calculating the corresponding coefficients. Here we first propagate the error gradient through our 2 layers in the CalculateKBufferGradient method. Then we distribute the resulting error gradient between the corresponding k coefficients and initial data in the CalculateInputKGradient method. However, instead of a buffer of error gradients from the previous layer, we receive data into a temporary buffer. Then we add the resulting gradient to the one previously accumulated in the gradient buffer of the previous layer using the SumAndNormilize method. At the last iteration, we average the accumulated error gradient.
At this stage, we have completely distributed the error gradient between all objects that influence the result in accordance with their contribution. All we have to do is update the model parameters. Previously, to perform this functionality, have we created the NODEF_UpdateWeightsAdam kernel. Now we have to organize a call to the specified kernel on the side of the main program. This functionality is performed in the updateInputWeights method.
bool CNeuronNODEOCL::updateInputWeights(CNeuronBaseOCL *NeuronOCL) { uint global_work_offset[3] = {0, 0, 0}; uint global_work_size[3] = {iDimension + 2, iDimension, iVariables};
In the parameters, the method receives a pointer to the object of the previous neural layer, which in this case is nominal and is necessary only for the method virtualization procedure.
Indeed, during the feed-forward and backward passes, we used the data from the previous layer. So, we will need them to update the parameters of the first layer of the ODE function. During the feed-forward pass, we saved the pointer to the results buffer of the previous layer in the iInputsK array with index 0. So, let's use it in our implementation.
In the body of the method, we first define a 3-dimensional problem space. Then we pass the parameters necessary to the kernel. First we update the parameters of layer 1.
if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_matrix_ik1, iInputsK[0])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_matrix_gk1, iMeadl[1])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_matrix_ik2, iInputsK[1])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_matrix_gk2, iMeadl[3])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_matrix_ik3, iInputsK[2])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_matrix_gk3, iMeadl[5])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_matrix_ik4, iInputsK[3])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_matrix_gk4, iMeadl[7])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_matrix_ik5, iInputsK[4])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_matrix_gk5, iMeadl[9])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_matrix_ik6, iInputsK[5])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_matrix_gk6, iMeadl[11])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_matrix_w, ((CBufferFloat*)cWeights.At(0)).GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_matrix_m, ((CBufferFloat*)cWeights.At(1)).GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_matrix_v, ((CBufferFloat*)cWeights.At(2)).GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_alpha, cAlpha.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_lenth, int(iLenth))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
if(!OpenCL.SetArgument(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_l, lr)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_b1, b1)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_b2, b2)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
Put the kernel in the execution queue.
if(!OpenCL.Execute(def_k_NODEF_UpdateWeightsAdam, 3, global_work_offset, global_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; }
Then we repeat the operations to organize the process of updating the parameters of layer 2.
if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_matrix_ik1, iMeadl[0])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_matrix_gk1, iBuffersK[6])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_matrix_ik2, iMeadl[2])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_matrix_gk2, iBuffersK[7])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_matrix_ik3, iMeadl[4])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_matrix_gk3, iBuffersK[8])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_matrix_ik4, iMeadl[6])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_matrix_gk4, iBuffersK[9])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_matrix_ik5, iMeadl[8])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_matrix_gk5, iBuffersK[10])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_matrix_ik6, iMeadl[10])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_matrix_gk6, iBuffersK[11])) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_matrix_w, ((CBufferFloat*)cWeights.At(3)).GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_matrix_m, ((CBufferFloat*)cWeights.At(4)).GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_matrix_v, ((CBufferFloat*)cWeights.At(5)).GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_alpha, cAlpha.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_lenth, int(iLenth))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_l, lr)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_b1, b1)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_NODEF_UpdateWeightsAdam, def_k_uwdoprif_b2, b2)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.Execute(def_k_NODEF_UpdateWeightsAdam, 3, global_work_offset, global_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; } //-- return true; }
2.8 File operations
We have looked at methods for organizing the main class process. However, I would like to say a few words about methods for working with files. If you look carefully at the structure of the internal objects of the class, you can select for saving only the cWeights collection, containing weights at the moments of their adjustment. Also you can save 3 parameters that determine the architecture of the class. Let's save them in the Save method.
bool CNeuronNODEOCL::Save(const int file_handle) { if(!CNeuronBaseOCL::Save(file_handle)) return false; if(!cWeights.Save(file_handle)) return false; if(FileWriteInteger(file_handle, int(iDimension), INT_VALUE) < INT_VALUE || FileWriteInteger(file_handle, int(iVariables), INT_VALUE) < INT_VALUE || FileWriteInteger(file_handle, int(iLenth), INT_VALUE) < INT_VALUE) return false; //--- return true; }
In the parameters, the method receives a file handle for saving data. Immediately, in the body of the method, we call the method of the parent class with the same name. Then we save the collection and constants.
The class saving method is quite concise and allows you to save maximum disk space. However, the savings come at a cost in the data loading method.
bool CNeuronNODEOCL::Load(const int file_handle) { if(!CNeuronBaseOCL::Load(file_handle)) return false; if(!cWeights.Load(file_handle)) return false; cWeights.SetOpenCL(OpenCL); //--- iDimension = (int)FileReadInteger(file_handle); iVariables = (int)FileReadInteger(file_handle); iLenth = (int)FileReadInteger(file_handle);
Here we first load the saved data. Then we organize the process of creating missing objects in accordance with the loaded parameters of the object architecture.
//--- CBufferFloat *temp = NULL; for(uint i = 0; i < 18; i++) { OpenCL.BufferFree(iBuffersK[i]); OpenCL.BufferFree(iInputsK[i]); //--- iBuffersK[i] = OpenCL.AddBuffer(sizeof(float) * Output.Total(), CL_MEM_READ_WRITE); if(iBuffersK[i] < 0) return false; iInputsK[i] = OpenCL.AddBuffer(sizeof(float) * Output.Total(), CL_MEM_READ_WRITE); if(iBuffersK[i] < 0) return false; if(i > 11) continue; //--- Initilize Output and Gradient buffers OpenCL.BufferFree(iMeadl[i]); iMeadl[i] = OpenCL.AddBuffer(sizeof(float) * Output.Total(), CL_MEM_READ_WRITE); if(iMeadl[i] < 0) return false; } //--- cTemp.BufferFree(); if(!cTemp.BufferInit(Output.Total(), 0) || !cTemp.BufferCreate(OpenCL)) return false; //--- return true; }
This concludes our discussion of the methods of our new CNeuronNODEOCL class. And you can find the complete code of all methods and programs used herein in the attachment.
2.9 Model architecture for training
We have created a new neural layer class based on ODE solver CNeuronNODEOCL. Let's add an object of this class to the architecture of the Encoder which we created in the previous article.
As always, the architecture of the models is specified in the CreateDescriptions method, in the parameters of which we pass pointers to 3 dynamic arrays to indicate the architecture of the models being created.
bool CreateDescriptions(CArrayObj *encoder, CArrayObj *actor, CArrayObj *critic) { //--- CLayerDescription *descr; //--- if(!encoder) { encoder = new CArrayObj(); if(!encoder) return false; } if(!actor) { actor = new CArrayObj(); if(!actor) return false; } if(!critic) { critic = new CArrayObj(); if(!critic) return false; }
In the method body, we check the received pointers and, if necessary, create new array objects.
We feed raw data describing the state of the environment into the Encoder model.
//--- Encoder encoder.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
The received data is preprocessed in the batch normalization layer.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = MathMax(1000, GPTBars); descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Next, we generate embeddings of the resulting states using an Embedding layer and a subsequent convolutional layer.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronEmbeddingOCL; { int temp[] = {prev_count}; ArrayCopy(descr.windows, temp); } prev_count = descr.count = GPTBars; int prev_wout = descr.window_out = EmbeddingSize / 2; if(!encoder.Add(descr)) { delete descr; return false; } //--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConvOCL; descr.count = prev_count; descr.step = descr.window = prev_wout; prev_wout = descr.window_out = EmbeddingSize; if(!encoder.Add(descr)) { delete descr; return false; }
The generated embeddings are supplemented with positional coding.
//--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronPEOCL; descr.count = prev_count; descr.window = prev_wout; if(!encoder.Add(descr)) { delete descr; return false; }
Then we use a complex, context-guided data analytics layer.
//--- layer 5 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronCCMROCL; descr.count = prev_count; descr.window = prev_wout; descr.window_out = EmbeddingSize; if(!encoder.Add(descr)) { delete descr; return false; }
Up to this point, we have completely repeated the model from the previous articles. But next, let's add 2 layers of a new class.
//--- layer 6 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronNODEOCL; descr.count = prev_count; descr.window = EmbeddingSize/4; descr.step = 4; if(!encoder.Add(descr)) { delete descr; return false; } //--- layer 7 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronNODEOCL; descr.count = prev_count; descr.window = EmbeddingSize/4; descr.step = 4; if(!encoder.Add(descr)) { delete descr; return false; }
The Actor and Critic models are copied from the previous article without changes. Therefore, we will not consider these models now.
Adding new layers does not affect the processes of interaction with the environment and model training. Consequently, all previous EAs are also used without changes. Again you can find the complete code of all programs in the attachment. We now move on to the next stage to test the work done.
3. Testing
We have considered a new family of models of Ordinary Differential Equations. Taking into account the proposed approaches, we implemented the new CNeuronNODEOCL class using MQL5 to organize the neural layer in our models. Now we are moving on to stage 3 of our work: training and testing models on real data in the MetaTrader 5 strategy tester.
As before, the models are trained and tested using historical data for EURUSD H1. We trained the models offline. For this purpose, we collected a training sample from various 500 trajectories based on historical data for the first 7 months of 2023. Most of the trajectories were collected by random passes. The share of profitable passes is quite small. In order to equalize the average profitability of passes during the training process, we use trajectory sampling with prioritization on their outcome. This allows assigning higher weights to profitable passes. This increases the probability of selecting such passes.
The trained models were tested in the strategy tester using historical data from August 2023, with the same symbol and timeframe. With this approach, we can evaluate the performance of the trained model on new data (not included in the training sample) while preserving the statistics of the training and testing datasets.
The testing results suggest that it is possible to learn strategies that generate profits both in the training and testing time periods. The screenshots of the tests are presented below.
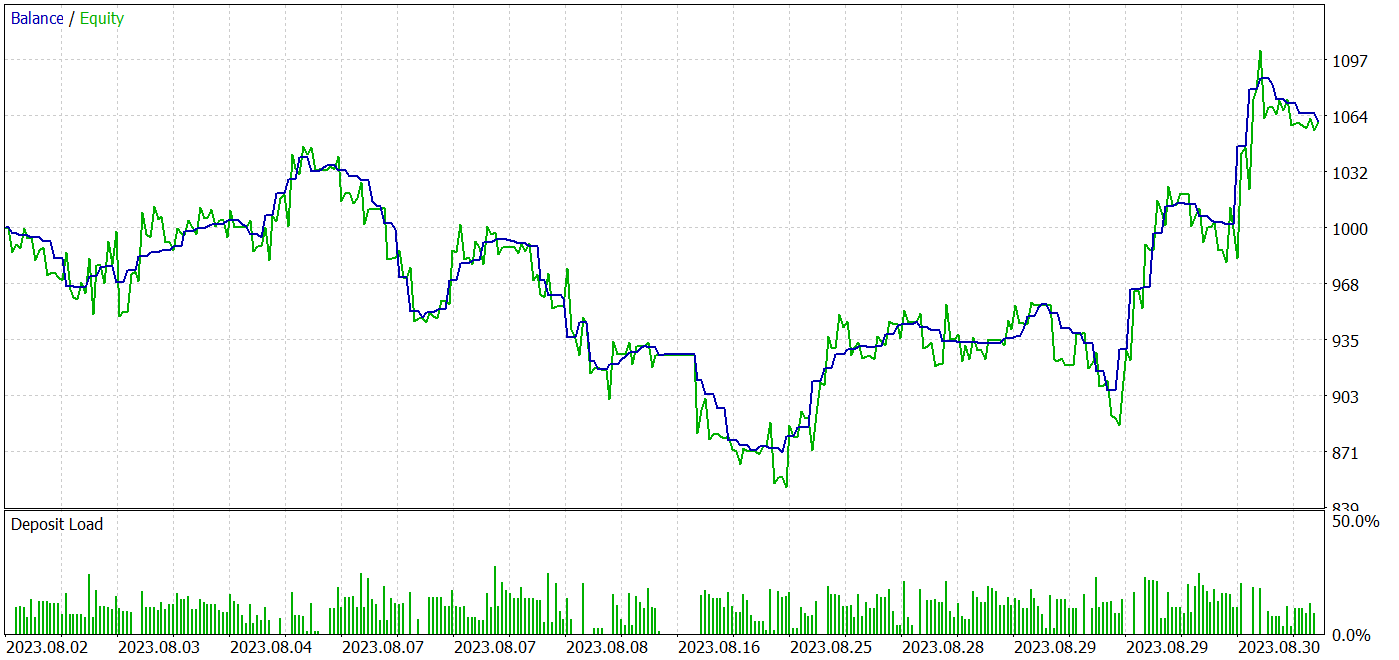
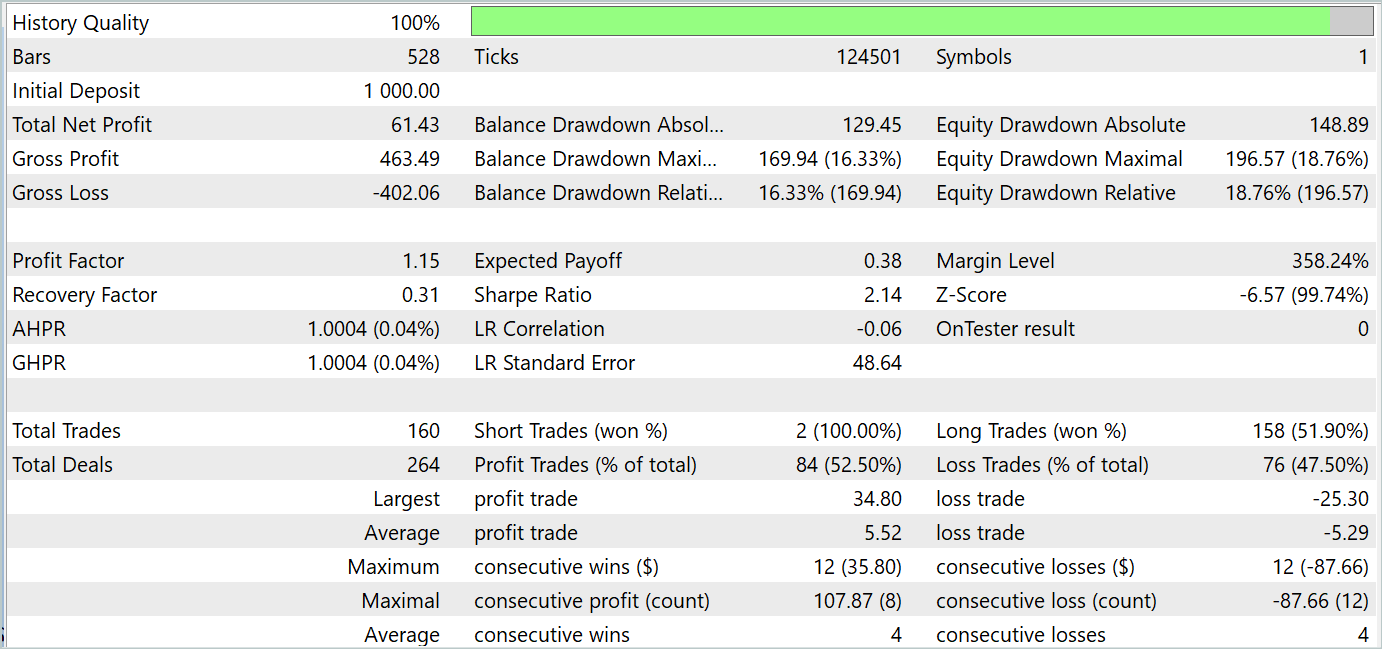
Based on the testing results for August 2023, the trained model made 160 trades, 84 of which were closed with a profit. This equals 52.5%. We can conclude that the trade parity has tilted slightly towards profit. The average profitable trade is 4% higher than the average losing trade. The average series of profitable trades is equal to the average series of losing ones. The maximum profitable series by the number of trades is equal to the maximum losing series by this parameter. However, the maximum profitable trade and the maximum profitable series in amount exceed similar variables of losing trades. As a result, during the testing period, the model showed a profit factor of 1.15 with a Sharpe ratio of 2.14.
Conclusion
In this article, we considered a new class of Ordinary Differential Equation (ODE) models. Using ODEs as components of machine learning models has a number of advantages and potentials. They allow you to model dynamic processes and changes in data, which is especially important for problems related to time series, system dynamics and forecasting. Neural ODEs can be successfully integrated into various neural network architectures, including deep and recurrent models, expanding the scope of these methods.
In the practical part of our article, we implemented the proposed approaches in MQL5. We trained and tested the model using real data in the MetaTrader 5 strategy tester. The testing results are presented above. They show the effectiveness of the proposed approaches to solving our problems.
However, let me remind you that all the programs presented in the article are of an informative nature and are intended only to demonstrate the proposed approaches.
References
Programs used in the article
| # | Name | Type | Description |
|---|---|---|---|
| 1 | Research.mq5 | EA | Example collection EA |
| 2 | ResearchRealORL.mq5 | EA | EA for collecting examples using the Real-ORL method |
| 3 | Study.mq5 | EA | Model training EA |
| 4 | Test.mq5 | EA | Model testing EA |
| 5 | Trajectory.mqh | Class library | System state description structure |
| 6 | NeuroNet.mqh | Class library | A library of classes for creating a neural network |
| 7 | NeuroNet.cl | Code Base | OpenCL program code library |
Translated from Russian by MetaQuotes Ltd.
Original article: https://www.mql5.com/ru/articles/14569
Warning: All rights to these materials are reserved by MetaQuotes Ltd. Copying or reprinting of these materials in whole or in part is prohibited.
This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.
 Time series clustering in causal inference
Time series clustering in causal inference
 MQL5 Wizard Techniques you should know (Part 30): Spotlight on Batch-Normalization in Machine Learning
MQL5 Wizard Techniques you should know (Part 30): Spotlight on Batch-Normalization in Machine Learning
 Implementing a Bollinger Bands Trading Strategy with MQL5: A Step-by-Step Guide
Implementing a Bollinger Bands Trading Strategy with MQL5: A Step-by-Step Guide
 Price-Driven CGI Model: Advanced Data Post-Processing and Implementation
Price-Driven CGI Model: Advanced Data Post-Processing and Implementation
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use