Funcionalidades do assistente MQL5 que você precisa conhecer (Parte 05): cadeias de Markov

Introdução

As cadeias de Markov são uma ferramenta matemática poderosa que pode ser usada para modelar e prever dados de séries temporais em vários campos, incluindo o financeiro. Na modelagem e previsão de séries temporais financeiras, as cadeias de Markov são frequentemente usadas para modelar a evolução de ativos financeiros ao longo do tempo, ativo esses como preços de ações ou pares de moedas. As principais vantagens dos modelos de cadeia de Markov são, entre outras, a simplicidade e a facilidade de uso. As cadeias de Markov se baseiam em um modelo probabilístico simples que descreve a evolução de um sistema ao longo do tempo e não requerem suposições matemáticas complexas ou suposições sobre as propriedades estatísticas dos dados. Isso as torna particularmente úteis para modelagem e previsão de dados de séries temporais financeiras, que podem ser muito complexas e apresentar comportamento não estacionário.

A modelagem de cadeias de Markov pode ser dividida em quatro tipos básicos: cadeias de Markov em tempo discreto, cadeias de Markov em tempo contínuo, modelos ocultos de Markov e modelos de Markov com mudança de estado. Os principais são as cadeias de Markov em tempo discreto, que são usadas para simular a evolução de um sistema em uma série de etapas de tempo discreto, e as cadeias de Markov em tempo contínuo, que são usadas para simular a evolução de um sistema em um intervalo de tempo contínuo. Ambos os tipos podem ser usados para modelar e prever dados financeiros de séries temporais.

A estimativa de probabilidade de um modelo de cadeia de Markov em dados de séries temporais financeiras pode ser realizada de diversas maneiras. Vou mencionar oito possíveis abordagens, sendo a maximização da expectativa a mais destacada delas. Este é o método implementado no ALGLIB.

Após estimar a probabilidade (ou os parâmetros de um modelo de cadeia de Markov), o modelo pode ser utilizado para prever estados ou eventos futuros. Por exemplo, no caso de séries temporais financeiras, um modelo de cadeia de Markov pode ser empregado para prever futuros preços de ações ou pares de moedas com base no estado atual do mercado e nas probabilidades de transição entre diferentes estados do mercado.

Modelagem de cadeias

Uma cadeia de Markov é um sistema matemático que realiza transições de um estado para outro de acordo com regras probabilísticas específicas. A característica definidora de uma cadeia de Markov é que, independentemente de como o sistema chegou ao seu estado atual, a probabilidade de transição para qualquer estado específico depende apenas do estado atual e do tempo decorrido. Uma cadeia de Markov pode ser representada usando um diagrama de estados, onde cada nó no diagrama representa um estado e as arestas entre os nós representam as transições entre os estados. A probabilidade de transição de um estado para outro é representada pelo peso da aresta correspondente.

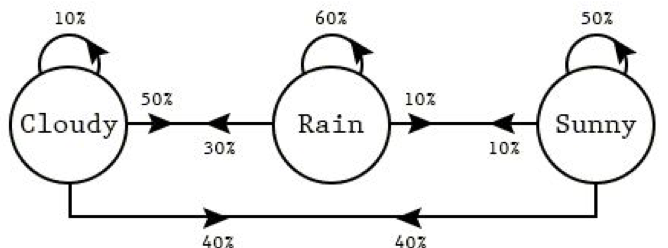
As setas no diagrama (cadeias de Markov) representam transições entre estados. A probabilidade de transição do estado 'rainy weather' (clima chuvoso) para o estado 'sunny weather' (clima ensolarado) pode ser representada pelo peso da aresta entre dois nós (neste caso, 0,1). O mesmo se aplica às outras transições. O mesmo se aplica às outras transições. 

Podemos usar esse diagrama de estados para modelar as probabilidades de transição entre estados em um sistema. O modelo que estamos criando é chamado de matriz estocástica.

Uma suposição importante da cadeia de Markov é que o comportamento futuro de um sistema depende apenas do estado atual e do tempo decorrido, e não do histórico passado do sistema. Isso é conhecido como a propriedade "sem memória" (sobre estados passados) de uma cadeia de Markov. Isso significa que a probabilidade de transição de um estado para outro é a mesma, independentemente de quantos estados intermediários o sistema possa percorrer para atingir seu estado atual.

As cadeias de Markov podem ser usadas para modelar uma ampla variedade de sistemas, incluindo sistemas financeiros, climáticos e biológicos. Elas são especialmente úteis para modelar sistemas que exibem dependências temporais, onde o estado atual do sistema depende de seus estados passados, como séries temporais.

As cadeias de Markov são amplamente utilizadas para modelar dados de séries temporais, que consistem em uma sequência de pontos de dados coletados em intervalos regulares. Dados de séries temporais podem ser encontrados em diversos campos, como finanças, economia, meteorologia e biologia.

Para usar uma cadeia de Markov na modelagem de dados de séries temporais, primeiro é necessário definir os estados do sistema e as transições entre eles. As probabilidades de transição de estado podem ser estimadas a partir dos dados utilizando métodos como a estimativa de máxima verossimilhança ou a maximização da expectativa. Depois de estimadas as probabilidades de transição, uma cadeia de Markov pode ser usada para prever estados ou eventos futuros com base no estado atual e no tempo decorrido.

As cadeias de Markov podem ser usadas para modelar dados de séries temporais de várias maneiras:

1. A cadeia de Markov em tempo discreto (discrete-time Markov chain) é um modelo matemático usado para descrever a evolução de um processo estocástico de tempo discreto ao longo de uma série de etapas de tempo. Ele pode ser usado para modelar uma sequência de eventos ou estados em que a probabilidade de transição para um determinado estado em um determinado momento depende apenas do estado atual. 

Aqui estão alguns exemplos de como uma cadeia de Markov em tempo discreto pode ser usada para modelar eventos diários:

• Previsão do tempo: Uma cadeia de Markov em tempo discreto pode ser usada para simular o clima diário em um local específico. Os estados da cadeia de Markov podem representar diferentes condições climáticas, como ensolarado, nublado, chuvoso ou com neve. As probabilidades de transição podem ser estimadas a partir de dados climáticos históricos, e uma cadeia de Markov pode ser usada para prever o clima do dia seguinte com base nas condições climáticas atuais.
• Movimentos de preços de ações: uma cadeia de Markov em tempo discreto pode ser usada para modelar os movimentos de preços diários de uma determinada ação. Os estados da cadeia de Markov podem representar diferentes níveis de movimento de preços, como ascendente, descendente ou nenhuma mudança. As probabilidades de transição podem ser estimadas com base nos dados históricos dos preços das ações, desse modo uma cadeia de Markov pode ser usada para prever a direção do preço das ações no dia seguinte com base no movimento atual dos preços.
• Padrões de tráfego: A cadeia de Markov em tempo discreto pode ser usada para simular padrões de tráfego diários em uma determinada estrada ou rodovia. Os estados da cadeia de Markov podem representar diferentes níveis de tráfego, como leve, médio ou pesado. As probabilidades de transição podem ser estimadas com base em dados históricos de tráfego, e uma cadeia de Markov pode ser usada para prever o nível de tráfego do dia seguinte com base no atual.

2. Cadeia de Markov em tempo contínuo (continuous-time Markov chain): aqui as transições entre os estados ocorrem continuamente, não em intervalos de tempo discretos. Isso significa que a probabilidade de uma transição de um estado para outro depende do tempo decorrido desde a última transição. As cadeias de Markov em tempo contínuo são comumente usadas para modelar sistemas que mudam continuamente ao longo de vários períodos de tempo, como o fluxo de tráfego em uma rodovia específica ou a taxa de reações químicas em uma fábrica de produtos químicos. Uma das principais diferenças entre cadeias de Markov em tempo discreto e em tempo contínuo é que as probabilidades de transição nas cadeias de Markov em tempo contínuo são caracterizadas por taxas de transição, que são a probabilidade de transição de um estado para outro na unidade de tempo. Essas taxas de transição são usadas para calcular a probabilidade de uma transição de um estado para outro dentro de um determinado intervalo de tempo.

3. O modelo oculto de Markov (Hidden Markov model, HMM) é um modelo estatístico no qual os estados de um sistema não são diretamente observáveis, mas inferidos a partir de uma sequência de observações. Aqui estão alguns exemplos de como um modelo oculto de Markov pode ser usado para modelar eventos cotidianos:

   • Reconhecimento de fala. O Modelo Oculto de Markov pode ser usado para modelar sons produzidos durante a fala e para reconhecer palavras faladas. Nesse caso, os estados do HMM podem representar diferentes fonemas (sons da fala) e as observações podem ser uma sequência de ondas sonoras representando palavras faladas. Com um grande conjunto de dados de palavras faladas e suas ondas sonoras correspondentes, o HMM pode ser treinado para reconhecer novas palavras faladas, determinando a sequência mais provável de fonemas com base nas ondas sonoras observadas.
   • Reconhecimento de caligrafia. O Modelo Oculto de Markov pode ser usado para modelar sequências de traços e reconhecer palavras manuscritas. Nesse caso, os estados do HMM podem ser traços diferentes e as observações podem ser uma sequência de imagens de palavras manuscritas. Com um grande conjunto de dados de palavras manuscritas e suas imagens correspondentes, o HMM pode ser treinado para reconhecer novas palavras manuscritas, determinando a sequência de traços mais provável com base nas imagens observadas.
   • Reconhecimento da atividade. O modelo oculto de Markov pode ser usado para reconhecer a atividade humana com base em uma sequência de observações, como leituras de sensores ou quadros de vídeo. Por exemplo, para reconhecer atividades como caminhar, correr ou pular.

4. O modelo de Markov com mudança de estado (Markov switching model, MSM) é um tipo de cadeia de Markov na qual os estados de um sistema podem mudar ao longo do tempo ou "alternar" dependendo de certas condições. Aqui estão alguns exemplos de como o modelo de Markov com mudança de estado pode ser usado para modelar eventos cotidianos:

   • Comportamento do consumidor. Para modelar o comportamento de compra dos consumidores, é possível utilizar o modelo de Markov com mudança de estado. Os estados no modelo podem representar diferentes tipos de comportamento de compra, como compras frequentes ou infrequentes. As transições entre estados podem ser baseadas em condições específicas, como mudança na renda ou introdução de novos produtos. Esse modelo pode ser usado para prever o comportamento de compra futuro com base no estado atual e nas probabilidades de transição entre estados.
   • Indicadores econômicos. Um modelo de Markov com mudança de estado pode ser aplicado na modelagem de indicadores econômicos, como o PIB ou a taxa de desemprego. Os estados no modelo podem representar diferentes condições econômicas, como expansão ou recessão, e as transições entre estados podem ser baseadas em condições específicas, como mudanças na política monetária ou no ciclo de negócios. O modelo pode ser usado para prever condições econômicas futuras com base no estado atual e nas probabilidades de transição entre estados.
   • Padrões de tráfego. Um modelo de Markov com mudança de estado pode ser empregado para simular padrões de tráfego em uma determinada estrada ou rodovia. Os estados no modelo podem representar diferentes níveis de congestionamento, como tráfego leve, médio ou pesado, e as transições entre estados podem ser baseadas em condições específicas, como hora do dia ou dia da semana. O modelo pode ser usado para prever padrões de tráfego futuros com base no estado atual e nas probabilidades de transição entre estados.

   
   

Assim como qualquer hipótese, ela sempre se baseia em suposições que, em geral, impõem certas limitações à ideia. As cadeias de Markov não são exceção. Aqui estão algumas das suposições:

1. Estacionaridade. Uma das suposições básicas de uma cadeia de Markov é que as probabilidades de transição entre os estados são constantes ao longo do tempo. Essa suposição é conhecida como estacionaridade.

2. Propriedade de Markov. Outra suposição da cadeia de Markov é que a evolução futura do sistema depende apenas do estado atual e do tempo decorrido, não dependendo do histórico passado do sistema além do estado atual. Essa suposição nem sempre pode ser válida na prática, especialmente para conjuntos de dados com dependências complexas ou memória de longo prazo.

3. Espaço de estados finitos: Uma cadeia de Markov geralmente é definida em um espaço de estados finitos, o que significa que há um número finito de estados possíveis nos quais o sistema pode estar. Isso pode não ser adequado para conjuntos de dados com muitos estados ou variáveis contínuas.

4. Homogeneidade no tempo. Uma cadeia de Markov é geralmente considerada homogênea no tempo, o que significa que as probabilidades de transição entre os estados não dependem do tempo específico em que a transição ocorre. Se as probabilidades de transição dependerem do momento em que a transição ocorre, o modelo da cadeia de Markov pode ser impreciso.

5. Ergodicidade. Uma cadeia de Markov é geralmente considerada ergódica, o que significa que é possível alcançar qualquer estado a partir de qualquer outro estado em um número finito de etapas. Se essa suposição não for atendida, o modelo da cadeia de Markov pode ser impreciso.

Em geral, os modelos de cadeia de Markov são mais adequados para conjuntos de dados com dependências relativamente simples e poucos estados ou variáveis. Se o conjunto de dados tiver dependências complexas ou um grande número de estados ou variáveis, outras técnicas de modelagem podem ser mais apropriadas.

Avaliação de probabilidade

Após modelar a cadeia de Markov, precisamos estimar as probabilidades de transição de cada estado. Há uma série de métodos que podem ser usados. Será útil revisá-los para entender melhor o escopo e as capacidades das cadeias de Markov. Existem vários métodos para estimar as probabilidades de transição entre estados em cadeias de Markov, incluindo:

1. Máxima verossimilhança (maximum likelihood estimation, MLE): O objetivo é estimar a probabilidade de um evento ou sequência de eventos com base em dados observados. No contexto das cadeias de Markov, isso significa que queremos estimar a probabilidade de uma transição de um estado para outro com base em um conjunto de transições observadas.

   Para implementar o MLE para cadeias de Markov, primeiro precisamos coletar um conjunto de transições observáveis. Isso pode ser feito executando uma simulação ou coletando dados reais. Uma vez que tenhamos as transições observadas, podemos usá-las para estimar as probabilidades de transição.

   Para estimar as probabilidades de transição, podemos usar os seguintes passos:

   • Especifique uma matriz para armazenar as probabilidades de transição. A matriz deve ter dimensões num_states x num_states, onde num_states é o número de estados na cadeia de Markov.
   • Inicialize a matriz com todas as probabilidades definidas como 0. Isso pode ser feito com um loop aninhado que itera sobre todos os elementos da matriz.
   • Repita as transições observadas e atualize as probabilidades de transição. Para cada transição observada do estado i para o estado j, aumente a probabilidade de transição_probs[i][j] em 1.
   • Normalize as probabilidades de transição de modo que sua soma seja igual a 1. Isso pode ser feito dividindo cada elemento da matriz pela soma dos elementos na linha correspondente.

   
   

   Uma vez estimadas as probabilidades de transição, podemos usá-las para prever a probabilidade de transição de um estado para outro. Por exemplo, se quisermos prever a probabilidade de uma transição do estado i para o estado j, podemos usar a fórmula P(j | i) = transition_probs[i][j].

2. Probabilidade Bayesiana: envolve o uso do teorema de Bayes para atualizar a distribuição de probabilidade dos parâmetros do modelo com base em novos dados. Para usar a estimativa de probabilidade bayesiana com uma cadeia de Markov, primeiro precisamos definir uma distribuição a priori sobre os estados da cadeia de Markov. Essa distribuição a priori representa nossa opinião inicial sobre as probabilidades dos vários estados da cadeia. Podemos então usar a atualização bayesiana para atualizar nossa compreensão das probabilidades de estado à medida que novas informações se tornam disponíveis. Por exemplo, suponha que temos uma cadeia de Markov de três estados: A, B e C. Começamos com um estado anterior, que pode ser representado como:

   P(A) = 0,4 P(B) = 0,3 P(C) = 0,3

   Isso significa que inicialmente assumimos que a probabilidade de estar no estado A é de 40%, a probabilidade de estar no estado B é de 30% e a probabilidade de estar no estado C é de 30%.

   Agora suponha que estamos observando o sistema passar do estado A para o estado B. Podemos usar essa nova informação para atualizar nosso entendimento das probabilidades de estado com uma estimativa de probabilidade bayesiana. Para fazer isso, precisamos conhecer as probabilidades de transição entre os estados. Suponha que as probabilidades de transição sejam:

   P(A -> B) = 0,8 

   P(A -> C) = 0,2 

   P(B -> A) = 0,1 

   P(B -> B) = 0,7 

   P(B -> C) = 0,2 

   P(C -> A) = 0,2 

   P(C -> B) = 0,3 

   P(C -> C) = 0,5

   Essas probabilidades de transição nos dizem a probabilidade de transição de um estado para outro. Por exemplo, a probabilidade de transição do estado A para o estado B é 0,8 e a probabilidade de transição do estado A para o estado C é 0,2.

   Usando essas probabilidades de transição, agora podemos atualizar nossa compreensão das probabilidades de estado usando a estimativa de probabilidade bayesiana. Em particular, podemos usar a regra de Bayes para calcular a distribuição posterior sobre os estados, dada a nova informação de que o sistema passou do estado A para o estado B. Essa distribuição posterior é nossa representação atualizada das probabilidades do estado, dada a nova informação que recebemos. .

   Por exemplo, usando a regra de Bayes, podemos calcular a probabilidade posterior de estar no estado A da seguinte forma:

   P(A | A -> B) = P(A -> B | A) * P(A) / P(A -> B)

   Substituindo valores de nossa distribuição anterior e probabilidade de transição, obtemos:

   P(A | A -> B) = (0,8 * 0,4) / (0,8 * 0,4 + 0,1 * 0,3 + 0,2 * 0,3) = 0,36

   Da mesma forma, podemos calcular as probabilidades posteriores de estar nos estados B e C:

   P(B | A -> B) = (0,1 * 0,3) / (0,8 * 0,4 + 0,1 * 0,3 + 0,2 * 0,3) = 0,09

3. Algoritmo de maximização de expectativa (Expectation-maximization, EM). Para usar o EM para estimar a probabilidade com uma cadeia de Markov, é necessário observar as transições entre os estados da cadeia de Markov durante um período específico de tempo. Com base nesses dados, podemos utilizar o algoritmo EM para estimar as probabilidades de transição, aprimorando de forma iterativa nossas estimativas com base nos dados observados. O algoritmo EM funciona alternando duas etapas: uma etapa de expectativa (E-step) e uma etapa de maximização (M-step). Na etapa E, estimamos o valor esperado do logaritmo da probabilidade total dos dados, considerando as estimativas atuais dos parâmetros. Na etapa M, maximizamos o valor esperado do logaritmo da verossimilhança total dos dados em relação aos parâmetros para obter estimativas atualizadas dos parâmetros. Em seguida, repetimos essas etapas até que as estimativas dos parâmetros convirjam para um valor estável. Por exemplo, se você observou uma cadeia de Markov com três estados (A, B e C) e deseja estimar as probabilidades de transição entre os estados, pode usar o algoritmo EM para refinar iterativamente suas estimativas de probabilidade de transição com base nos dados observados.

   A principal vantagem de usar o EM para estimativa de probabilidade é que o algoritmo pode lidar com dados incompletos ou ruidosos e pode estimar os parâmetros do modelo estatístico mesmo se a distribuição subjacente não for totalmente conhecida. No entanto, o algoritmo pode ser sensível à inicialização e nem sempre pode convergir para o máximo global da função de verossimilhança logarítmica. Além disso, requer recursos computacionais significativos, pois envolve avaliações múltiplas da função de log-verossimilhança e seu gradiente.

4. Avaliação paramétrica. Para utilizar a estimativa de probabilidade paramétrica com uma cadeia de Markov, é necessário observar as transições entre os estados da cadeia de Markov durante um período específico de tempo. Com base nesses dados, é possível ajustar um modelo paramétrico às probabilidades de transição, assumindo que a distribuição subjacente segue uma distribuição específica, como a distribuição normal ou a distribuição binomial. Podemos então usar esse modelo para estimar a probabilidade de transição de um estado para outro. Por exemplo, se observarmos uma cadeia de Markov com três estados (A, B e C) e descobrirmos que a transição do estado A para o estado B ocorreu 10 vezes em 20 transições, poderíamos ajustar um modelo binomial aos dados e usá-lo para estimar a probabilidade de transição do estado A para o estado B.

   A principal vantagem da estimativa de probabilidade paramétrica é que ela pode ser mais precisa do que os métodos não paramétricos, que não fazem suposições sobre a distribuição subjacente. No entanto, isso requer fazer suposições sobre a distribuição subjacente, que nem sempre são adequadas ou podem levar a estimativas enviesadas. Além disso, os métodos paramétricos podem ser menos flexíveis e menos confiáveis do que os métodos não paramétricos, pois são sensíveis a desvios da distribuição esperada.

5. Estimativa não paramétrica. Para utilizar a estimativa de probabilidade não paramétrica com uma cadeia de Markov, é necessário observar as transições entre os estados da cadeia de Markov durante um período específico de tempo. A partir desses dados, pode-se estimar a probabilidade de transição de um estado para outro, contando o número de vezes que a transição ocorreu e dividindo-o pelo número total de transições. Por exemplo, se observarmos uma cadeia de Markov com três estados (A, B e C) e descobrirmos que a transição do estado A para o estado B ocorreu 10 vezes em 20 transições, poderíamos estimar a probabilidade de transição do estado A para o estado B como 0,5.

   Esse método de estimativa de probabilidade é chamado de método de distribuição empírica e pode ser usado para estimar a probabilidade de qualquer conjunto de eventos, não apenas transições em uma cadeia de Markov. A principal vantagem da estimativa de probabilidade não paramétrica é que ela não requer suposições sobre a distribuição subjacente, tornando-a um método flexível e confiável para estimar probabilidades. No entanto, pode ser menos preciso do que os métodos paramétricos, que fazem suposições sobre a distribuição subjacente para obter estimativas de probabilidades mais precisas.

6. Bootstrapping. Este é um método geral que pode ser usado para estimar probabilidades em uma cadeia de Markov ou qualquer outro modelo probabilístico. A ideia básica consiste em utilizar um pequeno número de observações para estimar a distribuição de probabilidade dos estados do sistema e, em seguida, usar essa distribuição para criar um grande número de observações sintéticas. As observações sintéticas podem ser utilizadas para estimar com maior precisão a distribuição de probabilidade. O processo pode ser repetido até que o nível de precisão desejado seja alcançado.

   Para utilizar o bootstrapping para estimar probabilidades em uma cadeia de Markov, primeiro precisamos de uma cadeia de Markov inicial com seus estados. Semelhante ao método bayesiano, o bootstrapping atualiza e aprimora as cadeias de Markov existentes. Cada estado na cadeia está associado à probabilidade de transição para outros estados, e as probabilidades de transição entre diferentes pares de estados não dependem do histórico do sistema. Quando você possui a cadeia de Markov original, é possível utilizar o bootstrapping para estimar a distribuição de probabilidade de seus estados. Isso requer começar com um pequeno número de observações do sistema, como algumas configurações iniciais de estado ou uma curta sequência de transições de estado. Em seguida, essas observações podem ser utilizadas para estimar a distribuição de probabilidade dos estados do sistema.

   Por exemplo, se você tem uma cadeia de Markov com três estados A, B e C, e observou várias vezes a transição do sistema do estado A para o estado B e várias vezes do estado B para o estado C, você pode utilizar essas observações para estimar a probabilidade de transição do estado A para o estado B e do estado B para o estado C.

   Após estimar a distribuição de probabilidade dos estados do sistema, você pode utilizá-la para gerar um grande número de observações sintéticas do sistema. Isso pode ser feito através de amostragem aleatória da distribuição de probabilidade para simular transições entre os estados. Em seguida, as observações sintéticas podem ser usadas para estimar com maior precisão a distribuição de probabilidade e repetir o processo até que o nível de precisão desejado seja alcançado.

   O bootstrapping pode ser útil para estimar probabilidades em uma cadeia de Markov, pois permite usar um pequeno número de observações para criar um grande número de observações sintéticas, melhorando a precisão das estimativas. Além disso, é relativamente simples de implementar e pode ser aplicado a diversos modelos probabilísticos. No entanto, a precisão das estimativas obtidas com o bootstrapping depende da qualidade das observações iniciais e do modelo probabilístico subjacente. Em alguns casos, a precisão deste método pode ser inferior à de outros métodos de estimativa.

7. Método de reamostragem (Jackknife estimation). Este método realiza várias simulações de cadeias de Markov, excluindo a cada vez um estado diferente ou grupo de estados. A probabilidade de ocorrência de um evento é então estimada pela média das probabilidades do evento ocorrer em cada uma das simulações. A seguir, apresentamos uma explicação mais detalhada do processo:
   • Configure uma cadeia de Markov e defina o evento de interesse. Por exemplo, o evento pode ser alcançar um determinado estado na cadeia ou a transição entre dois estados específicos.
   • Realize várias simulações da cadeia de Markov, excluindo um estado diferente ou grupo de estados a cada vez. Isso pode ser feito simplesmente não considerando os estados excluídos ao executar a simulação ou definindo suas probabilidades de transição como zero.
   • Para cada simulação, calcule a probabilidade de ocorrência do evento. Isso pode ser feito realizando uma análise detalhada do equilíbrio ou usando métodos como amostragem de Monte Carlo ou multiplicação de matrizes.
   • Calcule a média das probabilidades do evento ocorrer em cada uma das simulações para obter uma estimativa da probabilidade do evento ocorrer na cadeia de Markov completa.

   Utilizar o método jackknife para estimar probabilidades em cadeias de Markov apresenta várias vantagens. Uma das vantagens é que ele permite estimar com maior precisão a probabilidade de um evento ocorrer, levando em consideração o impacto de cada estado individual na probabilidade geral. Outra vantagem é que ele é relativamente simples de implementar e pode ser facilmente automatizado. No entanto, o método jackknife também possui algumas limitações. Uma das limitações é que requer a realização de várias simulações de cadeias de Markov, o que pode exigir recursos computacionais significativos para cadeias grandes ou complexas. Além disso, a precisão da estimativa pode depender da quantidade e escolha dos estados excluídos durante a simulação.

8. Validação cruzada (cross-validation). Este método pode ser usado para estimar a probabilidade de um evento específico ocorrer em uma cadeia de Markov. Ele envolve dividir os dados em várias dobras ou subconjuntos e utilizar cada dobra como um conjunto de teste para avaliar o desempenho do modelo nesse subconjunto. Para aplicar a estimativa de probabilidade por validação cruzada com cadeias de Markov, primeiro precisamos configurar a cadeia de Markov com os estados e transições desejados Em seguida, dividimos os dados no número desejado de dobras. Depois, iteramos por cada dobra e a utilizamos como um conjunto de teste para avaliar o desempenho do modelo nesse subconjunto. Este processo envolve usar a cadeia de Markov para estimar a probabilidade de cada evento ocorrer no conjunto de teste e comparar essas estimativas com os resultados reais no conjunto de teste.

   Por fim, fazemos a média do desempenho em todas as dobras para obter uma estimativa geral do desempenho do modelo. Isso pode ser útil para avaliar o desempenho do modelo e ajustar os parâmetros da cadeia de Markov a fim de melhorar sua precisão. Para utilizar a estimativa de probabilidade por validação cruzada com cadeias de Markov, os dados devem ser independentes e identicamente distribuídos, o que significa que cada subconjunto de dados deve representar adequadamente o conjunto de dados completo.

Cada um desses métodos tem seus próprios pontos fortes e limitações, e a escolha do método dependerá das características específicas dos dados e dos objetivos da análise. 

Implementação usando o assistente MQL5

Para codificar uma classe de sinais que implemente cadeias de Markov, utilizamos a classe CMarkovCPD no arquivo dataanalysis.mqh na pasta alglib. Vamos modelar cadeias com tempo discreto. Uma cadeia de tempo discreto terá cinco estados, que correspondem às últimas cinco variações no preço de fechamento. Dessa forma, o período no qual o Expert Advisor é testado ou operado determinará a unidade de tempo discreta. Para estimar as probabilidades de transição entre os estados, a classe CMarkovCPD requer a inclusão de dados de rastreamento para treinar o modelo. A quantidade de dados de rastreamento a serem adicionados é determinada pelo parâmetro de entrada otimizável m_signal_tracks. A seguir, apresentamos como inicializar o modelo e adicionar dados de rastreamento (treinamento).

      CMCPDState _s;
      CMatrixDouble _xy,_p;
      CMCPDReport _rep;
      int _k=m_signal_tracks;
      
      _xy.Resize(m_signal_tracks,__S_STATES);
      
      m_close.Refresh(-1);
      
      for(int t=0;t<m_signal_tracks;t++)
      {
         for(int s=0;s<__S_STATES;s++)
         {
            _xy[t].Set(s,GetState(Close(Index+t+s)-Close(Index+t+s+1),Close(Index+t+s+1)-Close(Index+t+s+2)));
         }
      }

Os dados de preço de fechamento são normalizados em 1,0. Se a variação do preço de fechamento for negativa, o valor de entrada será menor que 1,0; se for positiva, o valor de entrada será maior que 1,0, sem alterações que resultem exatamente em 1,0. Essa normalização é realizada utilizando a função GetState, mostrada abaixo.

//+------------------------------------------------------------------+
//| Normalizer.                                                      |
//+------------------------------------------------------------------+
double CSignalMC::GetState(double NewChange,double OldChange)
   {
      double _state=0.0;
      
      double _norm=fabs(NewChange)/fmax(m_symbol.Point(),fabs(NewChange)+fabs(OldChange));
      
      if(NewChange>0.0)
      {
         _state=_norm+1.0;
      }
      else if(NewChange<0.0)
      {
         _state=1.0-_norm;
      }
      
      return(_state);
   }

Depois de adicionar os dados, precisamos inicializar uma instância da classe CMCPDState, pois esse é o objeto que trata todos os dados do nosso modelo e ajuda no cálculo das estimativas de probabilidade. Fazemos assim:

      CPD.MCPDCreate(__S_STATES,_s);
      
      CPD.MCPDAddTrack(_s,_xy,_k);
      
      CPD.MCPDSetTikhonovRegularizer(_s,m_signal_regulizer);
      
      CPD.MCPDSolve(_s);
      
      CPD.MCPDResults(_s,_p,_rep);

Idealmente, o parâmetro de entrada m_signal_regulazier não deve ser um valor duplo abstrato, mas um valor duplo que representa a quantidade de dados de rastreamento. Em outras palavras, deve ser proporcional aos dados de rastreamentorecebidos da função GetState. Isso significa que se você quiser otimizá-lo perfeitamente, digamos no intervalo de 0,5-0,0, você deve multiplicá-lo pela magnitude dos maiores dados de rastreamento ao usar o método de regularização de Tikhonov. 

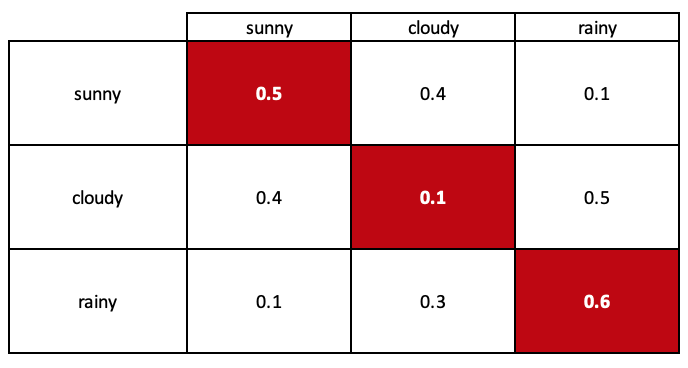
A matriz '_p' é a nossa matriz de transição com todas as probabilidades de transição entre os estados. Todo código de classe de sinal está anexado abaixo.

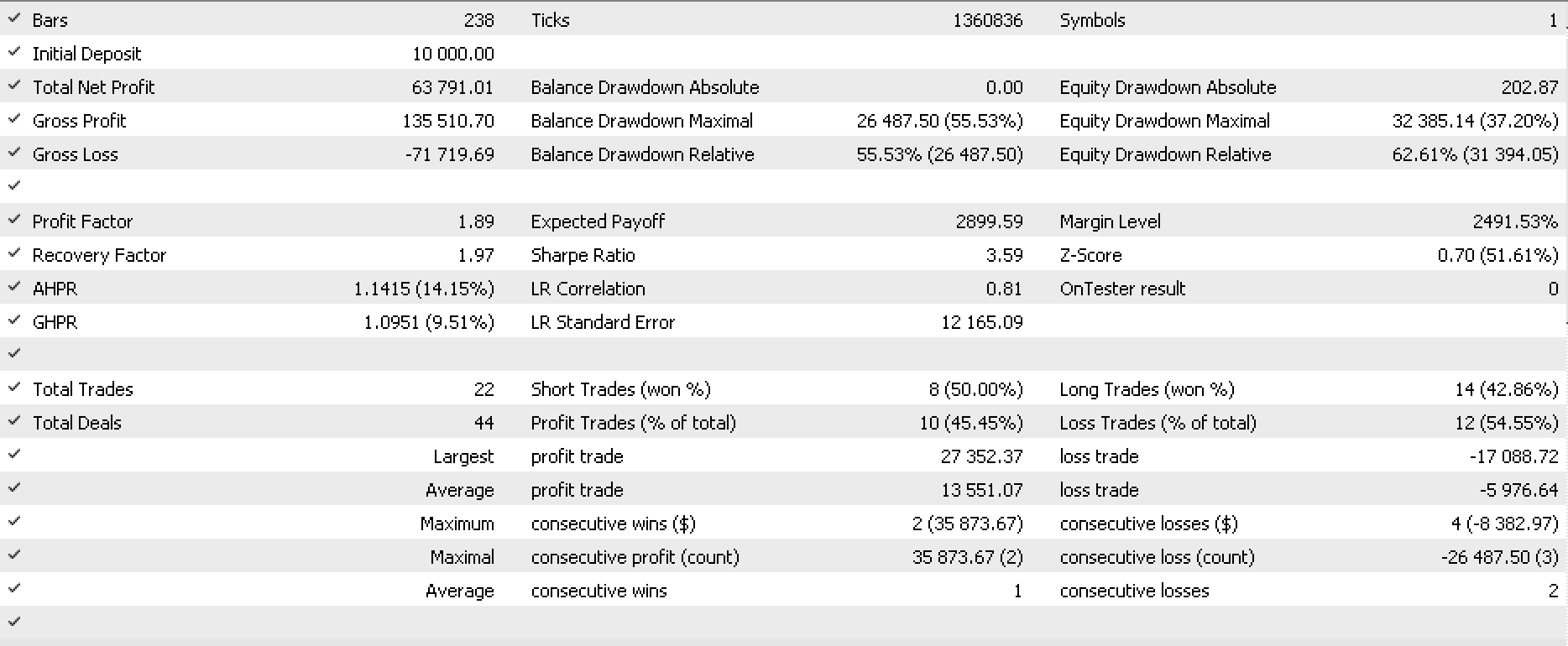
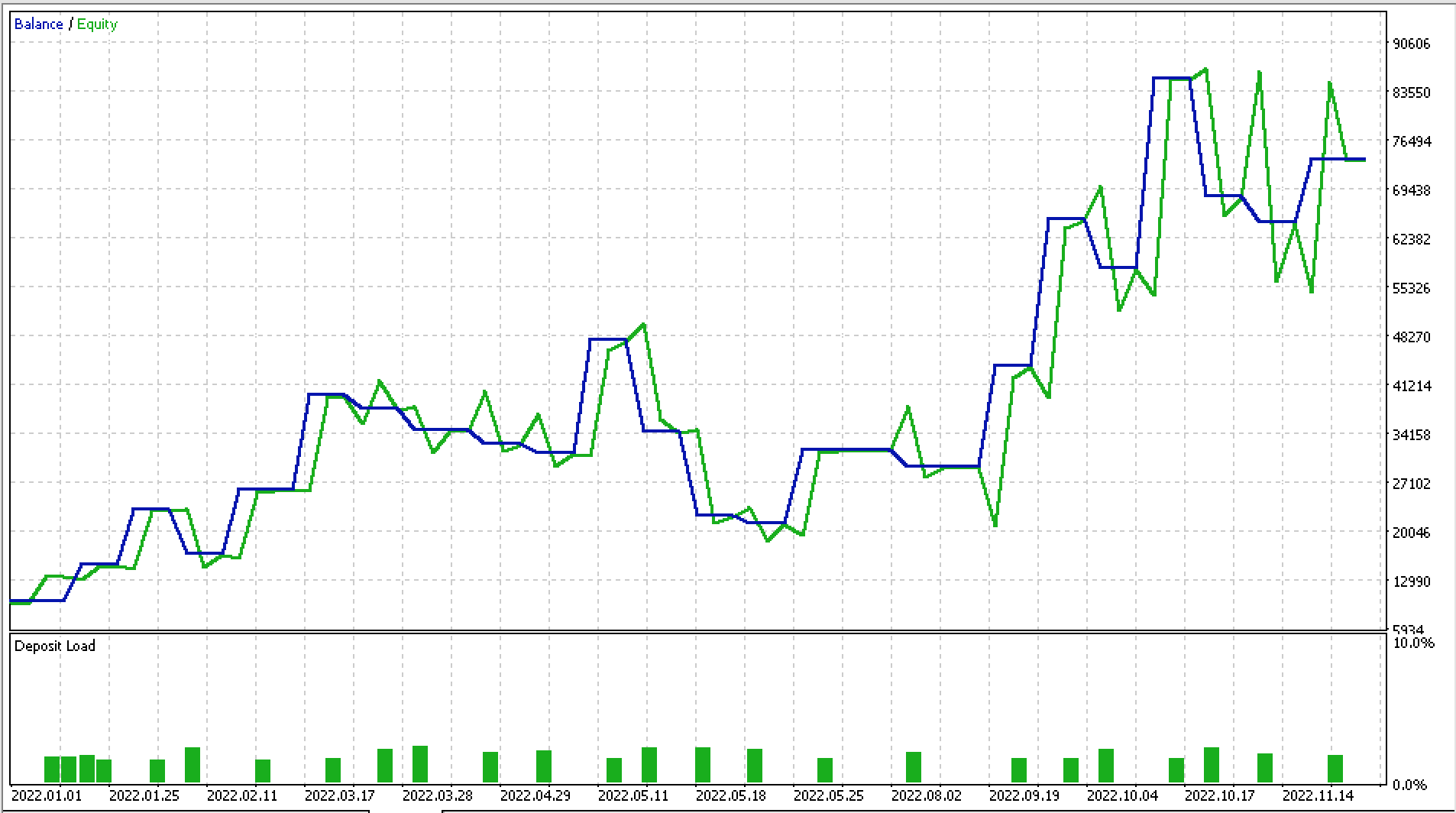
Fiz alguns testes com EURJPY D1 para 2022. Abaixo está uma parte do relatório e a curva de capital liquido.

Considerações finais

As cadeias de Markov são uma ferramenta matemática que podem ser utilizadas para modelar o comportamento dos mercados financeiros. Elas são especialmente úteis porque permitem que os traders analisem a probabilidade de futuros estados do mercado com base no estado atual do mercado. Isso pode ser extremamente vantajoso na negociação, uma vez que possibilita aos traders tomar decisões fundamentadas sobre quais operações realizar e em que momento fazê-las.

Um dos principais benefícios do uso das cadeias de Markov nos mercados financeiros é que elas possibilitam aos traders analisar e prever a evolução das tendências do mercado ao longo do tempo. Isso é especialmente relevante em mercados que mudam rapidamente, onde as tendências podem se alterar com rapidez e é difícil prever como o mercado se comportará. Ao utilizar cadeias de Markov, os traders podem determinar os caminhos mais prováveis que o mercado seguirá e usar essas informações para tomar decisões comerciais embasadas.

Outra vantagem das cadeias de Markov é a possibilidade de utilizá-las para analisar os riscos associados a diferentes negociações. Ao examinar as probabilidades de diferentes estados do mercado, os traders podem determinar o risco associado a diferentes operações e escolher aquelas que têm maior probabilidade de sucesso. Isso pode ser especialmente útil em mercados voláteis, onde o risco de perdas é maior.

Em resumo, as cadeias de Markov são uma ferramenta importante para os operadores nos mercados financeiros, pois permitem que analisem e prevejam o comportamento do mercado, determinem os caminhos mais prováveis que o mercado seguirá e avaliem o risco associado às negociações