Возможности Мастера MQL5, которые вам нужно знать (Часть 5): Цепи Маркова

Введение

Цепи Маркова представляют собой мощный математический инструмент, который можно использовать для моделирования и прогнозирования данных временных рядов в различных областях, включая финансы. При моделировании и прогнозировании финансовых временных рядов цепи Маркова часто используются для моделирования эволюции финансовых активов с течением времени, таких как цены акций или обменные курсы. Основными преимуществами моделей цепей Маркова являются, помимо прочего, их простота и удобство использования. Цепи Маркова основаны на простой вероятностной модели, описывающей эволюцию системы во времени, и не требуют сложных математических допущений или предположений о статистических свойствах данных. Это делает их особенно полезными для моделирования и прогнозирования данных финансовых временных рядов, которые могут быть очень сложными и демонстрировать нестационарное поведение.

Моделирование цепей Маркова можно разделить на четыре основных типа: цепи Маркова с дискретным временем, цепи Маркова с непрерывным временем, скрытые модели Маркова и модели Маркова с переключением. Основными среди них являются цепи Маркова с дискретным временем, которые используются для моделирования эволюции системы в течение ряда дискретных временных шагов, и цепи Маркова с непрерывным временем, которые используются для моделирования эволюции системы в течение непрерывного интервала времени. Оба типа могут использоваться для моделирования и прогнозирования данных финансовых временных рядов.

Оценка вероятности для модели цепи Маркова по данным финансовых временных рядов может быть выполнена несколькими способами. Я упомяну восемь возможных способов, наиболее заметным из которых является максимизация ожидания. Это метод, реализованный в ALGLIB.

После оценки вероятности (или параметров модели цепи Маркова) модель можно использовать для прогнозирования будущих состояний или событий. Например, в случае финансовых временных рядов модель цепи Маркова может использоваться для прогнозирования будущих цен на акции или обменных курсов на основе текущего состояния рынка и вероятностей перехода между различными состояниями рынка.

Моделирование цепей

Цепь Маркова — это математическая система, которая совершает переходы из одного состояния в другое по определенным вероятностным правилам. Определяющей характеристикой цепи Маркова является то, что независимо от того, как система пришла в свое текущее состояние, вероятность перехода в любое конкретное состояние зависит исключительно от текущего состояния и прошедшего времени. Цепь Маркова может быть представлена с помощью диаграммы состояний, где каждый узел на диаграмме представляет состояние, а ребра между узлами представляют переходы между состояниями. Вероятность перехода из одного состояния в другое представлена весом соответствующего ребра.

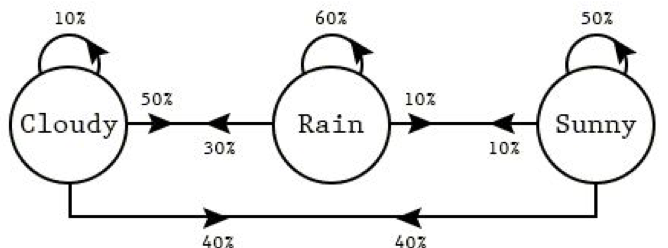
Стрелки на диаграмме (цепи Маркова) представляют собой переходы между состояниями. Вероятность перехода из состояния 'rainy weather' (дождь) к состоянию 'sunny weather' (солнечно) может быть представлено весом ребра между двумя узлами (в данном случае 0,1). Для других переходов аналогично. 

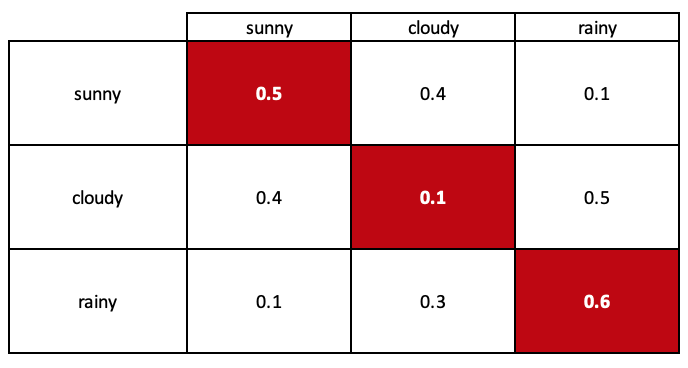
Мы можем использовать эту диаграмму состояний для моделирования вероятностей перехода между состояниями в системе. Модель, которую мы создаем, называется стохастической матрицей.

Одно важное предположение цепи Маркова состоит в том, что будущее поведение системы зависит только от текущего состояния и прошедшего времени, а не от прошлой истории системы. Это известно как свойство цепи Маркова «без памяти» (о прошлых состояниях). Это означает, что вероятность перехода из одного состояния в другое одинакова независимо от того, сколько промежуточных состояний может пройти система, чтобы достичь своего текущего состояния.

Цепи Маркова можно использовать для моделирования самых разных систем, включая финансовые, погодные и биологические. Они особенно полезны для моделирования систем, демонстрирующих временные зависимости, когда текущее состояние системы зависит от ее прошлых состояний, таких как временные ряды.

Цепи Маркова широко используются для моделирования данных временных рядов, которые представляют собой ряд точек данных, собираемых через равные промежутки времени. Данные временных рядов можно найти во многих областях, таких как финансы, экономика, метеорология и биология.

Чтобы использовать цепь Маркова для моделирования данных временных рядов, сначала необходимо определить состояния системы и переходы между ними. Вероятности перехода между состояниями можно оценить по данным с использованием таких методов, как оценка максимального правдоподобия или максимизация ожидания. После того как вероятности перехода были оценены, цепь Маркова можно использовать для прогнозирования будущих состояний или событий на основе текущего состояния и прошедшего времени.

Цепи Маркова можно использовать для моделирования данных временных рядов несколькими способами:

1. Цепь Маркова с дискретным временем (discrete-time Markov chain) - математическая модель, используемая для описания эволюции стохастического процесса с дискретным временем в течение ряда временных шагов. Ее можно использовать для моделирования последовательности событий или состояний, в которых вероятность перехода в любое заданное состояние в заданное время зависит только от текущего состояния. 

Вот несколько примеров того, как цепь Маркова с дискретным временем может быть использована для моделирования ежедневных событий:

• Прогнозирование погоды: Цепь Маркова с дискретным временем может использоваться для моделирования ежедневной погоды в определенном месте. Состояния цепи Маркова могут представлять различные погодные состояния, такие как солнечное, облачное, дождливое или снежное. Вероятности перехода можно оценить на основе исторических данных о погоде, а цепь Маркова можно использовать для прогнозирования погоды на следующий день на основе текущих погодных условий.
• Движения цен на акции: цепь Маркова с дискретным временем может использоваться для моделирования ежедневных движений цены конкретной акции. Состояния цепи Маркова могут представлять различные уровни движения цены, например вверх, вниз или без изменений. Вероятности перехода можно оценить на основе исторических данных о ценах на акции, а цепь Маркова можно использовать, чтобы спрогнозировать направление цены акции на следующий день на основе текущего движения цены.
• Схемы движения: цепь Маркова с дискретным временем можно использовать для моделирования ежедневных моделей движения на определенной дороге или шоссе. Состояния цепи Маркова могут представлять различные уровни загруженности дорог, например легкую, среднюю или тяжелую. Вероятности перехода можно оценить на основе исторических данных о движении, а цепь Маркова можно использовать для прогнозирования уровня загруженности на следующий день на основе текущего.

2. Цепь Маркова с непрерывным временем (continuous-time Markov chain): здесь переходы между состояниями происходят непрерывно, а не дискретными временными шагами. Это означает, что вероятность перехода из одного состояния в другое зависит от времени, прошедшего с момента последнего перехода. Цепи Маркова с непрерывным временем обычно используются для моделирования систем, которые непрерывно изменяются в течение различных промежутков времени, таких как транспортный поток на конкретном шоссе или скорость химических реакций на химическом заводе. Одно из основных различий между цепями Маркова с дискретным и непрерывным временем состоит в том, что вероятности перехода в цепи Маркова с непрерывным временем характеризуются скоростями переходов, которые представляют собой вероятность перехода из одного состояния в другое в единицу времени. Эти скорости перехода используются для вычисления вероятности перехода из одного состояния в другое в течение определенного интервала времени.

3. Скрытая марковская модель (Hidden Markov model, HMM) - это статистическая модель, в которой состояния системы не наблюдаемы напрямую, а вместо этого выводятся из последовательности наблюдений. Вот несколько примеров того, как можно использовать скрытую марковскую модель для моделирования повседневных событий:

   • Распознавание речи. Скрытую марковскую модель можно использовать для моделирования звуков, издаваемых во время речи, и для распознавания произносимых слов. В этом случае состояния HMM могут представлять разные фонемы (звуки речи), а наблюдения могут представлять собой последовательность звуковых волн, представляющих произнесенные слова. HMM можно обучить на большом наборе данных произносимых слов и соответствующих им звуковых волн и использовать для распознавания новых произнесенных слов путем определения наиболее вероятной последовательности фонем на основе наблюдаемых звуковых волн.
   • Распознавание почерка. Скрытая модель Маркова может использоваться для моделирования последовательности штрихов и распознавания рукописных слов. В этом случае состояния НММ могут представлять собой разные штрихи, а наблюдения могут представлять собой последовательность изображений рукописных слов. НММ можно обучить на большом наборе данных рукописных слов и соответствующих им изображений и использовать для распознавания новых рукописных слов путем определения наиболее вероятной последовательности штрихов на основе наблюдаемых изображений.
   • Распознавание деятельности. Скрытую марковскую модель можно использовать для распознавания человеческой деятельности на основе последовательности наблюдений, таких как показания датчиков или видеокадры. Например, HMM можно использовать для распознавания таких действий, как ходьба, бег или прыжки.

4. Модель с марковским переключением (Markov switching model, MSM) - тип цепи Маркова, в которой состояния системы могут изменяться во времени или «переключаться» в зависимости от определенных условий. Вот несколько примеров того, как модель марковского переключения можно использовать для моделирования повседневных событий:

   • Поведение потребителей. Для моделирования покупательского поведения потребителей можно использовать модель марковского переключения. Состояния MSM могут представлять различные типы покупательского поведения, такие как частые или редкие покупки. Переходы между состояниями могут быть основаны на определенных условиях, таких как изменение дохода или введение новых продуктов. MSM можно использовать для прогнозирования будущего покупательского поведения на основе текущего состояния и вероятностей перехода между состояниями.
   • Экономические индикаторы. Модель с переключением Маркова можно использовать для моделирования экономических индикаторов, таких как ВВП или уровень безработицы. Состояния MSM могут представлять различные экономические условия, такие как подъем или спад, а переходы между состояниями могут быть основаны на определенных условиях, таких как изменения в денежно-кредитной политике или цикле деловой активности. MSM можно использовать для прогнозирования будущих экономических условий на основе текущего состояния и вероятностей перехода между состояниями.
   • Схемы движения. Модель с переключением Маркова можно использовать для моделирования моделей движения на конкретной дороге или шоссе. Состояния MSM могут представлять различные уровни загруженности дорог, такие как легкая, средняя или тяжелая, а переходы между состояниями могут основываться на определенных условиях, таких как время суток или день недели. MSM можно использовать для прогнозирования будущих моделей трафика на основе текущего состояния и вероятностей перехода между состояниями.

   
   

Как и в случае с любой гипотезой, в основе всегда лежат допущения, которые, как правило, налагают на идею те или иные ограничения. Цепи Маркова не являются исключением. Вот некоторые из предположений:

1. Стационарность. Одно из основных предположений цепи Маркова состоит в том, что вероятности перехода между состояниями постоянны во времени. Это предположение известно как стационарность. Если вероятности перехода не являются постоянными во времени, модель цепи Маркова может быть неточной.

2. Марковское свойство. Еще одно предположение цепи Маркова состоит в том, что будущая эволюция системы зависит только от текущего состояния и прошедшего времени и не зависит от прошлой истории системы за пределами текущего состояния. Это предположение может не всегда выполняться на практике, особенно для наборов данных со сложными зависимостями или долговременной памятью.

3. Конечное пространство состояний. Цепь Маркова обычно определяется в конечном пространстве состояний, что означает, что существует конечное число возможных состояний, в которых может находиться система. Это может не подходить для наборов данных с большим количеством состояний или непрерывных переменных.

4. Однородность во времени. Цепь Маркова обычно считается однородной во времени. Это означает, что вероятности перехода между состояниями не зависят от конкретного времени, в которое происходит переход. Если вероятности перехода действительно зависят от времени, в которое происходит переход, модель цепи Маркова может быть неточной.

5. Эргодичность. Цепь Маркова обычно считается эргодичной, что означает, что можно достичь любого состояния из любого другого состояния за конечное число шагов. Если это предположение не выполняется, модель цепи Маркова может быть неточной.

В целом, модели цепи Маркова наиболее подходят для наборов данных с относительно простыми зависимостями и небольшим количеством состояний или переменных. Если набор данных имеет сложные зависимости или большое количество состояний или переменных, возможно, другие методы моделирования окажутся более подходящими.

Оценка вероятности

После моделирования цепи Маркова нам необходимо оценить вероятности перехода из каждого состояния. Существует ряд методов, которые можно использовать. Будет полезно повторить их, чтобы лучше понять область применения и возможности цепей Маркова. Существует несколько методов оценки вероятностей перехода между состояниями в цепях Маркова, в том числе:

1. Оценка максимального правдоподобия (maximum likelihood estimation, MLE): цель состоит в том, чтобы оценить вероятность события или последовательности событий на основе наблюдаемых данных. В контексте цепей Маркова это означает, что мы хотим оценить вероятность перехода из одного состояния в другое на основе набора наблюдаемых переходов.

   Чтобы реализовать MLE для цепей Маркова, нам сначала нужно собрать набор наблюдаемых переходов. Это можно сделать, запустив симуляцию или собрав реальные данные. Получив наблюдаемые переходы, мы можем использовать их для оценки вероятностей переходов.

   Чтобы оценить вероятности перехода, мы можем использовать следующие шаги:

   • Задать матрицу для хранения вероятностей перехода. Матрица должна иметь размеры num_states x num_states, где num_states — количество состояний в цепи Маркова.
   • Инициализировать матрицу со всеми вероятностями, установленными на 0. Это можно сделать с помощью вложенного цикла, перебирающего все элементы матрицы.
   • Повторить наблюдаемые переходы и обновить вероятности перехода. Для каждого наблюдаемого перехода из состояния i в состояние j увеличим вероятность transition_probs[i][j] на 1.
   • Нормализовать вероятности перехода так, чтобы их сумма равнялась 1. Это можно сделать, разделив каждый элемент матрицы на сумму элементов в соответствующей строке.

   
   

   Как только вероятности перехода были оценены, мы можем использовать их для прогнозирования вероятности перехода из одного состояния в другое. Например, если мы хотим предсказать вероятность перехода из состояния i в состояние j, мы можем использовать формулу P(j | i) = transition_probs[i][j].

2. Байесовская оценка: включает использование теоремы Байеса для обновления распределения вероятностей по параметрам модели на основе новых данных. Чтобы использовать байесовскую оценку вероятности с цепью Маркова, нам сначала нужно определить априорное распределение по состояниям цепи Маркова. Это априорное распределение представляет собой наше первоначальное мнение о вероятностях различных состояний в цепочке. Затем мы можем использовать байесовское обновление, чтобы обновить наши представления о вероятностях состояний по мере поступления новой информации. Например, предположим, что у нас есть цепь Маркова с тремя состояниями: A, B и C. Мы начинаем с априорного распределения по состояниям, которое можно представить как:

   P(A) = 0,4 P(B) = 0,3 P(C) = 0,3

   Это означает, что изначально мы считаем, что вероятность оказаться в состоянии А равна 40%, вероятность оказаться в состоянии В — 30%, а вероятность оказаться в состоянии С — 30%.

   Теперь предположим, что мы наблюдаем, как система переходит из состояния A в состояние B. Мы можем использовать эту новую информацию, чтобы обновить наши представления о вероятностях состояний с помощью байесовской оценки вероятности. Для этого нам нужно знать вероятности перехода между состояниями. Предположим, что вероятности перехода таковы:

   P(A -> B) = 0,8 

   P(A -> C) = 0,2 

   P(B -> A) = 0,1 

   P(B -> B) = 0,7 

   P(B -> C) = 0,2 

   P(C -> A) = 0,2 

   P(C -> B) = 0,3 

   P(C -> C) = 0,5

   Эти вероятности перехода говорят нам о вероятности перехода из одного состояния в другое. Например, вероятность перехода из состояния А в состояние В равна 0,8, а вероятность перехода из состояния А в состояние С равна 0,2.

   Используя эти вероятности перехода, мы теперь можем обновить наши представления о вероятностях состояний, используя байесовскую оценку вероятности. В частности, мы можем использовать правило Байеса для вычисления апостериорного распределения по состояниям с учетом новой информации о том, что система перешла из состояния A в состояние B. Это апостериорное распределение представляет собой наше обновленное представление о вероятностях состояний с учетом новой информации, которую мы получили.

   Например, используя правило Байеса, мы можем вычислить апостериорную вероятность пребывания в состоянии А следующим образом:

   P(A | A -> B) = P(A -> B | A) * P(A) / P(A -> B)

   Подставляя значения из нашего предыдущего распределения и вероятности перехода, мы получаем:

   P(A | A -> B) = (0,8 * 0,4) / (0,8 * 0,4 + 0,1 * 0,3 + 0,2 * 0,3) = 0,36

   Точно так же мы можем вычислить апостериорные вероятности пребывания в состояниях B и C:

   P(B | A -> B) = (0,1 * 0,3) / (0,8 * 0,4 + 0,1 * 0,3 + 0,2 * 0,3) = 0,09

3. EM-алгоритм (Expectation-maximization, EM). Чтобы использовать EM для оценки вероятности с помощью цепи Маркова, вам необходимо наблюдать за переходами между состояниями цепи Маркова в течение определенного периода времени. На основе этих данных мы можем использовать ЕМ-алгоритм для оценки вероятностей перехода, итеративно уточняя свои оценки на основе наблюдаемых данных. EM-алгоритм работает, чередуя два шага: шаг ожидания (E-шаг) и шаг максимизации (M-шаг). На шаге E мы оцениваем ожидаемое значение полной логарифмической вероятности данных с учетом текущих оценок параметров. На шаге М мы максимизируете ожидаемое значение полной логарифмической вероятности данных по отношению к параметрам, чтобы получить обновленные оценки параметров. Затем повторяем эти шаги, пока оценки параметров не сойдутся к стабильному значению. Например, если вы наблюдали цепь Маркова с тремя состояниями (A, B и C) и хотите оценить вероятности перехода между состояниями, вы можете использовать EM-алгоритм для итеративного уточнения ваших оценок вероятностей перехода на основе наблюдаемых данных.

   Основное преимущество использования EM для оценки вероятности заключается в том, что алгоритм может обрабатывать неполные или зашумленные данные и может оценивать параметры статистической модели, даже если лежащее в основе распределение известно не полностью. Однако алгоритм может быть чувствителен к инициализации и не всегда может сходиться к глобальному максимуму логарифмической функции правдоподобия. Также он требует значительных вычислительных ресурсов, поскольку предполагает многократную оценку функции логарифмического правдоподобия и ее градиента.

4. Параметрическая оценка. Чтобы использовать параметрическую оценку вероятности с цепью Маркова, нам необходимо наблюдать за переходами между состояниями цепи Маркова в течение определенного периода времени. На основе этих данных можно подобрать параметрическую модель к вероятностям перехода, предполагая, что базовое распределение следует определенному распределению, такому как нормальное распределение или биномиальное распределение. Затем мы можем использовать эту модель для оценки вероятности перехода из одного состояния в другое. Например, если бы мы наблюдали цепь Маркова с тремя состояниями (А, В и С) и обнаружили, что переход из состояния А в состояние В происходил 10 раз из 20 переходов, мы могли бы подогнать биномиальную модель к данным и использовать ее для оценки вероятности перехода из состояния A в состояние B.

   Основное преимущество параметрической оценки вероятности заключается в том, что она может быть более точной, чем непараметрические методы, которые не делают никаких предположений об основном распределении. Однако для этого необходимо делать предположения об основном распределении, что не всегда может быть уместным или может привести к необъективным оценкам. Кроме того, параметрические методы могут быть менее гибкими и менее надежными, чем непараметрические, поскольку они чувствительны к отклонениям от предполагаемого распределения.

5. Непараметрическая оценка. Чтобы использовать непараметрическую оценку вероятности с помощью цепи Маркова, нам необходимо наблюдать за переходами между состояниями цепи Маркова в течение определенного периода времени. По этим данным можно оценить вероятность перехода из одного состояния в другое, подсчитав количество раз, когда произошел переход, и разделив его на общее количество переходов. Например, если бы мы наблюдали цепь Маркова с тремя состояниями (А, В и С) и обнаружили, что переход из состояния А в состояние В происходил 10 раз из 20 переходов, мы могли бы оценить вероятность перехода из состояния A в состояние B как 0,5.

   Этот метод оценки вероятности называется методом эмпирического распределения, и его можно использовать для оценки вероятности любого набора событий, а не только переходов в цепи Маркова. Основное преимущество непараметрической оценки вероятностей заключается в том, что она не требует никаких предположений об основном распределении, что делает ее гибким и надежным методом оценки вероятностей. Однако она может быть менее точной, чем параметрические методы, которые делают предположения об основном распределении для более точной оценки вероятностей.

6. Бутстрэп (Bootstrapping). Это общий метод, который можно использовать для оценки вероятностей в цепи Маркова или в любой другой вероятностной модели. Основная идея состоит в том, чтобы использовать небольшое количество наблюдений для оценки распределения вероятностей по состояниям системы, а затем использовать это распределение для создания большого количества синтетических наблюдений. Затем синтетические наблюдения можно использовать для более точной оценки распределения вероятностей. Процесс можно повторять до тех пор, пока не будет достигнут желаемый уровень точности.

   Чтобы использовать начальную загрузку для оценки вероятности в цепи Маркова, у нас сначала должна быть начальная цепь Маркова с ее состояниями. Подобно байесовскому методу, бутстрэп обновляет и улучшает существующие цепи Маркова. Каждое состояние в цепочке связано с вероятностью перехода в другие состояния, а вероятности перехода между разными парами состояний не зависят от истории системы. Когда у вас есть исходная цепь Маркова, вы можете использовать бутстреп для оценки распределения вероятностей по ее состояниям. Для этого необходимо начать с небольшого количества наблюдений за системой, таких как несколько конфигураций начального состояния или короткая последовательность переходов между состояниями. Затем можно использовать эти наблюдения для оценки распределения вероятностей по состояниям системы.

   Например, если у вас есть цепь Маркова с тремя состояниями A, B и C, и вы несколько раз наблюдали переход системы из состояния A в состояние B и несколько раз из состояния B в состояние C, вы можете использовать эти наблюдения для оценки вероятности перехода из состояния А в состояние В и из состояния В в состояние С.

   После того, как вы оценили распределение вероятностей по состояниям системы, вы можете использовать его для создания большого количества синтетических наблюдений за системой. Это можно сделать путем случайной выборки из распределения вероятностей для имитации переходов между состояниями. Затем синтетические наблюдения можно использовать для более точной оценки распределения вероятностей и повторять процесс, пока не достигнут желаемый уровень точности.

   Бутстрэп может быть полезен для оценки вероятностей в цепи Маркова, поскольку позволяет использовать небольшое количество наблюдений для создания большого количества синтетических наблюдений, что может повысить точность оценок. Он также относительно прост в реализации и может использоваться с большим числом вероятностных моделей. Однако точность оценок, полученных с помощью бутстрэпа, зависит от качества первоначальных наблюдений и лежащей в основе вероятностной модели. Иногда точность метода может быть ниже, чем у других методов оценки.

7. Складной нож (Jackknife estimation). Этот метод запускает нескольких симуляций цепи Маркова, каждый раз исключая другое состояние или группу состояний. Затем вероятность возникновения события оценивается путем усреднения вероятностей события, происходящего в каждой из симуляций. Ниже приведено более подробное объяснение процесса:
   • Настройте цепь Маркова и определите интересующее вас событие. Например, событием может быть достижение определенного состояния в цепочке или переход между двумя конкретными состояниями.
   • Запустите несколько симуляций цепи Маркова, каждый раз исключая другое состояние или группу состояний. Это можно сделать, просто не рассматривая исключенные состояния при запуске моделирования или установив их вероятности перехода равными нулю.
   • Для каждой симуляции рассчитайте вероятность возникновения события. Это можно сделать, выполнив подробный анализ баланса или используя такие методы, как выборка методом Монте-Карло или умножение матриц.
   • Усредните вероятности события, происходящего в каждой из симуляций, чтобы получить оценку вероятности события, происходящего в полной цепи Маркова.

   Использование метода складного ножа для оценки вероятности в цепях Маркова имеет несколько преимуществ. Одним из преимуществ является то, что он позволяет более точно оценить вероятность возникновения события, поскольку учитывает влияние каждого отдельного состояния на общую вероятность. Еще одним преимуществом является то, что он относительно прост в реализации и может быть легко автоматизирован. Однако у метода складного ножа также есть некоторые ограничения. Одним из ограничений является то, что он требует выполнения нескольких симуляций цепи Маркова, что может потребовать значительных вычислительных ресурсов для больших или сложных цепей. Кроме того, точность оценки может зависеть от количества и выбора состояний, исключаемых при моделировании.

8. Перекрестная проверка (cross-validation). Этот метод можно использовать для оценки вероятности конкретного события, происходящего в цепи Маркова. Он включает в себя разделение данных на несколько сгибов или подмножеств и использование каждого сгиба в качестве тестового набора для оценки производительности модели на этом подмножестве. Чтобы использовать оценку вероятности перекрестной проверки с помощью цепей Маркова, нам сначала нужно настроить цепь Маркова с желаемыми состояниями и переходами. Затем мы разделим данные на желаемое количество сгибов. Затем мы перебираем каждый сгиб и используем его в качестве тестового набора для оценки производительности модели на этом подмножестве. Эта работа включает в себя использование цепи Маркова для оценки вероятности каждого события, происходящего в тестовом наборе, и сравнение этих оценок с фактическими результатами в тестовом наборе.

   Наконец, усредним производительность по всем сгибам, чтобы получить общую оценку производительности модели. Это может быть полезно для оценки производительности модели и тонкой настройки параметров цепи Маркова для повышения ее точности. Для использования оценки вероятности перекрестной проверки с цепью Маркова данные должны быть независимо и одинаково распределены, а это означает, что каждое подмножество данных должно представлять общий набор данных.

Каждый из этих методов имеет свои сильные стороны и ограничения, и выбор метода будет зависеть от конкретных характеристик данных и целей анализа. 

Реализация с помощью Мастера MQL5

Чтобы закодировать класс сигналов, реализующий цепи Маркова, используем класс CMarkovCPD в файле dataanalysis.mqh в папке alglib. Мы будем моделировать цепи с дискретным временем. Цепь с дискретным временем будет иметь пять состояний, которые являются последними пятью изменениями цены закрытия. Таким образом таймфрейм, на котором тестируется или работает советник, будет определять дискретную единицу времени. Чтобы оценить вероятности перехода между состояниями, класс CMarkovCPD требует добавления данных отслеживания для обучения модели. Количество добавляемых данных отслеживания определяется оптимизируемым входным параметром m_signal_tracks. Ниже показано, как мы будем инициализировать режим и добавлять данные отслеживания (обучения).

      CMCPDState _s;
      CMatrixDouble _xy,_p;
      CMCPDReport _rep;
      int _k=m_signal_tracks;
      
      _xy.Resize(m_signal_tracks,__S_STATES);
      
      m_close.Refresh(-1);
      
      for(int t=0;t<m_signal_tracks;t++)
      {
         for(int s=0;s<__S_STATES;s++)
         {
            _xy[t].Set(s,GetState(Close(Index+t+s)-Close(Index+t+s+1),Close(Index+t+s+1)-Close(Index+t+s+2)));
         }
      }

Данные о цене закрытия нормализованы на уровне 1,0. Если изменение цены закрытия отрицательное, входные данные меньше 1,0, если же оно положительное, входное значение будет больше 1,0 без изменений, дающих ровно 1,0. Эта нормализация выполняется с помощью функции GetState, показанной ниже.

//+------------------------------------------------------------------+
//| Normalizer.                                                      |
//+------------------------------------------------------------------+
double CSignalMC::GetState(double NewChange,double OldChange)
   {
      double _state=0.0;
      
      double _norm=fabs(NewChange)/fmax(m_symbol.Point(),fabs(NewChange)+fabs(OldChange));
      
      if(NewChange>0.0)
      {
         _state=_norm+1.0;
      }
      else if(NewChange<0.0)
      {
         _state=1.0-_norm;
      }
      
      return(_state);
   }

После добавления данных нам нужно инициализировать экземпляр класса CMCPDState, поскольку это объект, который обрабатывает все данные нашей модели и помогает в расчете оценок вероятности. Делаем это так:

      CPD.MCPDCreate(__S_STATES,_s);
      
      CPD.MCPDAddTrack(_s,_xy,_k);
      
      CPD.MCPDSetTikhonovRegularizer(_s,m_signal_regulizer);
      
      CPD.MCPDSolve(_s);
      
      CPD.MCPDResults(_s,_p,_rep);

В идеале входной параметр m_signal_regulazier должен быть не абстрактным двойным значением, а двойным значением, представляющим величину данных отслеживания. Другими словами, он должен быть пропорционален данным отслеживания, полученным из функции GetState. Это означает, что если вы хотите идеально оптимизировать его, скажем, в диапазоне 0,5-0,0, вы должны умножить его на величину самых больших данных отслеживания при использовании метода регуляризации Тихонова. 

Матрица ‘_p’ — это наша матрица переходов со всеми вероятностями перехода между состояниями. Полный код сигнального класса прикреплен внизу.

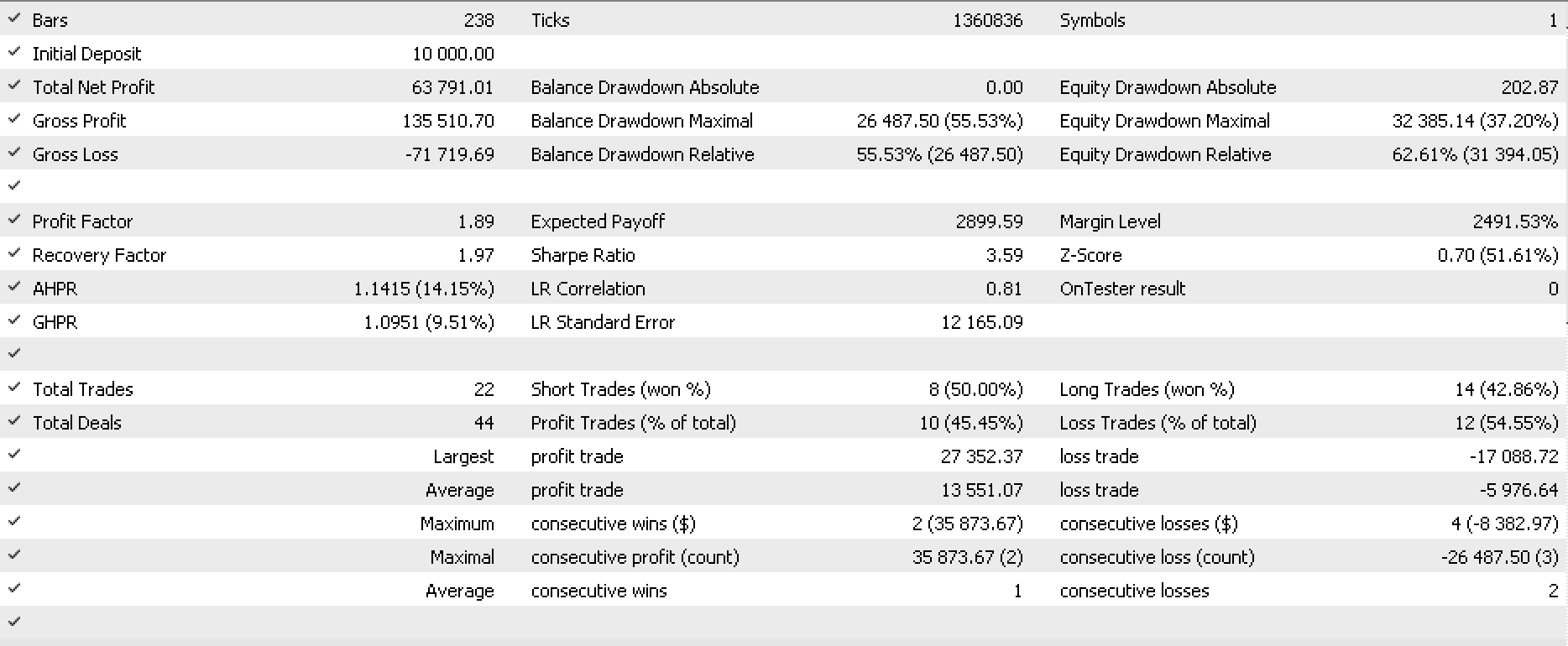
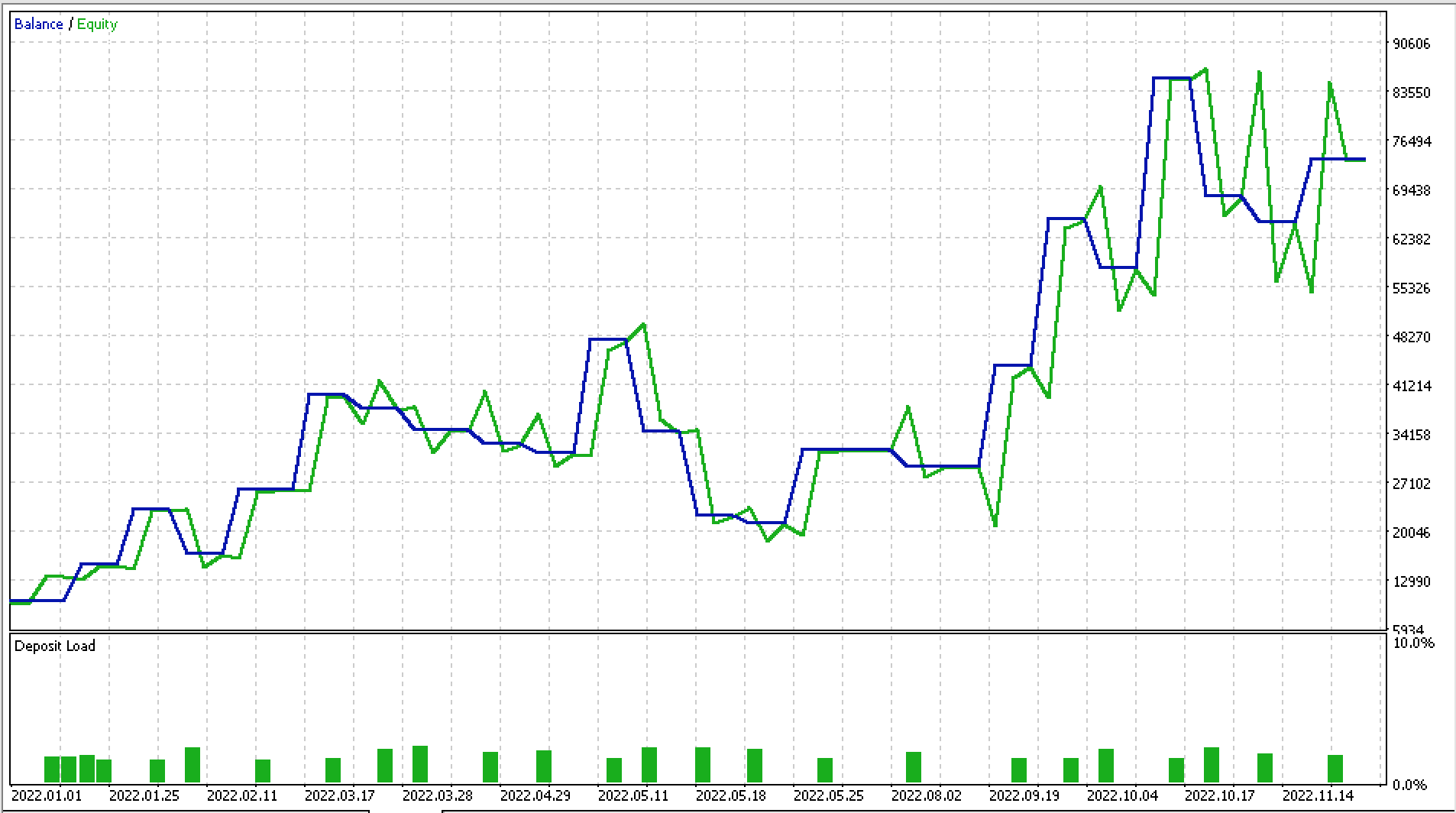
Я сделал несколько пробных прогонов на EURJPY D1 за 2022 год. Ниже приведены часть отчета и кривая эквити.

Заключение

Цепи Маркова — это математический инструмент, который можно использовать для моделирования поведения финансовых рынков. Они особенно полезны, поскольку позволяют трейдерам анализировать вероятность будущих состояний рынка на основе текущего состояния рынка. Это может быть очень полезно в трейдинге, поскольку позволяет трейдерам принимать обоснованные решения о том, какие сделки совершать и когда их совершать.

Одним из ключевых преимуществ использования цепей Маркова на финансовых рынках является то, что они позволяют трейдерам анализировать и прогнозировать эволюцию рыночных тенденций с течением времени. Это особенно важно на быстро меняющихся рынках, где тенденции могут быстро меняться и трудно предсказать, как поведет себя рынок. Используя цепи Маркова, трейдеры могут определить наиболее вероятные пути, по которым пойдет рынок, и использовать эту информацию для принятия обоснованных торговых решений.

Еще одним преимуществом цепей Маркова является то, что их можно использовать для анализа рисков, связанных с различными сделками. Анализируя вероятности различных состояний рынка, трейдеры могут определить риск, связанный с различными сделками, и выбрать сделки, которые, скорее всего, будут успешными. Это может быть особенно полезно на волатильных рынках, где риск потерь выше.

Обобщая, можно сказать, что цепи Маркова являются важным инструментом для трейдеров на финансовых рынках, поскольку они позволяют трейдерам анализировать и прогнозировать поведение рынка, определять наиболее вероятные пути, по которым пойдет рынок, и оценивать риск, связанный с различными сделками.