Características del Wizard MQL5 que debe conocer (Parte 5): Cadenas de Markov
Introducción
Las cadenas de Markov son una potente herramienta matemática que se puede usar para modelar y predecir los datos de las series temporales en varios campos, incluido el financiero. En el modelado y la previsión de series temporales financieras, las cadenas de Markov se usan a menudo para modelar la evolución de los activos financieros a lo largo del tiempo, como los precios de las acciones o los tipos de cambio. Las principales ventajas de los modelos de cadenas de Markov son, entre otras cosas, su simplicidad y sencillez de uso. Las cadenas de Markov se basan en un modelo probabilístico simple que describe la evolución de un sistema a lo largo del tiempo y no requiere suposiciones matemáticas complejas ni suposiciones sobre las propiedades estadísticas de los datos. Esto las hace especialmente útiles para modelar y pronosticar los datos de las series temporales financieras que pueden resultar muy complejos y mostrar un comportamiento no estacionario.
El modelado de cadenas de Markov se puede dividir en cuatro tipos principales: cadenas de Markov de tiempo discreto, cadenas de Markov de tiempo continuo, modelos de Markov ocultos y modelos de Markov de conmutación. Los principales son las cadenas de Markov de tiempo discreto, que se utilizan para modelar la evolución de un sistema en varios pasos de tiempo discretos, y las cadenas de Markov en tiempo continuo, que se usan para modelar la evolución de un sistema en un intervalo de tiempo continuo. Ambos tipos se pueden utilizar para modelar y pronosticar datos de series temporales financieras.
La estimación de la probabilidad para un modelo de cadenas de Markov a partir de los datos de las series temporales financieras se puede realizar de varias formas. Mencionaremos ocho formas posibles: la más notable de ellas es la maximización de las expectativas. Se trata de un método implementado en ALGLIB.
Una vez se haya estimado la probabilidad (o los parámetros de un modelo de cadenas de Markov), el modelo se podrá utilizar para predecir estados o eventos futuros. Por ejemplo, en el caso de series temporales financieras, se puede usar un modelo de cadenas de Markov para predecir precios de acciones o tipos de cambio futuros según el estado actual del mercado y las probabilidades de transición entre diferentes estados del mismo.
Modelado de cadenas
Una cadena de Markov es un sistema matemático que realiza transiciones de un estado a otro según ciertas reglas probabilísticas. La característica definitoria de una cadena de Markov es que no importa cómo haya llegado el sistema a su estado actual, la probabilidad de pasar a cualquier estado en particular dependerá únicamente del estado actual y el tiempo transcurrido. Una cadena de Markov se puede representar usando un diagrama de estado, donde cada nodo en el diagrama representa un estado, mientras que los bordes entre los nodos representan las transiciones entre los estados. La probabilidad de transición de un estado a otro estará representada por el peso del borde correspondiente.
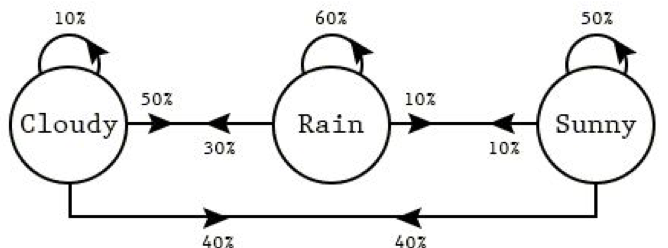
Las flechas en el diagrama (cadenas de Markov) representan transiciones entre estados. La probabilidad de transición del estado 'rainy weather' (tiempo lluvioso) al estado 'sunny weather' (tiempo soleado) se puede representar mediante el peso de la arista entre dos nodos (en este caso 0,1). Para las otras transiciones será similar.
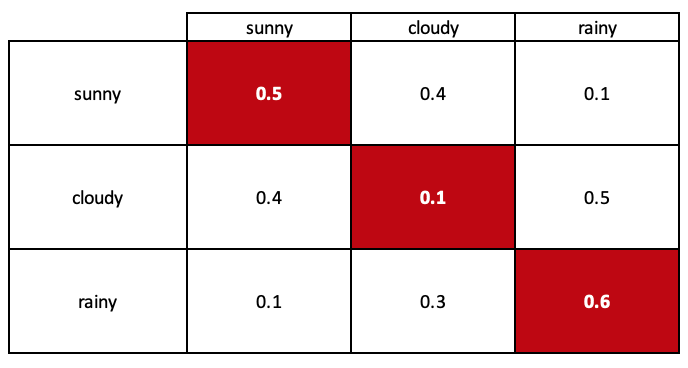
Podemos usar este diagrama de estado para modelar las probabilidades de transición entre los estados en un sistema. El modelo que estamos creando se llama matriz estocástica.
Una suposición importante de la cadena de Markov es que el comportamiento futuro de un sistema dependerá únicamente del estado actual y el tiempo transcurrido, y no de la historia pasada del sistema. Esto se conoce como la propiedad "sin memoria" (estado pasado) de una cadena de Markov. Esto significa que la probabilidad de transición de un estado a otro será la misma sin importar cuántos estados intermedios pueda atravesar el sistema para llegar a su estado actual.
Las cadenas de Markov se pueden usar para modelar una amplia variedad de sistemas, incluidos los sistemas financieros, meteorológicos y biológicos. Resultan especialmente útiles para modelar sistemas que muestren dependencias temporales donde el estado actual del sistema depende de sus estados pasados, como las series temporales.
Las cadenas de Markov se usan ampliamente para modelar datos de series temporales, que suponen una serie de puntos de datos recopilados a intervalos regulares. Los datos de las series temporales se pueden encontrar en muchos campos, como las finanzas, la economía, la meteorología y la biología.
Para usar una cadena de Markov a la hora de modelar datos de series temporales, primero deberemos definir los estados del sistema y las transiciones entre ellos. Las probabilidades de transición de estado se pueden estimar a partir de los datos usando métodos como la estimación de máxima verosimilitud o la maximización de la expectativa. Una vez se hayan estimado las probabilidades de transición, podremos usar una cadena de Markov para predecir estados o eventos futuros según el estado actual y el tiempo transcurrido.
Las cadenas de Markov se pueden usar para modelar los datos de las series temporales de varias formas:
-
La cadena de Markov con tiempo discreto (discrete-time Markov chain) es un modelo matemático que se utiliza para describir la evolución de un proceso estocástico de tiempo discreto en una serie de pasos de tiempo. Se puede usar para modelar una secuencia de eventos o estados en los que la probabilidad de transición a cualquier estado dado en un momento dado dependerá solo del estado actual.
- Predicción del tiempo atmosférico: Podemos usar una cadena de Markov de tiempo discreto para simular el clima diario en una ubicación específica. Los estados de la cadena de Markov pueden representar diferentes condiciones climáticas, como el tiempo soleado, nublado, lluvioso o con nieve. Las probabilidades de transición se pueden estimar partiendo de los datos meteorológicos históricos, mientras que podemos usar una cadena de Markov para predecir el clima del día siguiente en función de las condiciones climáticas actuales.
- Los movimientos de precio de las acciones: podemos usar una cadena de Markov de tiempo discreto para modelar los movimientos diarios de precios de una acción en particular. Los estados de la cadena de Markov pueden representar diferentes niveles de movimiento de precio, como ascendentes, descendentes o sin cambios. Podemos estimar las probabilidades de transición según los datos históricos del precio de las acciones, y usar una cadena de Markov para predecir la dirección del precio de las acciones del día siguiente en función del movimiento actual del precio.
- Patrones de tráfico: la cadena de Markov de tiempo discreto se puede usar para simular patrones de tráfico diarios en una carretera o autopista concreta. Los estados de la cadena de Markov pueden representar diferentes niveles de tráfico, como ligero, medio o denso. Podemos estimar las probabilidades de transición según los datos de tráfico históricos, y usar una cadena de Markov para predecir el nivel de densidad de tráfico del día siguiente en función del actual.
-
En la cadena de Markov de tiempo continuo (continuous-time Markov chain), las transiciones entre estados ocurren continuamente, no en pasos de tiempo discretos. Esto significa que la probabilidad de una transición de un estado a otro dependerá del tiempo transcurrido desde la última transición. Por lo común las cadenas de Markov de tiempo continuo se usan para modelar sistemas que cambian continuamente durante periodos de tiempo variables, como el flujo de tráfico en una carretera concreta o la tasa de reacciones químicas en una planta química. Una de las principales diferencias entre las cadenas de Markov de tiempo continuo y discreto es que las probabilidades de transición en las cadenas de Markov de tiempo continuo se caracterizan mediante tasas de transición, que suponen la probabilidad de transición de un estado a otro en la unidad de tiempo. Estas tasas de transición se usan para calcular la probabilidad de una transición de un estado a otro dentro de un cierto intervalo temporal.
-
El modelo oculto de Markov (HMM) es un modelo estadístico en el que los estados de un sistema no son directamente observables, sino que se infieren a partir de una secuencia de observaciones. Aquí tenemos algunos ejemplos de uso de un modelo oculto de Markov para modelar eventos cotidianos:
- Reconocimiento de voz. El modelo oculto de Markov se puede usar para modelar los sonidos que se producen durante el habla y para reconocer las palabras habladas. En este caso, los estados de HMM pueden representar diferentes fonemas (sonidos del habla), mientras que las observaciones pueden ser una secuencia de ondas sonoras que representan palabras habladas. Podemos entrenar una HMM con un gran conjunto de datos de palabras pronunciadas y sus correspondientes ondas sonoras y utilizar dicho método para reconocer nuevas palabras habladas mediante la determinación de la secuencia de fonemas más probable según las ondas sonoras observadas.
- Reconocimiento de la escritura a mano. El modelo oculto de Markov se puede usar para modelar secuencias de trazos y reconocer palabras escritas a mano. En este caso, los estados de HMM pueden ser diferentes trazos, mientras que las observaciones pueden ser una secuencia de imágenes de palabras escritas a mano. Una HMM puede entrenarse con un gran conjunto de datos de palabras escritas a mano y sus imágenes correspondientes y usarse para reconocer nuevas palabras escritas a mano determinando la secuencia de trazos más probable según las imágenes observadas.
- Reconocimiento de la actividad. Podemos usar un modelo oculto de Markov para reconocer la actividad humana según una secuencia de observaciones, como lecturas de sensores o fotogramas de vídeo. Por ejemplo, una HMM se puede usar para reconocer actividades como caminar, correr o saltar.
-
El modelo de conmutación de Markov (MSM) es un tipo de cadena de Markov en el que los estados de un sistema pueden cambiar con el tiempo o "alternar" según ciertas condiciones. Estos son algunos ejemplos de cómo podemos usar el modelo de conmutación de Markov para modelar eventos cotidianos:
- Comportamiento del consumidor. Para modelar el comportamiento de compra de los consumidores, podemos usar el modelo de conmutación de Markov. Los estados de MSM pueden representar diferentes tipos de comportamiento de compra, como compras frecuentes o poco frecuentes. Las transiciones de estado pueden basarse en ciertas condiciones, como un cambio en los ingresos o la introducción de nuevos productos. El MSM se puede usar para predecir un futuro comportamiento de compra en función del estado actual y las probabilidades de transición de estado.
- Indicadores económicos. Podemos utilizar el modelo de conmutación de Markov para modelar indicadores económicos como el PIB o la tasa de desempleo. Los estados de MSM pueden representar diversas condiciones económicas, como un ascenso o una caída, mientras que las transiciones de estado pueden basarse en condiciones específicas, como los cambios en la política monetaria o el ciclo económico. El MSM se puede utilizar para predecir las futuras condiciones económicas según el estado actual y las probabilidades de transición de estado.
- Esquemas de tráfico. El modelo de conmutación de Markov se puede usar para simular patrones de tráfico en una carretera o autopista concreta. Los estados de MSM pueden representar diferentes niveles de tráfico, como ligero, medio o denso, mientras que las transiciones de estado pueden basarse en ciertas condiciones, como la hora del día o el día de la semana. El MSM se puede utilizar para predecir futuros patrones de tráfico según el estado actual y las probabilidades de transición de estado.
Estos son algunos ejemplos de cómo podemos usar una cadena de Markov de tiempo discreto para modelar eventos diarios:
Como toda hipótesis, siempre se basa en suposiciones que, por regla general, imponen ciertas restricciones a la idea. Las cadenas de Markov no suponen una excepción. Estas son algunas de las suposiciones:
-
Estacionariedad. Una de las suposiciones básicas de una cadena de Markov es que las probabilidades de transición entre estados son constantes en el tiempo; Esta suposición se conoce como estacionariedad. Si las probabilidades de transición no son constantes en el tiempo, el modelo de la cadena de Markov puede resultar inexacto.
-
Propiedad de Markov. Otra suposición de la cadena de Markov es que la futura evolución de un sistema dependerá únicamente del estado actual y el tiempo transcurrido, y no de la historia pasada del sistema más allá del estado actual. Es posible que esta suposición no siempre se cumpla en la práctica, especialmente para conjuntos de datos con dependencias complejas o memoria a largo plazo.
-
Espacio de estado finito. Una cadena de Markov generalmente se define en un espacio de estado finito, lo cual significa que hay un número finito de estados posibles en los que puede estar el sistema. Esto podría no resultar adecuado para conjuntos de datos con muchos estados o variables continuas.
-
Uniformidad en el tiempo. Generalmente se considera que una cadena de Markov es homogénea en el tiempo, y esto significa que las probabilidades de transición entre estados no dependen del momento específico en el que sucede la transición. Si las probabilidades de transición dependen del momento en que ocurre la transición, el modelo de la cadena de Markov podría ser inexacto.
-
Ergodicidad. Una cadena de Markov generalmente se considera ergódica, lo cual significa que es posible llegar a cualquier estado desde cualquier otro estado en un número finito de pasos. Si no se cumple esta suposición, el modelo de la cadena de Markov puede resultar inexacto.
En general, los modelos de cadenas de Markov son más adecuados para conjuntos de datos con dependencias relativamente simples y pocos estados o variables. Si el conjunto de datos tiene dependencias complejas o una gran cantidad de estados o variables, otras técnicas de modelado pueden ser más apropiadas.
Estimación de la probabilidad
Después de modelar la cadena de Markov, necesitamos estimar la probabilidad de transición de cada estado. Hay una serie de métodos que podemos usar. Resultará útil repetirlos para comprender mejor el alcance y las capacidades de las cadenas de Markov. Existen varios métodos para estimar la probabilidad de transición entre los estados en las cadenas de Markov, estos incluyen:
- La estimación de máxima verosimilitud (maximum likelihood estimation, MLE): el objetivo es estimar la probabilidad de un evento o secuencia de eventos basada en los datos observados. En el contexto de las cadenas de Markov, esto significa que queremos estimar la probabilidad de una transición de un estado a otro según un conjunto de transiciones observadas.
Para implementar la MLE para cadenas de Markov, primero debemos recopilar un conjunto de transiciones observables. Podemos hacer esto ejecutando una simulación o recopilando datos reales. Una vez disponemos de las transiciones observadas, podemos usarlas para estimar las probabilidades de transición.
Para estimar las probabilidades de transición, podemos ejecutar los siguientes pasos:
- Especificamos una matriz para almacenar las probabilidades de transición. La matriz debe tener las dimensiones num_states x num_states, donde num_states será el número de estados en la cadena de Markov.
- Inicializamos la matriz con todas las probabilidades establecidas en 0. Esto se puede hacer con un ciclo anidado que itere por todos los elementos de la matriz.
- Repetimos las transiciones observadas y actualizamos las probabilidades de transición. Para cada transición observada del estado i al estado j, aumentaremos la probabilidad de transition_probs[i][j] en 1.
- Normalizamos las probabilidades de transición para que su suma resulte igual a 1. Esto se puede lograr dividiendo cada elemento de la matriz por la suma de los elementos en la fila correspondiente.
Una vez se hayan estimado las probabilidades de transición, podremos usarlas para predecir la probabilidad de transición de un estado a otro. Por ejemplo, si queremos predecir la probabilidad de una transición del estado i al estado j, podremos usar la fórmula P(j | i) = transition_probs[i][j].
- La probabilidad bayesiana implica utilizar el teorema de Bayes para actualizar la distribución de probabilidad de los parámetros del modelo en función de nuevos datos. Para utilizar la estimación de probabilidad bayesiana con una cadena de Markov, primero deberemos definir una distribución previa sobre los estados de la cadena de Markov. Esta distribución previa representará nuestra opinión inicial sobre las probabilidades de los distintos estados de la cadena. Luego podremos usar la actualización bayesiana para actualizar nuestra comprensión de las probabilidades de estado conforme dispongamos de nueva información. Por ejemplo, vamos a imaginar que tenemos una cadena de Markov de tres estados: A, B y C. Comenzaremos con el estado anterior, que se puede representar como:
P(A) = 0,4 P(B) = 0,3 P(C) = 0,3
Esto significa que inicialmente asumiremos que la probabilidad de estar en el estado A es del 40 %, la probabilidad de estar en el estado B es del 30 % y la probabilidad de estar en el estado C es del 30 %.
Ahora supongamos que vemos cómo el sistema pasa del estado A al estado B. Podemos usar esta nueva información para actualizar nuestra comprensión de las probabilidades de estado con una estimación de probabilidad bayesiana. Para hacer esto, necesitaremos conocer las probabilidades de transición entre estados. Supongamos que las probabilidades de transición son:
P(A -> B) = 0,8
P(A -> C) = 0,2
P(B -> A) = 0,1
P(B -> B) = 0,7
P(B -> C) = 0,2
P(C -> A) = 0,2
P(C -> B) = 0,3
P(C -> C) = 0,5
Estas probabilidades de transición nos indican la probabilidad de transición de un estado a otro. Por ejemplo, la probabilidad de transición del estado A al estado B es 0,8, mientras que la probabilidad de transición del estado A al estado C es 0,2.
Usando estas probabilidades de transición, ahora podremos actualizar nuestra comprensión de las probabilidades de estado usando la estimación de probabilidad bayesiana. En concreto, podemos usar la regla de Bayes para calcular la distribución posterior sobre estados dada la nueva información de que el sistema ha pasado del estado A al estado B. Esta distribución posterior será nuestra representación actualizada de las probabilidades de estado considerando la nueva información que hemos recibido.
Por ejemplo, usando la regla de Bayes, podremos calcular la probabilidad posterior de estar en el estado A de la siguiente manera:
P(A | A -> B) = P(A -> B | A) * P(A) / P(A -> B)
Sustituyendo valores de nuestra distribución anterior y la probabilidad de transición, obtendremos:
P(A | A -> B) = (0,8 * 0,4) / (0,8 * 0,4 + 0,1 * 0,3 + 0,2 * 0,3) = 0,36
De forma similar, podremos calcular las probabilidades posteriores de estar en los estados B y C:
P(B | A -> B) = (0,1 * 0,3) / (0,8 * 0,4 + 0,1 * 0,3 + 0,2 * 0,3) = 0,09
- Algoritmo EM (Expectation-maximization, EM). Para usar el EM para estimar la probabilidad con una cadena de Markov, deberemos observar las transiciones entre los estados de la cadena de Markov durante un periodo de tiempo. Usando dichos estados como base, podremos usar el algoritmo EM para estimar las probabilidades de transición, mejorando iterativamente nuestras estimaciones según los datos observados. El algoritmo de EM funciona alternando dos pasos: un paso de expectativa (paso E) y un paso de maximización (paso M). En el paso E, estimamos el valor esperado de log-verosimilitud total de los datos dadas las estimaciones de parámetros actuales. En el paso M, maximizamos el valor esperado de log-verosimilitud total de los datos respecto a los parámetros para obtener estimaciones de parámetros actualizadas. Luego repetimos estos pasos hasta que las estimaciones de los parámetros converjan en un valor estable. Por ejemplo, si hemos observado una cadena de Markov de tres estados (A, B y C) y deseamos estimar las probabilidades de transición entre estados, podemos usar el algoritmo EM para mejorar iterativamente nuestras estimaciones de probabilidad de transición según los datos observados.
La principal ventaja de usar EM para la estimación de la probabilidad es que el algoritmo puede procesar datos incompletos o con ruido, además de estimar los parámetros del modelo estadístico incluso si la distribución subyacente no se conoce por completo. No obstante, el algoritmo puede ser sensible a la inicialización y es posible que no siempre converja al máximo global de la función de verosimilitud logarítmica. También requiere importantes recursos computacionales, pues involucra la evaluación múltiple de la función de log-verosimilitud y su gradiente.
- Estadística paramétrica. Para usar la estimación de la probabilidad paramétrica con una cadena de Markov, necesitaremos observar las transiciones entre los estados de la cadena de Markov durante un periodo de tiempo. Usando como base estos datos, podremos ajustar el modelo paramétrico a las probabilidades de transición, asumiendo que la distribución subyacente siga una distribución particular, como la distribución normal o la distribución binomial. Luego podemos usar este modelo para estimar la probabilidad de una transición de un estado a otro. Por ejemplo, si observamos una cadena de Markov con tres estados (A, B y C) y descubrimos que la transición del estado A al estado B ha ocurrido 10 veces de 20 transiciones, podremos ajustar el modelo binomial a los datos y usarlo para estimar la probabilidad de transición del estado A al estado B.
La principal ventaja de la estimación de probabilidad paramétrica es que puede resultar más precisa que los métodos no paramétricos, que no hacen suposiciones sobre la distribución subyacente. Sin embargo, esto requiere hacer suposiciones sobre la distribución subyacente, lo cual puede no ser siempre apropiado o puede dar lugar a estimaciones sesgadas. Además, los métodos paramétricos pueden resultar menos flexibles y menos fiables que los métodos no paramétricos porque son sensibles a las desviaciones de la distribución esperada.
- Estimación no paramétrica. Para usar la estimación de probabilidad no paramétrica con una cadena de Markov, necesitaremos observar las transiciones entre los estados de la cadena de Markov durante un periodo de tiempo. A partir de estos datos, podremos estimar la probabilidad de una transición de un estado a otro contando el número de veces que ha sucedido la transición y dividiéndolo por el número total de transiciones. Por ejemplo, si observamos una cadena de Markov con tres estados (A, B y C) y descubrimos que la transición del estado A al estado B ha ocurrido 10 veces de 20 transiciones, podríamos estimar la probabilidad de pasar del estado A al estado B en 0,5.
Este método de estimación de la probabilidad se denomina método de distribución empírica y se puede utilizar para estimar la probabilidad de cualquier conjunto de eventos, no solo las transiciones en una cadena de Markov. La principal ventaja de la estimación de probabilidad no paramétrica es que no requiere ningún supuesto sobre la distribución subyacente, lo que la convierte en un método flexible y fiable para estimar probabilidades. No obstante, puede resultar menos precisa que los métodos paramétricos, que hacen suposiciones sobre la distribución subyacente para estimar mejor las probabilidades.
- Bootstrap (Bootstrapping). Este es un método general que se puede usar para estimar las probabilidades en una cadena de Markov o cualquier otro modelo probabilístico. La idea básica consiste en usar una pequeña cantidad de observaciones para estimar la distribución de probabilidad sobre los estados del sistema y luego utilizar esa distribución para generar una gran cantidad de observaciones sintéticas. Las observaciones sintéticas se pueden utilizar para estimar mejor la distribución de probabilidad. Podemos repetir el proceso hasta lograr el nivel deseado de precisión.
Para usar bootstrap a la hora de estimar la probabilidad en una cadena de Markov, primero necesitaremos tener una cadena de Markov inicial con sus estados. Al igual que el método bayesiano, el bootstrap actualiza y mejora las cadenas de Markov ya existentes. Cada estado de la cadena se vincula con la probabilidad de transición a otros estados, mientras que las probabilidades de transición entre diferentes pares de estados no dependen de la historia del sistema. Una vez tengamos la cadena de Markov original, podremos usar el bootstrap para estimar la distribución de probabilidad sobre sus estados. Esto requerirá comenzar con un pequeño número de observaciones del sistema, como algunas configuraciones de estado iniciales o una secuencia corta de transiciones de estado. Luego podremos usar estas observaciones para estimar la distribución de probabilidad sobre los estados del sistema.
Por ejemplo, si tenemos una cadena de Markov con tres estados A, B y C, y hemos observado la transición del sistema del estado A al estado B varias veces, y del estado B al estado C varias veces, podemos usar estas observaciones para estimar la probabilidad de transición del estado A al estado B y del estado B al estado C.
Una vez hayamos estimado la distribución de probabilidad sobre los estados del sistema, podremos usarla para generar una gran cantidad de observaciones sintéticas del sistema. Esto se puede hacer usando la muestra aleatoria de una distribución de probabilidad para simular transiciones de estado. Luego, las observaciones sintéticas se podrán usar para estimar mejor la distribución de probabilidad y repetir el proceso hasta lograr el nivel deseado de precisión.
El bootstrap puede resultar útil al estimar probabilidades en una cadena de Markov porque permite usar una pequeña cantidad de observaciones para generar una gran cantidad de observaciones sintéticas, lo que puede mejorar la precisión de las estimaciones. También es relativamente fácil de implementar y se puede usar con una gran cantidad de modelos de probabilidad. Sin embargo, la precisión de las estimaciones con bootstrap depende de la calidad de las observaciones iniciales y del modelo probabilístico subyacente. A veces, la precisión del método puede resultar menor que la de otros métodos de estimación.
- Estimación de jackknife (Jackknife estimation). Este método ejecuta varias simulaciones de cadenas de Markov, excluyendo cada vez un estado o grupo de estados diferente. Luego se estima la probabilidad de que ocurra un evento promediando las probabilidades de que suceda el evento en cada una de las simulaciones. A continuación, le mostraremos una explicación más detallada del proceso:
- Configure una cadena de Markov y defina el evento que le interese. Por ejemplo, el evento podría ser el logro de cierto estado en una cadena, o una transición entre dos estados específicos.
- Ejecute múltiples simulaciones de cadenas de Markov, excluyendo un estado o grupo de estados distinto cada vez. Esto se puede conseguir simplemente no considerando los estados excluidos al ejecutar la simulación, o estableciendo sus probabilidades de transición en cero.
- Para cada simulación, calcule la probabilidad de que suceda un evento. Esto se logra realizando un análisis detallado del balance general o utilizando métodos como el muestreo de Monte Carlo o la multiplicación de matrices.
- Promedie las probabilidades de que suceda un evento en cada una de las simulaciones para obtener una estimación de la probabilidad de que ocurra un evento en una cadena de Markov completa.
El uso del método jackknife para estimar la probabilidad en las cadenas de Markov tiene varias ventajas. Una de ellas es que nos permite estimar con mayor precisión la probabilidad de que ocurra un evento, ya que se tiene en cuenta el impacto de cada estado individual en la probabilidad general. Otra ventaja es que resulta relativamente fácil de implementar y se puede automatizar fácilmente. No obstante, el método jackknife también tiene algunas limitaciones. Una de sus limitaciones es que requiere ejecutar múltiples simulaciones de cadenas de Markov, lo cual puede resultar computacionalmente costoso para cadenas grandes o complejas. Además, la precisión de la estimación puede depender del número y la elección de los estados excluidos en la simulación.
- Validación cruzada (cross-validation). Este método se puede usar para estimar la probabilidad de que ocurra un evento particular en una cadena de Markov, e implica dividir los datos en varios pliegues o subconjuntos y utilizar cada pliegue como conjunto de prueba para evaluar el rendimiento del modelo en ese subconjunto. Para usar la estimación de la probabilidad de validación cruzada de una cadena de Markov, primero deberemos configurar la cadena de Markov con los estados y transiciones deseados. Luego dividiremos los datos por el número deseado de pliegues, iterando a continuación sobre cada pliegue y usándolo como un conjunto de prueba para evaluar el rendimiento del modelo en ese subconjunto. Este trabajo implicará usar una cadena de Markov para estimar la probabilidad de que ocurra cada evento en el conjunto de prueba y comparar estas estimaciones con los resultados reales en el conjunto de prueba.
Finalmente, promediaremos el rendimiento de todos los pliegues para obtener una estimación general del rendimiento del modelo. Esto puede resultar útil para evaluar el rendimiento del modelo y ajustar los parámetros de la cadena de Markov para mejorar su precisión. Para utilizar la estimación de la probabilidad de validación cruzada de la cadena de Markov, los datos deberán estar distribuidos de forma independiente e igual, lo cual significa que cada subconjunto de datos deberá representar un conjunto de datos común.
Cada uno de estos métodos tiene sus propias ventajas y desventajas, y la elección del método dependerá de las características específicas de los datos y los objetivos del análisis.
Implementación usando el Wizard MQL5
Para codificar una clase de señal que implemente cadenas de Markov, usaremos la clase CMarkovCPD en el archivo dataanalysis.mqh en la carpeta alglib. Modelaremos las cadenas de tiempo discreto. Una cadena de tiempo discreto tendrá cinco estados, que serán los últimos cinco cambios en el precio de cierre. Por lo tanto, el marco temporal en el que se prueba o funciona el asesor experto determinará una unidad de tiempo discreta. Para estimar las probabilidades de transición de estado, la clase CMarkovCPD necesitará la adición de datos de seguimiento para entrenar el modelo. La cantidad de datos de seguimiento para añadir estará determinada por el parámetro de entrada m_signal_tracks optimizado. A continuación, le mostramos cómo inicializar el modo y añadir los datos de seguimiento (entrenamiento).
CMCPDState _s; CMatrixDouble _xy,_p; CMCPDReport _rep; int _k=m_signal_tracks; _xy.Resize(m_signal_tracks,__S_STATES); m_close.Refresh(-1); for(int t=0;t<m_signal_tracks;t++) { for(int s=0;s<__S_STATES;s++) { _xy[t].Set(s,GetState(Close(Index+t+s)-Close(Index+t+s+1),Close(Index+t+s+1)-Close(Index+t+s+2))); } }
Datos de precios de cierre normalizados en 1.0. Si el cambio del precio de cierre es negativo, la entrada será inferior a 1,0; si es positivo, la entrada será superior a 1,0 sin cambios, dando exactamente 1,0. Esta normalización se realiza usando la función GetState, mostrada a continuación.
//+------------------------------------------------------------------+ //| Normalizer. | //+------------------------------------------------------------------+ double CSignalMC::GetState(double NewChange,double OldChange) { double _state=0.0; double _norm=fabs(NewChange)/fmax(m_symbol.Point(),fabs(NewChange)+fabs(OldChange)); if(NewChange>0.0) { _state=_norm+1.0; } else if(NewChange<0.0) { _state=1.0-_norm; } return(_state); }
Tras añadir los datos, deberemos inicializar un ejemplar de la clase CMCPDState, ya que este es el objeto que procesará todos los datos en nuestro modelo y ayudará a calcular las puntuaciones de probabilidad. Lo haremos así:
CPD.MCPDCreate(__S_STATES,_s); CPD.MCPDAddTrack(_s,_xy,_k); CPD.MCPDSetTikhonovRegularizer(_s,m_signal_regulizer); CPD.MCPDSolve(_s); CPD.MCPDResults(_s,_p,_rep);
De forma ideal, el parámetro de entrada m_signal_regulazier no debería ser un valor doble abstracto, sino un valor doble que represente la cantidad de datos de seguimiento. En otras palabras, debería ser proporcional a los datos de seguimiento obtenidos de la función GetState. Esto significa que si deseamos optimizarlo perfectamente, digamos en el rango de 0,5 a 0,0, deberemos multiplicarlo por la magnitud de los datos de seguimiento más grandes al usar el método de regularización de Tíjonov.
La matriz '_p' será nuestra matriz de transición con todas las probabilidades de transición entre estados. A continuación, se adjunta el código completo de la clase de señal.
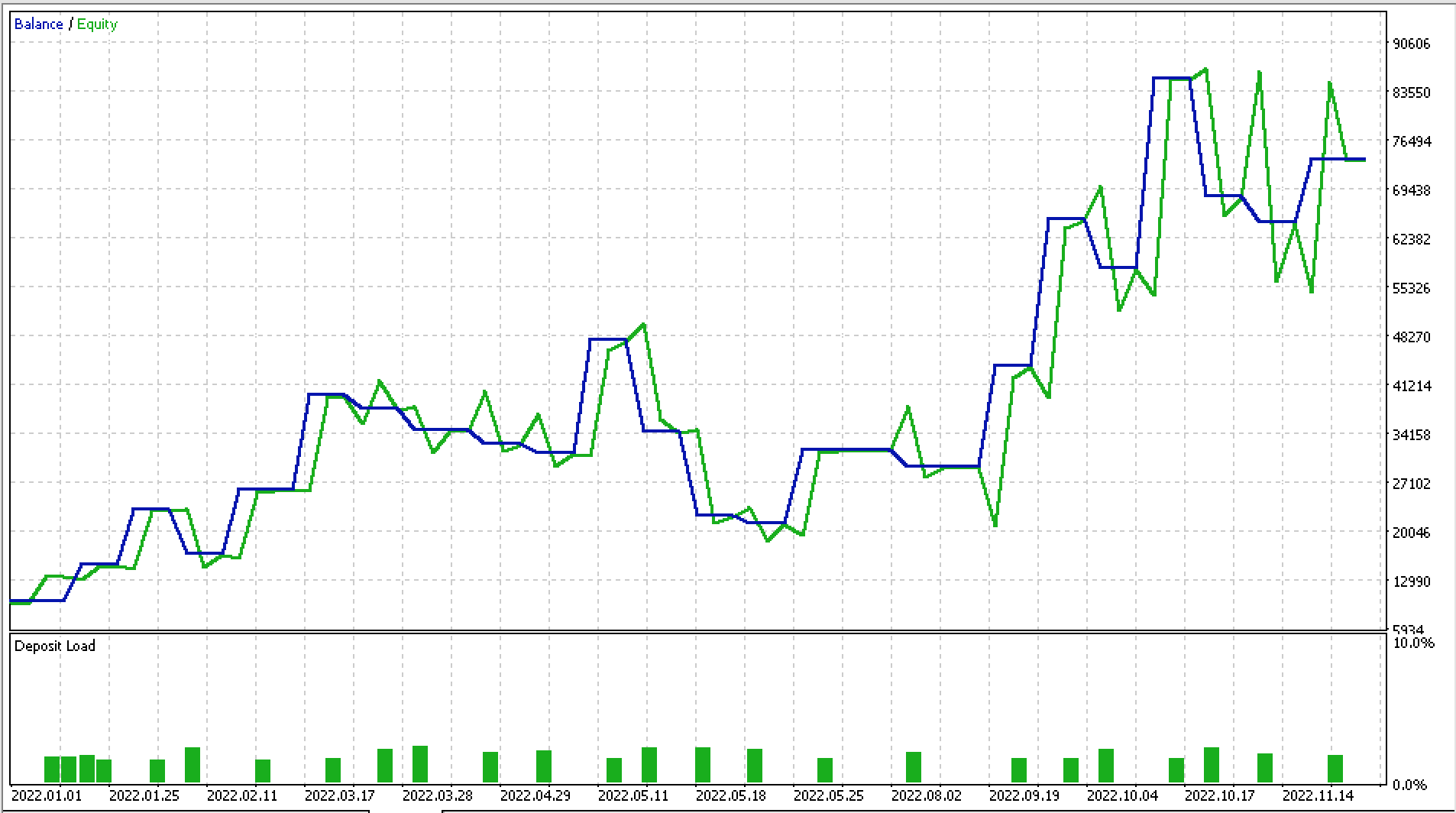
Hemos hecho algunas pruebas con EURJPY D1 para 2022. Más abajo, se muestra una parte del informe y la curva de equidad.
Conclusión
Las cadenas de Markov son una herramienta matemática que se puede usar para modelar el comportamiento de los mercados financieros. Resultan especialmente útiles porque permiten a los tráders analizar la probabilidad de las condiciones futuras del mercado en función del estado actual del mismo. Esto puede ser muy útil en el comercio, pues permite a los tráders tomar decisiones informadas sobre qué operaciones realizar y cuándo realizarlas.
Uno de los beneficios clave del uso de las cadenas de Markov en los mercados financieros es que permiten a los tráders analizar y predecir la evolución de las tendencias del mercado a lo largo del tiempo. Esto es sobre todo importante en mercados que cambian rápidamente, donde las tendencias pueden mudar al momento y resulta difícil predecir cómo se comportará el mercado. Usando las cadenas de Markov, los tráders pueden determinar los caminos más probables que tomará el mercado y usar esta información para tomar decisiones comerciales informadas.
Otra ventaja de las cadenas de Markov es que pueden utilizarse para analizar los riesgos vinculados a diferentes transacciones. Analizando las probabilidades de las diferentes condiciones del mercado, los tráders pueden determinar el riesgo asociado con las diferentes transacciones y seleccionar las que tengan más probabilidades de éxito. Esto puede ser especialmente útil en mercados volátiles donde el riesgo de pérdida resulta mayor.
En resumen, las cadenas de Markov son una herramienta importante para los tráders en los mercados financieros, ya que les permiten analizar y predecir el comportamiento del mercado, determinar los caminos más probables que tomará este y evaluar el riesgo vinculado a distintas transacciones.
Traducción del inglés realizada por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/en/articles/11930
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Aprendiendo a diseñar un sistema comercial con Gator Oscillator
Aprendiendo a diseñar un sistema comercial con Gator Oscillator
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso
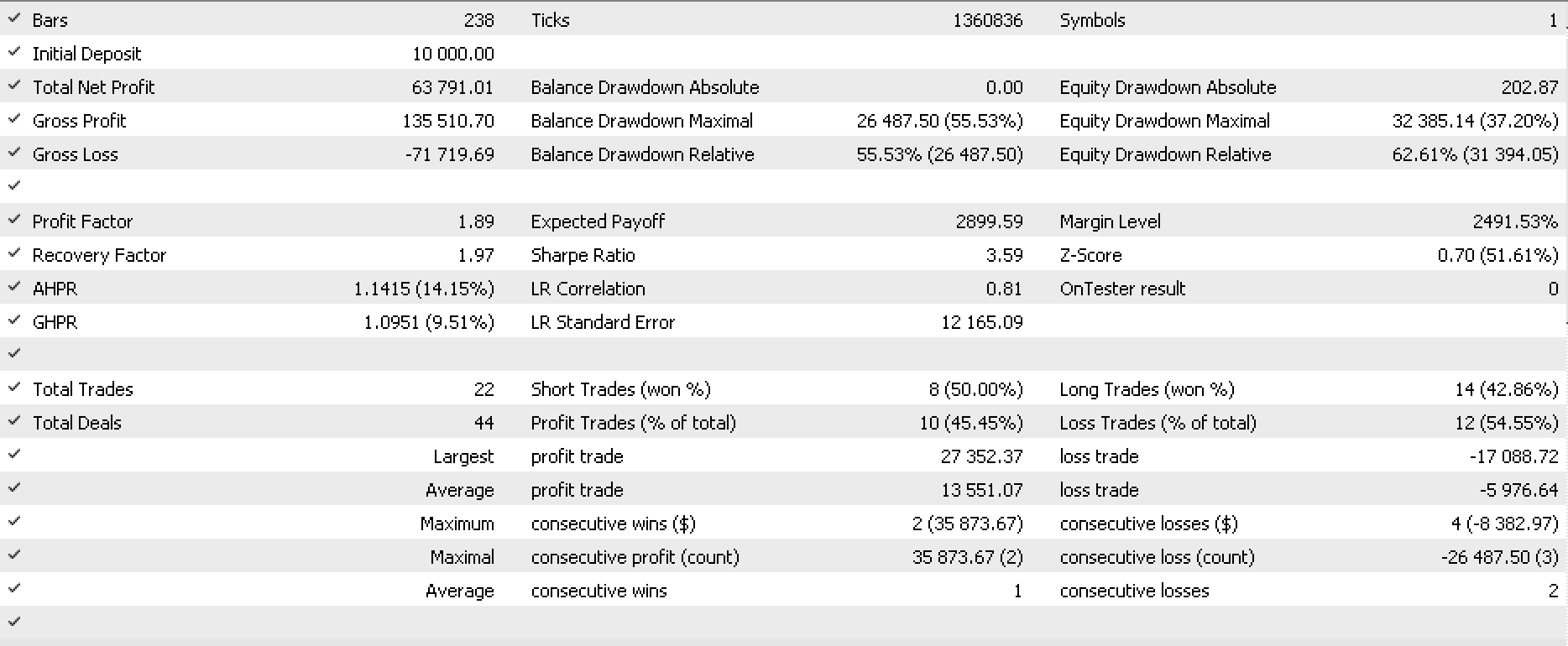
¿Puedes dar, la ea en esa foto?
El código no funciona
Hola Stephen,
Estoy obteniendo resultados interesantes utilizando esta clase MC. Sin embargo, estoy recibiendo muchas líneas de mensajes en la ficha Diario, como este: "CAp::Assert CMarkovCPD::MCPDAddTrack: XY contains infinite or NaN elements". ¿A qué se debe? ¿Debería preocuparme? ¿Qué me recomendáis para librarme de estos mensajes?
Gracias