
MQL5行列を使用した誤差逆伝播法によるニューラルネットワーク
機械学習、特にニューラルネットワークは、かなり前にトレーダーのツールボックスの一部になりました。ニューラルネットワークに関して言えば、それらの一部は「教師あり学習」手法を使用しており、その中でも誤差逆伝播法によるニューラルネットワーク(BPNN)は特別な位置を占めています。このようなアルゴリズムには、さまざまな変更が加えられています。たとえば、ディープニューラルネットワーク、回帰型ニューラルネットワーク、畳み込みニューラルネットワークの基礎として使用されています。したがって、このトピックに関する豊富な資料(およびこのサイトの記事)に驚くべきではありません。今日は、MQL5にとって比較的新しい方向でこのトピックについて詳しく説明します。少し前にMQL5で行列とベクトルで動作するように設計された新しいAPI機能が導入されたからです。これにより、データが全体として(ブロックで)処理されるときに、要素ごとではなくニューラルネットワークで一括計算を実装できるようになります。
行列演算を使用すると、ネットワークの順伝播(フィードフォワード)と誤差逆伝播法の式を具体化するプログラム命令が大幅に簡素化されます。これらの操作は実際には単一行の式に変換されるので、アルゴリズムを改善するための他の重要な側面に集中できます。
この記事では、誤差逆伝播法ネットワークの理論を簡単に復習し、この理論を使用してネットワークを構築するための汎用クラスを作成します。上記の式はソースコードにほとんどそのままに反映されます。したがって、初心者は、サードパーティの出版物を探す必要なく、このテクノロジを学習しながらすべての手順を実行できます。
すでに理論をご存じの方は、スクリプト、インジケータ、EAでのクラスの実用的な使用について説明する記事の第2部に安全に進むことができます。
ニューラルネットワークの理論の紹介
ニューラルネットワークは、単純な計算要素であるニューロンで構成されます。ニューロンは通常、論理的に層に結合され、信号が通過する接続(シナプス)によって結合されます。信号は、取引を含むさまざまなアプリケーション領域からの状況を表すために使用できる数学的抽象です。
シナプスは、あるニューロンの出力を別のニューロンの入力に接続します。これは、重みwiによって特徴付けられます。ニューロンの現在の状態は、その接続(入力)で受信した信号の加重和です。
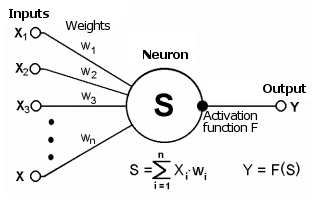
ニューロンの模式図
この状態は、特定のニューロンの出力値を生成する非線形活性化関数を使用してさらに処理されます。出力から、信号は次の接続されたニューロン(存在する場合)のシナプスに沿ってさらに進むか、ニューラルネットワークの応答のコンポーネントになります(現在のニューロンが最後の層にある場合)。
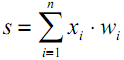 | (1) |
| | (2) |
非線形性の存在により、ネットワークの計算能力が向上します。双曲線正接やロジスティック関数など、さまざまな活性化関数を使用できます。どちらもいわゆるS字関数またはシグモイド関数です。
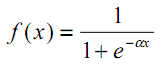 | (3) |
以下で説明するように、MQL5には組み込み活性化関数の大規模なセットがあります。関数は、特定の問題(回帰、分類)に基づいて選択する必要があります。通常、いくつかの関数を選択し、実験的に最適なものを見つけることができます。
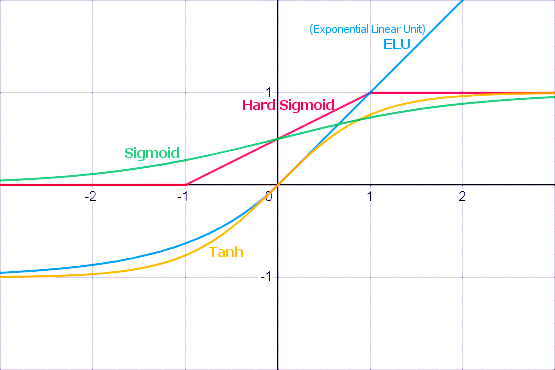
良く知られている活性化関数
活性化関数は、制限付きまたは無制限のさまざまな値の範囲を持つことができます。特に、シグモイド(3)はデータを範囲[0,+1]にマッピングするもので、分類問題に適しています。双曲線正接はデータを範囲[-1,+1]にマッピングするもので、回帰と予測の問題により適していると考えられます。
活性化関数の重要な特性の1つは、その導関数が軸全体に沿って定義される方法です。有限で非ゼロの導関数の存在は、後で説明する誤差逆伝播法アルゴリズムにとって重要です。S字関数はこの要件を満たします。さらに、標準の活性化関数は通常、導関数のかなり単純な分析表記法を持っているため、効率的な計算が保証されます。たとえば、シグモイド(3)の場合は次のようになります。
| | (4) |
単層ニューラルネットワークを次の図に示します。
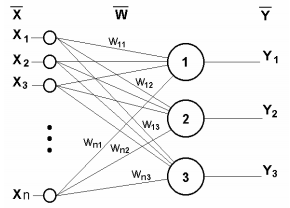
単層ニューラルネットワーク
その動作原理は、次の式で数学的に説明できます。
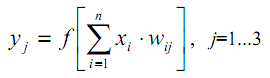 | (5) |
明らかに、1つの層のすべての重み係数はW行列に適合できます。この行列では、各wij要素がj番目のニューロンのi番目の接続の値を設定します。したがって、ニューラルネットワークで発生するプロセスは次の行列形式で記述できます。
| Y=F(XW) | (6) |
ここで、XとYはそれぞれ入力信号ベクトルと出力信号ベクトルです。F(V)は、ベクトルVのコンポーネントに要素ごとに適用される活性化関数です。
層の数と各層のニューロンの数は、入力データ(次元、データセットのサイズ、分布法則、その他の多くの要因)によって異なります。多くの場合、ネットワーク構成は試行錯誤によって選択されます。
これを説明するために、二層ネットワークの図を示します。
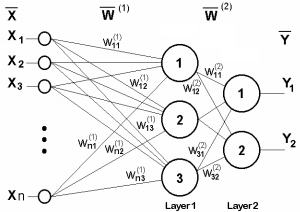
二層ニューラルネットワーク
ここで、見落としていた点を1つ考えてみましょう。活性化関数の図から、S字型の関数が最大の勾配を持ち、信号を適切に伝達するTの値があることは明らかですが、他の関数には1つ以上の特徴的な限界点があります。したがって、各ニューロンの主な作業はTの近くで発生します。通常、T=0または0の近くにあるため、活性化関数の引数をTに自動的にシフトする機能があることが望ましいです。
この現象は、次のようになるはずの式(1)には反映されていません。
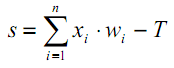 | (7) |
このようなシフトは通常、別の疑似入力をニューラル層に追加することによって実装されます。この疑似入力の値は常に1です。この入力に番号0を割り当てましょう。この場合、次のようになります。
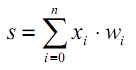 | (8) |
ここで、w0=–T、x0=1です。
教師あり学習アルゴリズムでは、人間の専門家によって事前に準備およびマークされた訓練データがあります。このデータでは、目的の出力ベクトルが入力ベクトルに関連付けられています。
訓練プロセスは、次の段階で実装されます。
1.重み行列要素を初期化します(通常は小さなランダム値)。
2.ベクトルの1つを入力し、ネットワークの反応を計算します。これは信号の順方向伝搬です。このフェーズは、訓練済みネットワークの通常の運用中にも使用されます。
3.理想的な出力値と生成された出力値の差を計算してネットワーク誤差を見つけ、この誤差に応じて何らかの式に従って重みを調整します。
4.誤差が指定された最小レベル以下に減少する(訓練が正常に完了する)まで、または事前定義された訓練ループの最大数に達する(ニューラルネットワークが失敗する)まで、データセットのすべての入力ベクトルに対してステップ2からのループを続行します。
単層ネットワークの場合、重み調整式は非常に単純です。
| | (9) |
| | (10) |
ここで、δはネットワーク誤差(ネットワーク応答と理想値の差)、tとt+1は現在の反復と次の反復の数、νは学習率(0<ν<1)、iは入力インデックス、jは層内のニューロンのインデックスです。
しかし、多層ネットワークの場合はどうすればよいでしょうか。これが、誤差逆伝播法のアイデアに行き着くところです。
誤差逆伝播法アルゴリズム
最もよく知られているニューラルネットワーク構造の1つは多層構造です。この構造では、特定の層の各ニューロンが前の層のすべてのニューロンに接続されるか、最初の層の場合はすべてのネットワーク入力に接続されます。このようなニューラルネットワークは、全結合と呼ばれます。この構造についてさらに説明します。他の多くのタイプのニューラルネットワーク、特に畳み込みネットワークでは、リンクは層の限られた領域、いわゆるコアを接続します。これは、ネットワーク要素のアドレス指定を多少複雑にしますが、誤差逆伝播法法の適用性には影響しません。
明らかに、誤差に関する情報はネットワーク出力からその入力に渡され、層の「導電率」、つまり重みを考慮してすべての層を徐々に通過する必要があります。
最小二乗法によると、最小化されるネットワーク誤差の目的関数は次の値です。
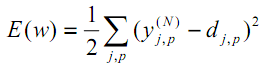 | (11) |
ここで、yjpᴺは、p番目の画像が入力されたときの出力層Nからのニューロンjの実際の出力状態です。djpは、このニューロンの理想的な(望ましい)出力状態です。
総和は、出力層のすべてのニューロンとすべての処理された画像に対して実装されます。1/2という比率は、Eの適切な導関数(2が約される)を取得するためだけに追加されます。これは訓練にさらに使用されます(式(12)を参照)。いずれの場合も、アルゴリズムの重要なパラメータ(比率(条件によっては2倍にしたりと動的に変更))によって重み付けされます。
関数を最小化する最も効果的な方法の1つは、以下に基づくものです。極値への最良の局地的な方向は、特定の点でのこの関数の導関数を示します。正の導関数は最大値になり、負の導関数は最小値になります。もちろん、最大値と最小値が(局地的な)極値であることが判明する可能性があり、最小値に進むには追加のトリックが必要になる場合がありますが、この問題は今のところ舞台裏に置いておきます。
説明されている方法は、勾配降下法です。それによると、重みは次のようにE導関数に基づいて調整されます。
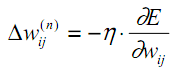 | (12) |
ここでwijは層n-1のi番目のニューロンと層nのj番目のニューロンの間の結合の重み、ηは学習率です。
ニューロンの内部構造に戻り、それに基づいて、式(12)の各計算段階を偏導関数に割り当てます。
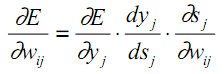 | (13) |
前述のように、yjはニューロンjの出力であり、sjはその入力信号の加重和、つまり活性化関数の引数です。係数dyj/dsjはこの関数の導関数であるため、考慮される逆伝播アルゴリズムで使用するために活性化関数がx軸全体で微分可能でなければならないという要件が設定されます。
次は双曲線正接の場合です。
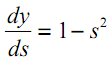 | (14) |
(13)の3番目の要素∂sj/∂wijは、前の層(n-1)のニューロン出力yiに等しくなります。なぜでしょうか。多層ネットワークでは、信号は前の層のニューロンの出力から現在の層のニューロンの入力に送られます。したがって、sjの式(1)は、次のように、より一般的な方法で書き直すことができます。
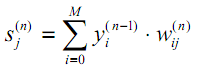 | (15) |
ここで、Mは層n-1のニューロンの数であり、オフセットを設定する一定の出力状態+1を持つニューロンを考慮に入れます。yi(n-1)=xij(n) は、(n-1)番目の層のi番目のニューロンの出力に接続される層nのニューロンjのi番目の入力です。
(13)の最初の要因については、次の上位層で誤差の増分で展開するのが論理的です(誤差値が反対方向に伝播するため)。
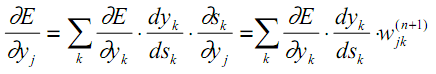 | (16) |
ここで、層n+1のニューロン間でkの合計が実装されます。
(13)での1つの層(ニューロンインデックスj)の最初の2つの因子は、次の層(インデックスk)の重みwjkの前の係数として(16)で繰り返されます。
次の2つの要因を含む中間変数を導入します。
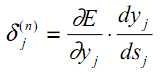 | (17) |
その結果、上位層n+1の値δk(n+1)を使用して、層nのδj(n)を計算するための再帰的な式が得られます。
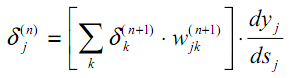 | (18) |
以前と同様に、出力層の新しい変数は、取得した結果と目的の結果の差に基づいて計算されます。
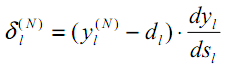 | (19) |
(9)と比較すると、ここに活性化関数の導関数があります。ネットワークの出力層では、タスクによっては活性化関数が存在しない場合があることに注意してください。
これで、式(12)の展開を記述して、学習プロセスで重みを調整できます。
| | (20) |
場合によっては、目的関数の表面上を移動するときに導関数の急激なジャンプを滑らかにする慣性を重み調整プロセスに与えるために、式(20)に前の反復での重み変更重みが追加されます。
| | (21) |
ここで、μは慣性係数、tは現在の反復回数です。
したがって、誤差逆伝播法手順を使用した完全なニューラルネットワーク訓練アルゴリズムは、次のように構築されます。
1.小さな乱数で重み行列を初期化します。
2.データベクトルの1つをネットワークに入力し、通常の操作モードで、信号が入力から出力に伝播するときに、重み付き合計(15)と活性化fの式に従って、層ごとに合計NN結果を計算します。
| | (22) |
ここで、ゼロ入力層のニューロンは、入力信号を供給するためだけに使用され、シナプスと活性化関数を持ちません。
| | (23) |
Iqは、ゼロ層に供給される入力ベクトルのq番目のコンポーネントです。
3.ネットワーク誤差が指定された小さな値よりも小さい場合、プロセスは成功として停止します。誤差が大きい場合は、次の手順に進みます。
4.式(19)を使用して出力層N:δを計算し、値の変化Δwを式(20)または(21)を使用して計算します。
5.逆順の他のすべての層、n=N-1,...1について、それぞれ式(18)と(20)(または(18)と(21))を使用してδとΔwを計算します。
6.前の反復t-1に基づいて、反復tのNNのすべての重みを調整します。
| | (24) |
7.手順2から始まるループでプロセスを繰り返します。
誤差逆伝播法アルゴリズムを使用して訓練されているネットワーク内の信号を、次の図に示します。
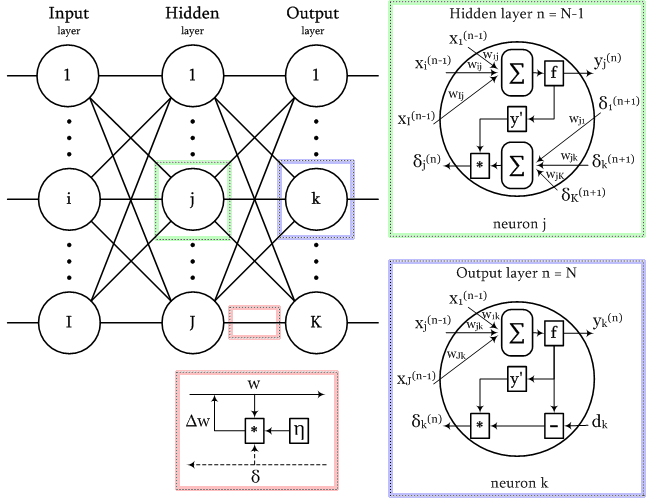
誤差逆伝播法アルゴリズムの信号
すべての訓練画像は交互にネットワークに供給されるため、他の画像を記憶するときに1つを「忘れる」ことはありません。通常、これはランダムな順序でおこなわれますが、データを行列に配置して単一のセットとして計算するため、実装に別のランダム要素を導入します。これについては後で説明します。
行列を使用するということは、入力およびターゲットの訓練データだけでなく、すべての層の重みが行列で表されることを意味します。したがって、上記の式、およびそれに応じて、アルゴリズムは行列形式を受け取ります。言い換えれば、入力データと降雨データの別々のベクトルを操作することはできませんが、ステップ2から7までのループ全体がデータセット全体に対して即座に計算されます。このようなループの1つを学習エポックと呼びます。
活性化関数の概要
記事の添付ファイルには、MQL5でサポートされているすべての活性化関数(青)とその派生関数(赤)のサムネイルをチャートに表示するAF.mq5スクリプトが含まれています。このスクリプトは、すべての関数がウィンドウに収まるようにサムネイルを自動的にスケーリングします。詳細な画像が必要な場合は、ウィンドウを最大化することをお勧めします。スクリプトによって生成された画像の例を以下に示します。
活性化関数の正しい選択は、NNのタイプと問題によって異なります。さらに、複数の異なる活性化関数を1つのネットワーク内で使用できます。たとえば、SoftMaxは、層の出力値を要素ごとではなく相互接続で処理するという点で、他の関数とは異なります。値を確率として解釈できるように値を正規化します(それらの合計は1)。これは複数の分類に使用されます。
このトピックは非常に広範であり、別の記事か連載が必要です。現時点では、すべての関数に長所と短所の両方があり、ネットワーク障害につながる可能性があることに注意してください。特に、S字関数は、信号がS字曲線の飽和セクションに落ち始め、したがって重みの調整がゼロになる傾向がある場合、「勾配消失」問題によって特徴付けられます。単調に増加する関数には、勾配が爆発的に増加するという問題があります(重みが絶えず増加し、数値オーバーフローとNaN(NotANumber)が発生するため、「勾配の爆発」)。ネットワークの層が増えるほど、これら2つの問題が発生する可能性が高くなります。これらの問題を解決するには、データの正規化(入力層と中間層の両方)、ネットワーク間引きアルゴリズム(「ドロップアウト」)、一括学習、ノイズ、その他の正則化方法など、さまざまな手法があります。それらのいくつかをさらに検討します。
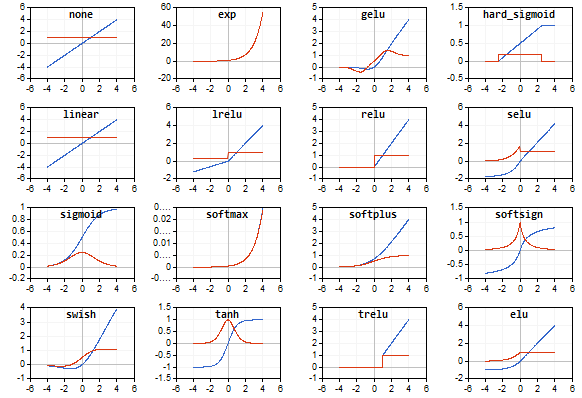
すべての活性化関数を備えたデモスクリプト
MatrixNetクラスにニューラルネットワークの実装
MQL5行列に基づくニューラルネットワーククラスの作成を開始しましょう。ネットワークは層で構成されているので、層ごとにニューロンの重みと出力値の配列を記述します。層の数はn変数に格納され、各層出力のニューロンの重みと信号はそれぞれ重み行列と出力'行列に格納されます。「出力」とは、ネットワーク出力だけでなく、任意の層のニューロン出力での信号を指すことに注意してください。したがって、outputs[i]は中間層も記述し、入力データが書き込まれるゼロ層も記述します。
重み配列と出力'配列のインデックス付けを次の図に示します(簡単にするために、各ニューロンと+1シフトソースとの接続は示していません)。
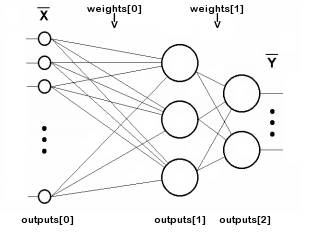
二層ネットワークでの行列配列のインデックス付け
この層は重みを必要としないため、数値nには入力層は含まれません。
class MatrixNet { protected: const int n; matrix weights[/* n */]; matrix outputs[/* n + 1 */]; ENUM_ACTIVATION_FUNCTION af; ENUM_ACTIVATION_FUNCTION of; double speed; bool ready; ...
私たちのネットワークは、2種類の活性化関数(ユーザーが選択)をサポートします。1つは出力を除くすべての層用(af変数に格納)で、もう1つは出力層用(of変数に格納)です。speed変数には、学習率(式(20)のη係数)が格納されます。
ready変数には、Nオブジェクトの初期化が成功したことを示す情報が含まれています。
ネットワークコンストラクタは、すべての層の数とサイズを定義する整数配列layersを受け取ります。ゼロ要素は、入力疑似層のサイズ、つまり各入力ベクトルの特徴の数を設定します。最後の要素は出力層のサイズを決定し、残りのすべての要素は中間の非表示層を定義します。最低でも2層は必要です。追加のallocateメソッドは、行列配列にメモリを割り当てるために記述されています(クラスが拡張されるにつれて、さらに開発します)。
public: MatrixNet(const int &layers[], const ENUM_ACTIVATION_FUNCTION f1 = AF_TANH, const ENUM_ACTIVATION_FUNCTION f2 = AF_NONE): ready(false), af(f1), of(f2), n(ArraySize(layers) - 1) { if(n < 2) return; allocate(); for(int i = 1; i <= n; ++i) { // NB: the weights matrix is transposed, i.e. indexes [row][column] specify [synapse][neuron] weights[i - 1].Init(layers[i - 1] + 1, layers[i]); } ... } protected: void allocate() { ArrayResize(weights, n); ArrayResize(outputs, n + 1); ... }
各重み行列を初期化するために、前の層のサイズ[i-1]が行数として取得され、一定の調整可能なシフトソース+1のために1つのシナプスがそれに追加されます。列の数として、現在の層の層[i]のサイズを使用します。各重み行列では、最初のインデックスは行列の左側の層を参照し、2番目のインデックスは右側の層を参照します。
このような番号付けは、順方向伝搬(通常のネットワーク操作)中の層行列による信号ベクトルの乗算の単純な記録を提供します。誤差逆伝播法プロセス中(訓練モード)、下位層の誤差を再計算するために、各上位層の誤差ベクトルをその転置された重み行列で乗算する必要があります。
言い換えると、ネットワーク内の情報は2つの反対方向に移動する(入力から出力への動作信号、および出力から入力への誤差)ため、これら2つの方向のいずれかの重み行列を通常の形式で使用し、2番目の方向では転置する必要があります。通常の構成では、直接信号の計算を容易にする行列マーキングを使用します。
ネットワークを通過する信号のプロセスに沿って「出力」行列を埋めます。重みに関しては、ランダムに初期化する必要があります。これは、コンストラクタの最後でrandomizeメソッドを呼び出すことによっておこなわれます。
public: MatrixNet(const int &layers[], const ENUM_ACTIVATION_FUNCTION f1 = AF_TANH, const ENUM_ACTIVATION_FUNCTION f2 = AF_NONE): ready(false), af(f1), of(f2), n(ArraySize(layers) - 1) { ... ready = true; randomize(); } // NB: set values with appropriate distribution for specific activation functions void randomize(const double from = -0.5, const double to = +0.5) { if(!ready) return; for(int i = 0; i < n; ++i) { weights[i].Random(from, to); } }
重み行列の存在は、ネットワーク入力から出力への順伝播パスを実装するのに十分です。訓練については後で扱うため、重みがまだ訓練されていないことは大きな問題ではありません。
bool feedForward(const matrix &data) { if(!ready) return false; if(data.Cols() != weights[0].Rows() - 1) { PrintFormat("Column number in data %d <> Inputs layer size %d", data.Cols(), weights[0].Rows() - 1); return false; } outputs[0] = data; // input the data to the network for(int i = 0; i < n; ++i) { // expand each layer (except the last one) with one neuron for the bias signal // (there is no weight matrix to the right of the last layer, since the signal does not go further) if(!outputs[i].Resize(outputs[i].Rows(), weights[i].Rows()) || !outputs[i].Col(vector::Ones(outputs[i].Rows()), weights[i].Rows() - 1)) return false; // forward the signal from i-th layer to the (i+1)-th layer: weighted sum matrix temp = outputs[i].MatMul(weights[i]); // apply the activation function, the result is received into outputs[i + 1] if(!temp.Activation(outputs[i + 1], i < n - 1 ? af : of)) return false; } return true; }
入力行列データの列数は、ゼロの重み行列の行数から1を引いた数(重みからバイアス信号)に一致する必要があります。
通常のネットワーク操作の結果を読み取るには、getResultsメソッドを使用します。デフォルトでは、出力画層状態行列を返します。
matrix getResults(const int layer = -1) const { static const matrix empty = {}; if(!ready) return empty; if(layer == -1) return outputs[n]; if(layer < -1 || layer > n) return empty; return outputs[layer]; }
testメソッドを使用して、入力データ行列だけでなく、目的のネットワーク応答を含む行列もフィードすることにより、モデルの現在の品質を評価できます。
double test(const matrix &data, const matrix &target, const ENUM_LOSS_FUNCTION lf = LOSS_MSE) { if(!ready || !feedForward(data)) return NaN(); return outputs[n].Loss(target, lf); }
feedForwardメソッドを使用した順伝播パスの後、ここで、指定されたタイプの「損失」を計算します。デフォルトでは、これは二乗平均平方根誤差(LOSS_MSE)であり、回帰および予測の問題に適しています。ただし、ネットワークを画像分類に使用する場合は、LOSS_CCEクロスエントロピーなど、別のタイプのスコアリングを使用する必要があります。
計算誤差が発生した場合、メソッドはNaN(数値ではない)を返します。
それでは、逆伝播に進みましょう。backPropメソッドも、ターゲットデータと出力層のサイズが一致するかどうかを確認することから始まります。これは、出力層(存在する場合)の活性化関数の導関数と、ターゲットデータに対する出力でのネットワークの「損失」を計算します。
bool backProp(const matrix &target) { if(!ready) return false; if(target.Rows() != outputs[n].Rows() || target.Cols() != outputs[n].Cols()) return false; // output layer matrix temp; if(!outputs[n].Derivative(temp, of)) return false; matrix loss = (outputs[n] - target) * temp; // all data line by line
損失行列には、式(19)のδ値が含まれます。
次に、出力層を除くすべての層に対して次のループが実行されます。
for(int i = n - 1; i >= 0; --i) // all layers except the output in reverse order { // remove pseudo-losses in the last element which we added as an offset source // since it is not a neuron and further error propagation is not applicable to it // (we do it in all layers except the last one where the shift element was not added) if(i < n - 1) loss.Resize(loss.Rows(), loss.Cols() - 1); matrix delta = speed * outputs[i].Transpose().MatMul(loss);
ここに正確な式(20)があります。現在の層の学習率η—δと前(下位)の層の関連する出力に基づいて、重みの増分を取得します。
次に、各層について、式(18)を計算して残りのδ値を再帰的に取得します。ここでも、活性化関数の導関数と、より高いδの転置された重み行列への乗算を使用します。入力疑似層(outputs[0])には重みがないため、outputs[]行列のインデックスiは、(i-1)番目のweights[]行列の重みを持つ層に対応します。つまり、順伝播では、重み[0]行列が出力[0]に適用され、出力[1]が生成されます。weights[1]は出力[2]などを生成します。対照的に、誤差逆伝播法では、インデックスは同じです。たとえば、outputs[2](微分後)に転置されたweights[2]が乗算されます。
if(!outputs[i].Derivative(temp, af)) return false; loss = loss.MatMul(weights[i].Transpose()) * temp;
下位層の「損失」δを計算した後、前に取得したデルタを補正することで、weights[i]行列の重みを調整できます。
weights[i] -= delta;
}
return true;
}
これで、エポックとfeedForwardメソッドおよびbackPropメソッドの呼び出しを反復する完全な学習アルゴリズムを実装する準備がほぼ整いました。ただし、最初に、以前に延期したいくつかの理論的なニュアンスに戻らなければなりません。
訓練と正規化
NNは、現在利用可能な訓練データで訓練されます。このデータに基づいて、ネットワーク構成(層の数、層内のニューロンの数など)、学習率などの特性が選択されます。したがって、訓練データで十分に小さい誤差を生成するのに十分強力なネットワークを構築することは常に可能です。ただし、ニューラルネットワークを使用する最終的な目的は、(訓練データセットと同じ暗黙的な依存関係を使用して)将来の未知のデータに対して適切に機能させることです。
訓練されたニューラルネットワークが訓練データでは非常にうまく機能したものの、フォワードテストで失敗した場合の影響は、過剰適合(過学習)と呼ばれます。この影響は、あらゆる方法で回避する必要があります。過剰適合を回避するには、正則化を使用できます。これは、ネットワークの一般化能力を評価するいくつかの追加条件の導入を意味します。正則化にはさまざまな方法がありますが、特に次の方法があります。
- 追加の検証データセット(訓練とは異なる)による訓練済みネットワークのパフォーマンス分析
- 訓練中のニューロンまたは接続の一部のランダムな破棄
- 訓練後のネットワークプルーニング
- 入力データへのノイズの導入
- 人工データ再生
- 訓練中の重みの振幅の弱い一定の減少
- ネットワークがまだ学習できるが、利用可能なデータに過剰適合しない場合の、ボリュームと細かいネットワーク構成の実験的選択
それらのいくつかをクラスに実装します。
まず、訓練メソッドへの入力(dataパラメータ)および出力訓練データ(target'パラメータ)だけでなく、検証データセット(入力および関連する出力ベクトル(validationとcheck)からも構成される)の入力も有効にします。
通常、訓練が進むにつれて、訓練データのネットワーク誤差は非常に単調に減少します(「通常」と言ったのは、学習率またはネットワーク容量が正しく選択されていないと、プロセスが不安定になる可能性があるためです)。ただし、このプロセスに沿って検証セットのネットワーク誤差を計算すると、最初は減少し(ネットワークがデータ内の最も重要なパターンを探している間)、次に過剰適合するにつれて増加し始めます(ネットワークが訓練データセットの特定の特徴に適合するが、検証セットには適合しない場合)。したがって、検証誤差が上昇し始めたら、学習プロセスを停止する必要があります。これが「早期停止」アプローチです。
2つのデータセットに加えて、trainメソッドを使用すると、訓練エポックの最大数、目的の精度(つまり、許容可能な平均最小誤差。この場合、訓練も成功の表示で停止する)、および誤差計算メソッド(lf)を指定できます。
学習率(speed)はaccuracyと同じに設定されていますが、設定の柔軟性を高めるために別の値に設定することもできます。これは、比率が自動的に調整されるためです。したがって、初期の概算値はそれほど重要ではありません。
double train(const matrix &data, const matrix &target, const matrix &validation, const matrix &check, const int epochs = 1000, const double accuracy = 0.001, const ENUM_LOSS_FUNCTION lf = LOSS_MSE) { if(!ready) return NaN(); speed = accuracy; ...
訓練セットと検証セットのために、現在のエポックネットワーク誤差値を変数mseとmsevに保存します。避けられないランダムな変動への応答を除外するには、指定されたエポック数の合計から計算される特定の期間pにわたって誤差を平均化する必要があります。平滑化された誤差値はmsema変数とmsevma変数に保存され、以前の値はmsemap変数とmsevmap変数に保存されます。
double mse = DBL_MAX; double msev = DBL_MAX; double msema = 0; // MSE averaging of the training set double msemap = 0; // MSE averaging of the training set in the previous epoch double msevma = 0; // MSE averaging of the validation dataset double msevmap = 0; // MSE averaging of the validation dataset in the previous epoch double ema = 0; // exponential smoothing factor int p = 0; // EMA period p = (int)sqrt(epochs); // empirically choose the period of the EMA averaging of errors ema = 2.0 / (p + 1); PrintFormat("EMA for early stopping: %d (%f)", p, ema);
次に、訓練エポックのループを実行します。後で別の正則化方法であるDropoutを実装するため、検証データを提供しないことを許可します。検証データセットが空でない場合、このセットに対してtestメソッドを呼び出してmsevを計算します。いずれにせよ、訓練セットに対してtestを呼び出してmseを計算します。testはfeedForwardメソッドを呼び出し、目的値に対するネットワーク結果の誤差を計算します。
int ep = 0; for(; ep < epochs; ep++) { if(validation.Rows() && check.Rows()) { // if there is validation, run it before normal pass/training msev = test(validation, check, lf); // smooth errors msevma = (msevma ? msevma : msev) * (1 - ema) + ema * msev; } mse = test(data, target, lf); // enable feedForward(data) run msema = (msema ? msema : mse) * (1 - ema) + ema * mse; ...
まず、誤差値が有効な数値であることを確認します。そうでなければ、ネットワークがオーバーフローしているか、不正なデータが入力されています。
if(!MathIsValidNumber(mse)) { PrintFormat("NaN at epoch %d", ep); break; // will return NaN as error indication }
新しい誤差が、訓練データセットと検証データセットのサイズの比率から決定される「許容範囲」で以前の誤差よりも大きくなった場合、ループは中断されます。
const int scale = (int)(data.Rows() / (validation.Rows() + 1)) + 1; if(msevmap != 0 && ep > p && msevma > msevmap + scale * (msemap - msema)) { // skip the first p epochs to accumulate values for averaging PrintFormat("Stop by validation at %d, v: %f > %f, t: %f vs %f", ep, msevma, msevmap, msema, msemap); break; } msevmap = msevma; msemap = msema; ...
誤差が減少し続けるか、増加しない場合は、新しい誤差値を保存して、次のエポック結果と比較します。
誤差が必要な精度に達した場合、訓練は完了したと見なされ、ループを終了します。
if(mse <= accuracy) { PrintFormat("Done by accuracy limit %f at epoch %d", accuracy, ep); break; }
さらに、progress仮想メソッドがループで呼び出され、ネットワークの派生クラスでオーバーライドできます。一部のユーザーアクションに応答して訓練を中断するために使用できます。progressの標準実装は後で示します。
if(!progress(ep, epochs, mse, msev, msema, msevma)) { PrintFormat("Interrupted by user at epoch %d", ep); break; }
最後に、上記の条件のいずれによってもループが中断されなかった場合は、backPropを使用して誤差逆伝播プロセスを開始します。
if(!backProp(target)) { mse = NaN(); // error flag break; } } if(ep == epochs) { PrintFormat("Done by epoch limit %d with accuracy %f", ep, mse); } return mse; }
デフォルトのprogressメソッドは、1秒に1回、学習指標をログに記録します。
virtual bool progress(const int epoch, const int total, const double error, const double valid = DBL_MAX, const double ma = DBL_MAX, const double mav = DBL_MAX) { static uint trap; if(GetTickCount() > trap) { PrintFormat("Epoch %d of %d, loss %.5f%s%s%s", epoch, total, error, ma == DBL_MAX ? "" : StringFormat(" ma(%.5f)", ma), valid == DBL_MAX ? "" : StringFormat(", validation %.5f", valid), valid == DBL_MAX ? "" : StringFormat(" v.ma(%.5f)", mav)); trap = GetTickCount() + 1000; } return !IsStopped(); }
trueが返された場合は訓練が続行され、falseが返された場合はループが中断されます。
「早期終了」に加えて、MatrixNetクラスは、ドロップアウトと同様に、接続の一部をランダムに無効にすることができます。
従来のドロップアウト法によれば、ランダムに選択されたニューロンがネットワークから一時的に除外されます。ただし、アルゴリズムは行列演算を使用するため、これを実装するにはコストがかかります。層からニューロンを除外するには、反復ごとに重み行列を再フォーマットし、部分的にコピーする必要があります。ランダムな重みを0に設定すると、接続が切断されるため、はるかに簡単で効率的です。もちろん、各エポックの開始時に、プログラムは一時的に無効にした重みを以前の状態に復元し、次のエポックで無効にする新しいものをランダムに選択する必要があります。
一時的にリセットされる接続の数は、enableDropOutメソッドを使用して、ネットワークの重みの合計数に対するパーセンテージとして設定されます。デフォルトでは、dropOutRate変数は0であるため、モードは無効になっています。
void enableDropOut(const uint percent = 10) { dropOutRate = (int)percent; }
ドロップアウトの原則は、重み行列の現在の状態を追加のストレージ(DropOutStateクラスによって実装)に保存し、ランダムに選択されたネットワーク接続をリセットすることです。1つのエポックに対して結果として得られる変更された形式でネットワークを訓練した後、リセットされた行列要素がストレージから復元され、手順が繰り返されます。他のランダムな重みが選択されてリセットされ、それらを使用してネットワークが訓練されます。DropOutStateがどのように機能するかをご自分で調べるようお勧めします。
適応学習率
これまでのところ、一定の学習率(speed変数)を使用していると仮定されてきましたが、これは実用的ではありません(低速では学習が非常に遅くなり、高速では「過度に興奮」する可能性がある)。
学習率調整形式の1つは、誤差逆伝播法アルゴリズムの特別な変更で使用されます。これはrprop (Resilient Propagation)と呼ばれます。このアルゴリズムは、重みごとに、前の反復と現在の反復でデルタ増分の符号が同じかどうかを確認します。符号が同じ場合、勾配の方向は保持され、この場合、特定の重みに対して選択的に速度を上げることができます。勾配の符号が変化した重みについては、速度を落としたほうがよい場合があります。
行列は各エポックで一度にすべてのデータを計算するため、各重みの勾配の値と符号は、データセット全体の動作を累積(および平均化)します。したがって、このテクノロジーはより正確には「一括rprop」と呼ばれます。
この拡張機能を実装するMatrixNetクラスのすべてのコード行は、BATCH_PROPマクロで提供されます。ヘッダーファイルMatrixNet.mqhをソースコードに含める前に、次のディレクティブを使用して適応率を有効にすることをお勧めします。
#define BATCH_PROP
このモードはspeed変数の代わりにspeed行列の配列を使用することに注意してください。また、最後のエポックからの重みの増分をdeltas行列の配列に格納する必要があります。
class MatrixNet { protected: ... #ifdef BATCH_PROP matrix speed[]; matrix deltas[]; #else double speed; #endif
加速係数と減速係数、および最大速度と最小速度は、4つの追加変数で設定されます。
double plus; double minus; double max; double min;
新しい配列にメモリを割り当て、既におなじみのallocateメソッドでデフォルトの変数値を設定します。
void allocate() { ArrayResize(weights, n); ArrayResize(outputs, n + 1); ArrayResize(bestWeights, n); dropOutRate = 0; #ifdef BATCH_PROP ArrayResize(speed, n); ArrayResize(deltas, n); plus = 1.1; minus = 0.1; max = 50; min = 0.0; #endif }
訓練を開始する前にこれらの変数に他の値を設定するには、setupSpeedAdjustmentメソッドを使用します。
MatrixNetコンストラクタでは、weight行列の配列をコピーしてspeed行列とdeltas行列を初期化します。これは、ネットワーク層に沿って同じサイズの行列を取得するためのより便利な方法です。次に、次のステップでspeedとdeltasに意味のあるデータが入力されます。trainメソッドの開始時に、単にspeedスカラー変数に精度を割り当てる代わりに、この値を使用してspeed配列のすべての行列を埋めます。
double train(const matrix &data, const matrix &target, const matrix &validation, const matrix &check, const int epochs = 1000, const double accuracy = 0.001, const ENUM_LOSS_FUNCTION lf = LOSS_MSE) { ... #ifdef BATCH_PROP for(int i = 0; i < n; ++i) { speed[i].Fill(accuracy); // adjust speeds on the fly deltas[i].Fill(0); } #else speed = accuracy; #endif ... }
backPropメソッド内のインクリメント式は、スカラーではなく、対応する層の行列を参照するようになりました。deltaの増分を受け取った直後に、delta*deltas[i]の積を渡して、adjustSpeedメソッド(以下参照)を呼び出し、前の方向と新しい方向を比較します。最後に、新しい重みの増分をdeltas[i]に保存して、次のエポックでそれらを分析します。
bool backProp(const matrix &target) { ... for(int i = n - 1; i >= 0; --i) // all layers except the output in reverse order { ... #ifdef BATCH_PROP matrix delta = speed[i] * outputs[i].Transpose().MatMul(loss); adjustSpeed(speed[i], delta * deltas[i]); deltas[i] = delta; #else matrix delta = speed * outputs[i].Transpose().MatMul(loss); #endif ... } ... }
adjustSpeedメソッドは非常に単純です。行列積要素の正の符号は、勾配が維持され、速度がplus倍増加するが、max値を超えないことを示します。負の符号は勾配の変化を示し、速度はminus倍減少しますが、min未満にはなりません。
void adjustSpeed(matrix &subject, const matrix &product) { for(int i = 0; i < (int)product.Rows(); ++i) { for(int j = 0; j < (int)product.Cols(); ++j) { if(product[i][j] > 0) { subject[i][j] *= plus; if(subject[i][j] > max) subject[i][j] = max; } else if(product[i][j] < 0) { subject[i][j] *= minus; if(subject[i][j] < min) subject[i][j] = min; } } } }
訓練済みネットワークの最良の状態の保存と復元
ネットワークは「エポック」と呼ばれる反復でループで訓練されます。各エポックでは、訓練データセットのすべてのベクトルがネットワークを通過し、行列に配置されます。行列では、レコードが行に配置され、符号が列に配置されます。.たとえば、各レコードにクウォートバーを格納し、列にOHLC価格と出来高を格納しりlptpができます。
重み調整プロセスは勾配に沿って実行されますが、解かれている問題の目的関数の不均一性と可変速度により、新しいネットワーク誤差の最小値を見つける前に定期的に「悪い」設定になる可能性があるという意味でランダムです。エポック数の増加によって、訓練済みモデルの品質がある程度向上し、ネットワーク誤差が減少するという保証はありません。
この点で、ネットワークの全体的な誤差を常に監視することは理にかなっています。現在のエポックの後に誤差が最小値を更新した場合、見つかった重みを記憶する必要があります。これらの目的のために、重み行列の別の配列と、学習指標を含むStats構造k体を使用します。
class MatrixNet { ... public: struct Stats { double bestLoss; // smallest error for all epochs int bestEpoch; // index of the epoch with the minimum error int epochsDone; // total number of completed epochs }; Stats getStats() const { return stats; } protected: matrix bestWeights[]; Stats stats; ...
trainメソッド内で、エポックのループを開始する前に、構造を統計で初期化します。
double train(const matrix &data, const matrix &target, const matrix &validation, const matrix &check, const int epochs = 1000, const double accuracy = 0.001, const ENUM_LOSS_FUNCTION lf = LOSS_MSE) { ... stats.bestLoss = DBL_MAX; stats.bestEpoch = -1; DropOutState state(dropOutRate);
ループ内で、既知の最小値より小さい誤差値が見つかった場合、すべての重み行列をbestWeightsに保存します。
int ep = 0; for(; ep < epochs; ep++) { ... const double candidate = (msev != DBL_MAX) ? msev : mse; if(candidate < stats.bestLoss) { stats.bestLoss = candidate; stats.bestEpoch = ep; // save best weights from 'weights' for(int i = 0; i < n; ++i) { bestWeights[i].Assign(weights[i]); } } } ...
訓練後、最終的なネットワークの重みと最適な重みの両方を簡単にクエリできます。
bool getWeights(matrix &array[]) const { if(!ready) return false; ArrayResize(array, n); for(int i = 0; i < n; ++i) { array[i] = weights[i]; } return true; } bool getBestWeights(matrix &array[]) const { if(!ready) return false; if(!n || !bestWeights[0].Rows()) return false; ArrayResize(array, n); for(int i = 0; i < n; ++i) { array[i] = bestWeights[i]; } return true; }
これらの行列の配列はファイルに保存できるため、後で訓練済みのすぐに使用できるネットワークを復元できます。これは別のコンストラクタでおこなわれます。
MatrixNet(const matrix &w[], const ENUM_ACTIVATION_FUNCTION f1 = AF_TANH, const ENUM_ACTIVATION_FUNCTION f2 = AF_NONE): ready(false), af(f1), of(f2), n(ArraySize(w)) { if(n < 2) return; allocate(); for(int i = 0; i < n; ++i) { weights[i] = w[i]; #ifdef BATCH_PROP speed[i] = weights[i]; // instead .Init(.Rows(), .Cols()) deltas[i] = weights[i]; // instead .Init(.Rows(), .Cols()) #endif } ready = true; }
後で、既製のネットワークを保存して読み取る方法を示す実用的な例を見ていきます。
ネットワーク訓練の進捗状況の可視化
定期的なログを出力するprogressメソッドの結果はあまり明確ではありません。したがって、MatrixNet.mqhファイルは、MatrixNetから派生したMatrixNetVisualクラスも実装します。このクラスは、エポックごとに訓練誤差が変化するグラフを表示します。
グラフィック表示は、標準のCGraphicクラス(MetaTrader5で利用可能)、またはそれから派生した小さなCMyGraphicクラスによって提供されます。
このクラスのオブジェクトは、MatrixNetVisualの一部です。また、「視覚化された」ネットワーク内には、5つの曲線の配列と、表示されたライン用のdoubleタイプの配列があります。
class MatrixNetVisual: public MatrixNet { CMyGraphic graphic; CCurve *c[5]; double p[], x[], y[], z[], q[], b[]; ...
ここで
MatrixNetVisualコンストラクタから呼び出されるgraphメソッドは、ウィンドウ全体のサイズのグラフィカルオブジェクトを作成します。前述の5つのカーブ(CCurve)もここに追加されます。
void graph() { ulong width = ChartGetInteger(0, CHART_WIDTH_IN_PIXELS); ulong height = ChartGetInteger(0, CHART_HEIGHT_IN_PIXELS); bool res = false; const string objname = "BPNNERROR"; if(ObjectFind(0, objname) >= 0) res = graphic.Attach(0, objname); else res = graphic.Create(0, objname, 0, 0, 0, (int)(width - 0), (int)(height - 0)); if(!res) return; c[0] = graphic.CurveAdd(p, x, CURVE_LINES, "Training"); c[1] = graphic.CurveAdd(p, y, CURVE_LINES, "Validation"); c[2] = graphic.CurveAdd(p, z, CURVE_LINES, "Val.EMA"); c[3] = graphic.CurveAdd(p, q, CURVE_LINES, "Train.EMA"); c[4] = graphic.CurveAdd(p, b, CURVE_POINTS, "Best/Minimum"); ... } public: MatrixNetVisual(const int &layers[], const ENUM_ACTIVATION_FUNCTION f1 = AF_TANH, const ENUM_ACTIVATION_FUNCTION f2 = AF_NONE): MatrixNet(layers, f1, f2) { graph(); }
オーバーライドされたprogressメソッドでは、引数が適切なdouble配列に追加され、plotメソッドが呼び出されて画像が更新されます。
virtual bool progress(const int epoch, const int total, const double error, const double valid = DBL_MAX, const double ma = DBL_MAX, const double mav = DBL_MAX) override { // fill all the arrays PUSH(p, epoch); PUSH(x, error); if(valid != DBL_MAX) PUSH(y, valid); else PUSH(y, nan); if(ma != DBL_MAX) PUSH(q, ma); else PUSH(q, nan); if(mav != DBL_MAX) PUSH(z, mav); else PUSH(z, nan); plot(); return MatrixNet::progress(epoch, total, error, valid, ma, mav); }
plotメソッドが完了し、曲線がプロットされます。
void plot() { c[0].Update(p, x); c[1].Update(p, y); c[2].Update(p, z); c[3].Update(p, q); double point[1] = {stats.bestEpoch}; b[0] = stats.bestLoss; c[4].Update(point, b); ... graphic.CurvePlotAll(); graphic.Update(); }
可視化プロセスの技術的な詳細はご自身でお調べになってください。画面上でどのように見えるかはすぐにわかります。
テストスクリプト
MatrixNetファミリクラスで最初のテストを実施できます。それはMatrixNet.mq5スクリプトで、初期データは既知の分析記録に基づいて人為的に生成されます。MachineLearningヘルプトピックの式を使用します。これは、クラスほど用途が広くないため、かなりのコーディングが必要なネイティブ逆伝播訓練の例を提供します(以下のクラスを使用する場合と使用しない場合の行数を比較してください)。
f=((x+y+z)^2/(x^2+y^2+z^2))/3
この式の唯一の小さな違いは、値が3で除算され、関数に0から1の範囲が与えられることです。
関数の形式は、次の図を使用して評価できます。ここでは、3つの異なるz値(0.05、0.5、5.0)に対する表面(x<->y)が示されています。
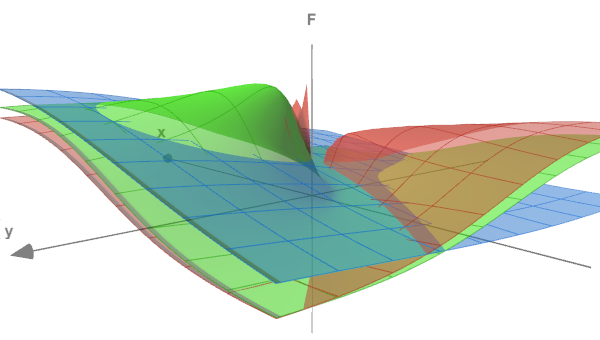
3つのセクションのテスト機能
スクリプト入力変数では、訓練エポックの数、精度(ターミナル誤差)、および生成されたデータにオプションで追加できるノイズ強度を指定します(これにより、実験が実際の問題に近づき、ノイズがあると、依存関係を特定するのが難しくなります)。RandomNoiseはデフォルトで0であるため、ノイズはありません。
input int Epochs = 1000; input double Accuracy = 0.001; input double RandomNoise = 0.0;
実験データはCreateData関数によって生成されます。そのdataと'target行列パラメータ'は、上記の関数のポイントで埋められます。ポイント数はcountです。1つの入力ベクトル(data行列の行)には3つの列(x、y、z)があります。出力ベクトル(target行列の行)は、fの単一の値です。ポイント(x,y,z)は、-10から+10の範囲でランダムに生成されます。
bool CreateData(matrix &data, matrix &target, const int count) { if(!data.Init(count, 3) || !target.Init(count, 1)) return false; data.Random(-10, 10); vector X1 = MathPow(data.Col(0) + data.Col(1) + data.Col(2), 2); vector X2 = MathPow(data.Col(0), 2) + MathPow(data.Col(1), 2) + MathPow(data.Col(2), 2); if(!target.Col(X1 / X2 / 3.0, 0)) return false; if(RandomNoise > 0) { matrix noise; noise.Init(count, 3); noise.Random(0, RandomNoise); data += noise - RandomNoise / 2; noise.Resize(count, 1); noise.Random(-RandomNoise / 2, RandomNoise / 2); target += noise; } return true; }
RandomNoiseのノイズ強度は、正しい座標とそれらに対して得られた関数値の追加の広がりの振幅として設定されます。関数の最大値が1.0であるとすると、このレベルのノイズではほとんど認識できなくなります。
ニューラルネットワークを使用するには、MatrixNet.mqhヘッダーファイルをインクルードし、このプリプロセッサディレクティブの前にBATCH_PROPマクロを定義して、可変レートで加速学習を有効にします。
#define BATCH_PROP #include <MatrixNet.mqh>
メインスクリプト関数では、layers配列を使用してネットワーク構成(層の数とサイズ)を定義し、これをMatrixNetVisualコンストラクタに渡します。訓練データセットと検証データセットは、CreateDataを2回呼び出すことによって生成されます。
void OnStart() { const int layers[] = {3, 11, 7, 1}; MatrixNetVisual net(layers); matrix data, target; CreateData(data, target, 100); matrix valid, test; CreateData(valid, test, 25); ...
実際には、ネットワークに送信する前に、ソースデータを正規化し、外れ値を削除し、要因の独立性を確認する必要があります。ただし、この場合、データは自分で生成します。
モデルは、dataおよびtarget行列でtrainメソッドを使用して訓練されます。有効な/テストセットでパフォーマンスが低下すると早期終了が発生しますが、ノイズのないデータでは、必要な精度または最大ループ数のいずれか早い方に到達する可能性があります。
Print("Training result: ", net.train(data, target, valid, test, Epochs, Accuracy)); matrix w[]; if(net.getBestWeights(w)) { MatrixNet net2(w); if(net2.isReady()) { Print("Best copy on training data: ", net2.test(data, target)); Print("Best copy on validation data: ", net2.test(valid, test)); } }
訓練後、見つかった最適な重みの行列を要求し、チェックするために、それらに基づいて別のネットワークインスタンスであるnet2オブジェクトを構築します。その後、両方のデータセットでネットワークを実行し、誤差値をログに出力します。
スクリプトは学習の進行状況を視覚化するネットワークを使用するため、ユーザーがグラフを学習できるように、ユーザーのコマンドがスクリプトを完了するのを待つループを開始します。
while(!IsStopped()) { Sleep(1000); } }
デフォルトのパラメータでスクリプトを実行すると、次の図のような結果が得られます(ランダムなデータ生成とネットワークの初期化により、実行間は異なります)。
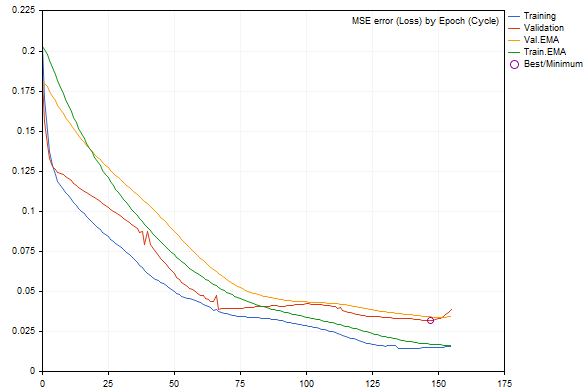
訓練中のネットワーク誤差ダイナミクス
訓練セットと検証セットの誤差は、それぞれ青と赤の線で示され、平滑化されたバージョンは緑と黄色です。訓練が進むにつれて、すべてのタイプの誤差が減少することがはっきりとわかりますが、ある瞬間の後、検証誤差が訓練セットの誤差よりも大きくなります。グラフの右端近くではその増加が顕著であり、「早期終了」につながります。最適なネットワーク構成は丸で囲まれています。
操作ログは次のようになります。
EMA for early stopping: 31 (0.062500)
Epoch 0 of 1000, loss 0.20296 ma(0.20296), validation 0.18167 v.ma(0.18167)
Epoch 120 of 1000, loss 0.02319 ma(0.02458), validation 0.04566 v.ma(0.04478)
Stop by validation at 155, v: 0.034642 > 0.034371, t: 0.016614 vs 0.016674
Training result: 0.015707719706513287
Best copy on training data: 0.015461956812387292
Best copy on validation data: 0.03211748853774414
RandomNoiseパラメータを使用してデータにノイズを追加し始めると、学習率が著しく低下し、ノイズが多すぎると、訓練済みネットワークの誤差が増加するか、学習が完全に停止します。
たとえば、ノイズ3.0のグラフは次のようになります。
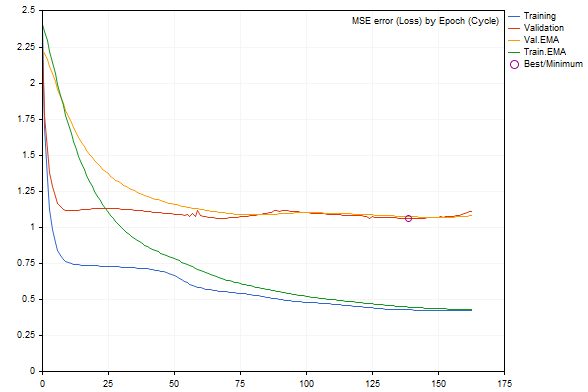
ノイズが追加された訓練でのネットワーク誤差ダイナミクス
ログによると、誤差値はさらに悪化しています。
Epoch 0 of 1000, loss 2.40352 ma(2.40352), validation 2.23536 v.ma(2.23536) Stop by validation at 163, v: 1.082419 > 1.080340, t: 0.432023 vs 0.432526 Training result: 0.4244786772678285 Best copy on training data: 0.4300476339855798 Best copy on validation data: 1.062895214094978
したがって、ニューラルネットワークツールうまく機能しています。それでは、より実用的な例に移りましょう。インジケータとEAです。
予測インジケータ
NNベースの予測インジケータの例として、CodeBaseの既存のインジケータを変更したBPNNMatrixPredictorDemo.mq5を考えてみましょう。NNは、行列を使用せずに、同じインジケータの以前のバージョンをC++から移植することによってMQL5に実装されます(NN理論の関連部分を含む詳細な説明付き)。
このインジケータは、フィボナッチ数列(1,2,3,5,8,13,21,34,55,89,144. ..)によって互いに間隔をあけられたバー間の間隔で、EMA平均価格の過去の増分から指定された長さの入力ベクトルを形成することによって動作します。この情報に基づいて、インディケータは次のバー(対応するベクトルに含まれる過去のバーの右側)の価格増分を予測する必要があります。ベクトルのサイズは、NN入力層(_numInputs)のユーザー指定のサイズによって決まります。層の数(最大6)とそのサイズは、他の入力変数で指定されます。
input int _lastBar = 0; // Last bar in the past data input int _futBars = 10; // # of future bars to predict input int _smoothPer = 6; // Smoothing period input int _numLayers = 3; // # of layers including input, hidden & output (2..6) input int _numInputs = 12; // # of inputs (that is neurons in input 0-th layer) input int _numNeurons1 = 5; // # of neurons in the 1-st hidden or output layer input int _numNeurons2 = 1; // # of neurons in the 2-nd hidden or output layer input int _numNeurons3 = 0; // # of neurons in the 3-rd hidden or output layer input int _numNeurons4 = 0; // # of neurons in the 4-th hidden or output layer input int _numNeurons5 = 0; // # of neurons in the 5-th hidden or output layer input int _ntr = 500; // # of training sets / bars input int _nep = 1000; // Max # of epochs input int _maxMSEpwr = -7; // Error (as power of 10) for training to stop; mse < 10^this
また、訓練データセットの最大サイズ(_ntr)、最大エポック数(_nep)、最小MSE誤差(_maxMSEpwr)も示します。
価格EMAの平均期間は_smoothPerで指定します。
デフォルトでは、インディケータは最後のバー(_lastBarは0に等しい)から始まる訓練データを取得し、_futBars先の予測をおこないます(明らかに、ネットワーク出力で1バーの予測があるため、それを徐々にいくつかの後続のバーを予測するための入力ベクトルに「プッシュ」できます)。_lastBarに正の数が指定されている場合、過去の対応するバー数の予測を取得し、既存のクウォートと比較して視覚的に評価することができます。
インディケータは3つのバッファを出力します。
- 訓練データセットの目標値を示す薄緑色の線
- 訓練データセットのネットワーク出力を示す青い線
- 予測の赤い線
データセットを生成し、結果を視覚化するインジケータのアプリケーション部分(初期データと予測の両方)は変更されていません。
主な変更は、TrainとTestの2つの関数でおこなわれました。これらは、NNの作業をMatrixNetクラスのオブジェクトに完全に委譲します。train関数は、収集されたデータに基づいてネットワークを訓練し、ネットワークの重みを含む配列を返します(テスターで実行する場合、訓練は1回だけおこなわれ、オンラインで実行する場合、新しいバーを開くと訓練が繰り返されます。これは、ソースコードで変更できます)。test関数は、重みによってネットワークを再作成し、通常の1回限りの予測計算を実行します。訓練済みネットワークのオブジェクトを保存し、それを再作成せずに利用することがより最適です。次の例では、EAを使用してこれをおこないます。インジケータに関しては、古いバージョンの元のコード構造を意図的に使用して、行列を使用する場合と使用しない場合のコーディングアプローチを比較しやすくしています。特に、行列バージョンでは、一度に1つずつループ内のネットワークを介してベクトルを実行し、その次元に従ってデータ配列を手動で再形成する必要がないという事実に注意を払うことができます。
以下は、EURUSD、H1チャートのデフォルト設定のインジケータです。
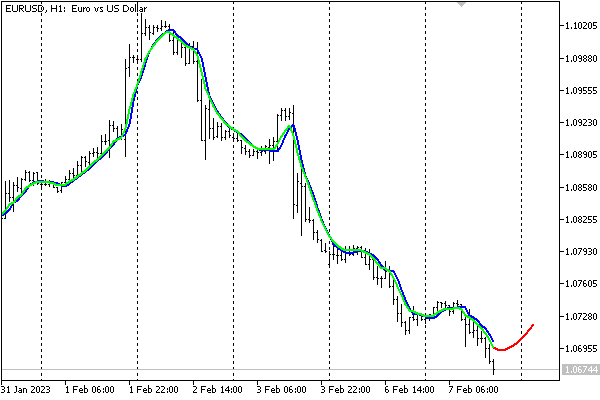
ニューラルネットワークベースのインジケータによる予測
このインジケータは、ニューラルネットワークのパフォーマンスを示すためにここに示されていることに注意してください。現在の簡略化された形式で取引の決定を下すために使用することはお勧めしません。
ファイルへのNNの保存
市場からのソースデータは急速に変化する可能性があるため、一部のトレーダーは、最新のデータセットでオンザフライ(毎日、すべてのセッションなど)でネットワークを訓練する価値があると考えます。ただし、コストがかかる可能性があり、日次データに基づいて動作する中期および長期の取引システムにはあまり適していません。このような場合、訓練済みネットワークを保存して、後ですばやく読み込んで使用できるようにすることをお勧めします。
この目的のために、この記事のフレームワーク内で、MatrixNetStore.mqhヘッダーファイルで定義されるMatrixNetStoreクラスを作成しました。このクラスには、MatrixNetファミリの任意のクラスをMテンプレートパラメータとして期待するsaveおよびloadテンプレートメソッドが含まれています(現在、MatrixNetVisualを含む2つのクラスしかありませんが、必要に応じてセットを拡張できます)。どちらのメソッドもファイル名の引数を持ち、標準のNNデータ(層の数、それらのサイズ、重み行列、活性化関数)を操作します。
これがネットワークの保存方法です。
class MatrixNetStore { static string signature; public: template<typename M> // M is a MatrixNet static bool save(const string filename, const M &net, Storage *storage = NULL, const int flags = 0) { // get the matrix of weights (the best weights, if any) matrix w[]; if(!net.getBestWeights(w)) { if(!net.getWeights(w)) { return false; } } // open file int h = FileOpen(filename, FILE_WRITE | FILE_BIN | FILE_SHARE_READ | FILE_SHARE_WRITE | FILE_ANSI | flags); if(h == INVALID_HANDLE) return false; // write network metadata FileWriteString(h, signature); FileWriteInteger(h, net.getActivationFunction()); FileWriteInteger(h, net.getActivationFunction(true)); FileWriteInteger(h, ArraySize(w)); // write weight matrices for(int i = 0; i < ArraySize(w); ++i) { matrix m = w[i]; FileWriteInteger(h, (int)m.Rows()); FileWriteInteger(h, (int)m.Cols()); double a[]; m.Swap(a); FileWriteArray(h, a); } // if user data is provided, write it if(storage) { if(!storage.store(h)) Print("External info wasn't saved"); } FileClose(h); return true; } ... }; static string MatrixNetStore::signature = "BPNNMS/1.0";
以下の点に注意してください。署名は、ファイル形式の正確性を確認するために使用できるように、ファイルの先頭に書き込まれます(署名は変更できます。クラスにはこのためのメソッドがあります)。さらに、saveメソッドを使用すると、必要に応じて、ユーザーデータをネットワークに関する標準情報に追加できます。特別なStorageインターフェイスのオブジェクトへのポインタを渡すだけです。
class Storage { public: virtual bool store(const int h) = 0; virtual bool restore(const int h) = 0; };
それに応じて、ファイルからネットワークを復元できます。
class MatrixNetStore { ... template<typename M> // M is a MatrixNet static M *load(const string filename, Storage *storage = NULL, const int flags = 0) { int h = FileOpen(filename, FILE_READ | FILE_BIN | FILE_SHARE_READ | FILE_SHARE_WRITE | FILE_ANSI | flags); if(h == INVALID_HANDLE) return NULL; // check the format by signature const string header = FileReadString(h, StringLen(signature)); if(header != signature) { FileClose(h); Print("Incorrect file header"); return NULL; } // read standard network metadata set const ENUM_ACTIVATION_FUNCTION f1 = (ENUM_ACTIVATION_FUNCTION)FileReadInteger(h); const ENUM_ACTIVATION_FUNCTION f2 = (ENUM_ACTIVATION_FUNCTION)FileReadInteger(h); const int size = FileReadInteger(h); matrix w[]; ArrayResize(w, size); // read weight matrices for(int i = 0; i < size; ++i) { const int rows = FileReadInteger(h); const int cols = FileReadInteger(h); double a[]; FileReadArray(h, a, 0, rows * cols); w[i].Swap(a); w[i].Reshape(rows, cols); } // read user data if(storage) { if(!storage.restore(h)) Print("External info wasn't read"); } // create a network object M *m = new M(w, f1, f2); FileClose(h); return m; }
これで、この記事の最後の例である自動売買ロボットに進む準備が整いました。
予測EA
TradeNN.mq5予測EAの戦略として、次のバーの予測された方向で取引するという、かなり単純な原則を使用します。私たちの目的は、ニューラルネットワークテクノロジの動作を実証することで、収益性の観点から予見可能なすべての適用可能性要因を調査することではありません。
初期データは、指定された数のバーでの価格増分です。必要に応じて、現在の銘柄だけでなく追加の銘柄も分析できます。これにより、理論的には相互依存関係を特定できます(たとえば、あるティッカーが別のティッカーまたはそれらの組み合わせを間接的に従っている場合)。ネットワークの唯一の出力は、目標価格としては解釈されません。代わりに、システムを単純化するために、正-買い、負-売りのサインを分析します。
言い換えれば、ネットワーク操作スキームはある意味でハイブリッドです。一方では、ネットワークは回帰問題を解決しますが、他方では、分類のように2つの取引アクションから選択します。将来的には、出力層のニューロンの数を取引状況の数まで増やし、SoftMax活性化関数を適用することが可能になります。ただし、そのようなネットワークを訓練するには、状況に応じてクウォートを自動または手動でラベル付けする必要があります。
戦略ではなく、ネットワークパラメータに焦点を当てるために、戦略は意図的に非常に単純化されています。
分析する商品のコンマ区切りのリストは、Symbols入力パラメータで指定されます。現在のチャートの銘柄が最初に表示されます。それは取引された銘柄にあります。
input string Symbols = "XAGUSD,XAUUSD,EURUSD"; input int Depth = 5; // Vector size (bars) input int Reserve = 250; // Training set size (vectors)
これらの銘柄をデフォルトとして選択したのは、銀と金が相関資産と見なされており、(通貨と比較して)影響力の大きいニュースは比較的少ないため、金に対した銀と(現在の状態)金に対した銀の両方を分析できるからです。EURUSDに関しては、このペアが市場全体の基準として追加されます。ニュースの存在は、予測変数ではなく予測因子として機能するため、重要ではありません。
他の最も重要なパラメータの中で、ベクトルを形成する各商品のバーの数(深さ)があります。たとえば、Symbolsが3ティッカーに設定され、Depthが5(デフォルト)に設定されている場合、ネットワークの入力ベクトルの合計サイズは15です。
Reserveパラメータを使用すると、サンプルの長さ(直近のクウォート履歴から形成されるベクトルの数)を設定できます。このテストでは毎日の時間枠を使用するため、デフォルト値は250です。250は約1年です。したがって、深さ5は1週間です。
もちろん、時間枠を含む任意の設定を変更できますが、D1のようなより高い時間枠では、基本的なパターンは、瞬間的な状況に対する自発的な市場の反応よりも顕著であると考えられます。
また、テスターで起動すると、約1年間のクウォートがプリロードされるため、D1+で要求された訓練データの量を増やすには、一定数の初期バーをスキップして、十分な数が蓄積されるのを待つ必要があることにも注意してください。
前の例と同様に、訓練エポックの数と精度(初期速度でもあり、速度はrpropによって各シナプスに対して動的に選択される)をパラメータで指定する必要があります。
input int Epochs = 1000; input double Accuracy = 0.0001; // Accuracy (and training speed)
このEAでは、NNは5つの層を持ちます(1つの入力層、3つの隠れ層、1つの出力層)。入力層のサイズによって入力ベクトルが決まり、2番目と3番目の層はHiddenLayerFactorで選択されます。最後から2番目の層については、経験式(以下のソースコードを参照)を使用して、前の層と出力層(単一)の間のサイズにします。
input double HiddenLayerFactor = 2.0; // Hidden Layers Factor (to vector size) input int DropOutPercentage = 0; // DropOut Percentage
また、この例を使用して、ドロップアウト正則化方法をテストします。ランダムにリセットされる重みのパーセンテージは、DropOutPercentageパラメータで指定されます。検証サンプリングはここでは提供されていませんが、クラスで許可されているため、必要に応じて両方の方法を組み合わせることができます。
NetBinFileNameパラメータは、ファイルからネットワークを読み込むために使用されます。ファイルは常に共通ターミナルフォルダに対して相対的に検索されます。それ以外の場合、ストラテジーテスターでエキスパートEAをテストするには、ソースコードで必要なすべてのネットワークの名前を#propertytester_fileディレクティブで事前に指定する必要があるためです。これが、エージェントに送信される唯一の方法です。
NetBinFileNameパラメータが空の場合、EAは新しいネットワークを訓練し、一意の一時的な名前でファイルに保存します。これは、最適化プロセス中にもおこなわれて、多数のネットワーク構成(さまざまなベクトルサイズ、層、ドロップアウト、履歴の深さ)を生成できます。
input string NetBinFileName = ""; input int Randomizer = 0;
さらに、Randomizerパラメータを使用すると、ランダムジェネレーターをさまざまな方法で初期化できるため、同じ他の設定で多くのネットワークインスタンスを訓練できます。ランダム化により、各ネットワークは一意であることに注意してください。統合された決定または多数決ルールが読み取られるNN委員会の使用は、別の種類の正規化である可能性があります。
Randomizerを特定の値に設定することで、デバッグ目的で同じ訓練プロセスを複製できます。
銘柄による価格情報は、Closes構造体とそのようなCC構造体の配列を使用して保存されます。その結果、配列の配列のようなものを取得します。
struct Closes { double C[]; }; Closes CC[];
Sグローバル配列とQ変数は、動作中の商品とその番号のために予約されています。それらはOnInitに入力されます。
string S[]; int Q; int OnInit() { Q = StringSplit(StringLen(Symbols) ? Symbols : _Symbol, ',', S); ArrayResize(CC, Q); MathSrand(Randomizer); ... return INIT_SUCCEEDED; }
Calc関数は、特定のバーoffsetから指定されたDepthへのクウォートを要求するために使用されます。この関数では、CC配列が埋められます。この関数がどのように呼び出されるかは後で説明します。
bool Calc(const int offset) { const datetime dt = iTime(_Symbol, _Period, offset); for(int i = 0; i < Q; ++i) { const int bar = iBarShift(S[i], PERIOD_CURRENT, dt); // +1 for differences, +1 for model const int n = CopyClose(S[i], PERIOD_CURRENT, bar, Depth + 2, CC[i].C); for(int j = 0; j < n - 1; ++j) { CC[i].C[j] = (CC[i].C[j + 1] - CC[i].C[j]) / SymbolInfoDouble(S[i], SYMBOL_TRADE_TICK_SIZE) * SymbolInfoDouble(S[i], SYMBOL_TRADE_TICK_VALUE); } ArrayResize(CC[i].C, n - 1); } return true; }
次に、特定のCC[i].C配列について、特別なDiff関数が、ネットワークの入力ベクトルに送信される価格増分を計算できます。この関数は、最後のインクリメントを除くすべてのインクリメントを、参照によって渡されたd配列に書き込み、目標予測値となる最後のインクリメントを直接返します。
double Diff(const double &a[], double &d[]) { const int n = ArraySize(a); ArrayResize(d, n - 1); // -1 minus the "future" model double overall = 0; for(int j = 0; j < n - 1; ++j) // left (from old) to right (toward new) { int k = n - 2 - j; overall += a[k]; d[j] = overall / sqrt(j + 1); } ... // additional normalization return a[n - 1]; }
時系列の「ランダムウォーク」理論に従って、バーの距離の平方根によって差を正規化することに注意してください(過去を既になされた予測と見なす場合、信頼区間に比例)。これは必須の手法ではありませんが、NNの操作はしばしば研究に似ています。
要素(価格だけでなく、インジケータ、ボリュームなど)を選択し、ネットワーク用のデータを準備する(正規化、コーディング)ための手順全体は、別の広範なトピックです。NNの計算作業をできる限り容易にすることが重要です。そうしないと、タスクに対処できなくなる可能性があります。
EAのOnTickメイン関数では、すべての操作はバーが開いた後にのみ実行されます。EAはさまざまな商品のクウォートを分析するため、操作を続行する前にそれらのバーを同期する必要があります。同期は、ここには示していないSync関数によって実行されます。興味深いことに、Sleep関数に基づいて適用された同期は、始値モードでのテストにも適しています。効率的な理由から、後でこのモードを使用します。
void OnTick() { ... static datetime last = 0; if(last == iTime(_Symbol, _Period, 0)) return; ...
ネットワークインスタンスは、オートポインタ型(AutoPtr.mqhヘッダーファイル)のrun変数に保存されます。したがって、メモリの解放を制御する必要はありません。std変数は、上記のCalcおよびDiff関数から取得されたデータセットで計算された分散を格納するために使用されます。データを正規化するには分散が必要です。
static AutoPtr<MatrixNet> run; static double std;
ユーザーがNetBinFileNameで読み込むファイル名を指定した場合、LoadNetを使用してネットワークの読み込みKが試みされます(以下を参照)。この関数は、成功するとネットワークオブジェクトへのポインタを返します。
if(NetBinFileName != "") { if(!run[]) { run = LoadNet(NetBinFileName, std); if(!run[]) { ExpertRemove(); return; } } }
ネットワークがある場合、予測と取引を実行します。TradeTestはこれらすべてを担当します(以下を参照)。
if(run[]) { TradeTest(run[], std); } else { run = TrainNet(std); } last = iTime(_Symbol, _Period, 0); }
ネットワークがまだない場合は、訓練データセットを生成し、TrainNetを呼び出してネットワークを訓練します。この関数は、新しいネットワークオブジェクトへのポインタも返します。さらに、参照によって渡されたstd変数に、計算されたデータ分散を入力します。
ネットワークは、すべての動作中の銘柄の履歴に少なくとも要求された数のバーが含まれている場合にのみ訓練できることに注意してください。オンラインチャートの場合、これはEAを起動するとすぐに発生する可能性が高くなります(ユーザーが法外な数値を入力しない限り)。テスターでは、プリロードされた履歴は通常1年に制限されているため、パスの開始を過去にシフトする必要がある場合があります。この場合、ネットワークを訓練するために必要なバーの数が得られます。
OnTick関数の先頭に十分なバーがあるかどうかのチェックが追加されていますが、この記事では提供されていません(完全なソースコードを参照してください)。
ネットワークが訓練された後、EAは取引を開始します。テスターにとって、これは、訓練済みネットワークの一種のフォワードテストを取得することを意味します。得られた金融測定値は、最も適切なネットワーク構成またはネットワークの委員会(構成が同一)を選択するために、最適化に使用できます。
以下はTrainNet関数です(CalcとDiffの呼び出しに注意してください)。
MatrixNet *TrainNet(double &std) { double coefs[]; matrix sys(Reserve, Q * Depth); vector model(Reserve); vector t; datetime start = 0; for(int j = Reserve - 1; j >= 0; --j) // loop through historical bars { // since close prices are used, we make +1 to the bar index if(!Calc(j + 1)) // collect data for all symbols starting with bar j to Depth bars { return NULL; // probably other symbols don't have enough history (wait) } // remember training sample start date/time if(start == 0) start = iTime(_Symbol, _Period, j); ArrayResize(coefs, 0); // calculate price difference for all symbols for Depth bars for(int i = 0; i < Q; ++i) { double temp[]; double m = Diff(CC[i].C, temp); if(i == 0) { model[j] = m; } int dest = ArraySize(coefs); ArrayCopy(coefs, temp, dest, 0); } t.Assign(coefs); sys.Row(t, j); } // normalize std = sys.Std() * 3; Print("Normalization by 3 std: ", std); sys /= std; matrix target = {}; target.Col(model, 0); target /= std; // the size of layers 0, 1, 2, 3 is derived from the data, always one output int layers[] = {0, 0, 0, 0, 1}; layers[0] = (int)sys.Cols(); layers[1] = (int)(sys.Cols() * HiddenLayerFactor); layers[2] = (int)(sys.Cols() * HiddenLayerFactor); layers[3] = (int)fmax(sqrt(sys.Rows()), fmax(sqrt(layers[1] * layers[3]), sys.Cols() * sqrt(HiddenLayerFactor))); // create and configure the network of the specified configuration ArrayPrint(layers); MatrixNetVisual *net = new MatrixNetVisual(layers); net.setupSpeedAdjustment(SpeedUp, SpeedDown, SpeedHigh, SpeedLow); net.enableDropOut(DropOutPercentage); // train the network and display the result (error) Print("Training result: ", net.train(sys, target, Epochs, Accuracy)); ...
可視化されたネットワーククラスを使用しているため、学習の進行状況がグラフに表示されます。訓練後、不要になった画像オブジェクトは手動で削除できます。EAをアンロードすると、画像は自動的に削除されます。
次に、ネットワークから最適な重み行列を読み取る必要があります。さらに、これらの重みを使用してネットワークを正常に再作成できることを確認し、同じデータを使用してそのパフォーマンスをテストします。
matrix w[]; if(net.getBestWeights(w)) { MatrixNet net2(w); if(net2.isReady()) { Print("Best result: ", net2.test(sys, target)); ... } } return net; }
最後に、ネットワークは、訓練条件(履歴間隔、銘柄リストと時間枠、データサイズ、ネットワーク設定)を説明する特別に準備された文字列と共にファイルに保存されます。
// the most important or all EA settings can be added to the network file const string context = StringFormat("\r\n%s %s %s-%s", _Symbol, EnumToString(_Period), TimeToString(start), TimeToString(iTime(_Symbol, _Period, 0))) + "\r\n" + Symbols + "\r\n" + (string)Depth + "/" + (string)Reserve + "\r\n" + (string)Epochs + "/" + (string)Accuracy + "\r\n" + (string)HiddenLayerFactor + "/" + (string)DropOutPercentage + "\r\n"; // prepare a temporary file name const string tempfile = "bpnnmtmp" + (string)GetTickCount64() + ".bpn"; // save the network and user data to a file MatrixNetStore store; // main class unloading/loading the networks BinFileNetStorage writer(context, net.getStats(), std); // optional class with our information store.save(tempfile, *net, &writer); ...
ここで言及されているBinFileNetStorageクラスは、EAに固有のものです。オーバーライドされた保存/復元メソッド(ストレージの親インターフェイス)を使用して、追加の説明、正規化値(新しいデータの定期的な作業に必要)、およびMatrixNet::Stats構造体の形式の訓練統計を処理します。.
さらに、EAの動作は、最適化モードで実行されるかどうかによって異なります。最適化中には、フレームメカニズムを使用してネットワークファイルをエージェントからターミナルに送信します(ソースコードを参照)。このようなファイルは、ローカルのMQL5/Files/フォルダのEAの名前のサブフォルダに保存されます。
if(!MQLInfoInteger(MQL_OPTIMIZATION)) { // set a new name in a more understandable time format, in the common folder string filename = "bpnnm" + TimeStamp((datetime)FileGetInteger(tempfile, FILE_MODIFY_DATE)) + StringFormat("(%7g)", net.getStats().bestLoss) + ".bpn"; if(!FileMove(tempfile, 0, filename, FILE_COMMON)) { PrintFormat("Can't rename temp-file: %s [%d]", tempfile, _LastError); } } else { ... // the file will be sent from the agent to the terminal as a frame }
それ以外の場合(単純なテストまたはオンライン作業)、ファイルは共通のターミナルフォルダに移動されます。これは、NetBinFileNameパラメータを介して単純にさらに読み込むためにおこなわれます。実際には、テスターで作業するためには、NetBinFileNameパラメータに入力する必要がある特定のファイル名で#propertytester_fileディレクティブを指定する必要があります。その後、EAを再コンパイルする必要があります。これらの追加操作がなければ、ネットワークファイルはエージェントにコピーされません。したがって、すべてのローカルエージェントからアクセスできる共通フォルダを使用する方が実用的です。
LoadNet関数は次のように実装されます。
MatrixNet *LoadNet(const string filename, double &std, const int flags = FILE_COMMON) { BinFileNetStorage reader; // optional user data MatrixNetStore store; // general metadata MatrixNet *net; std = 1.0; Print("Loading ", filename); ResetLastError(); net = store.load<MatrixNet>(filename, &reader, flags); if(net == NULL) { Print("Failed: ", _LastError); return NULL; } MatrixNet::Stats s[1]; s[0] = reader.getStats(); ArrayPrint(s); std = reader.getScale(); Print(std); Print(reader.getDescription()); return net; }
TradeTest関数はCalc(0)を呼び出して、実際の価格増分のベクトルを取得します。
bool TradeTest(MatrixNet *net, const double std) { if(!Calc(0)) return false; double coefs[]; for(int i = 0; i < Q; ++i) { double temp[]; // difference on the 0th bar is ignored, it will be predicted /* double m = */Diff(CC[i].C, temp, true); ArrayCopy(coefs, temp, ArraySize(coefs), 0); } vector t; t.Assign(coefs); matrix data = {}; data.Row(t, 0); data /= std; ...
ベクトルに基づいて、ネットワークは予測をおこなう必要があります。しかし、その前に、既存のポジションは強制的に決済されます。古い方向と新しい方向が一致するかどうかの分析はありません。決済に使用するClosePositionメソッドを以下に示します。次に、順伝播の結果に基づいて、意図した方向に新しいポジションを開きます。
ClosePosition();
if(net.feedForward(data))
{
matrix y = net.getResults();
Print("Prediction: ", y[0][0] * std);
OpenPosition((y[0][0] > 0) ? ORDER_TYPE_BUY : ORDER_TYPE_SELL);
return true;
}
return false;
}
OpenPosition関数とClosePosition関数は似ています。したがって、ここではClosePositionのみを示します。
bool ClosePosition() { // define an empty structure MqlTradeRequest request = {}; if(!PositionSelect(_Symbol)) return false; const string pl = StringFormat("%+.2f", PositionGetDouble(POSITION_PROFIT)); // fill in the required fields request.action = TRADE_ACTION_DEAL; request.position = PositionGetInteger(POSITION_TICKET); const ENUM_ORDER_TYPE type = (ENUM_ORDER_TYPE)(PositionGetInteger(POSITION_TYPE) ^ 1); request.type = type; request.price = SymbolInfoDouble(_Symbol, type == ORDER_TYPE_BUY ? SYMBOL_ASK : SYMBOL_BID); request.volume = PositionGetDouble(POSITION_VOLUME); request.deviation = 5; request.comment = pl; // send request ResetLastError(); MqlTradeResult result[1]; const bool ok = OrderSend(request, result[0]); Print("Status: ", _LastError, ", P/L: ", pl); ArrayPrint(result); if(ok && (result[0].retcode == TRADE_RETCODE_DONE || result[0].retcode == TRADE_RETCODE_PLACED)) { return true; } return false; }
実践研究の時間です。XAGUSD、D1チャート、始値モードで、デフォルト設定のテスターでEAを実行してみましょう。テスト開始日を2022.01.01に設定します。これは、EAの開始直後に、ネットワークが前年の2021年の価格を使用して学習を開始し、その信号に基づいて取引することを意味します。エポックごとの誤差変化グラフを表示するには、テスターをビジュアルモードで実行します。
ログには、NN訓練に関連するエントリが含まれます。
Sufficient bars at: 2022.01.04 00:00:00 Normalization by 3 std: 1.3415995381755823 15 30 30 21 1 EMA for early stopping: 31 (0.062500) Epoch 0 of 1000, loss 2.04525 ma(2.04525) Epoch 121 of 1000, loss 0.31818 ma(0.36230) Epoch 243 of 1000, loss 0.16857 ma(0.18029) Epoch 367 of 1000, loss 0.09157 ma(0.09709) Epoch 479 of 1000, loss 0.06454 ma(0.06888) Epoch 590 of 1000, loss 0.04875 ma(0.05092) Epoch 706 of 1000, loss 0.03659 ma(0.03806) Epoch 821 of 1000, loss 0.03043 ma(0.03138) Epoch 935 of 1000, loss 0.02721 ma(0.02697) Done by epoch limit 1000 with accuracy 0.024416 Training result: 0.024416206367547762 Best result: 0.024416206367547762 Check-up of saved and restored copy: bpnnm202302121707(0.0244162).bpn Loading bpnnm202302121707(0.0244162).bpn [bestLoss] [bestEpoch] [trainingSet] [validationSet] [epochsDone] [0] 0.024 999 250 0 1000 1.3415995381755823 XAGUSD PERIOD_D1 2021.01.18 00:00-2022.01.04 00:00 XAGUSD,XAUUSD,EURUSD 5/250 1000/0.0001 2.0/0 Best result restored: 0.024416206367547762
最終誤差の値に注意してください。後で、さまざまな強度でドロップアウトモードを有効にしてテストを繰り返し、結果を比較します。
次は取引レポートです。
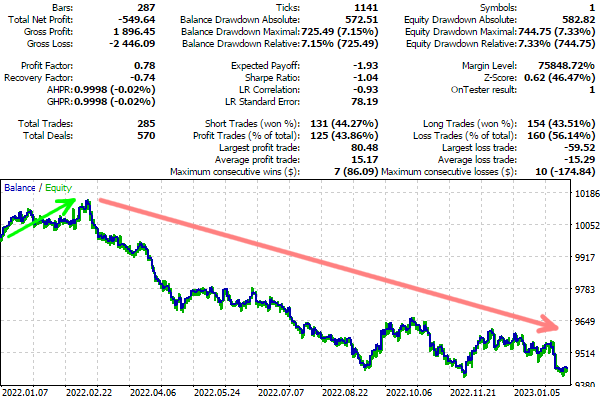
予想売買レポート例
明らかに、2022年のほとんどの期間、取引は満足のいくものではありませんでした。ただし、左側の訓練データセットである2021年直後には、短い収益期間があります。おそらく、ネットワークによって検出されたパターンは、しばらくの間動作し続けました。これが本当にそうであるかどうか、パフォーマンスを改善するためにネットワークまたは訓練セットの設定を何らかの方法で変更する必要があるかどうかを確認したい場合は、特定の取引システムごとに包括的な調査をおこなう必要があります。これは骨の折れる作業であり、ニューラルネットワークアルゴリズムの内部実装とは関係ありません。ここでは、最小限の分析のみをおこないます。
ログには、訓練済みネットワークを含むファイルの名前が表示されます。テスターでNetBinFileNameパラメータに指定し、テスト時間を2021年から拡張します。このモードでは、最初の2つ(SymbolsとDepth)を除くすべての入力パラメータは意味を持ちません。
延長された間隔でのテスト取引は、次のバランスダイナミクスを示しています(訓練データセットは黄色で強調表示)。
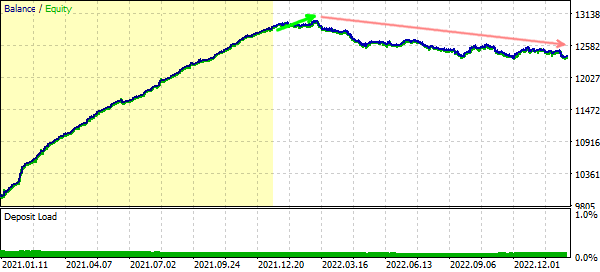
訓練セットを含む、延長された間隔で取引する場合の残高曲線
予想どおり、ネットワークは特定の間隔の詳細を学習しましたが、その完了後すぐに利益を上げなくなりました。
ドロップアウトを25%と50%にして、ネットワーク訓練を2回繰り返します(DropOutPercentageパラメータを25に設定し、次に50に順番に設定)。新しいネットワークの訓練を開始するには、NetBinFileNameパラメータをクリアし、テスト開始日を2022.01.01に戻します。
ドロップアウトが25%の場合、最初のケースよりも著しく大きな誤差が発生します。モデルを粗くすることにより、サンプル外のデータへの適用性を拡張しようとしているため、これは予想される結果です。
Epoch 0 of 1000, loss 2.04525 ma(2.04525) Epoch 125 of 1000, loss 0.46777 ma(0.48644) Epoch 251 of 1000, loss 0.36113 ma(0.36982) Epoch 381 of 1000, loss 0.30045 ma(0.30557) Epoch 503 of 1000, loss 0.27245 ma(0.27566) Epoch 624 of 1000, loss 0.24399 ma(0.24698) Epoch 744 of 1000, loss 0.22291 ma(0.22590) Epoch 840 of 1000, loss 0.19507 ma(0.20062) Epoch 930 of 1000, loss 0.18931 ma(0.19018) Done by epoch limit 1000 with accuracy 0.182581 Training result: 0.18258059873803228
ドロップアウトが50%になると、誤差はさらに増加します。
Epoch 0 of 1000, loss 2.04525 ma(2.04525) Epoch 118 of 1000, loss 0.54929 ma(0.55782) Epoch 242 of 1000, loss 0.43541 ma(0.45008) Epoch 367 of 1000, loss 0.38081 ma(0.38477) Epoch 491 of 1000, loss 0.34920 ma(0.35316) Epoch 611 of 1000, loss 0.30940 ma(0.31467) Epoch 729 of 1000, loss 0.29559 ma(0.29751) Epoch 842 of 1000, loss 0.27465 ma(0.27760) Epoch 956 of 1000, loss 0.25901 ma(0.26199) Done by epoch limit 1000 with accuracy 0.251914 Training result: 0.25191436104184456
次の図は、3つのバリアントの訓練グラフを示しています。
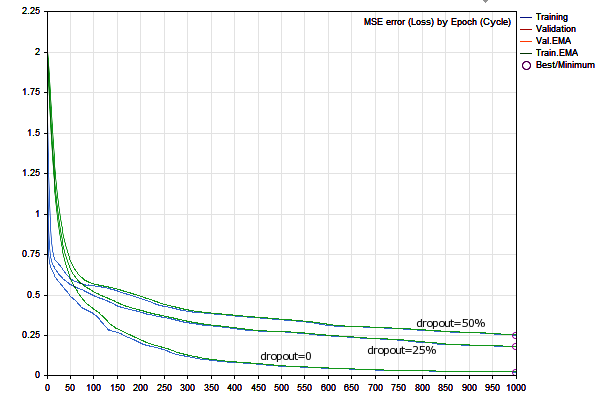
ドロップアウト値が異なる学習ダイナミクス
次が残高曲線です(訓練データセットは黄色で強調表示)。
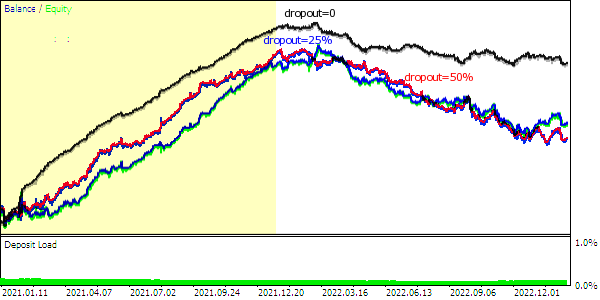
さまざまなドロップアウトを持つネットワークによっておこなわれた予測に基づく取引残高曲線
ドロップアウト中の重みのランダムな切断により、訓練期間の残高曲線は完全なネットワークほど滑らかではなくなり、総利益は自然に減少します。
この実験では、すべてのオプションがすぐに(1~2か月以内に)市場で機能しなくなりましたが、実験の本質は、完全なシステムを開発することではなく、作成されたニューラルネットワークツールをテストすることでした。
一般に、25%の平均ドロップアウト値がより最適であるように思われます。これは、正則化の程度が小さいと過剰適合に戻り、次数が大きいとネットワークの計算能力が破壊されるためです。しかし、予備的に引き出すことができる主な結論は、ニューラルネットワークアプローチは、あらゆる取引システムを「救う」ことができる万能薬ではないということです。特定の依存関係の存在に関する誤った仮定、異なるアルゴリズムモジュールの間違ったパラメータ、正しく準備されていないデータによって失敗が引き起こされる可能性があります。
この(または他の)取引システムを使用しないという決定を破棄する前に、AIを使用しないEAで通常おこなわれるように、最適なネットワーク設定を見つけるためにさまざまな方法を試す必要があります。条件の整った結論を出すには、より多くの統計を収集する必要があります。
特に、銘柄または時間枠の他のクラスタを検索したり、現在利用可能なpublicの変数で最適化を実行したり、それらのリストを拡張したりできます(たとえば、活性化関数、ベクトル生成メソッド、曜日によるフィルタリングなどを追加することによって)。
NNを使用しても、トレーダーが仮説を立てたり、アイデアをテストしたり、重要な要素をテストしたりする必要がなくなるわけではありません。唯一の違いは、取引システム設定の最適化がNNのメタパラメータによって補完されることです。
実験として、ベクトルのサイズ、ベクトルの数、隠れ層のサイズ係数、ドロップアウトの最適化を実行してみましょう。さらに、最適化にRandomizerパラメータを含めます。これにより、他の設定の組み合わせごとにネットワークの複数のインスタンスを生成できます。
- ベクトルサイズ(深さ):1~5
- 訓練セット(予備):50~400(50単位)
- 隠れ層係数:1~5
- ドロップアウト:0、25%、50%
- ランダマイザー:0~9
設定を含む.setファイルを以下に添付します。期間は2022.01.01~2023.02.15です。
最適化基準については、たとえばプロフィットファクターを使用します。ただし、組み合わせの数が少なく(6000)、それらの完全な反復(遺伝的最適化とは異なる)を考えると、これは重要ではありません。
最適化結果を分析するには、データをXMLファイルにエクスポートするか、「トレーディングにおけるOLAPの適用(その4)。テスターレポートの定量的・視覚的分析」稿のOLAPプログラムで説明されている.optファイル(optはオープンフォーマット)を直接使用するか、他のスクリプトを使用することができます。
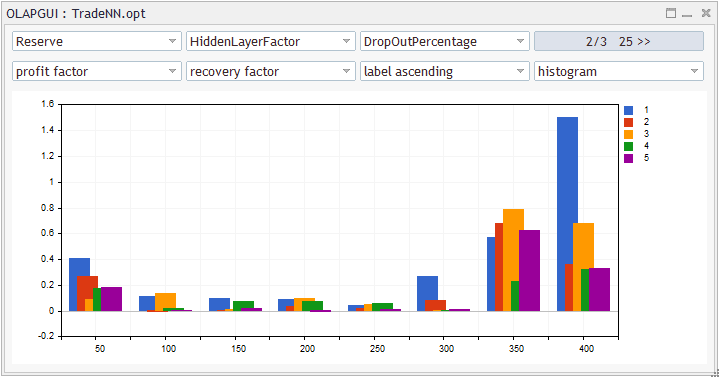
最適化レポートの統計分析
このスクリーンショットでは、変数は、回復係数から(最適化中のテスターの各パスから)特定の利益率計算(X/Y/Z 軸のセルごと)を使用して、要求された内訳(Y(色でマーク)によるHiddenLayerFactorに対するX(横軸)による予約、ZによるDropOutPercentage 25%)で集計されました。このような人為的な品質測定は理想的ではありませんが、すぐに使用できます。
同様の、またはより身近な統計はExcelで計算できます。
隠れ層係数を1(デフォルトの2ではなく)、ベクトルサイズを4(5ではなく)にすると、統計的に優れたパフォーマンスが得られました。推奨されるドロップアウト値は25%または50%ですが、0%ではありません。
また、予想どおり、より深い履歴が望ましいです(350または400、おそらくさらに増加することは正当化されます)。
見つかった作業設定を要約しましょう。
- ベクトルサイズ=4
- 訓練セット=400
- 隠れ層係数=1
Randomizerパラメータが最適化で使用されたため、この構成で訓練された30のネットワークインスタンスがあります。ドロップアウトレベル(0%、25%、50%)ごとに10個のネットワークです。25%と50%が必要です。最適化レポートをXMLでアップロードすることにより、必要なレコードをフィルターしてテーブルを取得できます(1より大きいフィルターを使用して収益性で並べ替えられます)。
Pass Result Profit Expected Profit Recovery Sharpe Custom Equity Trades Depth Reserve Hidden DropOut Randomizer Payoff Factor Factor Ratio DD % LayerF Perc 3838 1.35 336.02 2.41741 1.34991 1.98582 1.20187 1 1.61 139 4 400 1 25 6 838 1.23 234.40 1.68633 1.23117 0.81474 0.86474 1 2.77 139 4 400 1 25 1 3438 1.20 209.34 1.50604 1.20481 0.81329 0.78140 1 2.47 139 4 400 1 50 5 5838 1.17 173.88 1.25094 1.16758 0.61594 0.62326 1 2.76 139 4 400 1 50 9 5038 1.16 167.98 1.20849 1.16070 0.51542 0.60483 1 3.18 139 4 400 1 25 8 3238 1.13 141.35 1.01691 1.13314 0.46758 0.48160 1 2.95 139 4 400 1 25 5 2038 1.11 118.49 0.85245 1.11088 0.38826 0.41380 1 2.96 139 4 400 1 25 3 4038 1.10 107.46 0.77309 1.09951 0.49377 0.38716 1 2.12 139 4 400 1 50 6 1438 1.10 104.52 0.75194 1.09700 0.51681 0.37404 1 1.99 139 4 400 1 25 2 238 1.07 73.33 0.52755 1.06721 0.19040 0.26499 1 3.69 139 4 400 1 25 0 2838 1.03 34.62 0.24907 1.03111 0.10290 0.13053 1 3.29 139 4 400 1 50 4 2238 1.02 21.62 0.15554 1.01927 0.05130 0.07578 1 4.12 139 4 400 1 50 3
最良のものを見てみましょう。最初の行です。
最適化中、すべての訓練済みネットワークはMQL5/Files/<EA名>/<最適化の日>フォルダに保存されます。実際には、入力データが完全に一致する場合に限り、同様のネットワークをRandomizer値によって再訓練できることを考えると、これは省略できます。クウォート履歴が変更された場合(たとえば、別の証券会社を使用した場合)、これらの特性を正確に備えたネットワークを再現することはできません。
指定したフォルダ内のファイルには、最適化されたパラメータの名前と値で構成される名前が付けられます。したがって、ファイルシステムを簡単に検索できます。
Depth=4-Reserve=400-HiddenLayerFactor=1-DropOutPercentage=25-Randomizer=6
ファイルの名前が次のようになっているとします。
Depth=4-Reserve=400-HiddenLayerFactor=1-DropOutPercentage=25-Randomizer=6-3838(0.428079).bpn
ここで、括弧内の数字はネットワーク誤差、括弧の前の数字はパス番号です。
ファイル内を見てみましょう。ファイルはバイナリですが、訓練メタデータは末尾にテキストとして保存されています。したがって、訓練間隔は2021.01.1200:00-2022.07.2800:00(400バーD1)であることがわかります。
ファイルをtest3838.bpnなどの短い名前で共通ターミナルフォルダにコピーします。
NetBinFileNameパラメータに名前test3838.bpnを指定し、「ベクトルサイズ」(Depth)を4に設定します(予測モードでのみ作業する場合、他のすべてのパラメータは重要ではありません)。
さらに長い期間でEA取引を確認してみましょう:2022年から2023年が検証フォワードテストとして使用されたため、2020年を未知の期間として捉えます。
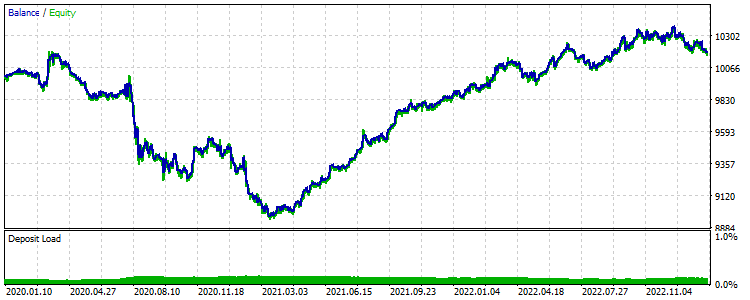
訓練セット外で失敗した予測取引テストの例
奇跡は起こりませんでした。システムは新しいデータでも不採算です。これは、他の設定でも同様です。
というわけで、良いニュースと悪いニュースの2つがあります。
悪いニュースは、提案されたアイデアが機能しないことです。まったく機能しないか、デモで調べた因子空間の制限が原因です(何十億もの組み合わせと何百もの銘柄に対して超大規模な最適化を実行していないため)。
良いニュースは、提案されたニューラルネットワークツールキットを使用してアイデアを評価し、(技術的な観点から)期待される結果を生成できることです。
結論
この記事では、MQL5行列を使用した誤差逆伝播法ニューラルネットワーククラスを紹介しました。実装は、Pythonなどの外部プログラムに依存せず、特別なファームウェア(OpenCLをサポートするグラフィックアクセラレータ)を必要としません。通常のニューラルネットワークの訓練モードと操作モードに加えて、クラスはプロセスの視覚化機能、ネットワークをファイルに保存および復元する機能を提供します。
これらのクラスを使用すると、ニューラルネットワークの使用を任意のプログラムに非常に簡単に統合できます。ただし、ネットワークは一部の資料(この場合は金融データ)に適用される単なるツールであることに注意してください。資料に十分な情報が含まれていない場合、情報に非常にノイズが多いまたは情報が無関係な場合、ニューラルネットワークはその中の聖杯を見つけることができません。
誤差逆伝播法アルゴリズムは、最も一般的な基本的な学習方法の1つであり、回帰型ネットワーク、畳み込みネットワーク、強化学習などのより複雑なニューラルネットワーク技術を構築するための基礎として使用できます。
MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/12187
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。
この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索
スタニスラフ・コロツキー
ニューラルネットワークのコンセプトをMQLに取り入れたあなたの努力は高く評価できる。これは私のような初心者にとって、本当に素晴らしい作品だ。ありがとう。)
バグを修正したファイルを更新してくれてありがとう。 しかし、ダウンロードエリアのファイルを差し替えた方がいいと思います。
幸いなことに、私はこのトピックに関するディスカッションを調べ、ファイルにバグがあることを知りました。そして、今、私は修正を探そうとしていたよりも、私はここにこのファイルのリンクを見つけました。
行番号490-493, 500, 515-527にバグフィックスのためのこれらの場所があることを望みます。それ以外の場所であれば、行番号に言及するか、//*BugFix ... をマークしてください。
よろしくお願いします。
ネッティング勘定を使用するには、ClosePosition 関数に明示的なシンボル 表示を追加する必要があります:
取引、自動取引システム、取引戦略のテストに関するフォーラム
記事 "MQL5行列上の逆伝播ニューラルネットワーク "の議論
Stanislav Korotky, 2024.04.16 17:34
ネット口座で動作するには、ClosePosition 関数でシンボルを明示的に指定する必要があります:
読む価値のある記事だ。
ありがとう!
ありがとう!
なぜか見落としていた。