Nöral Ağlar: Teoriden Pratiğe

Giriş

Günümüzde her yatırımcının, nöral ağlar hakkında bilgisi olması gerekir; bunları kullanmanın ne kadar havalı olduğunu bilirler. Çoğunluk, nöral ağlarla uğraşan kişilerin insanüstü olduklarına inanıyor. Bu makalede, sizlere nöral ağ mimarisini açıklamaya, uygulamalarını anlatmaya ve pratik kullanım örneklerini göstermeye çalışacağım.

 

Nöral Ağ Kavramı

Yapay nöral ağlar, insan sinir sistemini öğrenme ve uyum sağlama yeteneği konusunda simüle etme girişimlerine dayanan yapay zeka araştırmalarındaki alanlardan biridir ve bu, insan beyninin işleyişinin çok kabataslak bir simülasyonunu oluşturmamıza izin vermelidir.

İlginçtir ki, yapay nöral ağlar yapay nöronlardan oluşur.

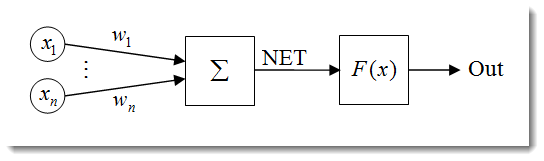
Şek. 1. Yapay nöron modeli

Bir nöronun yapısı, aşağıdaki birimlerin bir bileşimi olarak temsil edilebilir:

1. Girdiler ;
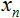2. Ağırlıklar ;
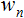3. Aktarım Fonksiyonu 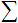ve Ağ Girişi ;
4. Aktivasyon Fonksiyonu ;
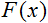5. Çıktı .

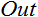Nöral ağların birçok özelliği vardır ve en önemlisi öğrenme yeteneğidir. Öğrenme süreci, ağırlıklarının değiştirilmesine indirgenir.

, burada nöronun net girdisidir.

Ağ girdisi daha sonra ele alacağımız aktivasyon fonksiyonu ile çıktıya dönüştürülür. Özetle, bir nöral ağ, sinyalleri girdi olarak alan ve sonucu çıktı olarak veren bir 'kara kutu' olarak görülebilir.

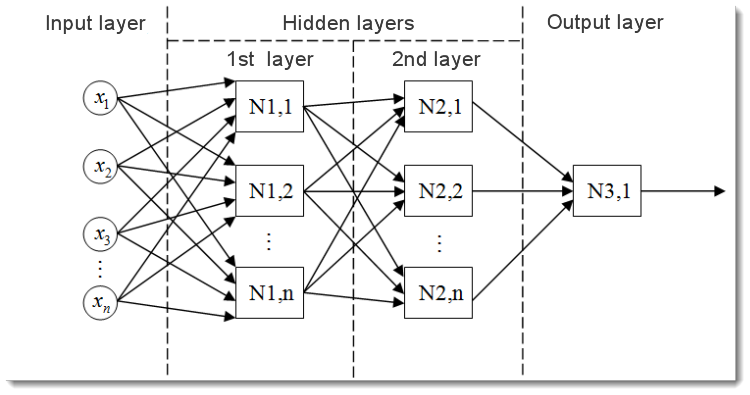
Şek. 2. Çok katmanlı bir nöral ağ modeli

Çok katmanlı bir nöral ağ, bu şekilde görünür. Şunları içerir:

• Verileri ağ üzerinde dağıtma işlevi gören ve herhangi bir hesaplama yapmayan girdi katmanı. Bu katmanın çıktıları, sinyalleri bir sonraki katmanın girdilerine (gizli veya çıktı) iletir;
• Çıktı katmanı, genellikle tüm nöral ağın çıktısını üreten bir (veya bazen birden fazla) nöron içerir. Bu sinyal, EA'nın gelecekteki kontrol mantığının temelini oluşturur;
• Gizli katmanlar, sinyalleri girdi katmanından çıktı katmanına ileten standart nöronların katmanlarıdır. Bunun girdisi bir önceki katmanın çıktısı iken çıktısı bir sonraki katmanın girdisi olarak işlev görür.

Bu örnekte, iki gizli katmana sahip nöral ağ gösterilmiştir. Ancak daha fazla gizli katmana sahip nöral ağlar olabilir.

 

Girdi Verilerini Normalleştirme

Girdi verilerinin normalleştirilmesi, tüm girdi verilerinin normalleştirildiği, yani [0,1] veya [-1,1] aralıklarına indirgendiği süreçtir. Normalleştirme yapılmazsa, girdi verileri nöron üzerinde ek bir etkiye sahip olacak ve yanlış kararlara yol açacaktır. Başka bir deyişle, farklı büyüklük derecelerine sahip değerleri nasıl karşılaştırabilirsiniz?

Standart formundaki normalleştirme formülü aşağıdaki gibidir:

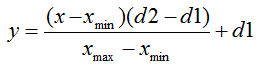
Burada:

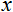• - normalleştirilecek değer;
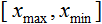• - х değer aralığı;
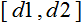• için etkili aralık - x değerinin indirgeneceği aralık.

Bunu bir örnekle açıklayayım:

Diyelim ki, [0,10] aralığında n girdi verisi var, = 0 ve = 10. Verileri, [0,1] aralığına, ardından = 0 ve = 1 aralığına indirgeyeceğiz. Şimdi, değerleri formüle yerleştirdikten sonra, n girdi verisinden herhangi bir x için normalleştirilmiş değerleri hesaplayabiliriz.

Bu, MQL5'te uygulandığında şöyle görünür:

double d1=0.0;
double d2=1.0;
double x_min=iMA_buf[ArrayMinimum(iMA_buf)];
double x_max=iMA_buf[ArrayMaximum(iMA_buf)];
for(int i=0;i<ArraySize(iMA_buf);i++)
  {
   inputs[i]=(((iMA_buf[i]-x_min)*(d2-d1))/(x_max-x_min))+d1;
  }

Önce çıktı değeri üst ve alt limitlerini belirleriz ve ardından gösterge minimum ve maksimum değerlerini elde ederiz (göstergeden veri kopyalama işlemi hariç tutulur ancak örneğin son 10 değer olabilir). Son olarak, her girdi öğesini normalleştiririz (farklı çubuklardaki gösterge değerleri) ve sonuçları daha sonra kullanmak üzere bir dizide saklarız.

 

Aktivasyon Fonksiyonları

Aktivasyon fonksiyonu, bir nöronun çıktısını hesaplayan bir fonksiyondur. Aldığı girdi, girdilerin tüm çarpımlarının ve bunların ilgili ağırlıklarının toplamını temsil eder (bundan böyle "ağırlıklı toplam" olarak anılacaktır):

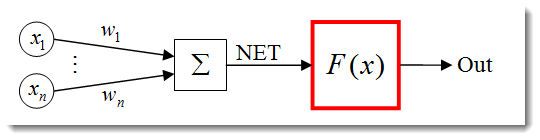
Şek. 3. Aktivasyon fonksiyonu ana hatlarıyla belirtilen yapay nöron modeli

Standart formundaki aktivasyon fonksiyonu formülü aşağıdaki gibidir:

Burada:

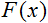• , aktivasyon fonksiyonudur;
• , bir nöronun çıktısının hesaplanmasının ilk aşamasında elde edilen ağırlıklı toplamdır;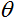
• , aktivasyon fonksiyonunun eşik değeridir. Bu, yalnızca sert eşik fonksiyonu için kullanılır ve diğer fonksiyonlarda sıfıra eşittir.

Ana aktivasyon fonksiyonu türleri şunlardır:

1. Birim adımı veya sert eşik fonksiyonu.
   
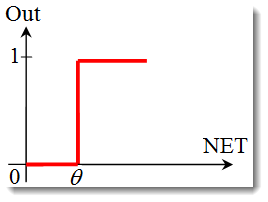
   Fonksiyon, aşağıdaki formülle tanımlanır:
   
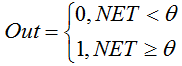
   Ağırlıklı toplam belirtilen değerden küçükse, aktivasyon fonksiyonu sıfır döndürür. Ağırlıklı toplam daha büyük olursa, aktivasyon fonksiyonu bir döndürür.

2. Sigmoid fonksiyonu.
   
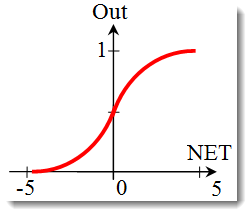
   Sigmoid fonksiyonunu açıklayan formül aşağıdaki gibidir:
   
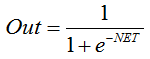
   Bu, genellikle çok katmanlı nöral ağlarda ve sürekli sinyalli diğer ağlarda kullanılır. Fonksiyon düzgünlüğü ve sürekliliği, çok olumlu özelliklerdir.

3. Hiperbolik tanjant.
   
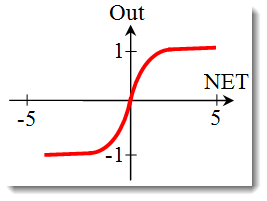
   Formül:
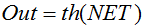   veya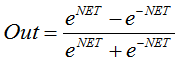
   Ayrıca bu, sürekli sinyalli ağlarda da sıklıkla kullanılır. Bunun, negatif değerleri döndürebilmesi alışılmamıştır.

 

Aktivasyon Fonksiyonunun Şeklini Değiştirme

Bir önceki bölümde, aktivasyon fonksiyonlarının türlerini ele aldık. Yine de dikkate alınması gereken bir başka önemli şey daha var; bir fonksiyonun eğimi (sert eşik fonksiyonu hariç). Sigmoid fonksiyonuna daha yakından bakalım.

Fonksiyon grafiğine bakıldığında, fonksiyonun [-5,5] aralığında düzgün olduğu kolaylıkla görülebilir. 10 girdisi ve bir çıktısı olan tek bir nörondan oluşan bir ağımız olduğunu varsayalım. Şimdi değişkeninin üst ve alt değerlerini hesaplamaya çalışalım. Her girdi, örneğin [-1,1] aralığından (Girdi Verilerini Normalleştirme'de daha önce belirtildiği gibi) normalleştirilmiş bir değer alacaktır.

Fonksiyon, negatif bir bağımsız değişkende dahi türevlenebilir olduğu için, negatif girdi değerlerini kullanacağız. Ağırlıklar da aynı aralıktan seçilecektir. Tüm olası girdi ve ağırlık kombinasyonlarıyla, [-10,10] aralığında uç değerlerini şu şekilde elde ederiz:

Formül, MQL5'te aşağıdaki gibi görünecektir:

for(int n=0; n<10; n++) 
  {
   NET+=Xn*Wn;
  }

Şimdi aktivasyon fonksiyonunu aralıkta, tanımlandığı gibi çizmemiz gerekiyor. Örnek olarak sigmoid fonksiyonunu alalım. Bunu yapmanın en kolay yolu, Excel kullanmaktır.

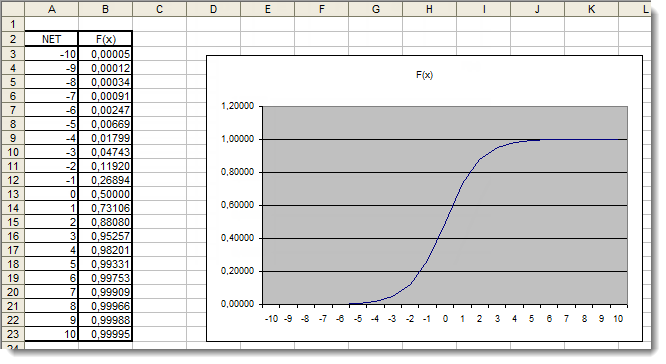
Şek. 4. Sigmoid fonksiyonunun Excel grafiği

Burada, [-5,5] aralığının dışındaki bağımsız değişken değerlerinin sonuçlar üzerinde kesinlikle hiçbir etkisi olmadığını açıkça görebiliriz. Bu, değer aralığının eksik olduğunu gösterir. Bunu düzeltmeye çalışalım. Bağımsız değişkene, değer aralığını genişletmemizi sağlayacak ek bir d katsayısı ekleyeceğiz.

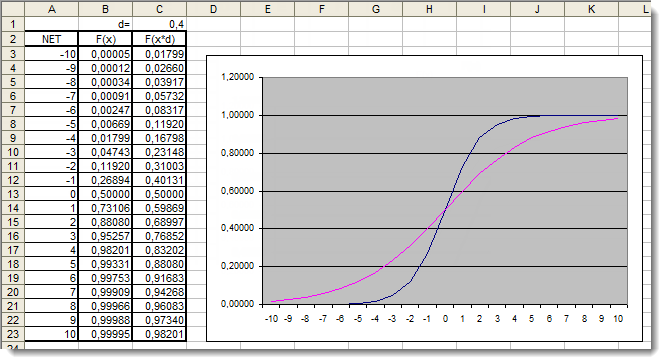
Şek. 5. Ek katsayı uygulanmış sigmoid fonksiyonunun Excel grafiği

Grafiklere bir kez daha göz atalım. Fonksiyon şeklini değiştiren ek bir d=0,4 katsayısı ekledik. Tablodaki değerlerin karşılaştırması, bunların artık daha düzgün dağıldığını göstermektedir. Dolayısıyla, sonuçlar aşağıdaki gibi ifade edilebilir:

for(int n=0; n<10; n++) 
  {
   NET+=Xn*Wn;
  }
NET*=0.4;

Şimdi hiperbolik tanjant aktivasyon fonksiyonunu inceleyelim. Önceki fonksiyonun incelemesinde ele alınan teoriyi atlayarak, hemen pratik uygulamaya geçelim. Buradaki tek fark, çıktının [-1,1] aralığında olabilmesidir. Ağırlıklı toplam ayrıca [-10,10] aralığından değerler alabilir.

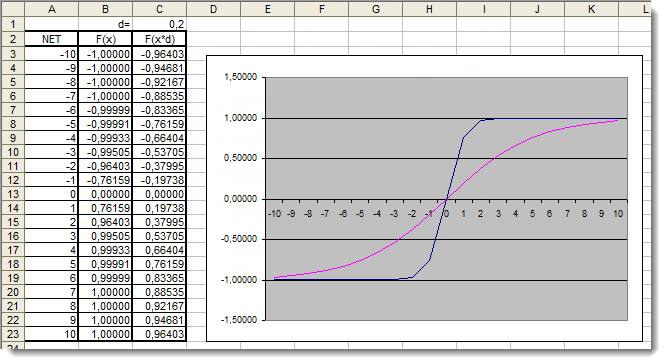
Şek. 6. Ek katsayı uygulanmış hiperbolik tanjant fonksiyonunun Excel grafiği

Grafik, d=0,2 ek katsayısının kullanılması nedeniyle fonksiyonun şeklinin iyileştirildiğini göstermektedir. Dolayısıyla, sonuçlar aşağıdaki gibi ifade edilebilir:

for(int n=0;n<10;n++) 
  {
   NET+=Xn*Wn;
  }
NET*=0.2;

Bu şekilde, herhangi bir aktivasyon fonksiyonunun şeklini değiştirebilir ve iyileştirebilirsiniz.

 

Uygulama

Şimdi pratik uygulamaya geçelim. İlk önce nöronun ağ girdisinin hesaplanmasını uygulamaya çalışacağız, ardından aktivasyon fonksiyonunu ekleyeceğiz. Nöronun ağ girdisini hesaplama formülünü hatırlayalım:

double NET;
double x[3];
double w[3];
int OnInit()
  {
   x[0]=0.1; // set the input value х1
   x[1]=0.8; // set the input value х2
   x[2]=0.5; // set the input value х3

   w[0]=0.5; // set the weight value w1
   w[1]=0.6; // set the weight value w2
   w[2]=0.3; // set the weight value w3

   for(int n=0;n<3;n++)
     {
      NET+=x[n]*w[n]; // add the weighted net input values together
     }
  }

O halde, onu inceleyelim:

1. Nöronun ağ girdisini ve iki diziyi depolamak için bir değişken bildirmekle başladık: Girdiler 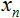ve ağırlıklar ;
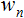2. Bu değişkenler, onlara genel bir kapsam vermek için (programın herhangi bir yerinden erişilebilir olmak üzere) tüm işlevlerin dışında en baştan bildirildi;
3. OnInit() başlatma işlevinde (aslında başka herhangi bir işlev olabilir), girdi dizisini ve ağırlık dizisini doldurduk;
4. Bunu, yalnızca üç girdimiz ve üç ilgili ağırlığımız olduğu için, n<3 toplama döngüsü takip etti;
5. Daha sonra ağırlıklı girdi değerleri ekledik ve bunları değişkende depoladık.

Böylece ilk görev tamamlandı - Toplamı elde ettik. Şimdi aktivasyon fonksiyonunun sırası. Aşağıda, Aktivasyon Fonksiyonları bölümünde incelenen aktivasyon fonksiyonlarını hesaplamaya yönelik kodlar bulunmaktadır.

Birim adımı veya sert eşik fonksiyonu

double Out;
if(NET>=x) Out=1;
else Out=0;

Sigmoid fonksiyonu

double Out = 1/(1+exp(-NET));

Hiperbolik tanjant fonksiyonu

double Out = (exp(NET)-exp(-NET))/(exp(NET)+exp(-NET));

 

Tümünü Bir Araya Getirme

Uygulamayı kolaylaştırmak için tek bir nörondan oluşan bir ağ alacağız. Bunu bir ağ olarak adlandırmak kesinlikle biraz zor ama önemli olan prensibi anlamak. Sonuçta, çok katmanlı bir nöral ağ, önceki nöron katmanının çıktısının bir sonraki katman için girdi olarak işlev gördüğü aynı nöronlardan oluşur.

Expert Advisor'ın "Yeni Başlayanlar için Hızlı Başlangıç veya Kısa Kılavuz" makalesinde geliştirilen ve tanıtılan biraz değiştirilmiş bir sürümünü kullanacağız. Dolayısıyla, örneğin Hareketli Ortalama trend göstergesini Göreceli Güç İndeksi osilatörü ile değiştireceğiz. Gösterge parametreleri ve bunların sırası hakkında bilgi yerleşik Yardım'da bulunabilir.

//+------------------------------------------------------------------+
//|                                                neuro-example.mq5 |
//|                        Copyright 2012, MetaQuotes Software Corp. |
//|                                              http://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2012, MetaQuotes Software Corp."
#property link      "http://www.mql5.com"
#property version   "1.00"
//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
#include <Trade\Trade.mqh>        //include the library for execution of trades
#include <Trade\PositionInfo.mqh> //include the library for obtaining information on positions

//--- weight values
input double w0=0.5;
input double w1=0.5;
input double w2=0.5;
input double w3=0.5;
input double w4=0.5;
input double w5=0.5;
input double w6=0.5;
input double w7=0.5;
input double w8=0.5;
input double w9=0.5;

int               iRSI_handle;  // variable for storing the indicator handle
double            iRSI_buf[];   // dynamic array for storing indicator values

double            inputs[10];   // array for storing inputs
double            weight[10];   // array for storing weights

double            out;          // variable for storing the output of the neuron

string            my_symbol;    // variable for storing the symbol
ENUM_TIMEFRAMES   my_timeframe; // variable for storing the time frame
double            lot_size;     // variable for storing the minimum lot size of the transaction to be performed

CTrade            m_Trade;      // entity for execution of trades
CPositionInfo     m_Position;   // entity for obtaining information on positions
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
int OnInit()
  {
//--- save the current chart symbol for further operation of the EA on this very symbol
   my_symbol=Symbol();
//--- save the current time frame of the chart for further operation of the EA on this very time frame
   my_timeframe=PERIOD_CURRENT;
//--- save the minimum lot of the transaction to be performed
   lot_size=SymbolInfoDouble(my_symbol,SYMBOL_VOLUME_MIN);
//--- apply the indicator and get its handle
   iRSI_handle=iRSI(my_symbol,my_timeframe,14,PRICE_CLOSE);
//--- check the availability of the indicator handle
   if(iRSI_handle==INVALID_HANDLE)
     {
      //--- no handle obtained, print the error message into the log file, complete handling the error
      Print("Failed to get the indicator handle");
      return(-1);
     }
//--- add the indicator to the price chart
   ChartIndicatorAdd(ChartID(),0,iRSI_handle);
//--- set the iRSI_buf array indexing as time series
   ArraySetAsSeries(iRSI_buf,true);
//--- place weights into the array
   weight[0]=w0;
   weight[1]=w1;
   weight[2]=w2;
   weight[3]=w3;
   weight[4]=w4;
   weight[5]=w5;
   weight[6]=w6;
   weight[7]=w7;
   weight[8]=w8;
   weight[9]=w9;
//--- return 0, initialization complete
   return(0);
  }
//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//--- delete the indicator handle and deallocate the memory space it occupies
   IndicatorRelease(iRSI_handle);
//--- free the iRSI_buf dynamic array of data
   ArrayFree(iRSI_buf);
  }
//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
//--- variable for storing the results of working with the indicator buffer
   int err1=0;
//--- copy data from the indicator array to the iRSI_buf dynamic array for further work with them
   err1=CopyBuffer(iRSI_handle,0,1,10,iRSI_buf);
//--- in case of errors, print the relevant error message into the log file and exit the function
   if(err1<0)
     {
      Print("Failed to copy data from the indicator buffer");
      return;
     }
//---
   double d1=0.0;                                 //lower limit of the normalization range
   double d2=1.0;                                 //upper limit of the normalization range
   double x_min=iRSI_buf[ArrayMinimum(iRSI_buf)]; //minimum value over the range
   double x_max=iRSI_buf[ArrayMaximum(iRSI_buf)]; //maximum value over the range

//--- In the loop, fill in the array of inputs with the pre-normalized indicator values
   for(int i=0;i<ArraySize(inputs);i++)
     {
      inputs[i]=(((iRSI_buf[i]-x_min)*(d2-d1))/(x_max-x_min))+d1;
     }
//--- store the neuron calculation result in the out variable
   out=CalculateNeuron(inputs,weight);
//--- if the output value of the neuron is less than 0.5
   if(out<0.5)
     {
      //--- if the position for this symbol already exists
      if(m_Position.Select(my_symbol))
        {
         //--- and this is a Sell position, then close it
         if(m_Position.PositionType()==POSITION_TYPE_SELL) m_Trade.PositionClose(my_symbol);
         //--- or else, if this is a Buy position, then exit
         if(m_Position.PositionType()==POSITION_TYPE_BUY) return;
        }
      //--- if we got here, it means there is no position; then we open it
      m_Trade.Buy(lot_size,my_symbol);
     }
//--- if the output value of the neuron is equal to or greater than 0.5
   if(out>=0.5)
     {
      //--- if the position for this symbol already exists
      if(m_Position.Select(my_symbol))
        {
         //--- and this is a Buy position, then close it
         if(m_Position.PositionType()==POSITION_TYPE_BUY) m_Trade.PositionClose(my_symbol);
         //--- or else, if this is a Sell position, then exit
         if(m_Position.PositionType()==POSITION_TYPE_SELL) return;
        }
      //--- if we got here, it means there is no position; then we open it
      m_Trade.Sell(lot_size,my_symbol);
     }
  }
//+------------------------------------------------------------------+
//|   Neuron calculation function                                    |
//+------------------------------------------------------------------+
double CalculateNeuron(double &x[],double &w[])
  {
//--- variable for storing the weighted sum of inputs
   double NET=0.0;
//--- Using a loop we obtain the weighted sum of inputs based on the number of inputs
   for(int n=0;n<ArraySize(x);n++)
     {
      NET+=x[n]*w[n];
     }
//--- multiply the weighted sum of inputs by the additional coefficient
   NET*=0.4;
//--- send the weighted sum of inputs to the activation function and return its value
   return(ActivateNeuron(NET));
  }
//+------------------------------------------------------------------+
//|   Activation function                                            |
//+------------------------------------------------------------------+
double ActivateNeuron(double x)
  {
//--- variable for storing the activation function results
   double Out;
//--- sigmoid
   Out=1/(1+exp(-x));
//--- return the activation function value
   return(Out);
  }
//+------------------------------------------------------------------+

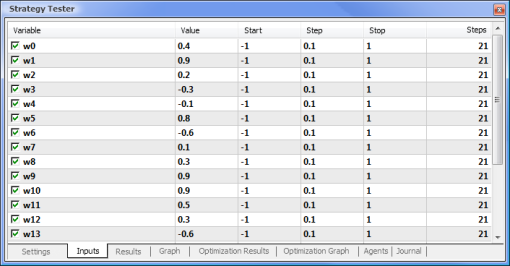
Yapmamız gereken ilk şey ağımızı eğitmek. Ağırlıkları optimize edelim.

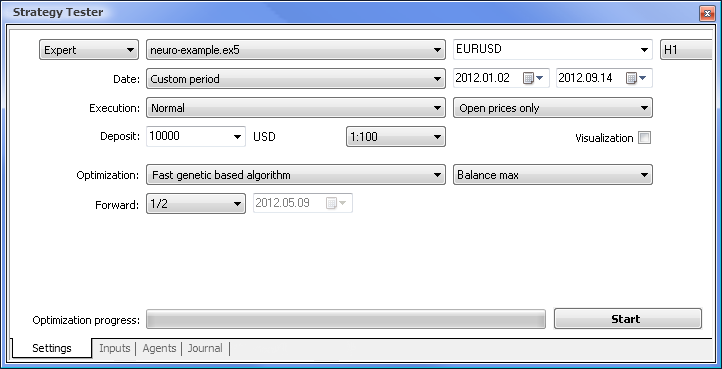
Şek. 7. Gerekli parametre kümesine sahip strateji test cihazı

Optimizasyonu aşağıdaki parametreleri kullanarak çalıştıracağız:

• Tarih - Örneğin yılın başından itibaren Dönem ne kadar uzun olursa, eğri uydurma olayı o kadar az olur ve sonuç o kadar iyi olur.
• Yürütme - Normal, Yalnızca açılış fiyatları. Expert Advisor'ımız, mevcut değer dışında göstergenin yalnızca son 10 değerini aldığı için, Her tick modunda test yapmanın bir anlamı yoktur.
• Optimizasyon, yavaş tamamlama algoritması kullanılarak çalışacak şekilde ayarlanabilir. Ancak genetik optimizasyon, bir algoritma değerlendirilirken özellikle kullanışlı olan daha hızlı sonuçlar verecektir. Sonuç tatmin ediciyse, daha doğru sonuçlar için yavaş tamamlama algoritmasını kullanmayı da deneyebilirsiniz.
• 1/2 ve üzeri Forward, EA'nızın bir sonraki optimizasyona kadar elde edilen sonuçları ne kadar süreyle oluşturabileceğini değerlendirmenize olanak tanır.
• Zaman dilimi ve Para birimi çifti uygun gördüğünüz şekilde ayarlanabilir.

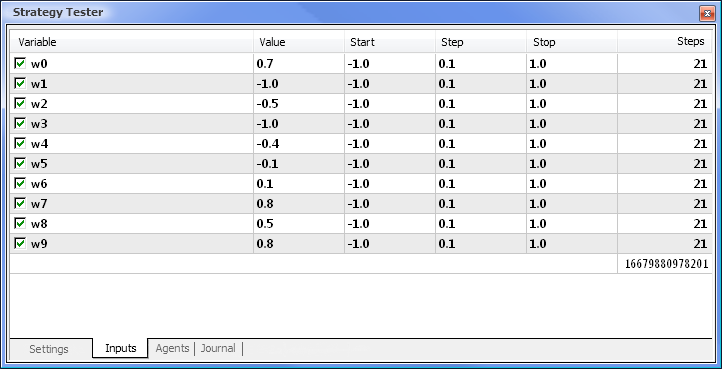
Şek. 8. Optimize edilecek parametreleri ve ilgili aralıklarını ayarlama

Optimizasyon, tüm ağırlıklara ve aralıklarına göre çalıştırılacaktır. Ayarlar sekmesine geri dönerek ve Başlat düğmesine tıklayarak optimizasyonu başlatın.

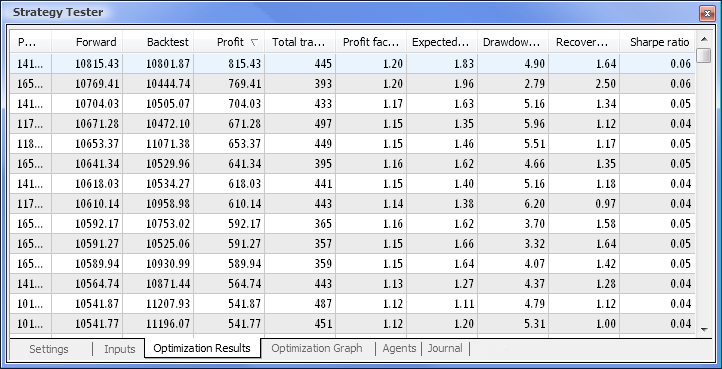
Şek. 9. Optimizasyondan sonra elde edilen veriler

Optimizasyon tamamlandıktan sonra Optimizasyon Sonuçları sekmesinde (parametrelerden birine göre sıralamak için ilgili sütun başlığına tıklayın) maksimum kar değeri olan geçişi seçeriz. Ardından diğer parametreleri değerlendirebilir ve gerekirse istediğiniz geçişi seçebilirsiniz.

Gerekli geçişe çift tıklama, sonuçları Sonuçlar ve Grafik sekmelerinde gösterilen testleri başlatır.

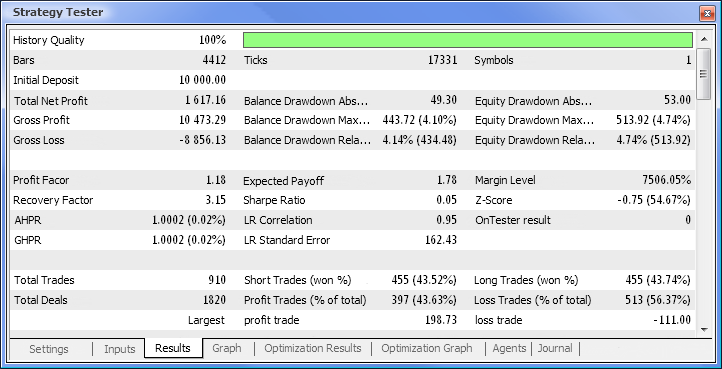
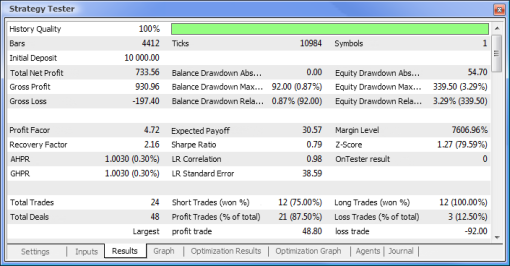
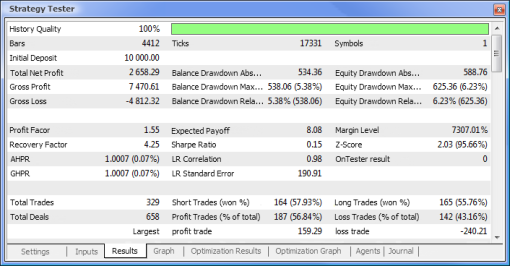
Şek. 10. Test raporu

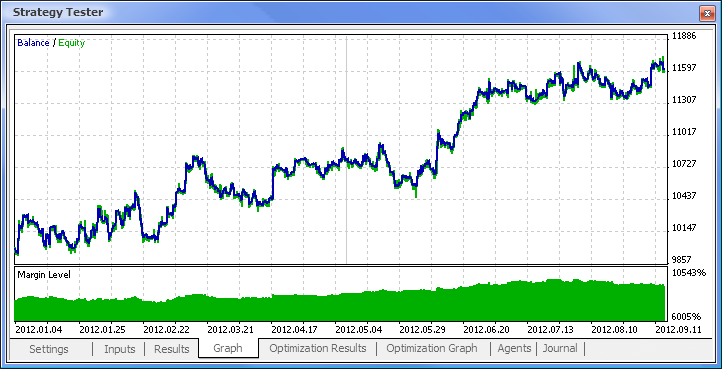
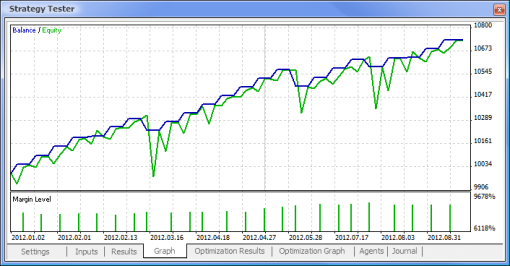
Şek. 11. Bakiye grafiği

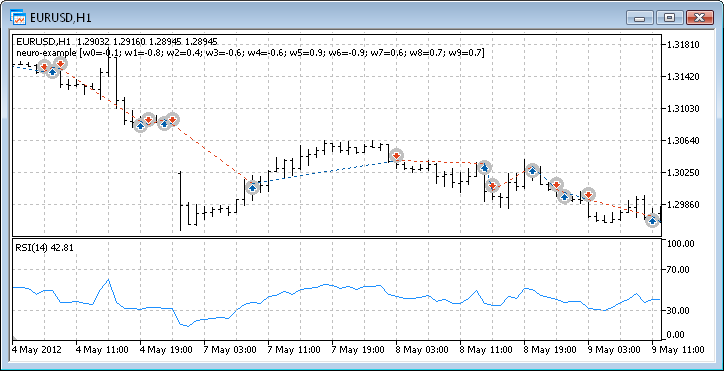
Şek. 12. Expert Advisor'ın alım satım performansı

Sonunda sonuçları aldık ve başlangıç için hiç de fena değiller. Yalnızca bir nöronumuz olduğunu unutmayın. Verilen örnek net bir şekilde ilkel ama kabul etmeliyiz ki tek başına dahi kar ettirebilir.

 

Nöral Ağların Avantajları

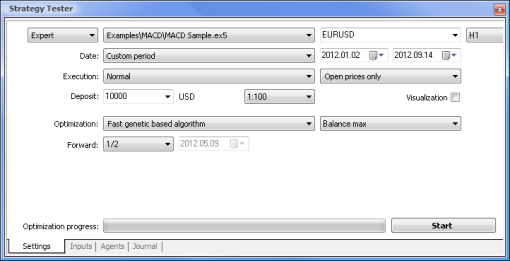
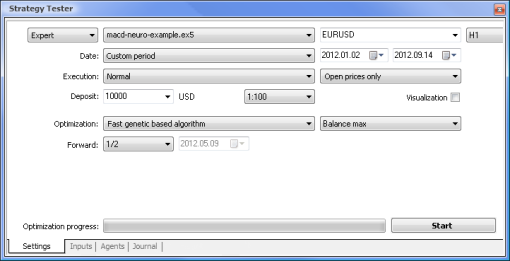
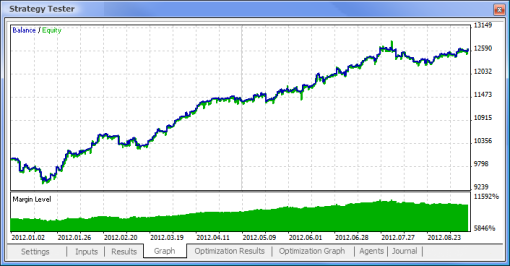
Şimdi standart mantığa dayalı bir EA ile nöral ağ destekli bir EA'yı karşılaştırmaya çalışalım. Terminal ile birlikte gelen MACD Örnek Expert Advisor'ının optimizasyon ve test sonuçlarını MACD tabanlı nöral ağ destekli EA'nın sonuçlarıyla karşılaştıracağız.

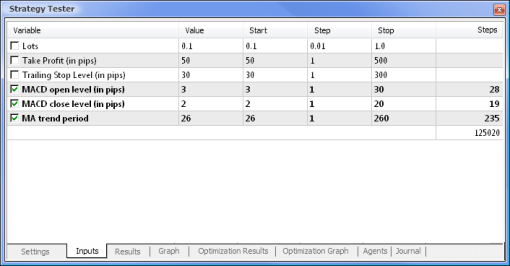
Kar Al ve Takip Eden Zarar Durdurucu değerleri, nöral ağ destekli EA'da eksik oldukları için optimizasyona dahil edilmeyecektir. Test edeceğimiz her iki Expert Advisor, aşağıdaki parametrelerle MACD'ye dayanmaktadır:

• Hızlı hareketli ortalamanın dönemi: 12;
• Yavaş hareketli ortalamanın dönemi: 26;
• Farkın ortalama alma dönemi: 9;
• Fiyat türü: Kapanış fiyatı.

Ayrıca gerekli para birimi çiftini ve zaman dilimini de ayarlayabilirsiniz, ancak bizim durumumuzda bunları değiştirmeden bırakacağız - sırasıyla EURUSD, H1,. Her iki durumda da test dönemi aynıdır: Açılış fiyatları kullanılarak yılın başından itibaren.

MACD Örneği	macd-neuro-examle

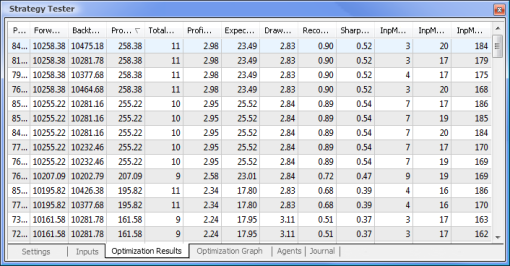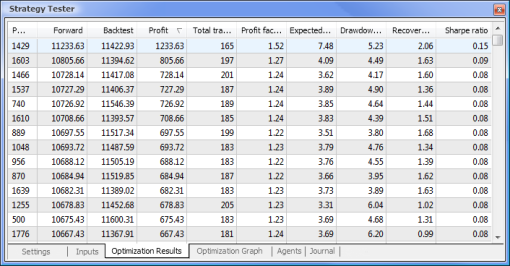Şimdi test edilen Expert Advisor'ların temel parametrelerini karşılaştıralım:

Parametre	MACD Örneği	macd-neuro-examle
Toplam Net Kar	733,56	2 658,29
Mutlak Bakiye Düşüşü	0,00	534,36
Maksimum Hisse Senedi Düşüşü	339,50 (%3,29)	625,36 (%6,23)
Kar Faktörü	4,72	1,55
Kurtarma Faktörü	2,16	4,25
Beklenen Kazanç	30,57	8,08
Sharpe Oranı	0,79	0,15
Toplam Alım Satım İşlemi	24	329
Toplam Yatırım	48	658
Kar Alım Satımları, (toplam %)	21 (%87,50)	187 (%56,84)
Ortalama Kar Alım Satımı	44,33	39,95
Ortalama Ardışık Kazançlar	5	2

 

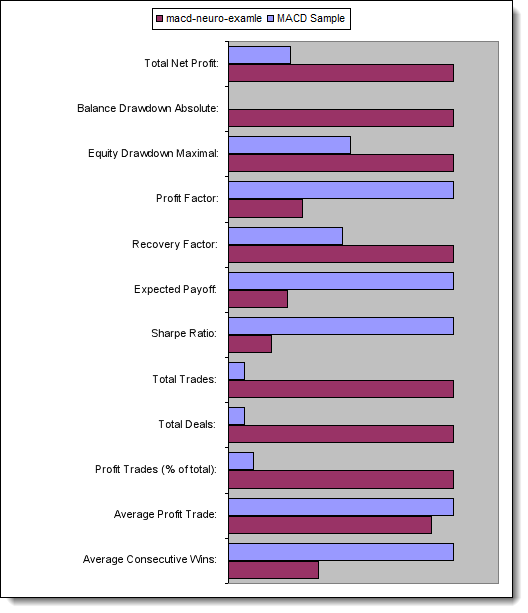
Şek. 13. Temel parametrelerin karşılaştırması

 

Sonuç

Bu makalede, nöral ağları kullanarak EA'ları tasarlarken bilmeniz gereken ana noktalar ele alınmıştır. Bunun yanı sıra, bir nöron ve nöral ağ mimarisinin yapısı gösterilmiş olup aktivasyon fonksiyonunun şeklini değiştirme yöntemleri ve aktivasyon fonksiyonları ve ayrıca optimizasyon ve girdi verilerini normalleştirme süreci özetlenmiştir. Ayrıca, standart mantığa dayalı bir EA ile nöral ağ destekli bir EA karşılaştırılmıştır.