
신경망 네트워크: 이론에서 실전까지
소개
요즘, 모든 거래자들은 신경망에 대해 들어봤을 것이고, 신경망을 사용하는 것이 얼마나 멋진지 알고 있을 것입니다. 대다수는 신경망을 다룰 수 있는 사람들이 일종의 초인적인 존재라고 믿습니다. 이 기사에서는 신경 네트워크 아키텍처를 설명하고, 그 적용 사례를 설명하며, 실제 사용 사례를 보여 드리겠습니다.
신경 네트워크의 개념
인공지능 연구의 한 분야로, 인공지능은 인간의 신경계를 학습하고 적응하는 능력에서 시뮬레이션하려는 시도를 바탕으로 하고 있습니다. 그러면 인간의 뇌 작동에 대한 매우 대략적인 시뮬레이션을 만들 수 있을 것입니다.
신기하게도 인공 신경망은 인공 뉴런으로 이루어져 있습니다.
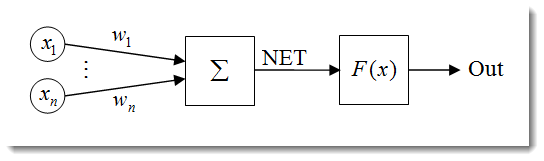
그림. 1. 인공 뉴런 모형
뉴런의 구조는 다음 단위의 구성으로 나타낼 수 있습니다:
- 입력
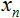 ;
; - 가중치
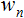 ;
; - 전송 기능
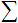 및 순 입력
및 순 입력  ;
; - 활성화 함수
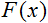 ;
; - 출력
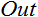 .
.
신경망은 많은 특성을 가지고 있고 학습 능력이 가장 중요합니다. 학습 프로세스는 가중치를 변경하는 것으로 귀결됩니다![]() .
.

![]() 여기 뉴런의 순입력이 있습니다.
여기 뉴런의 순입력이 있습니다.
![]()
그런 다음 우리가 나중에 다룰 활성화 함수에 의해 순 입력이 출력으로 변환됩니다. 한마디로 신경망은 신호를 입력으로 받고 그 결과를 출력하는 '블랙박스'로 볼 수 있습니다.
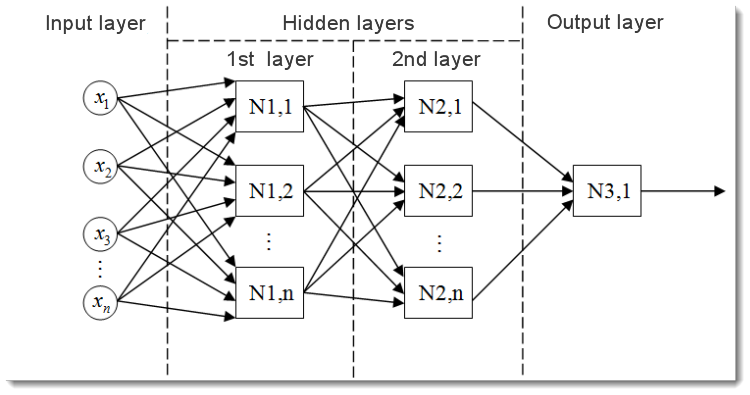
그림. 2. 다층 신경망의 모델
이것이 다층 신경망의 모습입니다. 구성 요소는 다음과 같습니다:
- 입력 계층은 데이터를 네트워크에 분산시키는 역할을 하고 계산을 수행하지 않습니다. 이 레이어의 출력은 다음 레이어의 입력(숨김 또는 출력)으로 신호를 전송합니다.
- 출력 계층은 일반적으로 전체 신경망의 출력을 생성하는 하나의 뉴런(또는 때로는 둘 이상의 뉴런)을 포함합니다. 이 신호는 EA의 미래 제어 논리의 기초가 됩니다;
- 숨겨진 계층은 입력 계층에서 출력 계층으로 신호를 전송하는 표준 뉴런 계층입니다. 입력은 이전 레이어의 출력인 반면, 출력은 다음 레이어의 입력 역할을 합니다.
이 예는 두 개의 숨겨진 층이 있는 신경망을 보여줍니다. 하지만 더 많은 숨겨진 층을 가진 신경망이 있을지도 모릅니다.
입력 데이터 정규화
입력 데이터 정규화는 모든 입력 데이터가 정규화되는 프로세스입니다. 즉, [0,1] 또는 [-1,1] 범위로 감소됩니다. 정규화가 수행되지 않으면 입력 데이터가 뉴런에 추가적인 영향을 미쳐 잘못된 결정을 내리게 됩니다. 즉, 크기가 서로 다른 값을 어떻게 비교할 수 있습니까?
표준 형식의 정규화 공식은 다음과 같습니다:
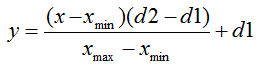
여기서:
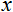 - 값을 정규화합니다;
- 값을 정규화합니다;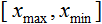 - х 값 범위;
- х 값 범위;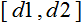 - x의 값이 감소하는 범위.
- x의 값이 감소하는 범위.
예를 들어 설명하겠습니다:
n 입력 데이터의 범위 [0,10], 그리고 ![]() = 0 and
= 0 and ![]() = 10 이라고 가정합니다. 데이터를 범위[0,1]로 줄인 다음, 그러면
= 10 이라고 가정합니다. 데이터를 범위[0,1]로 줄인 다음, 그러면 ![]() = 0 and
= 0 and ![]() = 1. 이제 수식에 값을 연결하면, 우리는 모든 x의 정규화 값을 n 입력 데이터로 부터 계산할 수 있습니다.
= 1. 이제 수식에 값을 연결하면, 우리는 모든 x의 정규화 값을 n 입력 데이터로 부터 계산할 수 있습니다.
다음은 MQL5에서 구현될 때의 모습입니다:
double d1=0.0; double d2=1.0; double x_min=iMA_buf[ArrayMinimum(iMA_buf)]; double x_max=iMA_buf[ArrayMaximum(iMA_buf)]; for(int i=0;i<ArraySize(iMA_buf);i++) { inputs[i]=(((iMA_buf[i]-x_min)*(d2-d1))/(x_max-x_min))+d1; }
먼저 출력 값 상한과 하한을 지정한 다음 지시자 최소값과 최대값을 구합니다(지시자의 데이터 복사는 생략되지만 10개의 마지막 값이 있을 수 있음). 마지막으로, 모든 입력 요소(다른 막대의 지시자 값)를 정규화하고 나중에 사용할 수 있도록 결과를 배열에 저장합니다.
활성화 기능
활성화 기능은 뉴런의 출력을 계산하는 기능입니다. 입력이 수신하는 입력은 입력의 모든 곱과 각 가중치의 합을 나타냅니다(이하 "가중합").
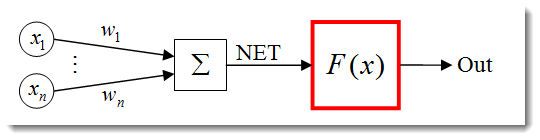
그림. 3. 활성화 기능이 약술된 인공 뉴런 모델
표준 형식의 활성화 함수 공식은 다음과 같습니다:
![]()
여기서:
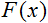 is the activation function;
is the activation function;-
 뉴런의 출력을 계산하는 첫 번째 단계에서 얻은 가중치 합입니다;
뉴런의 출력을 계산하는 첫 번째 단계에서 얻은 가중치 합입니다; 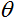 활성화 함수의 임계값입니다. 하드 임계값 기능에만 사용되며 다른 기능에서는 0입니다.
활성화 함수의 임계값입니다. 하드 임계값 기능에만 사용되며 다른 기능에서는 0입니다.
활성화 기능의 주요 유형은 다음과 같습니다:
-
단위 단계 또는 함드 임계값 함수.
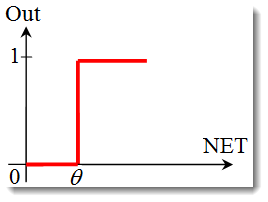
함수는 다음 공식으로 설명됩니다:
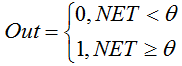
가중치 합계가 지정된 값보다 작으면 활성화 함수는 0을 반환합니다. 가중치 합계가 커지면 활성화 함수가 1을 반환합니다. -
시그모이드 함수.
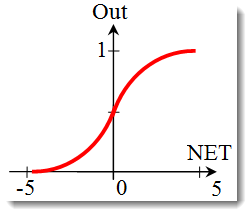
시그모이드 함수를 설명하는 공식은 다음과 같습니다:
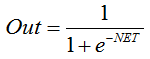
이것은 종종 연속 신호가 있는 다층 신경 네트워크와 다른 네트워크에서 사용됩니다. 기능의 매끄러움과 연속성은 매우 긍정적인 특성입니다. -
쌍곡선 접선.
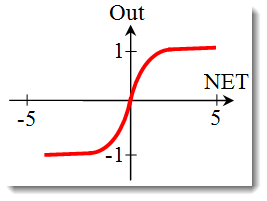
공식:
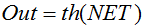 또는
또는 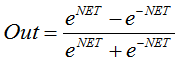
또한 연속 신호가 있는 네트워크에서도 자주 사용됩니다. 음수 값을 반환할 수 있다는 점에서 특이합니다.
활성화 함수 모양을 변경합니다.
이전 섹션에서는 활성화 기능의 유형에 대해 다루었습니다. 그러나 고려해야 할 또 다른 중요한 사항이 있습니다. 즉, 함수의 기울기입니다(하드 임계값 함수는 제외). 시그모이드 기능에 대해 자세히 살펴보겠습니다.
함수 그래프를 보면 [-5,5] 범위에 걸쳐 기능이 원활하다는 것을 쉽게 알 수 있습니다. 10개의 입력과 1개의 출력을 가진 단일 뉴런으로 구성된 네트워크가 있다고 가정해 보겠습니다. 이제 변수의 상한 및 하한 값을 계산해 보겠습니다![]() . 모든 입력은 정규화된 값을 사용합니다 (이미 언급했듯이, 입력 데이터 정규화), 예: 범위 [-1,1].
. 모든 입력은 정규화된 값을 사용합니다 (이미 언급했듯이, 입력 데이터 정규화), 예: 범위 [-1,1].
음의 인수에서도 함수가 미분 가능하기 때문에 음의 입력값을 사용할 것입니다. 가중치도 동일한 범위에서 선택됩니다. 가능한 모든 입력값과 가중치 조합을 통해 극한값을 다음과 같이 얻을 수 있습니다 ![]() 범위 [-10,10] :
범위 [-10,10] :

MQL5에서 공식은 다음과 같이 표시됩니다:
for(int n=0; n<10; n++) { NET+=Xn*Wn; }
이제 확인된 범위 내에서 활성화 기능을 플롯해야 합니다. 시그모이드 기능을 예로 들어 보겠습니다. 가장 쉬운 방법은 엑셀을 사용하는 것입니다.
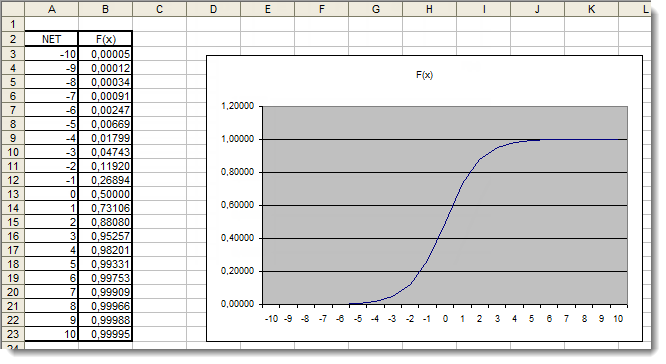
그림. 4. 시그모이드 함수의 Excel 그래프
여기서, 우리는 [-5,5] 범위를 벗어나는 인수 값이 결과에 전혀 영향을 미치지 않음을 명확히 알 수 있습니다. 이것은 값 범위가 불완전함을 나타냅니다. 우리가 이걸 고쳐보도록 하죠. 인수에 값의 범위를 확장할 수 있는 계수 d를 추가하겠습니다.
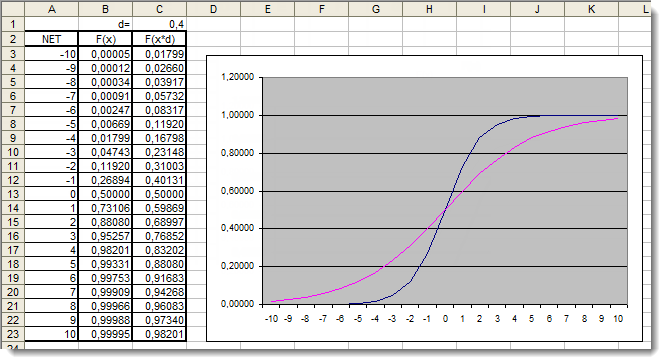
그림. 5. 추가 계수가 적용된 시그모이드 함수의 Excel 그래프입니다.
그래프를 다시 한 번 살펴보겠습니다. 함수 모양을 바꾼 계수 d=0.4 를 추가했습니다. 표의 값을 비교하면 이제 값이 더 균일하게 분포되어 있음을 알 수 있습니다. 따라서 결과는 다음과 같이 나타낼 수 있습니다:
for(int n=0; n<10; n++) { NET+=Xn*Wn; } NET*=0.4;
이제 쌍곡선 접선 활성화 기능을 살펴보겠습니다. 이전 기능에 대한 검토에서 다룬 이론을 건너뛰면 바로 실제 적용에 이르게 됩니다. 여기서 유일한 차이점은 출력이 [-1,1] 범위에 있을 수 있다는 것입니다. 가중치 합계는 [-10,10] 범위의 값도 취할 수 있습니다.
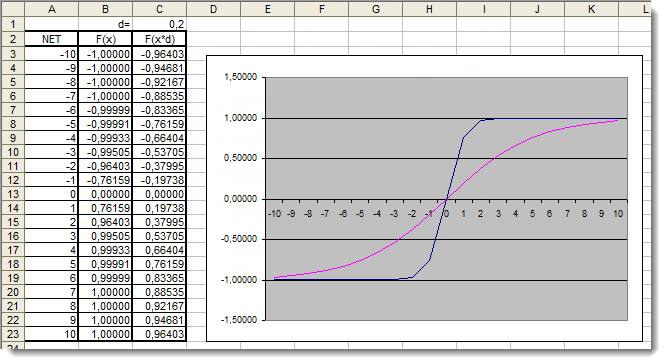
그림. 6. 추가 계수가 적용된 쌍곡선 접선 함수의 Excel 그래프
그래프에서는 추가 계수 d=0.2 를 사용하여 함수의 모양이 개선되었음을 보여 줍니다. 따라서 결과는 다음과 같이 나타낼 수 있습니다:
for(int n=0;n<10;n++) { NET+=Xn*Wn; } NET*=0.2;
이 방법으로 모든 활성화 기능의 모양을 변경하고 개선할 수 있습니다.
응용 프로그램
이제 실용적인 애플리케이션으로 넘어가겠습니다. 우선 뉴런의 순투입 계산부터 실행해 보고 활성화 기능을 추가하겠습니다. 뉴런의 순입력 계산 공식을 상기해 보겠습니다:

double NET; double x[3]; double w[3]; int OnInit() { x[0]=0.1; // set the input value х1 x[1]=0.8; // set the input value х2 x[2]=0.5; // set the input value х3 w[0]=0.5; // set the weight value w1 w[1]=0.6; // set the weight value w2 w[2]=0.3; // set the weight value w3 for(int n=0;n<3;n++) { NET+=x[n]*w[n]; // add the weighted net input values together } }
Let us look into it:
- 뉴런의 순 입력
 과 두 개의 배열
과 두 개의 배열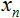 (입력 및 가중치)
(입력 및 가중치)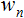 을 저장하기 위한 변수를 선언하는 것부터 시작했습니다;
을 저장하기 위한 변수를 선언하는 것부터 시작했습니다; - 이러한 변수들은 (프로그램 어디에서나 액세스할 수 있는) 글로벌 범위를 제공하기 위해 모든 기능의 맨 처음에 선언되었습니다.
- OnInit()초기화 함수(실제로는 다른 함수일 수 있음)에서는 입력 배열과 가중치 배열을 채웠습니다;
- 이어서 합계 루프, n<3 으로 나왔습니다. 입력값과 가중치가 각각 3개뿐이기 때문입니다;
- 그런 다음 가중 입력 값을 추가하여 변수에 저장했습니다
 .
.
첫 번째 작업이 완료되었습니다. 총합을 확보했습니다. 이제 활성화 기능의 차례입니다. 다음은 활성화 기능 섹션 섹션에서 검토한 활성화 기능 계산 코드입니다.
장치 스텝 또는 하드 임계값 기능
double Out; if(NET>=x) Out=1; else Out=0;
시그모이드 함수
double Out = 1/(1+exp(-NET));
쌍곡선 접선 함수
double Out = (exp(NET)-exp(-NET))/(exp(NET)+exp(-NET));
모든 것을 하나로 묶습니다.
보다 쉽게 구현할 수 있도록 단일 뉴런으로 구성된 네트워크를 구축하겠습니다. 네트워크라고 하기에는 분명 조금 무리가 있지만, 원칙을 이해하는 것이 중요합니다. 결국, 다층 신경망은 이전 뉴런 층의 출력이 다음 층의 입력 역할을 하는 동일한 뉴런으로 구성됩니다.
여기서는 Expert Advisor를 약간 수정하여 "초보자용 빠른 시작 또는 간단한 가이드"라는 기사에 소개하고자 합니다. 따라서, 예를 들어, 우리는 이동 평균 추세 표시기를 상대 강도 지수 오실레이터로 바꿀 것입니다. 지표의 파라미터 및 파라미터 시퀀스에 대한 정보는 내장된 도움말에서 확인할 수 있습니다.
//+------------------------------------------------------------------+ //| neuro-example.mq5 | //| Copyright 2012, MetaQuotes Software Corp. | //| http://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2012, MetaQuotes Software Corp." #property link "http://www.mql5.com" #property version "1.00" //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ #include <Trade\Trade.mqh> //include the library for execution of trades #include <Trade\PositionInfo.mqh> //include the library for obtaining information on positions //--- weight values input double w0=0.5; input double w1=0.5; input double w2=0.5; input double w3=0.5; input double w4=0.5; input double w5=0.5; input double w6=0.5; input double w7=0.5; input double w8=0.5; input double w9=0.5; int iRSI_handle; // variable for storing the indicator handle double iRSI_buf[]; // dynamic array for storing indicator values double inputs[10]; // array for storing inputs double weight[10]; // array for storing weights double out; // variable for storing the output of the neuron string my_symbol; // variable for storing the symbol ENUM_TIMEFRAMES my_timeframe; // variable for storing the time frame double lot_size; // variable for storing the minimum lot size of the transaction to be performed CTrade m_Trade; // entity for execution of trades CPositionInfo m_Position; // entity for obtaining information on positions //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ int OnInit() { //--- save the current chart symbol for further operation of the EA on this very symbol my_symbol=Symbol(); //--- save the current time frame of the chart for further operation of the EA on this very time frame my_timeframe=PERIOD_CURRENT; //--- save the minimum lot of the transaction to be performed lot_size=SymbolInfoDouble(my_symbol,SYMBOL_VOLUME_MIN); //--- apply the indicator and get its handle iRSI_handle=iRSI(my_symbol,my_timeframe,14,PRICE_CLOSE); //--- check the availability of the indicator handle if(iRSI_handle==INVALID_HANDLE) { //--- no handle obtained, print the error message into the log file, complete handling the error Print("Failed to get the indicator handle"); return(-1); } //--- add the indicator to the price chart ChartIndicatorAdd(ChartID(),0,iRSI_handle); //--- set the iRSI_buf array indexing as time series ArraySetAsSeries(iRSI_buf,true); //--- place weights into the array weight[0]=w0; weight[1]=w1; weight[2]=w2; weight[3]=w3; weight[4]=w4; weight[5]=w5; weight[6]=w6; weight[7]=w7; weight[8]=w8; weight[9]=w9; //--- return 0, initialization complete return(0); } //+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- delete the indicator handle and deallocate the memory space it occupies IndicatorRelease(iRSI_handle); //--- free the iRSI_buf dynamic array of data ArrayFree(iRSI_buf); } //+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { //--- variable for storing the results of working with the indicator buffer int err1=0; //--- copy data from the indicator array to the iRSI_buf dynamic array for further work with them err1=CopyBuffer(iRSI_handle,0,1,10,iRSI_buf); //--- in case of errors, print the relevant error message into the log file and exit the function if(err1<0) { Print("Failed to copy data from the indicator buffer"); return; } //--- double d1=0.0; //lower limit of the normalization range double d2=1.0; //upper limit of the normalization range double x_min=iRSI_buf[ArrayMinimum(iRSI_buf)]; //minimum value over the range double x_max=iRSI_buf[ArrayMaximum(iRSI_buf)]; //maximum value over the range //--- In the loop, fill in the array of inputs with the pre-normalized indicator values for(int i=0;i<ArraySize(inputs);i++) { inputs[i]=(((iRSI_buf[i]-x_min)*(d2-d1))/(x_max-x_min))+d1; } //--- store the neuron calculation result in the out variable out=CalculateNeuron(inputs,weight); //--- if the output value of the neuron is less than 0.5 if(out<0.5) { //--- if the position for this symbol already exists if(m_Position.Select(my_symbol)) { //--- and this is a Sell position, then close it if(m_Position.PositionType()==POSITION_TYPE_SELL) m_Trade.PositionClose(my_symbol); //--- or else, if this is a Buy position, then exit if(m_Position.PositionType()==POSITION_TYPE_BUY) return; } //--- if we got here, it means there is no position; then we open it m_Trade.Buy(lot_size,my_symbol); } //--- if the output value of the neuron is equal to or greater than 0.5 if(out>=0.5) { //--- if the position for this symbol already exists if(m_Position.Select(my_symbol)) { //--- and this is a Buy position, then close it if(m_Position.PositionType()==POSITION_TYPE_BUY) m_Trade.PositionClose(my_symbol); //--- or else, if this is a Sell position, then exit if(m_Position.PositionType()==POSITION_TYPE_SELL) return; } //--- if we got here, it means there is no position; then we open it m_Trade.Sell(lot_size,my_symbol); } } //+------------------------------------------------------------------+ //| Neuron calculation function | //+------------------------------------------------------------------+ double CalculateNeuron(double &x[],double &w[]) { //--- variable for storing the weighted sum of inputs double NET=0.0; //--- Using a loop we obtain the weighted sum of inputs based on the number of inputs for(int n=0;n<ArraySize(x);n++) { NET+=x[n]*w[n]; } //--- multiply the weighted sum of inputs by the additional coefficient NET*=0.4; //--- send the weighted sum of inputs to the activation function and return its value return(ActivateNeuron(NET)); } //+------------------------------------------------------------------+ //| Activation function | //+------------------------------------------------------------------+ double ActivateNeuron(double x) { //--- variable for storing the activation function results double Out; //--- sigmoid Out=1/(1+exp(-x)); //--- return the activation function value return(Out); } //+------------------------------------------------------------------+
우리가 가장 먼저 해야 할 일은 네트워크를 훈련하는 것입니다. 무게(가중치)를 최적화해 보겠습니다.
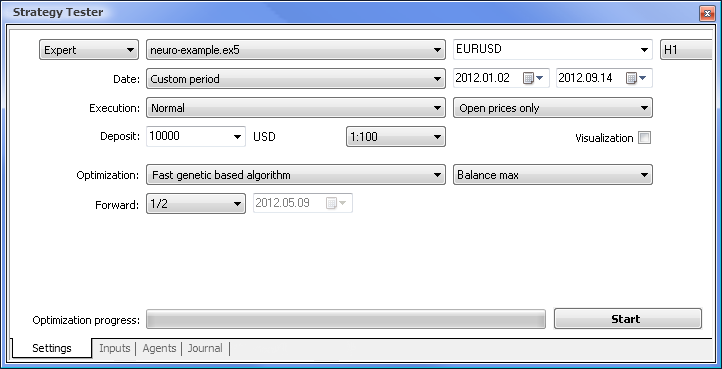
그림. 7. 필수 매개 변수가 설정된 전략 테스터
다음 매개 변수를 사용하여 최적화를 실행할 것입니다:
- 날짜 - 예를 들어 연초부터 기간이 길수록 원곡선 적합의 발생 횟수가 적어지고 결과가 좋아집니다.
- 실행 - 정상, 개시 가격만 적용. Expert Advisor는 현재 값을 제외하고 지표의 마지막 값을 10개만 취하기 때문에 Every tick(모든 틱) 모드에서는 테스트할 필요가 없습니다.
- 최적화는 느림 알고리즘을 사용하여 실행되도록 설정할 수 있습니다. 그러나 유전적 최적화는 알고리즘을 평가할 때 특히 유용한 결과를 더 빠르게 제공할 것입니다. 결과가 만족스러운 경우 더 정확한 결과를 위해 완료 느림 알고리즘을 사용할 수도 있습니다.
- Forward 1/2 를 사용하면 다음 최적화까지 EA가 얼마나 오랫동안 얻은 결과를 생성할 수 있는지 평가할 수 있습니다.
- 타임프레임 및 통화쌍은 사용자가 적합하다고 생각하는 대로 설정할 수 있습니다.
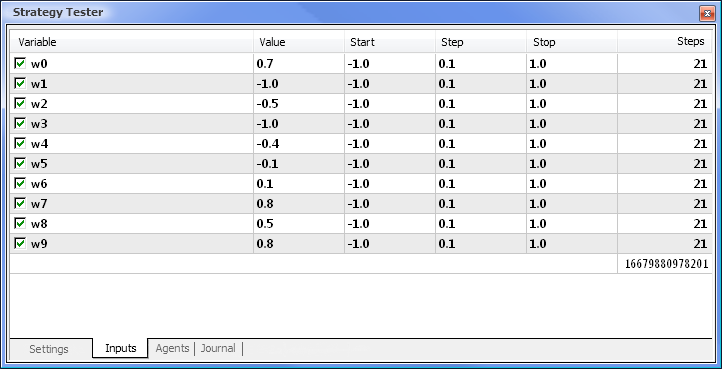
그림. 8. 파라미터 및 각각의 범위를 최적화하도록 설정하기
최적화는 모든 가중치와 해당 범위에 대해 실행됩니다. 설정 탭으로 돌아가서 시작 버튼을 클릭하여 최적화를 시작합니다.
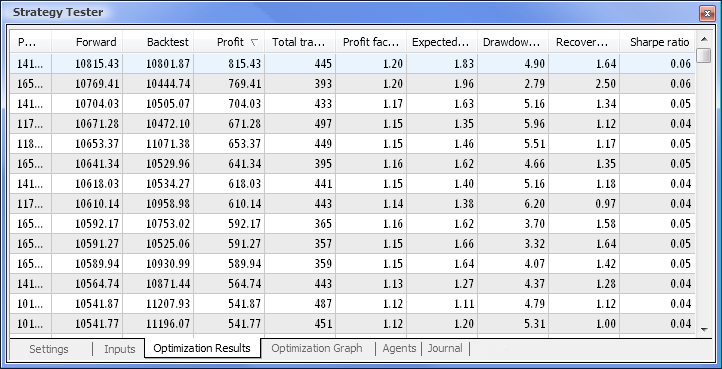
그림. 9. 최적화 후에 얻은 데이터
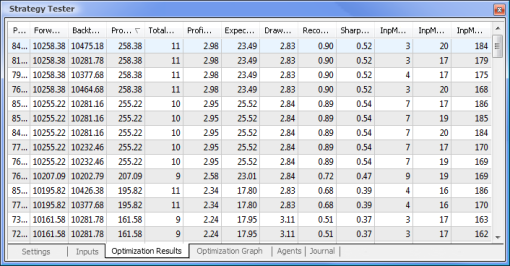
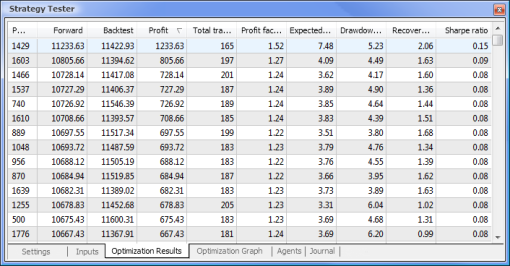
최적화가 완료되면 Optimization Results(최적화 결과) 탭에서 최대 수익 값을 가진 패스(매개 변수 중 하나를 기준으로 정렬하려면 관련 열 머리글 클릭)를 선택합니다. 그런 다음 다른 파라미터를 평가하고 필요한 경우 원하는 패스를 선택할 수 있습니다.
필요한 패스를 두 번 클릭하면 테스트 결과가 결과 및 그래프 탭에 표시됩니다.
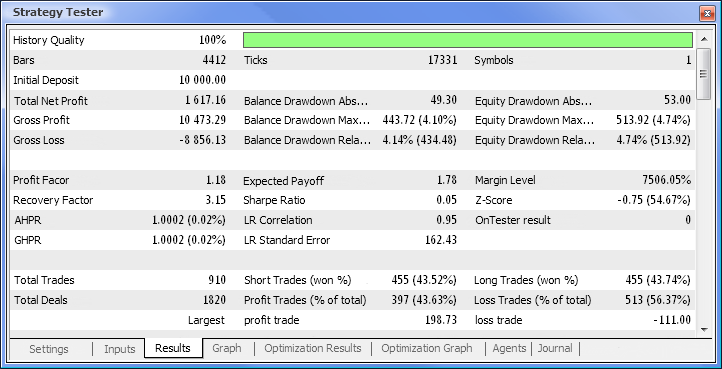
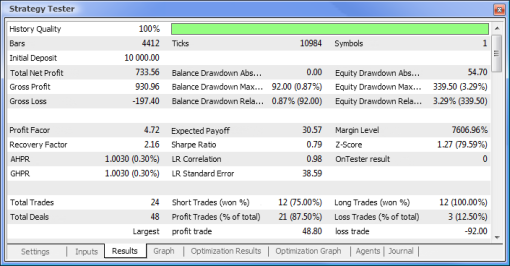
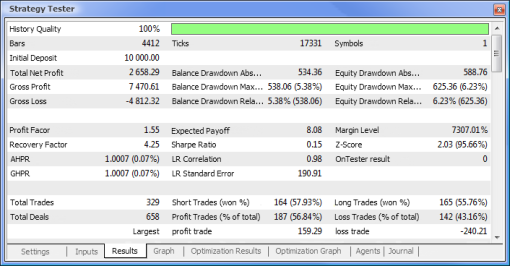
그림. 10. 테스트 보고서
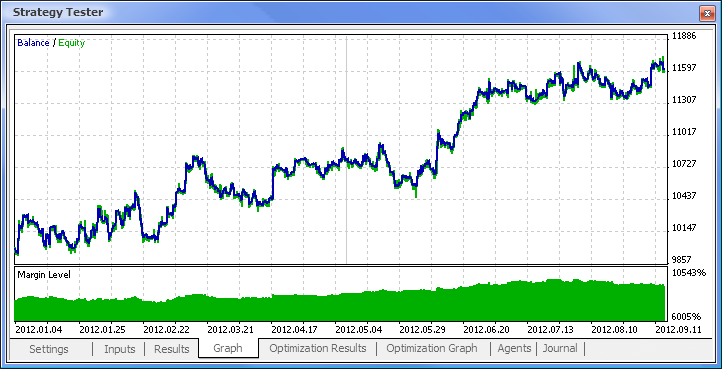
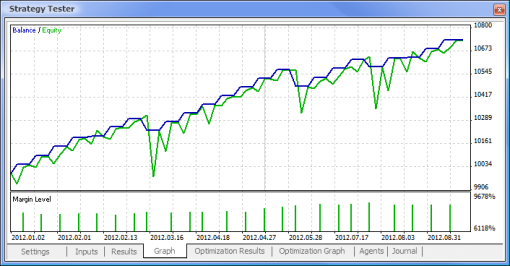
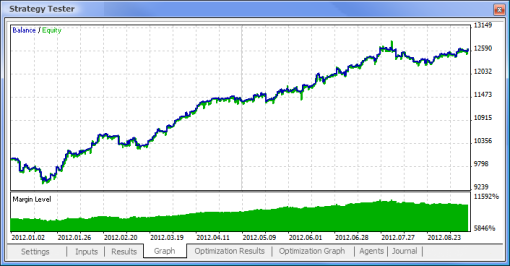
그림. 11. 잔액 차트
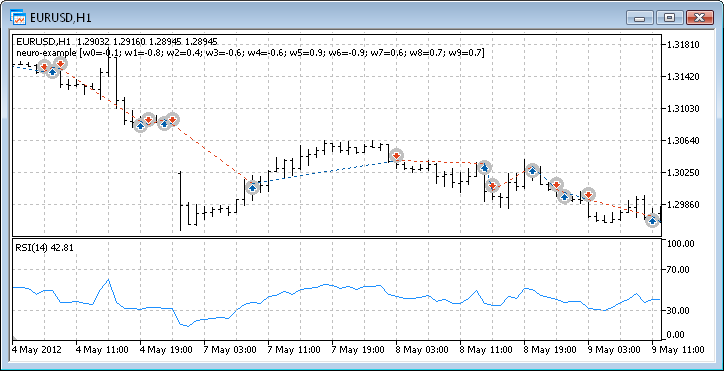
그림. 12. Expert Advisor의 거래 실적
그래서 우리는 마침내 그 결과를 얻었고 우선 그것들은 전혀 나쁘지 않습니다. 뉴런이 하나밖에 없었다는 걸 명심하세요. 제공된 예는 분명 원시적이지만 그것만으로도 이익을 얻을 수 있다는 것을 인정해야 합니다.
신경 네트워크의 장점
이제 표준 논리에 기반한 EA와 신경 네트워크 기반 EA를 비교해 보겠습니다. 터미널과 함께 제공되는 MACD Sample Expert Advisor의 최적화 및 테스트 결과를 MACD 기반의 신경 네트워크 기반 EA와 비교하겠습니다.
이익 취하기(Take Profit) 및 후행 중지(Trailing Stop) 값은 신경 네트워크 기반 EA에서 누락되므로 최적화에 관여하지 않습니다. 테스트할 Expert Advisor는 모두 다음 매개 변수를 사용하여 MACD를 기반으로 합니다:
- 빠른 이동 평균의 기간: 12;
- 느리게 움직이는 평균의 기간: 26;
- 평균화 기간의 차이: 9;
- 가격 유형: 마감 가격.
당신은 필요한 통화쌍과 기간을 설정할 수도 있지만 우리의 경우에는 각각 EURUSD, H1을 변경하지 않고 그대로 두겠습니다. 두 경우 모두 공시 가격을 사용하여 연초부터 시험 기간은 동일합니다.
| MACD 샘플 | macd-neuro-examle |
|---|---|
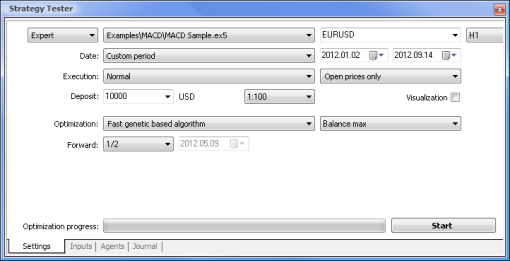 | 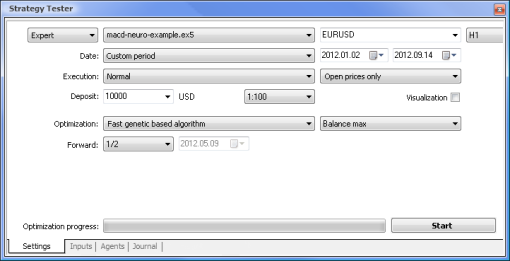 |
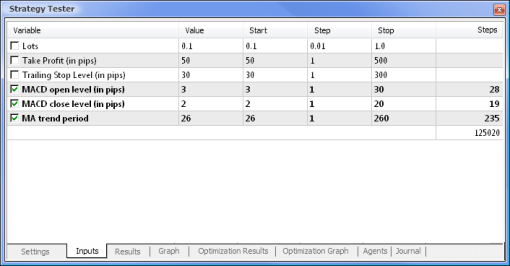 | 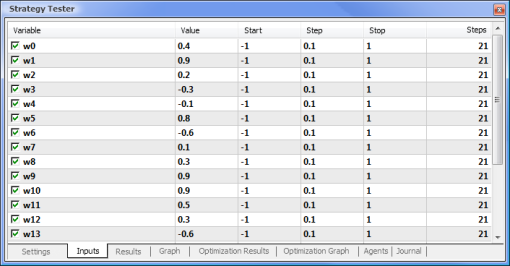 |
 |  |
 |  |
 |  |
이제 테스트를 거친 Expert Advisors의 주요 매개 변수를 비교해 보겠습니다:
| 매개 변수 | MACD 샘플 | macd-neuro-examle |
|---|---|---|
| 총 순이익 | 733,56 | 2 658,29 |
| 잔액 하락률 절대값 | 0,00 | 534,36 |
| 지분 하락률 최대값 | 339,50 (3,29%) | 625,36 (6,23%) |
| 수익률 | 4,72 | 1,55 |
| 복구 지수 | 2,16 | 4,25 |
| 예상 성과 | 30,57 | 8,08 |
| 샤프 지수 | 0,79 | 0,15 |
| 총 거래량 | 24 | 329 |
| 총 거래(Deals) | 48 | 658 |
| 이익 거래 (총 %) | 21 (87,50%) | 187 (56,84%) |
| 평균 이익 거래 | 44,33 | 39,95 |
| 평균 연속 획득 | 5 | 2 |
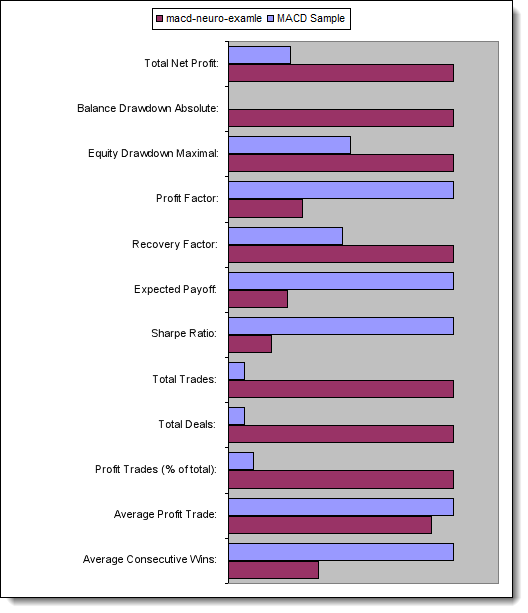
그림. 13. 주요 매개 변수의 비교
결론
이 글에서는 신경망을 사용하여 EA를 설계할 때 알아야 할 주요 사항에 대해 다룹니다. 뉴런과 신경망 아키텍처의 구조를 보여주었고, 활성화 기능과 활성화 기능 형태를 변경하는 방법, 최적화 및 입력 데이터 정상화 과정을 간략히 설명했습니다. 또한, 우리는 표준 논리에 기초한 EA와 신경 네트워크 기반 EA를 비교했습니다.
MetaQuotes 소프트웨어 사를 통해 러시아어가 번역됨.
원본 기고글: https://www.mql5.com/ru/articles/497
경고: 이 자료들에 대한 모든 권한은 MetaQuotes(MetaQuotes Ltd.)에 있습니다. 이 자료들의 전부 또는 일부에 대한 복제 및 재출력은 금지됩니다.
이 글은 사이트 사용자가 작성했으며 개인의 견해를 반영합니다. Metaquotes Ltd는 제시된 정보의 정확성 또는 설명 된 솔루션, 전략 또는 권장 사항의 사용으로 인한 결과에 대해 책임을 지지 않습니다.
 MetaTrader Market에서 거래용 로봇을 구입하여 설치하는 방법은 무엇입니까?
MetaTrader Market에서 거래용 로봇을 구입하여 설치하는 방법은 무엇입니까?
 통계 캐리 거래 전략
통계 캐리 거래 전략
 다른 애플리케이션에 대한 MetaTrader 5 Quotes을 준비하는 방법
다른 애플리케이션에 대한 MetaTrader 5 Quotes을 준비하는 방법
 표준 라이브러리의 거래 전략 클래스에 대해 알아보기 - 전략 사용자 정의하기
표준 라이브러리의 거래 전략 클래스에 대해 알아보기 - 전략 사용자 정의하기
백테스트에서 1건의 거래만 오픈
중요한 질문입니다:
RSI N 과거값은 14(N=14)로 설정됩니다.
입력 개수는 10(과거값)입니다.
문제가 있나요? ML 결과가 불안정한 것 같나요?
답변 부탁드립니다....
Thanks
중요한 질문입니다:
RSI N 과거값은 14(N=14)로 설정되어 있습니다.
입력 개수는 10(과거값)입니다.
문제가 있나요? ML 결과가 불안정한 것 같나요?
답변해 주세요....
Thanks
14는 RSI 지표를 계산하는 기간입니다. 입력은 RSI 버퍼에서 10개의 값을 입력합니다.