
Réseaux neuronaux : De la théorie à la pratique
Introduction
De nos jours, tout trader doit avoir entendu parler des réseaux neuronaux et sait à quel point il est cool de les utiliser. La majorité pense que ceux qui peuvent traiter les réseaux neuronaux sont des sortes de surhommes. Dans cet article, je vais essayer de vous expliquer l'architecture des réseaux neuronaux, de décrire leurs applications et de montrer des exemples d'utilisation pratique.
Le concept des réseaux neuronaux
Les réseaux neuronaux artificiels sont l'un des domaines de recherche en intelligence artificielle qui repose sur les tentatives de simulation du système nerveux humain dans sa capacité d'apprentissage et d'adaptation, ce qui devrait nous permettre de construire une simulation très grossière du fonctionnement du cerveau humain.
Curieusement, les réseaux neuronaux artificiels sont constitués de neurones artificiels.
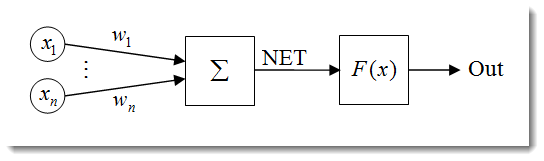
Fig. 1. Le modèle de neurone artificiel
La structure d’un neurone peut être représentée comme une composition des unités suivantes :
- Entrées
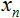 ;
; - Poids
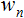 ;
; - Fonction de transfert
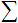 et Entrée nette
et Entrée nette  ;
; - Fonction d’activation
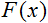 ;
; - Sortie
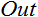 .
.
Les réseaux neuronaux possèdent de nombreuses propriétés, la capacité d'apprentissage étant la plus importante. Le processus d’apprentissage se résume à changer les poids ![]() .
.

![]() voici l’entrée nette du neurone.
voici l’entrée nette du neurone.
![]()
L’entrée nette est ensuite transformée en sortie par la fonction d’activation que nous aborderons plus tard. En un mot, un réseau neuronal peut être considéré comme une « boîte noire » qui reçoit des signaux en entrées et produit le résultat.
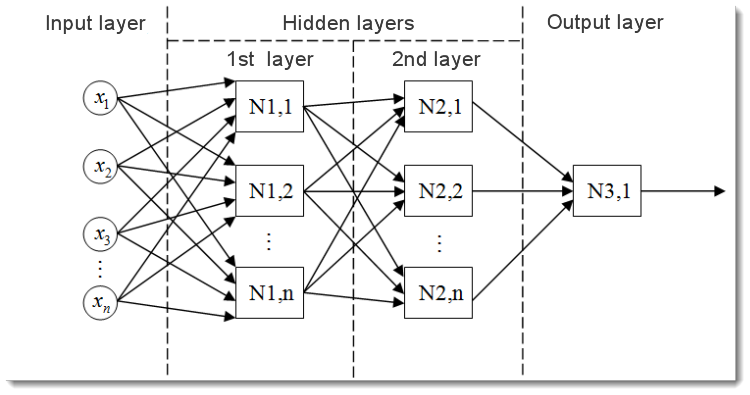
Fig. 2. Le modèle d’un réseau neuronal multicouche
Voici à quoi ressemble un réseau neuronal multicouche. Il comprend:
- La couche d’entrée qui sert à distribuer les données sur le réseau et n’effectue aucun calcul. Les sorties de cette couche transmettent des signaux aux entrées de la couche suivante (cachée ou de sortie) ;
- La couche de sortie qui contient généralement un neurone (ou parfois plus d’un) qui génère la sortie de l’ensemble du réseau neuronal. Ce signal est à la base de la logique de commande future de l'EA ;
- Les couches cachées qui sont des couches de neurones standard qui transmettent des signaux de la couche d’entrée à la couche de sortie. Son entrée est la sortie de la couche précédente, tandis que sa sortie sert d’entrée de la couche suivante.
Cet exemple a montré le réseau neuronal avec deux couches cachées. Mais il peut y avoir des réseaux neuronaux qui ont plus de couches cachées.
Normalisation des données d’entrée
La normalisation des données d’entrée est le processus par lequel toutes les données d’entrée sont normalisées, c’est-à-dire réduites aux intervalles [0,1] ou [-1,1]. Si la normalisation n'est pas effectuée, les données d'entrée auront un effet supplémentaire sur le neurone, ce qui entraînera des décisions erronées. En d’autres termes, comment pouvez-vous comparer des valeurs qui ont des ordres de grandeur différents ?
La formule de normalisation dans sa forme standard est la suivante :
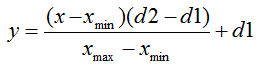
où :
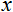 - valeur à normaliser ;
- valeur à normaliser ;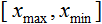 - х intervalle de valeurs ;
- х intervalle de valeurs ; 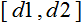 - intervalle à laquelle la valeur de x sera réduite.
- intervalle à laquelle la valeur de x sera réduite.
Permettez-moi de l’expliquer à l’aide d’un exemple :
Supposons que nous ayons n données d’entrée de l’intervalle [0,10], puis ![]() = 0 et
= 0 et ![]() = 10. Nous allons réduire les données à l'intervalle [0,1], puis
= 10. Nous allons réduire les données à l'intervalle [0,1], puis ![]() = 0 and
= 0 and ![]() = 1. Maintenant, après avoir introduit les valeurs dans la formule, nous pouvons calculer les valeurs normalisées pour tout x à partir de n données d’entrée.
= 1. Maintenant, après avoir introduit les valeurs dans la formule, nous pouvons calculer les valeurs normalisées pour tout x à partir de n données d’entrée.
Voici à quoi cela ressemble lorsqu'il est mis en œuvre dans MQL5 :
double d1=0.0; double d2=1.0; double x_min=iMA_buf[ArrayMinimum(iMA_buf)]; double x_max=iMA_buf[ArrayMaximum(iMA_buf)]; for(int i=0;i<ArraySize(iMA_buf);i++) { inputs[i]=(((iMA_buf[i]-x_min)*(d2-d1))/(x_max-x_min))+d1; }
Nous spécifions d’abord les limites supérieure et inférieure de la valeur de sortie, puis obtenons les valeurs minimales et maximales de l’indicateur (la copie des données de l’indicateur est laissée de côté, mais il peut y avoir, par exemple, 10 dernières valeurs). Enfin, nous normalisons chaque élément d’entrée (valeurs d’indicateur sur différentes barres) et stockons les résultats dans un tableau pour une utilisation ultérieure.
Fonctions d’activation
La fonction d’activation est une fonction qui calcule la sortie d’un neurone. L'entrée qu’il reçoit représente la somme de tous les produits des intrants et de leurs pondérations respectives (ci-après « somme pondérée ») :
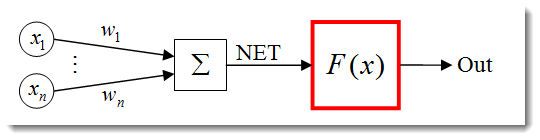
Fig. 3. Le modèle de neurone artificiel avec la fonction d’activation décrite
La formule de la fonction d’activation dans sa forme standard est la suivante :
![]()
où :
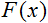 est la fonction d’activation ;
est la fonction d’activation ;-
 est la somme pondérée obtenue à la première étape du calcul de la sortie d’un neurone ;
est la somme pondérée obtenue à la première étape du calcul de la sortie d’un neurone ; 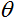 est une valeur seuil de la fonction d’activation. Il n’est utilisé que pour la fonction de seuil dur et est égal à zéro dans les autres fonctions.
est une valeur seuil de la fonction d’activation. Il n’est utilisé que pour la fonction de seuil dur et est égal à zéro dans les autres fonctions.
Les principaux types de fonctions d’activation sont :
-
La fonction d’étape unitaire ou de seuil dur.
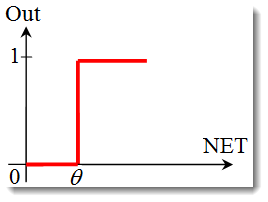
La fonction est décrite par la formule suivante :
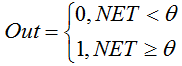
Si la somme pondérée est inférieure à la valeur spécifiée, la fonction d’activation renvoie zéro. Si la somme pondérée devient supérieure, la fonction d’activation en renvoie une. -
La fonction sigmoïde.
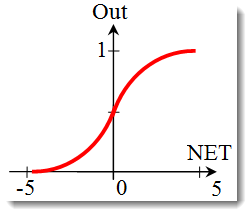
La formule qui décrit la fonction sigmoïde est la suivante :
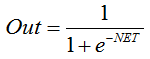
Il est souvent utilisé dans les réseaux de neurones multicouches et d’autres réseaux avec des signaux continus. La régularité et la continuité de la fonction sont des propriétés très positives. -
La tangente hyperbolique.
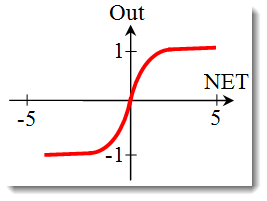
Formule :
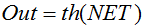 ou
ou 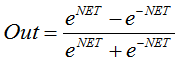
Il est également souvent utilisé dans les réseaux à signaux continus. Il a la particularité de pouvoir renvoyer des valeurs négatives.
Modification de la forme de la fonction d’activation
Dans la section précédente, nous avons traité des types de fonctions d’activation. Pourtant, il y a une autre chose importante à considérer - la pente d’une fonction (à l’exception de la fonction de seuil dur). Examinons de plus près la fonction sigmoïde.
En observant le graphique de la fonction, on peut facilement voir que la fonction est lisse sur l'intervalle [-5,5]. Supposons que nous ayons un réseau composé d’un seul neurone avec 10 entrées et une sortie. Essayons maintenant de calculer les valeurs supérieures et inférieures de la variable ![]() . Chaque entrée prendra une valeur normalisée (comme déjà mentionné dans la normalisation Normalisation des données d’entrée), par exemple à partir de l’intervalle [-1,1].
. Chaque entrée prendra une valeur normalisée (comme déjà mentionné dans la normalisation Normalisation des données d’entrée), par exemple à partir de l’intervalle [-1,1].
Nous utiliserons les valeurs d’entrée négatives puisque la fonction est différentiable même à un argument négatif. Les poids seront également sélectionnés dans la même gamme. Avec toutes les combinaisons possibles d’entrées et de poids, nous obtiendrons les valeurs extrêmes ![]() dans l’intervalle [-10,10] comme :
dans l’intervalle [-10,10] comme :

Dans MQL5, la formule se présentera comme suit :
for(int n=0; n<10; n++) { NET+=Xn*Wn; }
Nous devons maintenant tracer la fonction d'activation dans l’intervalle identifiée. Prenons l’exemple de la fonction sigmoïde. Le moyen le plus simple de le faire est d’utiliser Excel.
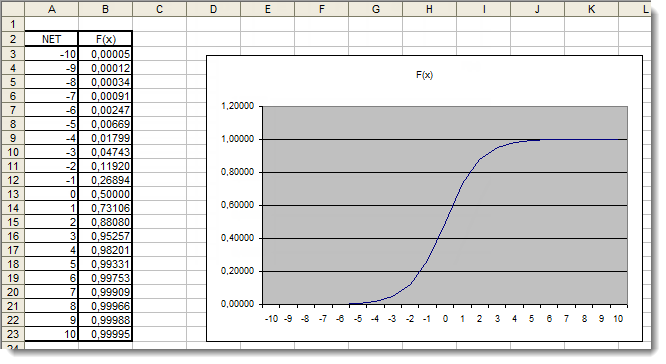
Fig. 4. Le graphique Excel de la fonction sigmoïde
Ici, nous pouvons clairement voir que les valeurs d’argument en dehors de l’intervalle [-5,5] n’ont absolument aucun effet sur les résultats. Cela suggère que l’intervalle de valeurs est incomplète. Essayons de résoudre ce problème. Nous ajouterons à l’argument un coefficient supplémentaire d qui nous permettra d’élargir l’intervalle de valeurs.
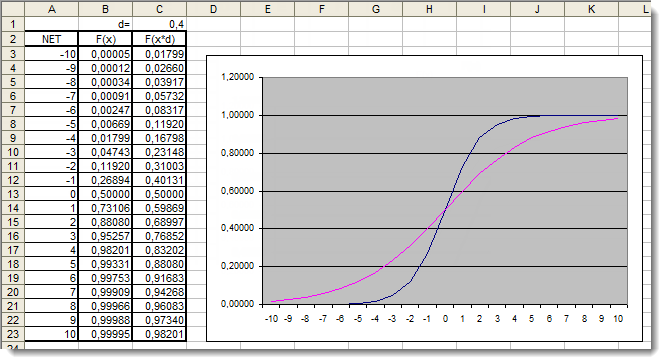
Fig. 5. Le graphique Excel de la fonction sigmoïde avec le coefficient supplémentaire appliqué
Examinons à nouveau les graphiques. Nous avons ajouté un coefficient supplémentaire d =0,4 qui a changé la forme de la fonction. La comparaison des valeurs dans le tableau suggère qu'elles sont maintenant plus uniformément distribuées. Les résultats peuvent donc être exprimés comme suit :
for(int n=0; n<10; n++) { NET+=Xn*Wn; } NET*=0.4;
Passons maintenant en revue la fonction d’activation de la tangente hyperbolique. Passant outre la théorie abordée dans l'examen de la fonction précédente, nous passons tout de suite à l'application pratique. La seule différence ici est que la sortie peut se situer dans l’intervalle [-1,1]. La somme pondérée peut également prendre des valeurs de l’intervalle [-10,10].
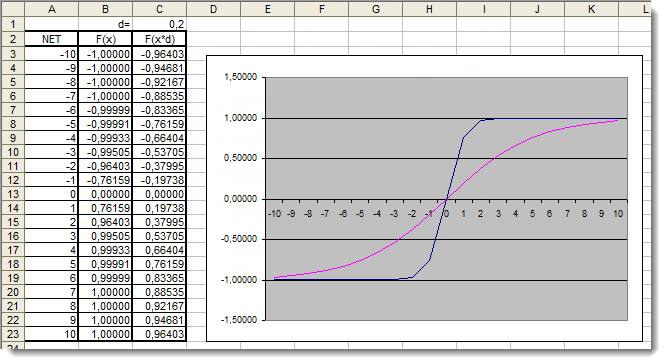
Fig. 6. Le graphique Excel de la fonction tangente hyperbolique avec le coefficient supplémentaire appliqué
Le graphique montre que la forme de la fonction a été améliorée grâce à l’utilisation du coefficient supplémentaire d= 0,2. Les résultats peuvent donc être exprimés comme suit :
for(int n=0;n<10;n++) { NET+=Xn*Wn; } NET*=0.2;
De cette manière, vous pouvez modifier et améliorer la forme de toute fonction d'activation.
Application
Passons maintenant à l’application pratique. Tout d’abord, nous allons essayer de mettre en œuvre le calcul de l’entrée nette du neurone, suivi de l’ajout de la fonction d’activation. Rappelons la formule de calcul de l’entrée nette du neurone :

double NET; double x[3]; double w[3]; int OnInit() { x[0]=0.1; // set the input value х1 x[1]=0.8; // set the input value х2 x[2]=0.5; // set the input value х3 w[0]=0.5; // set the weight value w1 w[1]=0.6; // set the weight value w2 w[2]=0.3; // set the weight value w3 for(int n=0;n<3;n++) { NET+=x[n]*w[n]; // add the weighted net input values together } }
Examinons la question :
- Nous avons commencé par déclarer une variable pour stocker l’entrée nette du neurone
 et deux tableaux : entrées
et deux tableaux : entrées 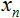 et poids
et poids 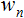 ;
; - Ces variables ont été déclarées au tout début, en dehors de toutes les fonctions afin de leur donner une portée globale (pour être accessibles de n’importe où dans le programme) ;
- Dans la fonction d’initialisation OnInit() (il peut en fait s’agir de n’importe quelle autre fonction), nous avons rempli le tableau d’entrées et le tableau de poids ;
- Elle est suivie par la boucle de sommation, n<3 puisque nous n'avons que trois entrées et trois poids respectifs ;
- Nous avons ensuite ajouté des valeurs d’entrée pondérées et les avons stockées dans la variable

La première tâche a donc été accomplie - nous avons obtenu la somme. C'est maintenant au tour de la fonction d'activation. Vous trouverez ci-dessous les codes permettant de calculer les fonctions d'activation examinées dans la section Fonctions d’activation.
La fonction d’étape unitaire ou de seuil dur
double Out; if(NET>=x) Out=1; else Out=0;
La fonction sigmoïde
double Out = 1/(1+exp(-NET));
La fonction tangente hyperbolique
double Out = (exp(NET)-exp(-NET))/(exp(NET)+exp(-NET));
Tout mettre en place
Pour faciliter la mise en œuvre, nous allons prendre un réseau composé d’un seul neurone. Il est certainement un peu exagéré d'appeler cela un réseau, mais il est important de comprendre le principe. Après tout, un réseau neuronal multicouche est constitué des mêmes neurones où la sortie de la couche précédente de neurones sert d'entrée à la couche suivante.
Nous allons utiliser une version légèrement modifiée de l’Expert Advisor développé et introduit dans l’article « Un démarrage rapide ou un guide court pour les débutants ». Ainsi, nous allons par exemple remplacer l’indicateur de tendance de la moyenne mobile par l’oscillateur de iRSI. Vous trouverez des informations sur les paramètres de l’indicateur et leur séquence dans l’aide intégrée.
//+------------------------------------------------------------------+ //| neuro-example.mq5 | //| Copyright 2012, MetaQuotes Software Corp. | //| http://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2012, MetaQuotes Software Corp." #property link "http://www.mql5.com" #property version "1.00" //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ #include <Trade\Trade.mqh> //include the library for execution of trades #include <Trade\PositionInfo.mqh> //include the library for obtaining information on positions //--- weight values input double w0=0.5; input double w1=0.5; input double w2=0.5; input double w3=0.5; input double w4=0.5; input double w5=0.5; input double w6=0.5; input double w7=0.5; input double w8=0.5; input double w9=0.5; int iRSI_handle; // variable for storing the indicator handle double iRSI_buf[]; // dynamic array for storing indicator values double inputs[10]; // array for storing inputs double weight[10]; // array for storing weights double out; // variable for storing the output of the neuron string my_symbol; // variable for storing the symbol ENUM_TIMEFRAMES my_timeframe; // variable for storing the time frame double lot_size; // variable for storing the minimum lot size of the transaction to be performed CTrade m_Trade; // entity for execution of trades CPositionInfo m_Position; // entity for obtaining information on positions //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ int OnInit() { //--- save the current chart symbol for further operation of the EA on this very symbol my_symbol=Symbol(); //--- save the current time frame of the chart for further operation of the EA on this very time frame my_timeframe=PERIOD_CURRENT; //--- save the minimum lot of the transaction to be performed lot_size=SymbolInfoDouble(my_symbol,SYMBOL_VOLUME_MIN); //--- apply the indicator and get its handle iRSI_handle=iRSI(my_symbol,my_timeframe,14,PRICE_CLOSE); //--- check the availability of the indicator handle if(iRSI_handle==INVALID_HANDLE) { //--- no handle obtained, print the error message into the log file, complete handling the error Print("Failed to get the indicator handle"); return(-1); } //--- add the indicator to the price chart ChartIndicatorAdd(ChartID(),0,iRSI_handle); //--- set the iRSI_buf array indexing as time series ArraySetAsSeries(iRSI_buf,true); //--- place weights into the array weight[0]=w0; weight[1]=w1; weight[2]=w2; weight[3]=w3; weight[4]=w4; weight[5]=w5; weight[6]=w6; weight[7]=w7; weight[8]=w8; weight[9]=w9; //--- return 0, initialization complete return(0); } //+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- delete the indicator handle and deallocate the memory space it occupies IndicatorRelease(iRSI_handle); //--- free the iRSI_buf dynamic array of data ArrayFree(iRSI_buf); } //+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { //--- variable for storing the results of working with the indicator buffer int err1=0; //--- copy data from the indicator array to the iRSI_buf dynamic array for further work with them err1=CopyBuffer(iRSI_handle,0,1,10,iRSI_buf); //--- in case of errors, print the relevant error message into the log file and exit the function if(err1<0) { Print("Failed to copy data from the indicator buffer"); return; } //--- double d1=0.0; //lower limit of the normalization range double d2=1.0; //upper limit of the normalization range double x_min=iRSI_buf[ArrayMinimum(iRSI_buf)]; //minimum value over the range double x_max=iRSI_buf[ArrayMaximum(iRSI_buf)]; //maximum value over the range //--- In the loop, fill in the array of inputs with the pre-normalized indicator values for(int i=0;i<ArraySize(inputs);i++) { inputs[i]=(((iRSI_buf[i]-x_min)*(d2-d1))/(x_max-x_min))+d1; } //--- store the neuron calculation result in the out variable out=CalculateNeuron(inputs,weight); //--- if the output value of the neuron is less than 0.5 if(out<0.5) { //--- if the position for this symbol already exists if(m_Position.Select(my_symbol)) { //--- and this is a Sell position, then close it if(m_Position.PositionType()==POSITION_TYPE_SELL) m_Trade.PositionClose(my_symbol); //--- or else, if this is a Buy position, then exit if(m_Position.PositionType()==POSITION_TYPE_BUY) return; } //--- if we got here, it means there is no position; then we open it m_Trade.Buy(lot_size,my_symbol); } //--- if the output value of the neuron is equal to or greater than 0.5 if(out>=0.5) { //--- if the position for this symbol already exists if(m_Position.Select(my_symbol)) { //--- and this is a Buy position, then close it if(m_Position.PositionType()==POSITION_TYPE_BUY) m_Trade.PositionClose(my_symbol); //--- or else, if this is a Sell position, then exit if(m_Position.PositionType()==POSITION_TYPE_SELL) return; } //--- if we got here, it means there is no position; then we open it m_Trade.Sell(lot_size,my_symbol); } } //+------------------------------------------------------------------+ //| Neuron calculation function | //+------------------------------------------------------------------+ double CalculateNeuron(double &x[],double &w[]) { //--- variable for storing the weighted sum of inputs double NET=0.0; //--- Using a loop we obtain the weighted sum of inputs based on the number of inputs for(int n=0;n<ArraySize(x);n++) { NET+=x[n]*w[n]; } //--- multiply the weighted sum of inputs by the additional coefficient NET*=0.4; //--- send the weighted sum of inputs to the activation function and return its value return(ActivateNeuron(NET)); } //+------------------------------------------------------------------+ //| Activation function | //+------------------------------------------------------------------+ double ActivateNeuron(double x) { //--- variable for storing the activation function results double Out; //--- sigmoid Out=1/(1+exp(-x)); //--- return the activation function value return(Out); } //+------------------------------------------------------------------+
La première chose à faire est de former notre réseau. Optimisons les poids.
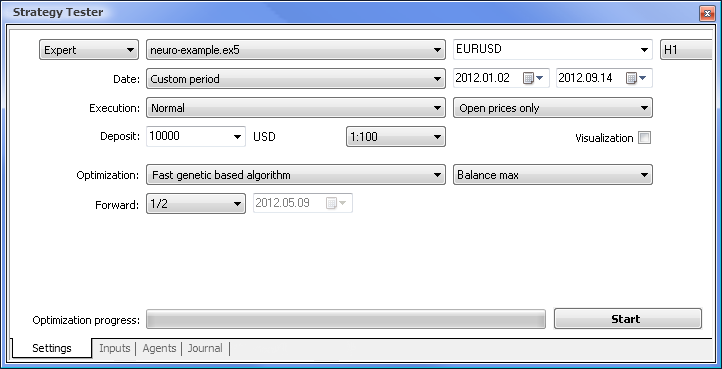
Fig. 7. Strategy tester avec les paramètres requis
Nous allons exécuter l'optimisation en utilisant les paramètres suivants :
- Date - par exemple à partir du début de l’année Plus la période est longue, moins il y a d’ajustement de courbe et meilleur est le résultat.
- Exécution - normale, prix d’ouverture uniquement. Il ne sert à rien de tester en mode Chaque tick puisque notre Expert Advisor ne prend que 10 dernières valeurs de l’indicateur, à l’exception de la valeur actuelle.
- L’optimisation peut être configurée pour s’exécuter à l’aide de l’algorithme complet lent. L’optimisation génétique donnera cependant des résultats plus rapides, ce qui est particulièrement utile lors de l’évaluation d’un algorithme. Si le résultat est satisfaisant, vous pouvez également essayer d’utiliser l’algorithme complet lent pour des résultats plus précis.
- Forward de 1/2 et plus vous permet d'évaluer combien de temps votre EA peut générer les résultats obtenus jusqu'à la prochaine optimisation.
- La période et la paire de devises peuvent être définies comme vous le souhaitez.
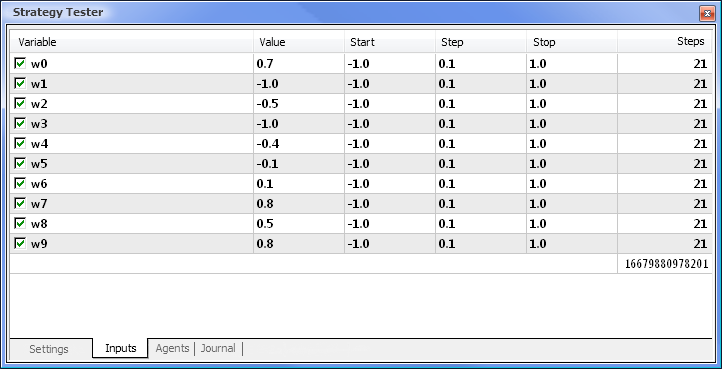
Fig. 8. Définition des paramètres et de leurs intervalles respectives à optimiser
L’optimisation sera effectuée en fonction de tous les poids et de leurs intervalles. Démarrez l’optimisation en revenant à l’onglet Paramètres et en cliquant sur le bouton Démarrer.
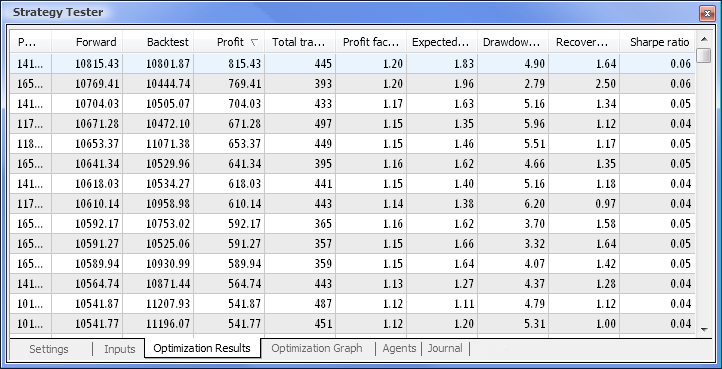
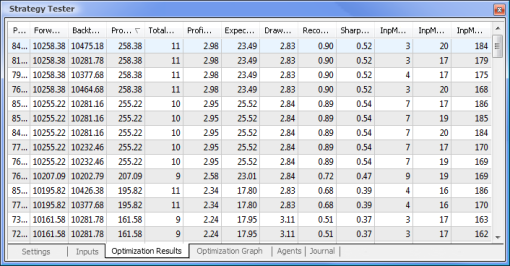
Fig. 9. Données obtenues suite à l’optimisation
Une fois l’optimisation terminée, nous sélectionnons la passe avec la valeur de profit maximale (pour trier par l’un des paramètres, cliquez sur l’en-tête de colonne correspondant) dans l’onglet Résultats de l’optimisation. Vous pouvez ensuite évaluer d’autres paramètres et sélectionner la passe souhaitée, si nécessaire.
Un double clic sur la passe requise lance le test dont les résultats sont affichés dans les onglets Résultats et Graphique.
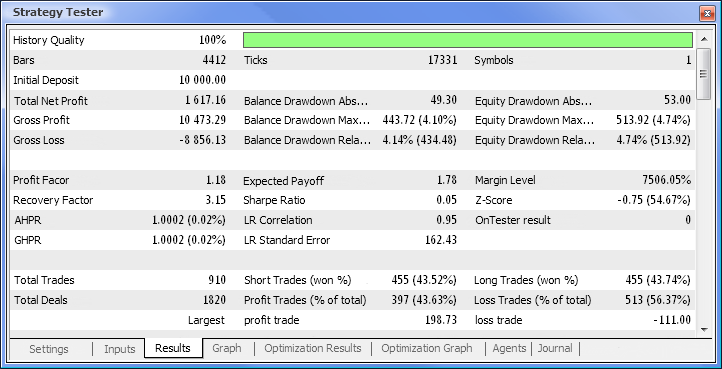
Fig. 10. Rapport d’essai
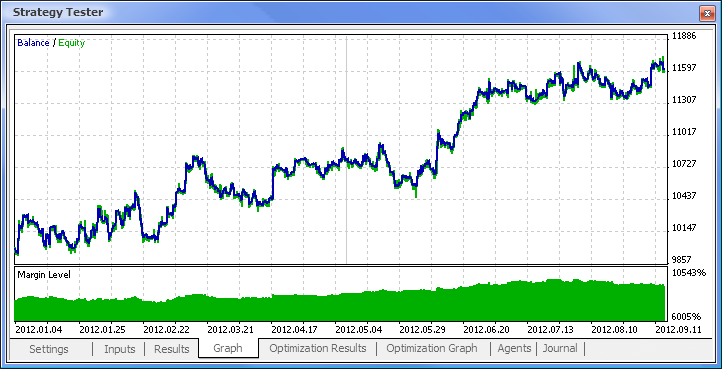
Fig. 11. Graphique d’équilibre
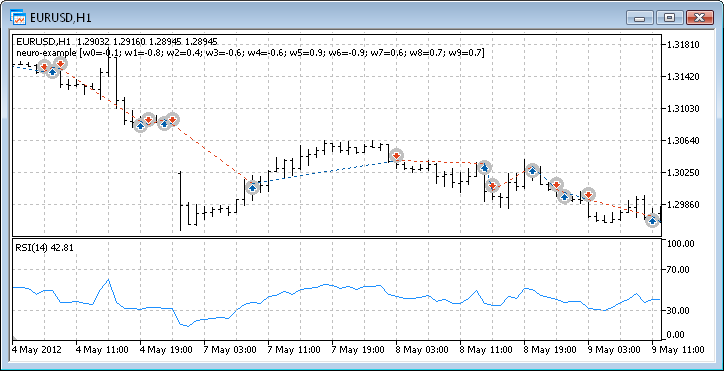
Fig. 12. Performance de trading de l’Expert Advisor
Nous avons donc enfin obtenu les résultats et pour commencer, ils ne sont pas mauvais du tout. Gardez à l’esprit que nous n’avions qu’un seul neurone. L'exemple fourni est clairement primitif mais il faut admettre que même lui seul peut rapporter.
Avantages des réseaux neuronaux
Essayons maintenant de comparer un EA basé sur la logique standard avec un EA piloté par un réseau neuronal. Nous allons comparer les résultats d'optimisation et de test de l'exemple de Expert Advisor MACD fourni avec le terminal avec ceux de l'EA basé sur le réseau neuronal MACD.
Les valeurs Take Profit et Trailing Stop ne seront pas impliquées dans l’optimisation car elles sont absentes de l’EA piloté par le réseau neuronal. Les deux Expert Advisors que nous allons tester sont basés sur le MACD avec les paramètres suivants :
- Période de la moyenne mobile rapide : 12 ;
- Période de la moyenne mobile lente : 26 ;
- Période de calcul de la moyenne de la différence : 9 ;
- Type de prix : cours de clôture.
Vous pouvez également définir la paire de devises et le délai requis, mais dans notre cas, nous les laisserons inchangés - EURUSD, H1, respectivement. La période de test dans les deux cas est la même: à partir du début de l’année en utilisant les prix d’ouverture.
| Echantillon MACD | macd-neuro-examle |
|---|---|
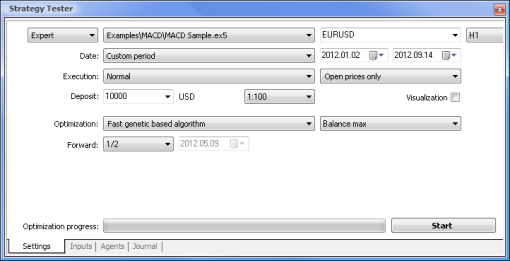 | 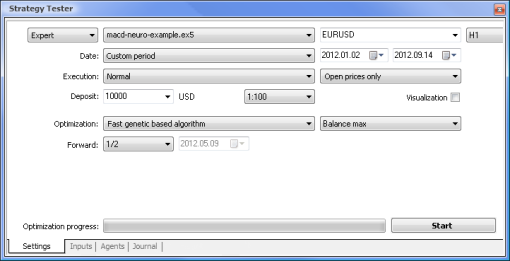 |
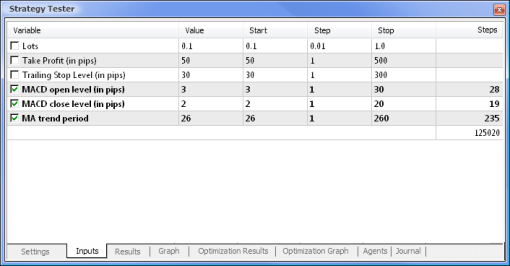 | 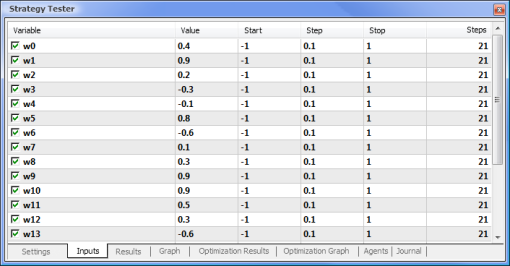 |
 | 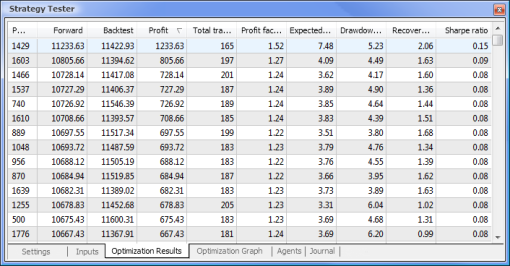 |
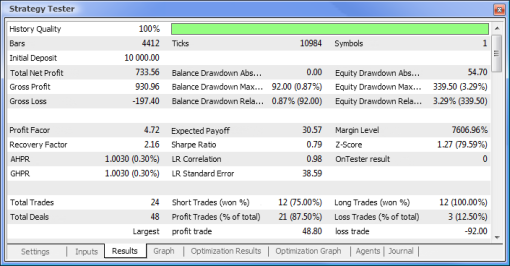 | 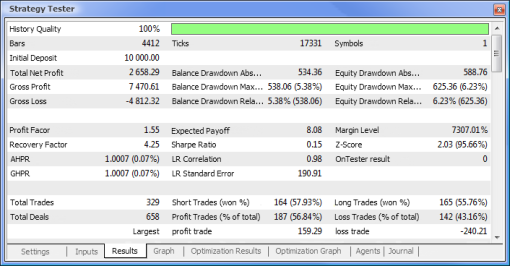 |
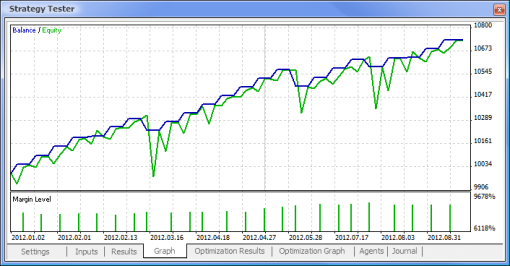 | 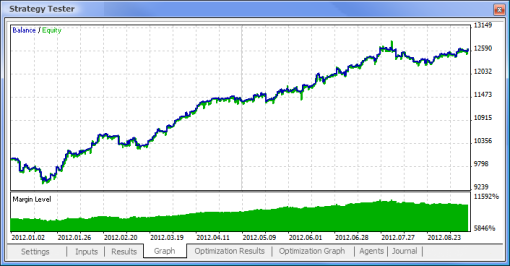 |
Comparons maintenant les paramètres clés des Expert Advisors testés :
| Paramètre | Echantillon MACD | macd-neuro-examle |
|---|---|---|
| Bénéfice net total | 733,56 | 2 658,29 |
| Solde prélèvement Absolu | 0,00 | 534,36 |
| Prélèvement Maximal sur actions | 339,50 (3,29 %) | 625,36 (6,23 %) |
| Facteur de profit | 4,72 | 1,55 |
| Facteur de récupération | 2,16 | 4,25 |
| Gain attendu | 30,57 | 8,08 |
| Ratio de Sharpe | 0,79 | 0,15 |
| Total des transactions | 24 | 329 |
| Nombre total de offres | 48 | 658 |
| Transactions sur profit (% du total) | 21 (87,50 %) | 187 (56,84 %) |
| Bénéfice moyen de trading | 44,33 | 39,95 |
| Moyenne de victoires consécutives | 5 | 2 |
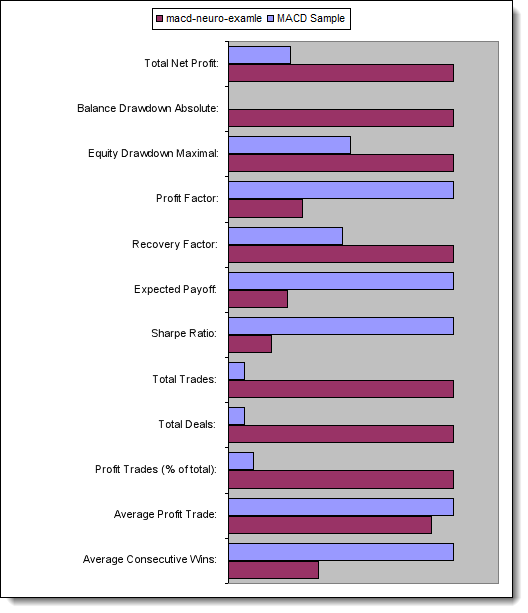
Fig. 13. Comparaison des paramètres clés
Conclusion
Cet article a abordé les principaux points que vous devez connaître lors de la conception d'EA utilisant des réseaux neuronaux. Il nous a montré la structure d'un neurone et l'architecture d'un réseau neuronal, décrit les fonctions d'activation et les méthodes permettant de modifier la forme de la fonction d'activation, ainsi que le processus d'optimisation et de normalisation des données d'entrée. De plus, nous avons comparé un EA basé sur la logique standard avec un EA piloté par un réseau neuronal.
Traduit du russe par MetaQuotes Ltd.
Article original : https://www.mql5.com/ru/articles/497
Avertissement: Tous les droits sur ces documents sont réservés par MetaQuotes Ltd. La copie ou la réimpression de ces documents, en tout ou en partie, est interdite.
Cet article a été rédigé par un utilisateur du site et reflète ses opinions personnelles. MetaQuotes Ltd n'est pas responsable de l'exactitude des informations présentées, ni des conséquences découlant de l'utilisation des solutions, stratégies ou recommandations décrites.
 Comment acheter un robot de trading sur MetaTrader Market et l'installer ?
Comment acheter un robot de trading sur MetaTrader Market et l'installer ?
 Stratégie statistique de Carry Trade
Stratégie statistique de Carry Trade
 Comment préparer des cotations MetaTrader 5 pour d'autres applications
Comment préparer des cotations MetaTrader 5 pour d'autres applications
 Exploration des classes de stratégies de trading de la bibliothèque standard - Personnalisation des stratégies
Exploration des classes de stratégies de trading de la bibliothèque standard - Personnalisation des stratégies
- Applications de trading gratuites
- Plus de 8 000 signaux à copier
- Actualités économiques pour explorer les marchés financiers
Vous acceptez la politique du site Web et les conditions d'utilisation
n'ouvre qu'une seule transaction dans le backtest
Une question importante :
Le RSI N valeurs passées est fixé à 14(N=14).
Le nombre d'entrées est de 10 (valeurs passées).
Y a-t-il un problème ? Il semblerait que les résultats de ML soient instables ?
Veuillez répondre à ....
Merci de votre compréhension.
Une question importante :
Le RSI N valeurs passées est fixé à 14(N=14).
Le nombre d'entrées est de 10 (valeurs passées).
Y a-t-il un problème ? Il semble que les résultats du ML soient instables ?
Veuillez répondre à la question suivante : ....
Merci de votre compréhension.
14 est la période de calcul de l'indicateur RSI. L'entrée est de 10 valeurs du tampon RSI.