戦略バランス曲線の品質評価としての R 乗

MetaTrader 5 — トレーディング | 18 12月 2017, 08:36

1 107

イントロダクション

すべてのトレーディング戦略は、その有効性に対する客観的評価が必要です。これには、さまざまな統計パラメータが使用されます。その多くは、計算しやすく、直感的です。他にも様々なものがありますが、構築や解釈が難しいものが多いです。このような多様性の中、非自明を推定するために定性的な指標があります。と同時に定量的なものもあります。-トレーディングシステムのバランスラインの滑らかさ。この記事では、この問題の解決策を提案します。このような非自明な測定を考慮してみましょう。係数として r-２乗 (r ^ 2), 定性的推定を計算します。

もちろん、MetaTrader5ターミナルはすでにトレードシステムの主要な統計情報を示す要約レポートを提供しています。しかし、提示されるパラメータは、必ずしも十分ではありません。幸い、MetaTrader5は、カスタム推定パラメータを記述する関数を提供しています。これだけでなく、決定係数 R ^ 2 を構築するだけでなく、その値を推定しようとすると、他の最適化基準と比較して、基本的な統計推定値を導出します。

トレーディングシステムの評価における共通の統計的批判

トレードレポートが生成されるか、またはトレードシステムのバックテストの結果が検査される度に、トレードの質について分析することができる複数の「マジックナンバー」があります。たとえば、MetaTrader5 ターミナルの代表的なテストレポートは次のようになります。

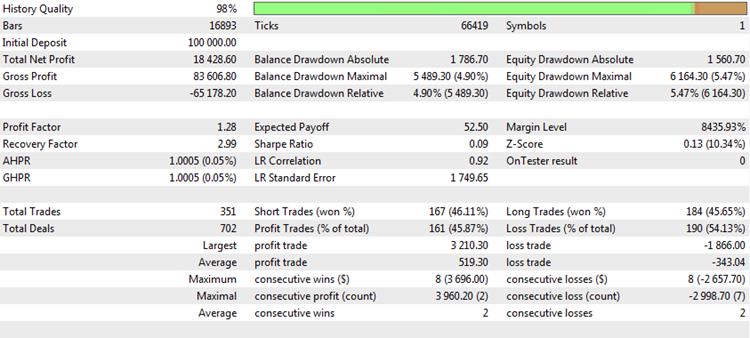
図1. トレード戦略のバックテスト

これには興味深い統計情報やメトリックがあります。最も人気のあるものを分析し、その長所と短所を客観的に考えてみましょう。

総純利益。このメトリックは、テストまたはトレード期間中の損益の合計を示します。最も重要なトレードパラメータの1つです。すべてのトレーダーの主な目的は、利益を最大化することです。これを行うには、さまざまな方法がありますが、最終的な結果は常に1つ、純利益です。純利益は、取引の量に依存せず、他のパラメータとは無関係です。したがって、他のメトリックに関連して不変であるため、独立して使用できます。しかし、これには、同様に深刻な欠点があります。

まず、純利益は、時価総額が使用されているかどうかに直接依存しています。時価総額を使用すると、利益は非直線的に増加します。しばしば、資産の爆発的な成長があります。このケースでは、テストの最後に純利益として記録された数字は、多くの場合、天文学的価値に到達し、現実とは何の関係もありません。固定ロットがトレードされている場合、デポジットの増分はより直線的ですが、この場合でも利益は選択されたボリュームに依存します。例えば、上記の表に示された結果を用いてテストを行った場合には、固定ロットを用いて行い、次いで $15757 の得られた利益を結果とみなすことができます。取引のボリュームが1.0 ロットなら、テスト結果は幾ばくかマシです。これが、経験豊富な開発者が、0.1 または0.01の固定ロットを外国為替相場に設定することを好む理由です。この場合、バランスの最小の変化は、この特性の分析をより客観的にするツールの1つのポイントに等しくなります。

第２に、最終結果は、テストされた期間またはトレード履歴の期間の長さに依存します。たとえば、上記の表で指定された純利益は、1年または5年でされている可能性があります。そして、それぞれのケースで、戦略の完全に異なる結果になることを意味します。

そして第３に、総利益は最終日の時点で固定されます。しかし、その時点で資本の強力なドローダウンがあるかもしれません。つまり、このパラメータは、レポートをテストする開始ポイントと終了ポイントに強く依存しています。

プロフィットファクター。これは間違いなくプロのトレーダーに最も人気のある指標です。初心者が全体の利益だけを見たいと思う反面、プロは投資された資金の転換を知ることが重要だとしています。取引の損失が一種の投資として考慮されれば、プロフィットファクターはトレードの利率を示します。たとえば、2つのトレードだけが行われた場合、最初の1つは $1000 を失い、2つ目は $2000 を獲得した場合、この戦略のプロフィットファクターは $ 2000/1000 = 2.0になります。非常に良い数字です。また、プロフィットファクターは、テストの時間にも、ボリュームにも依存しません。従って、プロはこれを好みます。しかし、同様に欠点があります。

その1つは、プロフィットファクターの値は、取引数に依存しているということです。取引が少ない場合、2.0 または3.0 のプロフィットファクターを得ることは容易です。一方で、多数の取引があれば、1.5 程度のプロフィットファクターを得ることは大きな成功です。

期待ペイオフ。平均取引のリターンを示す非常に重要な指標です。戦略が有益である場合、期待されるペイオフはプラスです。しかし、逆の場合マイナスになります。期待ペイオフがスプレッドや手数料のコストに匹敵する場合は、実際のアカウントで利益を獲得できるかどうかは疑わしいです。通常、予想されるペイオフは、理想的な実行条件の下でストラテジーテスターでポジティブになり、バランスのチャートは、上向きです。しかし、ライブトレードでは、平均的なトレードのリターンは、戦略の結果に重大な影響を与える可能性があります。また、実際の損失を引き起こすいわゆるリクオートまたはスリッページにより理論的に計算された結果よりもわずかに悪いことがあります。

また、欠点があります。取引の数に関連しています。取引の数が少なければ、予想されたペイオフを得ることは容易です。一方、取引回数が多い場合には、予想されたペイオフは悪くなることがあります。線形メトリックであるため、資金管理システムを実装する戦略では使用できません。しかし、プロのトレーダーは、固定ロットとリニアシステムを使用して、比較します。

トレード数。他のほとんどの特性に明示的または間接的に影響する重要なパラメータです。 70%の確率でトレードシステムが勝つと仮定します。同時に、勝ちトレードと負けトレードの絶対値が同じだとします。このようなシステムは素晴らしいように見えますが、最後の2つのトレードだけで評価したらどうなるでしょうか。 70%は、勝ちトレードですが、有益である両方の取引の確率は 49% だけです。つまり、2つのトレードの合計結果は、半分以上のケースでゼロになります。したがって、半分のケースでは、統計情報は、戦略が利益にならないことを表します。そのプロフィットファクターは、常に1に等しくなります。期待ペイオフと利益はゼロになります。他のパラメータもまた、ゼロを示します。

このため、取引数が十分に大きくなければなりません。しかし、何をもって十分と言えるでしょうか。一般に、任意のサンプルに少なくとも37の測定値が含まれていることが必要だと言われています。これは統計学におけるの特殊な数で、下限です。当然、取引におけるこの量はトレードシステムを評価するには十分ではありません。少なくとも100回の取引は信頼に必要な数です。また、多くのプロのトレーダーにとって、これは十分ではありません。少なくとも500-1000回の取引をし、ライブトレードのシステムを動かす可能性を考慮するために、システムを設計します。

トレーディングシステムをテストする際の共通統計パラメータの振る舞い

トレードシステムにおける主要な指標を考察しました。実際にそのパフォーマンスを見てみましょう。同時に、R ^ 2 の形で提案された方法を確認するためにネガティブな面に焦点を当てます。これを行うには、"ユニバーサルEA: 予約オーダーの使用" という記事に記載されている、CImpulse 2.0 EA を使用します。この記事の目的に非常に重要である標準的なMetaTrader5パッケージのEAとは異なり、そのシンプルさと最適化が選択の要です。また、すでに CStrategy トレードエンジンに書かれている特定のコードのインフラストラクチャが必要になりますので、同じタスクを2回行う必要はありません。決定係数のすべてのソースコードは、サードパーティのライブラリや手続き型のエキスパートなど、CStrategy の外部で使用できるように記述されています。

総純利益。すでに述べたように、収支 (または合計) 利益はトレーダーが取得したい最終的な結果です。利益が大きいほど、優れています。しかし、その最終的な利益に基づいた戦略の評価は、常に成功を保証するものではありません。 2015.01.15 から2017.10.10 の期間の EURUSD ペアの CImpulse 2.0 戦略の結果を考えてみましょう。

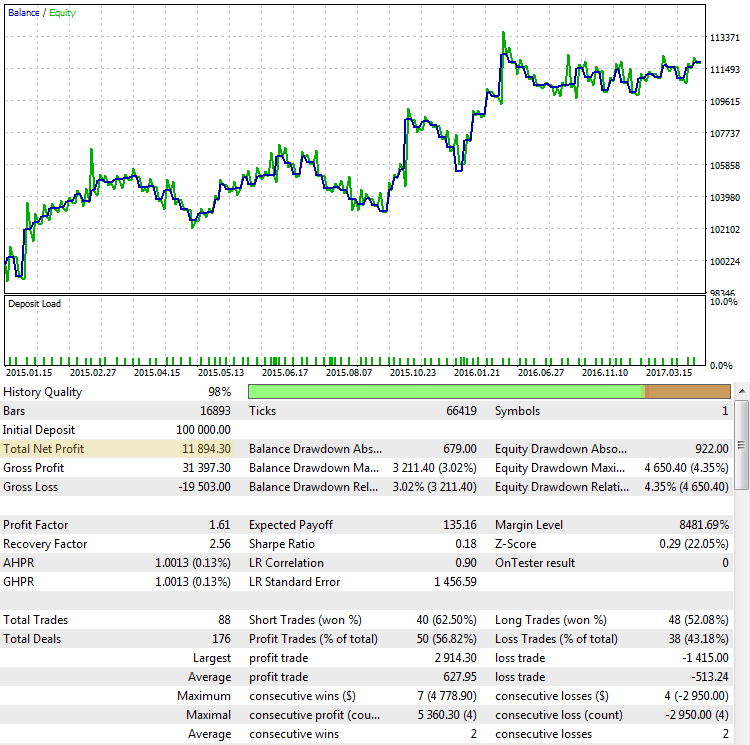
図2. CImpulse ストラテジー, EURUSD, 1h, 2015.01.15-2017.10.01, PeriodMA: 120, StopPercent: 0.67

この戦略は、このテスト期間の総利益の着実な成長を示していると見られています。ポジティブであり、1つの取引で11894ドルです。良い結果です。しかし、最終的な利益は、最初のケースに近いですが、別のように見えるものを見てみましょう:

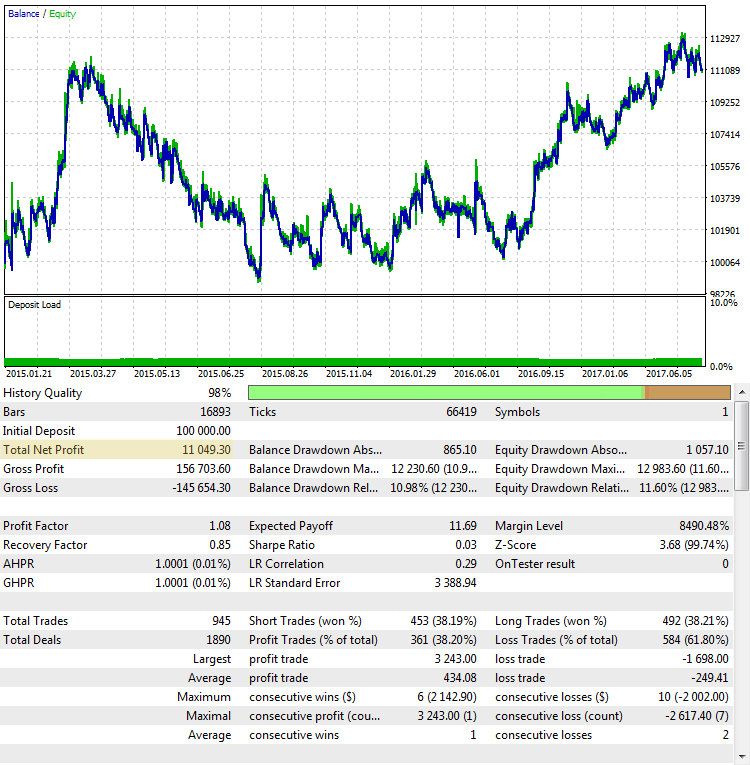
図3. CImpulse 戦略, EURUSD, 1h, 2015.01.15-2017.10.01, PeriodMA: 110, StopPercent: 0.24

利益は、両方のケースでほぼ同じであるという事実にもかかわらず、完全に異なるトレードシステムのように見えます。 2番目のケースでの最終的な利益もランダムに見えます。テストが2015の真中で終わったら、利益はゼロに近かった。

ここでは、最終的な結果として失敗していますが、最初のケースに非常によく似ています。

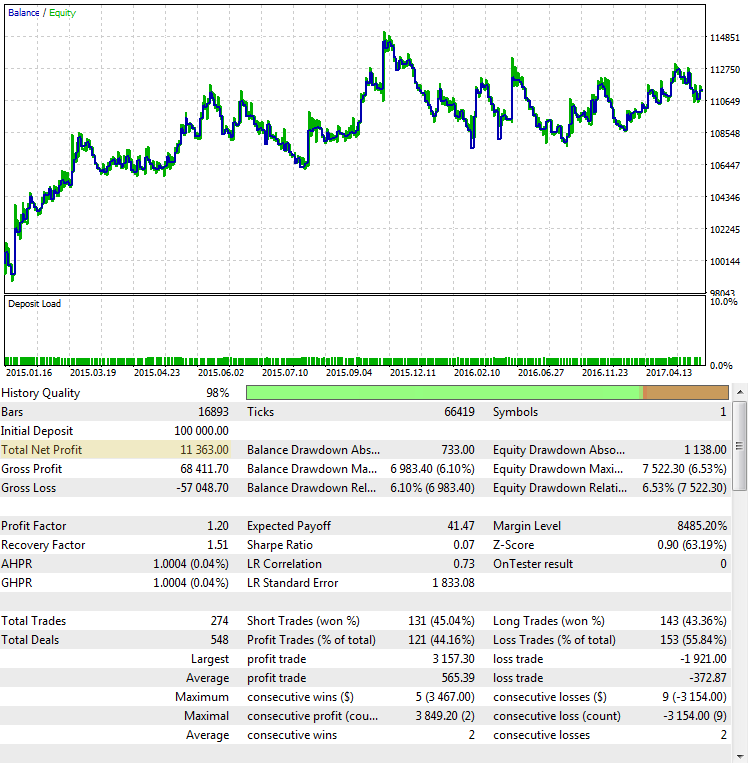
図4. CImpulse, EURUSD, 1H, 2015.01.15 - 2017.10.01, PeriodMA: 45, StopPercent: 0.44

2015の上半期に主な利益を出したのはチャートから明らかです。その後長引く停滞期が続いています。このような戦略は、ライブトレードの現実的な選択肢ではありません。

プロフィットファクター。プロフィトファクターの指標は、最終的な結果に大きく依存しています。この値は、各取引に依存し、すべての資金を失ったすべての勝率を示しています。図2においては、プロフィットファクターが非常に高いことがわかります。図4では、より低い。そして、図3では、収益性と不採算のシステムの境界線上にほぼあります。しかし、にもかかわらず、プロフィットファクターはだまされることができない普遍的な特性ではありません。プロフィットファクターの示す値が明確ではない他の例を調べてみましょう:

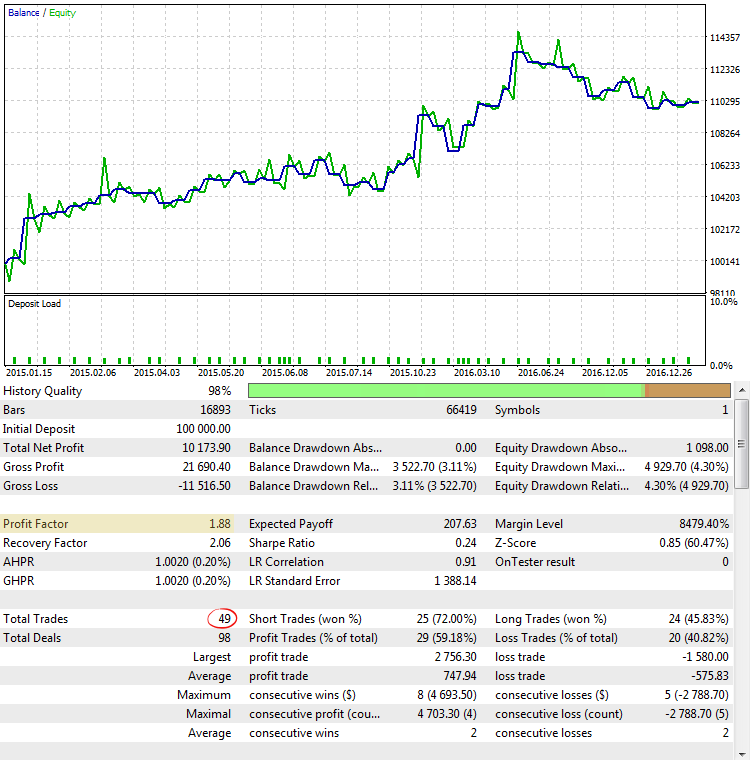
図5. CImpulse, EURUSD, 1 H, 2015.01.15-2017.10.01, PeriodMA:60, StopPercent: 0.82

図5は、最大のプロフィットファクター値のいずれかを使用した戦略テストの実行結果を示しています。バランスチャートは非常に有望に見えますが、得られた統計は、プロフィットファクターの値がトレードの非常に少ない数に誇張されているとして、誤解を招きます。

2つの方法でこのステートメントを確認してみましょう。 最初の方法: 取引数にプロフィットファクターの依存性を確認。これはさまざまなパラメータを使用してストラテジーテスターの CImpulse 戦略を最適化することによって行われます。

図6. 広範囲なパラメータを用いた CImpulse の最適化

最適化結果を保存します。

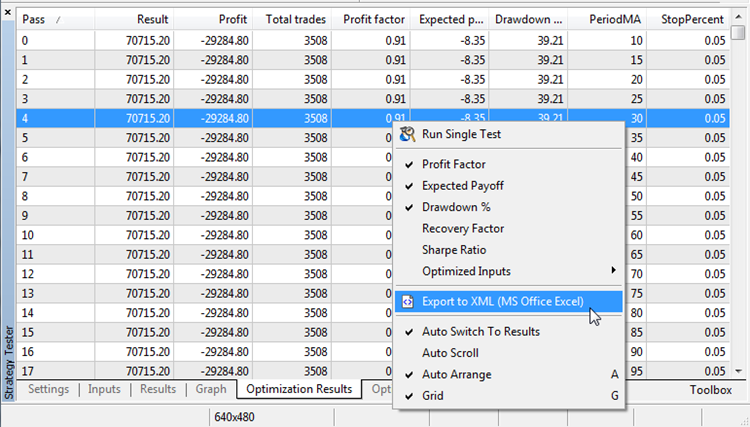
図7. 最適化結果のエクスポート

トレード数にプロフィットファクターの依存チャートを構築することができます。たとえば、Excel では、対応する列を選択し、[チャート] タブで散布図をプロットするだけで、これを行うことができます。

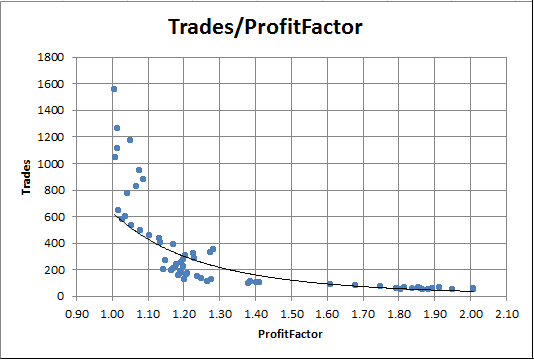
図8. トレード数に対するプロフィットファクターの依存性

チャートは明らかに高いプロフィットファクターを持ち、非常に少ないトレードであることを示しています。逆に、取引数が多いと、プロフィットファクターは実質的に1に等しくなります。

2 番目の方法は、ProfitFactor 値が取引数に依存し、戦略の品質がOut Of Sのテスト (OOS) を実行することに関連していると判断します。ところで、これは得られた結果のロバスト性を判断する最も確実な方法の1つです。ロバスト性は、推定における統計的手法の安定性の尺度です。 OOS は、プロフィットファクターだけでなく、他の徴候をテストするためにも有効です。同じパラメータが選択されますが、時間間隔が異なります-2012.01.01 から 2015.01.01:

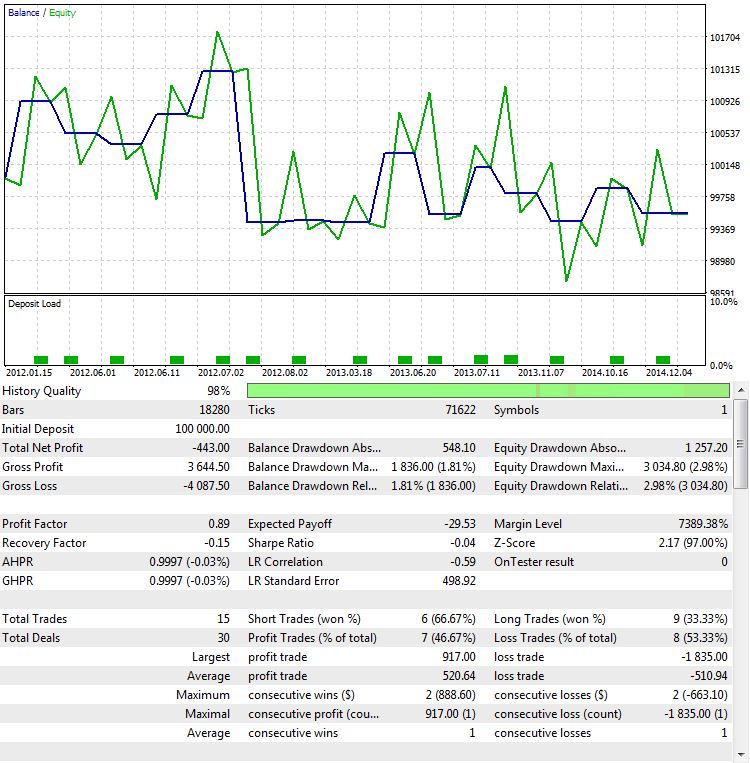
図9. サンプルから戦略をテスト

ご覧の通り、この戦略の振る舞いは、逆さまになります。利益の代りとして損失を発生させます。これは論理的な結果であり、得られた結果は、ほとんどの場合、ランダムです。 1つの時間間隔でのランダムな利益は別の損失によって補償されていることを意味します。図9.

期待ペイオフ。その欠点はプロフィットファクターに似ているので、このパラメータに多くこだわることはありません。ここではトレード数の期待ペイオフの依存チャートです:

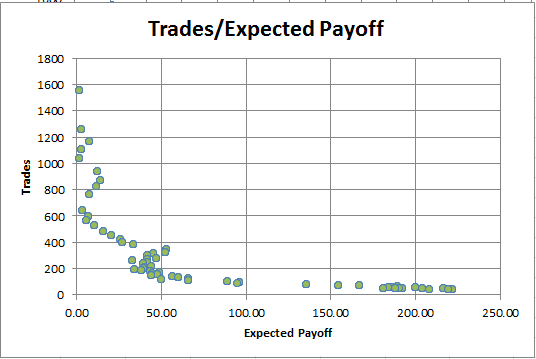
図10. トレード数に対する期待ペイオフの依存

より多くのトレードを見ることができ、小さい期待ペイオフになります。この依存性は、収益性と不採算の両方の戦略で常に観察されます。したがって、期待ペイオフは、トレード戦略の最適性の唯一の基準として機能することはできません。

トレーディングシステムのテスト基準の要件

トレードシステムの統計的評価の主な基準を検討した上で、各基準の適用可能性が限定的であると結論づけました。戦略自体はありませんが、メトリックは良い結果の例で反論することができます。

トレーディングシステムの堅牢性を判断するための理想的な基準はありません。しかし、強力な統計基準のプロパティを定式化することが可能です。

テスト期間の期間からの独立性。トレード戦略の多くのパラメータは、テスト期間の長さによって異なります。たとえば、収益性の高い戦略のテスト期間が大きいほど、最終損益が大きくなります。これは、期間と回復係数によって異なります。最大ドローダウンへの総利益の比率として計算されます。期間によって利益が決まるため、テスト期間の増加とともに回復要因も大きくなる。期間に対する不変性 (独立) は異なったテスト期間の異なった作戦の有効性を比較するために必要です。;
テストエンドポイントからの独立性。たとえば、損失するのを待つだけで、戦略が「浮いたまま」の場合、エンドポイントは最終的なバランスに重大な影響を与える可能性があります。このような "不法" の時点でテストが完了すると、フローティング損失 (エクイティ) は、バランスになり、重要なドローダウンがアカウント上で発生します。統計はそのような詐称から保護され、トレードシステム操作の客観性を提供するべきです。
解釈のシンプル。トレーディングシステムのすべてのパラメータは、定量的、すなわち、各統計は、特定の数字によって特徴付けられるべきです。この数字は直感的に理解できるものでなければなりません。得られた値の解釈がシンプルであるほど、パラメータがわかりやすくなります。また、パラメータが特定の範囲内にあることが望ましいため、大きなスケールで無限数の解析が複雑になることがよくあります。
少数の取引との代表的な結果。間違いなくなく、良い指標の特性の中で最も困難な要件です。すべての統計的なメソッドは測定の数によって決まります。多くは、より安定した統計情報になります。もちろん、小さなサンプルでこの問題を完全に解決することは不可能です。ただし、データ不足による影響を軽減することは可能です。この目的のため、R 乗を評価するための関数の2つのタイプを開発してみましょう。 1 つは、利用可能な取引数に基づいて、この基準を構築します。もう一つは、戦略 (エクイティ) の浮動利益を使用して基準を計算します。

決定係数 R ^ 2 の記述に進む前に、その内容を詳しく調べてみましょう。このパラメータの目的と基づく原則を理解するのに役立ちます。

線形回帰

線形回帰は、式y = ax + bで表される別の独立変数xからの1つの変数yの線形依存性です。この式において、 аは乗算器であり、 bはバイアス係数です。実際には、独立変数があり、そのようなモデルは、複数の線形回帰モデルと呼ばれます。しかし、最もシンプルなケースを検討しましょう。

線形依存性は、単純なグラフの形で視覚化することができます。 2017.06.21 から2017.09.21 に毎日の EURUSD チャートを取る。このセグメントは偶然には選択されていません。この期間中、この通貨ペアで緩やかな昇順トレンドが観察されました。これは、メタトレーダーでどのように見えるかです:

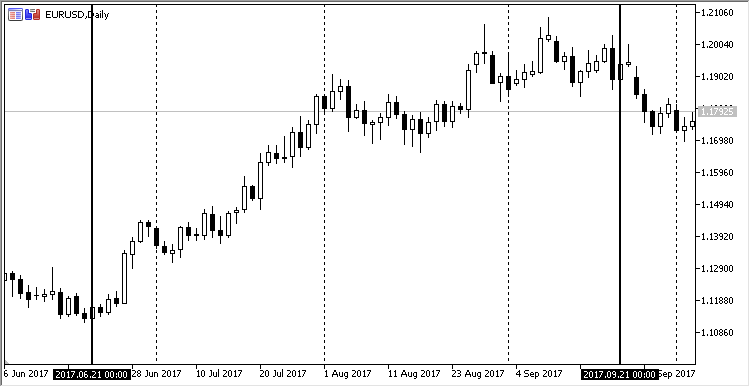
図11. 21.06.2017 から21.08.2017 への EURUSD 価格のダイナミクス, 日足

価格データを使用して、Excel でチャートをプロットします。

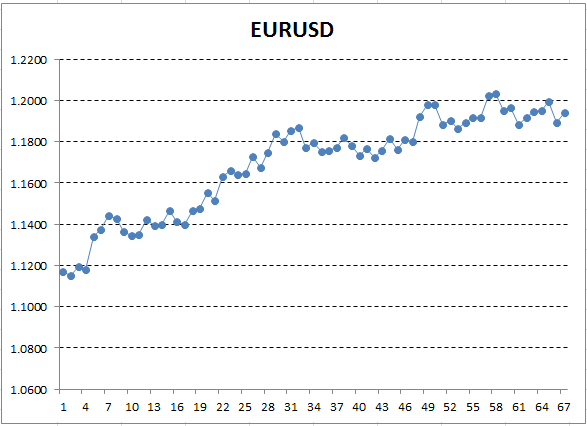
図12. エクセルのチャートとしての EURUSD 率 (終値)

ここで、Y 軸は価格に対応し、X は測定の序数 (日付は序数で置き換えられました) です。結果のチャートでは、昇順のトレンドは肉眼で表示されますが、このトレンドの定量的な解釈を取得する必要があります。最も簡単な方法は、検出されたトレンドが最も正確に収まる直線を描画することです。これは、線形回帰と呼ばれます。たとえば、次のように線を描画できます。

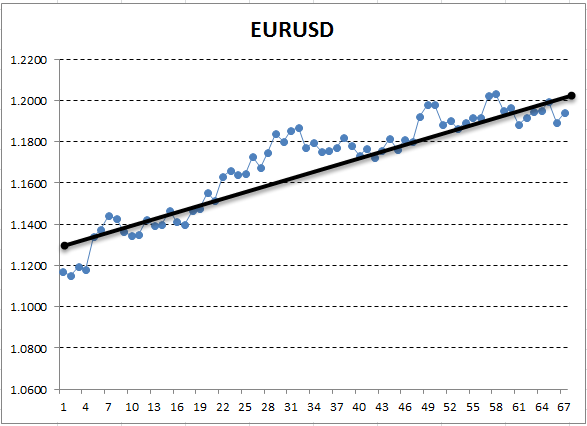
図13. 上昇トレンドを説明する線形回帰を目視で描画

グラフがかなり滑らかであれば、そのような線を描くことができ、チャートポイントが最小距離になるようにすることができます。逆に、振れ幅の大きいグラフの場合、その変更を正確に記述するラインを選択することはできません。これは、線形回帰には2つの係数しかないという事実によるものです。確かに、幾何学では、2つの点は、線をプロットするのに十分であることを示しています。このため、直線を「曲線」チャートに合わせることは容易ではありません。これは、さらに先に役立つ貴重なプロパティです。

しかし、どのすれば正しく直線を描画することができるでしょうか。数学的メソッドは、すべての利用可能なポイントがこのラインへの距離の最小の合計を持つような方法で線形回帰係数を最適に計算するために使用することができます。これについては、次の表で説明します。 5つの任意のポイントを通過する2つのラインがあると仮定します。 2つのラインから、ポイントまでの距離の最小合計を持つものを選択する必要があります:

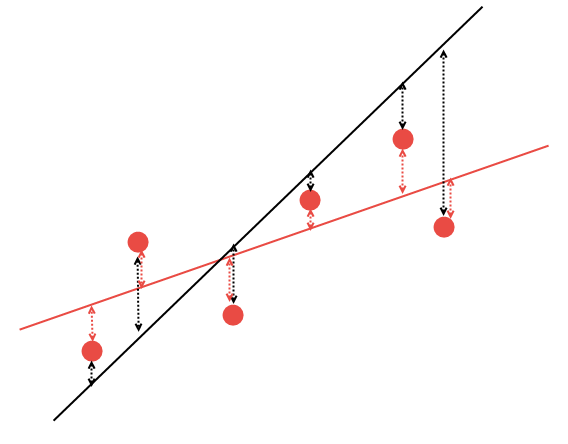
図14. 最適な線形回帰の選択

2つの線形回帰バリアントの、赤い線がより良い与えられたデータを記述することは明らかです。: ポイント #2 と #6 は黒い線よりも赤線に大幅に近いです。残りのポイントは、黒線と赤線の両方から約等距離です。数学的には、この規則を最もよく説明する線の座標を計算することが可能です。係数を裁量で計算せず、使用可能な AlgLib 数学ライブラリを代わりに使用します。

相関

線形回帰が計算されると、この線と計算されるデータとの間の相関関係を計算する必要があります。相関は、2つ以上のランダム変数の統計的な関係です。この場合、変数のランダム性は、変数の測定値が相互依存していないことを意味します。相関は-1.0 ~ + 1.0 で測定されます。ゼロに近い値は、検査された変数に相互がないことを示します。 + 1.0 の値は直接的な依存性を意味し、-1.0 は逆依存性を示しています。相関関係は、異なる数式によって計算されます。ここでは、ピアソンの相関係数が使用されます。

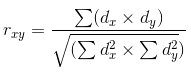
式の中のdxとdyは、ランダム変数xおよびyに対して計算された差異に対応しています。分散は、特性の変化の尺度です。一般的には、データと線形回帰の間の距離の平方和として記述することができます。

線形回帰に対するデータの相関係数は、直線がデータをどの程度記述しているかを示しています。データのポイントがラインから大きな距離にある場合、分散は高く、相関関係は低く、その逆も同様です。相関関係は非常に簡単に解釈することができます。ゼロは、回帰とデータの間に相関関係がないことを意味します。1に近い値は強い直接依存を示す。

メタトレーダーのレポートには、特別な統計指標があります。 LR 相関と呼ばれ、その曲線に対して検出されたバランスカーブと線形回帰の相関関係を示します。バランスカーブがスムーズであれば、直線への近似が良いでしょう。この場合、LR 相関係数は1.0 に近いか、少なくとも0.5 以上になります。バランスカーブが不安定な場合、上昇と下落は交互に行われ、相関係数はゼロになりがちです。

LR の相関関係は興味深いパラメータです。しかし、統計学では、相関係数を介してデータと記述回帰を直接比較することは慣習的ではありません。この理由については、次のセクションで説明します。

決定係数 R ^ 2

決定係数 R ^ 2 の計算メソッドは、LR 相関の計算メソッドに似ています。しかし、最終的な値は、さらに２乗されます。 0.0 ~ + 1.0 の値を取ることができます。この図は、合計サンプルからの説明値の共有を示しています。線形回帰は説明モデルとして機能します。厳密に言えば、説明モデルは線形回帰である必要はなく、他のものも同様に使用することができます。ただし、R ^ 2 の値では、線形回帰に対してさらに処理を行う必要はありません。より複雑なモデルでは、近似は通常より、R ^ 2 の値は「ペナルティ」によってさらに減らされなければならない。

モデルの内容を詳しく見てみましょう。プログラミング言語R プロジェクトを使用して、必須の係数が計算されるランダムウォークを生成する実験を行います。ランダムウォークは、実際の金融商品と非常によく似た特性を持つプロセスです。ランダムウォークを取得するには、通常の法則に従って分散された乱数を連続して追加するだけで十分です。

何が行われているかの詳細な説明と R のソースコード:

x <-rnorm (1000)  #通常の法則に従って配布される1000乱数を生成します。
                            #差異は1に等しく、期待値はゼロです。
walk <-cumsum (x) #累積的に数値を合計し、古典的なランダムウォークチャートを取得します。
plot(rwalk, type="l", col="darkgreen")       # 線形チャートの形式でデータを表示
rws <- lm(rwalk~c(1:1000))  # 線形モデル y = a * x + b をプロット、ここで x は測定の数であり、y は生成されたウォークベクトルの値
title("Line Regression of Random Walk")
abline(rws)                 # チャートの結果の線形回帰を表示

norm 関数は毎回異なるデータを返すので、この実験を繰り返す場合、チャートの外観は異なります。

提示されたコードの結果:

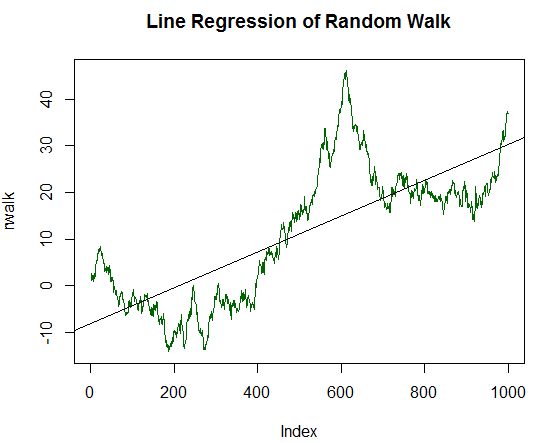
図15. ランダムウォークの線形回帰

結果のチャートは、任意の金融商品と似ています。その線形回帰が計算され、チャートの黒い線として出力します。一見すると、ランダムウォークダイナミクスの説明は非常に平凡です。しかし, 線形回帰の品質を定量的に推定する必要があります。このため、回帰モデルの集計統計を出力する ' summary ' 関数が使用されます。

summary(rws)
Call:
lm(formula = rwalk ~ c(1:1000))

Residuals:
    Min      1Q  Median      3Q     Max 
-16.082  -6.888  -1.593   4.174  30.787 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) -8.187185   0.585102  -13.99   <2e-16 ***
c(1:1000)    0.038404   0.001013   37.92   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 9.244 on 998 degrees of freedom
Multiple R-squared:  0.5903,    Adjusted R-squared:  0.5899 
F-statistic:  1438 on 1 and 998 DF,  p-value: < 2.2e-16

ここでは、最も関心のあるのはR の２乗です。このメトリックは、0.5903 の値を示します。したがって、線形回帰ではすべての値の 59.03% が記述され、残りの 41% は原因不明のままになります。

非常に敏感な指標で、データの平滑なレンジラインによく反応します。これを説明するために、実験を続けましょう。ランダムデータに安定した成長成分を導入します。これを行うには、最初に生成されたデータの分散の1/20 によって平均値または予期される値を変更します。

x_trend1 <- x+(sd(x)/20.0)      # 値の標準偏差 x を見つけ、20.0で除算し、得られた値を x の各値に加算します。
                                #x の各ような変更された値は、新しい値のベクトル x_trend1 に格納されます。
rwalk_t1 <- cumsum(x_trend1)    # 累積的に数値を合計し、シフトしたランダムウォークチャートを取得する。     
プロット (rwalk_t1, タイプ ="l", col = "セット") #データを線形チャートとして表示する
title("Line Regression of Random Walk #2")
rws_t1 <- lm(rwalk_t1~c(1:1000))# は、線形モデル y = a * x + b をプロットし、ここで x は測定の数であり、y は生成されたウォークベクトルの値です。
abline(rws_t1)                  # チャートの結果の線形回帰を表示します。

結果のチャートは、直線に近い位置になりました。

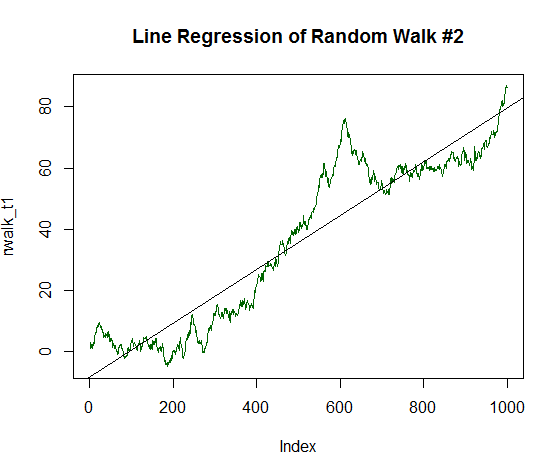
図16. 正の期待値を持つランダムウォーク（分散の1/20 に等しい）

統計量は次のとおりである:

summary(rws_t1)

Call:
lm(formula = rwalk_t1 ~ c(1:1000))

Residuals:
    Min      1Q  Median      3Q     Max 
-16.082  -6.888  -1.593   4.174  30.787 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) -8.187185   0.585102  -13.99   <2e-16 ***
C (1:1000) 0.087854 0.001013 86.75 <2E-16 * * *
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 9.244 on 998 degrees of freedom
Multiple R-squared:  0.8829,    Adjusted R-squared:  0.8828 
F-statistic:  7526 on 1 and 998 DF,  p-value: < 2.2e-16

R ２乗が有意に高く、値が0.8829 であることは明らかです。しかし、余分なマイルに行くと、最初のデータの標準偏差の1/10 まで、チャートの2倍の決定コンポーネントをみましょう。これを処理するコードは、前のコードと似ていますが、10.0 ではなく、20.0 で除算されています。新しいチャートは、ほぼ完全に直線です:

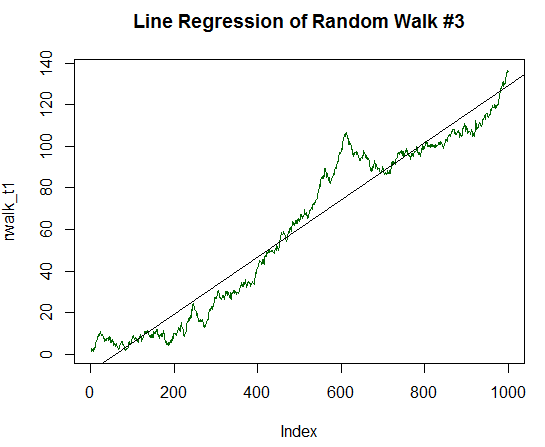
図17. 正の期待値を持つランダムウォーク（分散の1/10 に等しい）

統計を計算:

Call:
lm(formula = rwalk_t1 ~ c(1:1000))

Residuals:
    Min      1Q  Median      3Q     Max 
-16.082  -6.888  -1.593   4.174  30.787 
4
Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) -8.187185   0.585102  -13.99   <2e-16 ***
C (1:1000) 0.137303 0.001013 135.59 <2E-16 * * *
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 9.244 on 998 degrees of freedom
Multiple R-squared:  0.9485,    Adjusted R-squared:  0.9485 
F-statistic: 1.838e+04 on 1 and 998 DF,  p-value: < 2.2e-16

R２乗はさらに高くなり、0.9485 に達した。このチャートは、収益性の高いトレード戦略のバランスダイナミクスと非常に似ています。もう少し見てみましょう。標準偏差の1/5 までの期待値を上げます。

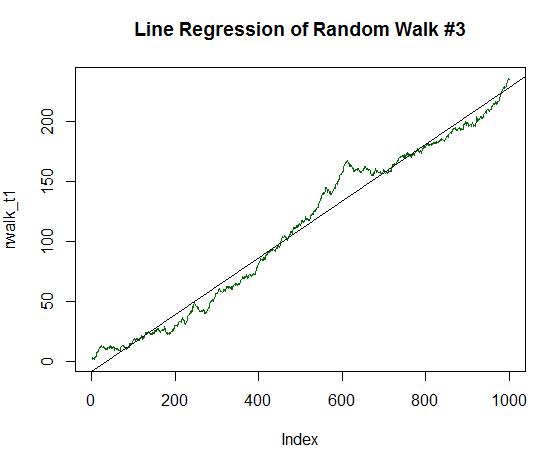
図18. 正の期待値を持つランダムウォーク（分散の1/5 に等しい）

次の統計情報になります。

Call:
lm(formula = rwalk_t1 ~ c(1:1000))

Residuals:
    Min      1Q  Median      3Q     Max 
-16.082  -6.888  -1.593   4.174  30.787 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) -8.187185   0.585102  -13.99   <2e-16 ***
C (1:1000) 0.236202 0.001013 233.25 <2E-16 * * *
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 9.244 on 998 degrees of freedom
Multiple R-squared:  0.982,     Adjusted R-squared:  0.982 
F-statistic: 5.44e+04 on 1 and 998 DF,  p-value: < 2.2e-16

R-２乗は、ほぼ1に等しいことは明らかです。緑線のランダムなデータは、ほぼ完全に平滑直線上にあることを示しています。

アークサイン定理とその線形回帰の推定への寄与

ランダムプロセスは、最終的には、元のポイントから遠くへ移動する数学的証拠があります。これは最初と2番目のアークサイン定理と命名されました。今回はこれを詳細に考察することはありません。定理の帰結だけ使います。

これらに基づいて、ランダムプロセスの傾きは、避けられない。つまり、このようなプロセスでは、最初のポイントの近くでランダムに変動するよりもランダムな傾向があります。これは非常に重要な特性であり、統計指標の評価に非常に有益です。線形回帰係数 (LR 相関) に特に顕著です。トレンドは線形回帰によって記述されています。トレンドが一つの方向に対する動きを含んでいるという事実によるものです。

そこにランダムプロセスのより多くのトレンドがある場合は、レンジ、LR の相関も一般的にその値が過大評価されます。このような効果を確認するには、1万の独立したランダムウォークを生成し、1.0 と期待値の値を0にしてみましょう。このようなチャートごとに LR の相関関係を計算し、値の分布をプロットしてみましょう。 R に簡単なテストスクリプトを記述します。

sample_r2 <- function(samples = 100, nois = 1000)
{
   lags <- c(1:nois)
   r2 <- 0  # R^2 rating
   lr <- 0  # Line Correlation rating
   for(i in 1:samples)
   {
      white_nois <- rnorm(nois)
      walk <- cumsum(white_nois)
      model <-  lm(walk~lags)
      summary_model <- summary(model)
      r2[i] <- summary_model$r.squared*sign(walk[nois])
      lr[i] <- (summary_model$r.squared^0.5)*sign(walk[nois])
   }
   m cbind (r2, lr)
}

このスクリプトは LR 相関と R ^ 2 の両方を計算します。差は後で見られます。スクリプトに小さな追加が行いました。得られた相関係数には合成チャートの最終的な符号が乗算されます。最終的な結果が0未満の場合、相関関係は負になります。それ以外の場合正です。他の統計に頼ることなく、ポジティブなものから簡単かつ迅速に負の結果を分離するために行われます。 MetaTrader5で LR の相関関係がどのように動作するか、同じ原理は、R ^ 2 に使用されます。

従って、1万の独立したサンプルの LR の相関の配分を、それぞれ1000の測定からプロットしてみましょう:

ms <- sample_r2(10000, nois=1000)
hist(ms[,2], breaks = 30, col="darkgreen", density = 30, main = "Distribution of LR-Correlation")

結果のグラフは、定義の正しさを明確に示します。:

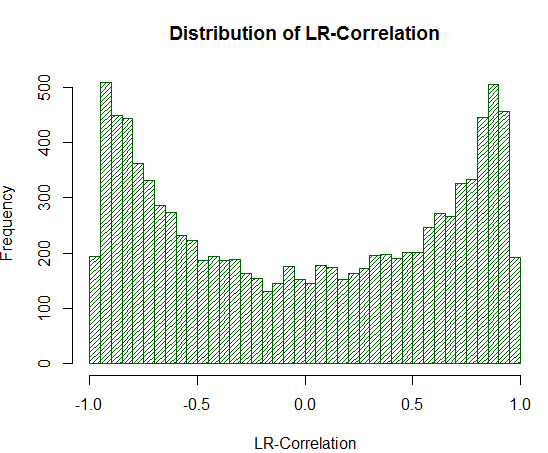
図19. 1万ランダムウォークにおける LR 相関の分布

実験から分かるように、LR-相関値は +/-0.75-0.95 の範囲で実質的に過大です。 LR-相関関係がしばしば不当に高い正の推定値を与えることを意味します。

ここで、R ^ 2 が同じサンプルでどのように動作するかを考えてみましょう。

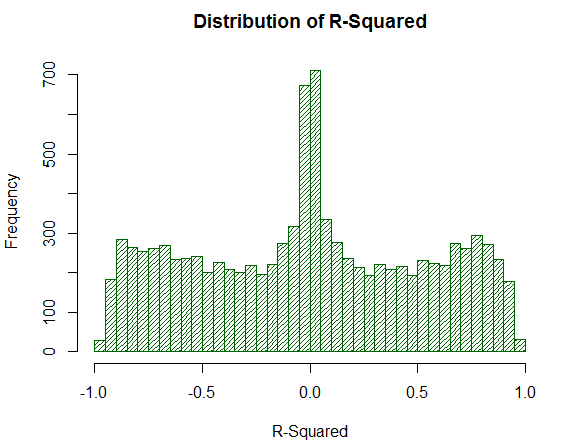
図20. 1万ランダムウォークにおける R ^ 2 の分布

R ^ 2 の値は、分布が均一であるにもかかわらず、高すぎません。数学的アクションの挙動は非常に驚きです。これがLR-相関関係が直接分析することができない理由です。つまり、追加の数学的な変換が必要です。また、R ^ 2 は、戦略の分析された仮想バランスのかなりの割合をゼロの近くに移動しますが、LR-相関によって安定した平均推定値が得られることに注意してください。これは正のプロパティです。

戦略エクイティの収集

メタトレーダーのターミナルで R-２乗を実装する方法が残っています。もちろん、ヒストリーの中でのトレードでこれを計算します。ただし、さらなる改善が必要です。前に述べたように、任意の統計パラメータは、情報の数が多い方が良いです。残念ながら、R-２乗は、他の統計のように、アカウント上で情報がある場合は、不当にその値を膨らませることができます。これを避けるためには、浮動利益を計算します。この背後にある概念は、例えば、EAが年間20のトレードを行う場合、その効率性を見積もることは非常に困難であるということです。その結果、最も可能性の高いのがランダムです。しかし、この EA のバランスが指定された周期 (例えば、1時間に一度) で測定されれば、統計量をプロットするためのかなりのポイントがあるでしょう。この場合、6000以上の測定が行われます。

さらに、そのような測定を打ち消すシステムは、その浮遊損失を修正しません。ドローダウンは存在しますが、これは残高によるものではありません。バランスに基づいて計算された統計は、発生する問題について警告しません。ただし、浮動損益を考慮して計算されたメトリックは、勘定の目標状況を反映します。

戦略のエクイティは、型破りな方法で収集されます。これは値のコレクションに2つの主要なポイントを考慮する必要があるためです。

統計収集の頻度
株式をチェックする必要がある受信イベントの決定。

たとえば、EAは、H1 の時間枠にタイマのみで動作します。 "始値のみ" モードでテストされています。したがって、この EA のデータを1時間に2回以上収集することはできず、データのスクリーニングは、OnTimer イベントが発生した場合にのみ実行できます。最も効果的なソリューションは、 CStrategy エンジンのパワーを使用することです。 CStrategy は、すべてのイベントを1つのイベントハンドラに収集し、必要な時間枠を自動的に監視するという事実です。したがって、最適解は、すべての必要な統計情報を計算する特別なエージェント戦略を記述することです。これはCManagerList 戦略マネージャによって作成されます。このクラスは、アカウントの変更を監視する戦略のリストにエージェントを追加します。

このエージェントのソースコードは以下のとおりです。

//+------------------------------------------------------------------+
//|                                                UsingTrailing.mqh |
//|                                 Copyright 2017, Vasiliy Sokolov. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2017, Vasiliy Sokolov."
#property link      "https://www.mql5.com"
#include "TimeSeries.mqh"
#include "Strategy.mqh"
//+------------------------------------------------------------------+
//| Integrated to the portfolio of strategies as an expert and       |
//| records the portfolio equity                                     |
//+------------------------------------------------------------------+
class CEquityListener : public CStrategy
{
private:
   //-- Recording frequency
   CTimeSeries       m_equity_list;
   double            m_prev_equity;
public:
                     CEquityListener(void);
   virtual void      OnEvent(const MarketEvent& event);
   void              GetEquityArray(double &array[]);
};
//+------------------------------------------------------------------+
//| Setting the default frequency                                    |
//+------------------------------------------------------------------+
CEquityListener:: CEquityListener (ボイド): m_prev_equity (EMPTY_VALUE)
{
}
//+------------------------------------------------------------------+
//| Collects the portfolio equity, monitoring all possible           |
//| events                                                           |
//+------------------------------------------------------------------+
void CEquityListener::OnEvent(const MarketEvent &event)
{
   if(!IsTrackEvents(event))
      return;
   double equity = AccountInfoDouble(ACCOUNT_EQUITY);
   if(equity != m_prev_equity)
   {
      m_equity_list.Add(TimeCurrent(), equity);
      m_prev_equity = equity;
   }
}
//+------------------------------------------------------------------+
//| Returns the equity as an array of type double                    |
//+------------------------------------------------------------------+
void CEquityListener::GetEquityArray(double &array[])
{
   m_equity_list.ToDoubleArray(0, array);
}

エージェント自体は、再定義された OnEvent と値を返すためのメソッドという2つのメソッドから成ります。ここで、主な関心は、初めて CStrategy に表示されるCTimeSeriesクラスです。シンプルなテーブルであり、データは日付、値、列番号の形式で追加されます。格納されている値はすべて時間順に並べ替えられます。必要な日付は、実質的にコレクションのタスクをスピードアップバイナリ検索を介してアクセスされます。 OnEvent メソッドは、現在のイベントが新しい足の開始であるかどうかをチェックし、その場合は、新しいエクイティ値を格納します。

R ^ 2 は長い間取引がない状態に反応します。このような時には、変更されていない株式価値が記録されます。エクイティチャートは、いわゆる "はしご" を形成しています。これを防ぐために、メソッドは値と前の値を比較します。値が一致すると、レコードはスキップされます。したがって、変更のみがリストに分類されます。

このクラスを CStrategy エンジンに統合してみましょう。統合は、CStrategyList のレベルで、上から実行されます。このモジュールは、カスタム統計の計算に適しています。カスタム統計情報があります。したがって、すべての可能な統計の種類を一覧表示する列挙体が導入されます。

//+------------------------------------------------------------------+
//| Determines the type of custom criterion calculated after         |
//| optimization.                                                    |
//+------------------------------------------------------------------+
enum ENUM_CUSTOM_TYPE
  {
   CUSTOM_NONE,                     //カスタム基準は計算されません
   CUSTOM_R2_BALANCE,               //戦略バランスに基づく R ^ 2
   CUSTOM_R2_EQUITY,                //戦略エクイティに基づく R ^ 2
  };

上記の列挙では、カスタム最適化基準には、トレードの結果に基づく r 乗、エクイティデータに基づく r 乗、統計の計算は3つのタイプがあります。

カスタム計算の種類を構成する関数を追加します。これを行うには、追加のSetCustomOptimaze* メソッドを使用して CStrategyList クラスを指定します。

//+------------------------------------------------------------------+
//| Sets R^2 as the optimization criterion. The coefficient is       |
//| calculated for the trades made.                                  |
//+------------------------------------------------------------------+  
void CStrategyList::SetCustomOptimizeR2Balance(ENUM_CORR_TYPE corr_type)
{
   m_custom_type = CUSTOM_R2_BALANCE;
   m_corr_type = corr_type;
}
//+------------------------------------------------------------------+
//| Sets R^2 as the optimization criterion. The coefficient is       |
//| calculated based on the recorded equity.                         |
//+------------------------------------------------------------------+  
+------------------------------------------------------------------+
{
   m_custom_type = CUSTOM_R2_EQUITY;
   m_corr_type = corr_type;
}

各メソッドは、ENUM_CUSTOM_TYPE の内部変数の値を m_custom_type と2番目のパラメータに設定し、相関型 ENUM_CORR_TYPE に等しくなります。

//+------------------------------------------------------------------+
//| Correlation type                                                 |
//+------------------------------------------------------------------+
enum ENUM_CORR_TYPE
  {
   CORR_PEARSON,     //ピアソンの相関関係
   CORR_SPEARMAN     //スピアのランク順位相関
  };

この追加パラメータは、個別に記述する必要があります。実際には、R ^ 2 は他にはありませんが、チャートとその線形モデルとの相関があります。ただし、相関型自体が異なる場合があります。 AlgLib の数学ライブラリを使用します。相関関係を計算するための2つのメソッドをサポートしています: ピアソンとスピア。ピアソンの公式は古典的であり、均質な、通常の分散データに適しています。スピアのランク順位の相関は、多くの場合、相場で観察される価格のスパイクに耐性があります。したがって、計算は、R ^ 2 を計算するの各バリアントでタスクできるようになります。

すべてのデータが準備されたので、R ^ 2 の計算に進みます。別の関数に移動します。

//+------------------------------------------------------------------+
//| Returns the R^2 estimate based on the strategy balance           |
//+------------------------------------------------------------------+
double CustomR2Balance(ENUM_CORR_TYPE corr_type = CORR_PEARSON);
//+------------------------------------------------------------------+
//| Returns the R^2 estimate based on the strategy equity            |
//| The values of equity are passed as the 'equity' array            |
//+------------------------------------------------------------------+
double CustomR2Equity(double& equity[], ENUM_CORR_TYPE corr_type = CORR_PEARSON);

RSquare という名前の別のファイルに配置されます。 mqh 計算は関数の形式で配置されるため、ユーザーはこの計算モードをプロジェクトに簡単かつ迅速に含めることができます。この場合、CStrategy を使用する必要はありません。たとえば、エキスパートで R ^ 2 を計算するには、OnTester システム関数を再定義するだけです。

double OnTester()
{
   return CustomR2Balance();
}

戦略エクイティを計算する必要がある場合は、しかし、CStrategy を採用していないユーザーは自分でを行う必要があります。

CStrategyList で最後に行う必要があるのは、OnTester メソッドを定義することです。

//+------------------------------------------------------------------+
//| Adds monitoring of equity                                        |
//+------------------------------------------------------------------+
double CStrategyList::OnTester(void)
{
   switch(m_custom_type)
   {
      case CUSTOM_NONE:
         return 0.0;
      case CUSTOM_R2_BALANCE:
         return CustomR2Balance(m_corr_type);
      case CUSTOM_R2_EQUITY:
      {
         double equity[];
         m_equity_exp.GetEquityArray(equity);
         return CustomR2Equity(equity, m_corr_type);
      }
   }
   return 0.0;
}

ここでは、関数CustomR2EquityとCustomR2Balanceの実装について検討します。

AlgLib を用いた決定係数 R ^ 2 の計算

決定係数 R ^ 2 は、数値解析のクロスプラットフォームライブラリである AlgLib を使用して実装されます。最も先進的なものに、様々な統計基準を計算することができます。

ここで係数を計算するための手順があります。

エクイティの値を取得し、行列の M [x, y] に変換します。ただし、x は測定の数, y はエクイティ値である.
得られた行列について、線形回帰式の a および b 係数を算出します。
各 X の線形回帰値を生成し、配列に格納します。
2つの相関式のいずれかを使用して、線形回帰の相関係数とエクイティ値を検索します。
R ^ 2 とその符号を計算します。
R ^ 2 の正規化された値を呼び出し元の関数に返します。

これらの手順は、CustomR2Equity 関数によって実行されます。そのソースコードを以下に示します。

//+------------------------------------------------------------------+
//| Returns the R^2 estimate based on the strategy equity            |
//| The values of equity are passed as the 'equity' array            |
//+------------------------------------------------------------------+
double CustomR2Equity(double& equity[], ENUM_CORR_TYPE corr_type = CORR_PEARSON)
{
   int total = ArraySize(equity);
   if(total == 0)
      return 0.0;
   //-- Y-エクイティ値、X-値の序数
   CMatrixDouble xy(total, 2);
   for(int i = 0; i < total; i++)
   {
      xy[i].Set(0, i);
      xy[i].Set(1, equity[i]);
   }
   //--線形モデル y = a * x + b の係数 a と b を検索します。
   int retcode = 0;
   double a, b;
   CLinReg::LRLine(xy, total, retcode, a, b);
   //--各 X の線形回帰値を生成します。
   double estimate[];
   ArrayResize(estimate, total);
   for(int x = 0; x < total; x++)
      estimate[x] = x*a+b;
   //--線形回帰による値の相関係数の検索
   double corr = 0.0;
   if(corr_type == CORR_PEARSON)
      corr = CAlglib::PearsonCorr2(equity, estimate);
   else
      corr = CAlglib::SpearmanCorr2(equity, estimate);
   //--R ^ 2 とその符号を見つける
   double r2 = MathPow(corr, 2.0);
   int sign = 1;
   if(equity[0] > equity[total-1])
      sign = -1;
   r2 *= sign;
   //--R ^ 2 の推定値を100分の1以内に正規化
   return NormalizeDouble(r2,2);
}

--R ^ 2 の推定値を100分の1以内に正規化主なものは、線形回帰係数を直接計算する CAlgLib:: LRLine です。

ここで、R ^ 2: CustomR2Balance を計算するための2番目の関数について説明します。名前が示すように、この関数は、行われたトレードに基づいて値を計算します。すべてのタスクは、ヒストリーの中ですべてのトレードを繰り返し処理することによって、バランスのダイナミクスを含む double 型の配列を形成することにあります。

//+------------------------------------------------------------------+
//| Returns the R^2 estimate based on the strategy balance           |
//+------------------------------------------------------------------+
double CustomR2Balance(ENUM_CORR_TYPE corr_type = CORR_PEARSON)
{
   HistorySelect(0, TimeCurrent());
   double deals_equity[];
   double sum_profit = 0.0;
   int current = 0;
   int total = HistoryDealsTotal();
   for(int i = 0; i < total; i++)
   {
      ulong ticket = HistoryDealGetTicket(i);
      double profit = HistoryDealGetDouble(ticket, DEAL_PROFIT);
      if(profit == 0.0)
         continue;
      if(ArraySize(deals_equity) <= current)
         ArrayResize(deals_equity, current+16);
      sum_profit += profit;
      deals_equity[current] = sum_profit;
      current++;
   }
   ArrayResize(deals_equity, current);
   return CustomR2Equity(deals_equity, corr_type);
}

配列が形成されると、前述の CustomR2Equity 関数に渡されます。実際には、CustomR2Equity 関数はユニバーサルです。エクイティ [] 配列に含まれているすべてのデータの R ^ 2 値を計算します。

最後のステップは、CImpulse EA、すなわち、OnTester システムイベントのオーバーライドのコードの小さな変更です。

//+------------------------------------------------------------------+
//| Tester event                                                     |
//+------------------------------------------------------------------+
double OnTester()
{
   Manager.SetCustomOptimizeR2Balance(CORR_PEARSON);
   return Manager.OnTester();
}

この関数は、カスタムパラメータの型を設定し、その値を返します。

計算された係数が表示されます。 CImpulse 戦略バックが開始されると、このパラメータはレポートに現れます。

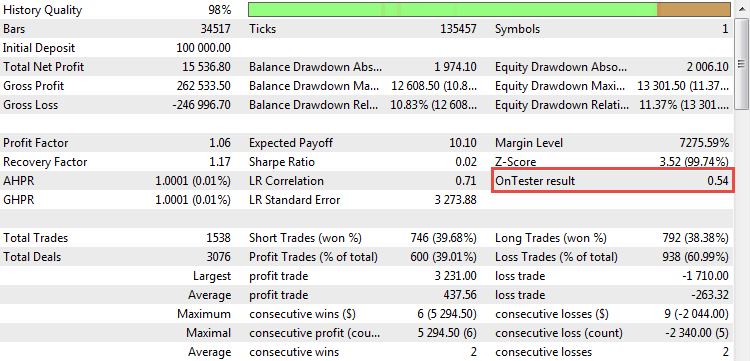
図21. カスタム最適化基準としての R ^ 2 の値

実習での R 乗パラメータの使用

R-２乗はカスタム最適化基準として組み込まれているので、実際に試してみる時間です。 EURUSD 通貨ペアのМ15時間枠で CImpulse を最適化することによって行われます。受信した最適化結果を Excel ファイルに保存し、取得した統計を使用して、異なる条件に従って選択された複数の実行を比較します。

最適化パラメータの完全なリストを以下に示します。

シンボル: EURUSD
期間: H1
期間: 2015.01.03-2017.10.10

EA パラメータの範囲は、次の表のとおりです。

Parameter	Start	Step	Stop Sign	Number of steps
PeriodMA	15	5	200	38
StopPercent	0.1	0.05	1.0	19

最適化の後で、722の変形から成っている最適化の雲が得られました。:

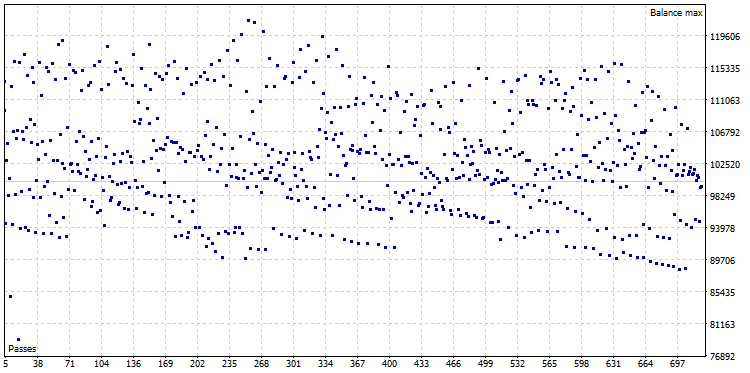
図22. CImpulse の最適化雲, シンボル-EURUSD, 時間枠-H1

最大利益で実行を選択し、残高チャートを表示します。

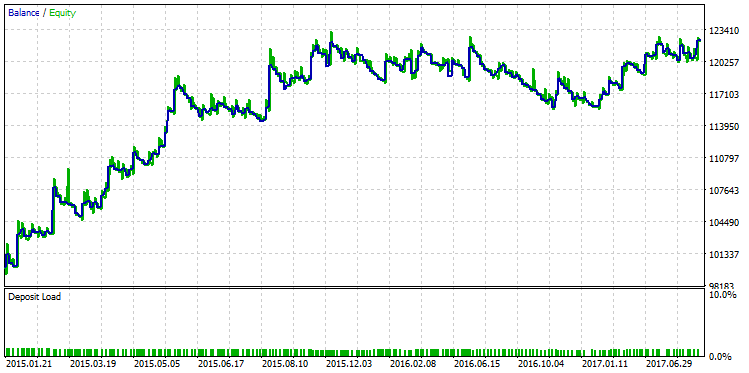
図23. 最大利益の基準に従って選択された戦略のバランスチャート

R-square パラメータに従って最高の実行を見つけます。 XML ファイルで実行される最適化を比較します。コンピュータに Microsoft Excel がインストールされている場合、ファイルは自動的に開かれます。このタスクには、並べ替えとフィルターが含まれます。テーブルのタイトルを選択し、同じ名前のボタン ([ホーム]-[並べ替えとフィルタ]-> [フィルタ]) を押します。これより、列の表示をカスタマイズできます。カスタム最適化基準に従って実行を並べ替えます。

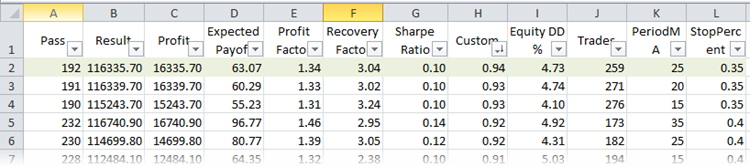
図24. R-２乗でソートされた、Microsoft Excel で実行された最適化

テーブルの最初の行には、サンプル全体の最高の R 乗値があります。上の図では、緑色でマークされています。ストラテジーテスタのこのパラメータセットは、次のようなバランスチャートになります。

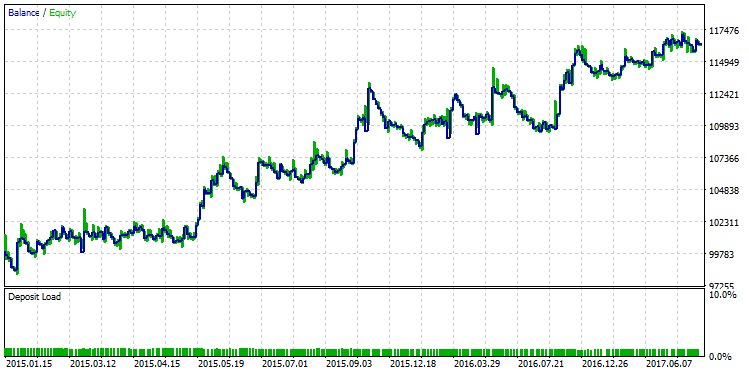
図25. 最大 R ２乗値の基準に従って選択されたストラテジーのバランスチャート

2つのバランスチャートの間の定性的な差は、肉眼で確認できます。最大利益を持つテストの実行は、12月2015で "決裂" が、最大 R ^ 2 と他のバリアントは、その着実な成長を続けた。

多くの場合 R ^ 2 は取引の数によって決まり、通常小さいサンプルの価値を過大評価するかもしれない。この点で、R ２乗は利益係数と相関します。特定の戦略では、プロフィットファクターの高い値と R ^ 2 の高い値が一緒になります。しかし、必ずしもそうではありません。実例として、サンプルからカウンタ例を選択し、R ^ 2 とプロフィットファクターの差を示します。次の図は、2.98 と等しい最高のプロフィットファクター値の1つを持つ戦略実行を示しています。

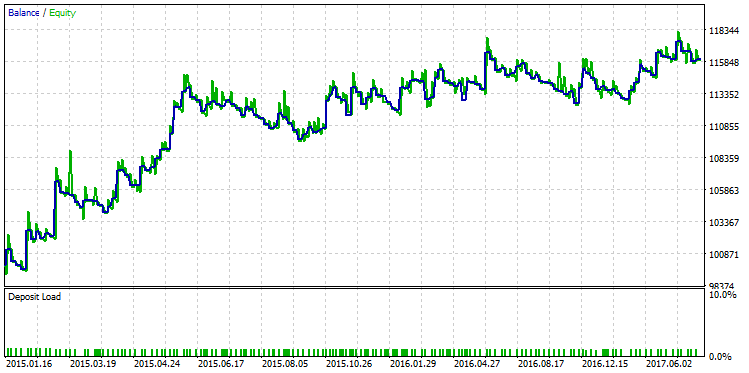
図26. プロフィットファクター2.98 に等しい戦略のテスト実行

このチャートは、戦略が着実な成長を示しているにもかかわらず、戦略バランス曲線の品質は、最大 R 乗のものよりも低いことを示しています。

利点と制限

各統計指標には長所と短所があります。 R２乗はこの点で例外ではありません。以下の表は、これを軽減することができる解決策です。

ドローバック	ソリューション
取引の数によって決まる。少数の取引との価値を過大評価する。	ストラテジーのエクイティに基づいて R ^ 2 値を計算すると、この問題が部分的に解決されます。
戦略効果の既存の指標と、特にプロフィットファクターと戦略の純利益との相関。	相関関係は 100% ではありません。戦略の特徴によっては、R２乗は他のすべてのメトリックと相関したり、弱く相関したりすることはできません。
この計算には複雑な数学的計算が必要です。	このアルゴリズムは、すべての複雑な計算をAlgLib ライブラリを使用して実装しています。
線形プロセスまたは固定ロットによるシステムトレードの推定にのみ適用されます。	資本化システム (資金管理) を使用するトレードシステムには適用しないでください。

ここでは、R^2 を非線形システム (たとえば、動的ロットを持つトレーディング戦略) に適用する問題について詳しく説明します。

すべてのトレーダーの主な目的は、利益の最大化です。こに必要な条件は、さまざまな資本システムの使用です。資本システムは、線形プロセスを非線形の1つに変換します (たとえば、指数プロセスに)。しかし、このような変換は、統計的パラメータのほとんどを無意味にレンダリングします。たとえば、「最終損益」パラメータは、資本化されたシステムでは無意味ですが、時間間隔のテストまたは 100% の戦略パラメータを変更することで、わずかなシフトでも、最終的な結果を数百または何百回も変更できます。

戦略の他のパラメータは、プロフィットファクター、期待ペイオフ、最大利益/損失などのように、その意味も失います。この意味では、R２乗も例外ではありません。バランス曲線平滑性の線形推定に作成された、非線形プロセスの評価が無力になります。したがって、任意の戦略は、線形形式でテストする必要がありますし、選択したオプションに資本システムを追加する必要があります。特別な統計指標 (たとえば GHPR) を使用して非線形システムを評価したり、年間のパーセンテージで利回りを計算したりすることをお勧めします。

結論

トレーディングシステムを評価するための標準的な統計パラメータは、考慮に入れなければならない既知の欠点があります。
MetaTrader5 の標準メトリクスの中で、LR 相関のみが戦略バランス曲線の滑らかさを推定するように設計されています。しかし、その値はしばしば過大です。
R乗は、バランス曲線と戦略の浮動利益曲線の両方の滑らかさを計算するメトリックの1つです。同時に、R-２乗は LR 相関の短所がありません。
AlgLib 数学ライブラリは、R ２乗の計算に使用されます。計算自体には多くの変更があり、例で十分に説明されています。
カスタム最適化基準はEAに組み込まれているため、すべてのEAがこのメトリックスを自動的に計算することはできません。これを行う方法については、CStrategy トレーディングエンジンに R-乗を統合する例で提供されています。
同様の統合メソッドを使用して、カスタム統計の計算に必要な追加データを計算することができます。 R乗の場合、このようなデータは、戦略 (エクイティ) の浮動利益に関するデータです。フローティング・プロフィット・ダイナミクスの記録は、CStrategy トレーディング・エンジンによって行われます。
決定係数は、バランス/エクイティの成長と戦略を選択することができます。この場合、他のパラメータに基づいて選択するプロセスは、そのようなバリアントを見逃すことがあります。
R２乗には、この値を使用するときに考慮する必要があるその他の統計指標と同様に、その欠点があります。

したがって、R２乗法の係数は、MetaTrader5のテストメトリクスの既存のセットにとって重要であると言っても過言ではありません。戦略のバランス曲線の滑らかさを見積もることができます。 R-乗は使いやすいツールです。その値は-1.0 〜 + 1.0 の範囲にバインドされ、戦略バランス (-1.0 に近い値)、トレンド (0.0 に近い値) とポジティブなトレンド (値は + 1.0 にトレンドがある) の負のトレンドについてシグナリングをします。すべてのプロパティ、信頼性とシンプルさのおかげで、R-乗は、収益性の高いトレーディングシステムを構築するために使用することができます。

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/2358

添付されたファイル |

ZIPをダウンロード

UnExpert.zip (114.84 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。