指定した価格変動に基づく極値点の自動検出

イントロダクション

多くの有名なトレード戦略は、さまざまなグラフィカルなパターンに基づいています: ヘッドアンドショルダー、ダブル トップ/ダブル、その他。いくつかの手法では、チャート上のダイバージェンスを分析に利用します。このようなトレードシステムの自動化、プロセスを見つけ、天井 ・ 底のチャートを解釈する必要が生じます。既存のツールは、必ずしも確立された基準による極値を見つけることができません。この記事では、効率的なアルゴリズムとプログラムの検索および処理によって、価格のチャートの極値発見ソリューションを示します。 

1. 極値を検索するための既存のツール

1.1. フラクタルおよび類似ツール

フラクタルは、極値を見つける人気あるツールです。一連の 5 本の足 (図1) の価格の高値と安値を検出します。極値は、強い価格と弱い価格の動きの間に定義されます。時間枠が正しく選択されている場合、相場の状況によって強く影響されますが、良いフラクタルが表示されます。

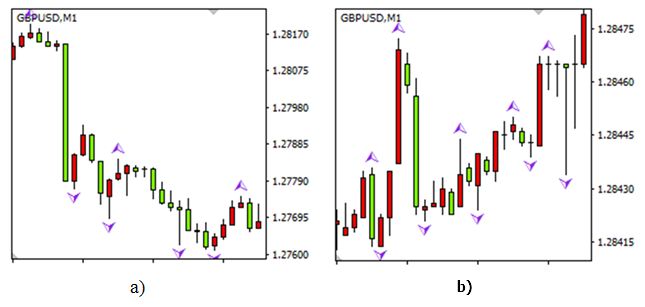
図1。フラクタルを使用した結果: トレンドがあるときは相対サイズで 140 から 420 pipsで(a)、レンジのときは相対的なサイズは50 ピップ以上ありません (b)

2番目のケースでは、極値 (極端な一点から別の価格の変化) の相対的なサイズがわずかなピップを超えることはできません。このような天井 ・ 底は通常見なされません。時間枠を切り替えることはできません。まだ長いレンジの中に定義されています。 

逆の問題がまたあります。すべての極値を定義することはできません。短時間間隔内で天井と底がたくさんあり、相場のボラティリティがある場合は検出されません。フラクタルは、現在の時間枠で 5 つの足で定義した間隔内でのみ 2 極値を検出することができます。したがって、自動トレードにフラクタルにすべて極値を検出させるのは勧めできません。 

「トーマス DeMark のテクニカル分析」の記事で説明したツールのフラクタルと同じ欠点があります。極値を検索するため、大きなスケールを選択すると、その多くは無視されるかもしれません。範囲が小さすぎる場合は、重要でない極端も検出されるかもしれません。いずれの場合も、結果の処理中、 些細な浮き沈みを破棄する特別なアルゴリズムを開発しなければなりません。

1.2. 極値を検索するときに移動平均を使用してください。

移動平均のような平均線を使用すれば、極値の検索を自動化するための基礎として実行可能です。価格が事前に定義されたポイント分だけ平均線から離れた場合、指定された足の数だけサーチされます。このツールは、フラクタルよりも良く、重要でない天井と底を発見します。ただし、まだ高値と安値を検出の問題を解決できていません (図2。

 

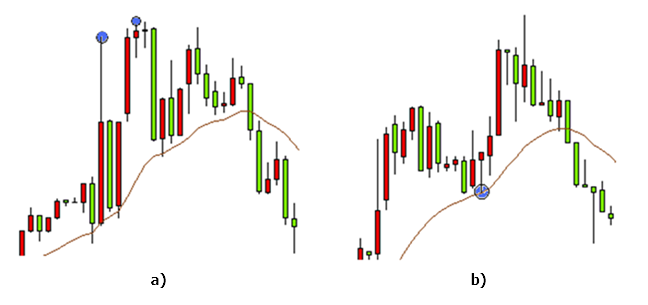
図2。極値を検索するときの平均移動: 2つの極値が定義されて(a)、移動平均の近くにある極値は無視されます (b)

一緒に移動平均とフラクタルを使っても良いかもしれません。移動平均を使用して、フラクタルは、指定した間隔内で検索されている間、些細な極値を整理します。ただし、このアプローチでは、すべて同様の問題を除去しません。常に最適な範囲のパラメータを選択する必要があります。そうしないと、1つの極値だけが2つのうちから定義されます (図2、a)。

また、この特定のメソッドに関連する別の問題があります。ボラティリティが高い間、移動平均期間に応じてそのようなシグナルを無視するかもしれません。この場合(図2 b)、底移動平均の近くと2 つの天井の間が認識されません。相場において非常に珍しいですが、移動平均の正しい選択について問題を提起します。 

したがって、極値だけでなく、上記の検索メソッドに欠点があり、追加のプログラミングソリューションを必要とします。アルゴリズムと同様、極値を検索するときに発生する問題を考えてみましょう。

2. 極値を検索するときに生じるあいまいさの問題

2.1. 天井と底を検索するための変動範囲を選択します。

よくある戦略と手法は、暗黙的または明示的に極値を使用する可能性があります。極値を見つけることは多くの場合、人が検出し、同じチャートで底を強調表示します。よく知られているグラフィカルなパターン-ダブルトップ

 

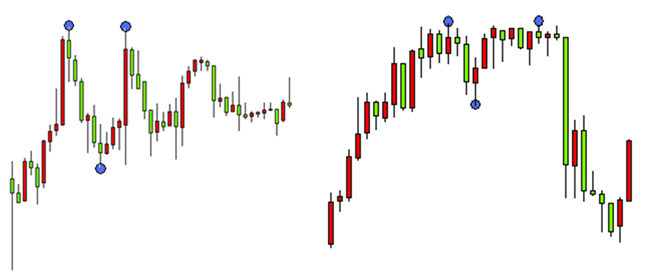
 図3。ダブル トップ パターン

2つのチャート (図3) には、同じパターンがあります。しかし、極値に依存せずに検出します。最初のチャートでは、最初の天井は底に続きます。したがって、天井の間にされていた場合、 ダブル トップ パターンを検出することができません。。このパターンは、普通の極値として定義されます。同じことは、底が２重の上部のパターンが、明確に表示されていない場合に発生します。したがって、唯一の違いは隣接する極値間の変化を比較すると、2 番目の最初のチャートのパターンを検出します。 

別の例を考えてみましょう。以降の極値 (天井 ・ 底) で前のものが上にある場合、上昇トレンドとします。下降トレンドは同様に定義されます。図4に、極値を使ったトレンドの方向を定義します。

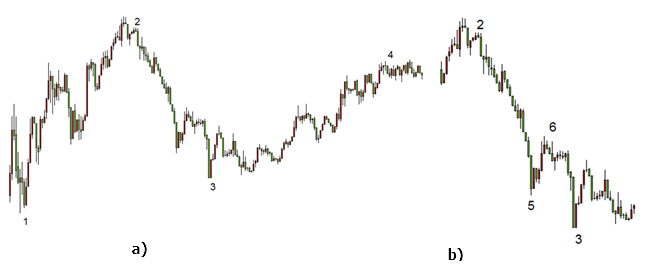
図4。同じチャートにおける正反対の価格の動き: 上昇 (a)、下降 (b)

1 つのチャートには、上昇と下降の両方があります。最初の場合では (図4、a)、極値 1、2、3、4 は明らかに上昇トレンドを示します。ただし、極値 2、5、6 と 3 (図4、b) を使用する場合 は下降トレンドです。したがって、異なる極値を使用して1つの結果を得ることが可能です。これを考慮し、選択範囲が極値の選定に大きくかかわってくるという問題があります。

2.2. 隣接した天井または底の効率的な分離

また、極値を定義する場合に起こる別の問題があります。2 つ以上の天井を分離するために、間に底があるはずです。最初の例 (上の下) の両方に当てはまります。さらに興味深いのが2つ目のケースです。。記載されている方法に従って、極値を見つけた後 (図5, 6) 下のチャートでトレンドを検出できます。 

 

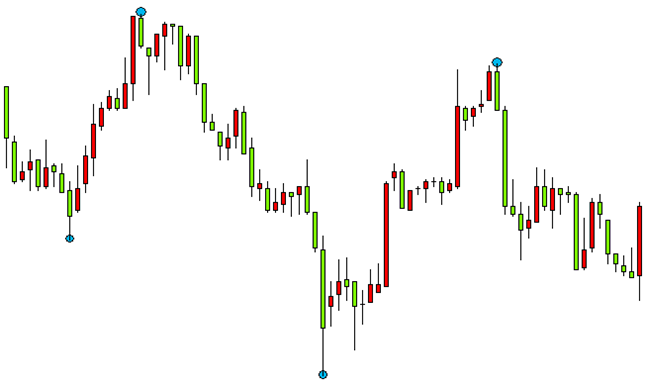
図5。長期的な中に天井 ・ 底を検出 

 

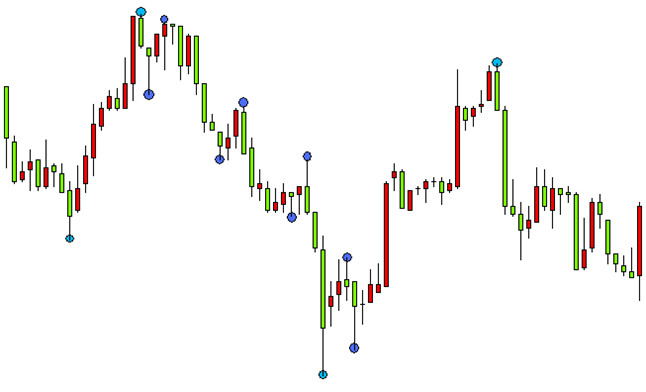
図6。かすかな天井 ・ 底を検出 

底の天井を分離することがない場合 (その逆もしかり)、この戦略はチャートのトレンドを見ることができるが、指定された基準に従って機能することはできません。典型的な例を考えてみましょう。強気トレンド中にある各天井は以前のものよりも高くなります。その間に底がない場合、またはそれが明確に表示されない場合は、最も高いピークだけが極端なポイントとして定義されます。極値は (移動平均) のように平均線を基準にして定義されている場合、2 つの隣接した天井や底を分離するタスクがあります。2 つの天井を分離するためには、間にある極値点使用してください。

したがって、 暗黙的または明示的に極値を使用して、次の仮定を適用します。:価格は天井から底に動き、底から天井に動く。この仮定を使用しない場合、主観的な視点に頼ることになります。

• いずれかが検出されると、
• 最高の天井のみが検出され、
• もしくは、どちらも検出されます。

底も同じです。この仮定では、選択されている可変範囲を使用して、極値の正確な検索のアルゴリズムを開発することが出来ます。

2.3. 最初の極値点の定義

3番目の問題は、価格の変動に関連し、最初の極値点を定義するときに発生します。トレードの戦術や戦略は、最も最近の極値点が古いものよりもより重要です。既に見てきたように、隣接した天井 ・ 底の位置に影響を与える単一の極値を定義します。したがって、現在の時刻から距離で極値を選択した場合、得られた結果により距離履歴データと最新の価格変動による影響をより強く受けます。この問題は、ジグザグを使用して場合顕著です。直近の極値点の場所は最後の価格変動に依存しません。  

ただし、チャートの端から極値を検索するとき、状況が全く異なります。この場合、まず天井または底を見つける必要があります。これ以外はあいまいなものになります。適応した戦略と選択した範囲に依存して、三つの選択肢が与えられます。

• 最も近い天井を見つける
• 最も近い底を見つける
• 最も近い極値 (天井、または底) を見つける

最も近い極値を見つけることを考えてみましょう。特定の変動範囲を選択した後、極値に最も近い場所を正確に定義することができるがおります。ただし、戦略の操作に悪影響を及ぼす可能性があります。極値を見るために、その点の変動範囲で指定された価格変更を定義する必要があります。価格の変動には多少の時間かかり、したがって遅延が生じます。天井や底に判明する実際には、極値として、最後の知られている価格の値を用いることもできなくはありません。 

この場合、他の極値を見つけるために使用される変動範囲の小数部分として、最初の極値を見つけます。たとえば、0.5 の値を選択してみましょう。  

選択した追加の比の値は、最小価格変動を定義します。 最も近い底の最安値を現在の値から極値として定義します。現在の極値と直近の極値の間の変位が特定の値よりも小さい場合、その極値は極値として定義されません。この場合、検出された最初の極値点が天井や底になります。同時に、極値の検出の問題を解決することができます。

140 pips を設定例として、考えてみましょう。追加比率は最初の極値点の検出に使用されます。最初のケースでは0.9 と等しく (図7、)、２番目は0.7です (図7 b)。ここでは、追加比率は、ピップの最初の極値点を検出することで最小価格変動を定義します。最初のケースでは、変位は126 ピップ、2番目は98 ピップです。同じチャートは、両方のケースと見なされます。垂直線は、現在の期間を表し、計算が実行された時間を表します。この期間内で検出された極値はドットとして表示されます。 

 

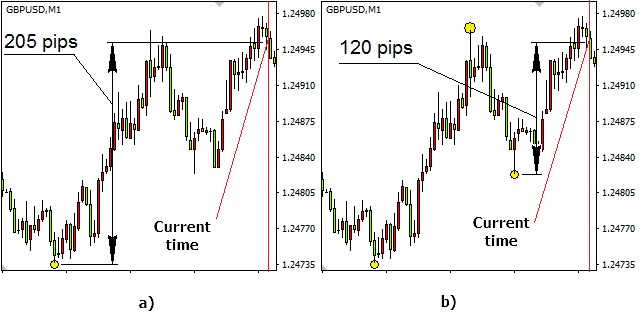
図7。追加比率は極値に影響します。: 最初の極値の検出には205ピップスで0.9 (126 pips)でした。120ピップスにした場合0.7 (98 pips)で、残りの 2 つが指定した変動範囲 (b) によって検出されました。

最初のケースで選択した追加比率は、最小価格変動は 126ピップで、205ピップの範囲でのみを定義されます。2番目の場合、 0.7 (98 pips)に等しく、現在の価格を基準にして 120 pipsの変動で定義されます。2つの極値は 140ピップと等しく、指定した変動範囲に従って検出されます。したがって、一番底と後続の天井の間の価格の変動は、140 pipsを超えています。２番目の底は、検出された天井を基準にしても 140 pipsを超える価格の変動によっても定義されます。

見てもわかるように、追加比率は最初検出された極値の位置に大きな影響を与えます。同様に、タイプにも影響があります。天井または底を同じチャートの最初に検出します。最初の2つの極値 (図7 b) の 2 番目のケースで検出された最初の 1 つは定義されていません。

さらに低率の場合、最初の極値はすぐに定義されます。後者の場合 (図7 b)、追加比率は0.4で、最初に検出された極値は5本足以前で定義 (現在の縮尺で5分) することができます。

3. 極値検索タスクとその実装のアルゴリズムの解法

3.1変動範囲によって極値を求めるアルゴリズム

まず、極値を構築するための価格範囲の選択から始めましょう。明らかに、足のサイズと極値のパラメータは、期間によって大きく異なります。天井/底の有無は、トレンド、時間帯、その他の要因によって影響を受けます。フラクタルや同様のツールのような既存のインジケーターにトレンドが存在するかどうかに関係なく、任意の期間に極値を見つけることができます。天井と底を検索するときに移動平均を使用する場合、移動平均を基準にして極値のサイズは 100 と同様に 2 ポイントを含んでもよいでしょう。日中のトレードで、極値 2 点に注意を払う必要がありますか?おそらく、ないでしょう。長期投資の場合、極値が20 ポイントより小さいかどうかは、時間枠に関係なく、どうでもよいでしょう。

これが「変動範囲」を使う理由でもあります。移動平均は、極値への距離の定義し、その最小値を制限することができる参照ポイントとして使用できます。ただし、移動平均期間は、検出された天井と底を参照して、位置に大きく影響します。

したがって、天井からの変動範囲は、極値に隣接する 2 つのポイントで最安値の変化として定義されます。極値のいくつかが既に定義されている場合、1つ置く必要があります。時間枠およびトレンドに関係なく、極値を定義します。このツールは、デイトレードと長期投資の両方に完全に適したものにする必要があります。

アルゴリズムを考えてみましょう。まず、最初のチャートの変動範囲は 60 のピップ (図8)、2 番目のチャートは 30 のピップ (図9)。同じチャートを使用して極値を視覚的に定義します。また、最初の極値点は既に仮定 (ポイント 1) を検出しています。 

 

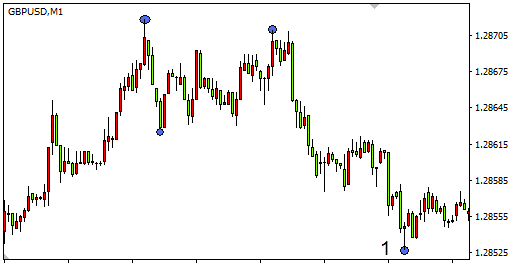
図8。60ピップの変動範囲

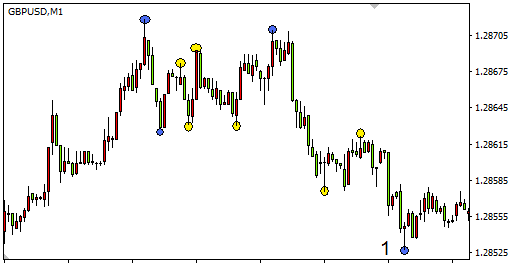
図9。30ピップの変動範囲

1ポイントからチャートの端から極値の検索を行いました最初のケースでは、4 つの極値点は、同じ間隔で検出された 10 の極値があった 2 番目のケースでの表示範囲で発見されました。チャートの指定した部分の変動範囲を増加すると、極値はまったく検出されません。したがって、極値の選択範囲を検索し、相場のボラティリティと期間を考慮すると、現実的になるはずです。ここでは、選択範囲は、足の数です。

上記したすべてのことを覚えておいて、極値の検索に対する解法をご紹介しましょう。”繰り返し”を使います。最初の天井の後、常に底が必要で、その後次々とそれが続きます。2番目の天井が検出されない場合 (チャートが上向きに動かない)、底の位置が再定義され、時系列に遠ざかって移動します。最初の天井の位置は、同じ方法で修正できます。天井と底の両方に同じ足が定義されている場合、 破棄する必要があります。

もちろん、このアプローチには、大量の計算が必要です。極値を検索するときに適用することをお勧めします。高速にプログラムが動作します。計算速度は、検索範囲によっても影響されます。この検索は正当化され、特定の天井および最も最近の価格変動の最大の影響を受け、底を定義することができます。複数の極値を見つける必要があり、ジグザグの使用をお勧めします。

3.2インジケーターの実装 

下記の繰り返しアルゴリズムのコードは、パフォーマンスを向上させる反復数が少ないようにしています。このシンプルさでは、極値検出の品質に重大な欠落は発生しません。メインの受信パラメータ-極値と変動範囲検索の範囲。

input int      bars=500;                 //極値範囲を検索
input double   delta_points=160;         //変動範囲のポイントの天井と底の間の最小距離を定義する
input double   first_extrem=0.9;         //最初の極値を検索するための追加比率
input double   reload_time=5;            //その後インジケーターの値が再計算され、秒単位での時間間隔

プログラム本体には、4 つの極値を定義するために必要な 3 つの入れ子になったループがあります。一番底と関連する極値だけは、プログラムのこの部分で定義されます。最初の天井と関連の極値を定義する、よく似た方法で実装されます。  

double High[],Low[];
datetime Time[];

ArraySetAsSeries(Low,true);
int copied1=CopyLow(Symbol(),0,0,bars+2,Low);
ArraySetAsSeries(High,true);
int copied2=CopyHigh(Symbol(),0,0,bars+2,High);
ArraySetAsSeries(Time,true);
int copied3=CopyTime(Symbol(),0,0,bars+2,Time);

double delta=delta_points*Point();  //極値間の変動範囲

int j, k, l;
int j2、k2、l2;
double  j1,k1,l1;
int min[6];  //底として検出された極値のインデックス
int max[6];  //天井として検出された極値のインデックス

int mag1=bars;
int mag2=bars;
int mag3=bars;
int mag4=bars;

j1=SymbolInfoDouble(Symbol(),SYMBOL_BID)+(1-first_extrem)*delta_points*Point();
//最安値で最初の極値を検索するとき

j2=0; //最初の反復で最後の足から検索を実行する

for(j=0;j<=15;j++) //min[1] - 最初の底を定義する
  {
   min[1]=minimum(j2,bars,j1);
   //指定した間隔内で最も近い底を定義

   j2=min[1]+1;     //すでに検出された底min [1] から次の繰り返しで、検索を行う
   j1=Low[min[1]]+delta;
   //現在の反復で下の価格よりも低くする必要があります

   k1=Low[min[1]];
   //次の高値を定義する底の安値

   k2=min[1];         //底の後の天井が形成された後

   for(k=0;k<=12;k++) //最初の天井のループ
     {
      max[1]=maximum(k2,bars,k1);
      //---指定された間隔に最も近い天井を定義する
      k1=High[max[1]]-delta;
      //次の反復の高値は、現在の反復で検出された天井の高値を超過するべき

      k2=max[1]+1;   //すでに検出された天井max [1] から次の繰り返しで、検索を行う

      l1=High[max[1]];
      //次の底を定義するための極値の高値
      l2=max[1];     //天井が形成された後の底の探索
      for(l=0;l<=10;l++) //2番目の底の決定のループ　min[2]と2番目の天井max[2]
        {
         min[2]=minimum(l2,bars,l1);
         //---指定された間隔内にある最も近い底を定義
         l1=Low[min[2]]+delta;
         //現在の反復で発見された底の安値よりも低い必要があります

         l2=min[2]+1;     //すでに検出された底min[2] から次の繰り返しで、検索を行う
         max[2]=maximum(min[2],bars,Low[min[2]]);
         //指定した間隔に最も近い天井を定義する

         if(max[1]>min[1] && min[1]>0 && min[2]>max[1] && min[2]<max[2] && max[2]<mag4)
           //極値と特殊なケースを整理
           {
            mag1=min[1];   //条件を満たした場合に各反復で検出される極値の場所が保存されます
            mag2=max[1];
            mag3=min[2];
            mag4=max[2];
           }
        }
     }
  }
min[1]=mag1; //極値が定義されて、すべての変数に割り当てられる
max[1]=mag2;
min[2]=mag3;
max[2]=mag4;

最も近い足を見つけ、特定の値以下の安値 (または指定した値を超えた高値)は、かなりシンプルなタスクです。

int minimum(int a,int b,double price0)
//この関数は、指定した間隔で最も近い底を定義します。底は、変動範囲以上で price0 の下に位置します。
  {
   double High[],Low[];
   ArraySetAsSeries(Low,true);
   int copied4=CopyLow(Symbol(),0,0,bars+2,Low);

   int i,e;
   e=bars;
   double pr=price0-delta_points*Point();    //追加の変動範囲が付いている底に置く必要がある価格
   for(i=a;i<=b;i++)                         //指定された範囲内の底の検索、および b パラメータ
     {
      if(Low[i]<pr && Low[i]<Low[i+1])       //価格の成長を開始した後、最も低い底を定義
        {
         e=i;
         break;
        }
     }

   return(e);
  }
int maximum(int a,int b,double price1)
//---この関数は、指定した間隔で最も近い天井を定義します。この底は、変動範囲を超える距離で price1 にある
  {
   double High[],Low[];
   ArraySetAsSeries(High,true);
   int copied5=CopyHigh(Symbol(),0,0,bars+2,High);

   int i,e;
   e=bars;
   double pr1=price1+delta_points*Point();   //上に追加された変動範囲で天井に位置する価格
   for(i=a;i<=b;i++)                         //指定された範囲内の天井の検索、および b パラメータ
     {
      if(High[i]>pr1 && High[i]>High[i+1])   //価格下落を開始した後の、最も近い天井を定義する
        {
         e=i;
         break;
        }
     }
   return(e);
  }

極値を見つけることのタスクは最初の近似でしか解決します。 は、(2 つのお尻の間にある) 天井検出アルゴリズムを使用して指定したアルゴリズム内で最高のものではない可能性があることを検討してください。チャートの端から検索を開始、天井と底の位置する必要がありますを明らかにする最初の端から第２に、第３に、以降極値します。検証・ 天井と下側の位置補正は、独立した関数として作られています。極値位置の明確化の実装は、次のように。

min[1]=check_min(min[1],max[1]); //指定した間隔内で最初の底の位置を修正、確認
max[1]=check_max(max[1],min[2]); //指定した間隔内で最初の天井の位置を修正、確認
min[2]=check_min(min[2],max[2]); //指定された間隔内の２番目の底の位置を修正、確認

 

int check_min (int ,int b)
//指定した間隔内で底の位置を修正するための関数
  {
   double High[],Low[];
   ArraySetAsSeries(Low,true);
   int copied6=CopyLow(Symbol(),0,0,bars+1,Low);
   int i,c;
   c=a;
   for(i=a+1;i<b;i++)                     //範囲で指定されたすべての足が検証されます
     {
      if(Low[i]<Low[a] && Low[i]<Low[c])  //底が見つかった場合
         c=i;                             //下の場所を再定義
     }
   return(c);
  }

int check_max (int ,int b)
//---指定した間隔内で天井の位置を修正するための関数
  {
   double High[],Low[];
   ArraySetAsSeries(High,true);
   int copied7=CopyHigh(Symbol(),0,0,bars+1,High);
   int i,d;
   d=a;
   for(i=(a+1);i<b;i++)                         //範囲で指定されたすべての足が検証されます
     {
      if(High[i]>High[a] && High[i]>High[d])    //上に位置する天井が検出された場合
         d=i;                                   //天井位置が再定義
     }
   return(d);
  }

4 つの極値が見つかった場合のみ、最初の 3 つの位置を明らかにする必要があります。検証・補正関数は、自身の位置と次の極値点の位置を使用して、現在の極値に対して定義されている範囲内で動作します。明確化後、設定した条件を確認できます。

その後、チャートの最後から最初の天井の検索を行い、最初の天井と底の位置が比較されます。実行された計算結果は、チャートの端に近い極値の位置を取得します。

最初の極値点を見つけましょう。追加検索率を導入しました。-たとえば 0.7。同時に、遅延を減少させますが、精度はその場合、減少します。したがって、追加比率は戦略に応じて選択する必要があります。

検出された天井 ・ 底は、矢印として表示されます。矢印は、極値の座標 (時系列と検出された天井/底の高値/安値) を表示します。多くの計算を必要とするので、プログラムはインジケーターの値を再計算するために使用する間隔を設定するエントリーパラメータを備えています。天井・底がない場合、インジケーターは適切なメッセージを生成します。極値のグラフィカル表示の実装は、次のようになります。

if(min[1]<Max[1]) //近くの位置、関連の極値の位置が底の場合
  {
   ObjectDelete(0,"id_1");       //前の段階で作られたラベルを削除
   ObjectDelete(0,"id_2");
   ObjectDelete(0,"id_3");
   ObjectDelete(0,"id_4");
   ObjectDelete(0,"id_5");
   ObjectDelete(0,"id_6");

   ObjectCreate(0,"id_1",OBJ_ARROW_UP,0,Time[min[1]],Low[min[1]]);         //一番の底を強調
   ObjectSetInteger(0,"id_1",OBJPROP_ANCHOR,ANCHOR_TOP);
   //---最初に検出された下のバインディングは時系列と安値上の位置によって実行される

   ObjectCreate(0,"id_2",OBJ_ARROW_DOWN,0,Time[max[1]],High[max[1]]);      //最初の天井を強調
   ObjectSetInteger(0,"id_2",OBJPROP_ANCHOR,ANCHOR_BOTTOM);
   //---検出された天井のバインディング、時系列と高値の位置によって実行されます

   ObjectCreate(0,"id_3",OBJ_ARROW_UP,0,Time[min[2]],Low[min[2]]);         //２番目の底を強調
   ObjectSetInteger(0,"id_3",OBJPROP_ANCHOR,ANCHOR_TOP);
   //---2番目に 検出された下のバインディングは時系列と安値の位置によって実行される
  }

 

if(min[1]>Max[1]) //天井がある場合、関連の極値の位置と同様、その位置が表示されます
  {
   ObjectDelete(0,"id_1");  //前の段階で作られたラベルを削除
   ObjectDelete(0,"id_2");
   ObjectDelete(0,"id_3");
   ObjectDelete(0,"id_4");
   ObjectDelete(0,"id_5");
   ObjectDelete(0,"id_6");

   ObjectCreate(0,"id_4",OBJ_ARROW_DOWN,0,Time[Max[1]],High[Max[1]]);         //最初の天井を定義
   ObjectSetInteger(0,"id_4",OBJPROP_ANCHOR,ANCHOR_BOTTOM);
   //最初に検出された天井のバインディングは時系列と高値の位置によって実行される

   ObjectCreate(0,"id_5",OBJ_ARROW_UP,0,Time[Min[1]],Low[Min[1]]);            //一番底を強調
   ObjectSetInteger(0,"id_5",OBJPROP_ANCHOR,ANCHOR_TOP);
   //時系列と安値の位置によって検出され、バインディングが実行されます

   ObjectCreate(0,"id_6",OBJ_ARROW_DOWN,0,Time[Max[2]],High[Max[2]]);         //2 番目の天井を定義する
   ObjectSetInteger(0,"id_6",OBJPROP_ANCHOR,ANCHOR_BOTTOM);
   //2番目の検出された天井のバインディングは時系列と高値の位置によって実行される
  }

if(min[1]==Max[1]) Alert("Within the specified range, ",bars," no bars and extreme points found");
//適切なメッセージが表示されます

インジケーターを初期化解除するときは、天井と底を定義するオブジェクトが削除されます。 

指定されたアルゴリズムは、チャート (図10) にハイライトされ、カスタムインジケーターの開発に使用されています。

 

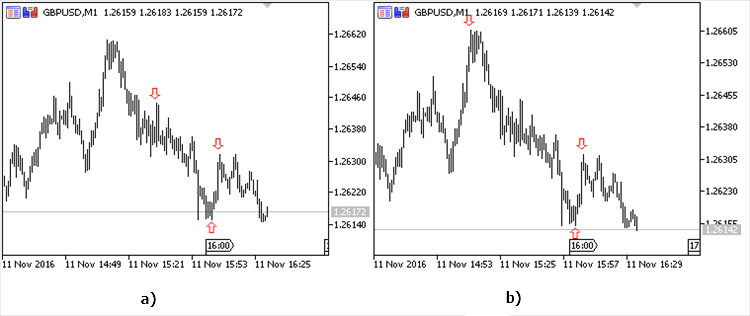
図10。インジケーターの操作の結果: 変動範囲 120 のピップ (a)、変動範囲 160 ピップ (b)

得られた結果は、変動の範囲によって定義されます。120ピップの値 (図10、a)は、極値がかなりお互いに近い存在で、範囲の大きさは重要です。160ピップの値および多くの(図10、b) 極値が十分あります。検索範囲を選択するとき、注意する必要があります。レンジ相場の場合、最適選択範囲が自動的に天井 ・ 底の弱い動きを見つけ、大きい時間間隔で区切られた (スキップ) 極値を整理するをことができます。

3.3MACD のヒストグラムと価格の間の分岐戦略を実装するEA

指定されたアルゴリズムで、さまざまな戦略を実装できます。Scale_factor インジケーターの操作結果は、ヘッドアンドショルダー、ダブルトップ、ダブルボトム等のグラフィカル モデルの操作に適しています。価格チャートやインジケーターの天井・底の相違の戦略で使用できます。1つ例として、MACDのヒストグラムのダイバージェンスのEAを作りましょう。この戦略は詳細に研究されています。 (アレキサンダーエルダーの"Trading for a Living"を参照)

その戦略によると、価格が上向きになり新しい天井になったにも関わらず、MACDの天井が低くなったら売りシグナルです。 

価格が下向きになり新しい底が形成され、MACDの底が高くなったら買いシグナルです。 

このアルゴリズムを実装するEAには、最新の変更に従って、変位範囲で天井と底を検出します。 

受信パラメータ-極値と検索の範囲。最後の2つの天井におけるダイバージェンスの最小価格を設定する必要があります。リスクとその他の比率は、資産通貨の各トレードに設定されています。Guard_points パラメータは、ロングポジションを開く場合に、最寄りの下の安値を基準にして追加のストップロスを定義します。したがって、ストップロスは、ショートポジションを開くときには上向きに移動します。また、トレードするときに検出された極値のパラメータを推測することが可能です (show_info = 1)。

input int      bars=500;                 //極値の検索範囲
input double   delta_points=160;         //変動範囲のポイントの天井と底の間の最小距離を定義する
input double   first_extrem=0.9;         //最初の極値を検索するための追加比率
input int      orderr_size=10;           //各トレード当たりのリスク
input double   MACD_t=0.00002;           //MACDヒストグラムの最小バラツキ
input double   trend=100;                //最も近い 2 つの天井/底の最小価格偏差
input double   guard_points=30;          //ストップロスの移動
input int      time=0;                   //秒単位での遅延時間
input int      show_info=0;              //極値に関するデータを表示

各ティックあたり計算できます。トレードの場合も同じです。この戦略は、遅延があってもうまく動作します。定義する主なパラメータと、 極値探索に渡す必要があります。プログラムの最初の部分では、最初が底の場合、極値を見つけることができます。その後、その状態は明らかになります。コードの2 番目の部分は、天井が最初にある場合に極値を見つけます。天井・底のパラメータを次の手順で明らかにしましょう。

void OnTick()
  {
   Sleep(1000*time);                //遅延を導入

   double High[],Low[];

   ArraySetAsSeries(Low,true);
   int copied1=CopyLow(Symbol(),0,0,bars+2,Low);
   ArraySetAsSeries(High,true);
   int copied2=CopyHigh(Symbol(),0,0,bars+2,High);
   ArraySetAsSeries(Time,true);
   int copied3=CopyTime(Symbol(),0,0,bars+2,Time);

   MqlTick last_tick;
   double Bid=last_tick.bid;
   double Ask=last_tick.ask;

   double delta=delta_points*Point();  //固定期間の変動値
   double trendd=trend*Point();        //最も近い2つの天井/底の最小価格偏差
   double guard=guard_points*Point();  //ストップロスの移動


   int j,k,l;
   int j2,k2,l2;
   double  j1,k1,l1;
   int min[6];  //最初の検出の極値が下の場合の底の配列を定義する
   int max[6];  //配列を定義する天井が検出された最初の極値が下の場合、値は足に対応して検出された極値のインデックス
   int Min[6];  //最初の検出の極値が天井の場合の底の配列を定義、値は足に対応検出された極端なインデックス
   int Max[6];  //配列を定義する天井が検出された最初の極値が天井の場合、値は足に対応して検出された極値のインデックス

   int mag1=bars;
   int mag2=bars;
   int mag3=bars;
   int mag4=bars;

   j1=SymbolInfoDouble(Symbol(),SYMBOL_BID)+(1-first_extrem)*delta_points*Point();
   //最初の極値を探索するとき、追加比率が最小価格を定義します。

   j2=0;                         //最初の反復で、最後の履歴足から検索を実行
   for(j=0;j<=15;j++)            //ループmin[1] - 最初の底を定義する
     {
      min[1]=minimum(j2,bars,j1);
      //指定した間隔内で最も近い底を定義

      j2=min[1]+1;              //すでに検出された底min [1] から次の繰り返しで、検索を行う
      j1=Low[min[1]]+delta;
      //---安値は現在の反復で下の安値よりも低くする必要があります
      k1=Low[min[1]];
      //次の極値の探索が高値を定義するとき、底の安値

      k2=min[1];                 //底min[1] から底が検出された後

      for(k=0;k<=12;k++)         //ループの最初の天井 - max[1] の定義
        {
         max[1]=maximum(k2,bars,k1);
         //---指定された間隔に最も近い天井を定義する
         k1=High[max[1]]-delta;
         //---次の反復の高値は、現在の反復で検出された天井の高値を超過するべき
         k2=max[1]+1;            //すでに検出された天井max[1] から次の繰り返しで、検索を行う
         l1=High[max[1]];
         //---次の底を定義するための極値の高値
         l2=max[1];              //底の検索位置の天井が検出された天井max[1] から実行された後
         for(l=0;l<=10;l++)      //2番目の底を定義するループ
           {
            min[2]=minimum(l2,bars,l1);
            //---指定された間隔内にある最も近い底を定義
            l1=Low[min[2]]+delta;
            //後続の繰り返しで検出される底の安値は、現在の反復で発見される安値よりも低い必要があります

            l2=min[2]+1;         //すでに検出された底min[2] から次の繰り返しで、検索を行う

            max[2]=maximum(min[2],bars,Low[min[2]]);
            //指定した間隔に最も近い天井を定義する
            if(max[1]>min[1] && min[1]>0 && min[2]>max[1] && min[2]<max[2] && max[2]<mag4)
              //---極値と特殊なケースを整理
              {
               mag1=min[1];      //条件を満たした場合、各反復で検出される極値の場所が保存されます
               mag2=max[1];
               mag3=min[2];
               mag4=max[2];

              }
           }
        }

     }

//---極値が定義され、すべての変数に割り当てられる
   min[1]=mag1;
   max[1]=mag2;
   min[2]=mag3;
   max[2]=mag4;
//---指定された間隔内の極値の位置を修正

   min[1]=check_min(min[1],max[1]);  
   max[1]=check_max(max[1],min[2]);
   min[2]=check_min(min[2],max[2]);

//---------------------------------------------------------------------------------------------------------------
   mag1=bars;
   mag2=bars;
   mag3=bars;
   mag4=bars;

   j1=SymbolInfoDouble(Symbol(),SYMBOL_BID)-(1-first_extrem)*delta_points*Point();
   //最初の極値を検索するとき、追加比率の最初の天井が配置される上に最高値を定義します

   j2=0;  //最初の反復で最後の足から検索を実行

   for(j=0;j<=15;j++)      //ループの最初の天井 - max[1] の定義
     {
      Max[1]=maximum(j2,bars,j1);
      //指定した間隔内で最も近い天井を決定

      j1=High[Max[1]]-delta;
      //次の反復の高値は、現在の反復で検出された天井の高値を超過するべき
      j2=Max[1]+1;         //次の反復ですでに検出された天井max[1] から検索を実行する

      k1=High[Max[1]];
      //次の底を定義するための極値の高値

      k2=Max[1];           //天井max[1]が形成された後の底の探索

      for(k=0;k<=12;k++)   //ループの最初の天井 - min[1]の定義
        {
         Min[1]=minimum(k2,bars,k1);
         //---指定された間隔内にある最も近い底を定義
         k1=Low[Min[1]]+delta;
         //後続の繰り返しの検出の底の安値は、現在の反復の安値よりも低い必要があります
         k2=Min[1]+1;      //すでに検出された底min[1] から次の繰り返しで、検索を行う
         l1=Low[Min[1]];
         //---底の次の極値定義上には天井があり、高値を捜すとき安値
         l2=Min[1];        //天井の検索位置検出の底min[1] から下が実行された後
         for(l=0;l<=10;l++)//ループの 2 番目の天井 - Max[2] と２番目の底min[2] を定義する
           {
            Max[2]=maximum(l2,bars,l1);
            //指定した間隔内で最も近い天井を定義

            l1=High[Max[2]]-delta;
            //次の反復の高値は、現在の反復で検出された天井の高値を超過するべき
            l2=Max[2]+1;  //次の反復で,すでに検出された天井Max[2] から検索を実行する

            Min[2]=minimum(Max[2],bars,High[Max[2]]);
            //---指定された間隔内にある最も近い底を定義
            if(Max[2]>Min[1] && Min[1]>Max[1] && Max[1]>0 && Max[2]<Min[2] && Min[2]<bars)
              //---一致の極値と特殊なケースを整理
              {
               mag1=Max[1];  //条件を満たした場合、各反復で検出される極値の場所が保存されます
               mag2=Min[1];
               mag3=Max[2];
               mag4=Min[2];
              }
           }
        }
     }
   Max[1]=mag1;  //極値が定義されて、すべての変数に割り当てられる
   Min[1]=mag2;
   Max[2]=mag3;
   Min[2]=mag4;

   Max[1]=check_max(Max[1],Min[1]);  //指定された間隔内にある極値点の位置を修正
   Min[1]=check_min(Min[1],Max[2]);
   Max[2]=check_max(Max[2],Min[2]);

さらに、最初渡された天井または最初に検出した底のいずれかを使用します。しかし、天井・底の取得だけでなく最寄の極値を使用するより合理的です。 

どちらの場合も、極値の位置に対応するインジケーターの値と同様に、ロットサイズが計算されます。正しい極値の検出とオープンポジションの条件が確認されます。

極値価格と MACD のヒストグラムに相違があり、エントリーによって設定された値未満ではない、適切なポジションが開かれます。ダイバージェンスは逆に検知する必要があります。

   double lot_buy=NormalizeDouble(0.1*orderr_size/(NormalizeDouble(((SymbolInfoDouble(Symbol(),SYMBOL_BID)-Low[min[1]]+guard)*10000),0)+0.00001),2);
   //買う際にロットを計算

   double lot_sell=NormalizeDouble(0.1*orderr_size/(NormalizeDouble(((High[Max[1]]-SymbolInfoDouble(Symbol(),SYMBOL_ASK)+guard)*10000),0)+0.00001),2);
   //---売りの際にロットの計算
   int index_handle=iMACD(NULL,PERIOD_CURRENT,12,26,9,PRICE_MEDIAN);
   double MACD_all[];
   ArraySetAsSeries(MACD_all,true);
   int copied4=CopyBuffer(index_handle,0,0,bars+2,MACD_all);
   double index_min1=MACD_all[min[1]];
   double index_min2=MACD_all[min[2]];
   //---最初の極値が底の場合、極値に対応するインジケーター値を計算
   double index_Max1=MACD_all[Max[1]];
   double index_Max2=MACD_all[Max[2]];
   //最初の極値が天井の場合、極値に対応するインジケーター値を計算
   bool flag_1=(min[2]<bars && min[2]!=0 && max[1]<bars && max[1]!=0 && max[2]<bars && max[2]!=0); //適切な極値条件の状態をチェック
   bool flag_2=(Min[1]<bars && Min[1]!=0 && Max[2]<bars && Max[2]!=0  && Min[2]<bars && Min[2]!=0);
   bool trend_down=(Low[min[1]]<(Low[min[2]]-trendd));
   bool trend_up=(High[Max[1]]>(High[Max[2]]+trendd));
   //---極値の差は設定値より小さくならない
   openedorder=PositionSelect(Symbol());  //オープンポジションがないことを確認してください
   if(min[1]<Max[1] && trend_down && flag_1 && !openedorder && (index_min1>(index_min2+macd_t)))
      //買いトレードを開いた最初の極値点が底の場合
      //極値の MACD の値の差がMACD_t の値よりも小さい
      //トレードが開かれ、インジケーターは、極値に基づいて計算されます
     {
      if(show_info==1) Alert("For the last",bars," bars, the distance in bars to the nearest bottom and extreme points",min[1]," ",max[1]," ",min[2]);
      //---極値にデータを表示
      MqlTradeResult result={0};
      MqlTradeRequest request={0};
      request.action=TRADE_ACTION_DEAL;
      request.magic=123456;
      request.symbol=_Symbol;
      request.volume=lot_buy;
      request.price=SymbolInfoDouble(Symbol(),SYMBOL_ASK);
      request.sl=Low[min[1]]-guard;
      request.tp=MathAbs(2*SymbolInfoDouble(Symbol(),SYMBOL_BID)-Low[min[1]])+guard;
      request.type=ORDER_TYPE_BUY;
      request.deviation=50;
      request.type_filling=ORDER_FILLING_FOK;

      OrderSend(request,result);
     }

   if(min[1]>Max[1] && trend_up && flag_2 && !openedorder && (index_Max1<(index_Max2-macd_t)))
      //売りトレードを開いた最初の極値点が天井の場合
      //極値の MACD の値の差がMACD_t の値よりも小さい
      //価格の逆方向の運動の場合、インジケーターは、極値に基づいて計算されます
     {
      if(show_info==1) Alert("For the last ",bars," bars, the distance in bars to the nearest peak and extreme points",Max[1]," ",Min[1]," ",Max[2]);
      //---極値にデータを表示
      MqlTradeResult result={0};
      MqlTradeRequest request={0};
      request.action=TRADE_ACTION_DEAL;
      request.magic=123456;
      request.symbol=_Symbol;
      request.volume=lot_sell;
      request.price=SymbolInfoDouble(Symbol(),SYMBOL_BID);
      request.sl=High[Max[1]]+guard;
      request.tp=MathAbs(High[Max[1]]-2*(High[Max[1]]-SymbolInfoDouble(Symbol(),SYMBOL_ASK)))-guard;
      request.type=ORDER_TYPE_SELL;
      request.deviation=50;
      request.type_filling=ORDER_FILLING_FOK;

      OrderSend(request,result);
     }

ポジションを開くときに、相場が動いているときと動いていないとき両方の現実的な目標を確立し、最も近い底の位置で設定されています。どちらの場合も、利益を取る現在の価格の値を基準にしてストップロスが対称に設定されています。デイトレードの場合範囲は狭く、長期的な投資の場合、大きく範囲を設定することをお勧めします。

EAの操作 (図11) の例を考えてみましょう。主な適用パラメータ: 変動範囲-160ピップ、最小 MACD ヒストグラムダイバージェンス-0,0004; 最安値のダイバージェンス、2 最も近い天井/底-120 のピップおよび追加比率-0.9。 

図11。EAの実行結果

まず、EAは最後の3つの極値を検索します。瞬間的にEAは1つの天井と 2 つの底 (矢印としてマーク) を検出します。インジケーターと異なり、EAは極値を強調表示しません。ただし、show_info によってトレードを開くとき位置データを取得できます。

最も近い底価格のダイバージェンスは、指定した値148ピップを超えています。MACDヒストグラムのダイバージェンスも指定した値を超え、0.00062です。最後2つの底によって検出された、追加比率 (150ピップ) によって定義された点でロングポジションを開きます。追加比率を使用している場合、ポジションがすでに開かれている可能性があります。

EAのテスト結果 (図12) MACD_t とトレンドのパラメータの最大の効果は、テスト中に明らかにされています。パラメータの値が大きいほど収益の額が大きいパーセンテージの値でトレードされています。しかし、収益性の増加は総トレード数の減少と同時に起こる。 

たとえば、MACD_t = 0.0006 でtrend=160の場合、56%のトレードが利益になります。MACD_t = 0.0004 でトレンド = 120の場合、84のトレードが収益性の高くなります。

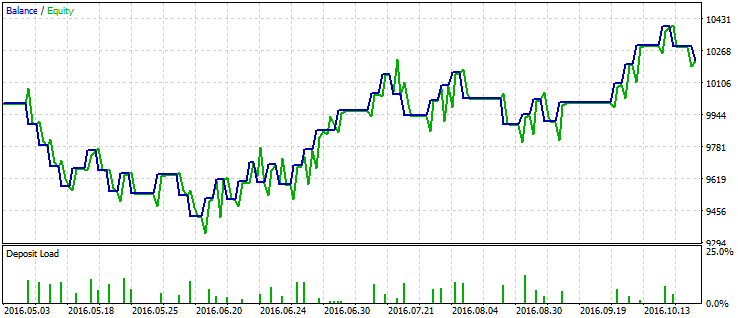
 図12。EA のテスト結果

戦略を最適化するとき、MACD_t とトレンドのパラメータを正しく設定することが重要です。変動範囲とトレードパラメータにも影響します。可変範囲は、検出された極値とトレードの数を定義します。追加比率は、エントリー時にテイクプロフィットとストップロスを厳密に決定づけます。

この戦略だけでなく、上記提案ツールを使用した場合にのみ、可能な限り正常に動作する可能性があります。それ以外の場合、現在の価格から200ポイント離れた場所にテイクプロフィットとストップロスを配置するトレードを行う可能性があります。この場合、そのような極値の重要性は非常に低いです。他の多くのケースは、従来のツールでは細かい極値が多すぎ、天井や底が検出されません。また、時系列の最後で極値を定義する際に問題が生じます。

結論

この記事におけるソリューションは、価格のチャートに極値を正確に定義することが可能です。得られた結果は、グラフィカルパターンを定義するとき、インジケーターを使用するとき、トレード戦略を実装する場合の両方に適用されます。開発したツールは、よく知られているソリューションに対して数々の利点があります。トレンドまたはレンジ相場の状況に関係なく、重要な極値のみが定義されます。定義済みの値を超える極値のみが検出されます。他の天井 ・ 底は無視されます。極値の探索はチャートの終わりから実行され、直近の価格変動に基づいて出力されます。これらの結果は、選択した期間による影響を強く受けません。指定された価格の変化によってのみ決定されます。