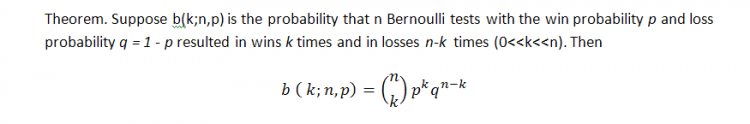Irrtümer, Teil 2. Statistiken sind eine Pseudo-Wissenschaft, oder eine Chronik des Nase Eintauchen in Brot und Butter
Einführung
Der erste Teil der Überschrift ist ein Zitat aus dem Beitrag von SergNF datiert aus den 17. April 2008 14:04, https://www.mql5.com/ru/forum/108164. Nun, sogar strenge Mathematik verwandelt sich in eine Pseudo-Wissenschaft, wenn sie von einem "Forscher" verwendet wird, der entscheidet mit attraktiven Formeln ohne praktische Anwendung zu spielen.
Die Skepsis des zitierten Autors, auch mit drei "Lächeln" abgemildert, ist offensichtlich. Der Grund dafür ist ziemlich klar: Die zahlreichen Versuche statistische Methoden auf die objektive Realität anzuwenden, das heißt auf Finanzreihen, stürzen ab wenn sie auf die Nichtstationarität von Verfahren treffen, "Fat Tails" begleitender Wahrscheinlichkeitsverteilung und unzureichendes Volumen an Finanzdaten. Keines der bestehenden Marktmodelle kann als ausreichend adäquat zur Wirklichkeit anerkannt werden. Und auch wenn wir es schaffen einige statistische Regelmäßigkeiten zu finden, scheinen die Ergebnisse ihrer Nutzung unverhältnismäßig zu den in ihre Bildung investierten Mühen.
In dieser Veröffentlichung werde ich versuchen nicht auf die Finanzreihe als solches zu beziehen, sondern auf ihre subjektive Darstellung - in diesem Fall, auf die Art, wie ein Trader versucht die Reihen zu halftern, d.h. auf das Handelssystem. Die Bildung von statistischen Regelmäßigkeiten des Handelsergebnis-Verfahren ist eine ziemlich fesselnde Aufgabe. In einigen Fällen können durchaus wahre Schlüsse über das Modell dieses Verfahren gezogen werden, und diese können an dem Handelssystem angewandt werden.
Ich entschuldige mich bei den Lesern, die weniger mit Mathematik zu tun haben, für die Kompliziertheit der Exposition, aber offensichtlich ist es eine unvermeidliche Folge der Artikelinhalte. Es scheint, dass das Versprechen am Ende meines vorherigen Artikels, nicht erfüllt ist. Fangen wir also mit unserer Suche an
In dem Artikel schafften wir es ein künstliches Beispiel aufzubauen, das uns anschaulich eine rentable Strategie mit der Money-Management (MM) Regel "Lot=0.1" zeigt, die mit einem geometrischen MM ins Verlieren dreht. Eine sehr regelmäßige Abfolge von Gewinntrades und Verlusttrades wurde dort verwendet, die man wohl kaum in der Realität antrifft: P L P L P L P L P L P L ... Die erste Frage ist: Warum analysiere ich genau solch eine "regelmäßige" Reihenfolge?
Verlustreihen: Kurze Übersicht
Der Grund ist einfach, er ist in dem Artikel Mein erster "Gral" angegeben:
Gleichzeitig können wir nie vorhersagen, wie genau verlierende Ordern unter den rentablen verteilt sein werden. Diese Verteilung ist überwiegend zufälliger Natur.
P P P L P P P L P P P L P P P L P P P L P P P L P P P L ...
B. Unten ist ein Beispiel der sehr wahrscheinlichen Situation von nicht einheitlicher Verteilung von rentablen und verlierenden Trades während realem Trading:
P P P P P P P P P P P P P P P L L L L P P P L P P P L ...
Eine Reihe von 5 aufeinander folgenden Verlusten wird oben gezeigt, obwohl solche Reihen sogar länger sein können. Sie sollten beachten, dass, in diesem Fall, das Verhältnis zwischen rentablen und verlierenden Ordern als 3:1 gehalten wird.
Somit ist der "regelmäßige" Wechsel von rentablen und Verlusttrades ideal in Bezug auf minimale Rückgänge (und maximalen Erholungsfaktor). Und wenn, wie in dem vorherigen Artikel, wir es schaffen zu zeigen, dass auch in diesem idealen Fall (wenn rentable und Verlusttrades sich abwechseln) das System mit einem geometrischen MM in ein verlierendes dreht, mit den gleichen Werten der mathematischen Erwartung an rentablen und verlierenden Trades, dann ist es mit Sicherheit noch schlechter, mit einer nicht gleichmäßigen Verteilung der Handelsergebnisse.
Hinweis: Angenommen das Verhältnis zwischen rentablen und verlierenden Trades ist gleich 14:9. Wie müssen wir die Trades in Reihen verteilen, um minimalen Rückgang zu haben? Dies ist keine einfache Sache, auch wenn wir die MM Regel "Lot=0.1" berücksichtigen und versuchen zu beweisen, dass die Reihe optimal sein wird. Es ist fast klar, dass die Verluste "gleichmäßig" in Reihen verteilt sein müssen - sagen wir, auf diese Weise:
P L P L P P L P P L P P L P L P L P P L P P L...
Dies ist eine "elementare Reihe", bestehend aus 23 Trades, 14 von ihnen sind rentabel. Danach wiederholt sich die Reihe. Es ist klar, dass ein solche Reihe in beiden MM Arten viel niedrigere Rückgänge hat als, zum Beispiel, diese:
P P P P P P P P P P P P P P L L L L L L L L L…
Es ist besonders anschaulich mit geometrischem MM (die Gründe wurde in dem Artikel) erklärt. Allerdings ist auch eine solche Serie an Verlusten ("Verlust-Cluster") nicht begrenzt. Um dies zu verstehen, frischen wir die Grundlage der Wahrscheinlichkeitstheorie auf. Aber zuerst bestimmen wir einige Begriffe.
Terminologie
Dieser Artikel enthält viele Begriffe, die mit Bernoulli Reihen und Histogrammen verbunden sind, die verschiedene Wahrscheinlichkeitsverteilungen visualisieren. Um diese nicht zu vermischen, lassen Sie uns die Terminologie bestimmen. Also:
- Eine vollständige Reihe von Trades wird hier einfach eine Reihe genannt. Dieser Begriff bezieht sich sowohl aus die erhaltene Reihe während der Verarbeitung der Ergebnisse eines einzelnen realen Tests, als auch auf die synthetisch erhaltene Reihe während der Erzeugung einer entsprechenden Bernoulli Reihe. Wenn die Reihenlänge angegeben werden muss, werden wir sie auf diese Art bezeichnen: 3457-Reihe (eine aus 3457 Trades bestehende Reihe).
- Eine Abfolge von aufeinanderfolgenden Trades des gleichen Zeichens innerhalb einer Reihe (rentable oder verlierende Trades, oder "Erfolge" oder "Ausfälle") werden hier ein Cluster genannt. muss die Länge angegeben werden, wird sie, Zum Beispiel, ein 7-Cluster genannt (ein Cluster mit einer Länge von 7).
- Eine Vielzahl an Reihen (in diesem Kontext werden wir in der Hauptsache über synthetische Reihen sprechen) wird ein Array an Reihen genannt werden. Die Anzahl kann auch bezeichnet werden: 65000-Array aus 5049-Reihen (65000 Bernoulli Reihen, jede 5049 Trades lang).
- Wenn Histogramme aufgebaut werden, müssen wir manchmal den nicht nur zu bestimmten Reihen, sondern auch zu dem ganzen Array an Reihen gehörenden Cluster berücksichtigen, Der Histogramm-Name entspricht dem Parameter Verteilung, von dem er visualisiert wird. Statt zu schreiben "Histogramm der Verteilung von Clustern mit der Länge 4 in einem Array aus 5000 Reihen, jede 3174 Trades lang" werden wir es so bezeichnen: "4-Cluster in 5000-Array aus 3174-Reihen».
Bernoulli Schema: Die Grundlagen
Sehr oft können viele praktische Aufgaben, in denen eine Folge von Ereignissen berücksichtigt wird, auf das folgende Schema reduziert werden:
- Jedes Ereignis hat nur zwei Ergebnisse - "Erfolg" und "Ausfall" ("Gewinn" und "Verlust"). Die Wahrscheinlichkeit von "Erfolg" ist p, und die von "Ausfall" ist q = 1-p.
- Die Wahrscheinlichkeit des Ereignis-Ergebnisses hängt nicht von der Historie von Ereignissen ab, die ihm vorausgingen.
Dies nennt sich Bernoulli Schema (oder Bernoulli Probe). Unsere farbig codierte Abfolge könnte als Bernoulli Schema betrachtet werden, wenn wir in dem zweiten oben angegebenen Kriterium sicher wären.
Der Autor denkt, dies ist für die meisten Handelssysteme wahr. Hier sind einige indirekte Beweise:
- Alle Informationen über ein System Z-Konto, nach der Meinung derjenigen, die versucht haben es für MM-Optimierung anzuwenden, erscheint nutzlos, wenn versucht wird die Wahrscheinlichkeit eines bestimmten Trade zu berechnen – auch wenn die Gewinnwahrscheinlichkeit größer als 90% ist,
- Die Effizienz verschiedener Martingale-Schemen, allem Anschein nach, ist auch gleich Null oder sogar negativ, während es zu unzulässigen Rückgängen führt.
Aus diesem Grund wäre es logisch, anzunehmen, dass für die Mehrheit von Handelssystemen eine Reihe ihrer aufeinanderfolgenden Trades den Kriterien des Bernoulli Schemas entspricht. Eine solche Hypothese führt zu sehr tiefen Konsequenzen.
Die klassische Formel für die Wahrscheinlich von k Gewinnen (wir können hier übrigens auch auf Verluste verweisen!) in der Reihe von n Tests in dem Bernoulli Schema ist die folgende (die Wahrscheinlichkeit eines Gewinns ist gleich p):
Diese Formel zeigt einige integrale Parameter der Reihen, Anzahl an Gewinnen, erzählt aber nichts darüber, wie gleichmäßig diese Gewinne verteilt sind, d.h. wir wisse nichts über die mögliche Länge von Cluster. Die Suche nach der Länge von wahrscheinlichen Verlust-Cluster i Bernoulli Reihen ist eine viel schwierigere Aufgabe, ihre Lösung wird von Feller [1] beschrieben. Und sind Formeln für die mathematische Erwartung einer Testreihenlänge und ihre Verteilung mit den festgelegten Parametern p (Wahrscheinlichkeit eines Gewinn), q (Wahrscheinlichkeit eines Verlusts), r (gewinnende Cluster-Länge) - vorausgesetzt wir haben eine Reihe von Tests, passend zu dem Bernoulli Schema: math. Erwartung und Verteilung der Rückkehrzeit für die Gewinnreihe von r Länge sind entsprechend gleich
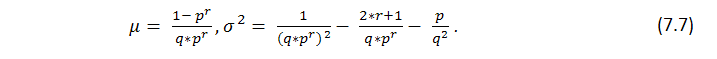
Aus dem Satz folgt, dass mit großem n die Anzahl ![]() von r in n Tests erhaltenen Reihen, annähernd eine Normalverteilung hat, d.h. mit festem
von r in n Tests erhaltenen Reihen, annähernd eine Normalverteilung hat, d.h. mit festem ![]() die Wahrscheinlichkeit der Ungleichung
die Wahrscheinlichkeit der Ungleichung
neigt zu
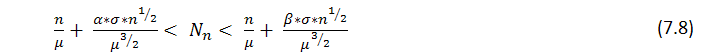
Die Tabelle enthält mathematische Erwartungen für eine Anzahl typischer Rückkehrzeiten.
| Reihenlänge, r | p = 0.6 | p=0.5 (Münze) | p=1/6 (Würfel) |
|---|---|---|---|
| 5 | 30.7 Sek. | 1 Min. | 2.6 Stunden |
| 10 | 6.9 Min. | 34.1 Min. | 28.0 Monate |
| 15 | 1.5 Stunden | 18.2 Stunden | 18 098 Jahre |
| 20 | 19 Stunden | 25.3 Tage | 140.7 mln. Jahre |
Tabelle 1. Durchschnittliche Rückkehrzeit für Gewinnreihen (pro Sekunde wird ein Test durchgeführt).
Konsequenz 2: Begrenzung, erhebliche Verlangsamung oder, im Gegenteil, erhebliche Überschreitung des Verlust-Cluster, abhängig von der Länge der Testreihen kann zu der Tatsache führen, dass das Handelssystem das Bernoulli Schema nicht erfüllt. Zum Beispiel, wenn bei dem vorher zugewiesenen
Konsequenz 3: wenn die "Bernoulli Schema" Hypothese wahr ist, unterscheidet sich ein solche Strategie nicht von dem Schema des Werfens einer asymmetrischen Münze mit, mit entsprechenden Wahrscheinlichkeiten gleich p, q = 1-p (oder dem Hochwerfen einer mit Butter bestrichenen Scheibe Brot).
Lassen Sie uns nun ein paar "interessante" Strategien aus diesem Gesichtspunkt analysieren.
Scalping: "Lucky", Teil 1
Alle oder fast alle Scalping Systeme besitzen eine Reihe gemeinsamer Eigenschaften:
- SL ist viel mehr als TP (typische Werte – 20 und 2, die Kommawerte entsprechen 4-Ziffern Kursen von EURUSD),
- p ist viel mehr als q (die Wahrscheinlichkeit eines rentablen Trades ist über 80%, manchmal bis zu 99%),
- die Anzahl an Trades ist sehr groß und kann für den Zeitraum von einem Jahr Zehntausende betragen.
Wir werden nicht bei dem dritten Punkt verweilen - ob dies in Handelszentren möglich ist oder nicht. Dieses Thema wird in dem erwähnten Artikel von SK besprochen, sowie im Forum. Wir nehmen an, dass ein Handelszentrum unseren Trader nicht behindert mit Requotes, Slippage, erhöhtem MODE_STOPLEVEL und so weiter.
Ein Trader, der ein Scalping Handelssystem (TS - Trading System) erstellt hat, irrt sich sehr oft über die Häufigkeit von Verlusttrades. Die Wurzeln dieser Illusion führen zurück zu der Idee über den Wiener Charakters von Schlusskurs Verfahren und des wahren Charakters der Einstein-Formel für die Braunsche Bewegung: "wenn wir SL=20, TP=2 einstellen, ist die Wahrscheinlichkeit des Auslösens von Stop-Loss (20/2)^2=100 Mal niedriger als die Wahrscheinlichkeit den TP zu treffen. Deshalb muss ein solcher TP rentabel sein". Der Trugschluss dieser Konzeption liegt in der Tatsache, dass dieses Verfahren nicht das Wiener Verfahren ist und entsprechende Wahrscheinlichkeiten tatsächlich in weniger als 100 Mal abweichen!
Genau in diesem Fall ist die "Bernoulli Schema" Hypothese sehr wahrscheinlich - einfach deswegen, weil die Scalping Handelsstrategien oft versuchen zufällige Besonderheiten des Verfahrens und seiner in einigen Handelszentren akzeptierten Filtration zu verwenden.
Jetzt wollen wir die Parameter der uns unter dem Namen "Lucky" (https://www.mql5.com/en/code/7464) bekannten Handelsstrategie nehmen. In ihrer ursprünglichen Form (in dem gleichen Abschnitt, Lucky_new.mq4) ist dieser EA nur ein Spielzeug, weil es kaum ein Handelszentrum gibt, welches das Öffnen von mehreren hundert Trades am Tag akzeptiert, mit der mathematischen Erwartung an Rentabilität von ungefähr ein-zwei Punkten. Allerdings kann man den Code leicht verändern und strengere Anforderungen für die TP Ebene einstellen, und erhält trotzdem manchmal ziemlich zufriedenstellende Kontostand/Kapital Kurven. Der Code des modifizierten EA (unter Berücksichtigung der Beschränkungen der Anzahl an gleichzeitig geöffneten Trades, was in diesem Fall gleich 1 ist. Siehe Erklärungen weiter unten) ist an diesen Artikel angehangen.
Der wichtigste Vorteil von diesem EA ist, dass eine riesige Anzahl an Trades ausführt und reichlich Material für Statistiken erzeugt - dies wird weiter bewiesen. Nun ist unser Ziel nur die Entdeckung von Beweisen um die Hypothese zu bestätigen oder zu widerlegen: " die Handelsergebnisse stimmen mit dem Bernoulli Schema überein". Für diejenigen, die über den nicht-zufälligen Charakter von Marktbewegungen streiten möchten, gebe ich an: Ich bezweifele nicht, dass Marktbewegungen nicht immer zufällig sind. Ich werde nicht den Markt (genau Markt!) an einen Münzwurf anpassen a la Bachelier, ich bin nur an den statistischen Handelsergebnissen interessiert - und sonst nichts. Außerdem werden Sie sehen, dass einige Sätze externer Parameter absichtlich als "verlierend" gewählt sind - nur um die angegebene Hypothese zu überprüfen.
Hier snd die Ergebnisse des ersten Tests:
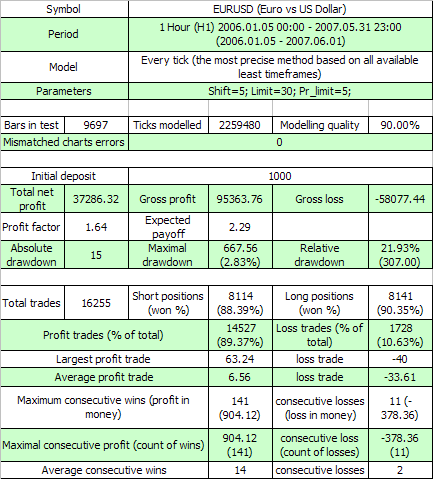
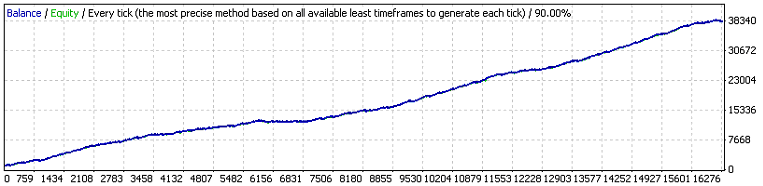
Die beiden ersten externen Variablen haben die gleiche Bedeutung wie in dem ursprünglichen Code, die dritte ist der Wert des Gewinn in Punkten, den eine Order überschreiten muss um ein Take Profit Ereignis zu veranlassen. Lassen Sie uns schätzen, nach (7.7). ist die mathematische Erwartung der minimalen Testreihe um den 11-Cluster an Verlusten (p=0.8937, q=0.1063, r_loss=11) zu erfüllen:
N_loss = 1 / (p * q^r_loss) – 1 / p ~ 57 140 275 804
Hier ist eine analoge Einschätzung der mathematischen Erwartung der Testreihenlänge um den rentablen 141-Cluster zu erfüllen:
N_profit = 1 / (q * p^r_profit) – 1 / q ~ 71 685 085
Nun... Wie wir wissen, ist die tatsächliche Länge von Reihen nur gleich 16255 Trades, und nicht zehn Milliarden oder Millionen. Ein solch riesiges überschreiten der tatsächlichen Reihenlänge ist das Zeichen, dass für dieses TS die Bernoulli Schema Hypothese kaum direkt funktioniert. Vielleicht gibt es es hier den Einfluss eines Faktors, den wir nicht berücksichtigt haben?
Bernoulli Schema: Ein Interessantes Ergebnis
Es gibt einen solchen Faktor: Ein Expert Advisor (EA) kann viel mehr als einen Trade gleichzeitig öffnen: in den zweiten hundert Trades (Ordern 158…163) öffnete er 6 Trades in Folge (und er schließt sie auch in "Haufen")! Dieser "Multiplikationsfaktor" ist wahrscheinlich verantwortlich für die erheblich erhöhten Cluster-Längen, verglichen mit den erwarteten: bewegt der Markt sich mit einem erheblichen Volumen seitwärts, beginnt der EA sehr viele Positionen bei fast jedem Zick zu öffnen. Allerdings, durch seine Arbeitseinstellung, werden bei einem seitwärts bewegenden Markt und die kleine Größe des Take Profit, verglichen mit dem Stop-Loss, die meisten von ihnen, wenn nicht alle, rentabel geschlossen. Auf der anderen Seite, wenn eine starke Bewegung in eine Richtung beginnt, wird der EA viele unidirektionale Trades in entgegengesetzter Richtung zur Markt Bewegung öffnen - und schließlich die meisten von ihnen mit Verlust schließen, und auch das "massiv".
Führen wir einfache Berechnungen durch. Wir nehmen beide Formeln für mathematische Erwartung der vollen Testreihenlänge des vorherigen Absatz. Hier sind r_loss_real, r_profit_real tatsächliche Längen maximaler verlierender und gewinnender Cluster. Während die erhaltenen N_xxxx Werte ziemlich groß sind, machen die gestutzten zweiten Bedingungen (1/p und 1/q) praktisch keine Fehler, wenn wir diese Gleichheiten gliedweise untereinander teilen:
N_loss / N_profit = q * p ^ r_profit_real / ( p * q ^ r_loss_real ) =
p ^ ( r_profit_real – 1) / q ^ (r_loss_real – 1)
Ermitteln wir den Logarithmus und vereinfachen ihn:
ln( N_loss / N_profit ) = ( r_profit_real – 1 ) * ln( p ) - ( r_loss_real – 1 ) * ln( q )
Jetzt markieren wir, dass, wenn die Tests dem Bernoulli Schema unterliegen und die Längen der längsten Cluster und beider Möglichkeiten p und q nicht sehr klein sind, dann sollten N_loss und N_profit Werte annähernd gleich sein. Also haben wir eine interessante annähernde Korrelation erhalten:
( r_profit_real – 1 ) / ( r_loss_real – 1 ) * ln( p ) / ln( q ) ~ 1 (*)
Und wenn wir es auf eine andere Weise neu schreiben:
p ^ ( r_profit_real – 1 ) ~ q ^ ( r_loss_real – 1 )
wird die Bedeutung der Korrelation (*) deutlich: In dem Bernoulli TS (bei einer ziemlich langen Testreihe und nicht zu kleinen p und q Möglichkeiten) sind die Möglichkeiten von zwei maximal langen Cluster ("Gewinne" und "Verluste") praktisch gleich. Tatsächlich kann dieses Prinzip auch auf jedes andere TS angewendet werden, die auch nicht-Bernoulli sein können, aber die Bildung der (*) Korrelation ist spezifisch für das Bernoulli Schema. Diese Korrelation kann ein grober Test eines TS für eine "Bernoullität" genannt werden.
Scalping: "Lucky", Teil 2
Lassen Sie uns den Multiplikationsfaktor ausschließen: setzen Sie die Begrenzung für die Anzahl gleichzeitig geöffneter Orden auf 1. Während die Anzahl der Ordern mehrmals für den gleichen Zeitraum verringert wird, werden wir den Bereich des Tests erweitern und ihn vom 1. Januar 2004 bis zum 4. April 2008 festlegen. Im Folgenden ist die Tabelle der Ergebnisse und einige Berechnungen (BS ist eine Abkürzung für das "Bernoulli Schema" (siehe Analyse unten), das erste "+" bezeichnet eine gute Übereinstimmung mit dem Bernoulli Schema für rentable Cluster, das zweite für verlierende Cluster, "-" ist eine widerlegte Hypothese "Das System erfüllt das BS", "0" bedeutet Zweifel in der Richtigkeit):
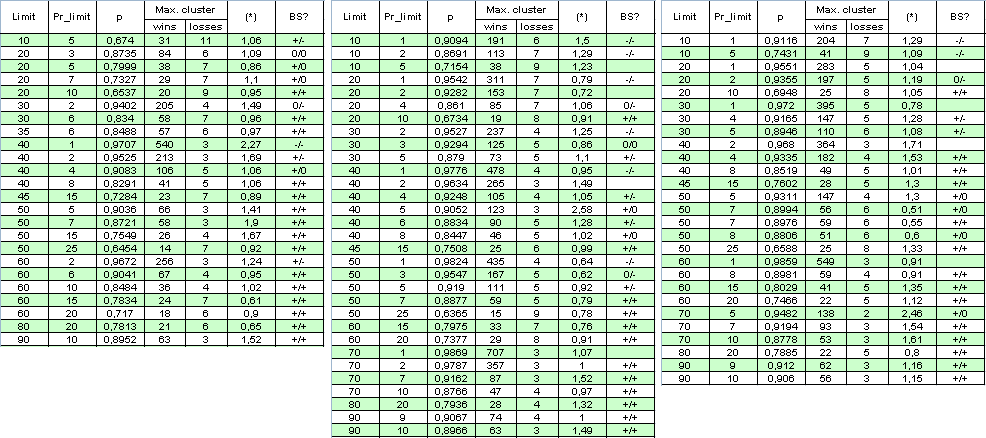
Der Autor entschuldigt sich für die große Größe der Tabelle, um das volle Bild zu erhalten. Der Parameter (*) scheint unzureichend um über die "Bernoullität" des Systems zu entscheiden, weil manchmal, wenn er nah an 1 ist, das System kaum auf das Bernoulli Schema bezogen werden kann.
P.S. Auch trotz der Tatsache, dass die Multiplikatoren in (*) manchmal weit von 1 abweichen können, ist der (*) weiterhin nah an 1. Zum Beispiel, wir haben:
( * ) = ( 478 - 1 ) / ( 4 - 1 ) * ln( 0.9776 ) / ln( 0.0224 ) ~
477 / 3 * ( -0.02265 ) / ( - 3.7987 ) ~ 0.95
Diese Tatsache erkennt übrigens auch eine andere Vermutung an: Auch wenn die System Bernoulli-Hypothese verzögert wird, die Abhängigkeit der Tades ist hier "fast die gleiche" für rentable und verlierende.
Kriterium der Übereinstimmung eines Handelssystems mit dem Bernoulli Schema.
Beschreibung der Skript Operation
Wie können wir zuverlässigere Testergebnisse in zwei Gruppen unterteilen - Bernoulli Systeme und "nicht-Bernoulli Systeme"? Wir können verschiedene Methoden versuchen, aber die einfachste, nach meiner Meinung, ist die folgende: Wenn wir viele Bernoulli Reihen mit Parametern entsprechend den wirklich in Tests erkannten erzeugen, im Falle der "Bernoullität" des Systems sollte die Wahrscheinlichkeitsverteilungsfunktion (p.d.f. - probability distribution funtcion) des Cluster nahezu unverändert bleiben. Diese Tatsache resultiert offensichtlich aus der Annahme über die Unveränderlichkeit der Gewinnwahrscheinlichkeit und der Unabhängigkeit von Trades.
Leider ist die theoretische Funktion der Verteilung von Gewinn/Verlust Cluster entsprechend ihrer Länge mir nicht bekannt. Unfortunately, the theoretical function of distribution of win/loss clusters according to their length is unknown to me. Obern habe ich einige Formeln eingeschlossen, die ermöglichen die mathematische Erwartung der Gewinn Cluster Anzahl in den Testreihen abzuschätzen, abhängig von ihrer Länge und Gewinnwahrscheinlichkeit (siehe (7.8) oben). Zu diesem Zweck bietet Feller ([1]) eine spezielle Methode, folgend aus der Theorie der wiederkehrenden Ereignisse, zu denen Cluster gehören. Auf den ersten Blick ist diese Methode nicht völlig passend nach dem Verständnis eines Traders des "Gewinnreihe" Begriffs, aber diese Methode vereinfacht die Theorie selbst wesentlich., so dass die Identifizierung des "r-Cluster Registrierung" Ereignis nicht von der Zukunft abhängt ([1], Seite 302):
Gewinnreihen in Bernoulli Tests. Der Begriff "Gewinnreihe der r Länge" wurde durch verschiedene Methoden bestimmt. Die Frage, ob eine Folge von drei aufeinanderfolgenden Gewinnen als mit 0, 1 oder 2 Reihen der Länge 2 zu betrachten ist, ist vor allem eine Frage der Zweckdienlichkeit, und für verschiedene Zwecke akzeptieren wir verschiedene Bezeichnungen. Wenn wir jedoch die Theorie der wiederkehrenden Ereignisse anwenden wollen, sollte die Bedeutung der r langen Reihen so definiert werden, das nach dem Ende der Reihe der Vorgang jedes Mal neu beginnt. Es bedeutet, wir sollten die folgende Definition akzeptieren: Die Folge n aus Buchstaben W und L enthält so viele r lange Reihen, wie sie kontinuierliche Untersequenzen enthält, von denen jede aus r Buchstaben W besteht, die zusammen bleiben. Wenn in der Abfolge von Bernoulli Tests als Ergebnis von n- Tests eine neue Reihe erscheint, werden wir sagen, dass diese Reihe in dem Test mit der Nummer n erscheint.
Somit gibt es in der Reihe WWW|WL|WWW|WWW drei Reihen der Länge 3, die im 3ten, 8ten und 11ten Test auftreten. Die gleiche Abfolge enthält fünf Reihen der Länge 2, sie treten in dem 2ten, 4ten, 7ten, 9ten und 11ten Tests auf. Die Definition vereinfacht die Theorie wesentlich, weil eine Reihe der festen Länge wiederkehrende Ereignisse werden. Es entspricht dem Zählen von aus mindestens r aufeinanderfolgenden Gewinnen gemachten Reihen mit dem Vorbehalt, dass 2*r von aufeinanderfolgenden Gewinnen als zwei Reihen betrachtet werden, und so weiter.
Andererseits, für einen Trader wird die Anzahl der Gewinn-Cluster ("Gewinnreihen" von Feller) in der angegebenen Reihe (WWWWLWWWWWW) die folgende sein: zuerst ein 4-Cluster aus Gewinnen, dann, nach einem Verlust, 6-Cluster aus Gewinnen. Es gibt dort keine "kompletten" Cluster der Länge 1, 2, 3 und 5 für einen Trader, obwohl nach Feller solche dort sind. Dieser Auszug aus [1] ist hier nur veröffentlicht um die Schwierigkeit des Problems anzuzeigen. Somit werden wir nur eine große Anzahl an Bernoulli Reihen erzeugen und Reihen in diesen erfassen, die dem Verständnis eines Traders von ihnen entsprechen (15 Gewinne in einer Reihe die mit einem Verlust endet, sind nicht 15 Registrierungen von 1-Cluster, oder 5 Registrierungen von 3-Cluster, wie nach Feller, sondern es ist nur eine Registrierung eines "wahren" 15-Cluster) Zum Prüfen der Reihen auf "Bernoullität" sind 1000 Bernoulli Reihen ausreichend.
Nach dieser Idee wurde zunächst ein Skript geschrieben, das ermöglicht die Abfolge von echten Handelsergebnissen in ein Array zu hochzuladen und dann Daten zu erhalten für das Zeichnen eines Histogramms von Cluster-Längen in MS Excel. Dieses Skript enthält außerdem die Funktionen, die Bernoulli Reihen erzeugen und die Daten vorbereiten um Histogramme in MS Excel zu machen. Ich möchte den Skriptcode nicht in den Artikel einfügen, stattdessen werde ich allgemeine Kommentare zu dem Code geben. Das Skript ist unten angehangen. Die Tester Bericht-Datei sollte als erstes platziert werden in das Verzeichnis experts\files\Sequences\, und ihr Name sollte in externe Skript-Parameter verschoben werden.
Am Anfang werden, auf Grundlage der Tester Bericht-Datei, mit Hilfe der readIntoArray() Funktion, die binären Ergebnisse von Trades (1 oder -1) in ein globales Array _res[] eingegeben. Um den Vorgang zu verstehen illustrieren wir unsere Erklärungen mit einem kleinen Array. Dieser Funktionsbetrieb resultiert schließlich in, zum Beispiel, dem folgenden Array _res[] (die Anzahl der Trades, d.h. die Reihenlänge ist 50):
1,1,-1,-1,1,1,1,1,1,-1,1,1,1,1,1,1,1,-1,1,1,-1,-1,-1,-1,1,1,1,-1,1,1,1,1,-1,1,-1,1,-1,-1,-1,1, 1,-1,1,1,1,1,1,1,1,1
Danach berechnet die Funktion formClustersArray( int results[], int& sequences[], int& h, int nr ) die Längen von Cluster und dann, abhängig von dem globalen Parameter _what, die definiert woran wir interessiert sind - Gewinne oder Verluste, schreibt sie die Längen von Reihen in dieses Array sequences[] (tatsächlich in das globale Array _seq[]). Zählen wir die Cluster in diesem Array:
2,-2,5,-1,7,-1,2,-4,3,-1,4,-1,1,-1,1,-3,2,-1,8
Negative Werte beziehen sich auf die Verlust-Cluster. Es ist klar, dass die Summe aller absoluten Werte der Anzahl gleich ist mit der Reihenlänge, 50. Angenommen wir sind an Verlusten interessiert, d.h. _what = -1. Then the array _seq[] werden wir nur negative Werte speichern, aber mit dem "Plus" Zeichen:
2,1,1,4,1,1,1,3,1
Danach wird das Array _seq[] verarbeitet mit dem Ziel das Array _histogramReal[] zu bilden. Jetzt müssen wir nur noch die Mengen berechnen von 1-, 2-, 3- usw. Cluster und diese in einer Folge in das Array schreiben. Als Ergebnis wird das Array _histogramReal[] die folgenden Werte enthalten:
6,1,1,1
Das Bedeutet, dass unsere Reihe 6 verlierende 1-Cluster, 1 verlierenden 2-Cluster, 1 verlierenden 3-Cluster und 1 verlierenden 4-Cluster enthält. Ferner wird das letztere Array in eine Ausgabedatei geschrieben. Die Datei ist nicht geschlossen, weil wir analoge "Histogramme" von synthetischen Reihen von Tests nach dem Bernoulli Schema in sie schreiben müssen.
Beim Bilden von "Synthetik" ist die Schlüsselfunktion der Generator eines einzelnen Tests nach dem Bernoulli Schema. Trotz dieses einfachen Code, arbeitet es recht gut: keine verantwortlichen "Randeffekte" verantwortlich für die Verzerrung der regelmäßigen Verteilung in dem Segment [0, 32767] wurden beobachtet.
// generates a single Bernoulli test (+-1 with different probabilities) int genBernTest( double probab ) { int rnd = MathRand(); if( rnd < probab * 32767 ) return( _what ); else return( -_what ); }
Nach einen einzelnen Aufruf von MathSrand( GetTickCount() ), diese Funktion wird oft aufgerufen, da dort echte Trades in dem Testzeitraum (_testsTotal) sind. Dann, wenn wir die erzeugten Bernoulli Reihen haben, werden die Ergebnisse entsprechend verarbeitet durch Cluster-Zählung und "Histogramm" Konstruktionsfunktionen. Diese Vorgänge sind verantwortlich für das Erstellen eines Histogramms, entsprechend dem einen Test (die Funktion genSynthHistogr( int& h, int nr ) ). Und schließlich die letzte Funktion wird in der Schleife aufgerufen, so dass im Ergebnis das Array der Bernoulli Reihen erzeugt wird, Histogramme für diese werden gebildet und sie werden in eine Ausgabedatei geschrieben.
Jetzt können wir diese Datei in MS Excel öffnen, notwendige Diagramme aufbauen und Schlüsse ziehen über die Übereinstimmung des Systems mit dem Bernoulli Schema. Zahlen haben in der Datei die folgende Bedeutung (die Tabelle ist beschnitten, und wir zeigen hier nicht die Daten von 5-Claster und darüber hinaus):
1 9 1639 1058 724 440
Nr. der Testreihe
Länge von max. Cluster
Anzahl von 1-Cluster
Anzahl von 2-Cluster
Anzahl von 3-Cluster
Anzahl von 4-Cluster
0
11
1649
1044
688
478
1
8
1681
1093
675
458
2
13
1628
1067
701
461
3
7
1616
1039
726
474
4
12
1601
1054
699
465
Die erste Zeile der Datei (grün) zeigt das Ergebnis von echtem Test, und die Zeilen darunter entsprechen synthetischen Testreihen, mit der Nummer bei 0 beginnend.
Und schließlich die letzte Stufe - Einschätzen von realen Testergebnissen zu ihrer Übereinstimmung mit dem Bernoulli Schema: Von den Bernoulli Reihen werden entsprechende Spalten gewählt, um ein Histogramm ein mit Clustern der erforderlichen Länge zu konstruieren. Zum Beispiel, um ein Histogramm von Gewinn 1-Cluster Mengenverteilung zu konstruieren, müssen wir die dritte Spalte nehmen (1649, 1681, 1628, 1616, 1601….), die Gesamtmenge solcher Zahlen ist gleich zu synthetischen Bernoulli Reihen). Für Gewinn 2-Cluster nehmen wir die vierte Spalte (1044, 1093, 1067, 1039, 1054…), und so weiter.
Solche Histogramme werden nach der von Bulashev [7] beschriebenen Methode konstruiert, und dann prüfen wir die Null Hypothese über die Gleichheit der Anzahl im realen Test zu dem Durchschnitt in synthetischen Reihen. Die vor-akzeptierte Bedeutungsebene für Hypothese Null, "Realzahl entspricht einem Durchschnitt für synthetische", ist gleicht 0.05 (sie bezieht sich auf annähernd zwei Standardabweichungen).
Erste Ergebnisse
Starten wir das Skript auf Lucky Testergebnisse bei den Parametern 3, 20, 10. Die Skript Parameter: _what = 1 (rentable Cluster), _globalSeriesQty = 5000. Parameter (*) in der großen Tabelle ist gleich 1, das heißt, wir können erwarten, dass die Skript Arbeitsergebnisse die Übereinstimmung mit dem Bernoulli Schema zeigen sollten. Wir zeigen hier nur die Datei-Datensätze, zur direkten Prüfung der Null Hypothese für Cluster-Längen 1-6 (sie werden leicht geändert in eine Tabellenform zur besseren Wahrnehmung):
// Die erste Zeile der Datei sind Ergebnisse des realen im Tester gemachten Tests. Die zwei ersten Zahlen sind die Anzahl an Reihen und die Lände eies maximalen Cluster.
1,20,1639,1058,724,440,271,212,137,91,62,30,26,22,5,7,1,4,1,0,1,1,
…
// Ende der Datei (teilweise):

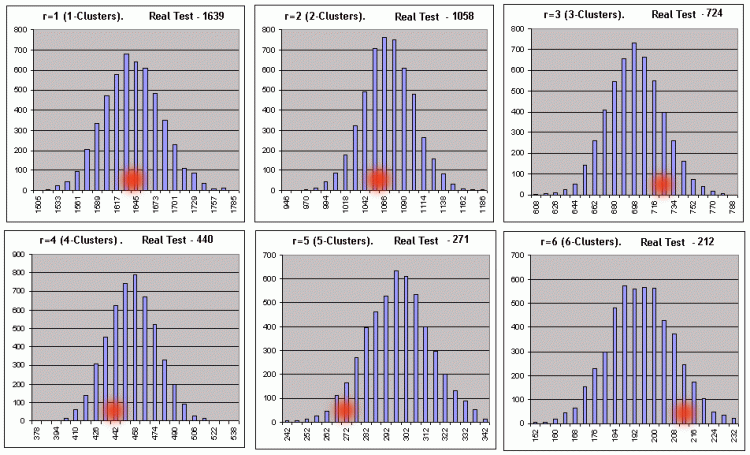
In jeder der 6 zweizeiligen Tabellen entspricht die obere Linie linken Werten von Histogramm-Intervallen, und die untere der Anzahl an Bernoulli Reihen (aus 5000), in denen die Anzahl an Clustern der gegebenen Länge innerhalb dieser Intervalle waren. Unten ist das gliche grafisch dargestellt (die Anzahl der in Bernoulli Reihen bereitgestellten rentablen r-Cluster entspricht der Gesamtzahl an Reihen gleich 5000) :
Die Abzissen aus roten Punkten entsprechen der Anzahl der in dem realen Test erhaltenen Cluster. Das gliche Skript für Verlust-Cluster (_what = -1) mit den gleichen Parametern ergibt auch ein recht gutes Bild - mit dem Abstrich für die sinnvolle Länge von Verlust-Clustern: Sobald die Anzahl der nach den Empfehlungen [7] berechneten Intervalle beginnt die Verbreitung von Daten in Synthetik zu überschreiten, ist die Konstruktion von Histogrammen mit der eingestellten Anzahl an Intervallen unmöglich. Trotzdem sollten formale Nullen in dem Skript-Bericht Sie nicht erschrecken, weil alle notwendigen Parameter ohne Histogramm berechnet werden können. Nur bei den voreingestellten Parametern für die 3- und 7-Cluster wurde die Null Hypothese zurückgewiesen. Als Hauptkriterium für den Bezug eines getesteten Systems auf das Bernoulli System, wurde das sehr zweifelhafte Kriterium des Fuzzy-Typ gewählt. Betrachten wir das Prinzip der Entscheidungsfindung am Beispiel der Skript-Arbeitsergebnisse für Verlust-Cluster:
Die Differenz eines realen Tests von der Schätzung eines Durchschnitts = -0.37 SD (Standardabweichung)
Die Differenz eines realen Tests von der Schätzung eines Durchschnitts = 0.95 SD
Die Differenz eines realen Tests von der Schätzung eines Durchschnitts = -2.04 SD
Die Differenz eines realen Tests von der Schätzung eines Durchschnitts = -0.45 SD
Die Differenz eines realen Tests von der Schätzung eines Durchschnitts = 0.36 SD
Die Differenz eines realen Tests von der Schätzung eines Durchschnitts = 1.13 SD
Die Differenz eines realen Tests von der Schätzung eines Durchschnitts = 3.27 SD
Die Differenz eines realen Tests von der Schätzung eines Durchschnitts = 0.11 SD
Die Differenz eines realen Tests von der Schätzung eines Durchschnitts = 0.46 SD
Die Differenz eines realen Tests von der Schätzung eines Durchschnitts = -0.47 SD
Also, hier ist das Hauptkriterium:
- Wenn der Mittelwert der Zahl-Module 1.5 nicht überschreitet (hier ist es 0.96),
- der Mittelwert an Zahlen nicht mehr als 1.2 pro Modul ist,
- die Anzahl der Ausreißer (hier sind sie Fett und entsprechen der Differenz über 2 SD) nicht 20% der Gesamtmenge überschreitet,
wird ein System als "sicher bernoullisch" betrachtet. Wenn die entsprechenden "kritischen" Zahlen 2, 1.5 und 30% sind, ist das System "zweifelhaft bernoullisch". Werden diese Zahlen überschritten, ist die Hypothese widerlegt. Ich halte den zweiten Punkt für sinnvoll, weil Abweichungen nicht in erster Linie von einem Zeichen abhängen sollten.
Statistische Kriterien der Übereinstimmung mit dem Bernoulli Schema sind mir nicht bekannt, weshalb ich mir ein solches Kriterium ausdenken musste. Die Ergebnisse eines solchen improvisierten entscheidenden Kriteriums sind in dem Skript-Arbeitsbericht angegeben. Ein interessierter Leser kann gerne ein sinnvolleres Kriterium anbieten.
Für diesen Fall können wir "sicher zu dem Schluss kommen". dass das Lucky_ System mit den Parametern 3, 20, 10 wirklich mit dem Bernoulli Schema übereinstimmt, das heißt, mit dem Schema einer zufällig geworfenen Scheibe Bot mit Butter.
Nehmen wir jetzt einen der "schlimmsten" Fälle und führen die gleichen Berechnungen mit der Anzahl an Bernoulli Reihen gleich 1000 durch, die Parameter von Lucky sind 5, 10, 1. Betrachten wir einen rentablen 1-Cluster:
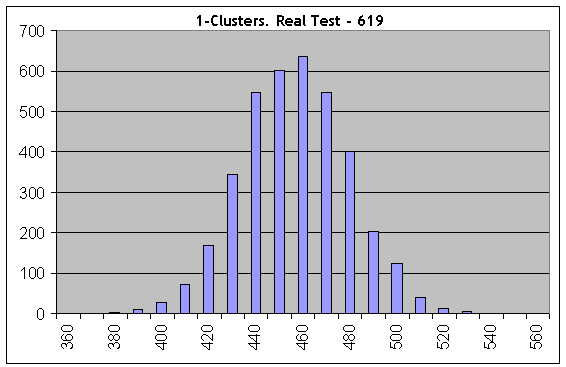
Bereits auf dem ersten Histogramm ist alles komplett anders: reale Testergebnisse (619 1-Cluster) stimmen nicht überein mit den "synthetischen" mit der gleichen länge an Testreihen und der gleichen Gewinnwahrscheinlichkeit. Deshalb sind die Trades nicht unabhängig.
Bitte beachten Sie, dass ähnlich eingeschätzte Tests mit vielen anderen Sätzen an Parameter einer großen Tabelle die Schlussfolgerung ermöglichen, dass das Bernoulli Schema ("Hochwerfen einer Scheibe Brot mit Butter") mehr eine Regel als eine Ausnahme ist. Außerdem gibt es Fälle, in denen für eine Gruppe aus Trades (z.B. "rentable Trades") das Bernoulli Schema erfüllt ist, und für eine andere Gruppe nicht. Des hindert nicht das System zumindest teilweise zu verwenden, um nützliche Informationen zu erhalten, die später in diesem Artikel besprochen werden. Und die letzte Sache: das entscheidende Kriterium ist nicht so zuverlässig für Verlust-Cluster, wegen der unzureichenden Menge an statistischen Daten, aber ich habe das Skript dafür auch angewandt- nur um das vollständige Bild zu erhalten.
"Universum" System: Wieder Bernoulli Schema!
Jetzt nehmen wir ein absolut unterschiedliches System für unsere Studie - "Universum". Sein Quellcode ist veröffentlicht auf https://www.mql5.com/en/code/7999. Der Autor behauptet, dass das System auf den gebildeten Balken arbeitet, weshalb das Testen "aller Ticks" nicht notwendig ist. Der anfängliche Kontostand, bei dem das System Handelsstatistiken für den Zeitraum vom 01.01.2001 bis zum 04.04.2008 sammeln kann, wurde auf ungefähr $10M eingestellt. das erste geöffnete Lot ist 0.1. Die drei tatsächlich geänderten Parameter sind p, tp, sl. Es sind keine Multiplikatoren anwesend, also ist die Studie einfach: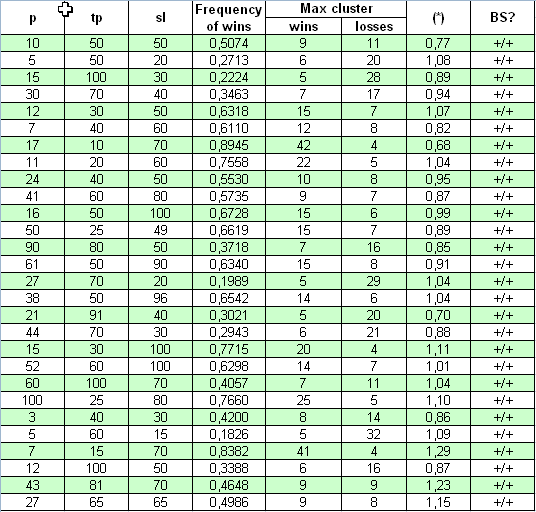
Sieh an, hier ist die Konformität des (*) Parameter mit 1 viel besser, als in dem vorherigen Fall: (*) Werte weichen leicht von 1 ab. Die Prüfung mit einem entscheidenden Kriterium zeigt auch, dass in allen Fällen, bei einem sehr breiten Parameter-Bereich, dieses System dem Bernoulli Schema entspricht.
Vorläufiges Fazit
Ralph Vince in [4] bietet ein anderes Verfahren zur Überprüfung von Testreihen auf die Übereinstimmung mit dem Bernoulli Schema. Dies ist die Berechnung des Z-Score und Prüfung von Handelsergebnissen auf eine spezielle Korrelation (Autokorrelation einer Quellreihe und einer um Eins verschobenen Reihe). Ich glaube nicht, dass sein Verfahren vielmehr aussagekräftige Ergebnisse ergibt als die oben beschriebene (wo die Abweichung von Cluster-Zahlen mit unterschiedlichen Längen in realen Reihen gegenüber Modellreihen geprüft wird). Stimmt, das angebotene entscheidende Kriterium ist ziemlich frei und benötigt eine Begründung. Außerdem, wie ich früher anmerkte, ist die Zuverlässigkeit dieser Prüfung bei einer kurzen Länge des maximalen Cluster nicht hoch (für Lucky sind dies in der Regel Verlust-Reihen Tests). Allerdings, meiner Meinung nach, obwohl dieses entscheidende Kriterium umfangreichere Berechnungen benötigt, ist es besser den spezifischen Charakter von Testreihen in dem Kontext ihrer Konformität mit dem Bernoulli Schema abzudecken. Diese Frage benötigt weitere Untersuchungen und, natürlich, ist noch nicht abgeschlossen.
Dennoch wurden die Erwartungen bewiesen: in den meisten Fällen, bei sehr unterschiedlichen Sätzen externer Parameter, stimmen die Trade-Reihen mit dem Bernoulli Schema überein, und die Abweichungen von dem Bernoulli Schema resultieren fast immer aus dem systematischen Ausnutzen von Regelmäßigkeiten, die charakteristisch sind für den Folterprozess von Kursen und häufiger inhärent sind zu den Systemen mit dem kleinen Pr_limit Wert. Dies wird besonders deutlich in der großen Tabelle mit Lucky_ Prüfergebnissen.
Vince stellt fest, dass, wenn die empirische Prüfung der Reihenkorrelation oder Z-Score Prüfung die Abhängigkeit zwischen Trades ergab, dann ist das System suboptimal, und die Abhängigkeit sollte explizit in das TS eingeschlossen sein, um es in des Testergebnissen zu senken und das TS-Optimum zu erhöhen. Um die Testergebnisse der beiden Systeme abzufertigen, müssen wir zugeben, dass das "Universum" System allgemein optimaler als das "Lucky" System ist. Allerdings rechtfertigt das nicht das in Universum verwendete MM.
Wie Verwendet man Möglicherweise die Bernoullität des Systems?
1. Was wissen wir?
Vorher zu wissen, dass zumindest in einigen Fällen die Abfolge von durch 1 ("Erfolg", d.h. Gewinn) ausgedrückten Handelsergebnissen und -1 ("Ausfall", d.h. Verlust) das Bernoulli ist, erhalten wir ein adäquates Modell dieses Vorgangs. Jetzt wissen wir genug über diesen Prozess, denn eigentlich ist dies eine Modifikation einer üblichen Braunschen Bewegung mit einer Abweichung. P. Samuelson hat geometrische (oder, wie er es nennt, ökonomische) Braunsche Bewegung in der Finanz-Theorie und-Praxis eingeführt ([6]):
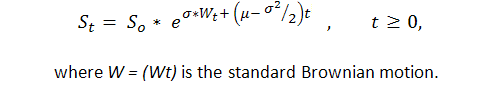
Somit können wir starke Ergebnisse theoretischer Untersuchungen der Standard Braunschen Bewegung (Arkussinus Gesetze, zum Beispiel) auf die Kontostand-Kurve anwenden. Allerdings ist die Braunsche-Bewegung-Theorie ziemlich kompliziert und kann nur durch die enge Zahl der Menschen mit einer soliden mathematischen Ausbildung in stochastischer Integration verstanden werden.
Der zweite Ansatz ist, von hoch theoretischen Berechnungen abzusehen, direkte Programmerzeugung von langen Bernoulli Reihen durchzuführen und diese dann in Kontostand-Kurven umzuwandeln zum "Testen von MM 0.1 Lot". Hier müssen wir nur Mittelwerte von rentablen und verlierenden Trades und die Gewinnhäufigkeit p kennen. Auch mehrere hundert solcher Reihen (zum Beispiel, 1000-Array von Bernoulli Reihen) können uns eine ziemlich gute Vorstellung davon geben, wozu eine Strategie, die mit dem Bernoulli Schema übereinstimmt, in der Lage ist.
Es ist wichtig, klar zu verstehen, dass ein solches synthetisches Testen eine gute Alternative zu einem ermüdenden Pardo Testen ist ([5]): wenn wir in der Lage sind die Null Hypothese zu bestätigen ("Trade-Abfolge ist bernoullisch" ist nicht widerlegt), kann er uns ausreichend Informationen bieten, über den wesentlichen Unterschied des Systems von dem gegebenen in der Walk-Forward-Analyse, beschrieben in [5]. Natürlich kann die Kontostand-Kurv viel von der in realem Test erhaltenen Kurve abweichen.
***********
Im Allgemeinen behindert nicht die Umsetzung eines solchen Ansatzes, weil eine solche Prüfung auf einem Computer in mehreren Minuten durchgeführt wird, als Ergebnis erhalten wir breite Informationen, die gründlich untersucht werden können. Leider erlaubt der Artikelumfang nicht die Veröffentlichung aller Ergebnisse. Hier sind mehrere Diagramme mit den Parametern 4, 70, 10 in dem gleichen Testzeitraum wie in der Tabelle. Die Aufgabe der Erzeugung synthetischer Bernoulli Systeme ist viel einfacher, als die von dem oben beschriebenen Skript durchgeführten Aufgaben, so dass die Mittel von MS Excel völlig ausreichend sind.
Realer Test auf 0.1:
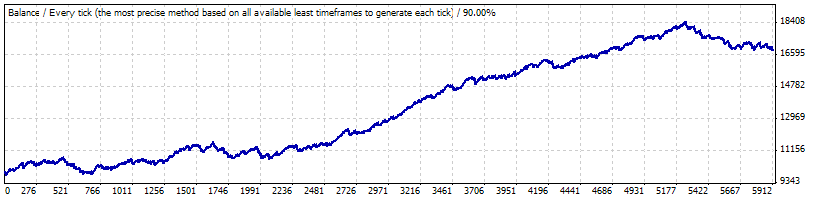
Die folgenden Parameter aus dem Bericht sind für uns wichtig. Wir werden sie einstellen bei der Erzeugung von Bernoulli Reihen und der Umwandlung von Reihen in Kurven:
Häufigkeit rentabler Trades (p)
0.8765
Durchschn. Gew. Trade
11.71
Durchschn. Verl. Trade
-73.73
Gesamtzahl an Trades
5904
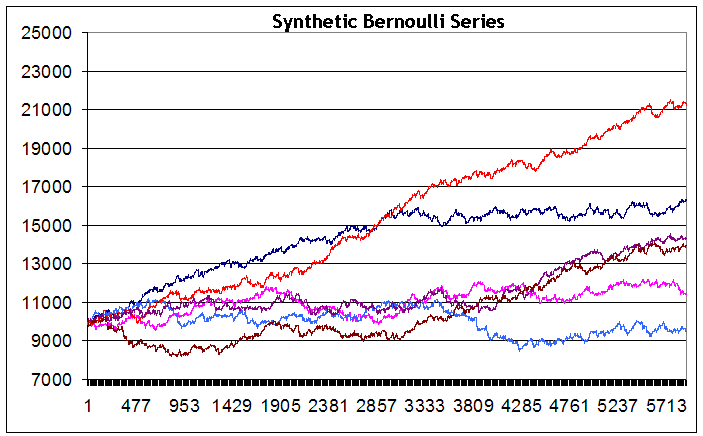
Wir sehen, trotz der Tatsache, dass die Reihen mit identischen Eingabedaten erzeugt wurden, unterscheiden sich die integralen Kontostandergebnisse am Ende des Testzeitraumes von Reihe zu Reihe erheblich - von einem kleinen Verlust (blaue Linie) zu einem großen Gewinn (rote Linie). Ich muss zugeben, ich habe es nicht geschafft eine Reihe mit einem deutlich fallenden Kontostand zu erzeugen (obwohl ich ein solches Diagramm erreichen wollte und ungefähr 200 Versuche machte). Vielleicht kann dies bei einer großen Anzahl an Reihen erreicht werden. Es scheint aber, ein solcher Fall ist nicht typisch für diese Strategie. Außerdem habe ich in keiner der Reihen einen Rückgang von mehr als 2500 Punkten gesehen.
Betrachten wir nun ein paar isolierte Ergebnisse in Verbindung mit der Einschätzung einiger Parameter einer Strategie mit dem Bernoulli Schema.
2. Einschätzung des maximalen Verlust-Cluster größer als Berichtswerte ("Schwarzer Schwan")
Mit den erhaltenen Beweisen der Bernoullität, können wir realistisch die maximale Länge eines Verlust-Cluster einschätzen, die uns in der gleichen Anzahl an Trades in realem Testen erwarten kann. Hier können wie nur viele Bernoulli Reihen erzeugen und dann de Chancen eines echten "Schwarzen Schwan" abschätzen (siehe [2, 3]), d.h. ein solches Ereignis, für das wir nie in der Lage sind die Möglichkeit nur basierend auf den Testergebnissen einzuschätzen, weil es einfach in dem Testzeitraum nicht passiert ist. Es ist einfach ein Wahrscheinlichkeit-theoretisches Modell, dass wir die notwendigen Statistiken für jedes Volumen das wir brauchen sammeln können.
Verwenden wir die Handelsergebnisse von allen gleichen Lucky_ Systemen mit den Parametern 4, 50, 7:

Nach dem Bericht, ist die Länge des maximalen Verlust-Cluster gleich 5. Lassen Sie uns nun eine sehr große Anzahl an Bernoulli Reihen festlegen, 65000, mit dem Parameter _what gleich -1 (Verlust-Cluster), und dann unser Skript auf dem Tester-Bericht anwenden. Lassen Sie uns die längste Linie ermitteln (die erste Nummer ist eine # der Bernoulli Reihe, die 2te ist eine der Länge des maximalen Cluster, und dann kommen Nummern von Clustern jeder Länge):
26001 9 1030 136 13 4 0 0 0 0 1
Sie sehen, die Länge des maximalen Verlust-Cluster kann viel größer sein als 5 (hier ist es 9)! Vielleicht ist das zu selten ein Ereignis? Stimmt, es ist sehr selten: es wurde nur einmal in 65000 Reihen erfüllt, also kann ihr Auftreten in einem realen Test als verschwindend betrachtet werden, unter Berücksichtigung "der Ergodizität-Hypothese" (siehe etwas später). Trotzdem ist diese Häufigkeitsschätzung sehr unzuverlässig: dieser Reihen können auftreten, zum Beispiel, unter nur 20 Bernoulli Reihen. Als Ergebnis, wenn die statistischen Kriterien der Zuverlässigkeitsschätzung nicht kennen, würden wir fälschlicherweise in Betracht ziehen, dass die Schätzung eine hohe Wahrscheinlichkeit hat.
In der Version die ich anbiete, ist die "der Ergodizität-Hypothese" die folgende: die Wahrscheinlichkeit eines Ereignisses in dem "synthetischen Testraum" (basierend auf dem adäquaten Modell des Ereignis) ist annähernd gleich zu der Wahrscheinlichkeit des gleichen Ereignisses in dem Zeitraum, d.h. für das reale Trading - das Bereitstellen der Anzahl an Trades in dem realen Test ist gleich der in Modell-Tests. Es wird berücksichtigt, natürlich, dass die Abfolge an Handelsergebnissen in realen Tests stationär ist, wie das Bernoulli Schema. Bei einer großen Menge an Trades ist diese Aussage nicht weit davon entfernt wahr zu sein, weil die einzige Quelle von Nichtstationarität kann hier, wahrscheinlich, die sogenannte "Gewinnverschiebung" sein, verteilt nach dem normalen Gesetz und weiter unten beschrieben.
Im Folgenden ist eine Tabelle von Verlust-Cluster Zahlen in dem 65000-Array von Bernoulli Reihen:
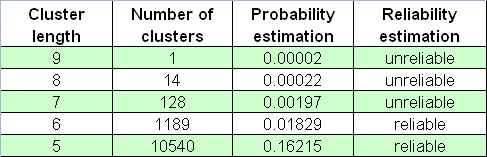
Wir sollten darüber "Schwarze Schwäne" nicht vergessen, die genau dann kommen, wenn Sie sie nicht erwarten.
Im Kontrast zu den obigen Berechnungen, können wir Schätzungen für "Schwarze Schwäne" mit einem entgegengesetzten Charakter verwenden, nämlich rentable Cluster der erhöhten Länge. Wir erinnern uns, dass der reale Test zeigt, dass die Länge des maximalen Gewinn-Cluster gleich 59 ist. Bei der Ausführung der analogen Modellierung für 65000 Modellreihen, finden wir die längste Linie wieder in dem Skript-Bericht:
44118 153 115 117 111 87 70 71 52 51 50 40 36 42 42 34 20 32 15 20 20 13 10 11 12 8 5 7 3 5 4 2 2 6 7 0 2 1 2 1 1 5 0 0 1 0 0 0 0 0 0 1 0 0 2 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
Dies ist eine Modell-Reihe #44118, mit der maximalen Gewinn-cluster Länge gleich 153 Trades (2te Zahl in der Liste), ungefähr 2,6 Mal länger als der maximale Cluster in dem realen Test! Allerdings, die statistisch signifikanten Schätzungen von Cluster-Häufigkeit können bei ihrer Länge beginnend ab ungefähr 80 (die Wahrscheinlichkeitsschätzung der Reihe ist 0.0088) und niedriger, und 80 ist viel mehr als 59. Das Quantil einer ½ Order (der Wert der Cluster-Länge, bei dem die integrale Verteilungsfunktion den Wert von 0,5 erhält, d.h. ein solcher Wert, bei dem die Verteilung in zwei Teile geteilt ist, gleich dem Bereich unter der Funktion der Wahrscheinlichkeitsdichteverteilung) für Gewinn-Cluster ist ungefähr 62, d.h. etwas mehr als 59. Das Histogramm von maximaler Cluster-Längenverteilung auf dem Bernoulli Reihen Array ist hier zu Ihrer Referenz enthalten:
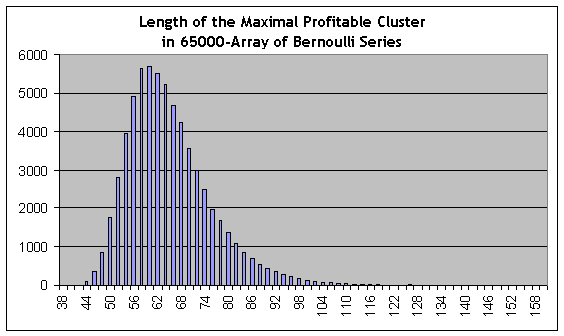
Natürlich, der "Schwarzer Schwan" Begriff wird hier nicht sehr sorgsam verwendet, weil nach Taleb scheint dies ein Ereignis der Wahrscheinlichkeit zu sein, die unberechenbar ist. Dennoch können wir feststellen, dass wir, nur beurteilt durch empirische Daten (Testbericht) und der Verwendung theoretischer Modelle, kaum eine statistisch zuverlässige Schlussfolgerung über die Wahrscheinlichkeiten von Verlust 6-Cluster oder Gewinn 80-Cluster machen können, das heißt, die die Ereignisse, die wir nicht in dem Bericht antreffen!
3. "Ausfall Verschiebung": Eine Ungünstige Verschiebung der Ausfallwahrscheinlichkeit von Empirischer Häufigkeit.
Annähernder Apparat, Versuch Nr. 1
Bei der großen Menge Tests durch das Bernoulli Schema (etwa mehrere tausend oder so) weicht die Ausfallhäufigkeit f leicht von der Ausfallwahrscheinlichkeit q ab und folgt der "korrekten" Normalverteilung mit einer kleinen Varianz: das Gesetz der großen Zahlen (hier Laplace-Theorem) ist weiter wirksam. Trotzdem kann auch f abweichen, und für Scalping Strategien mit einer sehr kleinen mathematischen Erwartung eines Trades, kann eine solche Verschiebung kritisch sein und ist in der Lage ein System über den gesamten Testintervalls in ein verlierendes zu drehen. Wir haben nun die ausreichende Ausstattung für die statistische Einschätzung von Chancen einer solchen Verschiebung - wenn ein Beweis dafür vorhanden ist, dass das Bernoulli Schema in diesem Fall "funktioniert".
Leider ist auch der EA Lucky_ in seinen Möglichkeiten begrenzt, bis ein Trade für eine feste Zeit zu viele Statistiken gibt.
Diese Aussage ist falsch, aber es wurde mir erst klar, nachdem der Originalartikel auf Russisch erschienen ist: trotzdem, ich entschied es in dieser Übersetzung so zu lassen "wie es ist", um sie authentisch zu machen. - Mathemat.
Für einen ernsthaften Strategie-Entwickler ist das mehr eine Ausnahme als eine Regel, weil man normalerweise schlangenartige Schlussfolgerungen treffen muss, basierend auf Testergebnissen mit mehreren Hunderten oder auch Dutzenden von Trades (siehe Erklärung weiter unten). Die angemessene Erhöhung des Statistik-Volumens führt zu der entsprechenden Absenkung der Breite der Gaußschen Verteilung und senkt erheblich die Chancen für große Abweichungen von ihrem zentralen Wert.
Als ein Beispiel betrachten wir Lucky_ mit Parametern, alles andere als günstig für den EA: 4, 80, 20, mit dem Lot 0.1. Zuerst führen wir seinen Test über den vollen Zeitintervall aus ("Intervall A") – vom 01. Januar 2004 bis zum 04. April 2008 (EURUSD H1). Hier ist das Kontostand-Diagramm aus dem Bericht:
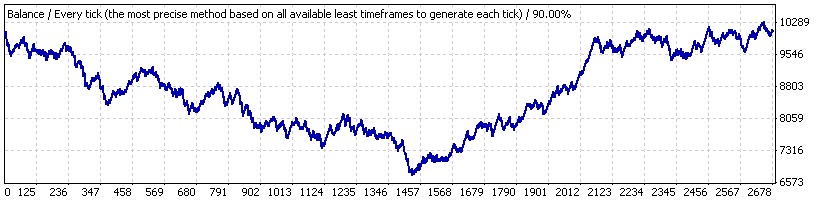
Was wir sehen ist alles andere als erstaunlich. Nach der Prüfung der Abfolge der Trades mit unserem Skript (auf 1000 Modell Bernoulli Reihen) stellen wir fest, dass die volle Trade-Reihe dem Bernoulli Schema entsprechend betrachtet werden kann - für Gewinn- und Verlust-Cluster.
Beachten wir die Parameter der durchschnittlichen Trades:
Durchschn. Gewinntrade
21.71
Verlusttrade
-83.32
Jetzt nehmen wir an, wir haben den EA nur für einen kurzen Zeitraum getestet, vom 21.10.2005 bis 07.06.2007 ("Intervall B"), wo die Strategie ein stabiles Wachstum zeigt. Das Diagramm ist unten:
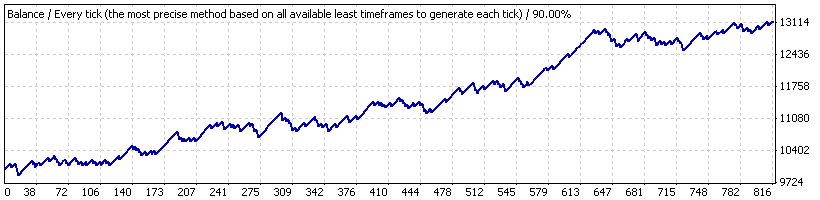
Hier die Ergebnisse der durchschnittlichen Trades:
| Durchschn. Gewinntrade | 21.69 | Verlusttrade | -82.94 |
Im Durchschnitt haben sich die Trades nur leicht verändert, deshalb können sie als annähernd unveränderlich, unerheblich von der Strategie-Rentabilität für die Testperiode betrachtet werden. Tatsächlich können wir dies früher sehen, wenn wir berücksichtigen, dass die Trades nur geschlossen werden, nachdem sie eine bestimmte Gewinn/Verlust Ebene erreicht haben, festgelegt durch die strikten externen Parameter.
Die zweite Express-Prüfung auf Bernoullität (1000 Modell Reihen) bestätigt noch einmal die Einhaltung des Bernoulli Schemas. Jetzt wenden wir unser Skript mit einer großen Anzahl Bernoulli Reihen (65000) auf die Ergebnisse des kurzen Test-Intervalls (Intervall B) an, und dann importieren wir die Ergebnisse der 65000 Bernoulli Modell Reihen in MS Excel, um ein Histogramm für die Verteilung des Gewinntrade-Verhältnis aufzubauen:
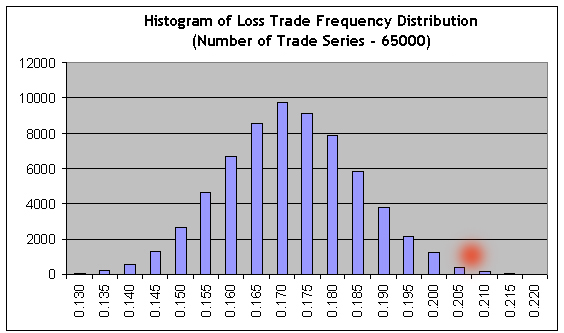
Es ist offensichtlich, dass zum Erreichen der Non-Profit, die Häufigkeit von Gewinnen und Verlusten umgekehrt auf das Verhältnis ihrer Mittelwerte bezogen werden muss: r = 21.69/82.94 = 0.2615. Folglich muss die Häufigkeit von Verlusttrades gleich f = r / ( 1+r ) = 0.2073 sein. Wir sehen, dass dieser Wert (siehe den roten Punkt) befindet sich weit in dem Bereich des rechten Schwanzes, wo die Summe an Balken nach rechts ungefähr 0,3% aller Histogramm ist, das heißt, die Non-Profit/Verlust Chance Wahrscheinlichkeit ist ungefähr 0,003. Annähernd der gleiche Wert wird erreicht bei der direkten Verwendung des Laplace Theorem.
Etwas ist faul im Staate Dänemark: Die Berichtdaten von Intervall A erzählen uns, dass in der ersten Hälfte von A, vor diesem wachsenden Intervall, fast genauso schnell fiel, und die fallende Periode ist nicht kürzer ist als B für die Anzahl an Trades. Wenn wir die Wahrscheinlichkeit von annähernd dem gleichen Intervall von fallendem Kontostand (stabiler Verlust) auf Grundlage unserer Testdaten von Intervall B schätzen, wird sie verschwinden (weil die Grenz-Häufigkeit f noch mehr nach rechts verschoben wird), und dies scheint widersprüchlich zu den experimentellen Daten.
Wahrscheinlich ist das Problem, dass solch lange Trade-Reihen mit der Rentabilität entsprechend des Intervall B eine sehr große Abweichung ist: der Test von Januar 1999 bis zum Anfang Mai 2008 zeigt, dass diese Strategie weder rentabel noch verlierend ist:
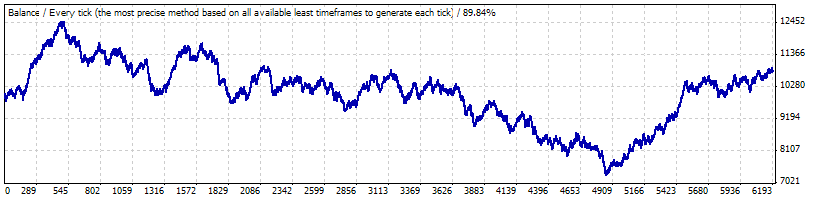
Die mathematische Erwartung eines Trade ist lediglich 0,17, und die "natürliche" Häufigkeit von Verlusttrades ist annähernd gleich zu den früher berechneten f (0.2073) und ergibt 0.2054.
Es ist klar, dass die Schätzung von Wahrscheinlichkeiten, basieren auf den Statistiken von seltenen Ereignissen (die Häufigkeit von Verlusttrades in Intervall B ist gleich 0.1706, und sie unterscheidet sich von der "natürlichen" in ungefähr 2.8 "Sigma" in die günstige Richtung) kann nicht zuverlässig genug sein. Aber wir können sie "wahre" Häufigkeit nicht mit Sicherheit kennen. Dennoch, kann der Begriff "Ausfall Verschiebung" für uns von Nutzen sein?
4. "Ausfall Verschiebung": Wahrscheinlichkeitsschätzung von Kurzfristigen "Schock" Rückgängen.
Annähernder Apparat, Versuch Nr. 2
Augenscheinlich können wir - wenn wir angemessene, nicht zu extreme Ziele setzen, entsprechend den "Schwänzen" der Verteilungen. Stellen wir die Aufgabe folgendermaßen: angenommen wir haben Testergebnisse für Intervall B. Wir sind sicher, dass dies Bernoulli Schema ist, und die mathematische Erwartung von Gewinn- und Verlusttrades hängt praktisch nicht davon ab, was mi dem Kontostand passiert. Basierend auf sehr optimistischen (tatsächlich falschen!) Schätzungen der Verlustwahrscheinlichkeit, versuchen wir unsere Chancen für kurze, aber tiefe "Schock" Rückgänge zu schätzen. Genau solche Rückgänge haben die verheerendsten Auswirkungen auf die Psyche eines Traders, weil ein Trader danach anfängt mystische Sätze zu sprechen, wie "der Markt hat sich geändert" oder sogar "hat einen Befehl bekommen".
Ich sollte hier hinzufügen, dass das Laplace Theorem hier keine große Hilfe wäre, weil der in seiner Formel enthaltene Wert n*p*q klein sein wird, ungefähr 10 und niedriger (dies entspricht ungefähr mehreren Dutzend Trades). Der Grundgedanke in der Grundlage dieser Berechnung ist, dass in sehr kurzen Trade-Reihen die Häufigkeit von Verlusten ausreichend von der "wahren" unterscheiden kann, d.h. von der Wahrscheinlichkeit: die Verteilung der Verlusthäufigkeit ist weit verbreitet, aufgrund der kleinen Anzahl an Tests.
Beachten Sie, dass die Schätzung von kurzfristigen Rückgängen die Aufgabe ist, die sich stark von dem Problem der Schätzung der maximalen Reihen-Länge unterscheidet, weil ein Rückgang nicht notwendigerweise nur aus Verlusttrades besteht. Verwenden wir unser Skript zum Erzeugen von 65000 Reihen der Länge 40 be einer "sehr günstigen" Verlusthäufigkeit 0.1706 ("Intervall B"), und dann bauen wir das Histogramm, wir das in Annähernder Apparat, Versuch Nr. 1:
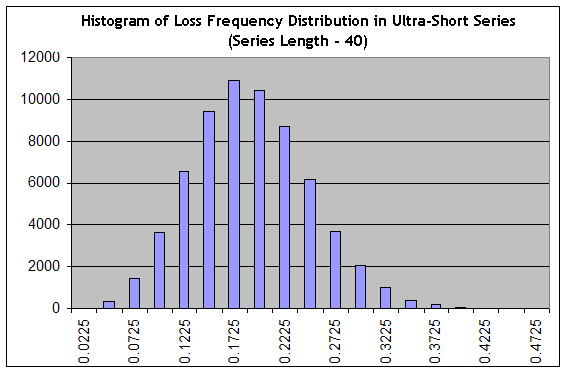
Wir sehen, dass das Setup sich entscheidend verändert hat: von einer scharfen hat die Verteilung sich in eine glatte gedreht, das heißt, ihre "relative Breite" ist gestiegen. Die Wahrscheinlichkeit, dass wir in 40-langen Reihen etwas in den Bereich von praktisch profitlosem Trading (z.B. bei der Häufigkeit von Verlusttrades gleich 0.1975 macht ein durchschnittlicher Trade 0,25 Punkte) zu einem stark verlierenden Trading (bei der Häufigkeit von Verlusttrades 0.3000, ist die Schätzung der mathematischen Erwartung in dieser Reihe gleich 0.7*20-0.3*80=-10 Punkte) erhalten werden, ist gleich zu der Summe von Spalten aus "0.2225" Spalte und rechts von ihr, was ungefähr 34% der Gesamtsumme an Spalten (65000) ist. Immerhin ist dies eine optimistische Einschätzung, weil die Verteilungsspitze bei der "optimistischen" Häufigkeit 0.1706 ist!
Rufen wir die Ergodizität Hypothese ins Gedächtnis, die eine Brücke zwischen der Wahrscheinlichkeitsverteilung und dem Handelsraum schafft, d.h. der reale Zeitraum, erhalten wir, dass mindestens 34% der Handelszeit das System keinen Gewinn machen oder im Durchschnitt verlieren wird. Diese Zahl korreliert sehr gut mit sen Daten in [4], nach denen ein Bernoulli System ungefähr in 35 bis 55% der gesamten Handelszeit im Rückgang bleibt.
Achten Sie auf die Tatsache, dass die tatsächliche Wahrscheinlichkeit auf einen Schock-Rückgang zu treffen nicht stark von der anfänglichen "günstigen" Häufigkeit anhängt, egal wie attraktiv sie aussieht. Dies ist das charakteristische Merkmal des Systems, das mit seiner Bernoullität verbunden ist, und dieses Ereignis kann nur durch das verbesserte Verhältnis von durchschnittlichen Gewinn- und Verlusttrades Ergebnissen geglättet werden.
Im Übrigen, genau diese Erwartung, basierend auf der Erzeugung von ultra-kurzen Reihen, ermöglicht häufig sehr zuverlässig die Testergebnisse eines ziemlich "rentablen" Systems durchzusieben, mit nur dutzenden von Trades in dem Testintervall: trotz der sehr positiven "mathematischen Erwartung" eines Trades, sind durch die kleine Anzahl an Trades die "Schock" Rückgänge unvermeidlich, im Fall der System-Bernoullität.
Fazit
Trotz der Tatsache, dass wir die logischen Konstruktionen, stolz " Mechanisches Handelssystem" genannt;, bauen möchten, erkennen wir oft nicht wie viel Zufälligkeit sie enthalten - eischließlich der, die wir nicht in den Testergebnissen antreffen ("Schwarze Schwäne").
Wie die Ergebnisse von aufeinanderfolgenden Trades in der binären Schreibweise ausgedrückt ("Erfolg" oder "Ausfall") sehr häufig dem Bernoulli Schema entsprechen, haben sie keinen ausdrücklichen Unterschied von der dem Hochwerfen einer Scheibe Brot mit Butter. Das bedeutet natürlich nicht, dass rentable Systeme unmöglich sind: eine Strategie kann sowohl rentabel als auch robust sein, auch wenn es idealerweise dem Bernoulli Schema entspricht. Diese klaren Ergebnisse aus einer Idee, dass wenn beides, die Wahrscheinlichkeit eines Gewinntrades und seine mathematische Erwartung, stabil höher sind als die von Verlusttrades, ist die Strategie offensichtlich rentabel.
Ein Leser, der zumindest manchmal in der Lage ist mit Mathematik als ein "Verwandter" zu "kommunizieren", sollte den Vorteil der Modelle recht gut verstehen - auch wenn sie bei weitem nicht deterministisch sind. Der Hauptwert von Modellen, die adäquat zu dem realen statistischen Phänomen sind ist, dass sie ermöglichen ein wertvolles Wissen über das Universum zu erhalten - das heißt, die Informationen, die nicht aus direkt aus spärlichen experimentellen Daten erhalten werden können. In diesem Fall ist der Wert des Bernoulli Schema wesentlich höher, wegen der extremen Einfachheit seiner Erzeugung und dem Fehlen "dicker Schwänze" in wichtigen Wahrscheinlichkeitsverteilungen.
Lassen Sie uns den Artikel mit einer sehr schwierigen Frage abschließen: Wahrscheinlich ist der analytische Teil der meisten TS nutzlos, und die wichtigsten Anstrenguen müssen in die effizienten und gut begründeten Money-Management Methoden investiert werden ("Analyse ist nichts, Money-Management ist alles"), nicht wahr?
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/1530
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Zweistufige Modifizierung von Offenen Positionen
Zweistufige Modifizierung von Offenen Positionen
 Show Must Go On, oder WIeder Einmal über ZigZagl
Show Must Go On, oder WIeder Einmal über ZigZagl
 Interaktion zwischen MetaTrader 4 und Matlab über DDE
Interaktion zwischen MetaTrader 4 und Matlab über DDE
 Integration von MetaTrader 4 Client Terminal mit MS SQL Server
Integration von MetaTrader 4 Client Terminal mit MS SQL Server
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.