知っておくべきMQL5ウィザードのテクニック（第82回）：DQN強化学習でTRIXとWPRのパターンを使用する

はじめに

ロボットやエキスパートアドバイザー(EA)を用いた取引では、構造化され再現性のある取引ルールの追求は、馴染みのあるテクニカル指標から始まることが一般的です。多くの場合、オシレーターや移動平均、価格ベースのパターンを組み合わせ、市場レジームの変化にも耐え得る戦略を構築しようとします。その中でも、TRIX（Triple Smoothed Exponential Moving Average、三重指数平滑移動平均）とWPR (Williams Percent Range)は、古典的かつ相性の良い組み合わせです。TRIXは短期的な価格ノイズを除去しながらモメンタムを捉え、WPRは買われ過ぎや売られ過ぎの状態を示します。この2つを組み合わせることで、トレンド転換点や継続局面をより明確に把握できる可能性があります。

従来、これらのインジケーターを用いた戦略は、固定ルールに依存する傾向がありました。たとえば、「TRIXがゼロラインを上抜け、かつWPRが-80以下のときに買い」や、「TRIXがピークを形成し、WPRが-20以上のときに売り」といった具合です。これらのルールは決定論的でバックテストもしやすい一方、市場が極めて動的であるにもかかわらず、関係性が静的であることを前提としているという共通の弱点があります。その結果、市場環境が変化すると有効性が低下し、こうした「絶対的な閾値」は頻繁な調整を必要とします。 

この課題に対するアプローチとして、強化学習が有力な選択肢となります。強化学習は、環境との相互作用や経験を通じて適切な行動を学習する機械学習手法です。あらかじめ決め打ちしたインジケーターの閾値に依存するのではなく、RLエージェントはさまざまな閾値や条件を探索し、長期的な報酬を最大化するよう取引判断を適応させていきます。トレーダーの視点では、単なるルールベースではなく、状況に応じて適応するシステムを構築できる可能性があります。

取引への応用において有望なRL手法の一つが、DQN (Deep Q Network)です。教師あり学習が入力と出力の直接的なマッピングを目的とするのに対し、DQNは特定の状態において、ある行動を取る価値を評価します。取引の文脈では、状態はインジケーターから得られる特徴量（変換済みデータ、バイナリ形式、あるいは生値）で表現できます。本記事では、その状態としてTRIXとWPRを用います。一方、行動は買い、売り、様子見といった選択肢になります。DQNフレームワークでは、これらの行動価値を固定ルールではなく、経験に基づいて評価し、調整していくことが可能です。

本記事は、連載「知っておくべきMQL5ウィザードのテクニック」の一環として、第82回ではTRIXとWPRのパターンをDQNベースの強化学習で扱います。まず、DQNの概要と強化学習アルゴリズム全体における位置付けを整理します。次に、「QuantileNetwork」クラスとして実装したQuantile Regression DQNのPython実装を紹介します。さらに、MetaTrader環境に強化学習モデルをデプロイする際の課題についても触れます。最後に、TRIXとWPRにおいて特定した3つのパターン（1、4、5）について、ストラテジーテスターの結果を確認します。本記事の全体的なテーマは、理論と実運用の橋渡しです。MQL5ウィザードを用いたハイブリッドなワークフローを通じて、強化学習の可能性と同時に、その実装上の落とし穴についても明らかにしていきます。

Pattern_1、Pattern_4、Pattern_5はチャート上で次のように表されます。

Pattern_1

弱気シグナルは、TRIXにおけるネガティブダイバージェンスと、WPRがレジスタンスまたは買われ過ぎ領域にある場合に記録されます。

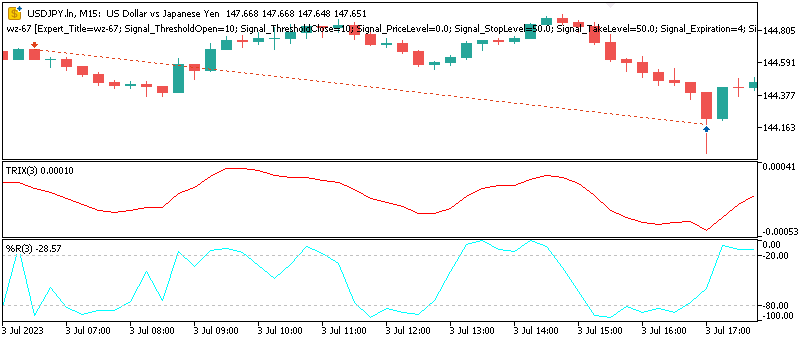
Pattern_4

強気シグナルは、TRIXが抵抗線を上抜けし、かつWPRが-50から-20の範囲に位置している場合に成立します。

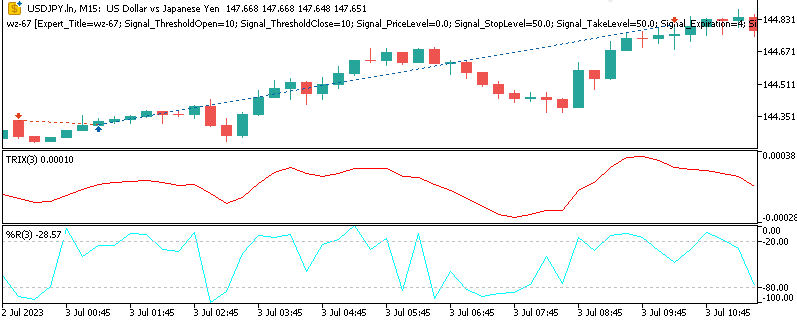
Pattern_5

弱気シグナルは、TRIXが売られ過ぎ水準から反転し、同時にWPRが売られ過ぎゾーンを抜けることで、弱気トレンドへの戻りが起こる可能性を示唆する場合に発生します。

DQN：価値ベース強化学習

DQNが金融取引に適している理由を理解するためにはまず強化学習の基本を整理することが有益です。強化学習とはエージェントが環境と相互作用しながら学習を進める体系的な手法です。各時間ステップにおいてエージェントは現在の状態を観測し行動を選択しその行動の望ましさに応じた報酬を受け取ります。エージェントの目的は時間を通じて累積報酬を最大化することであり、そのためには状態から行動への対応関係である方策を継続的に改善していく必要があります。 

金融市場において、状態は前述したような複数の技術指標で構成されることが一般的であり、生の数値から前処理を施した特徴量まで幅広く含まれます。行動は、買い、売り、様子見といった取引判断に対応します。報酬は通常、損益として定義され、取引コストや含み損益の変動を考慮する場合もあります。重要な点として、教師あり学習とは異なり、正解ラベルが存在しません。エージェントは、探索を通じて、どの選択が一貫して高い報酬につながるのかを、自ら発見する必要があります。

DQNはQ学習の考え方を基盤としています。Q学習は価値ベース強化学習の代表的手法の一つであり、Q値関数の概念を導入します。Q値関数Q(s,a)は状態sにおいて行動aを選択し、その後最適方策に従った場合に得られる、将来報酬の期待値を推定するものです。この関数が正確であれば、任意の時点における最適行動は最も高いQ値を持つものになります。従来のQ学習ではQ値を表形式で管理しますが、これは状態空間と行動空間が小さい場合にのみ現実的です。

しかし、金融市場では状態が連続的かつ高次元になるため表形式の手法は実用的ではありません。この制約を解決するのが深層学習です。ルックアップテーブルの代わりにニューラルネットワークを用いてQ値関数を近似します。この強化学習と深層学習の融合がDQNの本質です。

DQNの学習プロセスは、実際の取引と同様に反復的かつ適応的です。状態、行動、報酬、次状態、終了フラグからなる遷移データはリプレイバッファに保存されます。学習時には、このバッファからランダムに抽出されたミニバッチが使用されます。ランダムサンプリングをおこなうことで、連続データ間の相関を低減し学習の安定性を高めます。

さらにターゲットネットワークが用いられます。これはQネットワークのコピーであり、一定間隔または徐々に更新されます。目的は、自己更新による不安定なフィードバックループを防ぐことです。この更新はベルマン方程式に基づき、将来報酬を割り引いた推定値と実際の報酬との差を最小化するようにおこなわれます。探索性を維持するために、行動選択にはランダム性が導入されます。一般的にはεグリーディ方策が用いられ、εはほぼゼロに近い小さな浮動小数点値として設定されます。これにより単一パターンへの早期収束を防ぎます。

取引の観点では、このプロセスはネットワークが徐々に、どのインジケーターのパターンが特定の利益が見込める局面の前に現れやすいかを学習し、処理できるようになることを意味します。この過程は、履歴データへの過剰適合や直近データへの偏り(Recency Bias)を避けるために、代替のインジケーターオプションも試しながら進行します。  DQNはこの環境で優れた成果を発揮しやすい傾向があります。なぜなら、買い、売り、様子見といった離散的な行動空間に自然に適応できる能力を持っているからです。固定的な閾値に依存せず、適応的に学習できる点で優れています。さらに重要なのは、意思決定を行った直後に必ずしも収益性が顕在化するとは限らないという、遅延報酬の現実を取り込める能力を持っている点です。そのため、将来の報酬を割引して評価することで、DQNは短期的な利益と長期的な収益性とのバランスを取る傾向があります。

本記事の検証では、状態入力を決定するための特徴量としてTRIXとWPRを用いています。離散的な行動は、取引者が選択可能な取引ポジションに対応します。より高度な設計をおこなう場合には指値注文なども含めることができますが、ここでは買い、売り、様子見の3つに限定します。履歴データを用いてDQNを学習させることで、固定ルールを適用しただけでは把握しにくい、これら指標間の相互作用をモデルが捉えることが可能になります。このアプローチにより、ネットワークは行動に応じた相対的な価値を割り当てられるようになります。その結果、生のテクニカル指標シグナルは、適応性と先見性を兼ね備えた実行可能な取引方針へと変換されます。

価値ベース強化学習と方策・Actor-Critic手法の比較

ここで、これら2つの手法の違いについても触れておきます。DQNは価値ベース強化学習アルゴリズムに属し、状態から行動への直接的な擬似マッピングを学習するのではなく、行動の価値を推定することに重点を置いています。言い換えれば、価値ベースのエージェントは「今この行動を取った場合、長期的にどれだけの報酬を得られるか」という問いに答えようとします。一方で、他の強化学習手法は、行動の価値評価に重点を置くのではなく、方策を直接形成したり、価値評価と方策学習の両方を何らかの形で組み合わせたりすることに焦点を置きます。これらの違いを理解することは、各手法が市場での取引にどの程度適合するかを検討する際に非常に重要です。 

方策ベースの手法、例えばREINFORCEや近接方策最適化(PPO: Proximal Policy Optimization)は、Q値の推定自体をおこないません。代わりに、方策自体をパラメータ化して、可能な行動に対する確率分布として表現します。学習の過程では、累積報酬が高くなる行動がより頻繁にサンプリングされるように方策が調整されます。このアプローチは、行動空間が連続であり、すべての選択肢を離散化することが現実的でない環境に特に有効です。トレーダーにとって、方策ベースの手法は、理論上、ポジションサイズを連続的に決定したり、売り/買いを+/-で表すことも可能で、本記事で扱う買い、売り、様子見という離散的選択肢に制限されません。しかし、方策勾配法は更新時の分散が大きく、DQNのような価値ベース手法と比べると安定化のためにより多くのデータを必要とする傾向があります。

Actor-Critic手法は、これら2つの利点を組み合わせることを目指します。この場合、Actorは方策を指し、どの行動を取るかを決定します。一方Criticは、選択された行動の価値を評価します。この2つの要素が協働することで、学習過程の安定性を高め、方策の更新効率を向上させることができます。金融市場では、Actor-Critic手法により、モデルは取引行動の強度を変化させながら提案でき、同時にCriticがその行動を洗練させることが可能です。代表的な手法としてA2C (Advantage Actor-Critic)、DDPG (Deep Deterministic Policy Gradient)、TD3 (Twin Delayed DDPG)などがあります。

価値ベース手法と方策ベース手法の大きな違いは、簡便さと柔軟性のトレードオフにあります。DQNは、行動空間が自然に離散的な場合には実装が比較的簡単であり、遅延があるものの離散的な報酬が多い環境では収束も速い傾向があります。これは、限られた選択肢の中で意思決定を行う取引シナリオにおいて有利です。一方で方策ベースやActor-Critic手法は強力ですが、理論上の話ではありますが、計算リソースの消費が増え、MetaTraderのようなプラットフォーム上でONNXモデルを効率的にバックプロパゲーションすることがネイティブに扱えないため、実装が難しくなる場合があります。この点については後述します。

PythonによるQuantileNetworkの実装

この記事のエキスパートアドバイザー(EA)で用いる理論を支えるコードは、分位点回帰(Quantile Regression)を用いてDQNを取引コンテキストに適応させる具体例として非常に参考になります。以下に示します。

# ---------------------------- QR-DQN Core ---------------------------

class QuantileNetwork(nn.Module):
    def __init__(self, state_dim: int, action_dim: int, hidden: int = 256, num_quantiles: int = NUM_QUANTILES):
        super().__init__()
        self.num_quantiles = num_quantiles
        self.action_dim = action_dim
        self.fc1 = nn.Linear(state_dim, hidden)
        self.fc2 = nn.Linear(hidden, hidden)
        self.fc3 = nn.Linear(hidden, hidden)
        self.fc4 = nn.Linear(hidden, action_dim * num_quantiles)
        fanin_init(self.fc1.weight); nn.init.zeros_(self.fc1.bias)
        fanin_init(self.fc2.weight); nn.init.zeros_(self.fc2.bias)
        fanin_init(self.fc3.weight); nn.init.zeros_(self.fc3.bias)
        nn.init.uniform_(self.fc4.weight, -3e-3, 3e-3); nn.init.zeros_(self.fc4.bias)

    def forward(self, x):
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = F.relu(self.fc3(x))
        q = self.fc4(x)  # [batch, action_dim * num_quantiles]
        # FIX: only one inferred dimension allowed — reshape explicitly
        return q.view(x.size(0), self.num_quantiles, self.action_dim)  # [batch, N, A]

    def q_values(self, x):
        q = self.forward(x)            # [batch, N, A]
        return q.mean(dim=1)           # [batch, A]

Pythonでの中心的なクラスであるQuantileNetworkは、Q関数の近似を担当します。これは価値ベース強化学習の中核となる部分です。通常のDQNでは各行動に対して単一のQ値を出力しますが、Quantile DQNでは、複数の分位点を用いることで、結果の分布全体を予測できるように拡張されています。これは、取引において、市場の不確実性が平均的な期待値と同じくらい重要である場合に特に有用です。複数の分位点を用いて完全な分布をモデル化することで、ネットワークは期待される報酬だけでなく、各行動に伴うリスクも捉えることが可能になります。

QuantileNetworkクラスは、4層の全結合ニューラルネットワークとして構成されます。この4層のうち最初の3層は線形変換をおこない、その後にReLUなどの非線形活性化関数が適用されます。これは、入力状態と出力行動の間の非線形関係をネットワークが認識できるようにするためです。4層目であるヘッド層が出力層に相当し、その形状は行動次元と分位点数に対応するように設定されています。

学習および推論時には、このフラットな出力をバッチサイズ×分位点数のテンソルに変換します。実務上、これは各状態入力に対して、すべての可能な行動に対する分位点ベースのQ値セットが必要であることを意味します。これらの分位点を平均することで、意思決定に用いる従来型のQ値を得ることも可能であり、必要に応じてリスク分析に不可欠な柔軟性を保持できます。

重みの初期化は非常に慎重におこなわれます。最初の層にはfan-inスケーリングを用い、出力層には小さな一様分布を使用しています。強化学習では、初期の重み分布が不安定だと、データ中のノイズが増幅され学習が不安定になる傾向があります。初期重みにバランスを持たせることで、QuantileNetworkは最適化やバックプロパゲーションの過程で、早期発散をある程度防ぎつつ収束性を向上させることが可能になります。

私たちのDQNで使用するエージェントは、メインのQuantileNetworkとそのコピーであるターゲットネットワークを保持し、学習過程を統括します。このコピーはソフト更新機構によって定期的に更新され、学習で用いるターゲットが不規則に変化するのではなく、滑らかに変化するようにします。さらに、エージェントは最適化手法の起動にも関与します。今回の目的ではAdamを用いており、これは強化学習で特徴的なノイズの多い勾配更新に適しています。エージェントのコードは以下の通りです。

class QRDQNAgent:
    def __init__(self, state_dim: int, action_dim: int, hidden: int = 256):
        self.state_dim = state_dim
        self.action_dim = action_dim
        self.num_quantiles = NUM_QUANTILES

        self.net        = QuantileNetwork(state_dim, action_dim, hidden).to(DEVICE)
        self.target_net = QuantileNetwork(state_dim, action_dim, hidden).to(DEVICE)
        self.target_net.load_state_dict(self.net.state_dict())

        self.optimizer = optim.Adam(self.net.parameters(), lr=LR)
        self.replay_buffer = ReplayBuffer(capacity=100_000, state_dim=state_dim)

        # quantile fractions τ_i (midpoints)
        self.taus = torch.linspace(0.0 + 1.0/(2*self.num_quantiles),
                                   1.0 - 1.0/(2*self.num_quantiles),
                                   self.num_quantiles, device=DEVICE).view(1, -1)  # [1, N]

    @torch.no_grad()
    def act(self, state: torch.Tensor, epsilon: float = 0.1) -> int:
        if np.random.rand() < epsilon:
            return np.random.randint(self.action_dim)
        q_vals = self.net.q_values(state.unsqueeze(0).to(DEVICE))  # [1, A]
        return int(torch.argmax(q_vals, dim=1).item())

    def _quantile_huber_loss(self, preds: torch.Tensor, target: torch.Tensor, taus: torch.Tensor) -> torch.Tensor:
        """
        preds:  [B, N]   (predicted quantiles for chosen action)
        target: [B, N]   (target quantiles)
        taus:   [1, N]
        """
        diff = target.unsqueeze(1) - preds.unsqueeze(2)  # [B, N, N]
        huber = torch.where(diff.abs() <= KAPPA,
                            0.5 * diff.pow(2),
                            KAPPA * (diff.abs() - 0.5 * KAPPA))
        tau = taus.view(1, -1, 1)  # [1, N, 1]
        loss = (torch.abs(tau - (diff.detach() < 0).float()) * huber).mean()
        return loss

    def learn(self, batch_size: int = BATCH_SIZE):
        if self.replay_buffer.size < batch_size:
            return

        s, a, r, ns, d = self.replay_buffer.sample(batch_size)

        with torch.no_grad():
            # Double DQN selection w/ target evaluation (simple variant)
            q_next_online = self.net.q_values(ns)                  # [B, A]
            a_next = q_next_online.argmax(dim=1, keepdim=True)     # [B,1]
            q_next_all = self.target_net(ns)                       # [B, N, A]
            q_next_sel = q_next_all.gather(2, a_next.unsqueeze(1).expand(-1, self.num_quantiles, 1)).squeeze(-1)  # [B, N]
            target = r + (1.0 - d) * GAMMA * q_next_sel            # broadcast [B,1] + [B,N] -> [B,N]

        q_preds_all = self.net(s)                                  # [B, N, A]
        a_expanded  = a.view(-1, 1, 1).expand(-1, self.num_quantiles, 1)  # [B, N, 1]
        q_preds     = q_preds_all.gather(2, a_expanded).squeeze(-1)       # [B, N]

        loss = self._quantile_huber_loss(q_preds, target, self.taus)

        self.optimizer.zero_grad()
        loss.backward()
        self.optimizer.step()

        # Soft update target
        with torch.no_grad():
            for tp, sp in zip(self.target_net.parameters(), self.net.parameters()):
                tp.data.mul_(1.0 - TARGET_TAU)
                tp.data.add_(TARGET_TAU * sp.data)

    # -------------------- ONNX Export --------------------
    def export_qnet_onnx(self, path: str):
        """
        Export a wrapper that outputs mean Q-values: [1, action_dim]
        """
        class QValuesHead(nn.Module):
            def __init__(self, net: QuantileNetwork):
                super().__init__()
                self.net = net
            def forward(self, x):
                return self.net.q_values(x)

        wrapper = QValuesHead(self.net).to(DEVICE).eval()
        dummy = torch.zeros(1, self.state_dim, dtype=torch.float32, device=DEVICE)
        torch.onnx.export(
            wrapper, dummy, path,
            export_params=True, opset_version=17, do_constant_folding=True,
            input_names=["state"], output_names=["q_values"], dynamic_axes=None
        )
        return path

状態遷移を保存するために、リプレイバッファの実装も必要です。エージェントはこのバッファからランダムに小さなバッチをサンプリングすることができ、前述の通り学習データの相関を減らして安定的な学習を支援します。

学習過程では、Quantile Huber Lossを計算します。これは予測分位点とターゲット分位点とのギャップを評価する指標であり、外れ値に対しても頑健に設計されています。ターゲットの構築には従来のDQNアプローチを用い、次の行動はオンラインネットワークに従って選択されますが、その価値の評価はターゲットネットワークによっておこなわれます。これにより、選択と評価に同じネットワークを使用した場合に生じやすいバイアスを低減できます。Quantile Huber Lossは、予測の平均がずれている場合だけでなく、可能なリターン分布全体の偏差に対してもペナルティを与えます。この設計により、変動が大きく不確実な市場でもモデルの頑健性が向上します。

また、環境クラスであるCustomDataEnvも用意しています。このクラスは、エージェントが履歴データとどのように相互作用するかを定義します。環境は、TRIXとWPRのインジケーターパターンから作成された特徴量行列と、これらのパターン出現後の価格変動を示すターゲット配列を入力として受け取ります。各ステップでエージェントは、買い、売り、様子見のいずれかの行動を選択します。環境は次の状態と、行動と観測リターンの積に取引コストを差し引いた報酬を返します。これにより、履歴データを逐次的な意思決定環境に変換し、擬似的なライブ取引を模倣することが可能になります。

最後に、ONNXへのエクスポート機能があります。MetaTraderでは、エクスポートされたONNXモデルのバックプロパゲーションは使用できませんが、これはPythonで学習したモデルを使用する場合の唯一の方法です。エクスポートは推論専用であり、QuantileNetworkクラスを軽量のヘッドでラップし、平均Q値を出力します。これにより、EAでの評価に十分な効率性とコンパクトさが確保されます。過去の記事でも述べた通り、入力層と出力層のサイズを確認することは、学習済みモデルをライブ環境で安全に使用する上で非常に重要です。

まとめると、QuantileNetworkとそのエージェントラッパーは、強化学習の概念を実用的なコードに落とし込む方法を示しています。分位点回帰の使用により報酬分布を捉えて適応性を高め、リプレイバッファやターゲットネットワークによって学習の安定性を確保し、ONNXにより実運用への統合も可能になります。トレーダーにとって、このPythonコードは、単なるインジケーターシグナルから堅牢でデータ駆動型の意思決定へ移行するための重要な第一歩を示しています。

強化学習とMQL5統合の課題

Pythonでの利用やMQL5への橋渡しにより、強化学習を履歴データ上で学習させる方法を示すことはできますが、こうしたモデルをMetaTraderに移行する際にはいくつかの問題が生じます。これらの問題については、過去の記事でも触れており、特に前回の記事の結論では、強化学習で学習させたモデルを使用した際の制約について示しました。主な制約は、MQL5やその他のプラットフォームではONNXファイルのバックプロパゲーションがサポートされていないことです。ONNXは少なくとも最新バージョンでは、順伝播のみを目的として設計されています。 

Python内では、オリジナルのネットワークコードと高速なテンソル演算ライブラリを用いることで、効率的にネットワークを学習させ、バックプロパゲーションをおこなうことができます。しかし、MQL5は本質的に取引ロジックを効率的かつ軽量に実行するために設計されており、大規模な数値計算には適していません。このため、ONNXをEAに埋め込む、もしくはサンドボックスから参照する場合、順伝播による推論のみが可能です。最新のONNX仕様では、エクスポートされたモデルの重みを更新することはできません。 

この制約により、妥協策を取らざるを得ません。つまり、学習済みモデルの重みをそのまま利用する以外の方法は現状ではなく、これが理由でMQL5で強化学習を活用する際には、ONNXとして1つのネットワークモデルだけをエクスポートすることになります。従来の強化学習ループでは、エージェントは環境と継続的に相互作用し、経験を蓄積すると同時にQ値をリアルタイムで調整します。しかし、MQL5の文脈では、学習はPython上で完全にオフラインでおこなわれるべきです。モデルは履歴データで一度学習した後、そのネットワークの重み、層、バイアスをエクスポートし、静的な「Actor」としてデプロイされます。

このため、MetaTrader内でのいわゆる強化学習システムは、実質的には教師あり学習モデルとなります。入力特徴量であるTRIXやWPRから、取引行動の相対的望ましさを示す出力値をマッピングするだけであり、ライブ取引中やフォワードテスト中に新しい状態に適応することはできません。

もう一つの問題は、ONNXランタイムとMQL5のインターフェースにおける期待値の整合性です。ONNXモデルは基本的に定数変数であり、各層に対して特定の入力および出力形状を期待します。これらの形状はPythonでバッチ次元や浮動小数点精度（32または64ビット）とともに定義されます。MQL5でONNXハンドルを初期化する際に、Pythonで設定した形状と一致しない場合、ランタイムの初期化は失敗します。多くの場合これは解決可能ですが、入力層と出力層の形状を確認せずにエクスポートしてしまうと問題が発生しやすく、注意が必要です。

幸いなことに、Pythonで層の形状を出力して確認できるほか、MetaEditorにはツールメニューからニューラルネットワークビューアが用意されています。このアプリケーションを起動すると、別ウィンドウでエクスポートされたONNXファイルを開き、入力層と出力層のサイズや形状など詳細なレイアウトを確認できます。

教師あり学習としての妥協策

Pythonで学習させた強化学習モデルをONNXとしてエクスポートすると、MQL5内での用途は大きく変わります。このモデルはもはや本来意図されていた通りの適応型学習器ではなく、静的な意思決定エンジンとして扱われます。実務上は、エクスポートされた「Actor」ネットワークは、他の予測用教師あり学習ネットワークと同様に使用されます。ただし、このモデルは強化学習ネットワークとして学習されているため、層数や各層のサイズ、その他のアーキテクチャの構成が、教師あり学習モデルとして設計され、学習されたものほど扱いやすくはない場合があります。それでも、この妥協策により、PythonやONNXなしでも可能ではありますが、MQL5内で効率的に組み込むことが難しい追加ロジックを統合することが可能になります。

この妥協策に基づく実装では、まずActorのONNXファイルをMQL5にリソースとして埋め込むところから始めます。これらのONNXファイルには、学習済みQuantileNetworkの重み、バイアス、層のサイズなどが含まれています。ファイルはMQL5ランタイムが効率的に処理できる形式に圧縮されます。カスタムシグナルクラスでは、Pattern_1、Pattern_4、Pattern_5用の3つのモデルが参照されます。それぞれのモデルは、TRIXとWPRから抽出された独自のインジケーターパターンセットに対応しています。初期化時に、EAはこれらのバッファからONNXハンドルを作成し、取引エントリー条件の評価時にすべてのネットワークが呼び出せるようにします。この時点では、モデルは再学習や変更はおこなわれず、単にメモリ上にロードされ、参照用ツールとして利用可能な状態になります。

シグナルロジック

ONNXをエクスポートしてMQL5に埋め込んだ後の重要なステップの一つは、シグナルコードとポジション条件の作成です。ここで作成するコードは、QuantileNetworkの出力を実際の取引条件に変換する役割を担います。このロジックは、カスタムシグナルクラス内のLongConditionおよびShortCondition関数に記述されており、以下のように実装されます。

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalRL_TRX_WPR::LongCondition(void)
{  int result  = 0, results = 0;
   vectorf _x;
   _x.Init(2);
   _x.Fill(0.0);
//--- if the model 1 is used
   if(((m_patterns_usage & 0x02) != 0) && IsPattern_1(POSITION_TYPE_BUY))
   {  _x[0] = 1.0f;
      double _y = RunModel(0, POSITION_TYPE_BUY, _x);
      if(_y > 0.0)
      {  result += m_pattern_1;
         results++;
      }
   }
//--- if the model 4 is used
   if(((m_patterns_usage & 0x10) != 0) && IsPattern_4(POSITION_TYPE_BUY))
   {  _x[0] = 1.0f;
      double _y = RunModel(0, POSITION_TYPE_BUY, _x);
      if(_y > 0.0)
      {  result += m_pattern_4;
         results++;
      }
   }
//--- if the model 5 is used
   if(((m_patterns_usage & 0x20) != 0) && IsPattern_5(POSITION_TYPE_BUY))
   {  _x[0] = 1.0f;
      double _y = RunModel(0, POSITION_TYPE_BUY, _x);
      if(_y > 0.0)
      {  result += m_pattern_5;
         results++;
      }
   }
//--- return the result
//if(result > 0)printf(__FUNCSIG__+" result is: %i",result);
   if(results > 0 && result > 0)
   {  return(int(round(result / results)));
   }
   return(0);
}
//+------------------------------------------------------------------+
//| "Voting" that price will fall.                                   |
//+------------------------------------------------------------------+
int CSignalRL_TRX_WPR::ShortCondition(void)
{  int result  = 0, results = 0;
   vectorf _x;
   _x.Init(2);
   _x.Fill(0.0);
//--- if the model 1 is used
   if(((m_patterns_usage & 0x02) != 0) && IsPattern_1(POSITION_TYPE_SELL))
   {  _x[1] = 1.0f;
      double _y = RunModel(0, POSITION_TYPE_SELL, _x);
      if(_y < 0.0)
      {  result += m_pattern_1;
         results++;
      }
   }
//--- if the model 4 is used
   if(((m_patterns_usage & 0x10) != 0) && IsPattern_4(POSITION_TYPE_SELL))
   {  _x[1] = 1.0f;
      double _y = RunModel(0, POSITION_TYPE_SELL, _x);
      if(_y < 0.0)
      {  result += m_pattern_4;
         results++;
      }
   }
//--- if the model 5 is used
   if(((m_patterns_usage & 0x20) != 0) && IsPattern_5(POSITION_TYPE_SELL))
   {  _x[1] = 1.0f;
      double _y = RunModel(0, POSITION_TYPE_SELL, _x);
      if(_y < 0.0)
      {  result += m_pattern_5;
         results++;
      }
   }
//--- return the result
//if(result > 0)printf(__FUNCSIG__+" result is: %i",result);
   if(results > 0 && result > 0)
   {  return(int(round(result / results)));
   }
   return(0);
}

これら2つのメソッドは、EAが買いまたは売りのポジションをオープンするタイミングを決定する核となる部分です。これは、テクニカルインジケーターによるパターン認識と強化学習ネットワークの出力による意思決定を統合しておこなわれます。

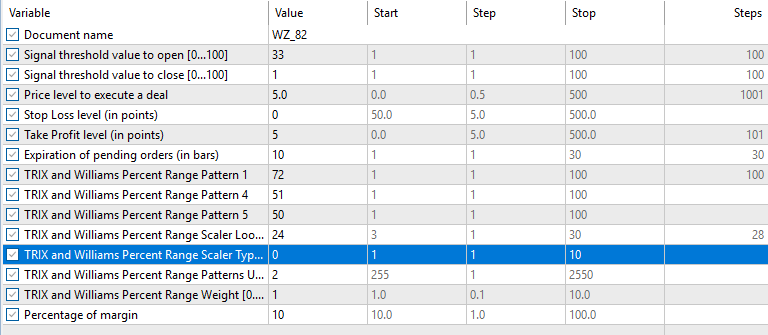
Long関数はまず、入力状態を表す特徴量ベクトルを宣言することから始まります。このベクトルxは初期化され、ゼロで埋められます。その後、使用されるパターンに応じて、2つのインデックスのうち1つに1を割り当てます。ここで重要なのが入力パラメータ「patterns-used」の意味です。

たとパターンのインデックスが1の場合、パラメータ「Patterns-Used」は2の1乗、つまり2に設定します。同様に、インデックスが2の場合は2^2=4と計算できます。このパラメータの最大値は1023で、10パターンすべてを利用する場合に対応します。0から1023の範囲で、2の累乗でない値を設定すると複数のパターンを組み合わせることを意味します。読者はEAに複数パターンを使用させる設定を試すことも可能です。しかし、過去の記事で提示した議論やテスト結果に基づき、本連載では現時点でこの方法は扱いません。

実装ではPattern_1、Pattern_4、Pattern_5のみを使用するため、チェック対象もこの3つだけです。Pattern_1の条件が満たされると、ベクトルの最初のインデックスに1を割り当てます。Pattern_4やPattern_5の場合も同様です。紙面上は複数パターン使用に対応させることも可能ですが、ここでは必ず1パターンずつのみを使用します。実際、複数パターンを使用するとシグナル同士が打ち消し合い、テスト結果が非常に不安定になることが予想されます。

使用中のパターンが一致した場合、最適化済みの重みとONNXによる順伝播が条件の最終結果に反映されます。ShortConditionも同様のロジックで、売りパターンの機会に焦点を当てています。x特徴量ベクトルを宣言し、同様のパターンチェックをおこないます。主な違いは、パターンがQuantileNetworkで確認された場合、1を割り当てるインデックスが買い条件では最初のインデックスですが、売り条件では2番目のインデックスに割り当てられる点です。その他の重み平均や最終結果の計算は、LongConditionと同じ手順でおこなわれます。

テスト結果

EURUSDの4時間足を対象に、2023年7月1日から2024年7月1日までの期間で学習および最適化をおこないました。フォワードウォークの期間は2024年7月1日から2025年7月1日までで、Pattern_1、Pattern_4、Pattern_5に対して以下の結果が得られました。

Pattern_1

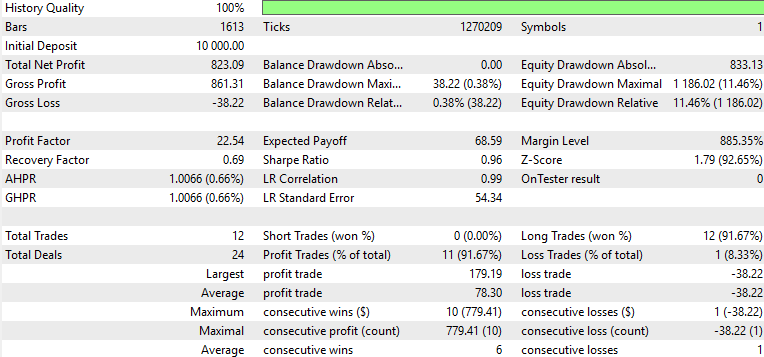
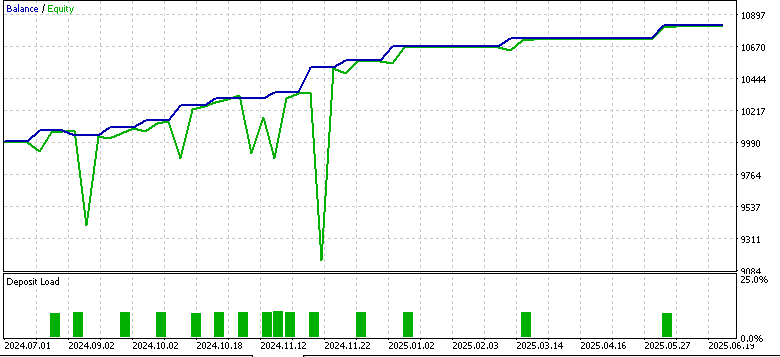
Pattern_4

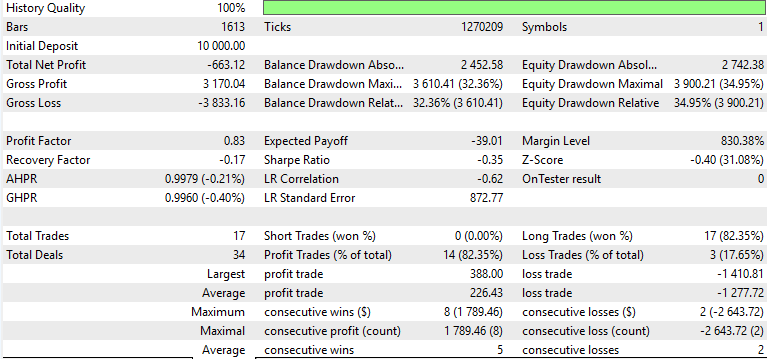
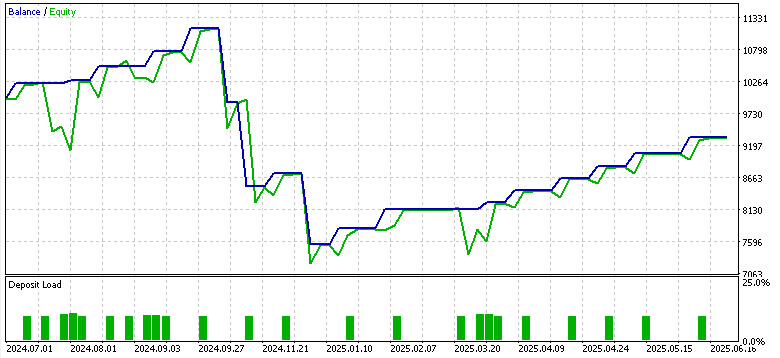
Pattern_5

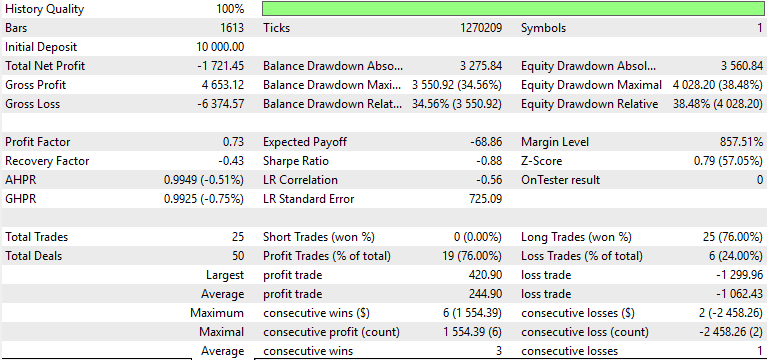
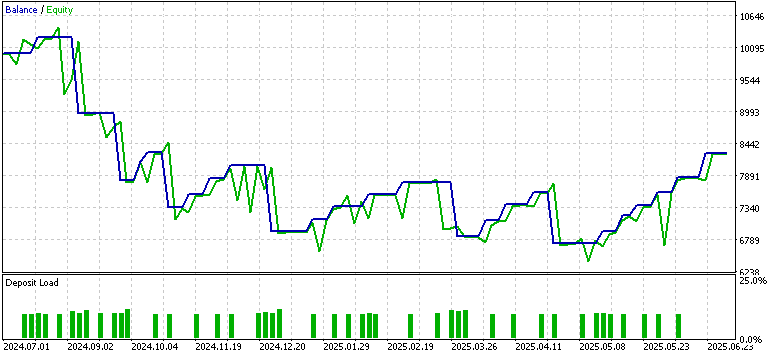
フォワードウォークで利益を上げたのはPattern_1のみで、Pattern_4およびPattern_5は苦戦しました。もちろん、これは金融アドバイスではない点にご注意ください。利益が出なかった原因としては、弱いまたは適応されていないActorネットワークを教師あり学習モデルとして使用したことが影響している可能性があります。ここでの目的は、従来どおり「即時に使える解決策」を提供することではなく、多様な可能性を探求し、どのようなことが可能かを示すことにあります。最終的な作業や重要な検証と判断は、読者ご自身が責任を持っておこなう必要があります。

結論

本記事では、TRIXとWPRのシグナルパターンを強化学習フレームワークで扱い、MQL5の現状における可能性と限界の両方を示しました。Pythonモジュールは常に更新されているため、将来的にはONNXでエクスポートしたネットワークもバックプロパゲーションで更新可能になる可能性があります。しかし現状ではそれは不可能であり、これが制約となります。モデルはオフラインで学習させた後、「固定」された状態で推論エンジンとして運用する必要があります。

名前	説明
WZ_82.mq5	ヘッダに参照ファイルを示すウィザード組み立てEAのメインファイル
SignalWZ_82.mqh	DQNをインポートするカスタムシグナルクラス
82_5_0.onnx	エクスポートされたPattern_5用のONNXモデル
82_4_0.onnx	エクスポートされたPattern_4用のONNXモデル
82_1_0.onnx	エクスポートされたPattern_1用のONNXモデル

新規読者向けの添付ファイルの使用方法に関するガイダンスは、こちらでご覧いただけます。