機械学習における量子化（第1回）：理論、コード例、CatBoostでの実装解析

はじめに

この記事では、ツリーモデルの構築における量子化の理論的応用について考察します。複雑な数式は使用しません。この記事を書いている間に、さまざまな著者の科学的著作では統一された用語が確立されていないことがわかりました。したがって、私の意見で、意味を最もよく反映する用語オプションを選択します。それに、他の研究者が放置している事柄については、私自身の用語を使用するつもりです。この記事では、私が以前「PythonやRの知識が不要なYandexのCatBoost機械学習アルゴリズム」稿で説明した用語や概念を使用します。従って、今回の記事を読む前に、その記事をよく理解しておくことをお勧めします。

この記事では、訓練済みニューラルネットワークのサイズを小さくするために量子化を適用する可能性については考えません。現時点でこの問題に関して個人的な経験を持っていないからです。

期待できることは以下の通りです。 

• 記事の最初の部分には量子化についての入門的な理論的資料が含まれており、プロセスの目標と本質を理解するのに役立つ
• 記事の第2部では、一様量子化法について、MQL5コードを例にして説明される
• 記事の第3部では、CatBoostを例に量子化処理の実装について考える

 

1. 標準用途

では、量子化とは何で、何故使用されるのかを考えてみましょう。

まず、データについて少しお話します。モデルを作る（訓練をおこなう）ためには、テーブルに綿密に収集されたデータが必要になります。そのようなデータのソースは、ターゲット（モデルによって決定される、例：取引シグナル）を説明することができる任意の情報とすることができます。データソースは、予測子、特徴、属性、因子など、さまざまに呼ばれます。データラインの発生頻度は、その現象に匹敵するプロセス観測の発生頻度によって決定され、それについて情報が収集され、機械学習を使用して研究されます。得られたデータの総体をサンプルと呼びます。

サンプルは代表的であることもあります。これは、その中に記録された観測が、研究対象の現象のプロセス全体を記述している場合です。また、非代表的であることもあります。これは、収集可能な限りのデータがあり、研究対象の現象のプロセスの部分的な記述しかできない場合です。原則として、金融市場を扱う場合、起こりうることすべてがまだ起こっていないという事実のために、代表的でないサンプルを扱うことになります。このため、（過去に発生したことのない）新たな事象が発生した場合に、金融商品がどのように動くかはわかりません。しかし、「歴史は繰り返す」という知恵は誰もが知っています。アルゴリズムトレーダーが調査において依拠するのはこの観測であり、新しい事象の中に以前の事象と類似したものがあり、その結果が特定された確率と類似していることを期待します。

その論理的内容に従って（測定尺度に従って）、予測子の数値指標は次であることができます。

• 両極的：観察された現象の固定した属性の存在を確認または否定します。
• 定量的（計量尺度）：ある種の測定指標を使用して現象を説明します。例えば、速度、何かの座標、サイズ、イベントの開始からの経過時間、および測定可能なその他の多くの特性（それらの派生物を含む）が挙げられます。
• カテゴリカル（名義尺度）：1つの論理的グループに含まれる異なる観察可能な対象や現象に関する信号で、原則として整数で表されます。例は、曜日、価格トレンドの方向、指示/抵抗レベルの通し番号です。
• ランク（順序尺度）：何かの優劣の度合いを表します。文脈やロジックによっては他のタイプの指標に分類されることもあるため、独立したグループに割り当てられることはほとんどありません。例は、行動の順番や、他の同様の実験との相対的な結果の評価という形での実験結果です。

したがって、サンプルは、それ自身の数値指標を持つ異なる予測子を含み、これらのデータは、全体として、観察された現象を記述し、その特徴またはタイプは、目的関数に記述されます。サンプルの目的関数は、数値指標でもカテゴリカル指標でも大丈夫です。さらに本文では、カテゴリカル目的関数、そしてより大きな範囲での、両極的目的関数について考えてみます。

ウィキペディアには次のような定義があります。

量子化とは、数学およびデジタル信号処理において、大きな集合（多くの場合、連続集合）からの入力値を、（可算な）小さな集合（多くの場合、有限個の要素を持つ）の出力値にマッピングするプロセスのことです。信号値は、エンコード方法に応じて、直近のレベル、または直近のレベルの低い方か高い方に丸めることができます。これはスカラー量子化と呼ばれます。ベクトル量の取り得る値の空間を有限個の領域に分割し、これらの値をこれらの領域の識別子に置き換えるベクトル量子化もあります。 

 私はこの短い定義が好きです。

データの量子化とは、観測情報を圧縮（符号化）する方法であり、その測定尺度の精度を許容できる範囲で損なうことです。圧縮（符号化）はオブジェクトの離散性を意味し、それはそれらの同じタイプと均質性、または単に類似性を意味します。類似性の基準は、選択されたアルゴリズムとそれに組み込まれたロジックによって異なる場合があります。

データの量子化は、特にアナログ信号からデジタル信号への変換や、それに続くデジタル信号の圧縮など、あらゆるところで使われています。例えば、カメラ行列から受信したデータは、RAWファイルとして記録し、すぐに（または後でコンピュータで）jpgまたは他の便利なデータ保存形式に圧縮することができます。

MetaTrader 5ターミナルのローソク足またはバーの形でデータのグラフ表示を見ると、選択した時間尺度でティックを量子化する作業の結果がすでに表示されています。連続的なデータストリームを時間的に量子化することは、通常、標本化（または離散化）と呼ばれます。

一般的に、標本化とは、ある頻度で観測された特性を時間にわたって記録するプロセスです。しかし、これがサンプルとしてデータが収集される頻度であると仮定するならば、定義は以下のように調整されるべきです。「標本化とは、観測特性を記録するプロセスであり、その頻度は閾値の活性化中に与えられた関数によって決定される」。ここでいう関数とは、それ自身の固有の論理に従って、データを受け取るための信号を与えるあらゆるアルゴリズムを意味します。例えば、MetaTrader 5では、まさにこのアプローチが見られます。非取引日には、終値が時間経過とともに繰り返されるのではなく、チャート上に情報がない、つまり標本化レートがゼロになるのです。

量子化アルゴリズムの簡単な例は、ヒストグラムの構築です。この方法のアルゴリズムは非常にシンプルです。

• 指標（ここでの場合は予測子）の最大値と最小値を求めます。
• 指標の最大値と最小値の差を計算します。
• 上の手順の結果のデルタを整数、例えば10、または観測の数に応じて（KarlPearsonが推奨しているように）で割ります。最初の測定単位での分割手順を取得します。これが、新しい測定尺度の読み取り値となります。
• 次に独自の分割で独自の尺度を構築する必要があります。これは、単純に手順に読み取り値の通し番号を掛けることでおこなわれます。
• 次に、各観測値が新しい測定尺度の範囲に割り当てられ、各範囲の観測が別々に合計されます。

このアルゴリズムの結果、図1に示すヒストグラムが得られます。

 

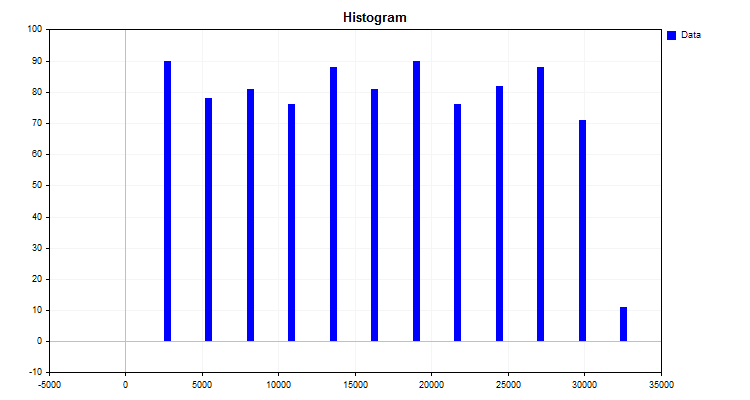
図1

ヒストグラムは、新しい測定尺度にしたがってデータがどのように分布しているかを示しています。その分布の外観から、記述統計の装置を通して、分布密度のタイプを仮定することができ、これは有限量子化法を選択するのに有用です。分布密度については以下の記事をご参照ください。

• 未知の確率密度関数のカーネル密度推定
• Rを使って高速化したMQL5の統計分布
• 統計的推定

つまり、ヒストグラムを作成することで次を得たのです。

• データをグループに分けるレベル（カットオフ）または境界：一連のレベルは量子グリッドまたは辞書と呼ばれ、これらのレベルでデータの符号化がおこなわれ、グループ化と圧縮がおこなわれます。境界は、量子化アルゴリズムに組み込まれたさまざまなルールに従って設置することができます。レベル（カットオフ）は、観測指標を測定するための新しい尺度を形成します。他の著者の作品では「区間」、「レンジ」、「量子化手順」など他の呼び方がありますが、私は2つのレベル間の範囲を「量子セグメント」と呼ぶのに慣れています。
• 各観測値（指標）が、与えられたグループ（ヒストグラムの列）に属するかどうか：量子化の場合、これは圧縮アルゴリズムの仕事であり、その本質は、量子グリッドの特定の範囲に観測値を割り当てる瞬間に、元のデータを圧縮データに変換することです。圧縮の結果は、変数値のさまざまな数値変換になります。2つのオプションが最も頻繁に発生します。1つ目は変換で、カットオフ（境界）の値の間の範囲の数値に応じて変数にランク（インデックス）が割り当てられます。2つ目のオプションはレベルの割り当てです。例えば、観測値が1.2～1.4の範囲にある場合、適切な値(1.4)が割り当てられます。ただし、量子化テーブルの境界の外側の任意の値を扱うことができる最初のオプションに対して、2つ目のオプションを使用するには、データがそれを超えないように制限を設定する必要があります。2つ目のオプションについては、かなり離れたところにレベル（境界）を強制的に追加するのが良い解決策かもしれません。そのため、スパイクや欠落データの形でエラーが発生する可能性があります。
• 精度を失った各数値の復元能力（脱量子化）は、次のようにおこなわれます。
• -区間の中心に沿って：これは数字のインデックスに対応します。
• -区間の左または右（多くの場合は右）のレベル値（境界/カットオフ）で：量子化テーブルの境界は、通常、最初と最後の区間で定義されていないことを考慮すると、区間の平均範囲または区間幅の最初と最後の値を使用して決定することができます。

量子化を適用するタスクと領域に応じて、変数のさまざまな指定や方程式の記述スタイルに対処する必要があります。これにより、アルゴリズムの本質を理解することが困難になります。これは、アルゴリズムを説明する著者が、アルゴリズムが適用された特定の領域の知識を前提としているためです。異なるアルゴリズムの本質は、レベル（カットオフ）の構成方法の違いに帰結するので、いくつかの基準に従ってそれらを分類することを提案します。

一定の区間を持つ量子化

• ピアソンヒストグラムに似た方法で一定区間に分割
• 数字の桁を減らす変換

可変区間量子化

• 各区間の観測の一定割合の累積
• 理論分布または近似分布の曲線下面積で固定値の使用
• 係数に応じて量子化手順を変更する所定の関数を使用（多くの場合、端や中央に向かって間隔を広げる関数）
• 値の密度によって区間に影響を与える重み付け係数を使用
• 反復法（適応的なものを含む）：データ構造に関する情報を境界を設定するために使用し、誤差を減らすための措置を取る
• その他の方法

経験的に決定された区間による量子化

• 数列
• 観測の性質に関する知識により、意味の類似した指標をグループ化
• 手動マーキング

選択されたメトリックの量子化誤差は、反復プロセスとして、または与えられた方程式を使用して一度だけ計算することによって減らすことができます。結果を評価するには，サンプル中の予測子の値をとる数値の全範囲に対する誤差の平均割合を使用するのが便利です。

 

2.MQL5での量子化アルゴリズムの実装

前回は、量子化がどのように機能するかの簡単な例を見ましたが、量子化でよく使われる手順の1つが欠けていました。つまり、いくつかの計算の後に得られた尺度を再分割して、区間（しばしばセントロイドと呼ばれる）の平均値を求めることです。量子化の間隔は、近接する2つのセントロイドの境界間の距離の半分で最終的に決定されます。

メモリ上で8バイトを占有するdoubleのような実数を、8ビットしか占有しないucharデータ型全体に段階的に量子化することを考えてみましょう。

• 1. 入力データの最大値と最小値を求める。
• 1.1.arr_In_Data配列の変数MaxとMinから最大値と最小値を求める。
• 2.区間間のウィンドウサイズを計算する。
• 2.1.最大値と最小値の差を求め、Delta変数に格納する。
• 2.2.1つのウィンドウのサイズDelta/nQを求め（nQはセパレータ（境界）の数）、結果をInterval_Size変数に保存する。
• 3.量子化と誤差計算をおこなう。
• 3.1.入力データの最小値をarr_In_Data-Minゼロにシフトする。
• 3.2.3.1の結果をInterval_Sizeの区間数で割る。
• 3.3.3.2で得られた結果に、最も近い整数に丸めるround関数を適用し、結果をarr_Output_Q_Interval配列に保存する。
• 3.4.配列arr_Output_Q_Intervalの値にInterval_Sizeを掛け、最小値を足す。これで変換された（量子化された）数値が得られたので、これをarr_Output_Q_Data配列に保存する。
• 3.5.誤差を累積で計算する。これをおこなうには、元の値と量子化の結果得られた値の絶対値の差をレンジで割る。結果の合計をarr_In_Data配列の要素数で割る。
• 4.セパレータ（境界）をarr_Output_Q_Book配列に保存する。
• 4.1.最初の区間については、最小値(Min)に区間(Interval_Size)の半分のサイズを追加する。
• 4.2.それ以降の区間は、区間の値を前の手順のarr_Output_Q_Book配列の値に加算することで計算する。

以下は、変数と配列の説明を含む関数コードの例です。

/+---------------------------------------------------------------------------------+
//|Quantization of transformation (encoding) type to a given integer bitness
//+---------------------------------------------------------------------------------+
double Q_Bit(
   double &arr_Input_Data[],//Quantization data array
   int &arr_Output_Q_Interval[],//Outgoing array with intervals containing data 
   double &arr_Output_Q_Data[],//Outgoing array with restored values of the original data 
   float &arr_Output_Q_Book[],//Outgoing array - "Book with boundaries" or "Quantization table"
   int N_Intervals=2,//Number of intervals the original data should be divided (quantized) into
   bool Use_Max_Min=false,//Use/do not use incoming maximum and minimum values
   double Min_arr=0.0,//Maximum value
   double Max_arr=100.0//Minimum value
)
{
   if(N_Intervals<2)return -1;//There may be at least two intervals, in this case, there is one separator
//---0. Initialize the variables and copy the arr_Input_Data array
   double arr_In_Data[];
   double Max=0.0;//Maximum
   double Min=0.0;//Minimum
   int Index_Max=0;//Maximum index in the array
   int Index_Min=0;//Minimum index in the array
   double Delta=0.0;//Difference between maximum and minimum
   int   nQ=0;//Number of separators (borders)
   double Interval_Size=0.0;//Interval size
   int Size_arr_In_Data=0;//arr_In_Data array size
   double Summ_Error=0.0;//To calculate error/data loss
   nQ=N_Intervals-1;//Number of separators
   Size_arr_In_Data=ArrayCopy(arr_In_Data,arr_Input_Data,0,0,WHOLE_ARRAY);
   ArrayResize(arr_Output_Q_Interval,Size_arr_In_Data);
   ArrayResize(arr_Output_Q_Data,Size_arr_In_Data);
   ArrayResize(arr_Output_Q_Book,nQ);

//---1. Finding the maximum and minimum in the input data
   if(Use_Max_Min==false)//If enforced array limits are not used
   {
      Index_Max=ArrayMaximum(arr_In_Data,0,WHOLE_ARRAY);
      Index_Min=ArrayMinimum(arr_In_Data,0,WHOLE_ARRAY);
      Max=arr_In_Data[Index_Max];
      Min=arr_In_Data[Index_Min];
   }

   else//Otherwise enforce the maximum and minimum 
   {
      Max=Max_arr;
      Min=Min_arr;
   }

//---2. Calculate the window size between intervals
   Delta=Max-Min;//Difference between maximum and minimum 
   Interval_Size=Delta/nQ;//Size of one window

//---3. Perform quantization and error calculation
   for(int i=0; i<Size_arr_In_Data; i++)
   {
      arr_Output_Q_Interval[i]=(int)round((arr_In_Data[i]-Min)/Interval_Size);
      arr_Output_Q_Data[i]=arr_Output_Q_Interval[i]*Interval_Size+Min;
      Summ_Error=Summ_Error+(MathAbs(arr_Output_Q_Data[i]-arr_In_Data[i]))/Delta;
   }
//---4. Save separators (borders) into the array
   for(int i=0; i<nQ; i++)
   {
      switch(i)
      {
      case 0:
         arr_Output_Q_Book[i]=float(Min+Interval_Size*0.5);
         break;
      default:
         arr_Output_Q_Book[i]=float(arr_Output_Q_Book[i-1]+Interval_Size);
         break;
      }
   }
   return Summ_Error=Summ_Error/(double)Size_arr_In_Data*100.0;
} 

以下は、データ量子化の実際の使用例です。

• データの保存と処理に必要なメモリを削減：この効果は、指標番号の数値が該当する量子セグメントのインデックスのみを保存すれば十分であることによって得られます。この場合、データ型をdoubleやfloatからintやucharのような整数型に変更することは理にかなっています。
• 計算の加速：整数を扱い、使用する数の集合を減らすことで、アルゴリズムのサイクル数を減らすことで達成されます。
• 雑音低減：ソースデータの品質には、証券会社からのデータ損失という一次的なものと、遅延、丸め誤差、測定誤差といった形で、測定誤差という雑音が含まれている可能性があります。量子化は、量子セグメントの範囲内で指標を平均化することで、そのような雑音を平滑化し、モデルがそのような雑音に注意を集中させないようにします。
• 近接観測値の不足を補う：時々、予測値は観測値の不足のために非常にまれであり、スパイクと見なすことができません。量子化は、そのような観測値に十分な値の分散範囲を与えることができ、サンプルがなかった新しいデータでもモデルを使用できるようにします。
• 次元の呪縛との戦い：可能な組み合わせの数を減らすことで、測定空間の可能な座標のグリッドを減らし、訓練のスピードアップと向上を図ることができます。

2つの例で、2つの主な量子化戦略を紹介しました。

• データ近似戦略
• データ集約戦略

最初のタイプの戦略は、特性値の分布が連続的なものに近い指標を測定する、計量尺度に最も適しています。理論的には、値の範囲を区切る区間が多ければ多いほど、数列の全範囲にわたって再構成された値の散布の誤差が小さくなるので良くなります。このタイプは数学関数の復元に適しています。

2つ目の戦略は、データをグループ化することです。特徴量の一般化されたカテゴリカルな値が作成されることが想像でき、ここで境界を正しく推定する作業はより困難になります。私の経験では、サンプルからの観測値の少なくとも5%が区間に入ることを保証する必要があります。

特筆すべきは、慣習にとらわれず、すでにカテゴリかるな意味を持つ特徴は、非常に慎重に量子化し、本当に似ているものだけを組み合わせるべきだということです。さらに、ここでいう類似性とは、サンプルを部分サンプルに分けたときの類似性を意味します。

この記事には、量子化処理の例となるスクリプトQ_Transが添付されています。量子化のためのデータは無作為に生成されます。このスクリプトには、以下の主な関数が含まれています。

• Q_Bit：変換（エンコード）タイプを、与えられた整数ビット深度に量子化
• Book_to_cifra：デコーダーは量子化テーブルから数値の近似値を復元。インデックスを含む配列が必要
• Book_to_cifra_v2：デコーダーは量子化テーブルから数値の近似値を復元。インデックスを含む配列は不必要
• Q_Random：無作為な境界を持つ量子化

スクリプトには以下の設定が含まれています。

• 元のデータを分割（量子化）する区間数
• 乱数発生器の初期化
• チャートの保存
• チャートを保存するディレクトリ
• チャートの幅
• チャートの高さ
• フォントサイズ

 

スクリプトの動作段階の説明

1. サンプルが無作為に作成されます。

2. 取引商品のチャートには、前述したように構築されたヒストグラムチャート（図1）と、生成された予測子の値が時系列に分布し、量子化後に得られた境界で分割されたチャート（図2）が表示されます。「Save charts」がtrueの場合、チャートはカスタムターミナルファイルのあるディレクトリ「Files\Q_Trans\Grafics」に保存されます。

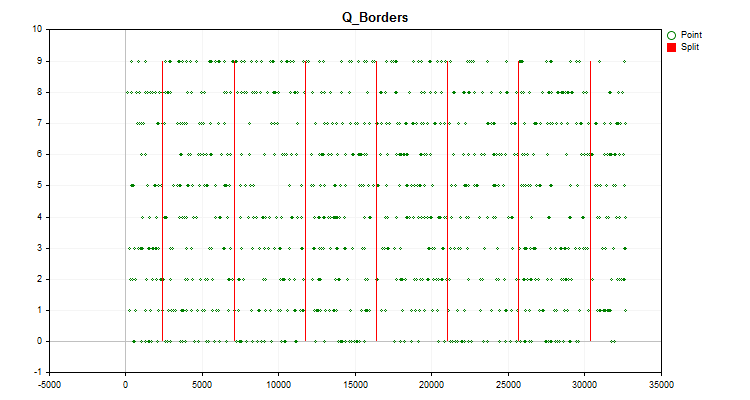   図2

3. 量子化をおこない、サンプル値の全範囲に対する再構成値のオフセットの形で誤差を計算します（Q_Bit関数）。
4. 重心に沿って非量子化をおこない、再構成された値のオフセットという形で誤差を計算します（Book_to_cifra関数）。
5. 右境界に沿って非量子化をおこない、再構成された値のオフセットという形で誤差を計算します（Book_to_cifra関数）。
6. 重心に沿って非量子化をおこない、再構成された値のオフセットという形で誤差を計算します（Book_to_cifra_v2関数）。
7. 予測子を分割する最適な区間を見つけるために1000回試行します（Q_Random関数）。
8. 無作為に得られた最適なグリッドを用いてセントロイドに沿って非量子化をおこない、再構成値のオフセットという形で誤差を計算します（Book_to_cifra関数）。

デフォルトの設定でスクリプトを実行すると、[エキスパート端末のログでは、Message欄に以下の情報が表示されます。

Average data recovery error size = 3.52% of full range when using 8 intervals
Average error size via quantum table for centroid conversion (Book_to_cifra) = 1145.62263
Average error size via quantum table for right boundary conversion (Book_to_cifra) = 2513.41952
Average error size via quantum table for centroid transformation (Book_to_cifra_v2) = 1145.62263
Average error size via quantum table for centroid transformation (Q_Random) = 1030.79216

興味深いのは、境界を無作為に選択する方法が、先に検討した方法（一様量子化に基づく）よりもさらに良い結果を示したことです。

 

3.CatBoostを使った量子化

以前、「PythonやRの知識が不要なYandexのCatBoost機械学習アルゴリズム」稿で紹介したCatBoostは、データの前処理に量子化を使用し、勾配ブースティングアルゴリズムの動作を大幅に高速化することができます。前回同様、CatBoostのコンソール版を使用することにします。コンピュータのセントラルプロセッサー上で作業をおこなう場合、追加のソフトウェアをインストールする必要がないからです。

以下の設定が必要です。

1. 量子化（分割）方法：キー「--feature-border-type」

• Median
• Uniform
• UniformAndQuantiles
• MaxLogSum
• MinEntropy
• GreedyLogSum

2.1～65535のセパレータ数：キー「--border-count」

3.量子化テーブルを指定ファイルに保存：キー「--output-borders-file」

4.指定されたファイルから量子化テーブルを読み込む：キー「--input-borders-file」

 

上記のキーを指定しない場合、記事で使用するモデルの構築には以下の設定が使用されます。

• CPU計算の場合、量子化方法はGreedyLogSum、セパレータの数は254
• GPU計算の場合、量子化方法はGreedyLogSum、セパレータの数は128

   

キーの登録方法

メソッドをUniform、セパレータの数を30に設定して量子化を設定し、量子化テーブルをQuant_CB.csvファイルに保存します。

catboost-1.0.6.exe fit --learn-set train.csv          --test-set test.csv --column-description Test_CB_Setup_0_000000000 --has-header --delimiter ; --train-dir ..\Rezultat --feature-border-type Uniform --border-count 30 --output-borders-file Quant_CB.csv 

Quant_CB.csvファイルから量子化テーブルを読み込み、モデルを訓練します。

catboost-1.0.6.exe fit --learn-set train.csv          --test-set test.csv --column-description Test_CB_Setup_0_000000000 --has-header --delimiter ; --train-dir ..\Rezultat --input-borders-file Quant_CB.csv

 量子化設定に関する開発者の指示のセクションは、こちらにあります。

 

具体的なデータに適用した場合、量子化方法がどのように異なるかを見てみましょう。以下はgifファイルのグラフです。それぞれの新しいフレームが次の方法となります。セパレータの数は16です。

 

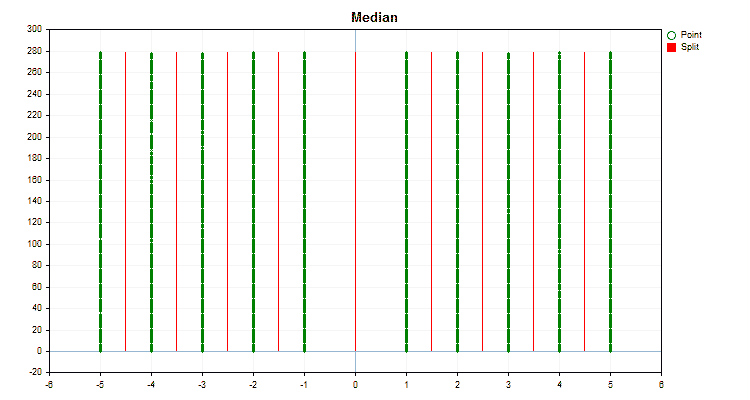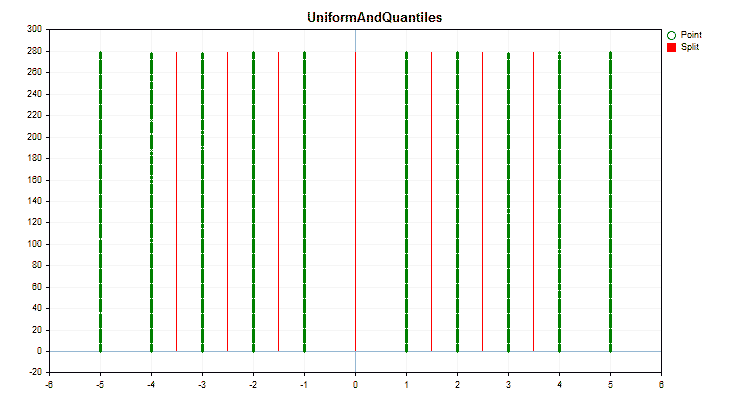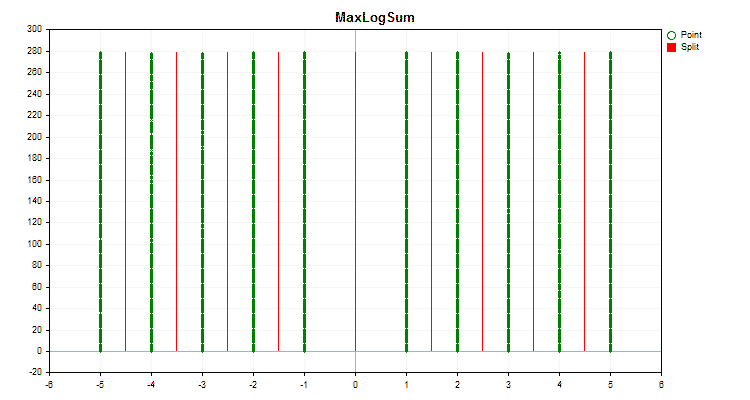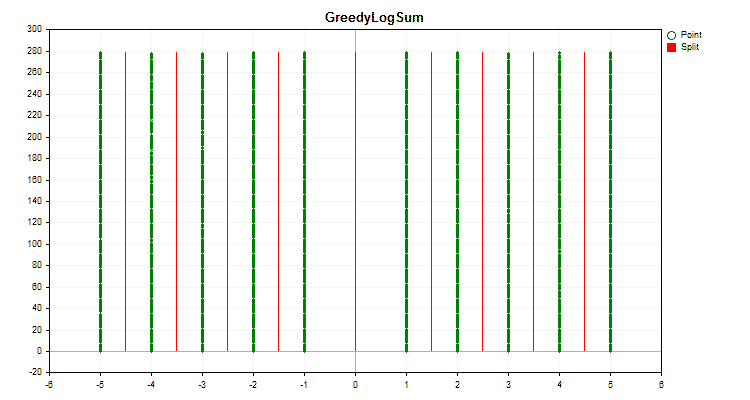
図2：カテゴリカル予測子のデータグラフ

 

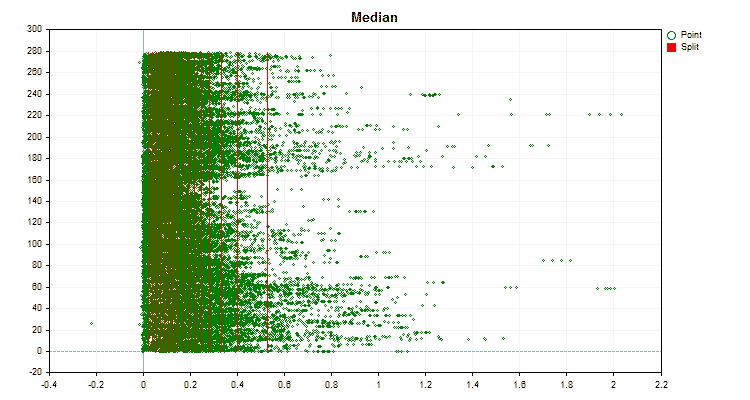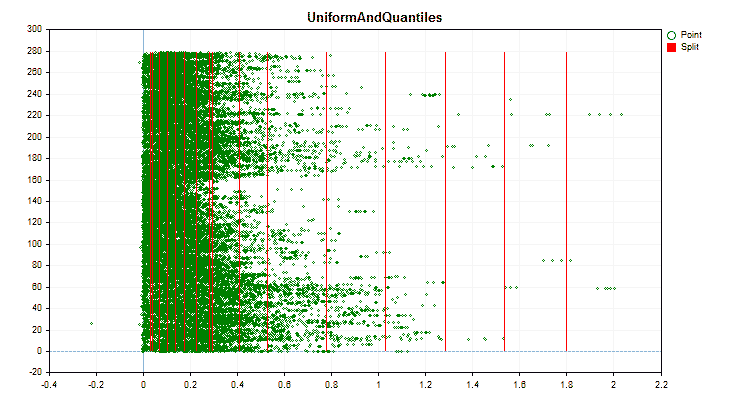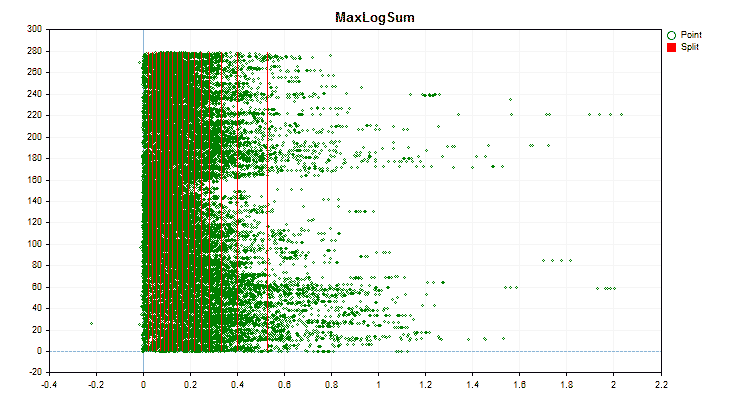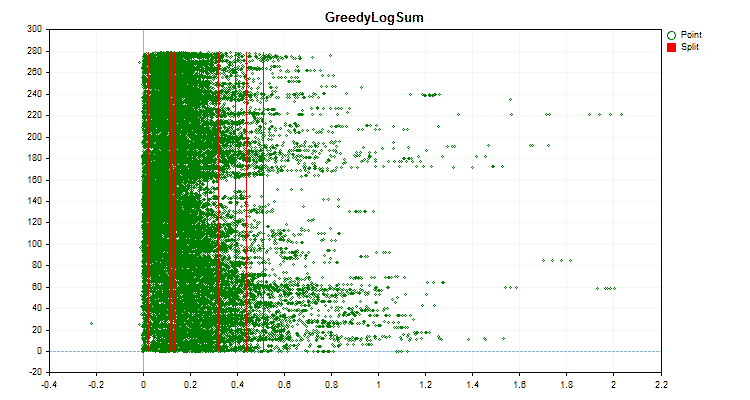
図3：左領域に値をシフトした予測値のデータグラフ

 

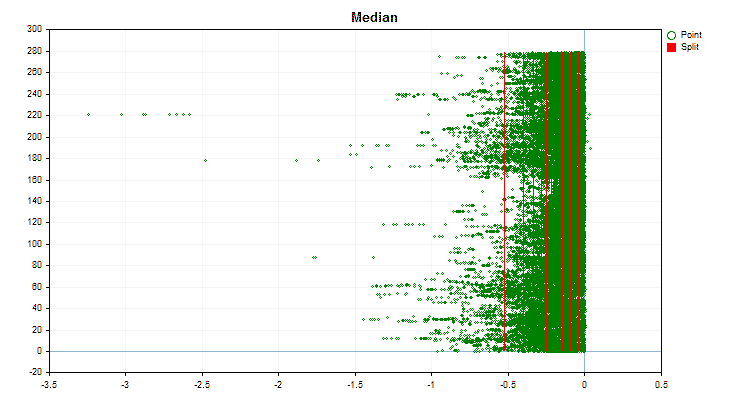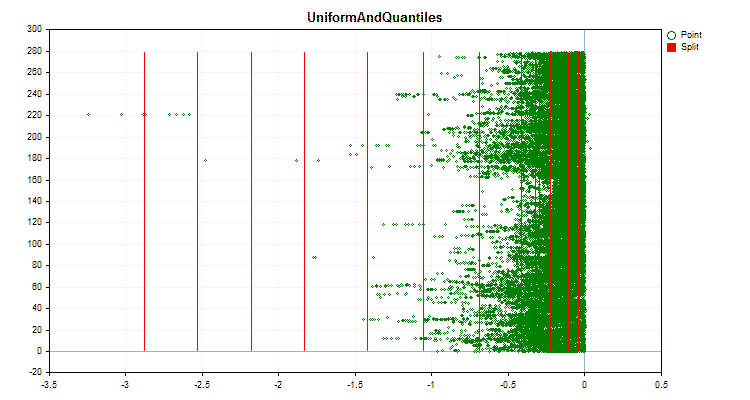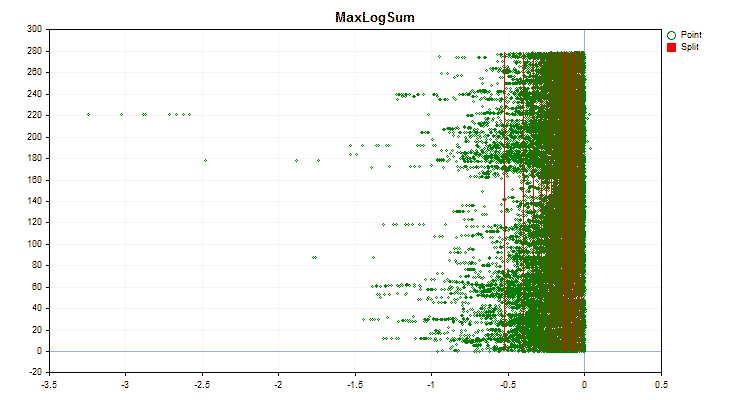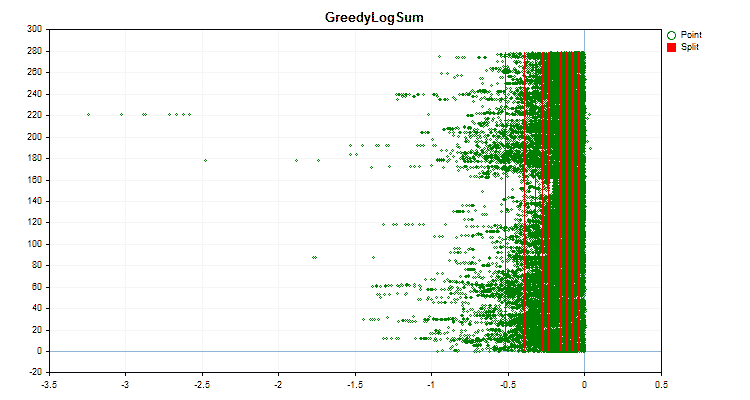
図4：右領域に値をシフトした予測値のデータグラフ

 

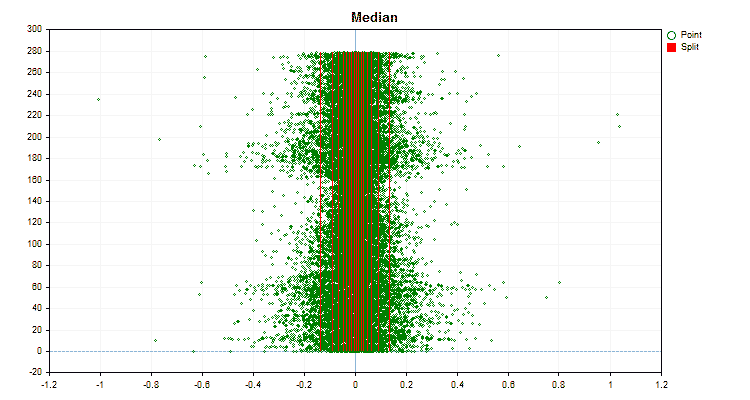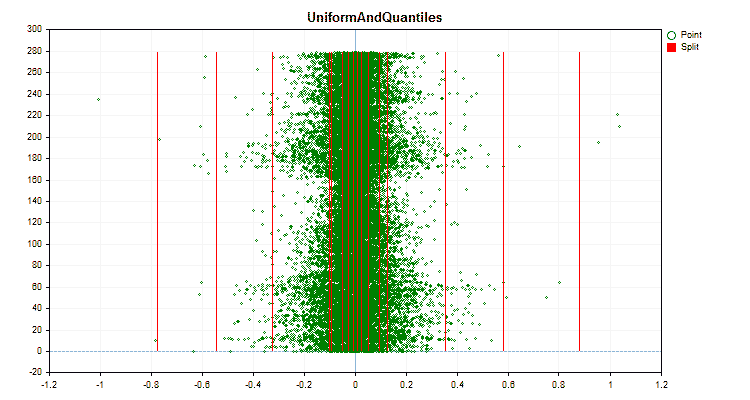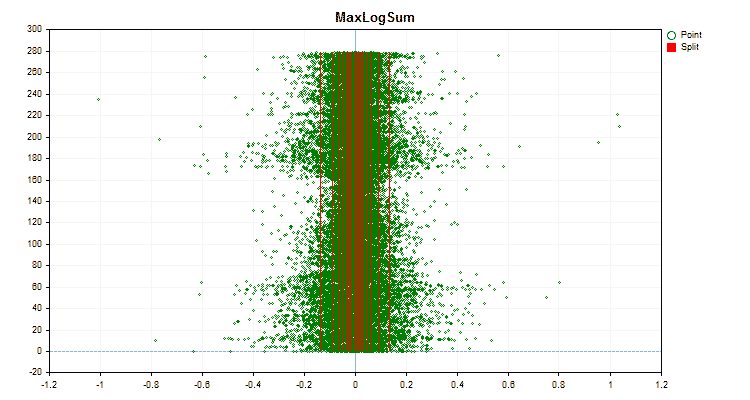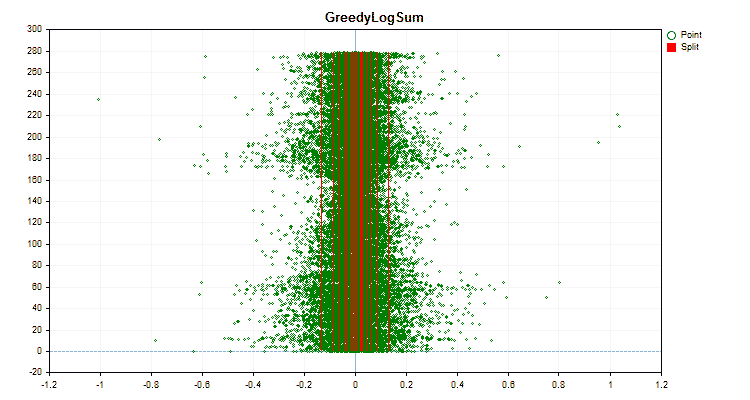
図5：中央領域に値を配置した予測子のデータグラフ

 

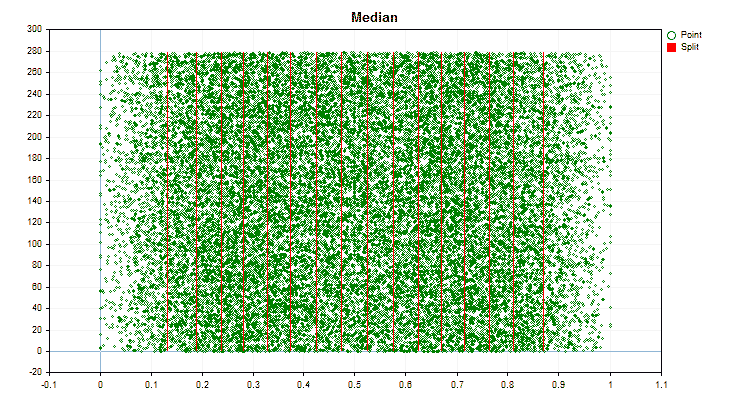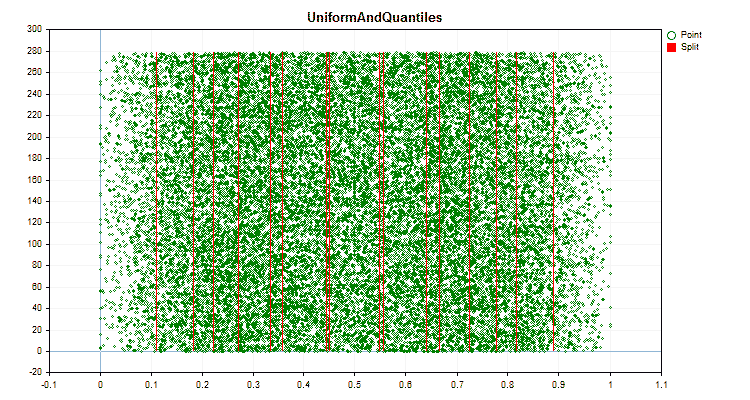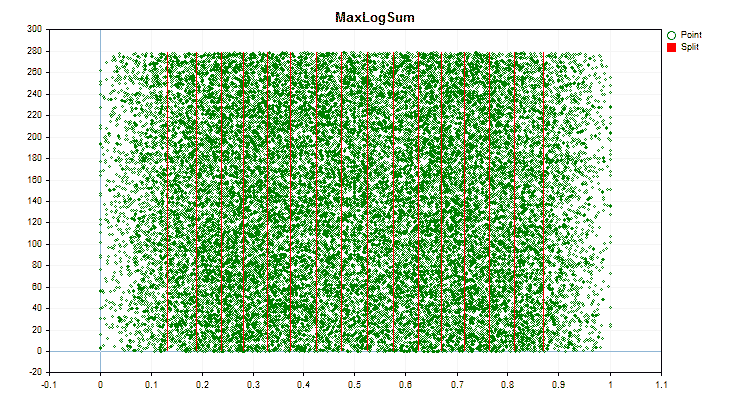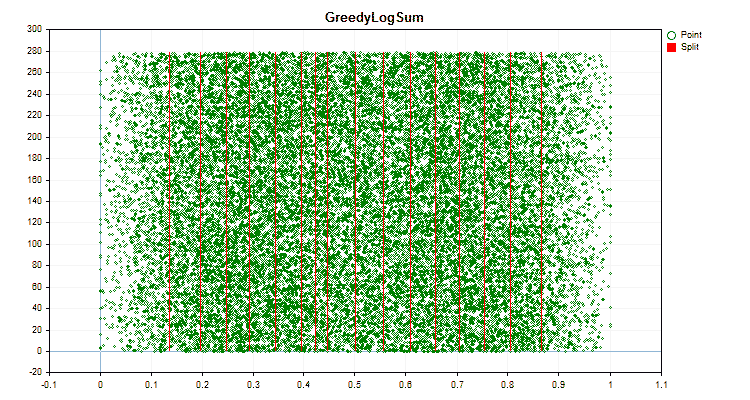
図6：値の一様分布を持つ予測子のデータグラフ

 

量子化テーブルを含むファイル（ここではQuant_CB.csv）の構造を見ると、2つの列と多くの行があることがわかります。最初の列は，モデルを訓練するときに使用される予測子の通し番号を格納し，2つ目の列はセパレータ（境界/レベル）を格納します。行数は区切り記号の累計に相当し、すべての区切り記号を列挙した後に最初の列の数字が変わります。

 

  

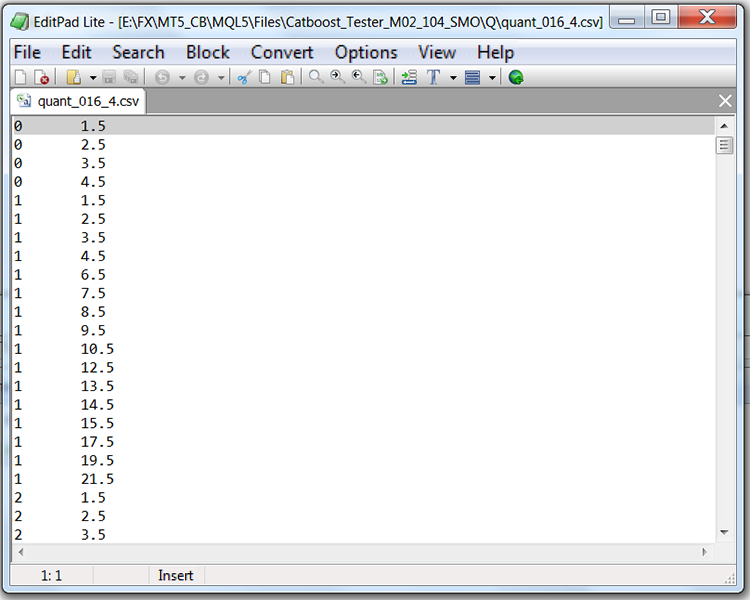
表1：セパレータ付きで保存されたCatBoostファイルの内容

 

結論

この記事では、量子化の概念を理解し、MQL5コードを例として量子化された予測値を得ることを分析し、CatBoostにおける量子化の実装を検討しました。

記事の中に用語や事実誤認を発見された方は、遠慮なくご連絡ください。

次回は、特定の予測子に対して量子化テーブルを選択する方法を考え、この選択の実現可能性を評価する実験もおこないます。

#	ファイル	詳細
1	Q_Trans.mq5	ランダムサンプルに対する一様量子化の例を含むスクリプト