MetaTrader 5 / 例
English Русский 中文 Español Deutsch Português 한국어 Français Italiano Türkçe
統計的推定

統計的推定

MetaTrader 5 — 例 | 29 10月 2015, 08:28
882 0
Victor
Victor

はじめに

今日、価格系列の予測、モデルを選択とその妥当性推定などをしている量子経済学を扱った記事や出版物を目にする機会が多くあります。ただしその大多数は、読者に数学統計の知識があり、分析されたシーケンスの統計パラメータを簡単に推定できるという前提に基づくものです。

シーケンスの統計的パラメータの推定はたいへん重要なものです。それはたいていの数学的モデルと手法が異なる前提に基づいているからです。たとえば、分布法則の正常化、分散値、その他パラメータです。よって時系列を分析し推定するとき、主要な統計的パラメータを素早く明確に推定できるシンプルで使い勝手のよいツールが必要です。本稿では、そのようなツールを作成していきたいと思います。

本稿では、もっともシンプルなランダムシーケンスの統計パラメータとビジュアル分析のメソッドをいくつか取り上げ述べていきます。それにより MQL5 でこれらメソッド、またニュープロットアプリケーションを用いて計算した結果の視覚メソッドを実装します。本稿はマニュアルや参照資料のようにはなっていません。用語や定義が当然のように登場するのはそのためです。


サンプル上でのパラメータ分析

時間内には無限に定常過程が存在するとします。それは離散サンプルのシーケンスとして表現することができます。このサンプルのシーケンスを一般集団と呼ぶことにします。一般集団から選ばれたサンプルの一部を一般集団からのサンプリングまたは N サンプルのサンプリングと呼びます。その上、真のパラメータは一つも分かっていないとします。よって有限のサンプリングにおいてそれらを推定していきます。


異常値の除外

パラメータの統計的推定を始める前に、サンプリングが大誤差（異常値）を含んでいたら、推定の精度が落ちることに注意が必要です。サンプリングのボリュームが小さければ、異常値は推定精度に多大な影響を与えます。異常値は分布の中央から異常に発散している値です。そのような偏差は滅多に起こらない異なる原因や、統計データ収集中またはシーケンス形成中に出現したエラーによって起こります。

異常値をフィルターにかけるかどうか判断するのは困難なことです。というのもほとんどの場合、値が異常値なのか分析途中のものなのか明確にすることは不可能だからです。異常値が検出され、それらをフィルターにかけるという判断をすれば、ここで問題が持ち上がります。そのエラー値をどう扱うか？です。もっとも理論的なバリアントはサンプリングから除くというものです。それで統計的特性の推定精度は上がります。ただし時系列を処理している場合はサンプリングから異常値を除外するのに注意が必要です。

サンプリングから異常値を除外するまたは少なくともそれらを検出する可能性には、S.V.Bulashev著 "Statistics for Traders" に述べられているアルゴリズムを実装します。

このアルゴリズムによると、分布中心の推定値を5個計算する必要があります。

  1. 中央値
  2. 四分位範囲の中央50% （中央四分位置、 MQR）
  3. サンプリング全体の算術平均値
  4. 四分位範囲の50% における算術平均値（第1四分位値、IQM）
  5. 範囲の中央（ミドルレンジ）- サンプリングの最大最小値の平均値として決定されます。

分布中央値の推定結果は昇順でソートされます。それから平均値または順序の3番目の値が分布の中心値Xcenとして選択されます。選ばれた推定値は異常値からの影響はもっとも少ないように思われます。

取得した分布中心の推定値Xcenを使って標準偏差 s、超過値 K、実験式に従って打ち切り比率を計算します。

 

ここでN はサンプリング内のサンプル値（サンプリングのボリューム）です。

それから範囲外に存在する値

 

は異常値として数えます。よってそれらはサンプリングから除外します。

この手法は本 "Statistics for Traders" に詳しく述べられています。それではさっそくアルゴリズムの実装にまいりましょう。異常値を検出し除外するアルゴリズムは erremove() 関数に実装されます。

以下の記述は本関数を検証するためのスクリプトです。

//----------------------------------------------------------------------------
//                                                                erremove.mq5
//                                   Copyright 2011, MetaQuotes Software Corp.
//                                                         https://www.mql5.com
//----------------------------------------------------------------------------
#property copyright "Copyright 2011, MetaQuotes Software Corp."
#property link      "https://www.mql5.com"
#property version   "1.00"

#import "shell32.dll"
bool ShellExecuteW(int hwnd,string lpOperation,string lpFile,
                  string lpParameters,string lpDirectory,int nShowCmd);
#import
//----------------------------------------------------------------------------
// Script program start function
//----------------------------------------------------------------------------
void OnStart()
  {
  int i;
  double dat[100];
  double y[];
  
  srand(1);
  for(i=0;i<ArraySize(dat);i++)dat[i]=rand()/16000.0;
  
  dat[25]=3;           // Make Error !!!
  
  erremove(dat,y,1);
  
  }
//----------------------------------------------------------------------------
int erremove(const double &x[],double &y[],int visual=1)
  {
  int i,m,n;
  double a[],b[5];
  double dcen,kurt,sum2,sum4,gs,v,max,min;
  
  if(!ArrayIsDynamic(y))                           // Error
    {
    Print("Function erremove() error!");
    return(-1);
    }
  n=ArraySize(x);
  if(n<4)                                          // Error
    {
    Print("Function erremove() error!");
    return(-1);
    }
  ArrayResize(a,n);
  ArrayCopy(a,x);
  ArraySort(a);
  b[0]=(a[0]+a[n-1])/2.0;                          // Midrange
  m=(n-1)/2;
  b[1]=a[m];                                       // Median
  if((n&0x01)==0)b[1]=(b[1]+a[m+1])/2.0;
  m=n/4;
  b[2]=(a[m]+a[n-m-1])/2.0;                        // Midquartile range
  b[3]=0;
  for(i=m;i<n-m;i++)b[3]+=a[i];                    // Interquartile mean(IQM)
  b[3]=b[3]/(n-2*m);
  b[4]=0;
  for(i=0;i<n;i++)b[4]+=a[i];                      // Mean
  b[4]=b[4]/n;
  ArraySort(b);
  dcen=b[2];                                       // Distribution center
  sum2=0; sum4=0;  
  for(i=0;i<n;i++)
    {
    a[i]=a[i]-dcen;
    v=a[i]*a[i];
    sum2+=v;
    sum4+=v*v;
    }
  if(sum2<1.e-150)kurt=1.0;
  kurt=((n*n-2*n+3)*sum4/sum2/sum2-(6.0*n-9.0)/n)*(n-1.0)/(n-2.0)/(n-3.0); // Kurtosis
  if(kurt<1.0)kurt=1.0;
  gs=(1.55+0.8*MathLog10((double)n/10.0)*MathSqrt(kurt-1))*MathSqrt(sum2/(n-1));
  max=dcen+gs;
  min=dcen-gs;
  m=0;
  for(i=0;i<n;i++)if(x[i]<=max&&x[i]>=min)a[m++]=x[i];
  ArrayResize(y,m);
  ArrayCopy(y,a,0,0,m);

  if(visual==1)vis(x,dcen,min,max,n-m);
  
  return(n-m);  
  }
//----------------------------------------------------------------------------
void vis(const double &x[],double dcen,double min,double max,int numerr)
  {
  int i;
  double d,yma,ymi;
  string str;
  
  yma=x[0];ymi=x[0];
  for(i=0;i<ArraySize(x);i++)
    {
    if(yma<x[i])yma=x[i];
    if(ymi>x[i])ymi=x[i];
    }
  if(yma<max)yma=max;
  if(ymi>min)ymi=min;
  d=(yma-ymi)/20.0;
  yma+=d;ymi-=d;
  str="unset key\n";
  str+="set title 'Sequence and error levels (number of errors = "+
        (string)numerr+")' font ',10'\n";
  str+="set yrange ["+(string)ymi+":"+(string)yma+"]\n";
  str+="set xrange [0:"+(string)ArraySize(x)+"]\n";
  str+="plot "+(string)dcen+" lt rgb 'green',";
  str+=(string)min+ " lt rgb 'red',";
  str+=(string)max+ " lt rgb 'red',";
  str+="'-' with line lt rgb 'dark-blue'\n";
  for(i=0;i<ArraySize(x);i++)str+=(string)x[i]+"\n";
  str+="e\n";
  if(!saveScript(str)){Print("Create script file error");return;}
  if(!grPlot())Print("ShellExecuteW() error");
  }
//----------------------------------------------------------------------------
bool grPlot()
  {
  string pnam,param;
  
  pnam="GNUPlot\\binary\\wgnuplot.exe";
  param="-p MQL5\\Files\\gplot.txt";
  return(ShellExecuteW(NULL,"open",pnam,param,NULL,1));
  }
//----------------------------------------------------------------------------
bool saveScript(string scr1="",string scr2="")
  {
  int fhandle;
  
  fhandle=FileOpen("gplot.txt",FILE_WRITE|FILE_TXT|FILE_ANSI);
  if(fhandle==INVALID_HANDLE)return(false);
  FileWriteString(fhandle,"set terminal windows enhanced size 560,420 font 8\n");
  FileWriteString(fhandle,scr1);
  if(scr2!="")FileWriteString(fhandle,scr2);
  FileClose(fhandle);
  return(true);
  }
//----------------------------------------------------------------------------

ではerremove() 関数を詳しく見ていきます。関数の最初のパラメータとして配列 array x[] のアドレスを渡します。ここに配列サンプリングの値が格納されます。サンプリングのボリュームは4エレメント以下にはなりません。配列 x[] のサイズはサンプリングサイズに等しいと思われます。それがサンプリングのボリューム N が渡されない理由です。配列 x[] に位置するデータは関数が実行された結果変化しません。 

次のパラメータは配列 y[] のアドレスです。関数が問題なく実行されると、この配列は除外される異常値のインプットシーケンスを持ちます。y[] 配列のサイズはサンプリングから除外された値の数 x[] 配列より小さくなっています。y[] ない列は動的配列として宣言される必要があります。そうでないと、関数本文内でサイズを変更するのは不可能になります。

最後の（オプションとしての）パラメータは計算結果を視覚化するためのフラグです。その値が1（初期値）であれば、関数実行終了前に次の情報を表示するチャートが別のウィンドウに描画されます。その情報というのは、インプットシーケンス、分布の中央と限度ライン、異常値とみなされるもの以外の値です。

チャート描画メソッドについてはのちほど述べます。問題なく実行された場合、関数はサンプリングから除外された値の数を帰ります。エラーとなった場合は、1を返します。エラー値（異常値）が見つからなければ、関数は0を返し y[] 配列のシーケンスは x[] 配列のシーケンスに等しくなります。

関数の冒頭では、 x[] 配列から a[] 配列に情報がコピーされ、そして昇順でソートされます。それから分布中央の推定が5回行われます。

範囲の中央（ミッドレンジ）は二分割されたソート済み配列 a[] の極値合計として決定されます。

中央値 はサンプリングの奇数ボリューム N に対して以下のように計算されます。

 

またサンプリングのボリュームに対しても計算されます。

 

ソートされた配列 a[] がゼロからスタートすることを考慮し、以下を取得します。

m=(n-1)/2;
median=a[m];                                       
if((n&0x01)==0)b[1]=(median+a[m+1])/2.0;

四分位範囲の50%の中央 （中央四分位置、 MQR）

 

ここでM=N/4 （整数除算）です。

ソートされた配列 a[] に対しては以下を取得します。

m=n/4;
MQR=(a[m]+a[n-m-1])/2.0;               // Midquartile range

四分位範囲の50% における算術平均値 （第1四分位値、IQM）です。サンプルの25% はそれぞれサンプリングの両端から切り落とされます。そして残りの 50% が数学的平均を計算するのに使われます。

 

ここでM=N/4 （整数除算）です。

m=n/4; IQM=0;
for(i=m;i<n-m;i++)IQM+=a[i];
IQM=IQM/(n-2*m);                       // Interquartile mean(IQM)

算術的平均 （平均値）がサンプリング全体に対して決定されます。

決定された値はそれぞれ b[] 配列に書き込まれ、配列は昇順でソートされます。b[2] 配列のエレメント値が分布の中央値として選択されます。この値を用いてのちに平均値および超過値係数の不偏推定計算を行います。この計算のアルゴリズムは追って記述します。

取得した推定値は打ち切り係数および異常値検出限界を計算するのに利用します。（式は上に示しています。）最後に、除外された異常値を伴うシーケンスが y[] 配列内に作成され、グラフ描画のために vis() 関数が呼ばれます。本稿で使用する視覚化メソッドを見ていきます。


視覚化

計算結果を視覚的に表示するのに、私は様々な 2Dグラフや3D グラフが描きたくてフリーアプリケーションのニュープロットを使います。ニュープロットには画面にチャートを表示する（個別のウィンドウに）機能や異なるグラフィックフォーマットでファイルにグラフを書き込む機能があります。グラフをプロットするコマンドはあらかじめ準備されたテキストファイルから実行されます。ニュープロットプロジェクトの公式ウェブサイトはgnuplot.sourceforge.netです。アプリケーションはマルチプラットフォームでソースコードファイルとしても特定のプラットフォームにコンパイルされているバイナリファイルとしても配布されています。

本稿の例は Windows XP SP3 で ニュープロットバージョン 4.2.2 により検証されました。The gp442win32.zip file can be downloaded at http://sourceforge.net/projects/gnuplot/files/gnuplot/4.4.2/. まだニュープロット別バージョンやビルドでは例の検証はしていません。

gp442win32.zip アーカイブをダウンロードしたらそれを解凍します。そうすると \gnuplot folder が作成されます。それにはアプリケーション、ヘルプファイル、ドキュメンテーション、用例が含まれています。アプリケーションと連携するには、お手持ちのMetaTrader 5 クライアント端末のルートファイルに\gnuplot folder全体を入れます。

\gnuplot 

 図1　フォルダ \gnuplot の配置

フォルダを移動したら、ニュープロットアプリケーションの操作性を変更することが可能です。それをするために、ファイル \gnuplot\binary\wgnuplot.exeを実行すると、"gnuplot>" コマンドプロンプトcommand prompt が表示されるので、 "plot sin(x)" コマンドをタイプします。そうすると、中に sin(x) 関数が描かれた他ウィドウが表示されます。またアプリケーションの配布時に同封されている例を試すこともできます。その場合はFile\Demos を選択しさらにファイル \gnuplot\demo\all.demを選択します。

ここでerremove.mq5 スクリプトをスタートすると、図2に示されているグラフが別のウィンドウに描かれます。

erremove.mq5 

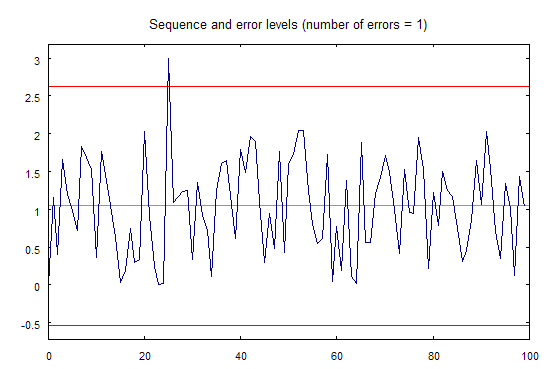
図2　erremove.mq5 スクリプトを使用し描画されるグラフ

本稿ではのちにニュープロットの利用特徴についてはほんの少しだけ触れるつもりです。というのもプログラム情報とその制御はドキュメンテーションで簡単に煮付けられるからです。それはニュープロットアプリケーションと共に提供されており、またhttp://gnuplot.ikir.ru/など様々なウェブサイトでも見つけることができます。

本稿用に書かれたプログラム例ではチャート描画目的でニュープロットとのもっともシンプルな連携を使用しています。まず、テキストファイル gplot.txt が作成されます。そこにはニュープロットコマンドと表示のための情報があります。それからコマンド行内で引数として渡されたファイル名で wgnuplot.exe アプリケーションが起動します。wgnuplot.exe アプリケーションはシステムライブラリ shell32.dllからインポートされたShellExecuteW() 関数を用いて呼ばれます。クライアント端末で外部 dlls のインポートができるのはそのためです。

既定バージョンのニュープロットではwxt および windowsの2タイプのターミナルに対し個別ウィンドウにチャートを描くことができます。wxt ターミナルはチャート描画にアンチエイリアスのアルゴリズムを使用しており、ウィンドウズのターミナルより描画が高画質です。ただし、本稿での例を書くのにはウィンドウズターミナルを利用しています。その理由はウィンドウズターミナルで作業をしている場合、ウィンドウを閉じると "wgnuplot.exe -p MQL5\\Files\\gplot.txt" の呼び出し結果作成されたシステム処理は自動的に終了され、グラフウィンドウも同様に閉じられてしまうためです。

wxt ターミナルを選んだら、チャートウィンドウを閉じても、システム処理 wgnuplot.exe は自動的にシャットダウンされません。このため上記のように wxt ターミナルを使用して wgnuplot.exe を何度も呼ぶと、システム内に処理のサインなしで複数処理が蓄積されてしまう可能性があります。"wgnuplot.exe -p MQL5\\Files\\gplot.txt" 呼び出しとウィンドウズターミナルを併用すると、不要なウィンドウを開いたり閉じられていないシステム処理が表示されたりするのを避けることができます。

チャートが表示されるウィンドウは連携していて、マウスのクリックやキーボードイベント処理を行います。ホットキーの初期設定に関してはwgnuplot.exeを実行し、「ターミナルウィンドウ設定」コマンドを使用してターミナルタイプを選択し、たとえば、 "plot sin(x)" コマンドを用いてチャートをプロットします。チャートウィンドウがアクティブ（ピントが合っている）ならば "h" ボタンを押すとすぐにwgnuplot.exeのテキストウィンドウにヒントが表示されているのがわかります。


パラメータの推定

チャート描画が少し解ったところで、有限サンプリングを基にした一般集団のパラメータ推定に戻ります。一般集団の統計パラメータはまったく未知だとして、これらパラメータの不偏推定のみ使用していきます。

数学的期待値の推定またはサンプリング平均値はシーケンス分布を決定する主要なパラメータであると考えられます。サンプリング平均値は次の式で計算されます。

 

ここで N はサンプリングにおけるサンプル数です。

平均値は分布中心の推定値で中心積率と連携したその他のパラメータを計算するのに利用されます。これによりこのパラメータは特に重要なものとなります。平均値に加え、統計パラメータとして分散（分散）の推定値、標準偏差、歪度（ひずみ）係数、超過指数（尖度）も使用します。

 

ここで m は中心積率です。 

中心積率は一般集団分布の数値特性です。

2番目～4番目の選択的 中心積率 は以下の式で計算されます。

 

ただし、これら値は不偏です。ここで、k 統計 とh 統計について述べます。一定条件下で、それら中心積率の不偏推定値を得られるようにします。よって離散の不偏推定値、標準偏差、歪度、 尖度を計算できるようになります。

k および h推定の4番目の積率計算は異なる方法で行われることに注意が必要です。k や hを使うと尖度の推定に異なる式を取得することになってしまいます。たとえば、Microsoft Excel では k推定に対応した式を使って超過値を計算します。一方 "Statistics for Traders" では、尖度の不偏推定は h推定値を用いて行われます。

h-推定を選び、以前の式では'm'でしたが代わりに今回は置換によって必要なパラメータを計算します。

分散と標準偏差

 

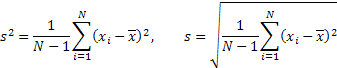
歪度

 

尖度

 

既定の式により正規分布法則について計算された過剰係数（尖度）は3です。

計算値から3を引いて得られる値は尖度値として用いられることが多く、そのため取得した値は正規分布法則に対して正規化されることに注意が必要です。最初のケースでは、この係数は尖度と呼ばれ、二番目のケースでは「過剰尖度」と呼ばれます。

既定の式によるパラメータ計算は dStat() 関数で行われます。

struct statParam
  {
  double mean;
  double median;
  double var;
  double stdev;
  double skew;
  double kurt;
  };
//----------------------------------------------------------------------------
int dStat(const double &x[],statParam &sP)
  {
  int i,m,n;
  double a,b,sum2,sum3,sum4,y[];
  
  ZeroMemory(sP);                                      // Reset sP
  n=ArraySize(x);
  if(n<4)                                             // Error
    {
    Print("Function dStat() error!");
    return(-1);
    }
  sP.kurt=1.0;
  ArrayResize(y,n);
  ArrayCopy(y,x);
  ArraySort(y);
  m=(n-1)/2;
  sP.median=y[m];                                     // Median
  if((n&0x01)==0)sP.median=(sP.median+y[m+1])/2.0;
  sP.mean=0;
  for(i=0;i<n;i++)sP.mean+=x[i];
  sP.mean/=n;                                         // Mean
  sum2=0;sum3=0;sum4=0;  
  for(i=0;i<n;i++)
    {
    a=x[i]-sP.mean;
    b=a*a;sum2+=b;
    b=b*a;sum3+=b;
    b=b*a;sum4+=b;
    }
  if(sum2<1.e-150)return(1);
  sP.var=sum2/(n-1);                                  // Variance
  sP.stdev=MathSqrt(sP.var);                           // Standard deviation
  sP.skew=n*sum3/(n-2)/sum2/sP.stdev;                 // Skewness
  sP.kurt=((n*n-2*n+3)*sum4/sum2/sum2-(6.0*n-9.0)/n)*
                              (n-1.0)/(n-2.0)/(n-3.0); // Kurtosis
  
  return(1);  
dStat() が呼ばれるとき、x[] 配列のアドレスがこの関数に渡されます。それは初期値を持ち、計算されたパラメータ値を持つ statParam ストラクチャへリンクします。配列内のエレメントが4個以下のとき、エラーが発生すると、関数は -1を返します。


ヒストグラム

dStat() 関数で計算されるパラメータ以外に、一般集団の分布法則はわれわれにとって大きな興味を引くものです。有限サンプリングにおいて分布法則を視覚的に推定するのにヒストグラムを描きます。ヒストグラムを描画する際、サンプリング値の範囲を似通ったセクションに分割します。そして各セクションのエレメント数を計算します。（グループ度数）

グループ度数を基に棒グラが描かれます。これがヒストグラムと呼ばれます。範囲の幅を正規化したあと、ヒストグラムは乱数の分布の実験的蜜度を表します。ヒストグラムを描くのに適したセクション数を決定するため "Statistics for Traders"で述べられている実験式を使用します。

 

ここで L は要求されるセクション数、N はサンプリングボリューム、e は尖度です。

以下に dHist()があるのがわかります。これはセクション数を決定し、そのそれぞれのエレメント数を計算し、取得されるグループ度数を正規化します。

struct statParam
  {
  double mean;
  double median;
  double var;
  double stdev;
  double skew;
  double kurt;
  };
//----------------------------------------------------------------------------
int dHist(const double &x[],double &histo[],const statParam &sp)
  {
  int i,k,n,nbar;
  double a[],max,s,xmin;
  
  if(!ArrayIsDynamic(histo))                           // Error
    {
    Print("Function dHist() error!");
    return(-1);
    }
  n=ArraySize(x);
  if(n<4)                                             // Error
    {
    Print("Function dHist() error!");
    return(-1);
    }
  nbar=(sp.kurt+1.5)*MathPow(n,0.4)/6.0;
  if((nbar&0x01)==0)nbar--; if(nbar<5)nbar=5;          // Number of bars
  ArrayResize(a,n);
  ArrayCopy(a,x);
  max=0.0;
  for(i=0;i<n;i++)
    {
    a[i]=(a[i]-sp.mean)/sp.stdev;                     // Normalization
    if(MathAbs(a[i])>max)max=MathAbs(a[i]);
    }
  xmin=-max;
  s=2.0*max*n/nbar;
  ArrayResize(histo,nbar+2);
  ArrayInitialize(histo,0.0);
  histo[0]=0.0;histo[nbar+1]=0.0;
  for(i=0;i<n;i++)
    {
    k=(a[i]-xmin)/max/2.0*nbar;
    if(k>(nbar-1))k=nbar-1;
    histo[k+1]++;
    }
  for(i=0;i<nbar;i++)histo[i+1]/=s;
  
  return(1);
  }

x[] 配列のアドレスが関数に渡されます。そこには初期シーケンスが含まれています。配列コンテントは関数実行結果によって変わることはありません。次のパラメータは、計算された値が格納される動的配列 histo[] へのリンクです。その配列のエレメント数は計算に使用されるセクション数+2エレメントに一致します。

histo[] 配列の最初と最後にゼロ値を持つエレメントが加えられます。最後のパラメータは前に計算されたパラメータ値を格納している statParam ストラクチャのアドレスです。関数に渡される histo[] 配列が動的配列ではない、またはインプット配列 x[] に4個未満のエレメントしかない場合、関数は実行を停止し -1を返します。

取得した値でヒストグラムを描いたら、サンプリングが分布の正規法則に一致しているか視覚的に推定ができます。分布の正規化法則に一致したグラフ表現をより視覚的にするには、ヒストグラム以外に正規確率のスケールでグラフを描く（正常確率プロット）ことができます。


正常確率プロット

そのようなグラフを描く上のポイントは、正規分布のシーケンス値が同一線上に描かれるように X 軸を伸ばすことです。この方法で正規性仮説がグラフで確認できます。 そのタイプのグラフに関する詳細はこちらで確認することができます。： "Normal probability plot" または "e-Handbook of Statistical Methods"。

正規確率グラフを描くのに必要な値を計算するには以下に示される関数 dRankit() が使用されます。

struct statParam
  {
  double mean;
  double median;
  double var;
  double stdev;
  double skew;
  double kurt;
  };
//----------------------------------------------------------------------------
int dRankit(const double &x[],double &resp[],double &xscale[],const statParam &sp)
  {
  int i,n;
  double np;
  
  if(!ArrayIsDynamic(resp)||!ArrayIsDynamic(xscale))    // Error
    {
    Print("Function dHist() error!");
    return(-1);
    }
  n=ArraySize(x);
  if(n<4)                                            // Error
    {
    Print("Function dHist() error!");
    return(-1);
    }
  ArrayResize(resp,n);
  ArrayCopy(resp,x);
  ArraySort(resp);
  for(i=0;i<n;i++)resp[i]=(resp[i]-sp.mean)/sp.stdev;
  ArrayResize(xscale,n);
  xscale[n-1]=MathPow(0.5,1.0/n);
  xscale[0]=1-xscale[n-1];
  np=n+0.365;
  for(i=1;i<(n-1);i++)xscale[i]=(i+1-0.3175)/np;
  for(i=0;i<n;i++)xscale[i]=ltqnorm(xscale[i]);
  
  return(1);
  }
//----------------------------------------------------------------------------

double A1 = -3.969683028665376e+01, A2 =  2.209460984245205e+02,
       A3 = -2.759285104469687e+02, A4 =  1.383577518672690e+02,
       A5 = -3.066479806614716e+01, A6 =  2.506628277459239e+00;
double B1 = -5.447609879822406e+01, B2 =  1.615858368580409e+02,
       B3 = -1.556989798598866e+02, B4 =  6.680131188771972e+01,
       B5 = -1.328068155288572e+01;
double C1 = -7.784894002430293e-03, C2 = -3.223964580411365e-01,
       C3 = -2.400758277161838e+00, C4 = -2.549732539343734e+00,
       C5 =  4.374664141464968e+00, C6 =  2.938163982698783e+00;
double D1 =  7.784695709041462e-03, D2 =  3.224671290700398e-01,
       D3 =  2.445134137142996e+00, D4 =  3.754408661907416e+00;
//----------------------------------------------------------------------------
double ltqnorm(double p)
  {
  int s=1;
  double r,x,q=0;

  if(p<=0||p>=1){Print("Function ltqnorm() error!");return(0);}
  if((p>=0.02425)&&(p<=0.97575))    // Rational approximation for central region
    {
    q=p-0.5; r=q*q;
    x=(((((A1*r+A2)*r+A3)*r+A4)*r+A5)*r+A6)*q/(((((B1*r+B2)*r+B3)*r+B4)*r+B5)*r+1);
    return(x);
    }
  if(p<0.02425)                    // Rational approximation for lower region
    {
    q=sqrt(-2*log(p)); 
    s=1;
    }
  else      //if(p>0.97575)          // Rational approximation for upper region
    {
    q = sqrt(-2*log(1-p));
    s=-1;
    }
  x=s*(((((C1*q+C2)*q+C3)*q+C4)*q+C5)*q+C6)/((((D1*q+D2)*q+D3)*q+D4)*q+1);
  return(x);
  }

この関数にはx[] 配列のアドレスが入力されます。この配列には初期シーケンスが含まれます。次のパラメータはアウトプット配列 resp[] および xscale[]に対する参照です。関数実行後、配列には X 軸、 Y 軸についてグラフを描くのに使用する値がそれぞれ書かれます。それから statParam ストラクチャのアドレスが関数に渡されます。そこには前に計算されたインプットシーケンスの統計的パラメータ値があります。エラーの場合、関数は -1を返します。

X 軸に対する値を作成するときは関数 ltqnorm() が呼ばれます。この関数は正規分布の逆整関数を計算します。計算に使用されるアルゴリズムは "An algorithm for computing the inverse normal cumulative distribution function"から借用しています。


4種類のチャート

以前に統計パラメータが計算する dStat() 関数について述べました。その意味を手短に繰り返します。

Dispersion (variance) は算術期待値（平均値）からの無作為な値の分散deviationを二乗した平均値です。乱数の分散が分布の中心からどのくらい離れているかを示すパラメータです。このパラメータ値が大きいほど、より分散していることを表します。

標準分散 – 分散は乱数の二乗として計測されるため、標準分散は分散のよりわかりやすい特性として用いられることがよくあります。dispersion 、 standard deviation 分散の二乗に等しくなっています。

歪度 – 乱数分布曲線を描くと、歪度は分布中心に関して確率密度曲線がどの程度非対称であるかを示します。歪度がゼロより大きければ、確率密度曲線は左側が急な傾斜で右側は緩やかな傾斜を描きます。歪度がマイナスであれば、左側がゆるやかで右側が急な傾斜となります。確率密度曲線が分布中央について対称であれば、歪度はゼロです。

過剰係数（尖度） – 確率密度曲線の尖り方、分布の端の傾斜の角度をを表します。分布中心に近い曲線の頂点が鋭いほど、尖度の値は大きくなっています。

挙げられている統計パラメータがシーケンスを細かく述べているにもかかわらず、グラフ形式で表わされる推定結果を基に、シーケンスをもっと簡単に特徴づけられることがよくあります。たとえば、通常のシーケンスグラフは統計パラメータを分析するとき取得されるビューをおおきくgreatly完成することができます

本稿で前に、正規確率のスケールでヒストグラムやチャートを描くデータを準備することのできる関数 dHist() および dRankit() について述べました。正規分布のヒストグラムやグラフを同じシート上に通常グラフを共に表示することで、視覚的に分析されたシーケンスの主な特性を判断することができるのです。

ここに挙げた3種類のチャートはY 軸における現在値および X 軸における前回値を伴うもうひとつのチャートへの補足です。そのようなチャートは"Lag Plot"と呼ばれます。隣接するインディケータ同士に強い相関関係があれば、サンプリングの値は直線で伸びますstretch in a straight line. 隣接するインディケータ同士に相関関係がなければ、たとえば無作為なシーケンスを分析するときなど、その場合は値がチャート中に分散します。dispersed

最初のサンプリングを手短ンに推定するために提案するのは、統計パラメータの計算値を表示するため1つのシートに4種類のチャートを描くことです。これは目新しい考え方ではありません。4種類のチャートの分析利用に関してはこちらに記載があります。："4-Plot"

本稿末尾に「ファイル」の項がありそこにシート1枚にこれら4種類のチャートを描くスクリプ s4plot.mq5があります。dat[] 配列はスクリプトの OnStart() 関数で作成されます。そこには初期シーケンスも含まれています。関数dStat()、dHist()、 dRankit() は常にチャートを描くのに要求されるデータ計算に呼ばれます。次に呼ばれるのはvis4plot() 関数です。これは、計算されたデータを基 gnuplot コマンドでテキストファイルを作成し、別ウィンドウにチャートを描くためのアプリケーションを呼びます。

本稿でスクリプトの全コードを表示することに意味はありません。関数 dStat()、dHist() 、dRankit() に関しては以前に述べているからです。gnuplot コマンドのシーケンスを作成する vis4plot() 関数は特別なことはありません。significant peculiaritiesまた gnuplot コマンドについても本稿の範囲を超えているので省きます。その上 gnuplot アプリケーションの代わりに別の方法でチャートを描くことができます。

s4plot.mq5 の一部分、 OnStart() 関数の記述を示します。

//----------------------------------------------------------------------------
// Script program start function
//----------------------------------------------------------------------------
void OnStart()
  {
  int i;
  double dat[128],histo[],rankit[],xrankit[];
  statParam sp;
 
  MathSrand(1);
  for(i=0;i<ArraySize(dat);i++) dat[i]=MathRand();
  
  if(dStat(dat,sp)==-1)return;
  if(dHist(dat,histo,sp)==-1)return;
  if(dRankit(dat,rankit,xrankit,sp)==-1)return;
  
  vis4plot(dat,histo,rankit,xrankit,sp,6);
  }

この例では、MathRand()関数を使用して初期データを伴う dat[] 配列を書くのにランダムシーケンスが使われています。スクリプト実行結果は以下です。

4-プロット 

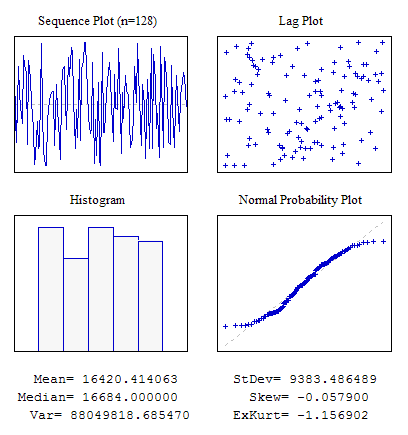
図3　4種類のチャートスクリプト s4plot.mq5

vis4plot() 関数の最後のパラメータに注意をはらう必要があります。それは出力された数値のフォーマットにとって合理的です。本稿では、値は6ケタで出力されています。six decimal placesこのパラメータはDoubleToString() 関数内でフォーマットを決めるパラメータと同じです。

インプットシーケンスの値が小さすぎたり大きすぎると、より判別可能な表示のために scientific フォーマットを使用することが可能です。そのために、たとえばそのパラメータを -5に設定します。値 -5 は vis4plot() 関数の初期値について設定されます。

シーケンスの特殊性を表示するための4種類のチャートのメソッドの明確性obviousnessを見せるためにはそのようなシーケンスのジェネレータが必要です。


疑似ランダムシーケンスのジェネレータ

クラス RNDXor128 疑似ランダムシーケンスを作成します。

以下にそのクラスを記述するインクルードファイルのコードを示します。

//-----------------------------------------------------------------------------------
//                                                                      RNDXor128.mqh
//                                                                      2011, victorg
//                                                                https://www.mql5.com
//-----------------------------------------------------------------------------------
#property copyright "2011, victorg"
#property link      "https://www.mql5.com"

#include <Object.mqh>
//-----------------------------------------------------------------------------------
// Generation of pseudo-random sequences. The Xorshift RNG algorithm 
// (George Marsaglia) with the 2**128 period of initial sequence is used.
//          uint rand_xor128()
//            {
//            static uint x=123456789,y=362436069,z=521288629,w=88675123;
//            uint t=(x^(x<<11));x=y;y=z;z=w;
//            return(w=(w^(w>>19))^(t^(t>>8)));
//            }
// Methods:
//  Rand()      - even distribution withing the range [0,UINT_MAX=4294967295].
//  Rand_01()   - even distribution within the range [0,1].
//  Rand_Norm() - normal distribution with zero mean and dispersion one.
//  Rand_Exp()  - exponential distribution with the parameter 1.0.
//  Rand_Laplace() - Laplace distribution with the parameter 1.0
//  Reset()     - resetting of all basic values to initial state.
//  SRand()     - setting new basic values of the generator.
//-----------------------------------------------------------------------------------
#define xor32  xx=xx^(xx<<13);xx=xx^(xx>>17);xx=xx^(xx<<5)
#define xor128 t=(x^(x<<11));x=y;y=z;z=w;w=(w^(w>>19))^(t^(t>>8))
#define inidat x=123456789;y=362436069;z=521288629;w=88675123;xx=2463534242

class RNDXor128:public CObject
  {
protected:
  uint      x,y,z,w,xx,t;
  uint      UINT_half;
public:
            RNDXor128()       {UINT_half=UINT_MAX>>1;inidat;};
  double    Rand()            {xor128;return((double)w);};
  int       Rand(double& a[],int n)
                              {int i;if(n<1)return(-1);
                               if(ArraySize(a)<n)return(-2);
                               for(i=0;i<n;i++){xor128;a[i]=(double)w;}
                               return(0);};
  double    Rand_01()         {xor128;return((double)w/UINT_MAX);};
  int       Rand_01(double& a[],int n)
                              {int i;if(n<1)return(-1);
                               if(ArraySize(a)<n)return(-2);
                               for(i=0;i<n;i++){xor128;a[i]=(double)w/UINT_MAX;}
                               return(0);};
  double    Rand_Norm()       {double v1,v2,s,sln;static double ra;static uint b=0;
                               if(b==w){b=0;return(ra);}
                               do{
                                 xor128;v1=(double)w/UINT_half-1.0;
                                 xor128;v2=(double)w/UINT_half-1.0;
                                 s=v1*v1+v2*v2;
                                 }
                               while(s>=1.0||s==0.0);
                               sln=MathLog(s);sln=MathSqrt((-sln-sln)/s);
                               ra=v2*sln;b=w;
                               return(v1*sln);};
  int       Rand_Norm(double& a[],int n)
                              {int i;if(n<1)return(-1);
                               if(ArraySize(a)<n)return(-2);
                               for(i=0;i<n;i++)a[i]=Rand_Norm();
                               return(0);};
  double    Rand_Exp()        {xor128;if(w==0)return(DBL_MAX);
                               return(-MathLog((double)w/UINT_MAX));};
  int       Rand_Exp(double& a[],int n)
                              {int i;if(n<1)return(-1);
                               if(ArraySize(a)<n)return(-2);
                               for(i=0;i<n;i++)a[i]=Rand_Exp();
                               return(0);};
  double    Rand_Laplace()    {double a;xor128;
                              a=(double)w/UINT_half;
                              if(w>UINT_half)
                                {a=2.0-a;
                                if(a==0.0)return(-DBL_MAX);
                                return(MathLog(a));}
                              else
                                {if(a==0.0)return(DBL_MAX);
                                return(-MathLog(a));}};
  int       Rand_Laplace(double& a[],int n)
                              {int i;if(n<1)return(-1);
                               if(ArraySize(a)<n)return(-2);
                               for(i=0;i<n;i++)a[i]=Rand_Laplace();
                               return(0);};
  void      Reset()           {inidat;};
  void      SRand(uint seed)  {int i;if(seed!=0)xx=seed;
                               for(i=0;i<16;i++){xor32;}
                               xor32;x=xx;xor32;y=xx;
                               xor32;z=xx;xor32;w=xx;
                               for(i=0;i<16;i++){xor128;}};
  int       SRand(uint xs,uint ys,uint zs,uint ws)
                              {int i;if(xs==0&&ys==0&&zs==0&&ws==0)return(-1);
                               x=xs;y=ys;z=zs;w=ws;
                               for(i=0;i<16;i++){xor128;}
                               return(0);};
  };
//-----------------------------------------------------------------------------------

ランダムシーケンス作成に使用されるアルゴリズムはGeorge Marsaglia著 "Xorshift RNGs" に詳しく述べられています。（本稿松木 xorshift.zip を参照ください。）RNDXor128 クラスのメソッドはファイル RNDXor128.mqh に記載があります。このクラスを用いてeven distribution、正規分布、指数分布、またはラプラス分布（二重指数分布）のシーケンスを取得することが可能です。

RNDXor128 クラスのインスタンスが作成されるときシーケンスの基本値は初期状態に設定されることに注意が必要です。このときスクリプトまたはRNDXor128を使うインディケータを新たに始めるとき MathRand() 関数を呼ぶのと反対ひとつ同じシーケンスが作成されます。MathSrand() を呼び、それから MathRand()を呼ぶときと同じです。


シーケンス例

以下は例としてプロパティが全く異なるシーケンス同士を分析するときに取得した結果です。

例1　分布のEven Law を伴うランダムシーケンス

#include "RNDXor128.mqh"
RNDXor128 Rnd;
//----------------------------------------------------------------------------
void OnStart()
  {
  int i;
  double dat[512];

  for(i=0;i<ArraySize(dat);i++) dat[i]=Rnd.Rand_01();
  ...  
  }

Even 分布

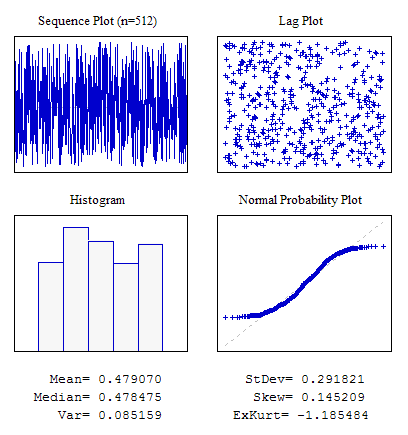
図4　Even 分布

例2　分布の正規法則を伴うランダムシーケンス

#include "RNDXor128.mqh"
RNDXor128 Rnd;
//----------------------------------------------------------------------------
void OnStart()
  {
  int i;
  double dat[512];

  for(i=0;i<ArraySize(dat);i++) dat[i]=Rnd.Rand_Norm();
  ...  
  }

正規分布

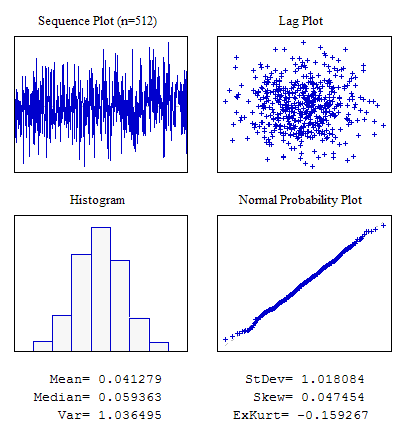
図5　正規分布

例31　分布の指数法則を伴うランダムシーケンス

#include "RNDXor128.mqh"
RNDXor128 Rnd;
//----------------------------------------------------------------------------
void OnStart()
  {
  int i;
  double dat[512];

  for(i=0;i<ArraySize(dat);i++) dat[i]=Rnd.Rand_Exp();
  ...  
  }

指数分布

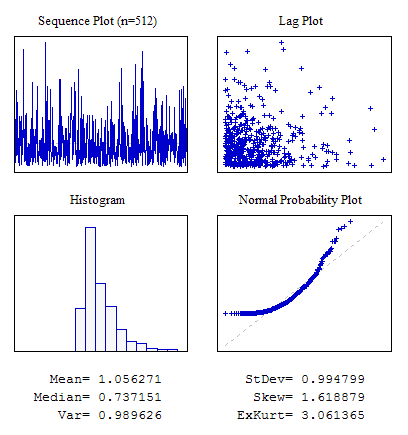
図6　指数分布

例4　分布のラプラス法則を伴うランダムシーケンス

#include "RNDXor128.mqh"
RNDXor128 Rnd;
//----------------------------------------------------------------------------
void OnStart()
  {
  int i;
  double dat[512];

  for(i=0;i<ArraySize(dat);i++) dat[i]=Rnd.Rand_Laplace();
  ...  
  }

ラプラス分布

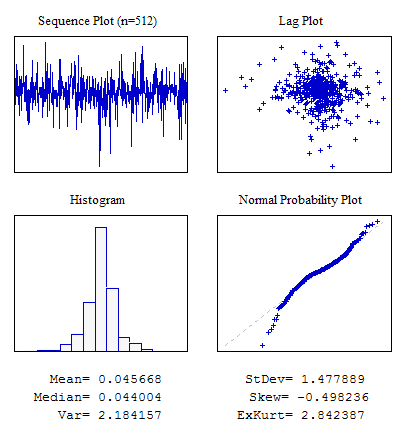
図7　ラプラス分布

例5　Sinusoidal シーケンス

//----------------------------------------------------------------------------
void OnStart()
  {
  int i;
  double dat[512];

  for(i=0;i<ArraySize(dat);i++) dat[i]=MathSin(2*M_PI/4.37*i);
  ...  
  }

Sinusoidal シーケンス

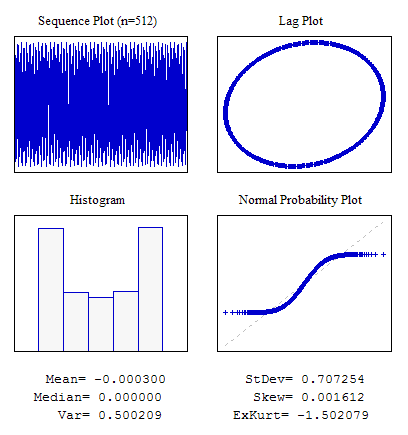
図8　Sinusoidal シーケンス

例6　隣接インディケータ間に可視相関関係を伴うシーケンス

#include "RNDXor128.mqh"
RNDXor128 Rnd;
//----------------------------------------------------------------------------
void OnStart()
  {
  int i;
  double dat[512],a;

  for(i=0;i<ArraySize(dat);i++) {a+=Rnd.Rand_Laplace();dat[i]=a;}
  ...  
  }

隣接インディケータ間の相関関係

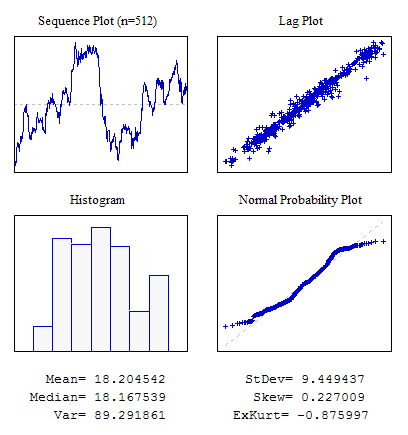
図9　隣接インディケータ間の相関関係


おわりに

あらゆる計算を実装するプログラムアルゴリズムの作成はつねに大変な仕事です。その理由は四捨五入、truncating 、変数オーバーフローの際に起こりうる誤りを最小限に留めるという多くの要件を考慮する必要があるからです。

本稿に挙げる例を書いているとき、プログラムアルゴリズムの分析を全く行いませんでした。関数を書いているとき、数学的アルゴリズムは直接実装されました。ですからみなさんがそれを「まじめな」アプリケーションで使用するなら、安定性と正確性を分析する必要があります。

本稿ではニュープロットアプリケーションについては全く触れませんでした。こういった内容は本稿のテーマから外れているからです。とはいえ、ニュープロットは MetaTrader 5と共に使用するのに適用できることはお伝えしたいと思います。このためにはそのソースコードにすこしばかり修正を加え再度コンパイルする必要があります。また、ファイルを使用してニュープロットにコマンドを渡す方法はおそらく最適な方法ではないでしょう。というのもニュープロットとの連携はプログラミングインターフェースによって形成されるからです。


ファイル

  • erremove.mq5 – サンプリングからエラーを除外するスクリプト例
  • function_dstat.mq5 – 統計パラメータを計算する関数
  • function_dhist.mq5 - ヒストグラム値を計算する関数
  • function_drankit.mq5 – 正規分布スケールを持ち手チャートを描く際に使用される値を計算する関数
  • s4plot.mq5 – 1シートに4種類のチャートを描くスクリプト例
  • RNDXor128.mqh – ランダムシーケンスのジェネレータクラス
  • xorshift.zip - George Marsaglia. "Xorshift RNGs".

 

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/273

添付されたファイル |
ZIPをダウンロード
erremove.mq5 (4.53 KB)
function_dhist.mq5 (1.21 KB)
function_drankit.mq5 (2.46 KB)
xorshift.zip (38.35 KB)
function_dstat.mq5 (1.35 KB)
s4plot.mq5 (10.52 KB)
rndxor128.mqh (12.01 KB)
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動
ソースコードのトレーシング デバッギング 構造分析 ソースコードのトレーシング デバッギング 構造分析
実行されたコードのストラクチャーの作成とトレーシングの複雑な問題は、特に困難なく解決することができます。これは、MetaTrader5から可能になりました。これは、MQL5言語の新しい機能である、様々な複雑なデータ型の自動生成やローカルスコープ外に出た際の除去などのおかでです。この記事は、その方法論や、すぐ使えるツールを紹介します。
Expert Advisors最適化のカスタム基準作成 Expert Advisors最適化のカスタム基準作成
MetaTrader 5 クライアント端末は Expert Advisor パラメータを最適化する幅広い機会を提供します。またストラレジーテスタに含まれる最適化評価基準に対して、開発者には自身の基準を作成するチャンスが与えられています。これは Expert Advisorsを検証し最適化する数えきれない可能性に導きます。本稿ではそのような基準を、複雑なもの単純なもの双方、作成する実践的方法について記述します。
MQL5での統計確率分布 MQL5での統計確率分布
本稿は、適用統計に使用されるランダム変数の確率分布（標準、対数正規分布、二項分布、ロジスティック分布、指数分布、コーシー分布、ストゥーデンとの t-分布、 ラプラス分布、 ポアソン分布、双曲線正割分布、 ベータ分布、ガンマ分布）について述べます。またこういった分布を処理するクラス特性についても述べます。
サルでも解るMQL5 ウィザード サルでも解るMQL5 ウィザード
2011年初頭、 MQL5 ウィザードの第一版を発売しました。この新しいアプリケーションはトレーディングロボットを自動で作成する便利なツールを提供します。MetaTrader 5 ユーザーはだれでも、MQL5でプログラミングする方法を知らなくても独自のExpert Advisor を作成することができるのです。