机器学习中的量化（第1部分）：使用 CatBoost 的理论、示例代码和实现分析

概述

本文探讨了量化在树模型构建中的理论应用，不使用复杂的数学方程。在写这篇文章的时候，我发现不同作者的科学著作中缺乏既定的统一术语，所以我会选择我认为最能反映其含义的术语选项。此外，在其他研究人员没有注意到的问题上，我将使用我自己的术语。本文将使用我之前在文章“来自Yandex的CatBoost机器学习算法而不学习Python或R”中描述的术语和概念。因此，我建议您在阅读当前文章之前先熟悉它。

本文不会探讨将量化应用于训练过的神经网络以缩小其规模的可能性，因为我目前在这方面没有个人经验。

以下是您可以期待的： 

• 文章的第一部分包含关于量化的介绍性理论材料，有助于理解量化过程的目标和本质。
• 在文章的第二部分中，将以MQL5代码为例讨论均匀量化方法。
• 在文章的第三部分中，我将以 CatBoost 为例探讨量化过程的实现。

 

1. 标准用途

那么什么是量化，为什么要使用量化呢？让我们来弄清楚！

首先，让我们谈谈数据。因此，为了创建模型（进行训练），我们需要在表中仔细收集数据。此类数据的来源可以是能够解释目标数据的任何信息（由模型确定，例如交易信号）。数据源被称为不同的预测因素、特征、属性或因素。数据线的出现频率由现象的可比过程观察的发生来确定，关于哪些信息正在被收集，哪些信息将使用机器学习进行研究。所获得的全部数据称为样本。

样本可以是有代表性的——这是指其中记录的观察结果描述了所研究现象的整个过程，也可以是不具有代表性的，因为有尽可能多的数据可以收集，这只允许对所研究现象过程进行部分描述。通常，当我们处理金融市场时，我们处理的是非代表性样本，因为可能发生的一切还没有发生。因此，我们不知道金融工具在发生新事件（以前从未发生过）时会如何表现。然而，每个人都知道“历史会重演”的格言。算法交易员在研究中依赖的正是这一观察结果，希望在新的事件中会有与以前类似的事件，并且它们的结果将与确定的概率相似。

根据其逻辑内容（根据测量量表），预测因子的数字指标可以是：

• 二元 - 确认或否认观察到的现象的固定属性的存在；
• 定量（公制）-用某种测量指标描述一种现象，例如，它可以是速度、某物的坐标、大小、自事件开始以来经过的时间以及许多其他可以测量的特征，包括它们的导数。
• 范畴（标称尺度）-关于一个逻辑组中包含的不同可观察对象或现象的信号，通常用整数表示。例如，一周中的几天，价格趋势的方向，支撑或阻力位的序列号。
• 等级（序数）-表征事物的优先性或有序性。它很少被分配到一个单独的组，因为它可以根据上下文和逻辑被归类为其他类型的指标。例如，这可以包括动作的顺序，实验的结果，以相对于其他类似实验的结果评估的形式。

因此，样本包含具有自己的数字指标的不同预测因子，这些数据总体上描述了观察到的现象，其特征或类型在目标函数（以下称为目标函数）中进行了描述。样本中的目标函数可以是数字指标，也可以是分类指标。在本文中，我将进一步探讨分类目标函数，并在更大程度上探讨二元目标函数。

维基百科提供了以下定义：

量化（Quantization）——在数学和数字信号处理中，是将大集合（通常是连续集合）的输入值映射到（可计数的）小集合中的输出值的过程，通常具有有限数量的元素。根据编码方法，信号值可以四舍五入到最近的电平，也可以四舍五入到最近水平中的较低或较高水平。这种量化称为标量。还有矢量量化——将矢量量的可能值的空间划分为有限数量的区域，并用其中一个区域的标识符替换这些值。 

 我喜欢较短的定义：

数据量化是一种压缩（编码）观测信息的方法，其测量尺度具有可接受的精度损失。压缩（编码）意味着对象的离散性，这意味着它们的类型和同质性，或者简单地说是相似性。相似性标准可能不同，这取决于所选择的算法和嵌入其中的逻辑。

数据量化在任何地方都被使用，特别是在模拟信号到数字信号的转换中，以及在数字信号的后续压缩中。例如，从相机矩阵接收的数据可以记录为原始文件，然后立即（或稍后在计算机上）压缩为jpg或其他方便的数据存储格式。

看看MetaTrader 5终端中蜡烛或柱形的数据图形表示，我们已经看到了在我们选择的时间尺度上量化刻度的结果。随着时间的推移对连续数据流进行量化通常称为采样（或离散化）。

通常，采样是在一段时间内以给定频率记录观测特征的过程。然而，如果我们假设这是将数据收集到样本中的频率，则定义应调整为以下内容：“采样是记录观测特征的过程，其频率由给定函数在其阈值激活期间确定”。这里的函数指的是根据其固有逻辑给出信号以接收数据的任何算法。例如，在MetaTrader 5中，我们看到的正是这种方法，因为在非交易日，收盘价不是一个持续一段时间的过程，而是图表上没有任何信息，即采样率降至零。

量化算法的一个简单例子是构造直方图。此方法的算法非常简单：

• 找到指标的最大值和最小值（在我们的例子中，是预测器）。
• 计算最大和最小指标之间的差值。
• 将第2点得到的增量除以一个整数，例如10，或，具体取决于观测次数（如Karl Pearson建议的）。获得初始测量单位中的除法步长，这将是新测量量表的读数。
• 现在，我们需要用自己的分部建立自己的尺度。这只需将步长乘以读数的序列号即可完成。
• 接下来，将每个观测值分配给新的测量尺度的范围，并分别对每个范围中的观测次数进行汇总。

算法结果是如图1所示的直方图。

 

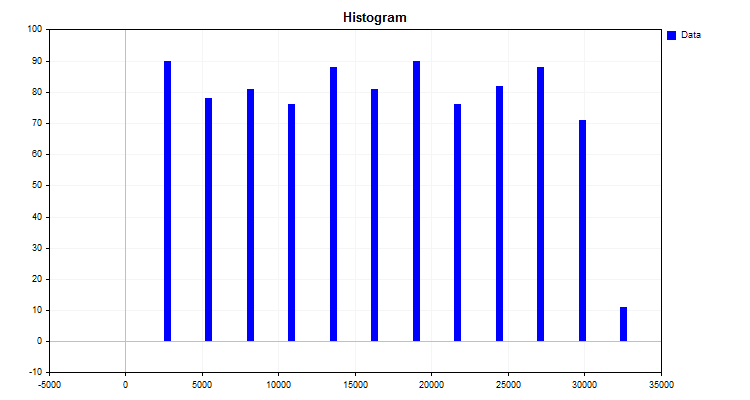
图1

直方图显示了数据是如何根据新的测量尺度分布的。基于分布的出现，通过描述性统计的装置，可以假设分布密度的类型，这对于选择有限量化方法是有用的。您可以在以下文章中阅读有关分布密度的信息：

• 未知概率密度函数的核密度估计；
• MQL5中的统计分布-充分利用R并使其更快；
• 统计估计。

所以，我们通过构建直方图得到了什么：

• 将数据分组的级别（截止）或边界。一组级别被称为量子网格或字典——正是在这些级别上进行数据编码，这确保了它们的分组和压缩。可以根据量化算法中嵌入的不同规则来安装边界。水平（临界值）形成了测量观测指标的新尺度。我习惯于将两个能级之间的范围称为“量子段”，尽管其他作者的作品中也有其他名称——“区间”、“范围”或“量化步长”；
• 每个观测值（指标）属于给定组（直方图列）。对于量化来说，这是一种压缩算法的工作，其本质是在将观测值分配给量子网格的某个范围时，将原始数据转换为压缩数据。压缩的结果可以是变量值的各种数值变换。最常见的有两种选择：第一种是变换，根据截断（边界）值之间的范围的数量为变量分配一个秩（索引），其中该数字位于截断（边界的值）的范围内，第二种选择是为变量分配水平标度值，例如，观察值的数值位于1.2和1.4之间，然后分配正确的值-1.4。然而，要使用第二个选项，我们需要设置限制，超过该限制数据将不会继续，而第一个选项允许您使用量子表边界之外的任何值。对于第二种选择，一个好的解决方案可能是强制在相当大的距离上添加级别（边界/边界），这将允许以尖峰或丢失数据的形式出现错误。
• 可以通过以下方式恢复每个数值的精度损失（去量化）：
• - 沿着区间的中心，对应于数字的索引。
• - 根据间隔的左侧或右侧级别值（边界/截止/边界），通常为右侧级别值。考虑到量化表中的边界通常不是为第一个和最后一个区间定义的，那么我们可以使用区间的平均范围或区间宽度的第一个和第二个值来确定它们。

根据量化应用的任务和领域，必须处理变量的不同名称和方程的写作风格，这使得很难理解算法的本质，因为描述它们的作者假设了来自应用算法的特定领域的知识。不同算法的本质归结为不同的构建级别（截止值）的方式，所以我建议根据一些标准对它们进行分类。

定间隔量化：

• 使用类似于Pearson直方图的方法划分为固定区间；
• 转换以减少数字的位数。

可变区间量化：

• 每个间隔的固定百分比观测值的累积。
• 对理论分布或近似分布曲线下的面积使用固定值。
• 使用根据系数改变量化步长的给定函数。这些通常是将间距向边缘或中心延伸的功能。
• 根据值的密度，使用影响间隔的加权系数。
• 迭代方法（包括自适应方法）。有关数据结构的信息用于配置边界，并采取措施减少错误。
• 其他方式。

以经验确定的区间量化：

• 数字序列；
• 了解观察的性质，允许对含义相似的指标进行分组；
• 手动标记。

减少所选度量中的量化误差可以是一个迭代过程，也可以使用给定的方程计算一次。为了评估结果，可以方便地使用相对于取样本中预测器值的整个数字范围的误差分布的平均百分比。

 

2. 在MQL5中实现量化算法

之前，我们看了一个量化如何工作的简单例子，但它缺少量化中经常使用的步骤之一，即对经过一些计算后获得的尺度进行重新划分，以找到区间的平均值，这通常被称为质心。量化的间隔将最终由两个附近质心的边界之间的距离的一半来确定。

让我们考虑将占用内存8个字节的实数（如double）逐步量化为仅占用8位的整个uchar数据类型：

• 1. 在输入数据中查找最大值和最小值：
• 1.1. 在arr_in_Data数组中查找最大值和最小值-Max和Min变量。
• 2. 计算间隔之间的窗口大小：
• 2.1. 找出最大值和最小值之间的差值，并将其存储在Delta变量中。
• 2.2. 查找一个窗口的大小Delta/nQ，其中nQ是分隔符（边界）的数量，将结果保存在Interval_size变量中。
• 3. 执行量化和误差计算：
• 3.1. 将输入数据的最小值移位为零arr_In_data_Min。
• 3.2. 将点3.1的结果除以Interval_Size间隔的数量，后者比分隔符的数量多一个。
• 3.3. 现在，我们应该将“round”函数应用于3.2中获得的结果，该函数将数字四舍五入到最接近的整数。结果将保存在arr_Output_Q_Interval数组中。
• 3.4. 将arr_Output_Q_Interval数组的值乘以Interval_Size，再加上最小值。现在我们有了这个数字的转换（量化）值，我们将把它保存在arr_Output_Q_Data数组中。
• 3.5. 让我们将误差计算为累计总数。为此，我们将原始值与量化结果之间的绝对值差除以范围。将得到的总数除以arr_in_Data数组中的元素数。
• 4. 将分隔符（边界）保存到arr_Output_Q_Book数组中：
• 4.1. 对于第一个间隔，我们进行了修改-将间隔大小的一半（interval_size）添加到最小值（Min）。
• 4.2. 随后的间隔是通过将间隔值与前一步的arr_Output_Q_Book数组的值相加来计算的。

下面是一个函数代码示例，其中包含变量和数组的描述。

/+---------------------------------------------------------------------------------+
//|Quantization of transformation (encoding) type to a given integer bitness
//+---------------------------------------------------------------------------------+
double Q_Bit(
   double &arr_Input_Data[],//Quantization data array
   int &arr_Output_Q_Interval[],//Outgoing array with intervals containing data 
   double &arr_Output_Q_Data[],//Outgoing array with restored values of the original data 
   float &arr_Output_Q_Book[],//Outgoing array - "Book with boundaries" or "Quantization table"
   int N_Intervals=2,//Number of intervals the original data should be divided (quantized) into
   bool Use_Max_Min=false,//Use/do not use incoming maximum and minimum values
   double Min_arr=0.0,//Maximum value
   double Max_arr=100.0//Minimum value
)
{
   if(N_Intervals<2)return -1;//There may be at least two intervals, in this case, there is one separator
//---0. Initialize the variables and copy the arr_Input_Data array
   double arr_In_Data[];
   double Max=0.0;//Maximum
   double Min=0.0;//Minimum
   int Index_Max=0;//Maximum index in the array
   int Index_Min=0;//Minimum index in the array
   double Delta=0.0;//Difference between maximum and minimum
   int   nQ=0;//Number of separators (borders)
   double Interval_Size=0.0;//Interval size
   int Size_arr_In_Data=0;//arr_In_Data array size
   double Summ_Error=0.0;//To calculate error/data loss
   nQ=N_Intervals-1;//Number of separators
   Size_arr_In_Data=ArrayCopy(arr_In_Data,arr_Input_Data,0,0,WHOLE_ARRAY);
   ArrayResize(arr_Output_Q_Interval,Size_arr_In_Data);
   ArrayResize(arr_Output_Q_Data,Size_arr_In_Data);
   ArrayResize(arr_Output_Q_Book,nQ);

//---1. Finding the maximum and minimum in the input data
   if(Use_Max_Min==false)//If enforced array limits are not used
   {
      Index_Max=ArrayMaximum(arr_In_Data,0,WHOLE_ARRAY);
      Index_Min=ArrayMinimum(arr_In_Data,0,WHOLE_ARRAY);
      Max=arr_In_Data[Index_Max];
      Min=arr_In_Data[Index_Min];
   }

   else//Otherwise enforce the maximum and minimum 
   {
      Max=Max_arr;
      Min=Min_arr;
   }

//---2. Calculate the window size between intervals
   Delta=Max-Min;//Difference between maximum and minimum 
   Interval_Size=Delta/nQ;//Size of one window

//---3. Perform quantization and error calculation
   for(int i=0; i<Size_arr_In_Data; i++)
   {
      arr_Output_Q_Interval[i]=(int)round((arr_In_Data[i]-Min)/Interval_Size);
      arr_Output_Q_Data[i]=arr_Output_Q_Interval[i]*Interval_Size+Min;
      Summ_Error=Summ_Error+(MathAbs(arr_Output_Q_Data[i]-arr_In_Data[i]))/Delta;
   }
//---4. Save separators (borders) into the array
   for(int i=0; i<nQ; i++)
   {
      switch(i)
      {
      case 0:
         arr_Output_Q_Book[i]=float(Min+Interval_Size*0.5);
         break;
      default:
         arr_Output_Q_Book[i]=float(arr_Output_Q_Book[i-1]+Interval_Size);
         break;
      }
   }
   return Summ_Error=Summ_Error/(double)Size_arr_In_Data*100.0;
} 

数据量化的实际应用：

• 减少存储和处理数据所需的内存。这种效果的实现是因为仅存储量子段的索引就足够了，其中指示符数的数值下降。在这种情况下，将数据类型从实数double或float更改为整数类型（如int甚至uchar）是有意义的。
• 加速计算。通过处理整数和减少所使用的数字集来实现，这减少了算法中的循环次数。
• 降噪。源数据的质量可能包含测量误差形式的噪声，既有来自代理的主要数据丢失，也有延迟、舍入和测量误差形式。量化将指标平均在量子段的范围内，这会消除这种噪声，不允许模型将注意力集中在它上。
• 对缺少近距离观测值的补偿。有时，由于缺乏观测，预测值非常罕见，不能被视为峰值。量化可以为这些观测提供足够的值离散范围，使模型可用于不在样本中的新数据。
• 与维度的诅咒作斗争。减少可能的组合的数量减少了测量空间的可能坐标的网格，从而加快和改进了训练。

两个例子展示了两种主要的量化策略：

• 数据近似策略。
• 数据聚合策略。

第一种策略最适合度量尺度，度量特征值分布接近连续的指标。从理论上讲，分隔值范围的间隔越多越好，因为重构值在数字序列的整个范围上的分散误差将更小。这种类型非常适合于恢复数学函数。

第二类策略旨在对数据进行分组。可以想象，特征的广义分类值正在被创建，而在这里，正确估计边界的任务要困难得多。根据我的经验，我们需要确保样本中至少有5%的观测结果落入区间。

值得注意的是，那些在意义上已经是分类的、没有任何约定的特征，应该非常仔细地量化，只结合那些真正相似的特征。此外，这里的相似性意味着将样本划分为子样本时的相似性。

文章附有脚本“Q_Trans”，作为量化过程的一个示例。用于量化的数据是随机生成的。该脚本包含以下主要函数：

• “Q_Bit”-将转换（编码）类型量化为给定的整数位深度
• “Book_to_cfra”-解码器从量化表中恢复数字的近似值，需要一个带索引的数组。
• “Book_to_cfra_v2”-解码器从量化表中恢复数字的近似值，不需要带索引的数组。
• “Q_Random”-具有随机边界的量化。

该脚本包含以下设置：

• 原始数据应划分（量化）为的区间数；
• 初始化随机数生成器的数字；
• 保存图表；
• 保存图表的目录；
• 图表宽度；
• 图表高度；
• 字体大小。

 

脚本操作阶段的描述：

1. 将随机生成一个样本。

2. 交易工具的图表将显示如文章前面所述构建的直方图（图1），以及生成的预测值按时间顺序分布并除以量化后获得的边界的图表（图2）。如果“Save charts”为“true”，则图表将与自定义终端文件“files\Q_Trans\Grafics”一起保存在目录中。

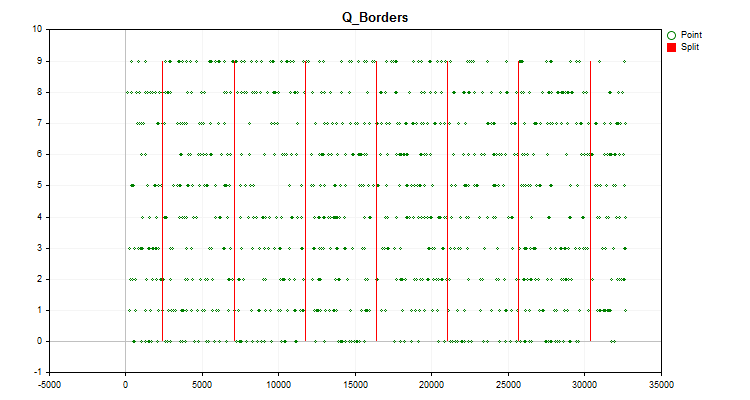   图 2

3. Q_Bit 函数用于执行量化并计算重构值相对于整个样本值范围的偏移形式的误差。
4. Book_to_cfra 函数用于沿着质心执行去量化，并以重构值的偏移的形式计算误差。
5. Book_to_cfra 函数用于沿右边界执行去量化，并以重构值的偏移量的形式计算误差。
6. Book_to_cfra_v2 函数用于沿着质心执行去量化，并以重构值的偏移的形式计算误差。
7. 使用Q_Random函数，将进行1000次尝试以找到分割预测器的最佳区间。
8. Book_to_cfra 函数用于使用随机获得的最佳网格沿着质心执行去量化，并以重构值的偏移的形式计算误差。

如果我们使用默认设置运行脚本，那么在专家终端日志中，我们将在消息列中看到以下信息

Average data recovery error size = 3.52% of full range when using 8 intervals
Average error size via quantum table for centroid conversion (Book_to_cifra) = 1145.62263
Average error size via quantum table for right boundary conversion (Book_to_cifra) = 2513.41952
Average error size via quantum table for centroid transformation (Book_to_cifra_v2) = 1145.62263
Average error size via quantum table for centroid transformation (Q_Random) = 1030.79216

有趣的是，选择边界的随机方法显示出比我们之前考虑的方法（基于均匀量化）更好的结果。

 

3. 使用 CatBoost 进行量化

我之前在我的文章《来自Yandex的CatBoost机器学习算法，无需学习Python或R》中写到过 CatBoost，它使用量化进行数据预处理，这可以显著加快梯度增强算法的操作。和以前一样，我将使用 CatBoost 的控制台版本，因为在计算机的中央处理器上执行工作时，它不需要安装额外的软件。

我们将需要以下设置：

1. 量化（划分）方法 —key “—feature-border-type”：

• Median
• Uniform
• UniformAndQuantiles
• MaxLogSum
• MinEntropy
• GreedyLogSum

2. 从1到65535分隔符的数目 –key “--border-count”

3. 将量化表保存到指定的文件 -key “-output-borders-file”

4. 从指定文件加载量化表 -key“-input-borders-file”

 

如果我们没有指定上述密钥，则使用以下设置来构建文章中使用的模型：

• 在CPU上计算，量化方法为“GreedyLogSum”，分隔符数为“254”；
• 对于GPU计算，量化方法为“GreedyLogSum”，分隔符的数量为“128”。

   

让我们来看看如何注册这些密钥：

通过将“Uniform”方法和分隔符的数量设置为30来设置量化，将量化表保存到Quant_CB.csv文件中

catboost-1.0.6.exe fit --learn-set train.csv          --test-set test.csv --column-description Test_CB_Setup_0_000000000 --has-header --delimiter ; --train-dir ..\Rezultat --feature-border-type Uniform --border-count 30 --output-borders-file Quant_CB.csv 

从Quant_CB.csv文件加载量化表并训练模型

catboost-1.0.6.exe fit --learn-set train.csv          --test-set test.csv --column-description Test_CB_Setup_0_000000000 --has-header --delimiter ; --train-dir ..\Rezultat --input-borders-file Quant_CB.csv

 您可以在此处找到与量化设置相关的开发人员说明部分。

 

让我们看看量化方法在应用于特定数据时有何不同。以下是gif文件形式的图形。每个新帧都是下一个方法。分离器的数量为16。

 

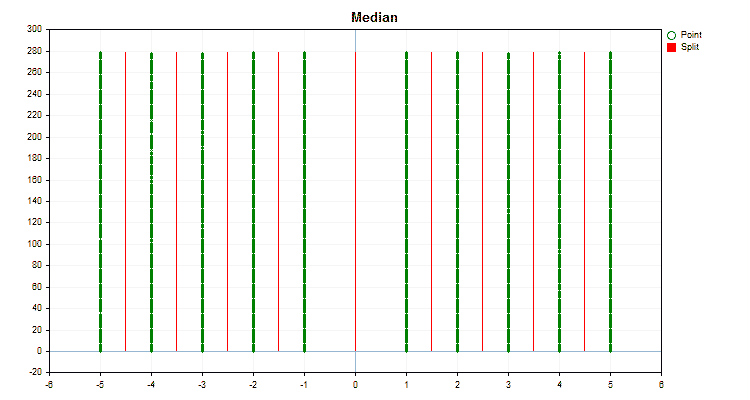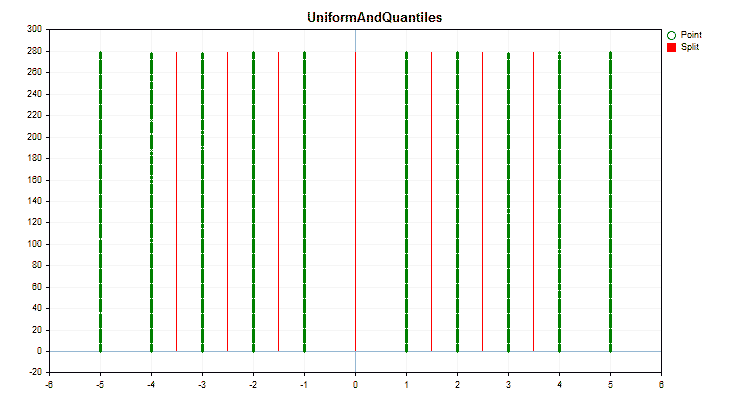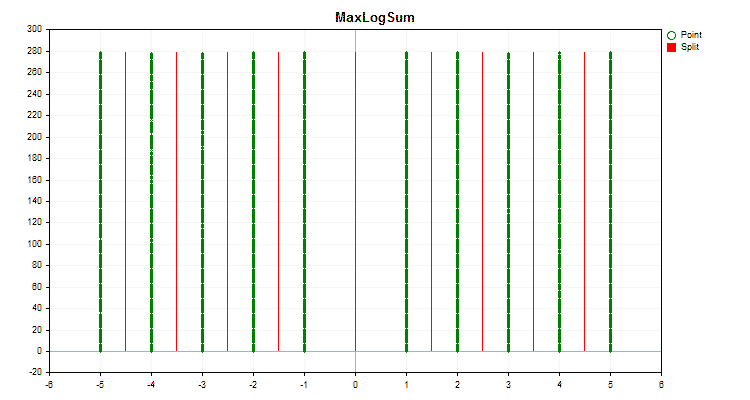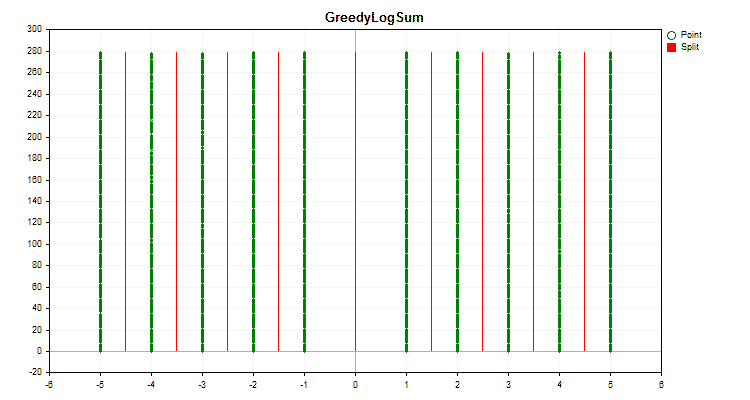
图2“分类预测器的数据图”

 

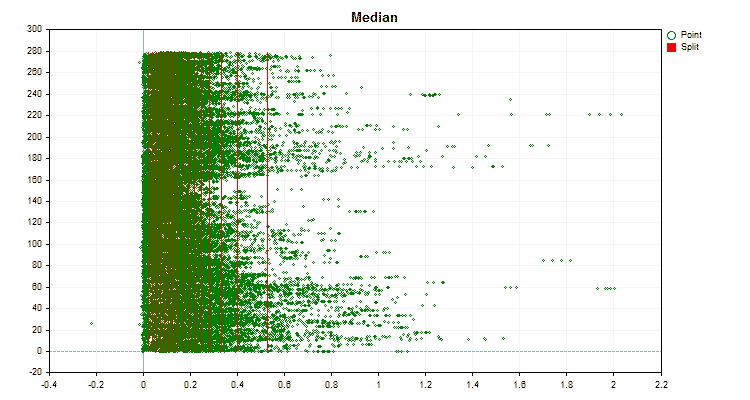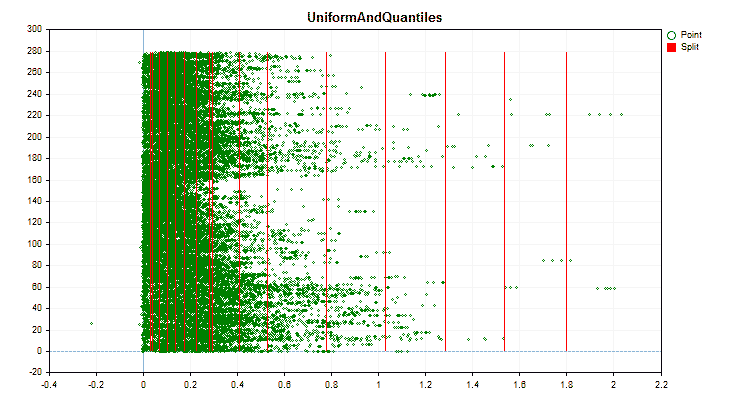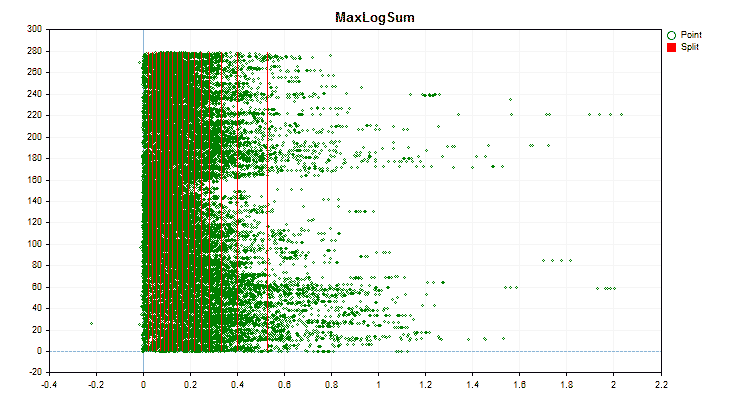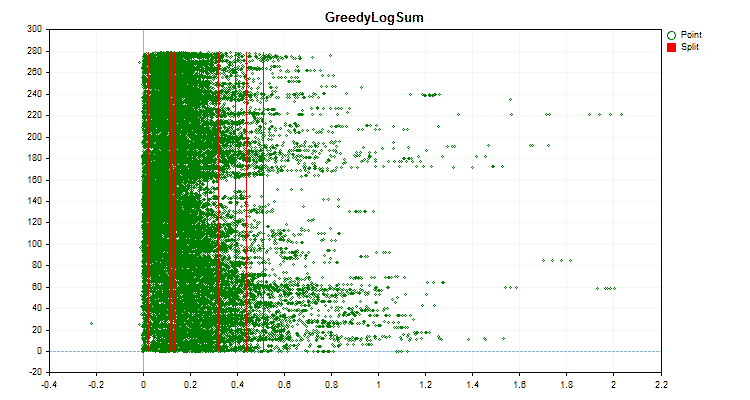
图3“值移到左侧区域的预测器数据图”

 

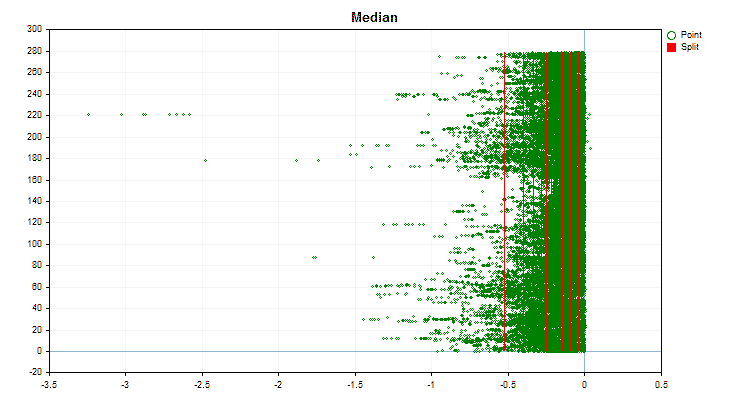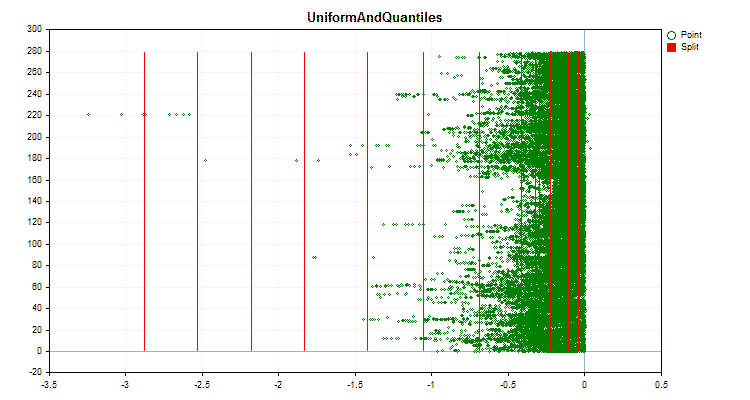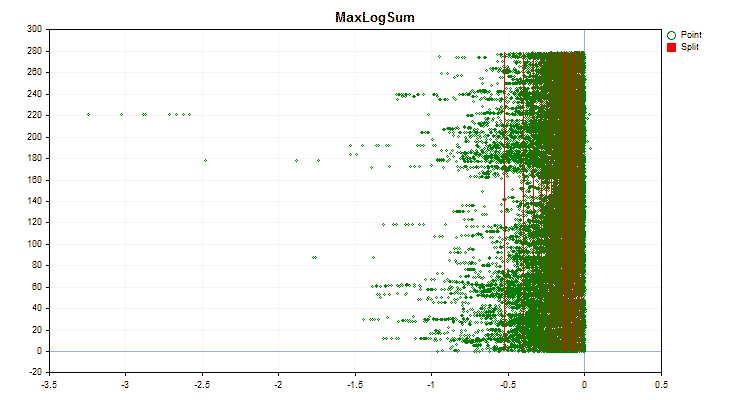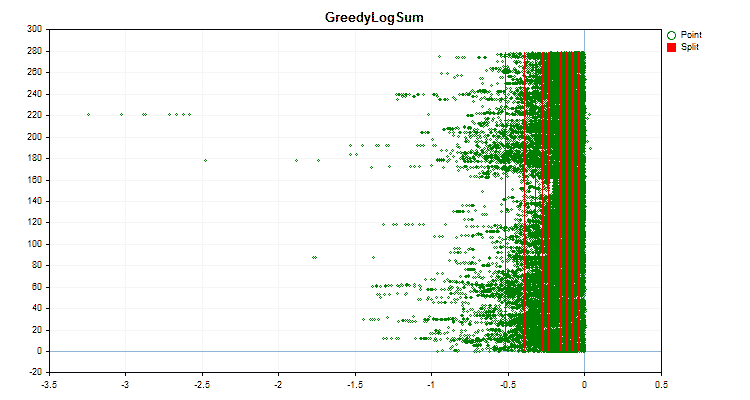
图4“值移到右侧区域的预测器数据图”

 

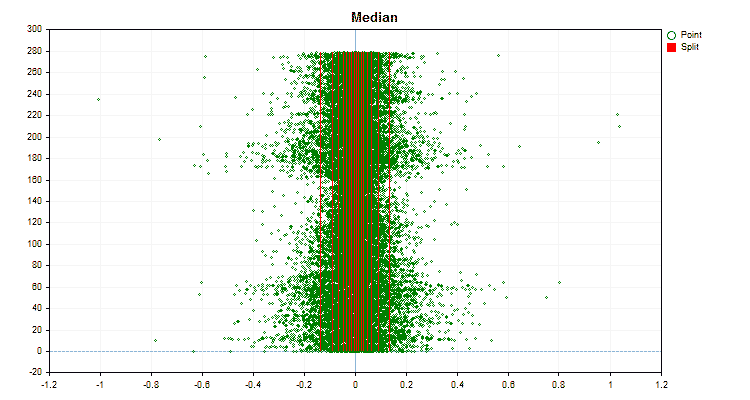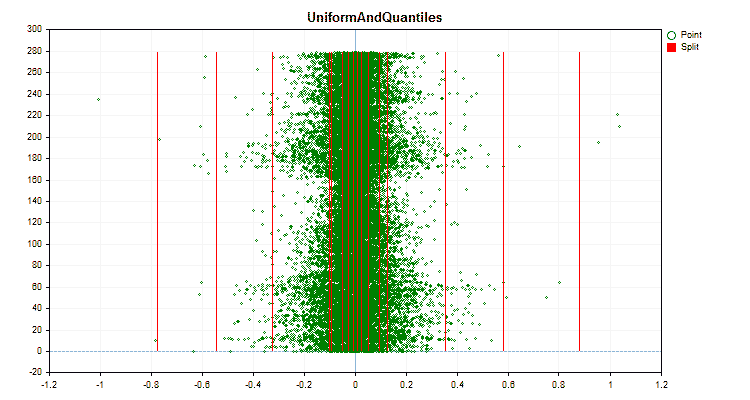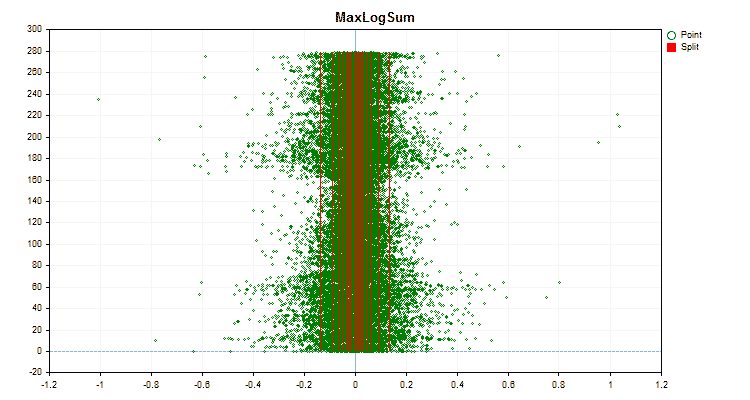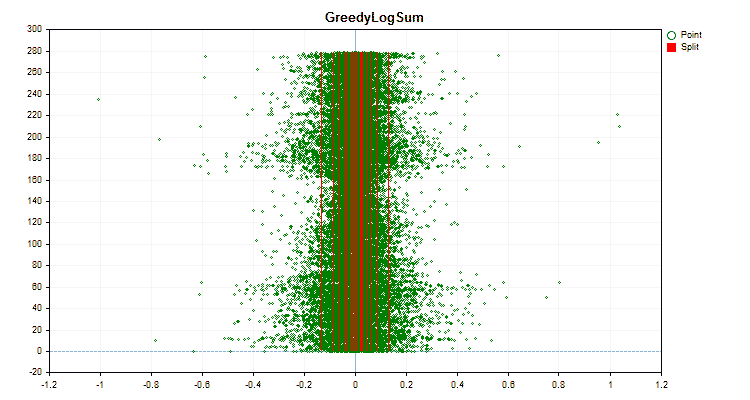
图5“预测值位于中心区域的数据图”

 

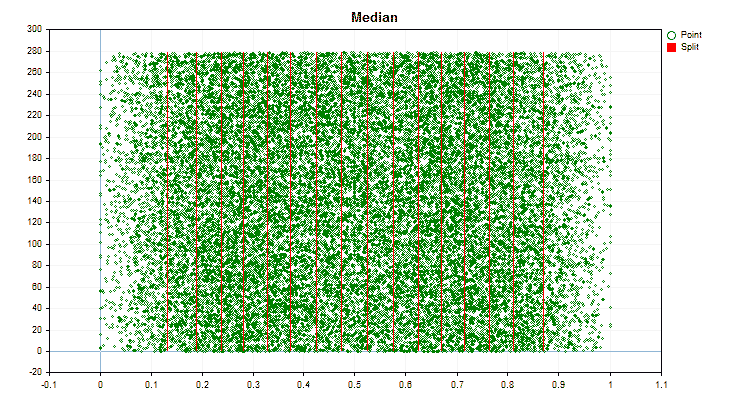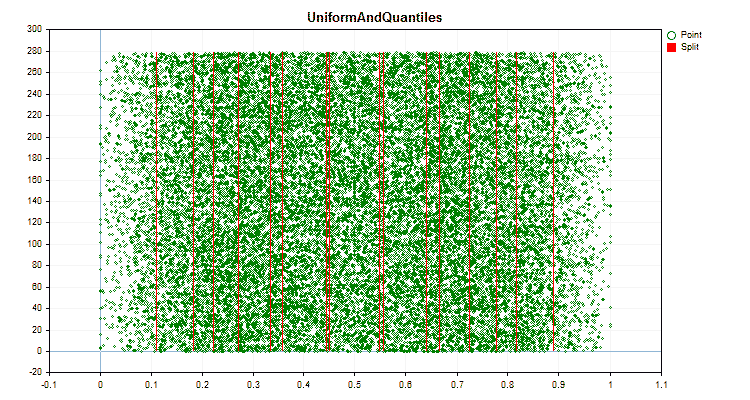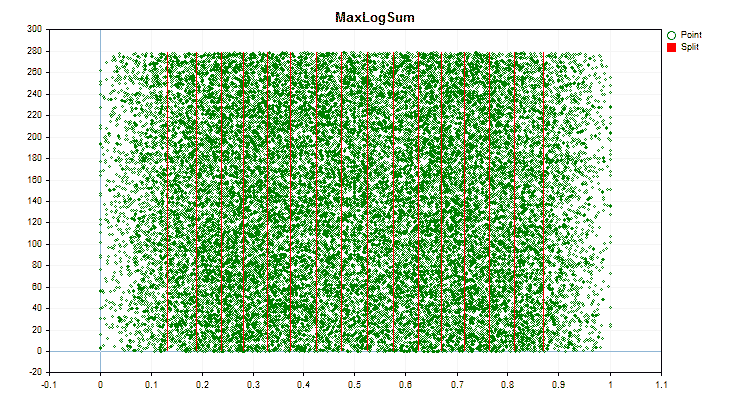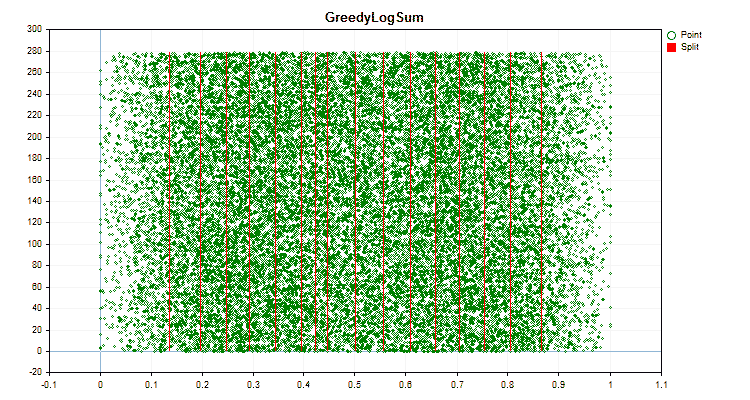
图6“具有均匀值分布的预测器的数据图”

 

如果我们用量化表查看文件的结构（在我们的例子中，它将是Quant_CB.csv），我们将看到两列和许多行。第一列存储训练模型时要使用的预测器的序列号，而第二列存储分隔符（边界/级别）。行数对应于分隔符的累积总和，并且在列出所有分隔符后，第一列中的数字会发生变化。

 

  

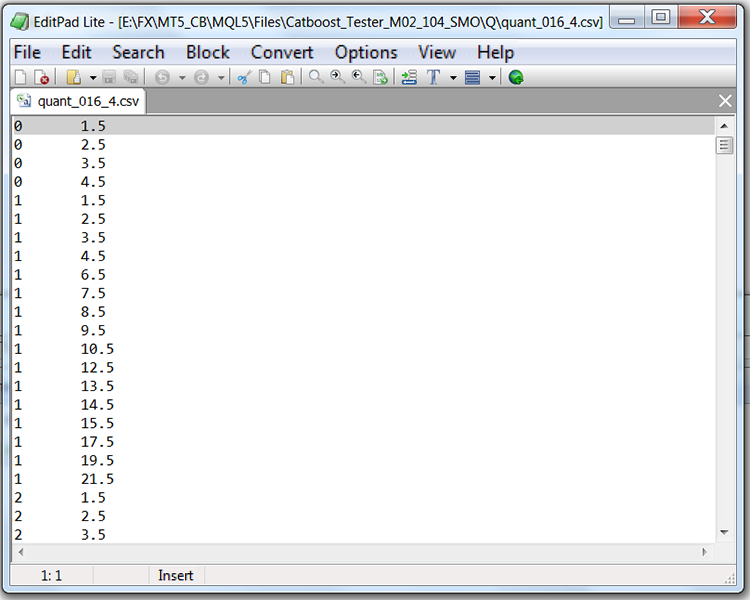
表1“使用分隔符保存的CatBoost文件的内容”

 

结论

在本文中，我们熟悉了量化的概念，以MQL5代码为例分析了量化预测值的获取，并考察了量化在CatBoost中的实现。

如果您在文章中发现术语或事实错误，请随时与我联系。

在下一篇文章中，我们将研究如何为特定的预测器选择量化表，并进行实验来评估这种选择的可行性。

#	应用程序	描述
1	Q_Trans.mq5	包含随机样本上的均匀量化示例的脚本。