
Gráfico PairPlot basado en CGraphic para analizar correlaciones entre los arrays de datos (series temporales)
Contenido
- Introducción
- 1. Planteamiento de la tarea
- 2. Creando clases base
- 2.1. «La base»
- 2.2. Gráfico de dispersión
- 2.3. Histograma
- 2.4. Clase para trabajar con series temporales
- 3. Ensablaje de PairPlot
- 4. Ejemplo del uso de la clase CPairPlot
- Conclusión
Introducción
No es ningún secreto que en el mercado de Forex el trading se realiza usando las cotizaciones de los pares de divisas, cuando el coste de la moneda de un país se expresa a través de la moneda de otro país. Además, es fácil de notar que la misma divisa figura en varios pares de divisas. Como se sabe, el coste de la moneda está condicionado al estado económico de su país. Entonces, surge la pregunta, ¿de la misma manera influye el cambio de la economía del país en el coste de su divisa en diferentes pares de divisas? Puede parecer que la respuesta positiva se ofrece. Pero es un caso ideal, cuando se cambia el estado económico sólo de un país. La verdad es que el mundo va cambiando constantemente. Y el cambio de la economía de un país provoca directa o indirectamente el cambio del estado económico global.
En Internet se puede encontrar bastante información sobre el análisis del cambio del coste de la moneda en diferentes pares de divisas y sobre la búsqueda de la correlación entre diferentes pares de divisas. Además, los artículos sobre el trading con las cestas de los pares de divisas se publicaba en este sitio web: [1, 2, 3]. No obstante, el problema del análisis de las dependencias de las series temporales queda abierto. En este artículo, yo propongo desarrollar una herramienta para el análisis gráfico de las correlaciones entre las series temporales lo que permitirá visualizar la presencia de las correlaciones entre las series temporales de las cotizaciones de los pares analizados.
1. Planteamiento del problema
Antes de empezar a trabajar, vamos a definir nuestros objetivos. ¿Qué tipo de herramienta queremos obtener al final? En primer lugar, tiene que ser un panel gráfico que contenga los gráficos de las correlaciones de las series temporales traspasadas. Además, la herramienta tiene que ser bastante universal y capaz de trabajar con diferente número de series temporales.
Para analizar las series temporales en el panel, vamos a construir un histograma de distribución para cada serie temporal. También vamos a construir a pares los gráficos de dispersión para las series analizadas con el fin de buscar la correlación. Añadimos las líneas de tendencia a los gráficos de dispersión, como una referencia visual.
La ubicación de los gráficos en forma de una tabla cruzada mejorará la legibilidad de toda la herramienta. Este enfoque permitirá unificar la representación de la información y simplificará la percepción visual. El modelo de la herramienta propuesta se encuentra más abajo.
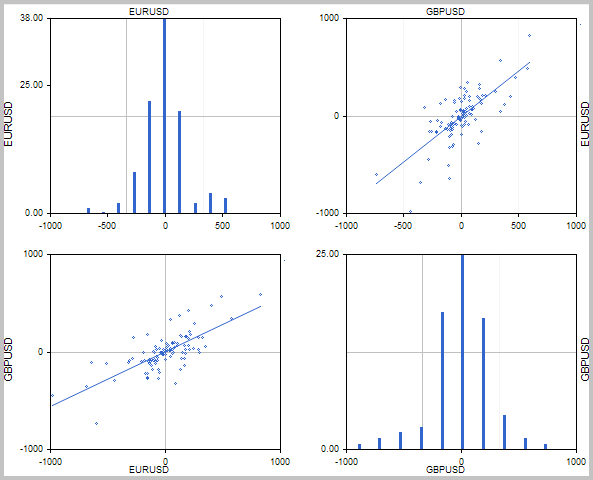
2. Creando las clases base
2.1. «La base»
A la hora de crear semejante herramienta, tenemos que comprender que el usuario puede trabajar con una cantidad diferentes de instrumentos. Según mi opinión, la solución perfecta de este problema consiste en usar el sistema de construcción basado en bloques, donde los gráficos estándar serán como «ladrillos» para la construcción de la tabla común de correlaciones.
Empezamos la creación de nuestra herramienta desde la preparación de la base para la construcción de los gráficos. En la entrega base de MetaTrader 5 hay clase CGraphic que sirve para construir los gráficos científicos. Puede encontrar la información detallada sobre esta clase en el artículo [4]. Precisamente esta clase nos servirá de base para la construcción de nuestros gráficos. Creamos la clase base CPlotBase y la asignamos como heredero de la clase estándar CGraphic. En esta clase, creamos los métodos para la creación del lienzo del gráfico. Habrán dos métodos: uno para construir el campo cuadrado del gráfico con el tamaño establecido del lado, y otro para construir el área rectangular usando las coordenadas establecidas. También añadimos los métodos para poder mostrar un texto aleatorio en los lados del gráfico (nos ayudarán a mostrar los nombres de los instrumentos). Añadimos un método para cambiar el color de la visualización de la serie temporal en el gráfico.
También tenemos que recordar que la clase base CGraphic no se deriva de la clase CObject y no contiene los métodos para el desplazamiento, ocultación y visualización del objeto en el gráfico. Dichos métodos se utilizan ampliamente en los paneles gráficos. Por tanto, es necesario añadir estos métodos a la clase creada para la compatibilidad de nuestra herramienta con las clases estándar para construir paneles gráficos.
class CPlotBase : public CGraphic { protected: long m_chart_id; // chart ID int m_subwin; // chart subwindow public: CPlotBase(); ~CPlotBase(); //--- Create of object virtual bool Create(const long chart,const string name,const int subwin,const int x1,const int y1,const int size); virtual bool Create(const long chart,const string name,const int subwin,const int x1,const int y1,const int x2,const int y2); //--- Change color of timeserie's label virtual bool SetTimeseriesColor(uint clr, uint timeserie=0); //--- Add text to chart virtual void TextUp(string text, uint clr); virtual void TextDown(string text, uint clr); virtual void TextLeft(string text, uint clr); virtual void TextRight(string text, uint clr); //--- geometry virtual bool Shift(const int dx,const int dy); //--- state virtual bool Show(void); virtual bool Hide(void); };
En el constructor de nuestra clase, quitamos la visualización de la leyenda del gráfico y colocamos el número máximo de las marcas en los ejes.
CPlotBase::CPlotBase()
{
HistoryNameWidth(0);
HistorySymbolSize(0);
m_x.MaxLabels(3);
m_y.MaxLabels(3);
}
Puede encontrar el código completo de todos los métodos de la clase en el anexo.
2.2. Gráfico de dispersión
El siguiente paso será la creación de la clase CScatter para visualizar el gráfico de dispersión. Esta clase va a contener sólo dos métodos de la creación y actualización de los datos de las series temporales.
class CScatter : public CPlotBase { public: CScatter(); ~CScatter(); //--- int AddTimeseries(const double ×eries_1[],const double ×eries_2[]); bool UpdateTimeseries(const double ×eries_1[],const double ×eries_2[],uint timeserie=0); };
Al método de la creación de la curva AddTimeseries le vamos a pasar dos arrays de las series temporales de los instrumentos analizados a base de los cuales vamos a construir el gráfico de dispersión. Prácticamente, la clase estándar CGraphic es capaz de visualizar el gráfico de puntos según dos arrays de datos. Pues, vamos a usar este recurso. Al principio del método, creamos la curva de puntos a base de dos arrays de datos obtenidos. Si la creación de la curva falla, salimos de la función con el resultado «-1». Si la curva ha sido creada con éxito, definimos el tamaño de los puntos de la curva y colocamos la bandera de visualización de la línea de tendencia. Después de ejecutar todas las operaciones, el método devuelve el índice de la curva creada.
int CScatter::AddTimeseries(const double ×eries_1[],const double ×eries_2[]) { CCurve *curve=CGraphic::CurveAdd(timeseries_1,timeseries_2,CURVE_POINTS); if(curve==NULL) return -1; curve.PointsSize(2); curve.TrendLineVisible(true); return (m_arr_curves.Total()-1); }
Para actualizar los datos de la curva, creamos el método UpdateTimeseries en el que vamos a pasar dos arrays de datos para construir la curva, y el número de la curva cuyos datos hay que sustituir. Al principio de la función, comprobamos la validez del número de la curva especificado. Si el número es erróneo, salimos de la función con el resultado false.
Luego, comparamos la dimensión de las series temporales obtenidas. Si los tamaños de los arrays se diferencian o los arrays están vacíos, terminamos la función con el resultado false.
En el siguiente paso, obtenemos el puntero al objeto de la curva por el índice. Si el puntero es erróneo, terminamos la función con el resultado false.
Después de todas las comprobaciones, pasamos las series temporales a la curva y terminamos la función con el resultado true.
bool CScatter::UpdateTimeseries(const double ×eries_1[],const double ×eries_2[], uint timeserie=0) { if((int)timeserie>=m_arr_curves.Total()) return false; if(ArraySize(timeseries_1)!=ArraySize(timeseries_2) || ArraySize(timeseries_1)==0) return false; //--- CCurve *curve=m_arr_curves.At(timeserie); if(CheckPointer(curve)==POINTER_INVALID) return false; //--- curve.Update(timeseries_1,timeseries_2); //--- return true; }
2.3. Histograma
El histograma es otro «ladrillo» para la construcción de nuestra herramienta. Creamos la clase CHistogram para su construcción. Igual como CScatter, esta clase recibe sus métodos de la creación y actualización de los datos de la curva. Pero a diferencia de su antecesor, la clase actual va a usar una serie temporal para la construcción de la curva. Los principios de la construcción de estos métodos son los mismos que para los métodos de la clase anterior.
Nótese que la clase base CGraphic puede construir el histograma sólo en su forma clásica. Para añadir la posibilidad de construir un histograma vertical tipo Market Profile, tendremos que reescribir el método HistogramPlot. Además de eso, añadimos la variable e_orientation para almacenar el tipo de la construcción del histograma, y reescribimos los métodos de la creación del lienzo del gráfico en los cuales añadimos la posibilidad de especificar el tipo del histograma.
Otra diferencia de nuestra clase de la clase base CGpraphic consiste en el tipo de datos iniciales obtenidos. En la clase base, el array de valores obtenidos se usa para la visualización directa sobre el gráfico. Nuestra clase va a obtener la serie temporal, y antes de construir el histograma habrá que procesar datos obtenidos. La preparación de datos para la construcción del histograma va a realizarse por el método CalculateHistogramArray, el número de las barras del histograma se establece por el método SetCells y se guarda en la variable i_cells.
class CHistogram : public CPlotBase { private: ENUM_HISTOGRAM_ORIENTATION e_orientation; uint i_cells; public: CHistogram(); ~CHistogram(); //--- bool Create(const long chart,const string name,const int subwin,const int x1,const int y1,const int size, ENUM_HISTOGRAM_ORIENTATION orientation=HISTOGRAM_HORIZONTAL); bool Create(const long chart,const string name,const int subwin,const int x1,const int y1,const int x2,const int y2, ENUM_HISTOGRAM_ORIENTATION orientation=HISTOGRAM_HORIZONTAL); int AddTimeserie(const double ×erie[]); bool UpdateTimeserie(const double ×erie[],uint timeserie=0); bool SetCells(uint value) { i_cells=value; } protected: virtual void HistogramPlot(CCurve *curve); bool CalculateHistogramArray(const double &data[],double &intervals[],double &frequency[], double &maxv,double &minv); };
El método CalculateHistogramArray se basa en el algoritmo propuesto en el Manual de referencia para MQL5, con una pequeña adición. Al principio del método, comprobamos la suficiencia de datos iniciales para construir el histograma, determinamos el valor mínimo y máximo, calculamos la anchura del rango para cada intervalo y preparamos los arrays para almacenar los intervalos y las frecuencias.
Después de eso, en el ciclo se establecen los centros de los intervalos, y se resetea el array de frecuencias.
En el siguiente ciclo, repasamos la serie temporal y calculamos la entrada de los valores en el intervalo correspondiente.
Al final, normalizamos las frecuencias expresando las entradas en por cientos del número total de los elementos en la serie temporal.
bool CHistogram::CalculateHistogramArray(const double &data[],double &intervals[],double &frequency[], double &maxv,double &minv) { int size=ArraySize(data); if(size<(int)i_cells*10) return (false); minv=data[ArrayMinimum(data)]; maxv=data[ArrayMaximum(data)]; double range=maxv-minv; double width=range/i_cells; if(width==0) return false; ArrayResize(intervals,i_cells); ArrayResize(frequency,i_cells); //--- establecemos los centros de intervalos for(uint i=0; i<i_cells; i++) { intervals[i]=minv+(i+0.5)*width; frequency[i]=0; } //--- llenamos las frecuencias de las entradas en el intervalo for(int i=0; i<size; i++) { uint ind=int((data[i]-minv)/width); if(ind>=i_cells) ind=i_cells-1; frequency[ind]++; } //--- normalizamos las frecuencias en representación porcentual for(uint i=0; i<i_cells; i++) frequency[i]*=(100.0/(double)size); return (true); }
El método HistogramPlot se usa para dibujar el histograma en el gráfico. Esta función se construye basándose en el algoritmo de la clase base CGraphic, indicando el uso de la serie temporal y orientación de la construcción del histograma.
Al principio del método, preparamos los datos para la construcción del histograma. Para eso, obtenemos la serie temporal desde los datos de la curva y llamamos al método CalculateHistogramArray. Después de que la función se ejecute con éxito, obtenemos la anchura de los bloques del histograma y comprobamos el tamaño de los arrays de datos para la construcción.
En el siguiente paso, formamos los valores por los ejes de acuerdo con el tipo de visualización del histograma.
Finalmente, organizamos el ciclo para visualizar las columnas del diagrama en el campo del gráfico.
CHistogram::HistogramPlot(CCurve *curve)
{
double data[],intervals[],frequency[];
double max_value, min_value;
curve.GetY(data);
if(!CalculateHistogramArray(data,intervals,frequency,max_value,min_value))
return;
//--- historgram parameters
int histogram_width=fmax(curve.HistogramWidth(),2);
//--- check
if(ArraySize(frequency)==0 || ArraySize(intervals)==0)
return;
//---
switch(e_orientation)
{
case HISTOGRAM_HORIZONTAL:
m_y.AutoScale(false);
m_x.Min(intervals[ArrayMinimum(intervals)]);
m_x.Max(intervals[ArrayMaximum(intervals)]);
m_x.MaxLabels(3);
m_x.ValuesFormat("%.0f");
m_y.Min(0);
m_y.Max(frequency[ArrayMaximum(frequency)]);
m_y.ValuesFormat("%.2f");
break;
case HISTOGRAM_VERTICAL:
m_x.AutoScale(false);
m_y.Min(intervals[ArrayMinimum(intervals)]);
m_y.Max(intervals[ArrayMaximum(intervals)]);
m_y.MaxLabels(3);
m_y.ValuesFormat("%.0f");
m_x.Min(0);
m_x.Max(frequency[ArrayMaximum(frequency)]);
m_x.ValuesFormat("%.2f");
break;
}
//---
CalculateXAxis();
CalculateYAxis();
//--- calculate original of y
int originalY=m_height-m_down;
int originalX=m_width-m_right;
int yc0=ScaleY(0.0);
int xc0=ScaleX(0.0);
//--- gets curve color
uint clr=curve.Color();
//--- draw
for(uint i=0; i<i_cells; i++)
{
//--- check coordinates
if(!MathIsValidNumber(frequency[i]) || !MathIsValidNumber(intervals[i]))
continue;
if(e_orientation==HISTOGRAM_HORIZONTAL)
{
int xc=ScaleX(intervals[i]);
int yc=ScaleY(frequency[i]);
int xc1 = xc - histogram_width/2;
int xc2 = xc + histogram_width/2;
int yc1 = yc;
int yc2 = (originalY>yc0 && yc0>0) ? yc0 : originalY;
//---
if(yc1>yc2)
yc2++;
else
yc2--;
//---
m_canvas.FillRectangle(xc1,yc1,xc2,yc2,clr);
}
else
{
int yc=ScaleY(intervals[i]);
int xc=ScaleX(frequency[i]);
int yc1 = yc - histogram_width/2;
int yc2 = yc + histogram_width/2;
int xc1 = xc;
int xc2 = (originalX>xc0 && xc0>0) ? xc0 : originalX;
//---
if(xc1>xc2)
xc2++;
else
xc2--;
//---
m_canvas.FillRectangle(xc1,yc1,xc2,yc2,clr);
}
}
//---
}
El código completo de todas las clases y métodos se encuentra en el anexo.
2.4. Clase para trabajar con series temporales
Para construir nuestra herramienta, necesitamos otro «ladrillo» que va a cargar los datos históricos necesarios y preparar las series temporales para construir los gráficos. Este trabajo va a realizarse en la clase CTimeserie. Al inicializar la clase, vamos a traspasar el nombre del instrumento, timeframe y el precio aplicado. Además, vamos a crear los métodos para el siguiente cambio del nombre del instrumento, timeframe, precio aplicado y la profundidad del histoial.
class CTimeserie : public CObject { protected: string s_symbol; ENUM_TIMEFRAMES e_timeframe; ENUM_APPLIED_PRICE e_price; double d_timeserie[]; int i_bars; datetime dt_last_load; public: CTimeserie(void); ~CTimeserie(void); bool Create(const string symbol=NULL, const ENUM_TIMEFRAMES timeframe=PERIOD_CURRENT, const ENUM_APPLIED_PRICE price=PRICE_CLOSE); //--- Change settings of time series void SetBars(const int value) { i_bars=value; } void Symbol(string value) { s_symbol=value; dt_last_load=0; } void Timeframe(ENUM_TIMEFRAMES value) { e_timeframe=value; dt_last_load=0; } void Price(ENUM_APPLIED_PRICE value) { e_price=value; dt_last_load=0; } //--- string Symbol(void) { return s_symbol; } ENUM_TIMEFRAMES Timeframe(void) { return e_timeframe; } ENUM_APPLIED_PRICE Price(void) { return e_price; } //--- Load data virtual bool UpdateTimeserie(void); bool GetTimeserie(double ×erie[]) { return ArrayCopy(timeserie,d_timeserie)>0; } };
El trabajo principal de la preparación de datos va a realizarse en el método UpdateTimeserie. Al principio del método, comprobamos si ha sido cargada la información necesaria en la barra actual. Si la información ya está lista, salimos de la función con el resultado true. Si hace falta preparar los datos, cargamos los datos históricos necesarios de acuerdo con el precio especificado. Si resulta imposible cargar la información, salimos fuera de la función con el resultado false. Obsérvese que en nuestro análisis no nos interesa el precio en sí, sino su cambio. Por eso, la carga de los datos históricos se realiza excediendo 1 barra más de la cantidad especificada. En la siguiente fase, recalculamos cíclicamente el cambio del precio en cada barra y guardamos en el array. En adelante, el usuario puede obtener esta información usando el método GetTimeserie.
bool CTimeserie::UpdateTimeserie(void) { datetime cur_date=(datetime)SeriesInfoInteger(s_symbol,e_timeframe,SERIES_LASTBAR_DATE); if(dt_last_load>=cur_date && ArraySize(d_timeserie)>=i_bars) return true; //--- MqlRates rates[]; int bars=0,i; double data[]; switch(e_price) { case PRICE_CLOSE: bars=CopyClose(s_symbol,e_timeframe,1,i_bars+1,data); break; case PRICE_OPEN: bars=CopyOpen(s_symbol,e_timeframe,1,i_bars+1,data); case PRICE_HIGH: bars=CopyHigh(s_symbol,e_timeframe,1,i_bars+1,data); case PRICE_LOW: bars=CopyLow(s_symbol,e_timeframe,1,i_bars+1,data); case PRICE_MEDIAN: bars=CopyRates(s_symbol,e_timeframe,1,i_bars+1,rates); bars=ArrayResize(data,bars); for(i=0;i<bars;i++) data[i]=(rates[i].high+rates[i].low)/2; break; case PRICE_TYPICAL: bars=CopyRates(s_symbol,e_timeframe,1,i_bars+1,rates); bars=ArrayResize(data,bars); for(i=0;i<bars;i++) data[i]=(rates[i].high+rates[i].low+rates[i].close)/3; break; case PRICE_WEIGHTED: bars=CopyRates(s_symbol,e_timeframe,1,i_bars+1,rates); bars=ArrayResize(data,bars); for(i=0;i<bars;i++) data[i]=(rates[i].high+rates[i].low+2*rates[i].close)/4; break; } //--- if(bars<=0) return false; //--- dt_last_load=cur_date; //--- if(ArraySize(d_timeserie)!=(bars-1) && ArrayResize(d_timeserie,bars-1)<=0) return false; double point=SymbolInfoDouble(s_symbol,SYMBOL_POINT); for(i=0;i<bars-1;i++) d_timeserie[i]=(data[i+1]-data[i])/point; //--- return true; }
En el anexo puede encontrar el código de todas las clases y sus métodos.
3. Ensablaje de PairPlot
Una vez creados los «ladrillos», podemos empezar a construir nuestra herramienta. Creamos la clase derivada CPairPlot usando la clase CWndClient. Dicho enfoque simplificará el uso de nuestra herramienta en los paneles gráficos construidos usando la clase estándar CAppDialog (se puede encontrar los detalles de su aplicación en los artículos [5,6]).
En el bloque private de nuestra clase, declaramos el array de punteros a los objetos de la clase CPlotBase para almacenar los punteros a los gráficos, objeto de la clase CArrayObj para almacenar los punteros a los objetos de las series temporales, así como las variables para almacenar el timeframe, precio, orientación del histograma, profundidad del historial y el color de la visualización del nombre del instrumento en el gráfico.
class CPairPlot : public CWndClient { private: CPlotBase *m_arr_graphics[]; CArrayObj m_arr_symbols; ENUM_TIMEFRAMES e_timeframe; ENUM_APPLIED_PRICE e_price; int i_total_symbols; uint i_bars; ENUM_HISTOGRAM_ORIENTATION e_orientation; uint i_text_color; public: CPairPlot(); ~CPairPlot(); //--- bool Create(const long chart,const string name,const int subwin,const int x1,const int y1,const int x2,const int y2, const string &symbols[],const ENUM_TIMEFRAMES timeframe=PERIOD_CURRENT, const int bars=1000, const uint cells=10, const ENUM_APPLIED_PRICE price=PRICE_CLOSE); bool Refresh(void); bool HistogramOrientation(ENUM_HISTOGRAM_ORIENTATION value); ENUM_HISTOGRAM_ORIENTATION HistogramOrientation(void) { return e_orientation; } bool SetTextColor(color value); //--- geometry virtual bool Shift(const int dx,const int dy); //--- state virtual bool Show(void); virtual bool Hide(void); };
Declaramos los métodos de la clase en el bloque public. La inicialización de la clase se ejecuta por el método Create, que durante la llamada obtiene el identificador del gráfico, número de la ventana utilizada, coordenadas para la construcción, array de símbolos utilizados, timeframe, precio, profundidad y el número de columnas del histograma.
Al principio del método, comprobamos el array de nombres traspasados de instrumentos y la profundidad del historial especificada. Si no van a cumplir con nuestros requerimientos mínimos, salimos de la función con el resultado false. Luego, guardamos los valores de los parámetros de entrada para construir los gráficos.
bool CPairPlot::Create(const long chart,const string name,const int subwin,const int x1,const int y1,const int x2,const int y2, const string &symbols[],const ENUM_TIMEFRAMES timeframe=PERIOD_CURRENT, const int bars=1000, const uint cells=10, const ENUM_APPLIED_PRICE price=PRICE_CLOSE) { i_total_symbols=0; int total=ArraySize(symbols); if(total<=1 || bars<100) return false; //--- e_timeframe=timeframe; i_bars=bars; e_price=price;
En la siguiente fase, creamos cíclicamente las instancias de las clases CTimeserie para cada instrumento. Si resulta imposible crear las series temporales para cada instrumento especificado, salimos fuera de la función con el resultado false.
for(int i=0;i<total;i++) { CTimeserie *temp=new CTimeserie; if(temp==NULL) return false; temp.SetBars(i_bars); if(!temp.Create(symbols[i],e_timeframe,e_price)) return false; if(!m_arr_symbols.Add(temp)) return false; } i_total_symbols=m_arr_symbols.Total(); if(i_total_symbols<=1) return false;
Después de realizar los trabajos preparatorios con éxito, pasamos a la creación de objetos gráficos. Primero, llamamos al método Create de la clase padre. Luego, ajustamos el tamaño del array m_arr_graphics (array para almacenar los punteros a los gráficos) de acuerdo con el número de instrumentos analizados. Calculamos la anchura y la altura de cada gráfico a base del tamaño de la herramienta entera y el número de instrumentos analizados.
Después de eso, organizamos dos ciclos anidados para repasar todos los instrumentos analizados y crear la tabla usando los objetos gráficos. Además, vamos a crear los histogramas en la intersección de instrumentos homónimos, y los gráficos de dispersión en los demás casos. Si todos los objetos se crean con éxito, salimos del método con el resultado true.
if(!CWndClient::Create(chart,name,subwin,x1,y1,x2,y2)) return false; //--- if(ArraySize(m_arr_graphics)!=(i_total_symbols*i_total_symbols)) if(ArrayResize(m_arr_graphics,i_total_symbols*i_total_symbols)<=0) return false; int width=Width()/i_total_symbols; int height=Height()/i_total_symbols; for(int i=0;i<i_total_symbols;i++) { CTimeserie *timeserie1=m_arr_symbols.At(i); if(timeserie1==NULL) continue; for(int j=0;j<i_total_symbols;j++) { string obj_name=m_name+"_"+(string)i+"_"+(string)j; int obj_x1=m_rect.left+j*width; int obj_x2=obj_x1+width; int obj_y1=m_rect.top+i*height; int obj_y2=obj_y1+height; if(i==j) { CHistogram *temp=new CHistogram(); if(CheckPointer(temp)==POINTER_INVALID) return false; if(!temp.Create(m_chart_id,obj_name,m_subwin,obj_x1,obj_y1,obj_x2,obj_y2,e_orientation)) return false; m_arr_graphics[i*i_total_symbols+j]=temp; temp.SetCells(cells); } else { CScatter *temp=new CScatter(); if(CheckPointer(temp)==POINTER_INVALID) return false; if(!temp.Create(m_chart_id,obj_name,m_subwin,obj_x1,obj_y1,obj_x2,obj_y2)) return false; CTimeserie *timeserie2=m_arr_symbols.At(j); if(timeserie2==NULL) continue; m_arr_graphics[i*i_total_symbols+j]=temp; } } } //--- return true; }
El método Refresh se encarga de actualizar los datos de las series temporales y visualizar la información en el gráfico. Al principio del método, tenemos organizado el ciclo para actualizar los datos de todas las series temporales. Obsérvese, cuando se construye el gráfico de distribución, las series temporales se usan en parejas. Por tanto, los datos tienen que ser compatibles. Para asegurar la compatibilidad, en caso de que si surja el error de la actualización por lo menos de una serie temporal, los datos de los objetos gráficos no se actualizan y el método devuelve false.
Tras la actualización de los datos de las series temporales, se organiza el ciclo del traspaso de las series temporales actualizadas para los objetos gráficos. Aquí, hay que prestar atención en la llamada al método Update del objeto gráfico con el parámetro false. Esta llamada asegura la actualización del objeto gráfico sin actualizar el gráfico en el que la aplicación haya sido iniciada. Este enfoque permite excluir la actualización del gráfico tras la actualización de cada objeto gráfico, lo que permitirá reducir la carga sobre el terminal y reducir los consumos temporales a la ejecución de la función. La actualización del gráfico se realiza una vez después de la actualización de todos los elementos gráficos, antes de salir de la función.
bool CPairPlot::Refresh(void) { bool updated=true; for(int i=0;i<i_total_symbols;i++) { CTimeserie *timeserie=m_arr_symbols.At(i); if(timeserie==NULL) continue; updated=(updated && timeserie.UpdateTimeserie()); } if(!updated) return false; //--- for(int i=0;i<i_total_symbols;i++) { CTimeserie *timeserie1=m_arr_symbols.At(i); if(CheckPointer(timeserie1)==POINTER_INVALID) continue; double ts1[]; if(!timeserie1.GetTimeserie(ts1)) continue; //--- for(int j=0;j<i_total_symbols;j++) { if(i==j) { CHistogram *temp=m_arr_graphics[i*i_total_symbols+j]; if(CheckPointer(temp)==POINTER_INVALID) return false; if(temp.CurvesTotal()==0) { if(temp.AddTimeserie(ts1)<0) continue; } else { if(!temp.UpdateTimeserie(ts1)) continue; } if(!temp.CurvePlotAll()) continue; if(i==0) temp.TextUp(timeserie1.Symbol(),i_text_color); if(i==(i_total_symbols-1)) temp.TextDown(timeserie1.Symbol(),i_text_color); if(j==0) temp.TextLeft(timeserie1.Symbol(),i_text_color); if(j==(i_total_symbols-1)) temp.TextRight(timeserie1.Symbol(),i_text_color); temp.Update(false); } else { CScatter *temp=m_arr_graphics[i*i_total_symbols+j]; if(CheckPointer(temp)==POINTER_INVALID) return false; CTimeserie *timeserie2=m_arr_symbols.At(j); if(CheckPointer(timeserie2)==POINTER_INVALID) continue; double ts2[]; if(!timeserie2.GetTimeserie(ts2)) continue; if(temp.CurvesTotal()==0) { if(temp.AddTimeseries(ts1,ts2)<0) continue; } else if(!temp.UpdateTimeseries(ts1,ts2)) continue; if(!temp.CurvePlotAll()) continue; if(i==0) temp.TextUp(timeserie2.Symbol(),i_text_color); if(i==(i_total_symbols-1)) temp.TextDown(timeserie2.Symbol(),i_text_color); if(j==0) temp.TextLeft(timeserie1.Symbol(),i_text_color); if(j==(i_total_symbols-1)) temp.TextRight(timeserie1.Symbol(),i_text_color); temp.Update(false); } } } //--- ChartRedraw(m_chart_id); //--- return true; }
Antes, ya mencionaba que nuestros elementos gráficos fueron construidos a base de la clase CGraphic, la que se derivaba de la clase CObject. Por esta razón, añadíamos los métodos Shift, Hide, Show a nuestra clase base. Por esta razón, también tendremos que reescribir los métodos correspondientes en la clase CPairPlot. En el anexo puede encontrar el código de todas las clases y sus métodos.
4. Ejemplo del uso de la clase CPairPlot
Es bastante lógico que después de tanto trabajo queremos ver el resultado de nuestra labor. Para demostrar el funcionamiento de la herramienta, yo propongo crear un indicador que visualice los gráficos de la correlación cuando aparezca una nueva barra (por ejemplo, para las últimas 1000 velas).
Como ya hemos mencionado antes, la herramienta ha sido construida para usarse en los paneles gráficos. Por eso, creamos primero la clase CPairPlotDemo, asignándola como clase derivada de la clase CAppDialog. Los detalles del trabajo con la clase CAppDialog se describen en los artículos [5, 6]. Por eso, aquí indicaré sólo en las particularidades de la aplicación de nuestra herramienta.
Declaramos la instancia de nuestra clase CPairPlot en el bloque private. Declaramos el método Create en el bloque public, indicando todos los parámetros de entrada que son necesarios para la inicialización y el funcionamiento de nuestra herramienta. Aquí mismo, declaramos los métodos Refresh y HistogramOrientation, que van a llamar a los métodos correspondientes de nuestra herramienta.
class CPairPlotDemo : public CAppDialog { private: CPairPlot m_PairPlot; public: CPairPlotDemo(); ~CPairPlotDemo(); //--- bool Create(const long chart,const string name,const int subwin,const int x1,const int y1,const int x2,const int y2,const string &symbols[],const ENUM_TIMEFRAMES timeframe=PERIOD_CURRENT, const int bars=1000, const uint cells=10); bool Refresh(void); //--- bool HistogramOrientation(ENUM_HISTOGRAM_ORIENTATION value) { return m_PairPlot.HistogramOrientation(value); } ENUM_HISTOGRAM_ORIENTATION HistogramOrientation(void) { return m_PairPlot.HistogramOrientation(); } };
En el método Create, primero llamamos al método correspondiente de la clase padre. Luego, llamamos al mismo método de la instancia de nuestro elemento, y después, añadimos el puntero a la instancia de la clase CPairPlot a la colección de controles.
bool CPairPlotDemo::Create(const long chart,const string name,const int subwin,const int x1,const int y1,const int x2,const int y2,const string &symbols[],const ENUM_TIMEFRAMES timeframe=PERIOD_CURRENT, const int bars=1000, const uint cells=10) { if(!CAppDialog::Create(chart,name,subwin,x1,y1,x2,y2)) return false; if(!m_PairPlot.Create(m_chart_id,m_name+"PairPlot",m_subwin,0,0,ClientAreaWidth(),ClientAreaHeight(),symbols,timeframe,bars,cells)) return false; if(!Add(m_PairPlot)) return false; //--- return true; }
Luego, creamos el indicador. La cadena con el nombre de los instrumentos utilizados separados por coma, la profundidad del historial analizado en barras, el número de las columnas y a orientación del histograma serán usados como los parámetros de entrada de nuestro indicador.
input string i_Symbols = "EURUSD, GBPUSD, EURGBP"; input uint i_Bars = 1000; input uint i_Cells = 50; input ENUM_HISTOGRAM_ORIENTATION i_HistogramOrientation = HISTOGRAM_HORIZONTAL;
En las variables globales, declaramos sólo la instancia de nuestra clase CPairPlotDemo.
CPairPlotDemo *PairPlot;
En la función OnInit. primero, creamos el array de instrumentos utilizados a partir de la cadena de los parámetros externos del indicador. Luego, creamos la instancia de la clase CPairPlotDemo, le pasamos la orientación establecida de los histogramas, y lo llamamos en el método Create. Tras una inicialización exitosa, iniciamos la ejecución de la clase usando el método Run, y actualizamos los datos usando el método Refresh.
int OnInit() { //--- string symbols[]; int total=StringSplit(i_Symbols,',',symbols); if(total<=0) return INIT_FAILED; for(int i=0;i<total;i++) { StringTrimLeft(symbols[i]); StringTrimRight(symbols[i]); } //--- PairPlot=new CPairPlotDemo; if(CheckPointer(PairPlot)==POINTER_INVALID) return INIT_FAILED; //--- if(!PairPlot.HistogramOrientation(i_HistogramOrientation)) return INIT_FAILED; if(!PairPlot.Create(0,"Pair Plot",0,20,20,620,520,symbols,PERIOD_CURRENT,i_Bars,i_Cells)) return INIT_FAILED; if(!PairPlot.Run()) return INIT_FAILED; PairPlot.Refresh(); //--- return INIT_SUCCEEDED; }
Cuando aparezca cada nueva barra, vamos a llamar al método Refresh dentro de la función OnCalculate. Vamos a llamar a los métodos correspondientes de nuestra clase desde la función OnChartEvent y OnDeinit.
Puede encontrar el código completo de todos las funciones y de las clases en el anexo.
Puede ver el funcionamiento de nuestro indicador más abajo.
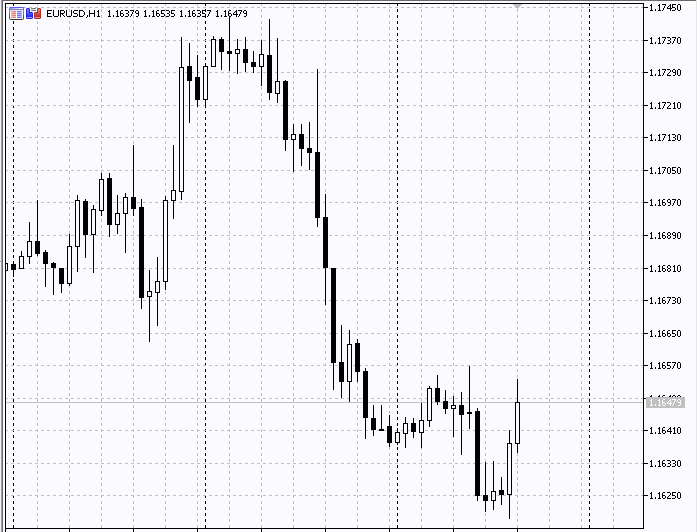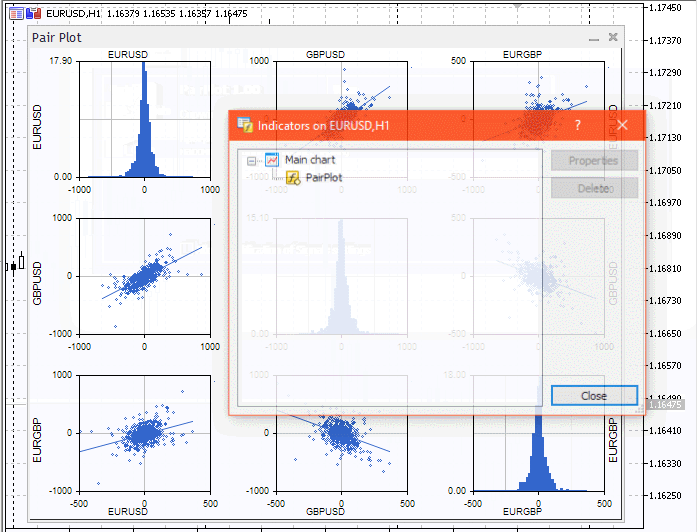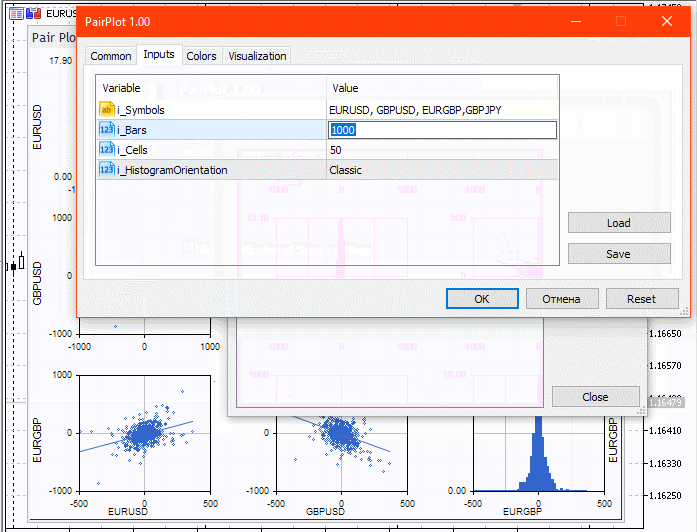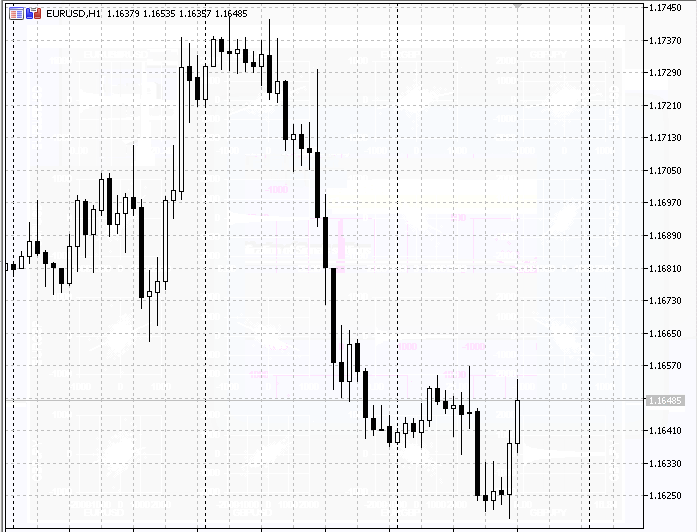
Conclusión
En este artículo, ofrecemos una herramienta bastante interesante. Permite visualizar de una manera fácil y rápida la presencia de una correlación entre prácticamente cualquier número de instrumentos financieros. La finalidad principal de la herramienta, según mi opinión, consiste en el análisis de los instrumentos y en el desarrollo de diferentes estrategias arbitrarias. Sin duda alguna, para el desarrollo de una estrategia completamente funcional, el uso de sólo esta herramienta no es suficiente, pero puede facilitar considerablemente la primera fase de la construcción de un sistema comercial: es decir, la búsqueda de los instrumentos correlacionados y sus dependencias.
Referencias
- Trabajo con las cestas de las parejas de divisas en el mercado Foresx
- Simulación de patrones que surgen al comerciar con cestas de parejas de divisas. Parte I
- Simulación de patrones que surgen al comerciar con cestas de parejas de divisas. Parte II
- ¡Visualice esto. La biblioteca gráfica en MQL5 como un análogo de PLOT del lenguaje R!
- Cómo crear un panel gráfico de cualquier nivel de complegidad
- Mejorando el trabajo con paneles: cómo añadir la transparencia, cambiamos el color del fondo y heredamos a partir de CAppDialog/CWndClient
Los programas usados en el artículo:
| # | Nombre | Tipo | Descripción |
|---|---|---|---|
| 1 | PlotBase.mqh | Librería de la clase | Clase base para construir gráficos |
| 2 | Scatter.mqh | Librería de la clase | Clase para construir gráfico de dispersión |
| 3 | Histogram.mqh | Librería de la clase | Clase para construir histograma |
| 4 | PairPlot.mqh | Librería de la clase | Clase de la herramienta PairPlot |
| 5 | PairPlotDemo.mqh | Librería de la clase | Clase para demostrar la conexión de la herramienta |
| 6 | PairPlot.mq5 | Indicador | Indicador para demostrar el funcionamiento de la herramienta |
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/4820
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Modelando series temporales con ayuda de símbolos personalizados según las leyes de distribución establecidas
Modelando series temporales con ayuda de símbolos personalizados según las leyes de distribución establecidas
 Desarrollo de indicadores bursátiles con control de volumen tomando como ejemplo el indicador delta
Desarrollo de indicadores bursátiles con control de volumen tomando como ejemplo el indicador delta
 Combinando una estrategia de tendencia y una de flat
Combinando una estrategia de tendencia y una de flat
 Integración de un experto en MQL y bases de datos (SQL Server, .NET y C#)
Integración de un experto en MQL y bases de datos (SQL Server, .NET y C#)
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso
Error. Sustituir la línea en el archivo Histogram.mqh:
por:
Los campos m_derecha, m_izquierda, m_arriba, m_abajo se especifican aquí incorrectamente y además contienen basura en tiempo de ejecución (porque se rellenan después), debido a lo cual puede que no salga el histograma (si la basura tiene un valor positivo grande).