
PairPlot graph based on CGraphic for analyzing correlations between data arrays (time series)
Contents
- Introduction
- 1. Setting a task
- 2. Creating base classes
- 2.1. "The basis"
- 2.2. Scatter plot
- 2.3. Histogram
- 2.4. Class for working with time series
- 3. Assembling PairPlot
- 4. Example of using the CPairPlot class
- Conclusion
Introduction
As we all know, forex traders perform transactions using currency pair quotes, in which the currency value of one country is expressed in the currency of another. It is easy to see that the same currency can be found in several currency pairs. Since the value of a currency is determined by the economic state of its country, we may ask whether changes in the country's economy affect its currency uniformly in different currency pairs. A positive answer seems inevitable here. But it is justified only in a perfect case when the economic state of only one country changes. The truth of life is that our world is constantly changing. A change in the economy of one country directly or indirectly entails a change in the global economy.
On the Internet, you can find plenty of information about analyzing changes of a currency price within various pairs and searching for correlation between different currency pairs. On this website, you can find articles about trading currency pair baskets [1, 2, 3]. Nevertheless, the question of analyzing the correlations between time series remains open. In this article, I suggest developing a tool for graphical analysis of correlations between time series, which allows visualizing correlations between time series of quotes of analyzed currency pairs.
1. Setting a task
Before we get to work, let's define our objectives. What kind of tool do we want to obtain in the end? First of all, it should be a graphical panel containing graphs of correlations between passed time series. The tool should be versatile enough and able to work with different number of time series.
To analyze the time series on the panel, we will build a distribution histogram for each time series. We will also prepare scatter plots to be displayed in pairs for analyzed time series in order to search for a correlation. Trend lines will be added to scatter plots as a visual reference.
The layout of the graphs in the form of a cross table will improve the readability of the entire tool. This approach unifies the data presentation and simplifies visual perception. The layout of the proposed tool is provided below.
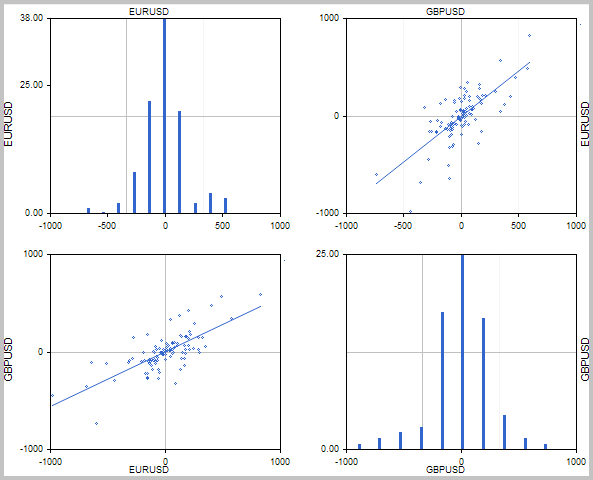
2. Creating base classes
2.1. "The basis"
While developing such a tool, we should keep in mind that users may work with a different number of trading instruments. I believe, the perfect visual solution is a block-based representation where standard graphs are used as "bricks" for building a common correlation table.
We will start developing our tool by preparing the basis for charts construction. MetaTrader 5 basic delivery features the CGraphic class meant for building scientific graphs. The article [4] provides a detailed description of this class. We will use it as the basis for constructing our graphs. Let's create the CPlotBase base class and assign it as the one derived from the CGraphic standard class. In this class, we will create methods for creating a graph canvas. There will be two such methods: the first one is to plot a square graph field with a given side dimension and the second one is to construct a rectangular area using given coordinates. We will also add the methods for displaying a text on the sides of the graph (they will help us in displaying the names of instruments). Besides, let's add the method for changing the display color on the time series graph.
We should also keep in mind that the applied CGraphic base class is not derived from the CObject class and does not contain the methods for relocating, hiding and displaying an object on a graph. Similar methods are widely used in graphical panels. Therefore, we need to add these methods to the created class for the compatibility of our tool with the standard classes for building graphical panels.
class CPlotBase : public CGraphic { protected: long m_chart_id; // chart ID int m_subwin; // chart subwindow public: CPlotBase(); ~CPlotBase(); //--- Create of object virtual bool Create(const long chart,const string name,const int subwin,const int x1,const int y1,const int size); virtual bool Create(const long chart,const string name,const int subwin,const int x1,const int y1,const int x2,const int y2); //--- Change color of timeserie's label virtual bool SetTimeseriesColor(uint clr, uint timeserie=0); //--- Add text to chart virtual void TextUp(string text, uint clr); virtual void TextDown(string text, uint clr); virtual void TextLeft(string text, uint clr); virtual void TextRight(string text, uint clr); //--- geometry virtual bool Shift(const int dx,const int dy); //--- state virtual bool Show(void); virtual bool Hide(void); };
In the class constructor, remove the graph legend display and set the minimum number of labels along the axes.
CPlotBase::CPlotBase()
{
HistoryNameWidth(0);
HistorySymbolSize(0);
m_x.MaxLabels(3);
m_y.MaxLabels(3);
}
Find the entire code of all class methods in the attachment.
2.2. Scatter plot
Next, develop the CScatter class for displaying the scatter plot. This class will only contain two methods for creating and updating the time series data.
class CScatter : public CPlotBase { public: CScatter(); ~CScatter(); //--- int AddTimeseries(const double ×eries_1[],const double ×eries_2[]); bool UpdateTimeseries(const double ×eries_1[],const double ×eries_2[],uint timeserie=0); };
Two time series arrays of analyzed instruments the scatter plot is based on are to be passed to the AddTimeseries curve creation method. The CGraphic standard class is able to display a point graph based on two data arrays. We will use this feature. At the beginning of the method, create a point curve based on two data arrays. If the curve creation fails, exit the function with the result "-1". If the curve is successfully created, set the size of the curve points and set the trend line display flag. After performing all operations, the method returns the index of the created curve.
int CScatter::AddTimeseries(const double ×eries_1[],const double ×eries_2[]) { CCurve *curve=CGraphic::CurveAdd(timeseries_1,timeseries_2,CURVE_POINTS); if(curve==NULL) return -1; curve.PointsSize(2); curve.TrendLineVisible(true); return (m_arr_curves.Total()-1); }
To update the curve data, create the UpdateTimeseries method. Two data arrays for creating the curve and the index of the curve, the data of which should be changed, are to be passed to it. At the beginning of the function, check the validity of the specified curve number. If the number is specified erroneously, exit the function with 'false'.
Then, compare the dimension of the received time series. If array sizes are different or the arrays are empty, end the function with 'false'.
The next step is specifying the pointer to a curve object by index. If the pointer is incorrect, end the function with 'false'.
After all the checks, pass the time series to the curve and end the function with 'true'.
bool CScatter::UpdateTimeseries(const double ×eries_1[],const double ×eries_2[], uint timeserie=0) { if((int)timeserie>=m_arr_curves.Total()) return false; if(ArraySize(timeseries_1)!=ArraySize(timeseries_2) || ArraySize(timeseries_1)==0) return false; //--- CCurve *curve=m_arr_curves.At(timeserie); if(CheckPointer(curve)==POINTER_INVALID) return false; //--- curve.Update(timeseries_1,timeseries_2); //--- return true; }
2.3. Histogram
The histogram is yet another "brick" for building our tool. We need the CHistogram class to create it. Like CScatter, the class receives its own curve data generation and update methods. However, unlike its predecessor, the current class applies one time series to build the curve. The principles of constructing these methods are similar to the methods of the previous class.
Keep in mind that the CGraphic base class can build the histogram only in its standard form. To add the possibility of constructing a vertical histogram of the Market Profile type, we will have to rewrite the HistogramPlot method. Besides, we should add the e_orientation variable for storing the histogram construction type and re-write the graph canvas creation methods by adding the ability to specify the histogram type to them.
Another difference between our class and the base class in CGpraphic is the type of initial data we get. In the base class, an array of obtained values is used for direct output to the graph. Our class will receive a time series, and before processing the histogram, it will be necessary to process the obtained data. Preparing the data for constructing the histogram is performed by the CalculateHistogramArray method, number of histogram columns is set by the SetCells method and saved in the i_cells variable.
class CHistogram : public CPlotBase { private: ENUM_HISTOGRAM_ORIENTATION e_orientation; uint i_cells; public: CHistogram(); ~CHistogram(); //--- bool Create(const long chart,const string name,const int subwin,const int x1,const int y1,const int size, ENUM_HISTOGRAM_ORIENTATION orientation=HISTOGRAM_HORIZONTAL); bool Create(const long chart,const string name,const int subwin,const int x1,const int y1,const int x2,const int y2, ENUM_HISTOGRAM_ORIENTATION orientation=HISTOGRAM_HORIZONTAL); int AddTimeserie(const double ×erie[]); bool UpdateTimeserie(const double ×erie[],uint timeserie=0); bool SetCells(uint value) { i_cells=value; } protected: virtual void HistogramPlot(CCurve *curve); bool CalculateHistogramArray(const double &data[],double &intervals[],double &frequency[], double &maxv,double &minv); };
The CalculateHistogramArray method is based on the algorithm offered in the MQL5 Reference with a small addition. At the beginning of the method, check the sufficiency of the initial data for plotting the histogram, determine the minimum and maximum values, calculate the range width of each interval and prepare arrays to store intervals and frequencies.
After that, the interval centers are set in the loop and the frequency array is set to zero.
In the next loop, iterate through the time series and count the values fitting the corresponding interval.
Finally, normalize the frequencies converting the mentioned fittings into percentage of the total number of elements in the time series.
bool CHistogram::CalculateHistogramArray(const double &data[],double &intervals[],double &frequency[], double &maxv,double &minv) { int size=ArraySize(data); if(size<(int)i_cells*10) return (false); minv=data[ArrayMinimum(data)]; maxv=data[ArrayMaximum(data)]; double range=maxv-minv; double width=range/i_cells; if(width==0) return false; ArrayResize(intervals,i_cells); ArrayResize(frequency,i_cells); //--- set the interval centers for(uint i=0; i<i_cells; i++) { intervals[i]=minv+(i+0.5)*width; frequency[i]=0; } //--- fill in the interval fitting frequencies for(int i=0; i<size; i++) { uint ind=int((data[i]-minv)/width); if(ind>=i_cells) ind=i_cells-1; frequency[ind]++; } //--- normalize frequencies into percentage for(uint i=0; i<i_cells; i++) frequency[i]*=(100.0/(double)size); return (true); }
The histogram is plotted on the graph by the HistogramPlot method. This function is built based on the CGraphic base class algorithm corrected for the use of time series and the histogram construction orientation.
At the beginning of the method, prepare the data for plotting the histogram. To do this, we get a time series from the curve data and call the CalculateHistogramArray method. After the function is executed successfully, we get the histogram blocks width and check the construction data array size.
Next, format the values by axes according to the histogram display type.
Finally, arrange the loop for displaying the diagram columns on the graph field.
CHistogram::HistogramPlot(CCurve *curve)
{
double data[],intervals[],frequency[];
double max_value, min_value;
curve.GetY(data);
if(!CalculateHistogramArray(data,intervals,frequency,max_value,min_value))
return;
//--- historgram parameters
int histogram_width=fmax(curve.HistogramWidth(),2);
//--- check
if(ArraySize(frequency)==0 || ArraySize(intervals)==0)
return;
//---
switch(e_orientation)
{
case HISTOGRAM_HORIZONTAL:
m_y.AutoScale(false);
m_x.Min(intervals[ArrayMinimum(intervals)]);
m_x.Max(intervals[ArrayMaximum(intervals)]);
m_x.MaxLabels(3);
m_x.ValuesFormat("%.0f");
m_y.Min(0);
m_y.Max(frequency[ArrayMaximum(frequency)]);
m_y.ValuesFormat("%.2f");
break;
case HISTOGRAM_VERTICAL:
m_x.AutoScale(false);
m_y.Min(intervals[ArrayMinimum(intervals)]);
m_y.Max(intervals[ArrayMaximum(intervals)]);
m_y.MaxLabels(3);
m_y.ValuesFormat("%.0f");
m_x.Min(0);
m_x.Max(frequency[ArrayMaximum(frequency)]);
m_x.ValuesFormat("%.2f");
break;
}
//---
CalculateXAxis();
CalculateYAxis();
//--- calculate original of y
int originalY=m_height-m_down;
int originalX=m_width-m_right;
int yc0=ScaleY(0.0);
int xc0=ScaleX(0.0);
//--- gets curve color
uint clr=curve.Color();
//--- draw
for(uint i=0; i<i_cells; i++)
{
//--- check coordinates
if(!MathIsValidNumber(frequency[i]) || !MathIsValidNumber(intervals[i]))
continue;
if(e_orientation==HISTOGRAM_HORIZONTAL)
{
int xc=ScaleX(intervals[i]);
int yc=ScaleY(frequency[i]);
int xc1 = xc - histogram_width/2;
int xc2 = xc + histogram_width/2;
int yc1 = yc;
int yc2 = (originalY>yc0 && yc0>0) ? yc0 : originalY;
//---
if(yc1>yc2)
yc2++;
else
yc2--;
//---
m_canvas.FillRectangle(xc1,yc1,xc2,yc2,clr);
}
else
{
int yc=ScaleY(intervals[i]);
int xc=ScaleX(frequency[i]);
int yc1 = yc - histogram_width/2;
int yc2 = yc + histogram_width/2;
int xc1 = xc;
int xc2 = (originalX>xc0 && xc0>0) ? xc0 : originalX;
//---
if(xc1>xc2)
xc2++;
else
xc2--;
//---
m_canvas.FillRectangle(xc1,yc1,xc2,yc2,clr);
}
}
//---
}
The full code of all classes and methods is available in the attachment.
2.4. Class for working with time series
To build the tool, we need yet another "brick" that will download required historical data and prepare timeseries for plotting graphs. This work will be performed in the CTimeserie class. The instrument name, the timeframe and the applied price are to be passed when initializing the class. Besides, the methods for subsequent change of the instrument name, timeframe, applied price and history depth are to be created.
class CTimeserie : public CObject { protected: string s_symbol; ENUM_TIMEFRAMES e_timeframe; ENUM_APPLIED_PRICE e_price; double d_timeserie[]; int i_bars; datetime dt_last_load; public: CTimeserie(void); ~CTimeserie(void); bool Create(const string symbol=NULL, const ENUM_TIMEFRAMES timeframe=PERIOD_CURRENT, const ENUM_APPLIED_PRICE price=PRICE_CLOSE); //--- Change settings of time series void SetBars(const int value) { i_bars=value; } void Symbol(string value) { s_symbol=value; dt_last_load=0; } void Timeframe(ENUM_TIMEFRAMES value) { e_timeframe=value; dt_last_load=0; } void Price(ENUM_APPLIED_PRICE value) { e_price=value; dt_last_load=0; } //--- string Symbol(void) { return s_symbol; } ENUM_TIMEFRAMES Timeframe(void) { return e_timeframe; } ENUM_APPLIED_PRICE Price(void) { return e_price; } //--- Load data virtual bool UpdateTimeserie(void); bool GetTimeserie(double ×erie[]) { return ArrayCopy(timeserie,d_timeserie)>0; } };
The main data preparation work is to be done in the UpdateTimeserie method. At the beginning of the method, check whether the necessary information has been previously loaded on the current bar. If the information is ready, exit the function with 'true'. If it is necessary to prepare the data, upload the necessary history data in accordance with the specified price. If it is impossible to upload the information, exit the function with 'false'. Note that we are not interested in the price itself but in its change. Therefore, the history data upload exceeds the specified amount by 1 bar. At the next stage, we recalculate the price change on each bar and save it to the array in a loop. Later, a user can get this information using the GetTimeserie method.
bool CTimeserie::UpdateTimeserie(void) { datetime cur_date=(datetime)SeriesInfoInteger(s_symbol,e_timeframe,SERIES_LASTBAR_DATE); if(dt_last_load>=cur_date && ArraySize(d_timeserie)>=i_bars) return true; //--- MqlRates rates[]; int bars=0,i; double data[]; switch(e_price) { case PRICE_CLOSE: bars=CopyClose(s_symbol,e_timeframe,1,i_bars+1,data); break; case PRICE_OPEN: bars=CopyOpen(s_symbol,e_timeframe,1,i_bars+1,data); case PRICE_HIGH: bars=CopyHigh(s_symbol,e_timeframe,1,i_bars+1,data); case PRICE_LOW: bars=CopyLow(s_symbol,e_timeframe,1,i_bars+1,data); case PRICE_MEDIAN: bars=CopyRates(s_symbol,e_timeframe,1,i_bars+1,rates); bars=ArrayResize(data,bars); for(i=0;i<bars;i++) data[i]=(rates[i].high+rates[i].low)/2; break; case PRICE_TYPICAL: bars=CopyRates(s_symbol,e_timeframe,1,i_bars+1,rates); bars=ArrayResize(data,bars); for(i=0;i<bars;i++) data[i]=(rates[i].high+rates[i].low+rates[i].close)/3; break; case PRICE_WEIGHTED: bars=CopyRates(s_symbol,e_timeframe,1,i_bars+1,rates); bars=ArrayResize(data,bars); for(i=0;i<bars;i++) data[i]=(rates[i].high+rates[i].low+2*rates[i].close)/4; break; } //--- if(bars<=0) return false; //--- dt_last_load=cur_date; //--- if(ArraySize(d_timeserie)!=(bars-1) && ArrayResize(d_timeserie,bars-1)<=0) return false; double point=SymbolInfoDouble(s_symbol,SYMBOL_POINT); for(i=0;i<bars-1;i++) d_timeserie[i]=(data[i+1]-data[i])/point; //--- return true; }
The full code of all classes and their methods is available in the attachment.
3. Assembling PairPlot
After creating "bricks", we can start developing our tool. Let's create the CPairPlot class derived from the CWndClient class. This approach will make it easier to use our tool in graphical panels built using the standard CAppDialog class (the details on its application can be found in the articles [5,6]).
In the 'private' block of our class, declare the array of pointers to the CPlotBase class objects for storing pointers to graphs, CArrayObj class object for storing pointers to time series objects, as well as the variables for storing the applied timeframe, price, histogram orientation, history depth and color for displaying instruments names on the graph.
class CPairPlot : public CWndClient { private: CPlotBase *m_arr_graphics[]; CArrayObj m_arr_symbols; ENUM_TIMEFRAMES e_timeframe; ENUM_APPLIED_PRICE e_price; int i_total_symbols; uint i_bars; ENUM_HISTOGRAM_ORIENTATION e_orientation; uint i_text_color; public: CPairPlot(); ~CPairPlot(); //--- bool Create(const long chart,const string name,const int subwin,const int x1,const int y1,const int x2,const int y2, const string &symbols[],const ENUM_TIMEFRAMES timeframe=PERIOD_CURRENT, const int bars=1000, const uint cells=10, const ENUM_APPLIED_PRICE price=PRICE_CLOSE); bool Refresh(void); bool HistogramOrientation(ENUM_HISTOGRAM_ORIENTATION value); ENUM_HISTOGRAM_ORIENTATION HistogramOrientation(void) { return e_orientation; } bool SetTextColor(color value); //--- geometry virtual bool Shift(const int dx,const int dy); //--- state virtual bool Show(void); virtual bool Hide(void); };
Declare the class methods in the 'public' block. The class initialization is performed by the Create method that receives the graph ID, object name, applied subwindow index, construction coordinates, array of used symbols, applied timeframes, price, history depth and number of histogram columns upon its call.
At the beginning of the method, check the array of passed instrument names and the depth of the specified history. If they do not satisfy our minimum requirements, exit the function with 'false'. Then save the values of the input parameters for plotting graphs.
bool CPairPlot::Create(const long chart,const string name,const int subwin,const int x1,const int y1,const int x2,const int y2, const string &symbols[],const ENUM_TIMEFRAMES timeframe=PERIOD_CURRENT, const int bars=1000, const uint cells=10, const ENUM_APPLIED_PRICE price=PRICE_CLOSE) { i_total_symbols=0; int total=ArraySize(symbols); if(total<=1 || bars<100) return false; //--- e_timeframe=timeframe; i_bars=bars; e_price=price;
Next, create instances of the CTimeserie classes for each instrument in a loop. If unable to create a time series for each specified instrument, exit the function with 'false'.
for(int i=0;i<total;i++) { CTimeserie *temp=new CTimeserie; if(temp==NULL) return false; temp.SetBars(i_bars); if(!temp.Create(symbols[i],e_timeframe,e_price)) return false; if(!m_arr_symbols.Add(temp)) return false; } i_total_symbols=m_arr_symbols.Total(); if(i_total_symbols<=1) return false;
After the successful completion of the preparatory work, proceed to the direct creation of graphical objects. First, call the Create method of the parent class. Then bring the size of the m_arr_graphics array (for storing pointers to graphs) into accordance with the number of analyzed instruments. Calculate the width and height of each graph based on the size of the entire instrument and the number of analyzed instruments.
After that, arrange two nested loops for iterating over all analyzed instruments and creating the table using graphical objects. Create the histograms at the intersection of same-name instruments and scatter plots in other cases. If all objects are successfully created, exit the method with 'true'.
if(!CWndClient::Create(chart,name,subwin,x1,y1,x2,y2)) return false; //--- if(ArraySize(m_arr_graphics)!=(i_total_symbols*i_total_symbols)) if(ArrayResize(m_arr_graphics,i_total_symbols*i_total_symbols)<=0) return false; int width=Width()/i_total_symbols; int height=Height()/i_total_symbols; for(int i=0;i<i_total_symbols;i++) { CTimeserie *timeserie1=m_arr_symbols.At(i); if(timeserie1==NULL) continue; for(int j=0;j<i_total_symbols;j++) { string obj_name=m_name+"_"+(string)i+"_"+(string)j; int obj_x1=m_rect.left+j*width; int obj_x2=obj_x1+width; int obj_y1=m_rect.top+i*height; int obj_y2=obj_y1+height; if(i==j) { CHistogram *temp=new CHistogram(); if(CheckPointer(temp)==POINTER_INVALID) return false; if(!temp.Create(m_chart_id,obj_name,m_subwin,obj_x1,obj_y1,obj_x2,obj_y2,e_orientation)) return false; m_arr_graphics[i*i_total_symbols+j]=temp; temp.SetCells(cells); } else { CScatter *temp=new CScatter(); if(CheckPointer(temp)==POINTER_INVALID) return false; if(!temp.Create(m_chart_id,obj_name,m_subwin,obj_x1,obj_y1,obj_x2,obj_y2)) return false; CTimeserie *timeserie2=m_arr_symbols.At(j); if(timeserie2==NULL) continue; m_arr_graphics[i*i_total_symbols+j]=temp; } } } //--- return true; }
The Refresh method is used to update the time series data and display data on the graph. The beginning of the method features the loop for updating the data of all time series. Note that when you build a distribution graph, time series are used in pairs. Therefore, the data should be comparable. To ensure the data compatibility, graphical object data are not updated and the method returns 'false' in case an error occurs when updating at least one of the time series.
After updating the time series data, the loop for passing updated time series to graphical objects is arranged. Pay attention to calling the Update method of a graphical object with the 'false' parameter. Such a call ensures that the graphical object is updated without updating the graph the application is running on. This approach excludes graph updates after updating each graphical object reducing the load on the terminal and cutting the function execution time. The graph is updated once after updating all graphical elements before exiting the function.
bool CPairPlot::Refresh(void) { bool updated=true; for(int i=0;i<i_total_symbols;i++) { CTimeserie *timeserie=m_arr_symbols.At(i); if(timeserie==NULL) continue; updated=(updated && timeserie.UpdateTimeserie()); } if(!updated) return false; //--- for(int i=0;i<i_total_symbols;i++) { CTimeserie *timeserie1=m_arr_symbols.At(i); if(CheckPointer(timeserie1)==POINTER_INVALID) continue; double ts1[]; if(!timeserie1.GetTimeserie(ts1)) continue; //--- for(int j=0;j<i_total_symbols;j++) { if(i==j) { CHistogram *temp=m_arr_graphics[i*i_total_symbols+j]; if(CheckPointer(temp)==POINTER_INVALID) return false; if(temp.CurvesTotal()==0) { if(temp.AddTimeserie(ts1)<0) continue; } else { if(!temp.UpdateTimeserie(ts1)) continue; } if(!temp.CurvePlotAll()) continue; if(i==0) temp.TextUp(timeserie1.Symbol(),i_text_color); if(i==(i_total_symbols-1)) temp.TextDown(timeserie1.Symbol(),i_text_color); if(j==0) temp.TextLeft(timeserie1.Symbol(),i_text_color); if(j==(i_total_symbols-1)) temp.TextRight(timeserie1.Symbol(),i_text_color); temp.Update(false); } else { CScatter *temp=m_arr_graphics[i*i_total_symbols+j]; if(CheckPointer(temp)==POINTER_INVALID) return false; CTimeserie *timeserie2=m_arr_symbols.At(j); if(CheckPointer(timeserie2)==POINTER_INVALID) continue; double ts2[]; if(!timeserie2.GetTimeserie(ts2)) continue; if(temp.CurvesTotal()==0) { if(temp.AddTimeseries(ts1,ts2)<0) continue; } else if(!temp.UpdateTimeseries(ts1,ts2)) continue; if(!temp.CurvePlotAll()) continue; if(i==0) temp.TextUp(timeserie2.Symbol(),i_text_color); if(i==(i_total_symbols-1)) temp.TextDown(timeserie2.Symbol(),i_text_color); if(j==0) temp.TextLeft(timeserie1.Symbol(),i_text_color); if(j==(i_total_symbols-1)) temp.TextRight(timeserie1.Symbol(),i_text_color); temp.Update(false); } } } //--- ChartRedraw(m_chart_id); //--- return true; }
Previously, I already mentioned that the graphical elements are based on the CGraphic class not derived from the CObject class. For this reason, we added the Shift, Hide and Show methods to the CPlotBase base class. For the same reason, we also have to rewrite the corresponding methods in the CPairPlot class. The full code of all classes and their methods is available in the attachment.
4. Example of using the CPairPlot class
Now, after so much work, it is time to have a look at the results. In order to demonstrate the tool in action, let's make an indicator that displays the correlation graphs, for example, for the last 1000 candles, at each new bar.
As already mentioned above, the tool is built for use in graphical panels. Therefore, let's first create the CPairPlotDemo class derived from the CAppDialog class. Details on working with the CAppDialog class can be found in the articles [5, 6]. Here, I will only point out the peculiarities of using the tool.
Declare the instance of the CPairPlot class in the 'private' block. In the 'public' block, declare the Create method with all the input parameters required for the tool initialization and operation. Here, we will also declare the Refresh and HistogramOrientation methods, that will call the corresponding methods of our tool.
class CPairPlotDemo : public CAppDialog { private: CPairPlot m_PairPlot; public: CPairPlotDemo(); ~CPairPlotDemo(); //--- bool Create(const long chart,const string name,const int subwin,const int x1,const int y1,const int x2,const int y2,const string &symbols[],const ENUM_TIMEFRAMES timeframe=PERIOD_CURRENT, const int bars=1000, const uint cells=10); bool Refresh(void); //--- bool HistogramOrientation(ENUM_HISTOGRAM_ORIENTATION value) { return m_PairPlot.HistogramOrientation(value); } ENUM_HISTOGRAM_ORIENTATION HistogramOrientation(void) { return m_PairPlot.HistogramOrientation(); } };
In the Create method, first call the appropriate method of the parent class, then call the same method of the element instance and add the pointer to the CPairPlot class instance to the collection of control elements.
bool CPairPlotDemo::Create(const long chart,const string name,const int subwin,const int x1,const int y1,const int x2,const int y2,const string &symbols[],const ENUM_TIMEFRAMES timeframe=PERIOD_CURRENT, const int bars=1000, const uint cells=10) { if(!CAppDialog::Create(chart,name,subwin,x1,y1,x2,y2)) return false; if(!m_PairPlot.Create(m_chart_id,m_name+"PairPlot",m_subwin,0,0,ClientAreaWidth(),ClientAreaHeight(),symbols,timeframe,bars,cells)) return false; if(!Add(m_PairPlot)) return false; //--- return true; }
Now, let's create the indicator. The string with the comma-separated names of the instruments used, the depth of the analyzed history in bars, the number of columns and histogram orientation are to be used as the input parameters of our indicator.
input string i_Symbols = "EURUSD, GBPUSD, EURGBP"; input uint i_Bars = 1000; input uint i_Cells = 50; input ENUM_HISTOGRAM_ORIENTATION i_HistogramOrientation = HISTOGRAM_HORIZONTAL;
Declare the CPairPlotDemo class instance in the global variables.
CPairPlotDemo *PairPlot;
In the OnInit function, create the array of applied instruments from the string of the indicator external parameters. Then create an instance of the CPairPlotDemo class, pass the specified histogram orientation to it and call its Create method. After successful initialization, launch the class execution by the Run method and update data using the Refresh method.
int OnInit() { //--- string symbols[]; int total=StringSplit(i_Symbols,',',symbols); if(total<=0) return INIT_FAILED; for(int i=0;i<total;i++) { StringTrimLeft(symbols[i]); StringTrimRight(symbols[i]); } //--- PairPlot=new CPairPlotDemo; if(CheckPointer(PairPlot)==POINTER_INVALID) return INIT_FAILED; //--- if(!PairPlot.HistogramOrientation(i_HistogramOrientation)) return INIT_FAILED; if(!PairPlot.Create(0,"Pair Plot",0,20,20,620,520,symbols,PERIOD_CURRENT,i_Bars,i_Cells)) return INIT_FAILED; if(!PairPlot.Run()) return INIT_FAILED; PairPlot.Refresh(); //--- return INIT_SUCCEEDED; }
In the OnCalculate function, call the Refresh method at each new bar. The appropriate class methods will be called from the OnChartEvent and OnDeinit functions.
Find the entire code of all the functions and classes in the attachment.
Below you can see how the indicator works.
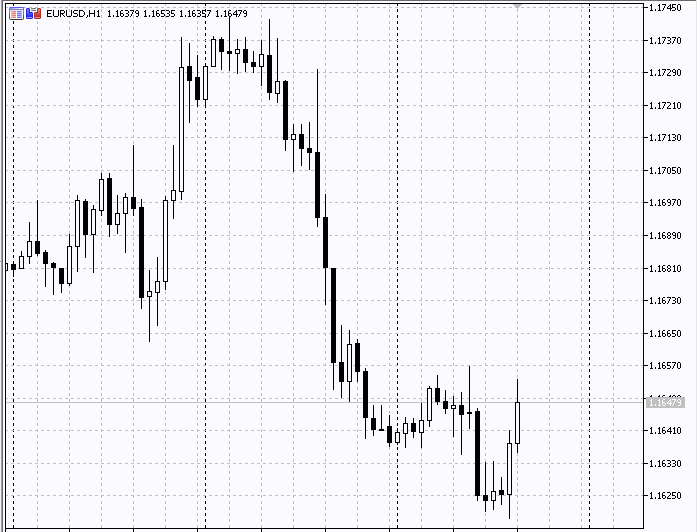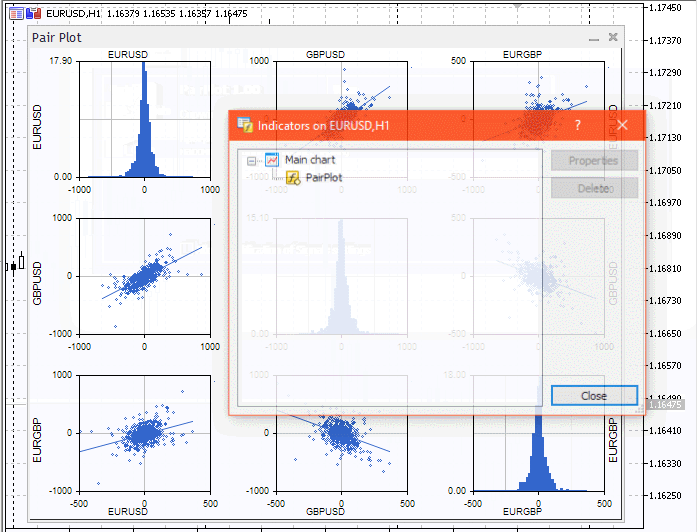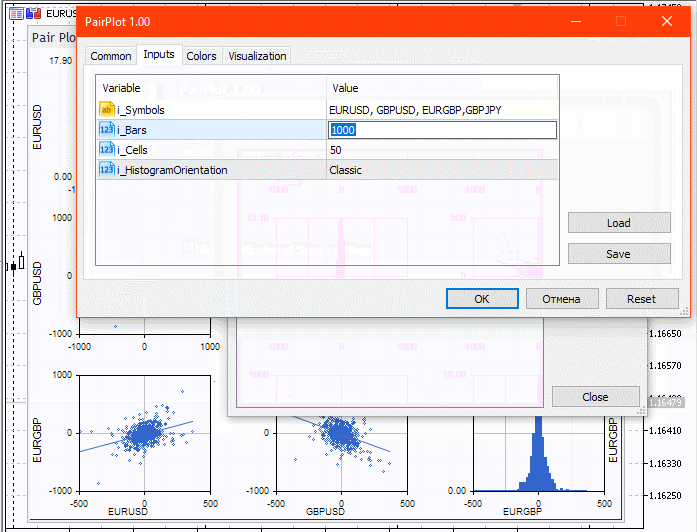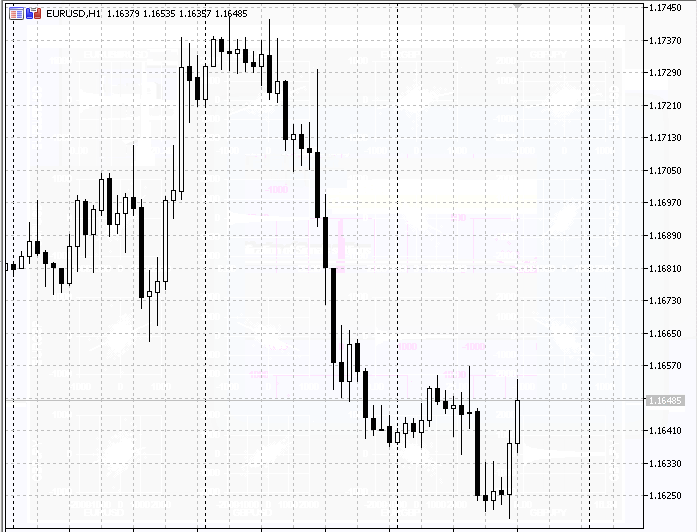
Conclusion
In this article, we offered quite an interesting tool. It allows traders to quickly and easily visualize the presence of a correlation between almost any number of trading instruments. The main purpose of the tool lies in the analysis of trading instruments and in the development of various arbitrage strategies. Of course, this tool alone is insufficient for developing a full-fledged trading system, but it can greatly facilitate the first stage of developing a trading system – the search for correlated instruments and their dependencies.
References
- Working with currency baskets in the Forex market
- Testing patterns that arise when trading currency pair baskets. Part I
- Testing patterns that arise when trading currency pair baskets. Part II
- Visualize this! MQL5 graphics library similar to 'plot' of R language
- How to create a graphical panel of any complexity level
- Improving panels: Adding transparency, changing background color and inheriting from CAppDialog/CWndClient
Programs used in the article
| # |
Name |
Type |
Description |
|---|---|---|---|
| 1 | PlotBase.mqh | Class library | Base class for building graphs |
| 2 | Scatter.mqh | Class library | Class for building scatter plots |
| 3 | Histogram.mqh | Class library | Class for building histograms |
| 4 | PairPlot.mqh | Class library | PairPlot tool class |
| 5 | PairPlotDemo.mqh | Class library | Class for demonstrating the tool connection |
| 6 | PairPlot.mq5 | Indicator | Indicator demonstrating the work of the tool |
Translated from Russian by MetaQuotes Ltd.
Original article: https://www.mql5.com/ru/articles/4820
Warning: All rights to these materials are reserved by MetaQuotes Ltd. Copying or reprinting of these materials in whole or in part is prohibited.
This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.
 Deep Neural Networks (Part VIII). Increasing the classification quality of bagging ensembles
Deep Neural Networks (Part VIII). Increasing the classification quality of bagging ensembles
 Combining trend and flat strategies
Combining trend and flat strategies
 Developing stock indicators featuring volume control through the example of the delta indicator
Developing stock indicators featuring volume control through the example of the delta indicator
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use
Bug. Replace the line in the Histogram.mqh file:
by:
Fields m_right, m_left, m_up, m_down are specified here incorrectly and moreover contain rubbish at runtime (because they are filled in later), because of which the histogram may not be output (if the rubbish has a large positive value).