
Fundamentos de la estadística
Introducción
¿Qué es la estadística? Esta es la definición que da Wikipedia: "La estadística es la rama del saber en la que se explican las cuestiones generales sobre la recopilación, la medición y el análisis de los datos de una muestra representativa (ya sean cuantitativos o cualitativos)." (Estadística). De esta definición podemos extraer las tres tareas básicas de la estadística: la recopilación de datos, la medición de datos y el análisis de datos. Para el trader, la tarea más útil es el análisis de datos, dado que la información le es proporcionada por el bróker o a través del terminal comrecial, y ya está medida de antemano.
los traders modernos (en su mayoría) utilizan el análisis técnico para la toma de decisiones sobre la compra o la venta. Los traders topan con la estadística prácticamente a cada paso cuando usan este o aquel indicador, o bien intentan pronosticar el nivel de los precios en el periodo de tiempo más cercano. Qué vamos a decir, el mismo gráfico de las oscilaciones de los precios constituye un cierto tipo de estadística de la acción o la divisa a lo largo del tiempo. Por eso es muy importante comprender los principios básicos de la estadística, sobre los que se basan y construyen multitud de mecanismos que facilitan el trabajo del trader a la hora de tomar decisiones.
Teoría de la probabilidad y estadística
Cualquier estadística es el resultado del cambio del estado de un objeto, de su causa. Estudiaremos el curso de la pareja de divisas EURUSD según los time frames por horas:
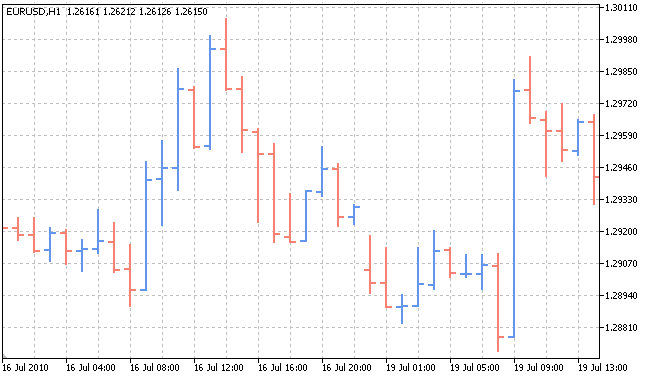
En este caso, el objeto de estudio es la relación entre las dos divisas, y la estadística es su curso en cada momento temporal. ¿De qué manera influye la correlación entre dos divisas en su curso? ¿Por qué en este segmento temporal tenemos precisamente este gráfico del curso, y no otro?. ¿Por qué en este momento del tiempo el curso de la divisa está descendiendo, y no ascendiendo? La respuesta a estas preguntas es la palabra "probabilidad". Cada objeto, depediendo de la probabilidad, puede adoptar este u otro valor.
Hagamos un experimento sencillo: tomemos una moneda. La lanzaremos al aire un número determinado de veces, anotando cada vez el resultado del lanzamiento. Supongamos que la moneda es ideal. Entonces, conforme a ella, podemos hacer la siguiente tabla:
| Resultado | Probabilidad |
|---|---|
| Cara | 0.5 |
| Cruz | 0.5 |
Partiendo de la tabla se puede llegar a la conclusión de que la moneda tiene las mismas probabilidades de caer del lado de la "cara", o del lado de la "cruz". Otro tipo de resultados resultan imposibles aquí (la variante "canto" ha sido excluida de antemano), dado que la suma de las probabilidades de todos los resultados posibles, deberá ser igual a uno.
Lanzamos la moneda 10 veces. Estudiamos el resultado de los lanzamientos:
| Resultado | Cantidad |
|---|---|
| Cara | 8 |
| Cruz | 2 |
¿Por qué ha resultado así, si la probabilidad de que caíga de ambos lados es igual? La probabilidad de que caiga boca arriba cualquiera de los lados es realmente la misma, pero eso no significa, que tras un cierto número de pruebas la moneda deba caer exactamente la mitad de las veces de un lado y la otra mitad del otro. La probabilidad sólo demuestra que, en este experimento (los lanzamientos), la moneda puede caer boca arriba, o bien del lado de la "cara", o bien del de la "cruz", y que la oportunidades de que se cumplan estos acontecimientos son iguales.
Lancemos la moneda ahora 100 veces. Obtenemos una nueva tabla de resultados:
| Resultado | Cantidad |
|---|---|
| Cara | 53 |
| Cruz | 47 |
Como podemos ver, la cantidad esta vez tampoco ha sido igual. Sin embargo, 53 y 47 es el resultado que confirma de manera ideal las presuposiciones iniciales sobre la probabilidad. Casi la mitad de las veces la moneda ha caído del lado de la "cara" o del lado de la "cruz".
Ahora hagamos el trabajo inverso. Supongamos que hay una moneda de la que desconocemos las probabilidades de que caiga de un lado u otro. Hay que determinar si la moneda es ideal, es decir, si tiene las mismas probabilidades de caer de ambos lados.
Tomemos los resultados de la primera experiencia. Dividamos la cantidad de resultados de cada uno de ambos lados entre la cantidad total de resultados. Obtemos las probabilidades:
| Resultado | Probabilidad |
|---|---|
| Cara | 0.8 |
| Cruz | 0.2 |
Como podemos ver, fijándonos en la primera experiencia resulta difícil llegar a la conclusión de que la moneda sea ideal. Hagamos lo mismo con la segunda expriencia:
| Resultado | Cantidad |
|---|---|
| Cara | 0.53 |
| Cruz | 0.47 |
Para estos resultados, ya con un elevado nivel de precisión, podemos asegurar que la moneda es ideal.
De este sencillo ejemplo podemos extraer una conclusión muy importante: cuantas más pruebas se realicen, mayor será la precisión con que reflejará la estadística las propiedades del objeto que la genera.
De esta forma, la estadística y la probabilidad se encuentran estrechamente entrelazadas. La estadística es el resultado de las pruebas realizadas sobre un objeto y depende directamente del estado de dicho objeto. A su vez, con ayuda de la estadística se pueden valorar las probabilidades de los estados de un objeto. Aquí es precisamente cuando surge la principal tarea del trader: conociendo los datos sobre los negocios en un intervalo de tiempo determinado (estadística), deberá pronosticar el comportamiento de los precios (el curso) en el siguiente intervalo de tiempo (obtener las probabilidades), y en base a ello tomar la decisión de comprar o vender.
Por ello, y volviendo a la introducción, es importante, asímismo, conocer y comprender la relación entre estadística y probabilidad, así como poseer conocimientos sobre valoración de riesgos y situaciones arriesgadas, pero esto ya no está relacionado con el tema del presente artículo.
Parámetros estadísticos básicos
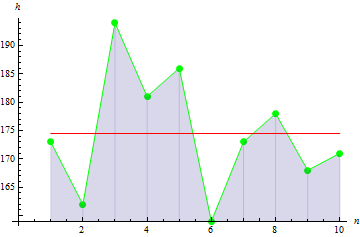
Veamos ahora los parámetros estadísticos básicos. Supongamos que disponemos de datos sobre la estatura en centímetros de diez personas de un grupo determinado:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Estatura | 173 | 162 | 194 | 181 | 186 | 159 | 173 | 178 | 168 | 171 |
Los datos en la tabla se denominan muestra, y su cantidad, el tamaño de la muestra. Veamos algunos de los parámetros de esta muestra. Todos los parámetros serán muestras, dado que se obtienen de los datos de la muestra, y no de magnitudes al azar.
1. Valor muestral esperado
El valor esperado de una muestra indica el valor medio de la muestra. En este caso se trata de la estatura media de un miembro del grupo.
Para calcular el valor esperado, es necesario:
- Sumar todos los valores de la muestra.
- Dividir el resultado obtenido entre el tamaño de la muestra.
Fórmula:
![]()
Donde:
- M - es el valor muestral esperado,
- a[i] - es el elemento de la muestra,
- n - es el tamaño de la muestra.
Tras calcular el resultado del valor esperado, . obtenemos 174.5 см.

2. Dispersión (varianza) muestral
La dispersión muestral indica hasta qué punto los valores de una muestra se desvían del valor esperado. Cuanto mayor sea el valor, más dispersos estarán los datos.
Para calcular la dispersión, hay que:
- Calcular el valor muestral esperado.
- Restar a cada elemento de la muestra el valor esperado. y elevar la diferencia al cuadrado.
- Sumar todos los resultados obtenidos más arriba.
- Y dividir la suma entre el tamaño de la muestra menos 1.
Fórmula:
![]()
Donde:
- D - es la dispersión muestral,
- M - es el valor muestral esperado,
- a[i] - es el elemento de la muestra,
- n - es el tamaño de la muestra.
Para esta muestra, el valor de la dispersión es igual a: 113.611.
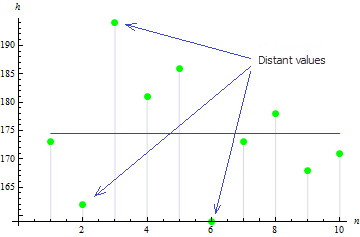
Como se puede ver en el dibujo, los tres valores distan del valor esperado, lo que conduce a un valor elevado de la dispersión.
3. Asimetría muestral
La asimetría muestral indica cuán asimétricos son los valores de la muestra con respecto al valor esperado. Cuanto más próximo sea el valor a cero, más simétricos serán los valores muestrales.
Para calcular la asimetría, hay que:
- Calcular el valor muestral esperado.
- Calcular la dispersión muestral.
- Sumar el cubo de la diferencia de cada elemento y el valor esperado.
- El resultado se dividirá entre el valor de la dispersión en un grado 2/3.
- El resultado se multiplicará por un coeficiente, igual al tamaño de la muestra dividido entre el producto del tamaño de la muestra menos uno y el tamaño de la muestra menos 2.
Fórmula:
![]()
Donde:
- A - es la asimetría muestral,
- D - es la dispersión muestral,
- M - es el valor muestral esperado,
- a[i] - es el elemento de la muestra,
- n - es el tamaño de la muestra.
Para esta muestra obtemos un valor de asimetría bastante reducido: 0.372981. Esto resulta así debido a que los valores alejados se compensan entre sí.
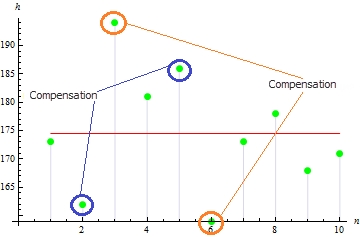
Para la asimetría muestral, el valor será mayor. Por ejemplo, para los datos siguientes, el valor será igual a: 1.384651.
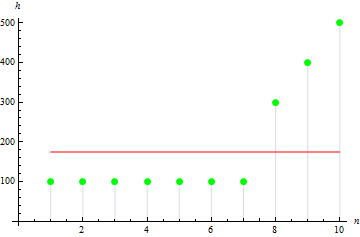
4. Exceso muestral
El exceso muestral indica la medida de la agudeza del pico de la muestra.
Para calcular el exceso, hay que:
- Calcular el valor muestral esperado.
- Calcular la dispersión muestral.
- Sumar la cuarta potencia de las diferencias de cada elemento y el valor esperado.
- Dividir el resultado entre el cuadrado de la dispersión.
- Multiplicar el resultado por un coeficiente, igual al producto del tamaño de la muestra por el tamaño de la muestra más 1, y dividido entre el producto del tamaño de la muestra menos 1, de tamaño de la muestra menos 2 y el tamaño de la muestra menos 3.
- Restar a este resultado el resultado obtenido al dividir la multiplicación por 3 del tamaño de la muestra menos 1, entre el producto del tamaño de la muestra menos 1 por el tamaño de la muestra menos 2.
Fórmula:
![]()
Donde:
- E - es el exceso muestral,
- D - es la dispersión muestral,
- M - es el valor muestral esperado,
- a[i] - es el elemento de la muestra,
- n - es el tamaño de la muestra.
Para los datos sobre la estatura obtenemos el valor: -0.1442285.
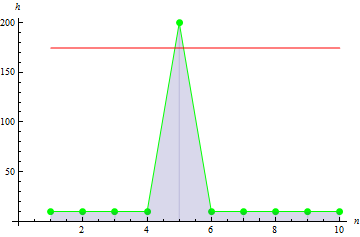
Para los datos con pico máximo, obtenemos el resultado mayor: 10.
5. Covariación muestral
La covariación muestral es la magnitud que indica el nivel de dependencia lineal entre dos muestras de datos. Entre dos datos linealmente independientes, la covariación será igual a 0.
Para demostrar este parámetro, introduciremos de manera adicional datos sobre el peso de 10 personas:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Peso | 65 | 70 | 83 | 60 | 105 | 58 | 69 | 90 | 78 | 65 |
Para calcular la covariación de dos muestras, hay que:
- Calcular el valor esperado de la primera muestra.
- Calcular el valor esperado de la segunda muestra.
- Sumar todos los productos de las dos diferencias: la primera será un elemento de la primera muestra menos el valor esperado de la primera muestra; la segunda será un elemento de la segunda muestra (que corresponda al elemento de la primera lista) menos el valor esperado de la segunda muestra.
- El resultado obtenido lo dividimos entre el tamaño de la muestra menos 1.
Fórmula:
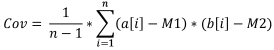
Donde:
- Cov es la covariación muestral,
- a[i] es el elemento de la primera muestra,
- b[i] es el elemento de la primera muestra,
- M1 es el valor muestral esperado de la primera muestra,
- M2 es el valor muestral esperado de la segunda muestra,
- n - es el tamaño de la muestra.
Calculamos el valor de la covariación para las dos muestras: 91.2778. Existe dependencia, como mostraremos en el gráfico superpuesto:
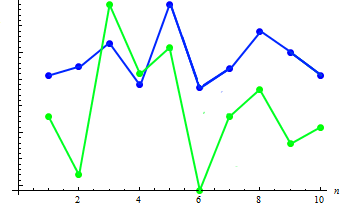
Como se puede ver (como norma) el aumento de la estatura se corresponde con la disminución del peso y viciversa.
6. Correlación muestral
La correlación muestral indica, asímismo, el grado de dependencia lineal entre dos muestras, pero su valor oscila entre -1 y 1.
Para calcular la correlación de dos muestras, hay que:
- Calcular la dispersión de la primera muestra.
- Calcular la dispersión de la segunda muestra.
- Calcular la covariación de estas muestras.
- Dividir la covariación por la raíz del producto de las dispersiones.
Fórmula:
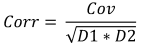
Donde:
- Corr es la correlación muestral,
- Cov es la covariación muestral,
- D1 es la dispersión muestral de la primera muestra,
- D2 es la dispersión muestral de la segunda muestra,
Para los datos sobre estatura y peso, el valor de la correlación será igual 0.579098.
Cómo se usa la estadística en el comercio
El ejemplo más simple del uso de los parámetros estadísticos es el indicador MovingAverage o media móvil. Al calcularla, se utilizan los datos de un periodo determinado, y luego se cuenta el valor aritmético medio del precio:
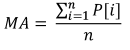
Donde:
- MA es el valor del indicador,
- P[i] es el precio,
- n es el periodo de medida de la MA
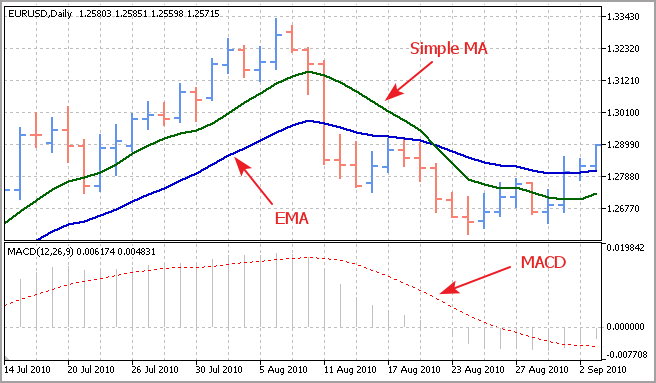
Como se puede ver, el indicador es un análogo pleno del valor muestral esperado. A pesar de su sencillez, este indicador se usa en el cómputo de la EMA, la media móvil exponencial, que a su vez es un elemento base para la construcción del indicador MACD, un instrumento clásico para le medición de la fuerza y dirección de la tendencia de mercado.
Estadística en MQL5
Veamos la realización de las parámetros estadísticos básicos expuestos más arriba, en MQL5. Estos métodos estadísticos, descritos más arriba (y no sólo más arriba), están realizados en el paquete Funciones estadísticas statistics.mqh. Veamos su código.
1. Valor muestral esperado
La función del paquete, capaz de calcular el valor muestral esperado, se llama Average:

En la entrada de la función se proporciona una muestra con los datos. En la salida tenemos el valor esperado.
2. Dispersión (varianza) muestral
La función del paquete, encargada de calcular la dispersión muestral, se llama Variance:
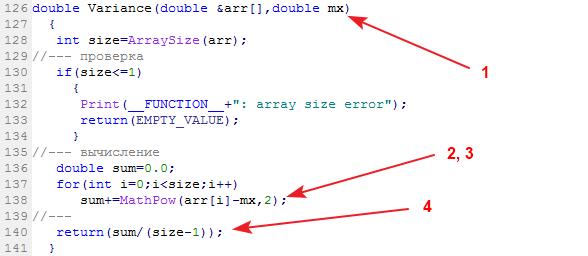
En la entrada de la función se proporciona una muestra con los datos y su valor esperado. En la salida tenemos la dispersión.
3. Asimetría muestral
La función del paquete, encargada de calcular la asimetría muestral, se llama Asymmetry:
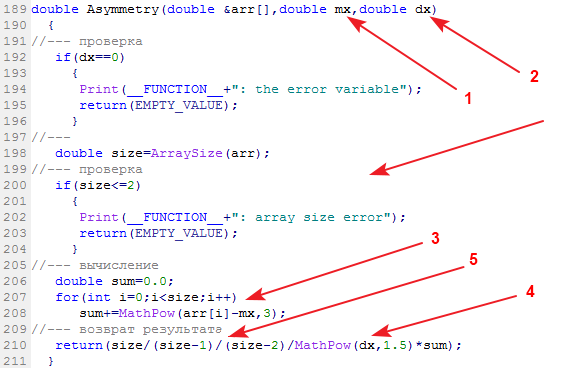
En la entrada se proporciona una muestra con los datos, su valor esperado y la dispersión. En la salida tenemos la asimetría.
4. Exceso muestral
La función del paquete, encargada de calcular el exceso muestral, se llama Excess (Excess2):
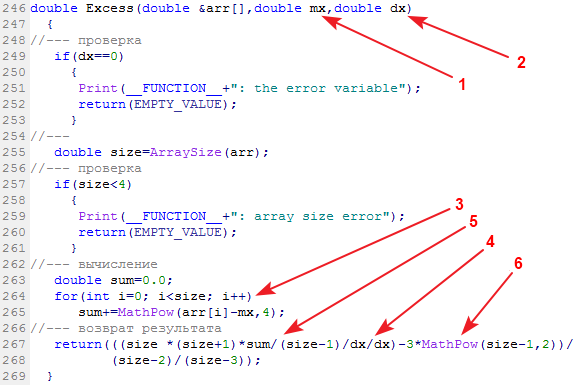
En la entrada se proporciona una muestra con los datos, su valor medio y la dispersión. En la salida tenemos el exceso.
5. Covariación muestral
La función del paquete, encargada de calcular la covariación muestral, se llama Cov:
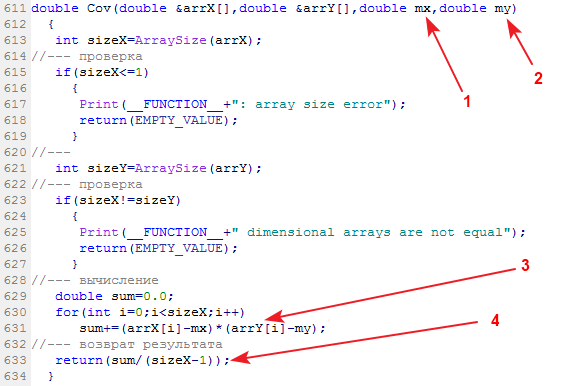
En la entrada se proporcionan dos muestras con datos y su valor esperado. En la salida tenemos la covariación.
6. Correlación muestral
La función del paquete, encargada de calcular la correlación muestral, se llama Corr:

En la entrada de la función se proporciona la covariación de las dos muestras, la dispersión de la primera muestra y la dispersión de la segunda muestra. En la salida tenemos la correlación.
Ahora introducimos la muestra con los datos sobre la estatura y el peso y las analizamos en el paquete.#include <Statistics.mqh> //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- introducimos las dos muestras de valores. double arrX[10]={173,162,194,181,186,159,173,178,168,171}; double arrY[10]={65,70,83,60,105,58,69,90,78,65}; //--- calculamos el valor esperado double mx=Average(arrX); double my=Average(arrY); //--- para el cálculo de la dispersión utilizamos el valor del valor esperado double dx=Variance(arrX,mx); double dy=Variance(arrY,my); //--- valores de la asimetría y el exceso double as=Asymmetry(arrX,mx,dx); double exc=Excess(arrX,mx,dx); //--- valores de covariación y correlación double cov=Cov(arrX,arrY,mx,my); double corr=Corr(cov,dx,dy); //--- salida de los resultados en un archivo log PrintFormat("mx=%.6e",mx); PrintFormat("dx=%.6e",dx); PrintFormat("as=%.6e",as); PrintFormat("exc=%.6e",exc); PrintFormat("cov=%.6e",cov); PrintFormat("corr=%.6e",corr); }
Después de completar el script, el terminal dará los siguientes resultados:
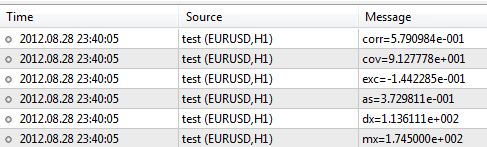
El paquete contiene muchas otras funciones, cuya descripción se encuentra en el CodeBase - https://www.mql5.com/es/code/866.
Conclusión
Ya se obtuvieron ciertas pequeñas al final del punto "Teoría de la rpobabilidad y estadística". Me gustaría añadir que, para estudiar estadística, como sucede con cualquier ciencia, hay que hacerlo desde el principio mismo. Gracias a sus elementos básicos se puede simplificar la percepción de muchos de los conceptos, mecanismos y leyes más complicados, que, a fin de cuentas, son parte imprescindible del trabajo de un trader.
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/387
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 ¡200 usd por su artículo de trading algorítmico!
¡200 usd por su artículo de trading algorítmico!
 Cómo crear un experto en sólo unos minutos con ayuda de EA Tree: Parte 1
Cómo crear un experto en sólo unos minutos con ayuda de EA Tree: Parte 1
 Estudiando las clases de estrategias comerciales de la Biblioteca Estándar - Estrategias personalizadas
Estudiando las clases de estrategias comerciales de la Biblioteca Estándar - Estrategias personalizadas
 Aplicación Práctica de Bases de Datos para Análisis de Mercados
Aplicación Práctica de Bases de Datos para Análisis de Mercados
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso
Debe haber un montón de algoritmos para determinar mods, por lo que una bicicleta universal no es útil aquí.
Usted debe mirar más bien ejemplos, lo que quiere conseguir y lo que no quiere conseguir.
Me ha gustado el artículo.
Es muy fácil de entender y contiene suficiente información.
Y, a juzgar por el título, no pretende ser más que eso.
No le veo ninguna utilidad a este artículo. Una serie de tópicos de la televisión. Y si este artículo no se publicara en un sitio web especializado y medio comercial, sería posible guardar silencio. Pero teniendo en cuenta el sitio, me gustaría señalar lo siguiente.
Existe una ciencia que mide, analiza y pronostica los datos económicos. Se llama econometría. Es un pariente cercano y consanguíneo de la estadística, pero hay diferencias significativas.
1. Para los operadores, el análisis en sí no tiene ningún valor si la previsión no se deriva del análisis. El artículo no menciona la previsión en absoluto.
2. La econometría parte inicialmente de la no estacionariedad de las series económicas. Y si al menos uno se acordara de ello, lo tuviera presente, por así decirlo, la historia de la estadística básica no sería tan halagüeña: para las series no estacionarias los conceptos básicos de mo, varianza, etc. pueden aplicarse con muchas reservas. En cualquier caso, siempre hay que tener dudas. Por ejemplo, para las series no estacionarias, la media no convergerá necesariamente a la mo. No hablo en absoluto de correlación.
3. la econometría se basa en muestras muy cortas: algunas decenas de observaciones. No le interesa la media de muchos años, ya que dicha media también implica estar en una pose durante varios años. En las crisis, las estimaciones de los resultados del cálculo cobran importancia. Son las estimaciones las que distinguen radicalmente la TV de la estadística y, sobre todo, de la econometría.
Artículo sobre la escuela. El nivel de una escuela especial, ni siquiera los cursos inferiores de un instituto.
"De este sencillo ejemplo podemos extraer una importante conclusión: a medida que aumenta el número de ensayos, la estadística refleja con mayor precisión las propiedades del objeto que los genera."
Para un proceso estacionario (Caballo Esférico en el Vacío) - Sí.
Para Series Temporales de datos reales esta afirmación es más bien una tontería.
Si Forex fuera una Serie Temporal Estacionaria - no se necesitaría MQL5 para estimarla - bastaría con simples cepillos de madera del supermercado.
Si los agujeros se perforan en la polilla en un orden caótico y en intervalos de tiempo caóticos.
entonces las estadísticas para todo el período serán más como un informe RosStat - o los desvaríos de un loco.
"Aquí es donde surge la principal tarea de un operador: conocer los datos de las operaciones de un determinado periodo de tiempo (estadísticas), predecir el comportamiento de los precios (tasa) para el siguiente periodo de tiempo (obtener probabilidad), y en base a ello tomar la decisión de comprar o vender."
otra afirmación en términos de significado no dista mucho de ser un disparate. Para pronosticar algo, primero hay que demostrarse a uno mismo que la serie no es aleatoria y puede pronosticarse. Es posible tener ingresos sobre series aleatorias. no se pueden predecir, pero se puede salir de ellas. asimetría de probabilidades y expectativa positiva/negativa.
.