Grundlagen der Statistik

Einleitung

Was ist Statistik? In dem Eintrag in der russischen Fassung von Wikipedia heißt es übersetzt: „Statistik ist der Wissenszweig, der sich mit den allgemeinen Fragen der Erfassung, Auswertung und Analyse großer Mengen (quantitativer und qualitativer) Daten befasst.“ (Statistics). Diese Definition beinhaltet die drei wesentlichen Bestandteile der Statistik: die Erfassung, Auswertung und Analyse von Daten. Für Devisenhändler ist die Datenanalyse besonders nützlich, da die über einen Makler oder an einem Börsenschalter bezogenen Informationen bereits ausgewertet wurden.

Moderne Devisenhändler (die meisten von ihnen) nutzen die technische Analyse, um über Kauf oder Verkauf zu entscheiden. Sie stoßen de facto bei jedem Schritt auf Statistik, wenn sie diesen oder jenen Indikator verwenden, oder versuchen, das Kursniveau für den nächsten Zeitraum vorherzusagen. Und was soll man sagen, selbst ein Kursschwankungsdiagramm ist eine statistische Abbildung des Verhaltens eines Wertpapiers oder einer Währung in der Zeit. Deshalb sollte man die grundlegenden Prinzipien der Statistik kennen, auf denen eine Vielzahl der Mechanismen beruht und aufgebaut ist, die dem Devisenhändler die Entscheidungsfindung erleichtern.

Wahrscheinlichkeitstheorie und Statistik

Jede Statistik ist das Ergebnis einer Veränderung des Zustandes des Objektes, das sie hervorbringt. Wir betrachten den Kurs des Währungspaares EURUSD anhand von Stundenzeiträumen (H1)

 

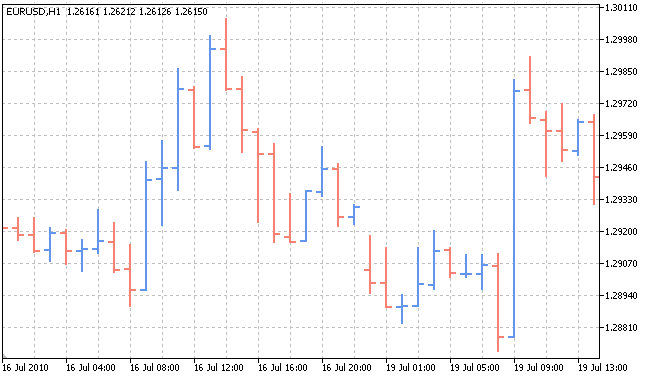
In diesem Fall ist das Beobachtungsobjekt die Beziehung zwischen zwei Währungen, und deren jeweiliger Kurs zu jedem Zeitpunkt die Statistik. Wie beeinflusst nun aber die Beziehung (Korrelation) zwischen zwei Währungen ihren jeweiligen Kurs? Warum erhalten wir zu einem bestimmten Zeitabschnitt genau dieses Kursdiagramm und kein anderes? Warum steigt der Kurs in diesem Moment, statt zu fallen? Die Antwort auf all diese Fragen liegt in einem Wort: Wahrscheinlichkeit. Jedes Objekt kann je nach Wahrscheinlichkeit diesen oder jenen Wert annehmen.

Machen wir ein einfaches Experiment: wir nehmen eine Münze und werfen sie eine bestimmte Anzahl mal hoch, wobei wir jeweils aufzeichnen, welche ihrer Seiten nach der Landung nach oben zeigte. Wir setzen voraus, dass es sich um eine „reelle“ Münze handelt. Dann kann für sie folgende Tabelle angelegt werden:

Ergebnis	Wahrscheinlichkeit
Kopf	0,5
Zahl	0,5

Ausgehend von der Tabelle kann der Schluss gezogen werden, dass die Münze „Kopf“ oder „Zahl“ mit derselben Wahrscheinlichkeit zeigt. Andere Ergebnisse sind hier nicht möglich (das Landen auf dem Rand wurde von Vornherein ausgeschlossen), da die Summe der Wahrscheinlichkeiten „1“ sein muss.

Wir werfen die Münze zehn Mal und erhalten folgende Tabelle:

Ergebnis	Ziffer
Kopf	8
Zahl	2

Wie kann das sein? Die Wahrscheinlichkeit für beide Seiten ist doch dieselbe! Die Wahrscheinlichkeit, dass jede der Seiten nach oben zeigt, ist tatsächlich dieselbe, was jedoch nicht bedeutet, dass die Münze nach einigen Würfen genauso oft auf der einen wie der anderen Seite landen muss. Die Wahrscheinlichkeit besagt lediglich, dass bei jedem einzelnen Versuch (Wurf) die Münze entweder „Kopf“ oder „Zahl“ zeigt, und dass die Chancen für das Eintreten beider Ergebnisse (Ereignisse) gleich stehen.

Jetzt werfen wir die Münze 100 Mal und erhalten eine andere Ergebnistabelle:

Ergebnis	Ziffer
Kopf	53
Zahl	47

Die Anzahl der Ergebnisse ist offenkundig wieder nicht identisch. Allerdings handelt es sich bei 53 gegenüber 47 um ein Ergebnis, das die anfänglichen Annahmen bezüglich der Wahrscheinlichkeit stützt. Die Münze ist in etwas genauso oft auf die eine wie die andere Seite gefallen.

Jetzt zäumen wir das Pferd einmal von hinten auf. Nehmen wir an, es gibt eine Münze, von der unbekannt ist, wie häufig sie auf eine ihrer beiden Seiten fällt. Es ist also zu ermitteln, ob es sich um eine „reelle“ Münze handelt, das heißt, ob sie mit derselben Wahrscheinlichkeit auf die eine wie die andere Seite fällt.

Wir bedienen uns der Daten aus dem ersten Versuch und teilen die Anzahl der Ergebnisse für jede Seite durch die Gesamtzahl der Ergebnisse. So erhalten wir folgende Wahrscheinlichkeiten:

Ergebnis	Wahrscheinlichkeit
Kopf	0,8
Zahl	0,2

Wie wir sehen, lässt sich aus dem ersten Versuch schwerlich folgern, dass die Münze „reell“ ist. Führen wir also denselben Vorgang mit den Daten aus dem zweiten Versuch durch:

Ergebnis	Ziffer
Kopf	0,53
Zahl	0,47

Anhand dieser Ergebnisse lässt sich mit einigermaßen großer Bestimmtheit sagen, dass die Münze tatsächlich „reell“ ist.

Dieses einfache Beispiel führt zu einem wichtigen Schluss: je größer die Zahl der Versuche desto genauer gibt die Statistik die Eigenschaften des sie hervorbringenden Objektes wieder.

Die Statistik und die Wahrscheinlichkeit sind also eng miteinander verwoben. Die Statistik ist das Ergebnis von mit dem Objekt gemachten Versuchen und hängt unmittelbar von der Wahrscheinlichkeit ab, mit der das Objekt bestimmte Zustände annimmt. Mithilfe der Statistik kann andererseits auch die Wahrscheinlichkeit des Eintretens bestimmter Zustände des Objektes ermittelt werden. Genau hier liegt die Hauptaufgabe für Devisenhändler: anhand der Daten zu den Abschlüssen in einem bestimmten Zeitraum (Statistik) das Kursverhalten (den Kurs) für den Folgezeitraum vorhersagen (Wahrscheinlichkeit) und auf dieser Grundlage eine Entscheidung in Bezug auf Kauf oder Verkauf zu fällen.

Deshalb ist es, um zu unserer Einleitung zurückzukommen, sowohl wichtig, die Wechselbeziehung zwischen Statistik und Wahrscheinlichkeit zu kennen und zu verstehen als auch über Kenntnisse der Beurteilung von Risiken und Gefahrensituationen zu verfügen, was allerdings nicht Thema dieses Beitrages ist.

Grundlegende statistische Kennziffern 

Wir befassen uns jetzt mit den grundlegenden Kennziffern der Statistik. Angenommen, uns liegen die Größenangaben von 10 Personen einer bestimmten Gruppe in Zentimetern vor:

	1	2	3	4	5	6	7	8	9	10
Größe	173	162	194	181	186	159	173	178	168	171

 

Die Daten in der Tabelle werden als Stichprobe bezeichnet und ihre Anzahl als Stichprobengröße. Wir schauen uns einige Kennziffern dieser Stichprobe etwas genauer an. Alle Kennziffern gehören zu der Stichprobe, da sie aus den Daten der Stichprobe gewonnen werden und nicht aus den Daten einer Zufallsgröße.

1. Der Erwartungswert der Stichprobe

Der Erwartungswert der Stichprobe weist den Durchschnittswert der Stichprobe aus. In unserem Fall ist dies die durchschnittliche Körpergröße der Gruppenmitglieder.

Zur Berechnung des Durchschnittswertes müssen wir:

1. die Summe aller Werte der Stichprobe bilden und
2. das Ergebnis durch die Stichprobengröße teilen. 

Die Formel lautet: 

 mit:

• M für den Durchschnittswert der Stichprobe,
• a[i] als Element der Stichprobe und
• n für die Stichprobengröße.

Die Berechnung des Erwartungswertes der Stichprobe ergibt: 174,5 cm

 

 

2. Varianz der Stichprobe

Die Stichprobenvarianz gibt an, wie weit die Werte der Stichprobe von dem Erwartungswert entfernt sind. Je größer dieser Wert desto größer die Streuung der Daten.

Zur Berechnung der Varianz müssen wir:

1. den Durchschnittswert der Stichprobe berechnen,
2. diesen von jedem Element der Stichprobe subtrahieren und die Differenz mit sich selbst multiplizieren,
3. die Summe der so erhaltenen Werte bilden und
4. die Summe durch die Stichprobengröße minus 1 dividieren.

Die Formel lautet:  

 

mit: 

• D für die Varianz der Stichprobe,
• M für den Durchschnittswert der Stichprobe,
• a[i] als Element der Stichprobe und
• n für die Stichprobengröße.

Für unsere Stichprobe beträgt der Wert der Varianz: 113,611.

 

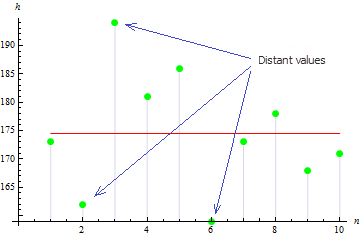
Wie die Abbildung zeigt, liegen 3 Werte weit von dem Erwartungswert entfernt, wodurch der hohe Varianzwert bedingt ist.

3. Schiefe der Stichprobe

Die Schiefe der Stichprobe gibt an, wie asymmetrisch die Stichprobenwerte in Bezug auf deren Erwartungswert verteilt sind. Je näher die Schiefe bei Null liegt, desto symmetrischer sind die Werte der Stichprobe.

Zur Berechnung der Schiefe müssen wir:

1. den Durchschnittswert der Stichprobe berechnen,
2. die Varianz der Stichprobe ermitteln,
3. die Summe der hoch drei genommenen Differenzen zwischen allen Elementen und dem Erwartungswert bilden,
4. das erhaltene Ergebnis durch den Varianzwert mit der Potenz 2/3 dividieren und
5. das Ergebnis mit dem Koeffizienten multiplizieren, der der durch das Produkt aus der Stichprobengröße minus 1 und der Stichprobengröße minus 2 dividierten Stichprobengröße entspricht.

Die Formel lautet:  

mit: 

• A für die Schiefe der Stichprobe, 
• D für die Varianz der Stichprobe,
• M für den Durchschnittswert der Stichprobe,
• a[i] als Element der Stichprobe und
• n für die Stichprobengröße.

Für diese Stichprobe erhalten wir einen recht kleinen Schiefewert von 0,372981. Das liegt daran, dass die weit entfernten Werte sich gegenseitig ausgleichen.

 

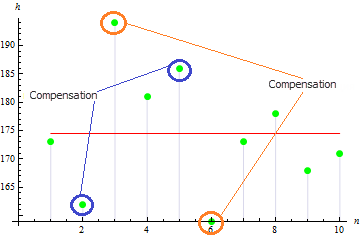
Bei einer schiefen oder asymmetrischen Stichprobe ist dieser Wert höher. Für die folgenden Daten liegt er beispielsweise bei 1,384651.

 

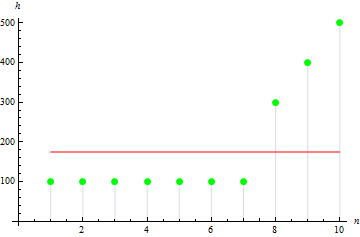
4. Wölbung der Stichprobe

Die Wölbung oder Kurtosis der Stichprobe ist das Maß dafür, wie „steil“ ihre Ausschläge sind.

Zur Berechnung der Wölbung müssen wir:

1. den Durchschnittswert der Stichprobe berechnen,
2. die Varianz der Stichprobe ermitteln,
3. die Summe der hoch vier genommenen Differenzen zwischen allen Elementen und dem Erwartungswert bilden,
4. das erhaltene Ergebnis durch die quadrierte (mit sich selbst multiplizierte) Varianz dividieren,
5. das Ergebnis mit dem Koeffizienten multiplizieren, der dem durch das Produkt aus der Stichprobengröße minus 1, der Stichprobengröße minus 2 und der Stichprobengröße minus 3 dividierten Produkt aus der Stichprobengröße und der Stichprobengröße plus 1 entspricht, und
6. von dem Ergebnis das durch das Produkt aus der Stichprobengröße minus 1 und der Stichprobengröße minus 2 dividierte Produkt aus 3 und dem Quadrat der Stichprobengröße minus 1 subtrahieren.

Die Formel lautet:  

mit: 

• E für die Wölbung der Stichprobe,
• D für die Varianz der Stichprobe,
• M für den Durchschnittswert der Stichprobe,
• a[i] als Element der Stichprobe und
• n für die Stichprobengröße.

Für die Körpergrößendaten erhalten wir -0,1442285.

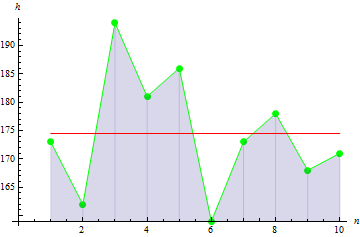
Für Daten mit „steileren“ Ausschlägen ist der Wert höher: 10.

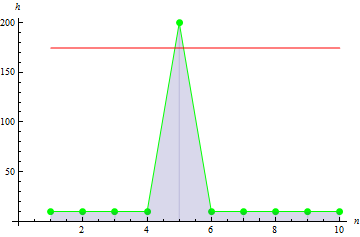
5. Kovarianz der Stichproben

Bei der Stichprobenkovarianz handelt es sich um eine Größe, die den Grad der linearen Abhängigkeit zwischen zwei Datenstichproben angibt. Zwischen linear unabhängigen Daten ist die Kovarianz gleich „0“.

Zur Veranschaulichung führen wir zusätzlich die Gewichtsdaten von 10 Personen ein:

	1	2	3	4	5	6	7	8	9	10
Gewicht	65	70	83	60	105	58	69	90	78	65

 

Zur Berechnung der Kovarianz zweier Stichproben müssen wir:

1. den Erwartungswert der ersten Stichprobe berechnen,
2. den Erwartungswert der zweiten Stichprobe berechnen,
3. die Summe der beiden Differenzen, (1) eines Elementes der ersten Stichprobe minus dem Erwartungswert derselben und (2) des dem Element aus (1) entsprechenden Elementes der zweiten Stichprobe minus dem Erwartungswert der zweiten Stichprobe, bilden sowie
4. die erhaltene Summe durch die Stichprobengröße minus 1 dividieren.

Die Formel lautet:  

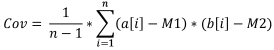
mit: 

• Cov für die Kovarianz der Stichproben,
• a[i] als Element der ersten Stichprobe,
• b[i] als Element der zweiten Stichprobe, 
• M1 für den Erwartungswert der ersten Stichprobe, 
• M2 für den Erwartungswert der zweiten Stichprobe und  
• n für die Stichprobengröße. 

Die Berechnung des Kovarianzwertes der beiden Stichproben ergibt: 91,2778. Wie das kombinierte Diagramm zeigt, liegt eine Abhängigkeit vor:

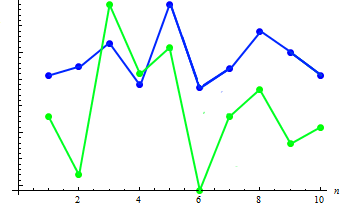
Unübersehbar entspricht eine größere Körperlänge (für gewöhnlich) auch einem höheren Gewicht und umgekehrt.

 6. Stichprobenkorrelation

Die Korrelation zwischen zwei Stichproben gibt ebenfalls den Grad der linearen Abhängigkeit zwischen diesen wieder, ihr Wert schwankt jedoch stets zwischen „-1“ und „1“.

Zur Berechnung der Korrelation zweier Stichproben müssen wir:

1. die Varianz der ersten Stichprobe berechnen,
2. die Varianz der zweiten Stichprobe berechnen,
3. die Kovarianz beider Stichproben berechnen, und
4. die Kovarianz durch die Wurzel aus dem Produkt der Varianzen dividieren.

Die Formel lautet: 

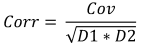
mit: 

• Corr für die Stichprobenkorrelation,
• Cov für die Kovarianz der Stichproben,
• D1 für die Varianz der ersten Stichprobe und  
• D2 für die Varianz der zweiten Stichprobe.  

Für die Größen- und Gewichtsangaben beträgt die Korrelation 0,579098.

Die Verwendung der Statistik im Handel

Das einfachste Beispiel für den Einsatz statistischer Kennziffern im Handel ist der Indikator des gleitenden Durchschnittswertes oder Moving Average (MA). Um ihn zu berechnen, werden die Daten für einen bestimmten Zeitraum verwendet, anhand derer das arithmetische Mittel des Kursverlaufs berechnet wird.

 

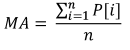
mit: 

• MA für den Indikatorwert,
• P[i] für den jeweiligen Kurswert und
• n für den Zeitraum, für den der MA ermittelt wird.

Wir sehen, der Indikator entspricht in vollem Umfang dem Erwartungswert für die Stichprobe. Ungeachtet seiner Einfachheit kommt dieser Indikator bei der Berechnung des exponentiellen gleitenden Durchschnittswertes (EMA) zum Einsatz, welcher seinerseits wiederum ein wesentlicher Baustein des Indikators MACD, eines klassischen Elementes zur Bestimmung der Stärke und der Richtung des Trends, ist.

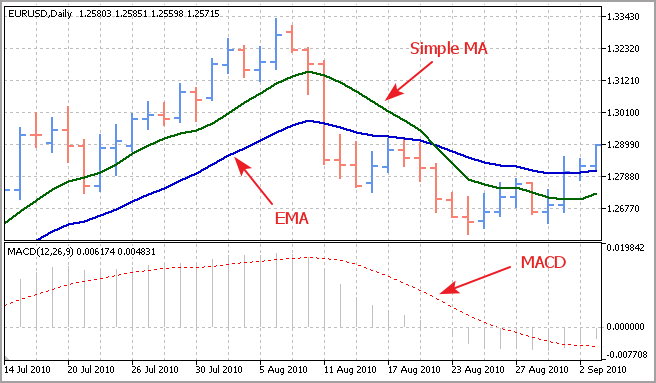
Statistik in MQL5

Wir sehen uns die Umsetzung der oben vorgestellten grundlegenden statistischen Kennziffern in MQL5 einmal genauer an. Die Umsetzungen der oben dargestellten statistischen Verfahren (und nicht nur die) befinden sich in der Bibliothek für die statistischen Funktionen (statistics.mqh). Wir untersuchen ihren Code in MQL5.

1. Der Erwartungswert der Stichprobe

 Die Bibliotheksfunktion zur Berechnung des Erwartungswertes der Stichprobe heißt „Average“:

Am Eingang der Funktion wird die Stichprobe mit den Daten eingegeben. An ihrem Ausgang erhalten wir den Erwartungs- oder Durchschnittswert.

2. Varianz der Stichprobe

Die Bibliotheksfunktion zur Berechnung der Varianz der Stichprobe trägt die Bezeichnung „Variance“:

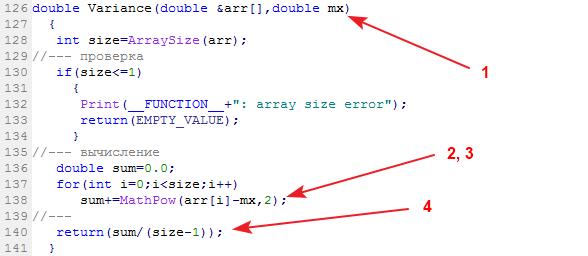
 Am Eingang der Funktion werden die Stichprobe mit den Daten sowie der ermittelte Erwartungswert eingegeben. An ihrem Ausgang erhalten wir den Streuungswert, die Varianz.

3. Schiefe der Stichprobe

Die Bibliotheksfunktion zur Berechnung der Schiefe der Stichprobe wird als „Asymmetry“ bezeichnet:

 

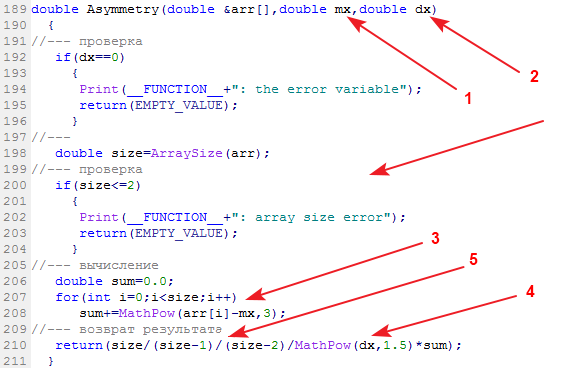
 Am Eingang der Funktion werden die Stichprobe mit den Daten, der ermittelte Erwartungswert und die Streuung eingegeben. An ihrem Ausgang erhalten wir den Wert für die Schiefe bzw. Asymmetrie.

4. Wölbung der Stichprobe

Die Bibliotheksfunktion zur Berechnung der Wölbung der Stichprobe finden wir unter „Excess“ (Excess2):

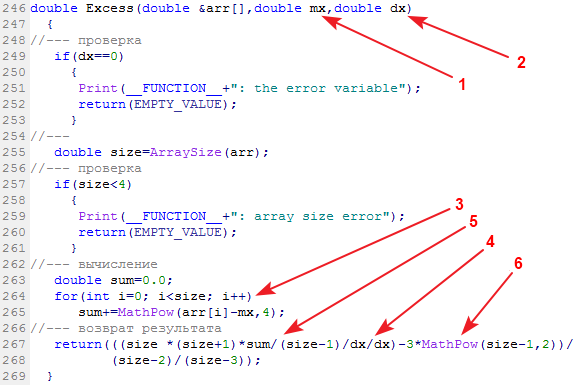
Am Eingang der Funktion werden die Stichprobe mit den Daten, der ermittelte Erwartungswert und die Streuung eingegeben. An ihrem Ausgang erhalten wir den Wert für die Wölbung, die Kurtosis.

5. Kovarianz der Stichproben

Die Bibliotheksfunktion zur Berechnung der Stichprobenkovarianz heißt „Cov“: 

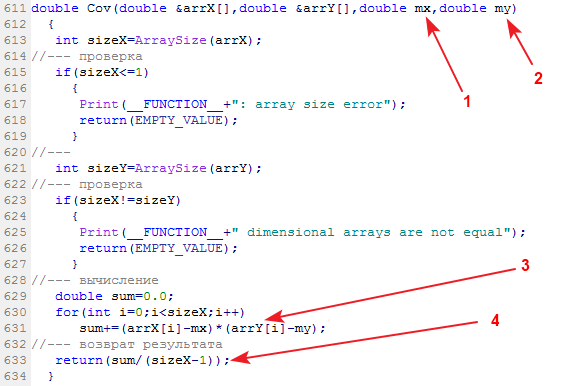
Am Eingang der Funktion werden zwei Stichproben mit den Daten sowie deren jeweilige Erwartungswerte eingegeben. An ihrem Ausgang erhalten wir den Wert für ihre Kovarianz.

6. Stichprobenkorrelation

Die Bibliotheksfunktion zur Berechnung der Korrelation zwischen zwei Stichproben hat die Bezeichnung „Corr“: 

 

Am Eingang der Funktion werden die Kovarianz zweier Stichproben sowie die Varianzen der ersten und der zweiten Stichprobe eingegeben. An ihrem Ausgang erhalten wir den Wert für ihre Korrelation.

Jetzt legen wir eine Stichprobe mit Größen- und Gewichtsangaben fest und analysieren sie mithilfe der Bibliothek.

#include <Statistics.mqh>
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//--- specify two data samples.
   double arrX[10]={173,162,194,181,186,159,173,178,168,171};
   double arrY[10]={65,70,83,60,105,58,69,90,78,65};
//--- calculate the mean
   double mx=Average(arrX);
   double my=Average(arrY);
//--- to calculate the variance, use the mean value
   double dx=Variance(arrX,mx);
   double dy=Variance(arrY,my);
//--- skewness and kurtosis values
   double as=Asymmetry(arrX,mx,dx);
   double exc=Excess(arrX,mx,dx);
//--- covariance and correlation values
   double cov=Cov(arrX,arrY,mx,my);
   double corr=Corr(cov,dx,dy);
//--- print results in the log file
   PrintFormat("mx=%.6e",mx);
   PrintFormat("dx=%.6e",dx);
   PrintFormat("as=%.6e",as);
   PrintFormat("exc=%.6e",exc);
   PrintFormat("cov=%.6e",cov);
   PrintFormat("corr=%.6e",corr);
  }

Nach der Ausführung des Skriptes sehen wir am Ausgabegerät die folgenden Ergebnisse:

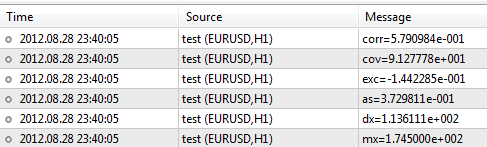
Die Bibliothek enthält eine Vielzahl weiterer Funktionen, deren Beschreibungen in der Codesammlung unter in https://www.mql5.com/de/code/866 zu finden sind.

Fazit

Ein kleines Zwischenfazit wurde bereits am Ende des Abschnitts Wahrscheinlichkeitstheorie und Statistik gezogen. Ergänzend sei hier noch angemerkt, dass man beim Studium der Statistik wie bei jeder anderen Wissenschaft mit den elementarsten Grundlagen beginnen sollte. Selbst Grundkenntnisse erleichtern das Verständnis zahlreicher komplexerer Angelegenheiten, Vorgänge und Gesetzmäßigkeiten, was sie für den Devisenhandel nahezu unverzichtbar macht.