İstatistik Temelleri

Giriş

İstatistik nedir? Wikipedia'da bulunan tanımı şu şekildedir: "İstatistik, verilerin toplanması, düzenlenmesi, analizi, yorumlanması ve sunulması çalışmasıdır." (İstatistik). Bu tanım, istatistiğin üç ana bileşenini ortaya koyar: Veri toplama, ölçüm ve analiz. Veri analizi, alınan bilgiler broker tarafından veya bir alım satım terminali aracılığıyla sağlandığı ve halihazırda ölçüldüğü için, bir yatırımcı için özellikle yararlı görünmektedir.

Modern yatırımcılar (çoğunlukla) satın alma veya satma konusunda karar vermek için teknik analizi kullanır. Belirli bir göstergeyi kullanırken veya gelecek dönem için fiyat seviyesini tahmin etmeye çalışırken yaptıkları hemen hemen her şeyde istatistiklerle uğraşırlar. Aslında, bir fiyat dalgalanma grafiğinin kendisi, bir hisse veya para biriminin zaman içindeki belirli istatistiklerini temsil eder. Bu nedenle, bir yatırımcı için karar verme sürecini kolaylaştıran mekanizmaların çoğunun altında yatan istatistiklerin temel prensiplerini anlamak çok önemlidir.

Olasılık Teorisi ve İstatistik

Herhangi bir istatistik, onu oluşturan nesnenin durumlarında meydana gelen değişikliğin sonucudur. Saatlik zaman dilimlerinde bir EURUSD fiyat grafiğini ele alalım:

 

Bu durumda, nesne iki para birimi arasındaki korelasyon iken, istatistikler her zaman noktasındaki fiyatlarıdır. İki para birimi arasındaki korelasyon bunların fiyatlarını nasıl etkiler? Neden belirli bir zaman aralığında farklı bir fiyat grafiğine değil de bu fiyat grafiğine sahibiz? Fiyatlar neden şu anda düşüyor da artmıyor? Bu soruların cevabı 'olasılık' sözcüğüdür. Olasılığa bağlı olarak her nesne bir veya başka bir değer alabilir.

Basit bir deney yapalım: Bir madeni para alın ve her seferinde yazı tura sonucunu kaydederek belirli sayıda çevirin. Diyelim ki aynı oranda yazı tura geldi. Bu durumda, bunun için tablo aşağıdaki gibi olabilir:

Sonuç	Olasılık
Tura	0,5
Yazı	0,5

Tabloda, madeni paranın tura veya yazı gelme olasılığının eşit olduğu gösterilmiştir. Tüm olası olayların olasılıklarının toplamı bire eşit olacağı için, burada başka bir sonuç mümkün değildir (madeni paranın dik gelme olasılığı hariç tutulmuştur).

Madeni parayı 10 kez çevirin. Şimdi yazı tura sonuçlarına bakalım:

Sonuç	Sayı
Tura	8
Yazı	2

Madeni paranın her iki tarafa da gelme olasılığı eşitse neden bu sonuçlara sahibiz? Madeni paranın her iki tarafa da gelme olasılığı gerçekten de eşittir, ancak bu, birkaç yazı tura atışından sonra madeni paranın bir tarafa diğer tarafa olduğu kadar çok denk geleceği anlamına gelmez. Olasılık yalnızca, bu belirli denemede (yazı tura atışı) tura ya da yazı geleceğini ve her iki olayın da eşit şansa sahip olduğunu gösterir.

Şimdi madeni parayı 100 kez çevirelim. Yeni sonuç tablosu şu şekildedir:

Sonuç	Sayı
Tura	53
Yazı	47

Görüldüğü gibi sonuç sayıları yine eşit değildir. Ancak, 53 ila 47, ilk olasılık varsayımlarını kanıtlayan sonuçtur. Madeni para, yazılarda olduğu kadar neredeyse turalarda geldi.

Şimdi aynı işlemi ters sırada yapalım. Diyelim ki bir madeni paramız var ama hangi tarafa denk geleceğine ilişkin olasılık bilinmiyor. Aynı oranda yazı tura gelip gelmeyeceğini, yani bu paranın tura veya yazı gelme olasılığı eşit olan bir madeni para olup olmadığını belirlememiz gerekiyor.

İlk deneydeki verileri alalım. Her iki tarafa göre sonuç sayısını toplam sonuç sayısına bölün. Aşağıdaki olasılıkları elde ederiz:

Sonuç	Olasılık
Tura	0,8
Yazı	0,2

İlk deneyden madeni paranın yazı ve tura gelme oranın eşit olacağı sonucuna varmanın çok zor olduğunu görebiliriz. Aynı işlemi ikinci deney için de yapalım:

Sonuç	Sayı
Tura	0,53
Yazı	0,47

Elimizde bu sonuçlar varken, bu madeni parada yazı tura gelme olasılığının eşit olduğunu yüksek bir doğrulukla söyleyebiliriz.

Bu basit örnek, önemli bir sonuca varmamızı sağlar: Deney sayısı ne kadar fazlaysa, nesne özellikleri, nesne tarafından oluşturulan istatistikler tarafından o kadar doğru bir şekilde yansıtılır.

Bu nedenle, istatistik ve olasılık ayrılmaz bir şekilde iç içedir. İstatistik bir nesneyle deneysel sonuçları temsil eder ve nesne durumlarının olasılığına doğrudan bağlıdır. Tersine, nesnenin durumlarının olasılığı istatistikler kullanılarak tahmin edilebilir. Bir yatırımcı için asıl zorluk burada yatmaktadır: Belirli bir zaman dilimindeki (istatistikler) alım satım işlemlerine ilişkin verilere sahip olmak, sonraki zaman dilimi (olasılık) boyunca fiyat davranışını tahmin etmek ve bu bilgilere dayanarak al veya sat kararı vermek.

Bu nedenle Giriş bölümünde değinilen noktalara geri dönersek, istatistik ve olasılık arasındaki ilişkiyi bilmek ve anlamak kadar risk değerlendirmesi ve risk durumları hakkında bilgi sahibi olmak da önemlidir. Ancak son ikisi bu makalenin kapsamı dışındadır.

Temel İstatistiksel Parametreler

Şimdi temel istatistiksel parametreleri gözden geçirelim. Bir gruptaki 10 kişiyle ilgili olarak cm cinsinden boy verimiz olduğunu varsayalım:

	1	2	3	4	5	6	7	8	9	10
Boy	173	162	194	181	186	159	173	178	168	171

 

Tabloda belirtilen verilere örnek, veri miktarına ise örnek boyutu diyelim. Verilen örneğin bazı parametrelerine bir göz atacağız. Tüm parametreler, rastgele değişken verisi yerine örnek veriden kaynaklandıkları için örnek parametreler olacaktır.

1. Örnek ortalaması

Örnek ortalaması, örnekteki ortalama değerdir. Bizim durumumuzda, bu, gruptaki insanların ortalama boyudur.

Ortalamayıhesaplamak için şu işlemleri gerçekleştirmeliyiz:

1. Tüm örnek değerleri toplayın.
2. Ortaya çıkan değeri örnek boyutuna bölün.

Formül: 

 Burada:

• M, örnek ortalamasıdır,
• a[i], örnek öğedir,
• n, örnek boyutudur.

Hesaplamaların ardından 174,5 cm ortalama değerini elde ederiz.

 

 

2. Örnek varyansı

Örnek varyansı, örnek değerlerinin örnek ortalamasından ne kadar uzakta olduğunu açıklar. Değer ne kadar büyük olursa, veriler o kadar geniş ölçüde yayılır.

Varyansı hesaplamak için şu işlemleri gerçekleştirmeliyiz:

1. Örnek ortalamasını hesaplayın.
2. Her örnek öğeden ortalamayı çıkarın ve farkın karesini alın.
3. Yukarıda elde edilen ortaya çıkan değerleri toplayın.
4. Toplamı, örnek boyutu eksi 1'e bölün

Formül:  

 

Burada: 

• D, örnek varyansıdır,
• M, örnek ortalamasıdır,
• a[i], örnek öğedir,
• n, örnek boyutudur.

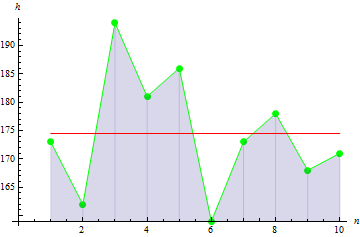
Bizim durumumuzdaki örnek varyansı 113,611'dir.

 

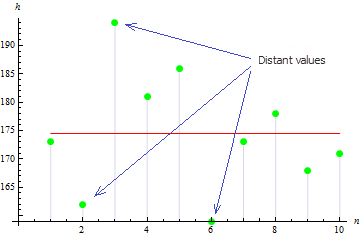
Şekilde, 3 değerin, büyük varyans değerine yol açan ortalamadan geniş ölçüde yayıldığı gösterilmiştir.

3. Örnek çarpıklığı

Örnek çarpıklığı, örnek değerlerinin ortalaması etrafındaki asimetri derecesini tanımlamak için kullanılır. Çarpıklık değeri sıfıra ne kadar yakınsa, örnek değerleri o kadar simetriktir.

Çarpıklığı hesaplamak için şu işlemleri gerçekleştirmeliyiz:

1. Örnek ortalamasını hesaplayın.
2. Örnek varyansını hesaplayın.
3. Her bir örnek öğenin küplü farklarını ve ortalamasını toplayın.
4. Yanıtı 2/3 kuvvetine yükseltilmiş varyans değerine bölün.
5. Yanıtı, örnek boyutu eksi 1 ve örnek boyutu eksi 2'nin çarpımı ile bölünen örnek boyutuna eşit katsayı ile çarpın

Formül:  

Burada: 

• A, örnek çarpıklığıdır, 
• D, örnek varyansıdır,
• M, örnek ortalamasıdır,
• a[i], örnek öğedir,
• n, örnek boyutudur.

Bu örnek için oldukça küçük bir çarpıklık değeri elde ederiz: 0,372981. Bunun nedeni, farklı değerlerin birbirini dengelemesidir.

 

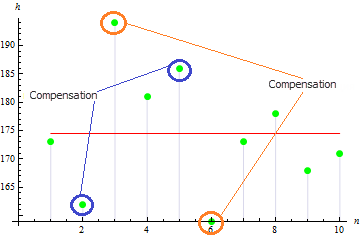
Değer, asimetrik örnek için daha büyük olacaktır. Örneğin aşağıdaki gibi veriler için değer 1,384651 olacaktır.

 

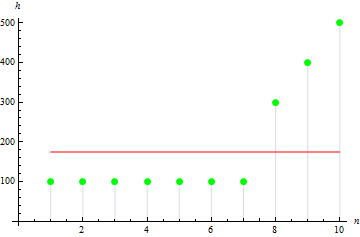
4. Örnek basıklığı

Örnek basıklığı, örneğin doruk noktasını tanımlar.

Basıklığı hesaplamak için şu işlemleri gerçekleştirmeliyiz:

1. Örnek ortalamasını hesaplayın.
2. Örnek varyansını hesaplayın.
3. Her örnek öğenin dördüncü kuvvet farklarını ve ortalamasını toplayın.
4. Yanıtı karesi alınmış varyansa bölün.
5. Ortaya çıkan değeri, örnek boyutu eksi 1, örnek boyutu eksi 2 ve örnek boyutu eksi 3'ün çarpımına bölünen örnek boyutu ve örnek boyutu artı 1 çarpımına eşit katsayı ile çarpın.
6. Ortaya çıkan değerden, örnek boyutu eksi 1 ve örnek boyutu eksi 2'ye bölünen 3'ün çarpımını ve örnek boyutu ile 1'in kare farkını çıkarın.

Formül:  

Burada: 

• E, örnek basıklığıdır,
• D, örnek varyansıdır,
• M, örnek ortalamasıdır,
• a[i], örnek öğedir,
• n, örnek boyutudur.

Verilen boy verileri için -0,1442285 değerini elde ederiz.

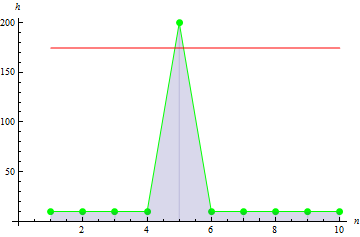
Daha keskin bir tepe verisi için daha büyük bir değer elde ederiz: 10.

5. Örnek kovaryansı

Örnek kovaryansı, iki veri örneği arasındaki doğrusal bağımlılığın derecesini gösteren bir ölçüdür. Doğrusal olarak bağımsız veriler arasındaki kovaryans, 0 olacaktır.

Bu parametreyi göstermek için, 10 kişinin her biri için ağırlık verileri ekleyeceğiz:

	1	2	3	4	5	6	7	8	9	10
Ağırlık	65	70	83	60	105	58	69	90	78	65

 

İki örneğin kovaryansını hesaplamak için şu işlemleri gerçekleştirmeliyiz:

1. İlk örneğin ortalamasını hesaplayın.
2. İkinci örneğin ortalamasını hesaplayın.
3. İki farkın tüm çarpımlarını toplayın: Birinci fark - ilk örneğin bir öğesi eksi ilk örneğin ortalaması; ikinci fark - ikinci örneğin bir öğesi (ilk örneğin öğesine karşılık gelen) eksi ikinci örneğin ortalaması.
4. Yanıtı, örnek boyutu eksi 1'e bölün

Formül:  

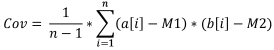
Burada: 

• Cov, örnek kovaryansıdır,
• a[i], ilk örneğin öğesidir,
• b[i], ikinci örneğin öğesidir, 
• M1, ilk örneğin örnek ortalamasıdır, 
• M2, ikinci örneğin örnek ortalamasıdır, 
• n, örnek boyutudur. 

İki örneğin kovaryans değerini hesaplayalım: 91,2778. Mevcut bağımlılık, birleşik grafikte gösterilebilir:

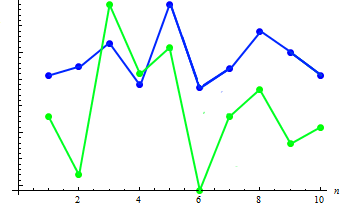
Görülebileceği gibi, boydaki artış (genel olarak) ağırlıktaki azalmaya karşılık gelir ve bunun tersi de geçerlidir.

 6. Örnek korelasyonu

Örnek korelasyonu, iki veri örneği arasındaki doğrusal bağımlılığın derecesini tanımlamak için de kullanılır, ancak değeri her zaman -1 ila 1 aralığındadır.

İki örneğin korelasyonunu hesaplamak için şu işlemleri gerçekleştirmeliyiz:

1. İlk örneğin varyansını hesaplayın.
2. İkinci örneğin varyansını hesaplayın.
3. Bu örneklerin kovaryansını hesaplayın.
4. Kovaryansı, varyansların çarpımının kareköküne bölün.

Formül: 

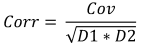
Burada: 

• Corr, örnek korelasyonudur,
• Cov, örnek kovaryansıdır,
• D1, ilk örnek için örnek varyansıdır, 
• D2, ikinci örneğin örnek varyansıdır,  

Verilen boy ve ağırlık verileri için korelasyon 0,579098'e eşit olacaktır.

İstatistik Alım Satımda Nasıl Kullanılır?

Alım satımda istatistiksel parametrelerin kullanımını gösteren en basit örnek MovingAverage göstergesidir. Hesaplanması, belirli bir zaman dilimi boyunca veri gerektirir ve fiyatın aritmetik ortalama değerini verir:

 

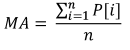
Burada: 

• MA, gösterge değeridir,
• P[i], fiyattır,
• n, MA ölçüm dönemidir

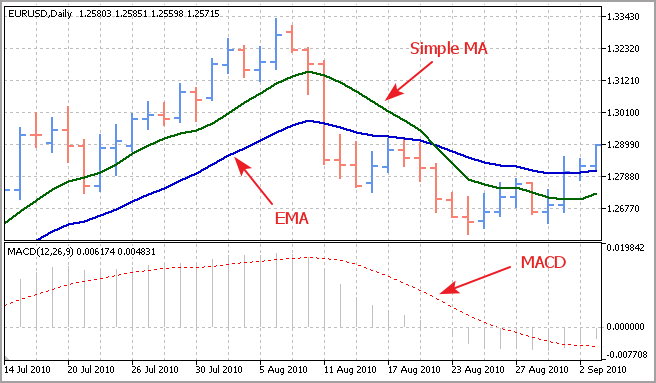
Göstergenin, örnek ortalamasının tam bir analogu olduğunu görebiliriz. Basitliğine rağmen, bu gösterge, trend gücünü ve yönünü belirlemek için klasik bir araç olan MACD göstergesi için gerekli olan temel bir unsur olan üstel hareketli ortalama (EMA) hesaplanırken kullanılır.

 

MQL5'teki istatistikler

Yukarıda açıklanan temel istatistiksel parametrelerin MQL5 uygulamasına bakacağız. Yukarıda incelenen istatistiksel yöntemler (ve çok daha fazlası), statistics.mqh istatistiksel işlev kitaplığında uygulanır. Bunların kodlarını inceleyelim.

1. Örnek ortalaması

 Örnek ortalamasını hesaplayan kitaplık işlevine Ortalama adı verilir:

Giriş verileri: Veri örneği. Çıkış verileri: Ortalama.

2. Örnek varyansı

Örnek varyansını hesaplayan kitaplık işlevine Varyans adı verilir:

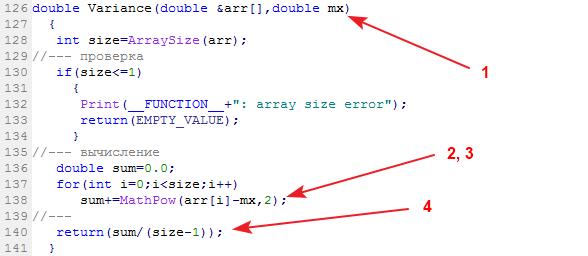
 Giriş verileri: Veri örneği ve ortalaması. Çıkış verileri: Varyans.

3. Örnek çarpıklığı

Örnek çarpıklığını hesaplayan kitaplık işlevine Asimetri adı verilir:

 

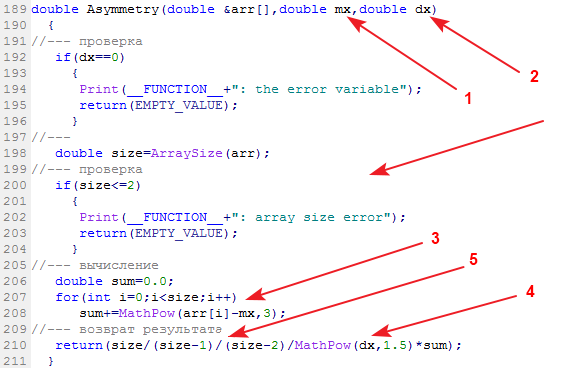
 Giriş verileri: Veri örneği, ortalaması ve varyansı. Çıkış verileri: Çarpıklık.

4. Örnek basıklığı

Örnek basıklığını hesaplayan kitaplık işlevine Excess (Excess2) adı verilir:

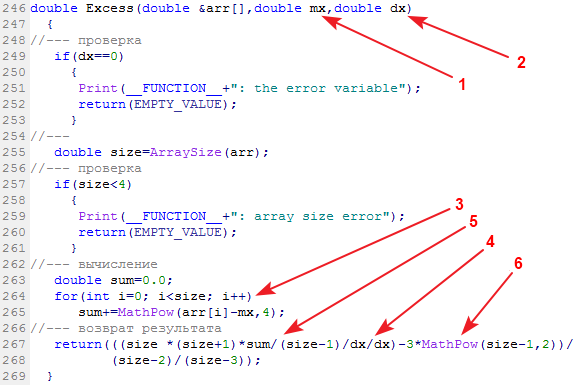
Giriş verileri: Veri örneği, ortalaması ve varyansı. Çıkış verileri: Basıklık.

5. Örnek kovaryansı

Örnek kovaryansını hesaplayan kitaplık işlevine Cov adı verilir: 

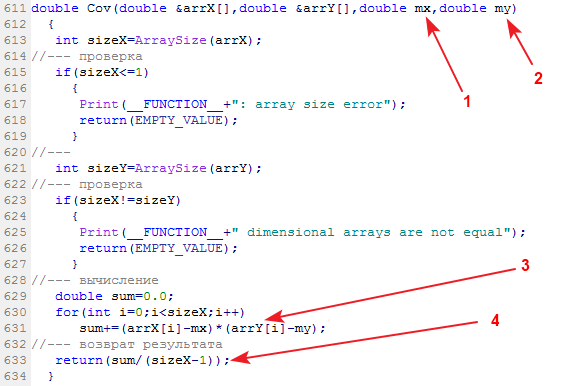
Giriş verileri: İki veri örneği ve bunların ilgili araçları. Çıkış verileri: Kovaryans.

6. Örnek korelasyonu

Örnek korelasyonunu hesaplayan kitaplık işlevine Corr adı verilir: 

 

Giriş verileri: İki örneğin kovaryansı, ilk örneğin varyansı ve ikinci örneğin varyansı. Çıkış verileri: Korelasyon.

Şimdi boy ve ağırlık örnek verilerini girelim ve kitaplığı kullanarak işleyelim.

#include <Statistics.mqh>
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//--- specify two data samples.
   double arrX[10]={173,162,194,181,186,159,173,178,168,171};
   double arrY[10]={65,70,83,60,105,58,69,90,78,65};
//--- calculate the mean
   double mx=Average(arrX);
   double my=Average(arrY);
//--- to calculate the variance, use the mean value
   double dx=Variance(arrX,mx);
   double dy=Variance(arrY,my);
//--- skewness and kurtosis values
   double as=Asymmetry(arrX,mx,dx);
   double exc=Excess(arrX,mx,dx);
//--- covariance and correlation values
   double cov=Cov(arrX,arrY,mx,my);
   double corr=Corr(cov,dx,dy);
//--- print results in the log file
   PrintFormat("mx=%.6e",mx);
   PrintFormat("dx=%.6e",dx);
   PrintFormat("as=%.6e",as);
   PrintFormat("exc=%.6e",exc);
   PrintFormat("cov=%.6e",cov);
   PrintFormat("corr=%.6e",corr);
  }

Script dosyasını yürüttükten sonra, terminal aşağıdaki gibi sonuçlar üretecektir:

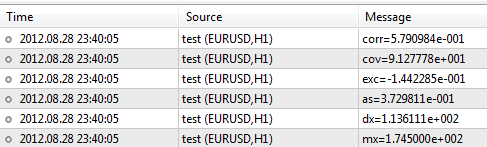
Kitaplık, açıklamaları Kod Tabanı'nda - https://www.mql5.com/tr/code/866 bulunabilecek çok daha fazla işlev içerir.

Sonuç

"Olasılık Teorisi ve İstatistik" bölümünün sonunda bazı sonuçlara halihazırda varılmıştı. Yukarıdakilere ek olarak, diğer bilim dalları gibi istatistiğin de ABC'sinden başlayarak incelenmesi gerektiğini belirtmekte fayda var. Temel öğeleri dahi, günün sonunda yatırımcının işinde fazlasıyla gerekli olabilecek çok sayıda karmaşık unsurun, mekanizmanın ve modelin anlaşılmasını kolaylaştırabilir.