Fondamentaux de la statistique

Introduction

Qu'est-ce que les statistiques ? Voici la définition trouvée sur Wikipédia : « La statistique est l'étude de la collecte, de l'organisation, de l'analyse, de l'interprétation et de la présentation des données ». (Statistique). Cette définition suggère trois composantes principales des statistiques : la collecte de données, la mesure et l'analyse. L'analyse des données semble être d'autant plus utile pour un trader que les informations reçues sont fournies par le courtier ou via un terminal de trading et sont déjà mesurées.

Les traders modernes utilisent (principalement) l'analyse technique pour décider d'acheter ou de vendre. Ils traitent des statistiques dans pratiquement tout ce qu'ils font lorsqu'ils utilisent un certain indicateur ou essaient de prédire le niveau des prix pour la période à venir. En effet, un graphique de fluctuation des prix représente en lui-même certaines statistiques d'une action ou d'une devise dans le temps. Il est donc très important de comprendre les principes de base des statistiques qui sous-tendent la majorité des mécanismes qui facilitent le processus de prise de décision d'un trader.

Théorie des probabilités et statistiques

Toute statistique est le résultat d'un changement dans les états de l'objet qui la génère. Considérons un graphique des prix EURUSD sur des périodes horaires :

 

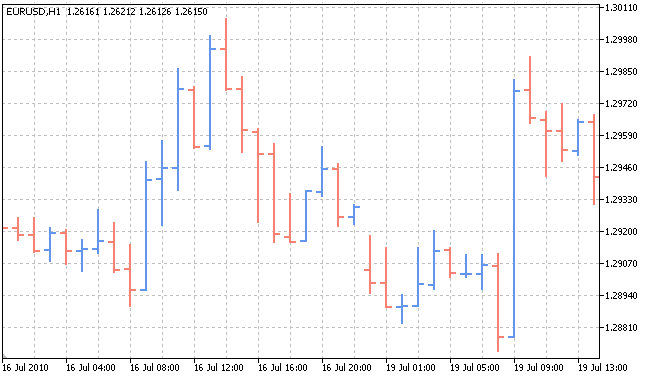
Dans ce cas, l'objet est la corrélation entre deux devises, tandis que les statistiques sont leurs prix à chaque instant. Comment la corrélation entre deux devises affecte-t-elle leurs prix ? Pourquoi avons-nous ce graphique de prix et pas un autre à l'intervalle de temps donné ? Pourquoi les prix sont-ils actuellement en baisse et non en hausse ? La réponse à ces questions est le mot « probabilité ». Chaque objet, selon la probabilité, peut prendre l'une ou l'autre valeur.

Faisons une expérience simple : prenez une pièce et lancez-la un certain nombre de fois, en notant à chaque fois le résultat du lancer. Supposons que nous ayons une pièce équilibrée. Le tableau peut alors être le suivant :

Résultat	Probabilité
Faces	0,5
Piles	0,5

Le tableau suggère que la pièce a autant de chances de tomber sur pile que sur face. Tout autre résultat n'est pas possible ici (l'atterrissage sur la tranche de la pièce a été exclu a priori) car la somme des probabilités de tous les événements possibles est égale à un.

Lancez la pièce 10 fois. Examinons maintenant les résultats du lancer :

Résultat	Nombre
Faces	8
Piles	2

Pourquoi avons-nous ces résultats si la pièce a autant de chances de tomber sur l'un ou l'autre des côtés ? La probabilité que la pièce tombe sur l'un ou l'autre des côtés est en effet égale, ce qui ne signifie pas pour autant qu'après quelques lancers, la pièce tombera sur un côté autant de fois que sur l'autre. La probabilité montre seulement que lors de cette tentative particulière (lancer), la pièce tombera soit sur pile, soit sur face, les deux événements ayant des chances égales.

Jouons maintenant 100 fois à pile ou face. Nous obtenons le nouveau tableau des résultats :

Résultat	Nombre
Faces	53
Piles	47

Comme on peut le voir, les nombres de résultats ne sont pas égaux. Cependant, 53 à 47 est le résultat qui prouve les hypothèses de probabilité initiales. La pièce a atterri sur face en presque autant de fois qu'elle est tombée sur pile.

Faisons maintenant la même chose dans l'ordre inverse. Supposons que nous ayons une pièce de monnaie mais que la probabilité qu'elle tombe sur ses côtés soit inconnue. Nous devons déterminer s'il s'agit d'une pièce équilibrée, c'est-à-dire d'une pièce qui a autant de chances de tomber sur pile que sur face.

Reprenons les données de la première expérience. Divisez le nombre de résultats par côté par le nombre total de résultats. Nous obtenons les probabilités suivantes :

Résultat	Probabilité
Faces	0,8
Piles	0,2

Nous pouvons voir qu'il est très difficile de conclure de la première expérience que la pièce est équilibrée. Faisons de même pour la deuxième expérience :

Résultat	Nombre
Faces	0,53
Piles	0,47

Avec ces résultats en main, nous pouvons dire avec un degré élevé de précision que cette pièce est équilibrée.

Cet exemple simple nous permet de tirer une conclusion importante : plus le nombre d'expériences est important, plus les propriétés de l'objet sont reflétées avec précision par les statistiques générées par l'objet.

Ainsi, les statistiques et les probabilités sont inextricablement liées. Les statistiques représentent les résultats expérimentaux avec un objet et dépendent directement de la probabilité des états de l'objet. Inversement, la probabilité des états de l'objet peut être estimée à l'aide de statistiques. C'est là que réside le principal défi pour un trader : disposer de données sur les transactions sur une certaine période (statistiques), prédire le comportement des prix pour la période suivante (probabilité) et, sur la base de ces informations, prendre une décision d'achat ou de vente.

Par conséquent, pour revenir aux points soulevés dans l'introduction, il est également important de connaître et de comprendre la relation entre les statistiques et les probabilités, ainsi que d'avoir des connaissances sur l'évaluation des risques et les situations à risque. Ces deux derniers points n'entrent toutefois pas dans le cadre de cet article.

Paramètres statistiques de base 

Passons maintenant en revue les paramètres statistiques de base. Supposons que nous disposions de données sur la taille en cm de 10 personnes d'un groupe :

	1	2	3	4	5	6	7	8	9	10
Hauteur	173	162	194	181	186	159	173	178	168	171

 

Les données présentées dans le tableau sont appelées échantillon, tandis que la quantité de données correspond à la taille de l'échantillon. Nous allons examiner certains paramètres de l'échantillon donné. Tous les paramètres seront des paramètres d'échantillon car ils résultent des données d'échantillon, plutôt que des données de variables aléatoires.

1. Moyenne de l'échantillon

La moyenne de l'échantillon est la valeur moyenne de l'échantillon. Dans notre cas, il s'agit de la taille moyenne des personnes du groupe.

Pour calculer la moyenne, il faut :

1. Additionnez toutes les valeurs de l'échantillon.
2. Diviser la valeur obtenue par la taille de l'échantillon. 

Formule : 

Où :

• M est la moyenne de l'échantillon,
• a[i] est l'élément échantillon,
• n est la taille de l'échantillon.

Suite aux calculs, on obtient la valeur moyenne de 174,5 cm

 

 

2. Variance de l'échantillon

La variance de l'échantillon décrit la distance entre les valeurs de l'échantillon et la moyenne de l'échantillon. Plus la valeur est élevée, plus les données sont dispersées.

Pour calculer la variance, il faut :

1. Calculer la moyenne de l'échantillon.
2. Soustrayez la moyenne de chaque élément de l'échantillon et mettez la différence au carré.
3. Additionnez les valeurs obtenues ci-dessus.
4. Divisez la somme par la taille de l'échantillon moins 1.

Formule :  

 

Où : 

• D est la variance de l'échantillon,
• M est la moyenne de l'échantillon,
• a[i] est l'élément échantillon,
• n est la taille de l'échantillon.

La variance de l'échantillon dans notre cas est de 113,611.

 

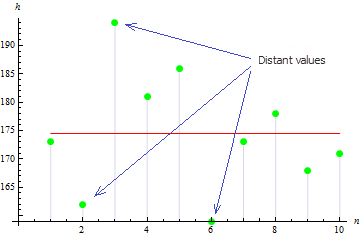
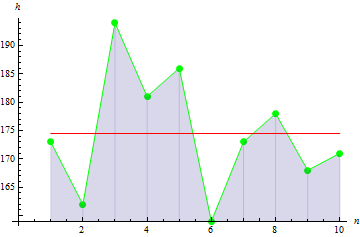
La figure suggère que 3 valeurs sont très éloignées de la moyenne, ce qui conduit à une grande valeur de variance.

3. Asymétrie de l'échantillon

L'asymétrie de l'échantillon est utilisée pour décrire le degré d'asymétrie des valeurs de l'échantillon autour de sa moyenne. Plus la valeur de l'asymétrie est proche de zéro, plus les valeurs de l'échantillon sont symétriques.

Pour calculer l'asymétrie, il faut :

1. Calculer la moyenne de l'échantillon.
2. Calculer la variance de l'échantillon.
3. Additionnez les différences au cube de chaque élément de l'échantillon et la moyenne.
4. Divisez la réponse par la valeur de la variance élevée à la puissance 2/3.
5. Multipliez la réponse par le coefficient égal à la taille de l'échantillon divisé par le produit de la taille de l'échantillon moins 1 et de la taille de l'échantillon moins 2.

Formule :  

Où : 

• A est l'asymétrie de l'échantillon, 
• D est la variance de l'échantillon,
• M est la moyenne de l'échantillon,
• a[i] est l'élément échantillon,
• n est la taille de l'échantillon.

Nous obtenons une valeur d'asymétrie assez faible pour cet échantillon : 0,372981. Cela est dû au fait que des valeurs divergentes se compensent.

 

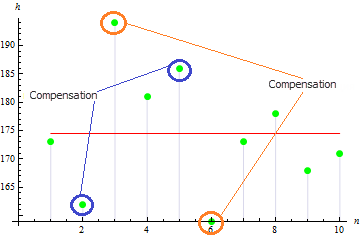
La valeur sera plus grande pour un échantillon asymétrique. Par exemple, la valeur des données ci-dessous sera de 1,384651.

 

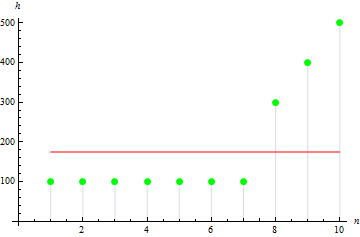
4. Exemple d'aplatissement

L'aplatissement de l'échantillon décrit le pic de l'échantillon.

Pour calculer l'aplatissement, nous devrions :

1. Calculer la moyenne de l'échantillon.
2. Calculer la variance de l'échantillon.
3. Additionnez les différences de quatrième puissance de chaque élément de l'échantillon et de la moyenne.
4. Divisez la réponse par la variance au carré.
5. Multipliez la valeur résultante par le coefficient égal au produit de la taille de l'échantillon et de la taille de l'échantillon plus 1, divisé par le produit de la taille de l'échantillon moins 1, de la taille de l'échantillon moins 2 et de la taille de l'échantillon moins 3.
6. Soustraire de la valeur résultante le produit de 3 et la différence au carré de la taille de l'échantillon et 1, divisé par le produit de la taille de l'échantillon moins 1 et de la taille de l'échantillon moins 2.

Formule :  

Où : 

• E est l'aplatissement de l'échantillon,
• D est la variance de l'échantillon,
• M est la moyenne de l'échantillon,
• a[i] est l'élément échantillon,
• n est la taille de l'échantillon.

Pour les données de hauteur données, nous obtenons la valeur de -0,1442285.

Pour un pic de données plus net, on obtient une valeur plus grande : 10.

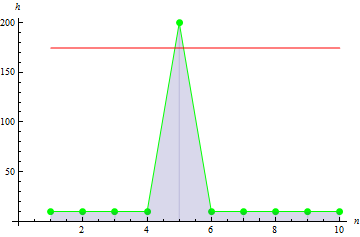
5. Exemple de covariance

La covariance d'échantillon est une mesure indiquant le degré de dépendance linéaire entre deux échantillons de données. La covariance entre les données linéairement indépendantes sera de 0.

Pour illustrer ce paramètre, nous allons ajouter des données de poids pour chacune des 10 personnes :

	1	2	3	4	5	6	7	8	9	10
Poids	65	70	83	60	105	58	69	90	78	65

 

Pour calculer la covariance de deux échantillons, il faut :

1. Calculer la moyenne du premier échantillon.
2. Calculer la moyenne du deuxième échantillon.
3. Additionnez tous les produits de deux différences : la première différence - un élément du premier échantillon moins la moyenne du premier échantillon ; la deuxième différence - un élément du deuxième échantillon (correspondant à l'élément du premier échantillon) moins la moyenne du deuxième échantillon.
4. Divisez la réponse par la taille de l'échantillon moins 1.

Formule :  

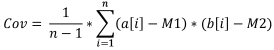
Où : 

• Cov est la covariance de l'échantillon,
• a[i] est l'élément du premier échantillon,
• b[i] est l'élément du deuxième échantillon, 
• M1 est la moyenne d'échantillon du premier échantillon, 
• M2 est la moyenne de l'échantillon du deuxième échantillon, 
• n est la taille de l'échantillon. 

Calculons la valeur de covariance des deux échantillons : 91,2778. La dépendance existante peut être montrée dans le graphique combiné :

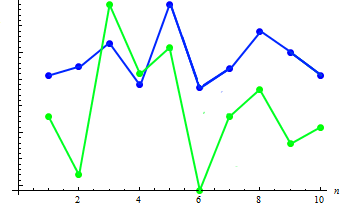
Comme on peut le voir, l'augmentation de la taille (en règle générale) correspond à la diminution du poids et vice versa.

 6. Corrélation de l'échantillon

La corrélation entre échantillons est également utilisée pour décrire le degré de dépendance linéaire entre deux échantillons de données, mais sa valeur est toujours comprise entre -1 et 1.

Pour calculer la corrélation de deux échantillons, il faut :

1. Calculer la variance du premier échantillon.
2. Calculer la variance du deuxième échantillon.
3. Calculer la covariance de ces échantillons.
4. Divisez la covariance par la racine carrée du produit des variances.

Formule : 

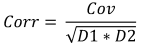
Où : 

• Corr est la corrélation de l'échantillon,
• Cov est la covariance de l'échantillon,
• D1 est la variance d'échantillon du premier échantillon, 
• D2 est la variance d'échantillon du deuxième échantillon,  

Pour les données de taille et de poids données, la corrélation sera égale à 0,579098.

Comment utiliser les statistiques dans le trading

L'exemple le plus simple illustrant l'utilisation de paramètres statistiques dans le trading est l'indicateur MovingAverage. Son calcul nécessite des données sur une certaine période de temps et donne la valeur moyenne arithmétique du prix :

 

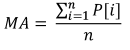
Où : 

• MA est la valeur de l'indicateur,
• P[i] est le prix,
• n est la période de mesure MA

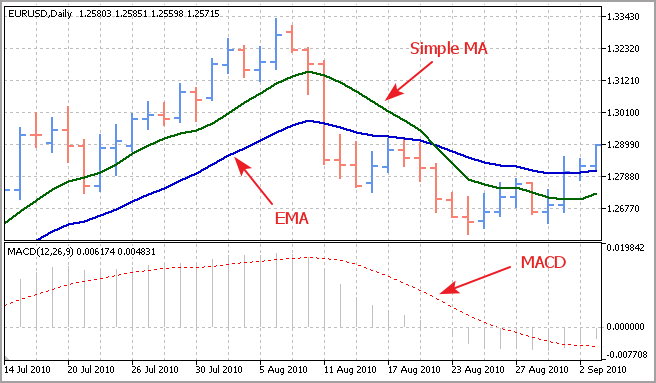
Nous pouvons voir que l'indicateur est un analogue complet de la moyenne de l'échantillon. Malgré sa simplicité, cet indicateur est utilisé lors du calcul de l'EMA, la moyenne mobile exponentielle qui, à son tour, est un élément de base requis pour l'indicateur MACD - un outil classique pour déterminer la force et la direction de la tendance.

 

Statistiques en MQL5

Nous allons examiner la mise en œuvre MQL5 des paramètres statistiques de base décrits ci-dessus. Les méthodes statistiques examinées ci-dessus (et bien d'autres encore) sont mises en œuvre dans la bibliothèque de fonctions statistiques statistics.mqh. Passons en revue leurs codes.

1. Moyenne de l'échantillon

 La fonction de bibliothèque calculant la moyenne de l'échantillon est appelée Moyenne :

Données d'entrée : échantillon de données. Données de sortie : moyenne.

2. Variance de l'échantillon

La fonction de bibliothèque calculant la variance de l'échantillon est appelée Variance :

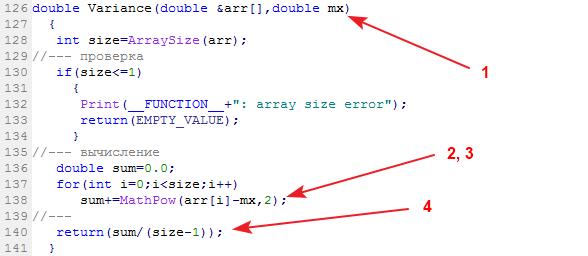
 Données d'entrée : échantillon de données et sa moyenne. Données de sortie : variance.

3. Asymétrie de l'échantillon

La fonction de bibliothèque calculant l'asymétrie de l'échantillon est appelée Asymétrie :

 

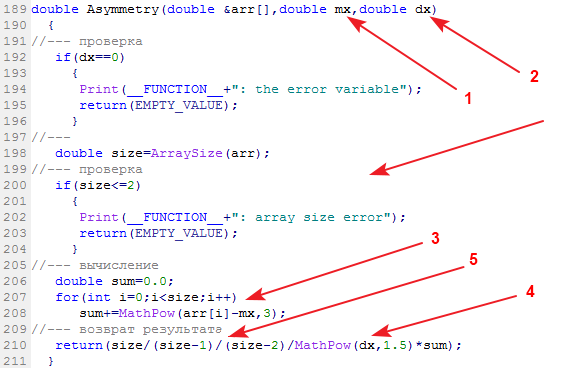
 Données d'entrée : échantillon de données, sa moyenne et sa variance. Données de sortie : asymétrie.

4. Exemple d'aplatissement

La fonction de bibliothèque calculant l'aplatissement de l'échantillon s'appelle Excess (Excess2) :

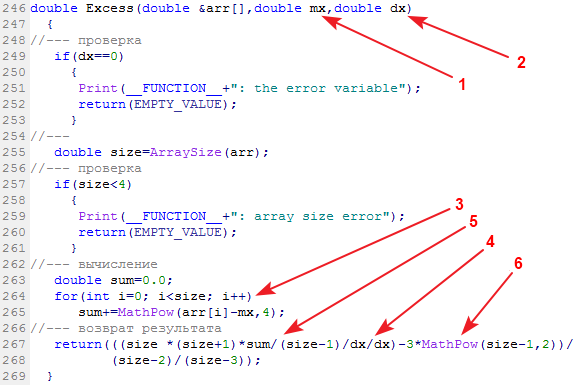
Données d'entrée : échantillon de données, sa moyenne et sa variance. Données de sortie : aplatissement.

5. Exemple de covariance

La fonction de bibliothèque calculant la covariance de l'échantillon s'appelle Cov : 

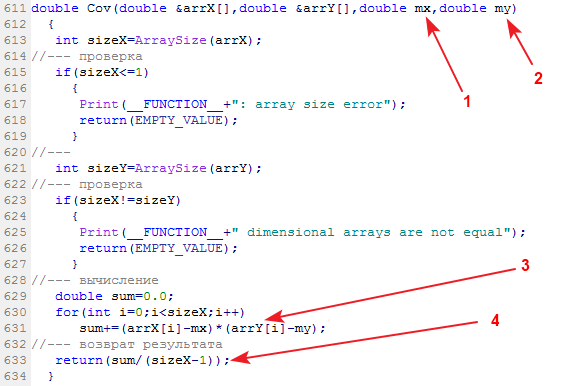
Données d'entrée : deux échantillons de données et leurs moyennes respectives. Données de sortie : covariance.

6. Corrélation de l'échantillon

La fonction de bibliothèque calculant la corrélation de l'échantillon s'appelle Corr : 

 

Données d'entrée : covariance de deux échantillons, variance du premier échantillon et variance du deuxième échantillon. Données de sortie : corrélation.

Entrons maintenant les données d'échantillon de taille et de poids et traitons-les à l'aide de la bibliothèque.

#include <Statistics.mqh>
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//--- specify two data samples.
   double arrX[10]={173,162,194,181,186,159,173,178,168,171};
   double arrY[10]={65,70,83,60,105,58,69,90,78,65};
//--- calculate the mean
   double mx=Average(arrX);
   double my=Average(arrY);
//--- to calculate the variance, use the mean value
   double dx=Variance(arrX,mx);
   double dy=Variance(arrY,my);
//--- skewness and kurtosis values
   double as=Asymmetry(arrX,mx,dx);
   double exc=Excess(arrX,mx,dx);
//--- covariance and correlation values
   double cov=Cov(arrX,arrY,mx,my);
   double corr=Corr(cov,dx,dy);
//--- print results in the log file
   PrintFormat("mx=%.6e",mx);
   PrintFormat("dx=%.6e",dx);
   PrintFormat("as=%.6e",as);
   PrintFormat("exc=%.6e",exc);
   PrintFormat("cov=%.6e",cov);
   PrintFormat("corr=%.6e",corr);
  }

Après avoir exécuté le script, le terminal produira les résultats suivants :

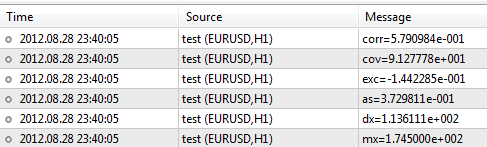
La bibliothèque contient beaucoup plus de fonctions dont les descriptions peuvent être trouvées dans CodeBase - https://www.mql5.com/fr/code/866.

Conclusion

Certaines conclusions ont déjà été tirées à la fin de la section « Théorie des probabilités et statistiques ». En plus de ce qui précède, il convient de mentionner que la statistique, comme toute autre branche de la science, doit être étudiée en commençant par sa base. Même ses éléments de base peuvent faciliter la compréhension d'un grand nombre de choses, de mécanismes et de modèles complexes qui, en fin de compte, peuvent être extrêmement nécessaires dans le travail d'un trader.