
统计学基础
简介
什么是统计学?以下是在维基百科中找到的定义:“统计学是对数据的采集、组织、分析、解释和表达进行的研究。”(统计学)。此定义提出了统计学的三个主要部分:数据采集、衡量和分析。数据分析对交易者而言尤其有用,因为收到的信息是经纪人提供的,或通过交易客户端得到的,已经经过衡量。
现代交易者(最)常用技术分析来决定是买还是卖。当使用某个指标或试图预测将来的价格水平时,他们几乎在一切事情中都应用统计学。事实上,价格波动图本身代表了股票或货币在时间上的某种统计。因此,理解促进交易者决策过程的主要机制下统计学的基本原则非常重要。
概率论和统计学
任何统计都是生成统计的对象的状态改变的结果。让我们讨论以小时为单位的时间框架中欧元兑美元 (EURUSD) 的价格图:
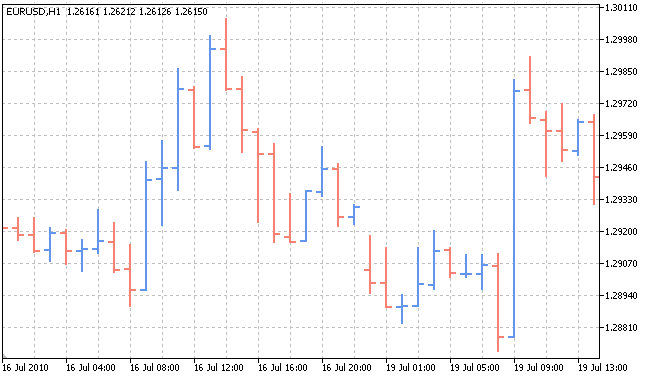
在这个例子中,对象是两种货币之间的关系,而统计是这两种货币在每一时间点的价格。两种货币之间的相关性如何影响它们的价格?为什么我们在给定的时间区间得到此价格图而不是另外的价格图?为什么价格当前是下跌的而不是上涨的?这些问题的答案是“概率”这一词。视概率而定,每一个对象能够取这个值,也能够取另一个值。
让我们进行一个简单的实验:拿一枚硬币,并且掷硬币若干次,每次都记录其正反面结果。假定我们有一枚公平的硬币。则结果可能如下表所示:
| 结果 | 概率 |
|---|---|
| 正面 | 0.5 |
| 反面 | 0.5 |
该表显示硬币出现正反面的可能性相同。在这里不可能出现其他结果(首先排除硬币直立的情况),因为所有可能的结果的概率之和应等于 1。
掷硬币 10 次。现在,让我们看一看掷硬币的结果:
| 结果 | 次数 |
|---|---|
| 正面 | 8 |
| 反面 | 2 |
为什么硬币出现正反面的可能性相同?硬币出现正反面的可能性确实相同,然而这并不意味着在掷过几次硬币之后,硬币出现正面的次数与出现反面的次数相同。概率仅说明在此具体尝试(掷硬币)中,硬币有可能出现正面,也有可能出现反面,并且正反面的机会相等。
让我们掷硬币 100 次。我们得到新的结果表:
| 结果 | 次数 |
|---|---|
| 正面 | 53 |
| 反面 | 47 |
如您所见,正反面的次数并不相等。然而,53 比 47 的结果证明了初始的概率假设。硬币出现正面的次数与出现反面的次数几乎相等。
现在,让我们以相反的顺序进行同样的实验。假定我们有一枚硬币,但是不知道其出现正面和反面的概率。我们需要确定它是否是一枚公平的硬币,即硬币出现正面的可能性与出现反面的可能性相同。
让我们采用首个实验中的数据。将每面的次数除以总次数。我们得到以下概率:
| 结果 | 概率 |
|---|---|
| 正面 | 0.8 |
| 反面 | 0.2 |
我们可以看到,从第一个实验得出硬币是公平的这一结论很难。现在,让我们对第二个实验进行相同的操作:
| 结果 | 次数 |
|---|---|
| 正面 | 0.53 |
| 反面 | 0.47 |
得到这些结果之后,我们可以非常准确地说硬币是一枚公平硬币。
这个简单的例子让我们能够得出一个重要的结论:实验次数越多,对象生成的统计所反映的对象特性就越准确。
因此,统计学和概率不可避免地交缠在一起。统计是对象的实验结果,并且直接取决于对象状态的概率。反过来说,可以使用统计估计对象状态的概率。交易者面临的主要挑战在于:拥有某个时间段内的交易数据(统计)、预测后续时间段的价格行为(概率)以及基于此信息做出买入或卖出的决定。
因此,回到在简介中指出的重点,知道并理解统计学和概率之间的关系,以及具有风险评估和风险状况的相关知识也非常重要。但是,后两者不在本文的讨论范围之内。
基本统计参数
现在,让我们回顾一下基本的统计参数。假定我们拥有一组中 10 个人的身高数据,以厘米为单位:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 身高 | 173 | 162 | 194 | 181 | 186 | 159 | 173 | 178 | 168 | 171 |
此表列出的数据称为样本,而数据数量称为样本大小。我们将看一看给定样本的某些参数。所有参数都是样本参数,因为它们是从样本数据得出的结果,而不是从随机变量数据。
1. 样本平均值
样本平均值指样本中的平均值。在我们的例子中,它是该组中人的平均身高。
要计算平均值,我们应:
- 求所有样本值之和。
- 将得到的值除以样本数量。
公式:
![]()
其中:
- M 是样本平均值,
- a[i] 是样本元素,
- n 是样本数量。
在计算之后,我们得到平均值 174.5 cm

2. 样本方差
样本方差描述样本值与样本平均值的偏离情况。值越大,则数据分布越广。
要计算方差,我们应:
- 计算样本平均值。
- 从每个样本元素减去平均值,并对差进行平方运算。
- 求上述结果之和。
- 将得到的值除以样本大小减 1 后的值。
公式:
![]()
其中:
- D 是样本方差,
- M 是样本平均值,
- a[i] 是样本元素,
- n 是样本数量。
在我们的例子中,样本方差为 113.611。
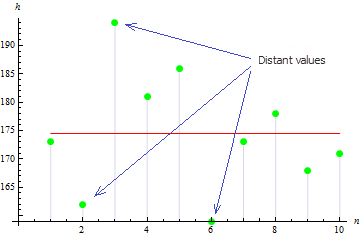
数字指出,3 个值离平均值较远,从而导致方差值较大。
3. 样本偏度
样本偏度用于描述样本值围绕其平均值的不对称度。偏度值越接近 0,则样本值越对称。
要计算偏度,我们应:
- 计算样本平均值。
- 计算样本方差。
- 求每个样本元素与平均值之差的立方和。
- 将得到的值除以方差值的 2/3 次幂。
- 将得到的值乘以样本数量,再除以样本数量减 1 后的值与样本数量减 2 后的值之积。
公式:
![]()
其中:
- A 是样本偏度,
- D 是样本方差,
- M 是样本平均值,
- a[i] 是样本元素,
- n 是样本数量。
对于这个例子,我们得到一个非常小的偏度值:0.372981. 这是发散的值相互补偿的结果。
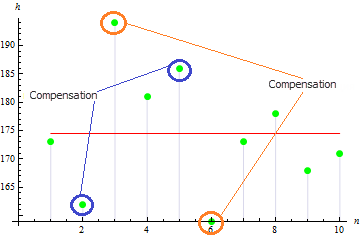
对于不对称的例子,这个值会较大,例如以下数据的偏度值为 1.384651。
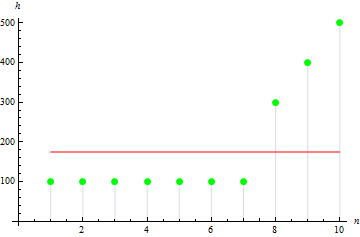
4. 样本峰度
样本峰度描述样本的峭度。
要计算峰度,我们应:
- 计算样本平均值。
- 计算样本方差。
- 求每个样本元素与平均值之差的四次方之和。
- 将得到的值除以方差的平方。
- 将得到的值乘以样本数量与样本数量加 1 后的值之积,再除以样本数量减 1 后的值与样本数量减 2 后的值及样本数量减 3 后的值之积。
- 求 3 与样本大小与 1 之差的平方之积,再除以样本数量减 1 后的值与样本数量减 2 后的值之差,再从上一步得到的值减去这个值。
公式:
![]()
其中:
- E 是样本峰度,
- D 是样本方差,
- M 是样本平均值,
- a[i] 是样本元素,
- n 是样本数量。
对于给定身高数据,我们得到的值为 -0.1442285。
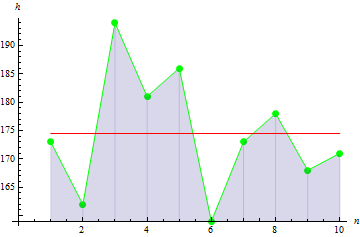
峰值数据越尖锐,我们得到的值越大: 10.
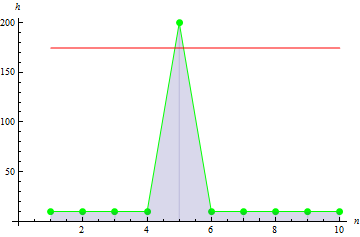
5. 样本协方差
样本协方差是两个数据样本之间的线性依存度的衡量。线性独立数据之间的协方差为 0。
为了说明这一参数,我们将添加 10 个人的体重数据:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 体重 | 65 | 70 | 83 | 60 | 105 | 58 | 69 | 90 | 78 | 65 |
要计算两个样本的协方差,我们应:
- 计算第一个样本的平均值。
- 计算第二个样本的平均值。
- 求所有两个差值之积的和:第一个差值 - 第一个样本的元素减去第一个样本的平均值;第二个差值 - 第二个样本的元素(对应于第一个样本的元素)减去第二个样本的平均值。
- 将得到的和除以样本数量减 1 后的值。
公式:
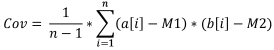
其中:
- Cov 是样本协方差,
- a[i] 是第一个样本的元素,
- b[i] 是第二个样本的元素,
- M1 是第一个样本的样本平均值,
- M2 是第二个样本的样本平均值,
- n 是样本数量。
让我们计算两个样本的协方差值:91.2778. 现有依存关系可显示在以下组合图中:
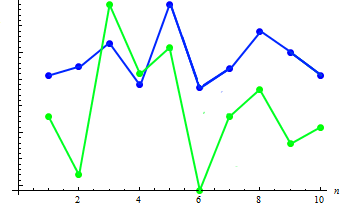
如图所示,身高的增加(通常)对应于体重的下降(反之亦然)。
6. 样本相关系数
样本相关系数也用于描述两个数据样本之间的线性依存度,但其值始终在 -1 至 1 的范围内。
要计算两个样本的相关系数,我们应:
- 计算第一个样本的方差。
- 计算第二个样本的方差。
- 计算这些样本的协方差。
- 将协方差除以两个方差之积的平方根。
公式:
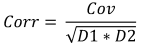
其中:
- Corr 是样本相关系数,
- Cov 是样本协方差,
- D1 是第一个样本的样本方差,
- D2 是第二个样本的样本方差,
对于给定的身高和体重数据,相关系数等于 0.579098。
如何在交易中应用统计学
说明在交易中使用统计参数的最简单的例子是移动平均线 (MovingAverage) 指标。其计算需要某个时间段内的数据并给出价格的算术平均值:
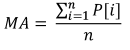
其中:
- MA 是指标值,
- P[i] 是价格,
- n 是 MA 衡量区间
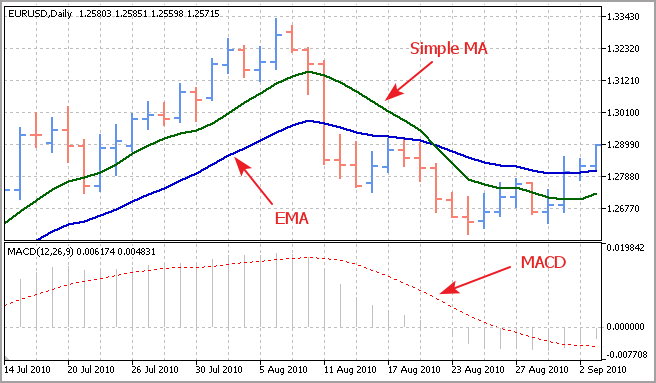
我们可以看到指标与样本平均值完全类似。尽管它很简单,这个指标在计算指数移动平均(EMA)时使用,并且是 MACD 指标需要的基本元素 - MACD 指标是一个用于确定趋势强度和方向的经典工具。
MQL5 中的统计
我们将讨论上述基本统计参数的 MQL5 实施。在统计函数库 statistics.mqh 中实施了上文讨论的统计方法(以及其他方法)。让我们回顾一下它们的代码。
1. 样本平均值
计算样本平均值的库函数称为 Average:

输入数据:数据样本。输出数据:平均值。
2. 样本方差
计算样本方差的库函数称为 Variance:
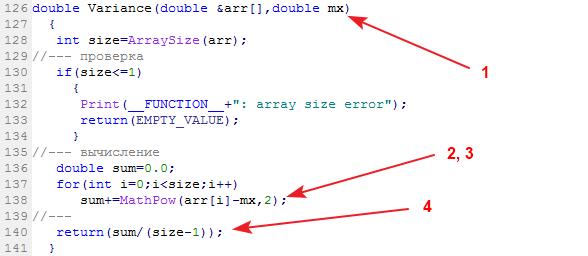
输入数据:数据样本及其平均值。输出数据:方差。
3. 样本偏度
计算样本偏度的库函数称为 Asymmetry:
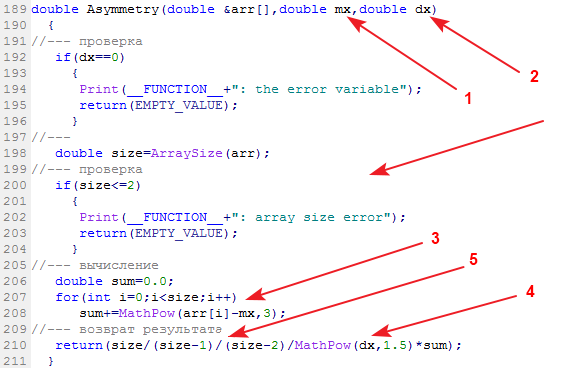
输入数据:数据样本、及平均值和方差。输出数据:偏度。
4. 样本峰度
计算样本峰度的库函数称为 Excess (Excess2):
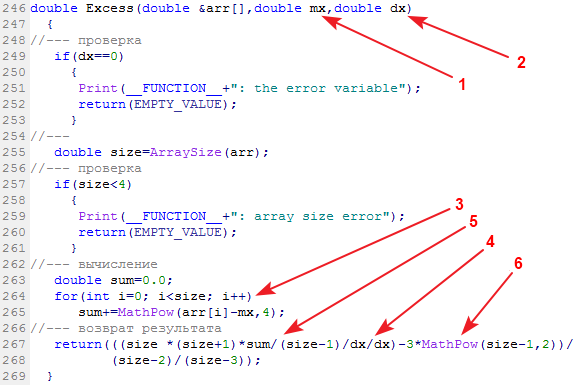
输入数据:数据样本、及平均值和方差。输出数据:峰度。
5. 样本协方差
计算样本协方差的库函数称为 Cov:
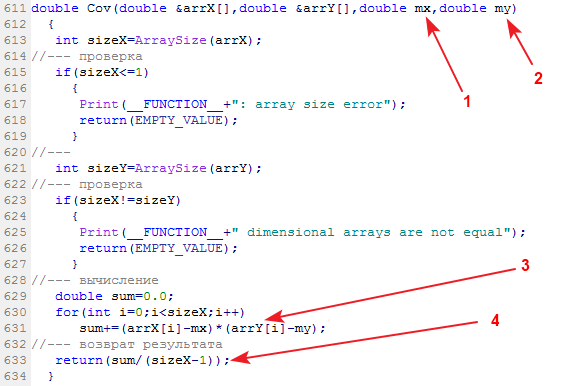
输入数据:两个数据样本及它们的相应平均值。输出数据:协方差。
6. 样本相关系数
计算样本相关系数的库函数称为 Corr:

输入数据:两个样本的协方差、第一个样本的方差和第二个样本的方差。输出数据:相关系数。
现在,让我们输入身高和体重样本数据并使用库函数进行处理。#include <Statistics.mqh> //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- specify two data samples. double arrX[10]={173,162,194,181,186,159,173,178,168,171}; double arrY[10]={65,70,83,60,105,58,69,90,78,65}; //--- calculate the mean double mx=Average(arrX); double my=Average(arrY); //--- to calculate the variance, use the mean value double dx=Variance(arrX,mx); double dy=Variance(arrY,my); //--- skewness and kurtosis values double as=Asymmetry(arrX,mx,dx); double exc=Excess(arrX,mx,dx); //--- covariance and correlation values double cov=Cov(arrX,arrY,mx,my); double corr=Corr(cov,dx,dy); //--- print results in the log file PrintFormat("mx=%.6e",mx); PrintFormat("dx=%.6e",dx); PrintFormat("as=%.6e",as); PrintFormat("exc=%.6e",exc); PrintFormat("cov=%.6e",cov); PrintFormat("corr=%.6e",corr); }
在执行脚本之后,客户端将生成以下结果:
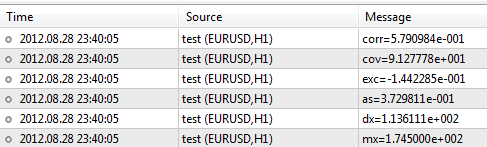
函数库包含很多函数,可以在代码库 - https://www.mql5.com/zh/code/866 中找到这些函数的说明。
总结
在“概率论和统计学”一节最后已经得出了某些结论。除了以上结论以外,值得指出,应如其他科学分支一样,从其基础开始研究统计学。即使其基础要素也有助于对大量复杂事物、机制和模式的理解,最终成为交易者的工作中必不可少的内容。
本文由MetaQuotes Ltd译自俄文
原文地址: https://www.mql5.com/ru/articles/387
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。
本文由网站的一位用户撰写,反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责,也不对因使用所述解决方案、策略或建议而产生的任何后果负责。
 MQL5.community 中的名人?
MQL5.community 中的名人?
 MQL5 编程基础:列表
MQL5 编程基础:列表
 MQL5-RPC来自 MQL5 的远程过程调用:针对乐趣及获利的网络服务访问及 XML-RPC 自动交易锦标赛分析程序
MQL5-RPC来自 MQL5 的远程过程调用:针对乐趣及获利的网络服务访问及 XML-RPC 自动交易锦标赛分析程序
应该有很多算法来确定 mod,所以通用自行车在这里没有用。
您应该多看看例子,看看您想得到什么,不想得到什么。
我喜欢这篇文章。
文章通俗易懂,包含足够的信息。
而且,从标题来看,这篇文章并没有故弄玄虚。
我看不出这篇文章有什么用。电视上的一些陈词滥调。如果这篇文章不是刊登在一个半商人的专业网站上,我还可以保持沉默。但考虑到这个网站,我想指出以下几点。
有一门测量、分析和预测经济数据的科学。这就是计量经济学。它与统计学有着血缘关系,但也有显著区别。
1.对于交易者来说,如果预测不能从分析中得出,那么分析本身就没有价值。这篇文章完全没有提到预测。
2.计量经济学最初是从经济序列的非平稳性出发的。如果人们至少能记住它,把它牢记在心,那么关于基本统计学的故事就不会那么美好了:对于非平稳序列,在应用摩、方差等基本概念时会有很多保留。无论如何,我们都应该心存疑虑。例如,对于非平稳序列,均值并不一定会趋近于 mo。我说的根本不是相关性。
3. 计量经济学基于非常短的样本--几十个观测值。它对多年的平均值不感兴趣,因为这样的平均值也意味着几年来一直处于一种姿势。在危机中,对 计算结果的估算 变得非常重要。正是估算结果从根本上区分了电视与统计,尤其是计量经济学。
学校文章。专门学校的水平,甚至不是学院的初级课程。
"从这个简单的例子中,我们可以得出一个重要的结论:随着试验次数的增加,统计数据可以更准确地反映产生试验的对象的属性。
对于静止过程(真空中的球形马)来说--是的。
对于真实数据的时间序列来说,这种说法更像是无稽之谈。
如果外汇是静止的时间序列--就不需要 MQL5 来估计它--杂货店里的简单木刷就足够了。
如果以混乱的顺序和时间间隔在飞蛾身上钻孔,
,那么整个期间的统计数据将更像是 RosStat 报告 - 或疯子的呓语。
"这就是交易者的主要任务:了解 某段时间的交易数据(统计数据),预测 下一段时间的价格行为(比率)(获得概率),并据此做出买入或卖出的决定"。
另一种说法在含义上与无稽之谈相去不远。要预测某种事物,首先要证明该序列不是随机的,是可以预测的。随机序列是可以有收入的。它们无法预测,但你可以从中获益。概率不对称和正/负期望。
。