Discusión sobre el artículo "Entrenamos un perceptrón multicapa usando el algoritmo de Levenberg-Marquardt"
Gracias por el interesante artículo.
Es una pena que haya pocas explicaciones sobre los códigos.
Y algo falla en el código python, he instalado todas las librerías, pero da lo siguiente en la terminal:
learning time = 1228.5106182098389
solver = lbfgs
loss = 0.0024399556870102
iter = 300
C:\Users\User\AppData\Local\Programs\Python\Python39\lib\site-packages\sklearn\neural_network\_multilayer_perceptron.py:545: ConvergenceWarning: lbfgs failed to converge (status=1): in '' (0,0)
STOP: TOTAL NO. of ITERATIONS REACHED LIMIT. in '' (0,0)
Increase the number of iterations (max_iter) or scale the data as shown in: in '' (0,0)
https://scikit-learn.org/stable/modules/preprocessing.html in '' (0,0)
self.n_iter_ = _check_optimize_result("lbfgs", opt_res, self.max_iter) in '' (0,0)
Traceback (most recent call last): in '' (0,0)
plt.plot(np.log(pd.DataFrame(clf.loss_curve_))) in 'SklearnMLP.py' (59,0)
AttributeError: 'MLPRegressor' object has no attribute 'loss_curve_' in 'SklearnMLP.py' (59,0)
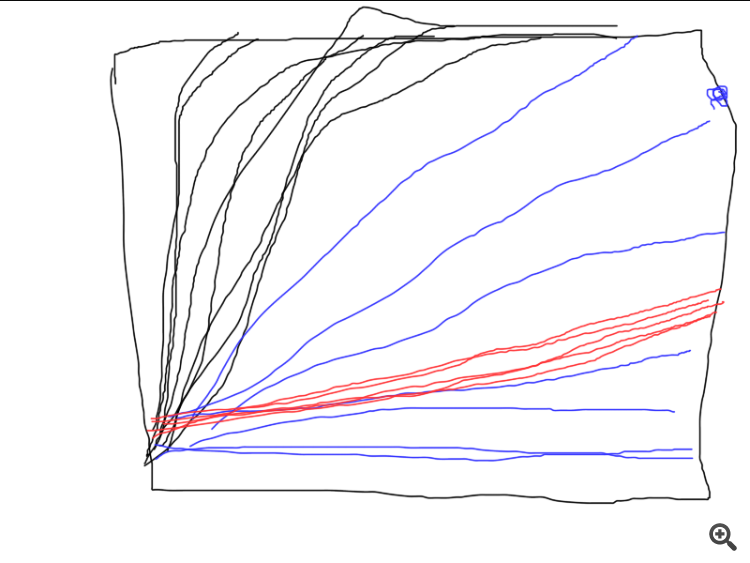
Una cosa más, el script SD en algunos casos dibuja tal cosa:
Es decir, el algo se atasca en, aparentemente, una simple fecha.
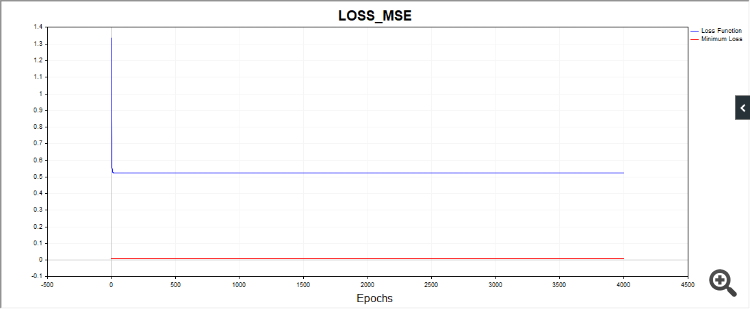
Otros códigos también producen resultados de convergencia muy diferentes. Por lo tanto, es deseable dar gráficos de una serie de pruebas independientes, las imágenes de pruebas únicas nos dicen poco (prácticamente nada).
Gracias por los comentarios.
En python. No es un error, avisa de que el algoritmo se ha parado porque hemos llegado al límite de iteración. Es decir, el algoritmo se ha parado antes de alcanzar el valor tol = 0.000001. Y luego avisa de que el optimizador lbfgs no tiene atributo "loss_curve", es decir, datos de la función de pérdida. Para adam y sgd sí, pero para lbfgs por alguna razón no. Probablemente debería haber hecho un script para que cuando se inicie lbfgs no pida esta propiedad para no confundir a la gente.
Sobre SD. Dado que empezamos cada vez desde diferentes puntos en el espacio de parámetros, los caminos a la solución también serán diferentes. He hecho muchas pruebas, a veces realmente se necesitan más iteraciones para converger. He intentado dar un número medio de iteraciones. Puede aumentar el número de iteraciones y verá que el algoritmo converge al final.
En SD. Como empezamos cada vez desde un punto diferente en el espacio de parámetros, los caminos para converger a una solución también serán diferentes. He hecho muchas pruebas, a veces realmente toma más iteraciones para converger. He intentado dar un número medio de iteraciones. Puede aumentar el número de iteraciones y verá que el algoritmo converge al final.
A eso me refiero. Es la robustez, o, la reproducibilidad de los resultados. Cuanto mayor sea la dispersión de los resultados, más cerca estará el algoritmo de RND para un problema dado.
He aquí un ejemplo de cómo funcionan tres algoritmos diferentes. ¿Cuál es el mejor? A menos que realice una serie de pruebas independientes y calcule la media de los resultados (idealmente, calcule y compare la varianza de los resultados finales), es imposible comparar.
A eso me refiero. Es la estabilidad, o, la reproducibilidad de los resultados. Cuanto mayor sea la dispersión de los resultados, más cerca estará el algoritmo de RND para un problema determinado.
Aquí tienes un ejemplo de cómo funcionan tres algoritmos diferentes. ¿Cuál es el mejor? A menos que realice una serie de pruebas independientes y calcule la media de los resultados (idealmente, calcule y compare la varianza de los resultados finales), es imposible comparar.
A continuación, es necesario definir el criterio de evaluación.
No, en este caso no tienes que tomarte tantas molestias, pero si estás comparando diferentes métodos, podrías añadir un ciclo más (pruebas independientes) y trazar los gráficos de las pruebas individuales. Quedaría muy claro quién converge, lo estable que es y cuántas iteraciones tarda. Y así resultó ser "como la otra vez", cuando el resultado es genial, pero sólo una vez entre un millón.
De todos modos, gracias, el artículo me ha dado algunas ideas interesantes.
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso
Artículo publicado Entrenamos un perceptrón multicapa usando el algoritmo de Levenberg-Marquardt:
El objetivo de este artículo será ofrecer a los tráders en activo un algoritmo eficaz para entrenar redes neuronales, una variante del método de optimización newtoniano conocido como algoritmo de Levenberg-Marquardt. Se trata de uno de los algoritmos más rápidos para entrenar redes neuronales de propagación directa, al que solo puede plantar cara el algoritmo Broyden-Fletcher-Goldfarb-Shanno (L-BFGS).
Los métodos de optimización estocástica, como el descenso de gradiente estocástico (SGD) y Adam, resultan muy adecuados para el entrenamiento offline cuando la red neuronal se reentrena durante largos periodos de tiempo. Si un tráder que utiliza redes neuronales quiere que el modelo se adapte rápidamente a unas condiciones comerciales en cambio constante, necesitará reentrenar la red online en cada nueva barra, o tras un breve periodo de tiempo. En tal caso, los algoritmos que, además de información sobre el gradiente de la función de pérdida, también usan información adicional sobre las segundas derivadas parciales, lo cual permitirá encontrar el mínimo local de la función de pérdida en unas pocas épocas de entrenamiento.
De momento, que yo sepa, no existe ninguna implementación de acceso abierto del algoritmo Levenberg-Marquardt en MQL5. Así que ha llegado la hora de llenar este vacío, y también de repasar brevemente los algoritmos de optimización más conocidos y sencillos, como el descenso de gradiente, el descenso de gradiente con impulso y el descenso de gradiente estocástico. Al final del artículo, realizaremos algunas pruebas de rendimiento del algoritmo Levenberg-Marquardt y de algoritmos de la biblioteca de aprendizaje automático scikit-learn.
Autor: Evgeniy Chernish