Falacias, Parte 1: La gestión del dinero es secundario y no muy importante

Introducción

En este artículo discutiremos cuestiones muy simples que pueden ser con frecuencia muy engañosas: los gráficos del balance de una cuenta en el informe de pruebas. En los informes de las pruebas de estrategias de los principiantes podemos ver a menudo gráficos de balance/valor neto exponenciales y resultados multimillonarios al final del periodo de prueba. Dichos resultados suelen suscitar comentarios escépticos de escritores de asesores expertos experimentados que saben de dónde proceden estos exponentes e inmediatamente recomiendan mostrar los resultados en un lote fijo (normalmente 0,1).

Se asume que los resultados de la prueba con el lote fijo 0,1 reflejan mejor todas las ventajas y desventajas de una estrategia. Los argumentos a favor de esta suposición son bastante claros: para la mayoría de los pares de divisas, este gráfico muestra cuántos puntos consigue una estrategia en un periodo de prueba. Hay una opinión justificada según la cual una estrategia puede considerarse difícil si es rentable en puntos, pero si una esperanza matemática es negativa, dicha estrategia es difícil que se convierta en rentable solo mediante la gestión del dinero.

Un argumento más convincente: una curva de "lote 0,1" cerca de una línea recta es una indicación de estabilidad de la estrategia que es difícil ver en un gráfico exponencial.

No obstante, a pesar de todas las ventajas, dichos gráficos presentan inconvenientes que no son tan obvios. Para comprender todo esto, vamos a analizar los resultados de la prueba de una estrategia simple con diferentes sistemas de gestión del dinero y comparar los gráficos.

Tipos de gestión del dinero (MM) analizadas en el artículo. Seleccionar un asesor experto

Ahora analizaremos 3 tipos de MM en las que el volumen de posiciones abiertas es fijo o es una función creciente de un depósito. La probabilidad de una MM eficiente teniendo en cuenta los resultados de la cuenta de transacciones previas me parece razonable solo cuando la probabilidad de una serie rentable/perdedora es considerablemente superior a la opción de que las transacciones con resultados opuestos se alternen. Por tanto, estas son las MM descritas en el artículo:

1. El lote se fija con independencia del tamaño del depósito y es igual a 0,1. Vamos a llamar a esta estrategia conservadora. En el artículo se llamará "lote 0,1" o "0,1".
2. El lote es proporcional al depósito. Esta es una gestión del dinero agresiva. La llamaremos "MM geométrica".
3. El lote crece proporcionalmente a la raíz cuadrada de un depósito. Vamos a llamarla estrategia moderada.

Vamos a analizar el asesor experto "20_200 expert_v4.2_AntS". No optimizaremos el asesor experto por los parámetros, ya que queda fuera del alcance de este artículo. Vamos a usar los parámetros por defecto del asesor experto. Lo probaremos en todos los ticks en EURUSD H1 desde el 7-6-2000 al 15-3-2008. Este periodo de prueba se seleccionó intencionadamente para tener un gráfico de balance bastante bueno en la prueba del lote 0,1. Precisamente se ha seleccionado este asesor experto para demostrar las afirmaciones principales de este artículo. El código fuente del asesor experto se encuentra en https://www.mql5.com/en/code/7891 .

La mayor parte del asesor experto es la función para seleccionar el lote LotSize() un poco más largo de 1000 líneas (o 44K de 50K del tamaño del código fuente), que condiciona parcialmente su singularidad. Este función podría implementarse de una forma mucho más corta si aproximamos la función de la dependencia del lote en un balance mediante una simple línea con el lote necesario redondeado a 0,01. Al menos la diferencia de la aproximación a partir de los cálculos en el código fuente en los "nodos" (puntos de medición del lote) se muestra solo en un nodo de entre un millar. Difícilmente puede incidir sobre los parámetros de la estrategia.

Decidí no estudiar la lógica exacta de la selección del tamaño del lote y cambié el código, haciendo de esta forma el código mucho más pequeño (inicialmente el código del asesor experto contenía solo MM activas correspondientes a esta función de la selección del lote). Las partes relacionadas con el incremento del lote no proporcional también se excluyeron del código, excluyéndose de esta forma los elementos de martingale del asesor experto. El código modificado del asesor experto se adjunta al artículo.

A continuación se muestra la función del cálculo del tamaño del lote adecuada para EURUSD:

double LotSize() 
{
   double size;
   switch( _MM )
   {
      case 0:  size = 0.1;  
               break;
      case 1:  size = 0.1 * AccountBalance() / 1000; 
               break;
      case 2:  size = 0.1 * MathSqrt( AccountBalance() / 1000 ); 
               //size = 1. * MathSqrt( AccountBalance() / 10000 ); 
               break;
      default: size = 0.1;  break;
   }  
   if( size < 0.1 )          // is money enough for opening 0.1 lot?
      if( ( AccountFreeMarginCheck( Symbol(), OP_BUY,  0.1 ) < 10. ) || 
          ( AccountFreeMarginCheck( Symbol(), OP_SELL, 0.1 ) < 10. ) || 
          ( GetLastError() == 134 ) )
                  lot = 0.0; // not enough
      else        lot = 0.1; // enough; open 0.1
   else           lot = NormalizeDouble( size, 2 ); 
   
   return( lot ); 
}

Hipótesis en el artículo

Más adelante en el artículo seguiremos la lógica de un principiante típico:

1. Un principiante visita el foro, entra en la Basede código, ve precisamente este asesor experto y decide ver qué es capaz de hacer el mismo. No está interesado en los detalles del código fuente, necesita un resultado rápido.
2. El principiante no está interesado en la cuestión de la fiabilidad de los resultados de la prueba relativos a la variabilidad del historial. Solo elije un periodo de prueba comenzando varios años atrás hasta el momento presente en el que el asesor experto muestra resultados muy buenos. El principiante cree que el asesor experto se comportará igual en el futuro, ya que para casi los 8 años ha mostrado buenos resultados.
3. Al haber recibido los resultados de la prueba en el lote fijo 0,1, visita el foro y ve las respuestas típicas de visitantes del foro experimentados que al probar el lote 0,1 muestran resultados muy veraces sobre la estabilidad de la estrategia, toma un paso hacia adelante y decide introducir la gestión del dinero geométrica, es decir, abrir posiciones cuyos tamaños sean proporcionales al tamaño del balance. Tampoco piensa que en realidad stop-loss es mucho mayor que take-profit porque no ha visto el código. No está seguro de cómo cambiará la curva de balance.
4. Y, finalmente, nuestro principiante intenta modificar la MM e inventa el tercer tipo de MM descrito anteriormente.

Analizaremos los resultados obtenidos y las acciones del principiante, observando principalmente varios parámetros integrales de los resultados de la prueba: beneficio neto, reducción máxima en porcentajes y factor de recuperación.

Prueba 1: Lote fijo, "0,1"

Estos son los resultados de la prueba:

Strategy Tester Report 20_200 expert_v4.2_AntS

Alpari-Demo (Build 215)

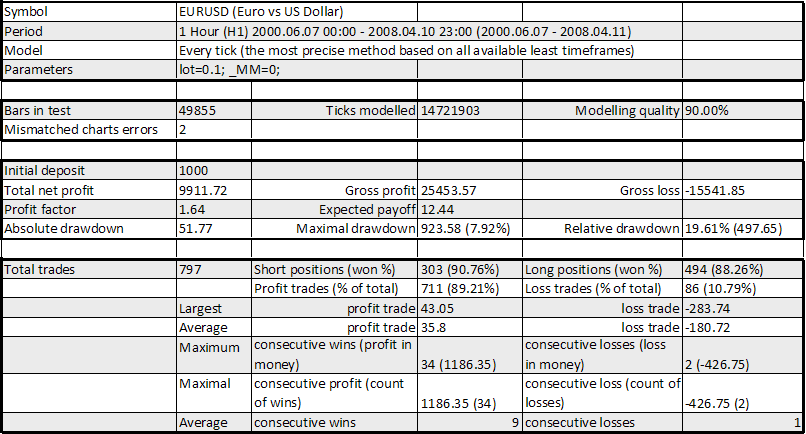
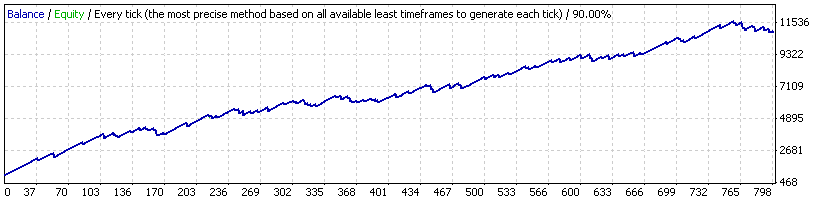
Expert Advisor 20_200 expert_v4.2_AntS, lot 0.1

Añadiremos un parámetro más, el factor de recuperación:

RF (factor de recuperación) = Beneficio neto total / Reducción máxima = 9911,72 / 923,58 = 10,73

La curva no tiene mal aspecto, RF está también OK, aunque es para casi 8 años. Todos los demás parámetros de la tabla también son bastante buenos: la esperanza matemática es 12,44 puntos (puede ser mayor, pero no está mal), la reducción máxima es del orden del 20 %. El coeficiente de una transacción de beneficio media respecto a una con pérdidas media es igual a 35,80/180,72 = 0,198 = 1/5,05; no obstante, el número de transacciones rentables es mayor que el de las transacciones perdedoras (89,21 %/10,79 %, es decir, en 8,27, que es mayor que 5,05). De esta forma una estrategia parece tener algo en la reserva.

Esto da confianza a nuestro principiante y este decide tomar el riesgo: en lugar de un lote fijo introduce la gestión de dinero geométrica en base a una "modesta" proporción "lote 0,1/$1000 de depósito". Es mucho más arriesgada la proporción ofrecida en el asesor experto original (un poco más que el lote 1/3 para $10.000 de depósito), pero nuestro héroe no presta atención a esto: quiere ganar todo el dinero posible...

Prueba 2, Parte 1: Lote proporcionado al balance, «0,1/$1000»

He dejado varias líneas en el informe que pueden serle interesantes.

Strategy Tester Report 20_200 expert_v4.2_AntS

Alpari-Demo (Build 215)

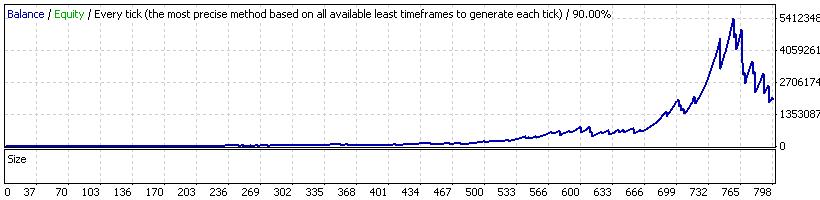
Expert Advisor 20_200 expert_v4.2_AntS, MM geométrica

Para una mejor visualización he grabado un vídeo que ayuda a hacer un seguimiento del proceso en la dinámica: el resultado estadístico final para la MM geométrica a menudo tienen mucho mejor aspecto que en la realidad debido a que los detalles se igualan. El vídeo ilustra perfectamente las reducciones intermedias que parecen abolladuras sin importancia en la figura. Podemos ver que estas reducciones intermedias no son tan pequeñas y alcanzan a veces el 50 % del balance máximo logrado (en realidad, el punto no está en la última reducción recibida después de que el balance ha alcanzado su máximo absoluto):

MM geométrica en la dinámica

Debido a características de la conversión desconocidas para mí, el vídeo debe verse hasta el segundo 34, después de que el mensaje sobre un modo de prueba se haya mostrado, se muestra el final repetido.

Puede verse que la situación es mucho peor ahora: visualmente el gráfico no es tan atractivo y los parámetros que nos interesan también han cambiado. No discutiremos si el volumen de la transacción abierta en el pico de balance (unos 540 lotes) es real para las empresas de corretaje. Vemos que el beneficio neto aumentó considerablemente, pero la reducción máxima es superior al 70 %, y el factor de recuperación

RF = 1989283,04 / 3883421,15 = 0,51 –

ha caído de forma crítica y ahora es inferior a uno. Por supuesto, un RF tan escaso es el resultado de la última reducción, pero no nos interesa la autodecepción, y no vamos a excluir la reducción del informe, ¿verdad? Esta situación ya se describió en el artículo famoso "Mi primer grial'", que es probablemente el artículo más citado del foro.

Esta es una doble lección para un principiante que ha aceptado las respuestas del "experimentado" que invariablemente solicita los resultados de la prueba en el lote fijo 0,1. Por tanto, hacer una prueba en "0,1" parece ser decepcionante: a pesar de la demostración evidente de la esperanza matemática positiva y la estabilidad de la estrategia en el lote 0,1, generalmente no es suficiente para añadir una MM agresiva mientras se confía en la esperanza matemática positiva que "debería" ayudar.

La razón de ese brusco cambio en el carácter de la curva y sus parámetros es evidente: cuando hacemos una prueba en "0,1" el crecimiento del depósito se ve acompañado por una disminución del riesgo relativo, ya que el tamaño del lote con relación al depósito disminuye sobre la hipérbola. Y en caso de una MM geométrica el riesgo no disminuye y sigue siendo el mismo. Esto explica el gran aumento de profundidad de las "abolladuras" al final del periodo de pruebas.

Hay una observación más: el coeficiente de transación rentable media con respecto a la transacción perdedora media también ha empeorado. Ahora es igual a 20051,69/142644,96 = 0,141 – en lugar de 35,80 / 180,72 = 0,198 en la prueba anterior "0,1". ¿Por qué? Esta es la respuesta: la pérdida en la MM geométrica se calcula para un tamaño de lote en el balance de una cuenta correspondiente al momento de la apertura de la transacción, es decir, en el punto superior de la trayectoria descendente del balance. Al mismo tiempo, se calcula el volumen de una transacción rentable debido al balance en el momento de su apertura, es decir, en el punto más bajo de la trayectoria del balance y parece ser un poco menor que para la transacción perdedora.

Un ejemplo numérico: supongamos que en un balance igual a $5000 y una MM geométrica hemos abierto una transacción con el volumen 0,1*($5K/$1K) = 0,5 lotes y ganó los 100 puntos de beneficio. Esto significa que el beneficio para EURUSD es igual a $500. Ahora supongamos que abrimos inmediatamente una transacción que trae 100 puntos de pérdidas. ¿Cuál es nuestra pérdida? El lote es igual a 0,1*($5K+$500)/$1K = 0,55,es decir, nuestra pérdida es -$550, que es un 10 % más que el beneficio. Esto no ocurrió en el primer caso con un lote fijo.

¿Qué conclusiones podemos extraer?

1. Si observamos una MM geométrica agresiva, para obtener una curva de balance realmente buena, debemos conocer claramente que la curva correspondiente de prueba en el lote 0,1 debe ser prácticamente ideal, sin "abolladuras". No debemos obviar ninguna de las variantes de la MM que vayamos a usar en el trading en directo. No nos dejemos llevar solo por la "prueba 0,1" si nuestra MM ha de ser distinta.
2. No olvidemos que una MM geométrica normalmente aumenta el porcentaje de reducción. Supongamos que tenemos una prueba en el lote 0,1 en un periodo de cinco años y que muestra un crecimiento del depósito de un 1.000 % (desde $1K a $11K). A propósito, es un valor bastante realista: corresponde a 10.000 puntos durante 60 meses, es decir, 167 puntos al mes. Supongamos que al final del periodo de 5 años cuando el depósito es igual a $11K teníamos una reducción muy pequeña en el lote 0,1, un 5 %, y que después de la última transacción fue rentable y el depósito ahora es de nuevo igual a $11K. ¿Cuál cree que será la reducción con la MM geométrica? 55 % de su depósito – con independencia de por cuánto haya aumentado antes esta "abolladura". La explicación va más allá.
3. Por tanto, esta es la recomendación: elija "la media de oro" en sus estrategias de MM. Esto no significa que siempre debamos usar el lote 0,1, sino que la MM geométrica en transacciones de un millón de valor es solo un sueño relacionado con la subestimación del riesgo.
   

La prueba de los argumentos de reducción de la MM geométrica:si durante la prueba en el lote 0,1 la reducción al final del periodo (cuando el balance antes de la transacción perdedora es igual a $11K) es igual al 5 %, esto significa que es igual a 5%*$11K = $550, es decir, 550 puntos. Ahora vamos a calcular lo mismo con la MM geométrica.

Si esta reducción deriva de solo una posición abierta (por ejemplo, no hay stop loss), nuestro razonamiento es simple: supongamos que antes de esta reducción en la "MM geométrica" el balance ha alcanzado X*$1K (debido a esta MM, X es probable que sea superior a 11 pero aquí no es importante). Entonces, la transacción de los lotes X*0,1 se abre y luego se cierra con la pérdida igual a lot*pips_value*pips = (X*0.1)*$10*550 = $550*X, que es igual al 100%*($550*X)/(X*$1K) = 55% del depósito antes de esta reducción.

El caso en que esta reducción es el resultado de varias transacciones perdedoras consecutivas es más difícil, pero formalmente estas transacciones pueden reunirse aproximadamente en una transacción y esta reducción puede considerarse el resultado de una transacción. No obstante, debido al efecto de la acumulación de numerosas transacciones opuestas, el resultado será algo diferente.

Este razonamiento se obtuvo precisamente en el proceso de escritura del artículo, cuando intentaba explicar lógicamente los resultados de la prueba de la MM geométrica. La radicalidad del resultado todavía me impresiona. Antes de este momento, era demasiado ingenuo para creer que a cualquier estrategia que mostrara en el lote 0,1 una curva atractiva con pequeñas reducciones, incluso una MM agresiva podía ser añadida, pero nunca pensé que las reducciones crecería tan desproporcionadamente en comparación con las demostradas en la "prueba 0,1". Y ahora soy absolutamente escéptico sobre el uso intensivo de una MM geométrica. La razón es que no hay estrategia sin reducciones...

Prueba 2, Parte 2: Asesor experto Lucky y MM geométrica

Vamos a considerar otro ejemplo asombroso que prueba nuestros argumentos sobre la reducción. Esta es una lección para los autores del asesor experto 'Lucky" que esperan usar con la MM geométrica (esta es la intención inicial: ver el código fuente en https://www.mql5.com/en/code/7464):

double GetLots()
{
   return (NormalizeDouble(AccountFreeMargin()/10000,1));
}

El asesor experto está ligeramente modificado para la prueba en el lote 0,1 y usa un take-profit mayor que 1 pip (con el límite del parámetro externo Pr_=1). Además, a diferencia del código fuente, en el asesor experto solo puede abrirse una orden al mismo tiempo (para este caso no cambia mucho el carácter de la curva de balance). No nos interesa si el asesor experto funcionará con una empresa de corretaje real, este no es nuestro propósito. Se adjunta a este artículo un código del asesor experto modificado.

La prueba se realiza con los parámetros Shift=4, Limit=10, Pr_limit=1 con un lote fijo 0,1 en el periodo histórico desde el 1-1-2004 al 4-4-2008 (el depósito inicial es $1K). Esta es la curva de balance:

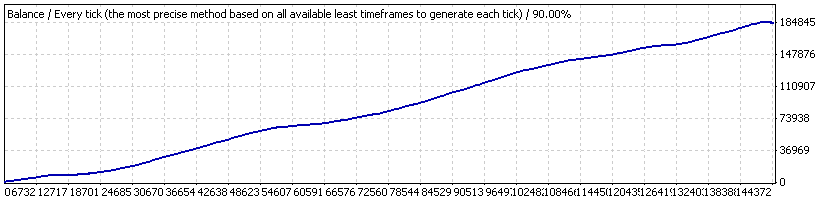
Asesor experto Lucky, "0,1"

Esta curva contiene una pequeña "abolladura" que es visible solo en el probador, pero invisible en la fig.: está en el periodo desde el 31-12-2004 al 7-1-2005 para los números de orden desde 57890 a 58857. Vamos a analizar la "abolladura" en detalle limitando el intervalo de prueba total para este periodo (el lote aún está fijo y es igual a 0,1. El balance inicial en esta parte no es importante y se asume igual a $1000 ya que nos interesa el tamaño de la reducción en puntos):

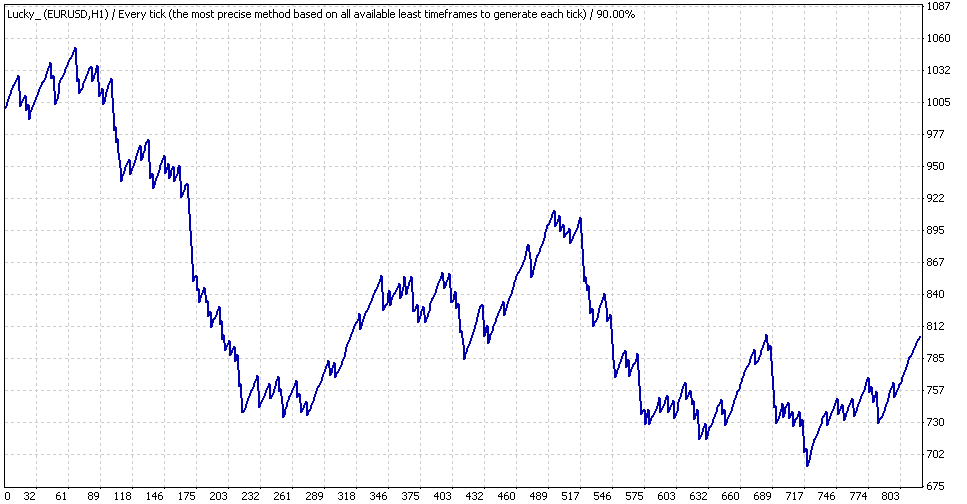
Asesor experto Lucky, "0,1", examen "microscópico"

Podemos ver que el balance máximo es aproximadamente igual a $1050 y el mínimo es $690. La reducción con el lote 0,1 es igual a $360, es decir 360 puntos. Realizando cálculos sencillos análogos a los descritos anteriormente, obtenemos que con la MM geométrica este valor se transforma en una reducción de casi el 36 %. Vamos a probarlo en la práctica haciendo una prueba en el mismo periodo corto con la MM geométrica (redondeando la precisión en GetLots() es 0,01, es decir, 2 dígitos):

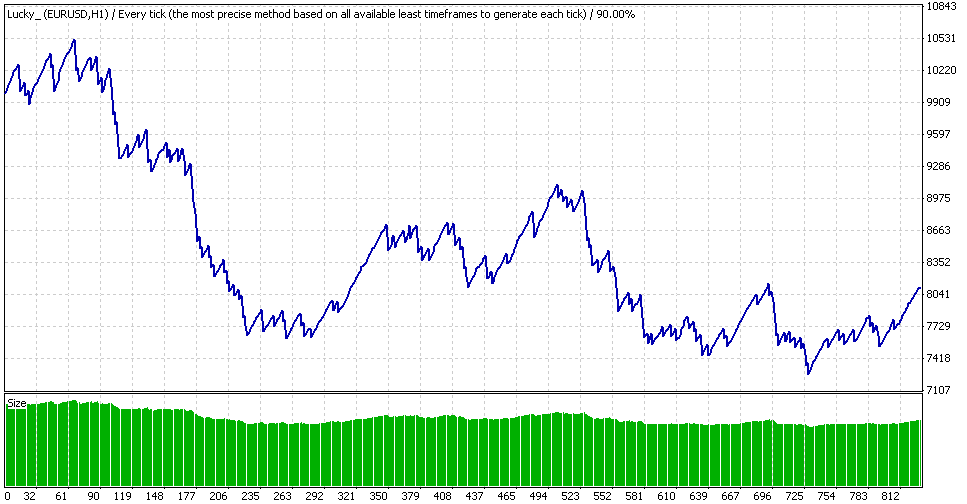
Asesor experto Lucky, MM geométrica en el mismo periodo

La reducción real es cerca del 32 % (ya que no se debe a una única orden), sin embargo, ¡qué demonios vemos aquí! Una abolladura casi invisible en el centro del gráfico (con el lote 0,1 la reducción es aproximadamente igual a 360/68000 ~ 0,5%) ha crecido en cifras relativas en más de 60 veces. Y esto es al margen de la reducción al final del periodo, que es solo del 0,89 % con "0,1" aunque 1660 en puntos. Esta reducción acabará prácticamente con el depósito, pero no es tan eficiente ahora...

Y ahora vamos a crear un ejemplo artificial que, a primera vista, es incompatible con el sentido común.

Ejemplo paradójico. Una investigación superficial

En base a la observación de que dos transacciones consecutivas con resultados en puntos idénticos en módulo pero opuestos en el signo puede obtener pérdidas en una MM considerablemente agresiva, podemos construir dicha curva de balance de crecimiento estable cuando se prueba con un lote 0,1, que, una vez probado con la MM geométrica cambia radicalmente de carácter y se convierte en una curva con una tendencia descendente estable. Los gráficos creados mediante MS Excel se muestran a continuación.

El ejemplo se basa en la idea de que nuestras transacciones se alternan en sus resultados (beneficio/pérdida): primero tenemos una transacción con 100 puntos de beneficio y luego va la transacción perdedora en la que la pérdida se calcula de forma que con la MM geométrica tenemos la pérdida como el total de dos operaciones: cuando es con la MM "0,1" tenemos el beneficio total.

Las limitaciones de las empresas de corretaje relativas al tamaño mínimo del lote y su incremento mínimo se tienen en cuenta (0,1 y 0,01 respectivamente, de acuerdo con los términos de Alpari-IDC). Por esta razón en cualquier caso el depósito no será mucho menor que $1000 debido a la limitación resultante del tamaño mínimo del lote, es decir, 0,1. Y por esta razón, para evitar dicho "efecto de frontera", el depósito inicial se toma 10 veces mayor que el anterior, $1000.

Lo que obtenemos: a pesar del hecho de que con un beneficio de 100 puntos hay un valor de pérdida precisamente calculado en puntos en los que la MM geométrica tiene pérdidas exactamente iguales al beneficio ganado anteriormente, en realidad aún hay un cierto rango de valores de transacciones perdedoras en las que el balance entra en un ciclo de valores estables en un cierto rango limitado. No sé aún la razón. A continuación podemos ver las ilustraciones: el depósito inicial es siempre $10.000, la transacción rentable es de 100 puntos, la proporción de la MM geométrica es de lote 0,1 por $1K del depósito.

Transacción perdedora: 91 puntos (la transacción rentable es mayor que la perdedora en 9 puntos)

La figura de arriba muestra ambas curvas para distintas MM. A continuación para la misma curva de balance con el lote 0,1 se amplía el encuadre para mostrar el carácter de dientes de sierra. Además, el segundo gráfico no se mostrará ya que su carácter es siempre análogo a este.

La cifra con la esperanza matemática de pérdidas igual a 91 se muestra para ilustrar el "umbral" de una transacción perdedora en que un sistema rentable formalmente con la MM "0,1" se convierte en uno sin beneficio y sin pérdidas cuando se usa con la MM geométrica.

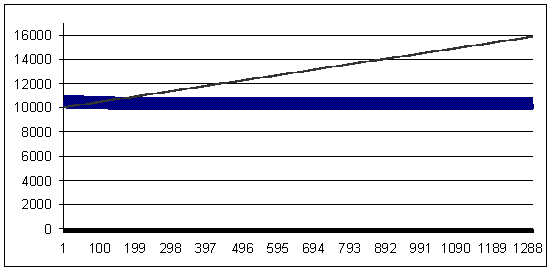
Pérdida 91, ММ geométrica 0,1/$1000

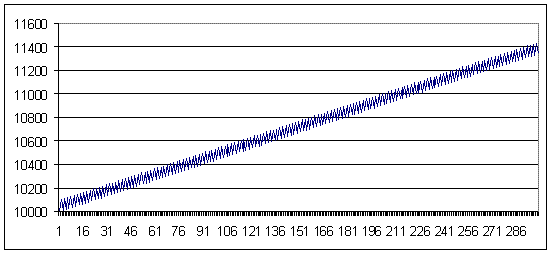
pérdida 91, lote = 0,1

Transacción perdedora: 92 puntos (la transacción rentable es mayor que la perdedora en 8 puntos)

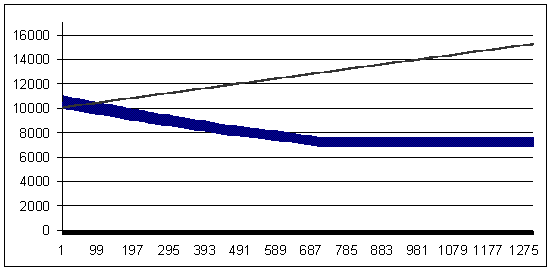
Pérdida 92, ММ geométrica 0,1/$1000

Transacción perdedora: 93 puntos (la transacción rentable es mayor que la perdedora en 7 puntos)

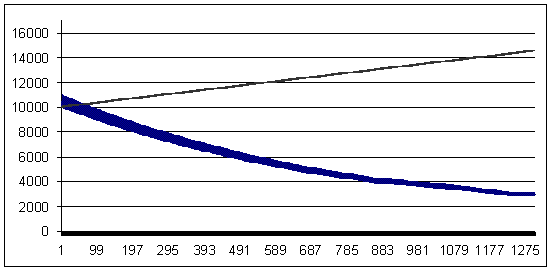
Pérdida 93, ММ geométrica 0,1/$1000

Transacción perdedora: 94 puntos (la transacción rentable es mayor que la perdedora en 6 puntos)

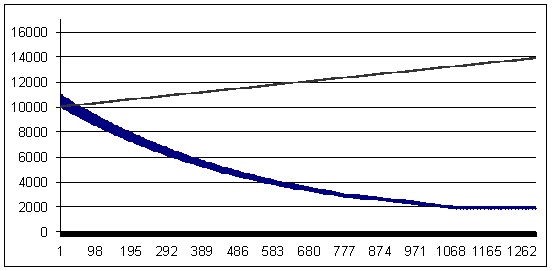
Pérdida 94, ММ geométrica 0,1/$1000

Transacción perdedora: 96 puntos (la transacción rentable es mayor que la perdedora en 4 puntos)

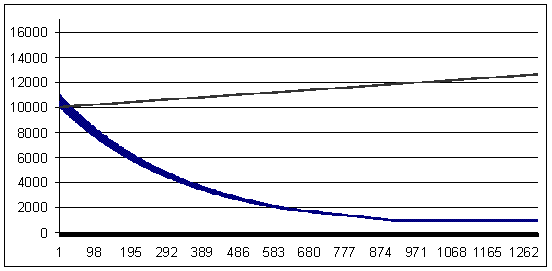
Pérdida 96, ММ geométrica 0,1/$1000

Vemos que las previsiones de las curvas son opuestas. Por supuesto, un sistema en vivo difícilmente puede ser tan "estable", pero he incluido este ejemplo solo para ilustrar lo que puede ocurrir si no tenemos en cuenta un gráfico de prueba con el "lote 0,1" muy críticamente.

Veamos ahora qué ocurrirá si hacemos que la MM geométrica sea más agresiva (por ejemplo 0,2 o incluso 0,33 lote por $1K de depósito. Puede encontrar estos casos en el foro). Además verá gráficos que solo pertenecen a los valores de frontera de las transacciones perdedoras (una transacción rentable todavía es igual a 100 puntos): si una transacción perdedora excede un valor límite, el comportamiento de las curvas en la MM geométrica incluso empeora.

Transacción perdedora: 84 puntos (la transacción rentable es mayor que la perdedora en 16 puntos) MM - geométrica, 0.2 lote/$1K de depósito.

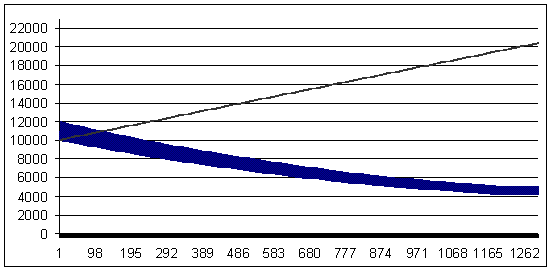
Pérdida 84, ММ geométrica 0,2/$1000

Transacción perdedora: 75 puntos (la transacción rentable es mayor que la perdedora en 25 puntos). MM - geométrica, 0.33 lote/$1K de depósito.

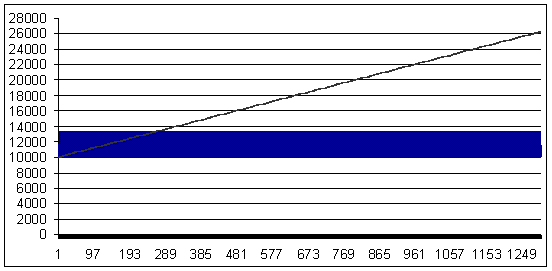
Pérdida 75, ММ geométrica 0,33/$1000

Conclusión: una mayor agresividad de una estrategia con una esperanza matemática sin cambios para una transacción rentable establece mayores requisitos para la estrategia: la esperanza matemática de una transacción en puntos debe incrementarse. Podemos determinar una formula definiendo un valor umbral de una transacción perdedora en puntos (pérdida) con los siguientes parámetros:

- beneficio de una transacción rentable (beneficio),

- agresividad de una MM geométrica (agr.), es decir, volumen de la posición en lotes por cada $10K de un depósito,

- valor de 1 punto para 1 lote de un valor bursátil (pointval).

Para probar la fórmula solo necesitamos abrir las primeras dos transacciones, comenzando por el depósito de $10K y luego esta correlación se cumplirá con independencia del depósito obtenido (se prueba un poco antes, ya que el parámetro X se cancela).

1. La primera transacción arroja un beneficio: el depósito es igual a $10K. Abre una posición con el volumen igual a los lotes aggr. Obtenemos un beneficio igual a aggr * profit * pointval. Cierra la transacción.
2. Abre la segunda transacción, obtiene pérdidas. En el momento de la apertura de la transacción, el depósito es igual a $10000+ aggr*profit*pointval = $10K*(1+ aggr*profit*pointval/10000). El volumen de la transacción es aggr*(1+ aggr*profit*pointval/10000). La pérdida de la transacción deseada en dólares es igual a aggr*(1+ aggr*profit*pointval/10000) * loss * pointval.
3. Iguala las dos expresiones obtenidas y obtiene una fórmula para la pérdida:

pérdida = beneficio / (1+ aggr*profit*pointval /10000)

Vamos a comprobar si es correcta la fórmula en EURUSD (pointval=$10):

-siprofit=100, aggr=1 obtenemospérdida = 100/(1+1*100*10/10000) = 100/1.1 ~ 90.91 pips. Como vimos anteriormente, el valor del umbral en este caso es igual a 91 puntos (ver el primer gráfico);

-sibeneficio=100, aggr=2 obtenemospérdida = 100/1.2 ~ 83.33. El valor del umbral obtenido anteriormente en un experimento es igual a 84 puntos;

-sibeneficio=100, aggr=3.33 obtenemospérdida = 100/1.33 ~ 75.19. El valor del umbral obtenido anteriormente en un experimento es igual a 75 puntos.

La adecuación con los datos del experimento no es mala. No obstante, el gráfico del balance real no puede tener este aspecto: normalmente el coeficiente porcentual de transacciones rentables y perdedoras no es igual. No intentaremos aplicar el modelo a casos más complejos ya que el principio general de la construcción de una curva de balance artificial está claro. Vamos a finalizar nuestra investigación probando el asesor experto con el tercer tipo de MM llamada "moderada".

Prueba 3: El lote es proporcional a la raíz cuadrada de un depósito

Strategy Tester Report 20_200 expert_v4.2_AntS

Alpari-Demo (Build 215)

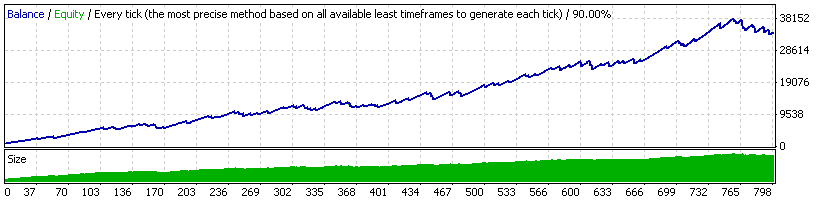
Expert Advisor 20_200 expert_v4.2_AntS, MM moderada

RF = 32764.09 / 5632.51 = 5.82

En este caso el depósito inicial es igual a $1K, lote inicial - 0.1.

Esta MM toma una posición intermedia entre las dos analizadas anteriormente. La reducción máxima no es muy grande, pero la reducción relativa todavía es bastante grande, aunque mucho menos en la variante con la MM geométrica. No obstante, la curva es bastante atractiva y mucho mejor que la segunda (para el asesor experto "20_200"). Además, es mucho más estable que la segunda variante.

Hay distintas variaciones de esta variante. Por ejemplo, si tomamos un depósito inicial igual a $10K y establecemos un lote inicial igual a 1.0 (comentando la variante del código previa):

caso 2: tamaño = 1. * MathSqrt( AccountBalance() / 10000 );

para casi 8 años el beneficio mostrado antes se incrementa en diez veces, pero las reducciones relativas no cambian.

Conclusión

La mayoría de conclusiones se extraen en la parte dedicada a la MM geométrica. El autor tiene pensado publicar el segundo artículo sobre las "Falacias" para cubrir algunas irregularidades estadísticas que aparecen en el análisis de los resultados de la transacción de algunas estrategias "interesantes". El nivel de descripción material es un poco mayor que en el artículo presente pero no demasiando incomprensible.

Y ahora tengo el comentario final al encabezado del artículo: sí, la gestión del dinero es secundaria, porque aparentemente la gestión del dinero difícilmente puede ayudarnos a salvar una estrategia que está obteniendo pérdidas con el lote 0,1 y convertirla en una rentable y robusta. No obstante, es cierta la segunda afirmación parcialmente refutando el proverbio "nunca demasiado de algo bueno": cualquier estrategia que permita dos tipos distintos de gestión del dinero, incluso si es muy rentable y robusta, puede ser eliminada por una MM inadecuadamente agresiva.