谬误，第 1 部分：资金管理排第二位，并不是很重要

简介

本文中我们将讨论一些非常简单但却往往具有欺骗性的东西 - 测试报告中的账户余额图。在新手们的策略测试报告中，我们经常会在测试结尾处看到指数余额/权益图和数十亿金额的结果。这种结果通常会引发经验丰富、知道这些指数的来龙去脉的 EA 编写者的质疑，并立即建议根据固定手数（通常是 0.1）显示结果。

人们认为基于固定 0.1 手的测试结果能更好地反应一个策略的所有优缺点。这种看法的论据相当明显：对于大部分货币对，这个图显示了策略在测试期间内获得了多少点。还有一种公允的看法，即如果某种策略是按点盈利的，则它可能被视为很有挑战性；但如果数学期望值为负值，则此类策略很难仅靠资金管理的方式获利。

另一个令人信服的论据是：“0.1 手”的曲线接近于一条直线，它是一种策略稳定性的指示，而这种指示很少能在指数图上看到。

但是，尽管有很多优势，但这种图也有一些不是那么明显的缺点。为了获得全面的了解，我们来分析一个使用不同资金管理系统的简单策略的测试结果，并比较各个图。

本文中分析的资金管理 (MM) 类型。选择 EA

现在我们将分析三种 MM，在这些 MM 中，已建立仓位的金额要么是固定的，要么是保证金的递增函数。对我来说，只有当获利/亏损系列的可能性大大高于产生相反结果的交易将取而代之的几率，有效 MM 才可以较为合理地把之前交易的结果纳入考虑范围。因此，本文中所述 MM 如下：

1. 手数固定为 0.1，无论保证金有多少。让我们把这种策略称为保守策略。本文中将用“0.1 手” 或“0.1”表示。
2. 手数与保证金成比例。这是一个积极的资金管理方法。我们将称其为“几何 MM”。
3. 手数按保证金的平方根成比例增长。我们将称其为温和策略。

让我们分析 Expert Advisor“20_200expert_v4.2_AntS一文中描述的游戏。我们不会通过参数优化 EA，因为这超出了本文的范围；让我们使用 Expert Advisor 的默认参数吧。我们将使以 EURUSD H1 在从 2000/06/07 到 2008/03/15 的所有价格变动来测试该 EA。我们特意选择这个测试周期，为的是在用 0.1 手测试时获得一个很好的余额图。选择这个 EA 正是为了展示本文的主张。此 EA 的源代码位于 Https://www.mql5.com/zh/code/7891 。

此 Expert Advisor 的主要部分是用于选择手数的函数LotSize()，占 1000 行略微出头（或源文件 50K 中占 44K），这一定程度上也决定了它的突出性。如果我们用简单的一行将必要手数舍入至 0.01 以逼近手数对余额的依赖关系的函数，则此函数可以用较短的形式实现。至少“节点”（手数测量的点）中源代码中的计算的逼近差异仅在千分之一的节点 (!!!) 内显示。它几乎不会影响策略的参数。

我决定不去研究选择手数的确切逻辑，并更改代码，以进一步缩减文件大小（EA 代码初始仅包含与此手数选择函数对应的活动 MM）。与非比例手数增加关联的部分也排除在代码之外，从而从 EA 中排除了马丁格尔的元素。本文随附了 EA 的变更代码。

以下是适用于此处 EURUSD 的手数计算函数：

double LotSize() 
{
   double size;
   switch( _MM )
   {
      case 0:  size = 0.1;  
               break;
      case 1:  size = 0.1 * AccountBalance() / 1000; 
               break;
      case 2:  size = 0.1 * MathSqrt( AccountBalance() / 1000 ); 
               //size = 1. * MathSqrt( AccountBalance() / 10000 ); 
               break;
      default: size = 0.1;  break;
   }  
   if( size < 0.1 )          // is money enough for opening 0.1 lot?
      if( ( AccountFreeMarginCheck( Symbol(), OP_BUY,  0.1 ) < 10. ) || 
          ( AccountFreeMarginCheck( Symbol(), OP_SELL, 0.1 ) < 10. ) || 
          ( GetLastError() == 134 ) )
                  lot = 0.0; // not enough
      else        lot = 0.1; // enough; open 0.1
   else           lot = NormalizeDouble( size, 2 ); 
   
   return( lot ); 
}

本文中的假设

本文中我们将进一步分析典型新手的逻辑：

1. 一位新手访问论坛，进入代码 库，看到这个代码，并决定了解此 EA 的倾向。他对源代码的细节不感兴趣；他需要一个快速结果。
2. 新手不关心测试结果相对于历史多变性的可靠性问题；他只是选择一个从几年前到现在的测试周期，在这个周期中，EA 表现出相当好的结果。他相信这个 EA 将来也能表现的很好，因为它在将近八年时间里一直都表现良好。
3. 在收到固定 0.1 手的测试结果后，他访问论坛并看到经验丰富的论坛访客的典型回答，即在 0.1 手时所做的测试具备较高的策略稳定性，能提供相当可靠的结果，然后他前进一步，决定引入几何资金管理系统，即建仓金额与余额大小成比例。他也并不认为实际的止损会远大于获利，因为他还没看代码。他不确定余额曲线会怎么变化。
4. 最终，我们的新手试着修改 MM，并发明了上述的第三种 MM。

我们将分析获得的结果和新手的操作，主要是观察测试结果的多个综合参数 - 净利润、最大亏损百分比和回收系数。

测试 1：固定手数“0.1”

以下是测试结果：

策略测试程序报告 20_200 expert_v4.2_AntS

Alpari-Demo (Build 215)

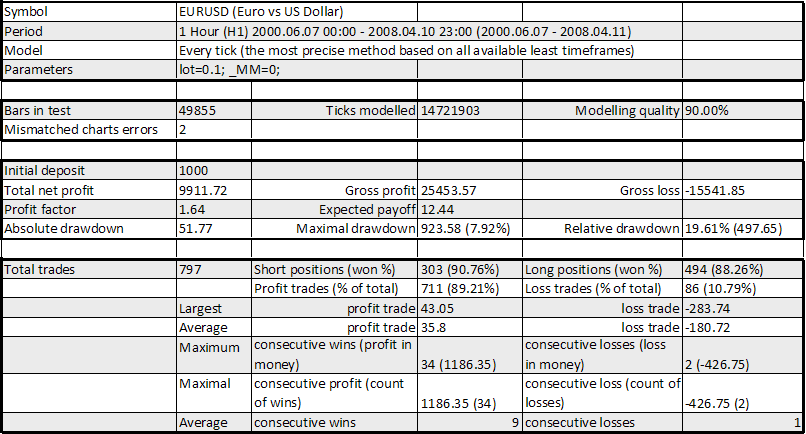
Expert Advisor 20_200 expert_v4.2_AntS，0.1 手

我们将再添加一个参数 - 回收系数：

RF（回收系数）= 总净利润/最大亏损 = 9911.72 / 923.58 = 10.73

曲线看上去不错，RF 也很好，尽管周期将近 8 年。表中的所有其他参数也相当好：数学期望值为 12.44 点（可以更大，但这就不错了），最大亏损约为 20%。平均获利交易数与平均亏损交易数之比为 35.80/180.72 = 0.198 = 1/5.05；但获利交易数大于亏损交易数（89.21%/10.79%，即 8.27，这个数字高于 5.05）。因此策略看起来大有可为。

这给了新手信心，他决定冒险一搏：不采用固定手数，而是基于“每 1000 美元保证金 0.1 手”的“适度”比例引入几何资金管理。这种比例的风险远大于原始 EA 中提供的比例（每 10000 美元保证金 1/3 手略多一点），但我们的英雄可没有注意到这一点：他只想赚到尽可能多的钱...

测试 2，第 1 部分：手数与余额成比例，«0.1/$1000»

我留下了报告中我们可能会感兴趣的几行内容。

策略测试程序报告 20_200 expert_v4.2_AntS

Alpari-Demo (Build 215)

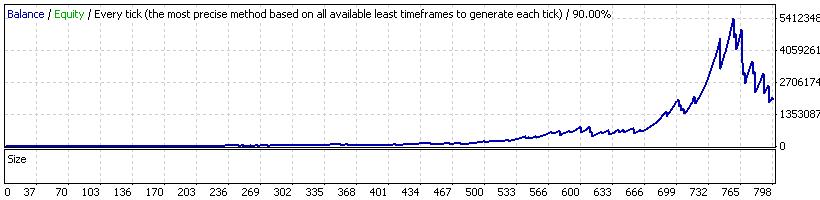
Expert Advisor 20_200 expert_v4.2_AntS，几何 MM

为了让视觉效果更好，我记录了一个可帮助跟踪动态流程的视频文件：几何 MM 的最终统计结果看上去通常比实际结果好得多，因为细节不会出错。视频完美展示了中间亏损，看上去就像图中不重要的凹陷。这些中间亏损并不那么小，有时达到已实现余额最大值的 50%（实际上，这个点不在余额达到其最大绝对值后发生的最后一次下跌中）：

动态学中的几何 MM

由于我不了解的转换功能，视频要观看至第 34 秒；在显示关于测试模式的消息后，就会出现重复的结尾。

看，现在情况更糟了：图形看上去并不那么好，我们感兴趣的参数也已经发生变化。我们不讨论余额峰值时的建仓手数（大约 540 手！）对于经纪公司来说是否现实。我们看到净利润大大增加，但最大亏损百分比超过 70%，而且回收系数

RF=1989283.04 /3883421.15 =0.51–

直线下跌，现在甚至小于 1！当然，这么差的 RF 是最后一次下跌的结果，但我们不想自欺欺人，我们也不会把该下跌排除在报告内容之外，对不对？！这种情况已经在著名的文章“我的第一个’圣杯’”中描述过，这篇文章也许是论坛上引用最多的文章。

对于接受了总是请求固定 0.1 手时测试结果的“老手”的说法的新手来说，这是双重的经验教训。所以“在 0.1”时测试看起来似乎有欺骗性：抛开明显展示的正数学期望值和 0.1 手的策略稳定性不论，一般来说，要依赖“应该”有帮助的正数学期望值时，仅添加一个积极的 MM 是不够的。

导致这种曲线特性及其参数发生急剧变化的原因很明显：“在 0.1”进行测试时，保证金的增长伴随的是相对风险的减小，因为相对于保证金的手数在双曲线上减小。在使用几何 MM 时，风险不会变低，而是保持不变。这解释了测试周期结尾时大大增加的“凹陷”深度。

还有一个发现：平均获利交易数与平均亏损交易数之比也变得更差。现在它等于 20051.69/142644.96 =0.141 - 而不是上一个“0.1”测试中的 35.80 / 180.72 = 0.198。原因何在？答案如下：几何 MM 的亏损是针对开始交易时对应的帐户余额的相对手数计算得出的，即在下降余额轨迹的上点中。同时，获利交易的金额是根据建仓时的余额计算得出的，即在下降余额轨迹的下点中，并且它看上去略小于亏损交易的金额。

数值示例：假设当余额为 5000 美元并使用了几何 MM 时，我们开仓交易，手数为 0.1*($5K/$1K) = 0.5 手，并赢得了 100 点利润。这意味着 EURUSD 货币对的利润为 500 美元。现在假设我们立即进行了一个带来 100 点亏损的开仓交易。那么我们亏损多少？手数为 0.1*($5K+$500)/$1K= 0.55，即我们的损失是 550 美元，比获利大 10%。而在使用固定手数的第一种情况下，这种情况并不会发生！

我们能得出什么结论？

1. 如果你想要使用一个积极的（几何）MM，则为了获取一个真正良好的余额曲线，你应该清醒地认识到，0.1 手测试的对应曲线应该是实际情况下的理想状态，没有“凹陷”。切勿忽视任何你要在实际交易中使用的 MM 类型。如果你的 MM 是不同的类型，不要盲目的完全遵循“0.1 测试”。
2. 别忘了几何 MM 通常会提高亏损百分比。假设基于 5 年周期的 0.1 手测试显示保证金增长 1000%（从 1000 美元到 11000 美元）。顺便说一下，这是一个很实际的值：它对应于 60 个月的 10000 个点，即每月 167 个点。假设在 5 年周期结束之前，当保证金为11000 美元时 ，你在 0.1 手时的亏损非常小，仅有 - 5%，之后交易就在盈利，且保证金现在再次等于 11000 美元。你认为使用几何 MM 时亏损将会如何？ 55% 的保证金 - 无论在此“凹陷”之前它已经增加了多少！下面将提供进一步的说明。
3. 所以，这里的建议是：选择你的 MM 策略的“黄金分割”。这并不意味着你应该始终使用 0.1 手，但在价值百万的交易中，几何 MM 仅仅是你在低估风险的情况下做的一场美梦。

几何 MM 亏损论点证明： 如果在 0.1 手测试期间，周期结束时的亏损（当出现亏损交易前的余额等于 11000 美元时）等于 5%，则表示亏损额为 5%*$11K = $550，即 550 个点。现在我们来对几何 MM 进行相同的计算。

如果这个亏损结果来自一个已建仓位（例如，在没有止损位的情况下），我们的推理很简单：假设在“几何 MM”中发生此亏损之前，余额达到了 X*$1K（由于此 MM，X 很可能大于 11，但这里的 X 并不重要）。则 X*0.1 手交易打开，然后在损失等于lot*pips_value*pips= (X*0.1)*$10*550 = $550*X时平仓，即等于此亏损之前的 100%*($550*X)/(X*$1K) = 55% 的保证金。

当此亏损是多个序列亏损交易的结果时，情况会更加复杂，但正式地看，这些交易大概可以组合成一个交易，那么此亏损也可视为一个交易的结果；但是由于大量反向交易累积的效应，这个结果将会略有不同。

这个推理就是在写下本文时想到的，当时我试着解释几何 MM 的逻辑测试结果；结果的激进程度至今仍让我惊叹。而在此之前，我曾那么天真的相信，可以向 0.1 手时显示的任何策略添加带少量亏损甚至是一个积极 MM 的漂亮曲线 - 但我从没料到亏损和“0.1 测试”中展示的结果是如此的不同。现在我对长期使用的几何 MM 产生了很大的怀疑。原因是根本没有不亏损的策略...

测试 2，第 2 部分：幸运的 EA 和几何 MM

让我们看看另一个令人震惊的例子，它证明了我们关于亏损的论点。这是 EA“幸运”的作者们要上的一堂课，这些作者们希望将 EA 与几何 MM 配合使用（这是初始意图：要查看源代码，请访问 (https://www.mql5.com/en/code/7464)：

double GetLots()
{
   return (NormalizeDouble(AccountFreeMargin()/10000,1));
}

Expert Advisor 已稍加修改以进行 0.1 手测试，并使用大于 1 价格利润点的获利（使用外部参数 Pr_limit01)。此外，与源代码不同，EA 中一次仅可打开一个订单（这种情况不会使余额曲线特征产生很大的变化）。我们对 EA 是否使用真实的经纪公司并不感兴趣，这不是我们的目的。更改的 EA 代码附于本文之后。

执行测试时，使用参数Shift=4,Limit=10,Pr_limit=1，并使用固定 0.1 手，所用历史周期为 2004.01.01 至 2008.04.04（初始保证金为 1000美元）。以下是其余额曲线：

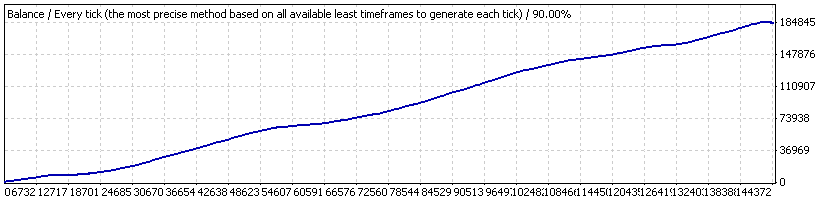
Expert Advisor Lucky，“0.1”

此曲线包含一个仅在测试程序中可见，而图中不可见的很小“凹陷”：对于 57890 到 58857 的订单号，周期为 2004/12/31 到 2005/01/07。让我们详细地分析这个“凹陷”，限制此周期的总测试间隔（手数仍是固定等于 0.1；此部分中的初始余额不重要，假定等于 1000 美元，因为我们关注的是以点为单位的亏损比例）：

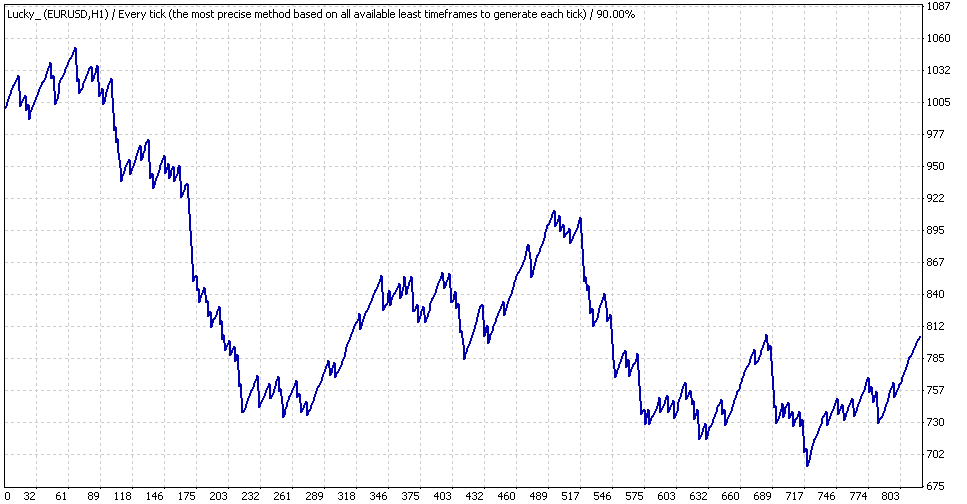
Expert Advisor Lucky，“0.1”，“微观”检查

我们可以看到，最大余额约为 1050 美元，最小余额为 690 美元。0.1 手时的亏损等于 360 美元，即 360 个点。执行类似于上述算法的简单计算，我们会发现，使用几何 MM 时，此值会转变为大约 35% 的亏损！让我们用几何 MM 进行同一个短周期的测试，以在实践中证明这一点（GetLots() 中的舍入精度为 0.01，即 2 位）：

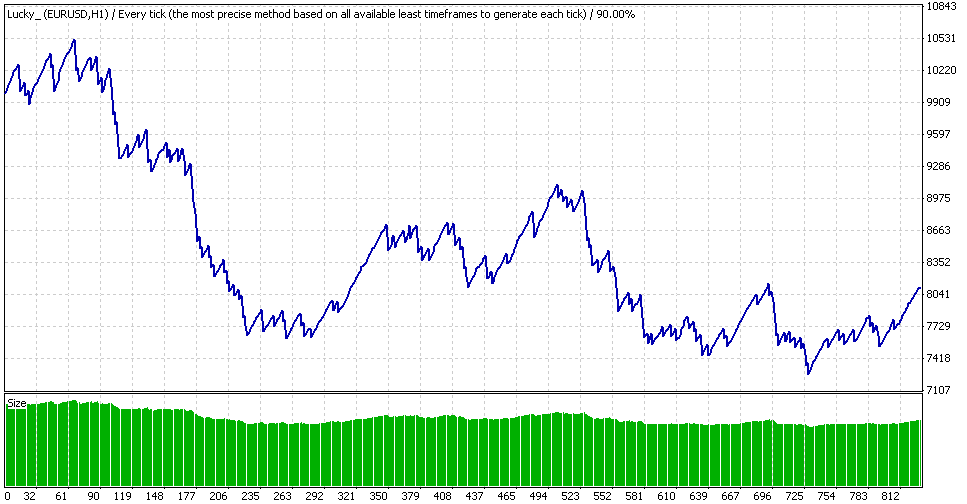
Expert Advisor Lucky，同一周期内的几何 MM

实际亏损将近 32%（因为此结果并非来自单个订单），但我们这里看到的到底是什么玩意！图表中心的一个几乎不可见的凹陷（0.1 手时，亏损约为 360/68000 ~ 0.5%） 在相关图中增大了 60 倍以上！这还没将周期末尾时的亏损计算在内，该亏损仅为 0.89%，但换成点数就是 1660 点；此亏损几乎抵消掉了保证金 - 但现在不那么有效了...

现在让我们创建一个人工示例，乍一看它并不符合常识。

矛盾的例子。肤浅的调查

我们观察到，当两个连续交易的结果点数在模块中完全一致但在符号中却相反时，这两个交易在使用相当积极的 MM 时会产生亏损，基于此发现，我们可以在用 0.1 手测试时构建一个稳定增长的余额曲线，此曲线的特征在使用几何 MM 测试时会发生剧烈变化，转变为一个稳定下降趋势的曲线！通过 MS Excel 的方式创建的图如下所示。

此示例的依据理论是我们的交易结果是交替的（获利/亏损）：首先我们进行一个盈利 100 点的交易，然后进行一个亏损交易，计算此亏损额时，如果使用了几何 MM，则此亏损额是两个操作的亏损总额，而使用“0.1”MM 时，我们就获得了利润总额。

还要考虑到经纪公司关于最小手数及其最小增量的限制（根据 Alpari-IDC 的条款，分别对应 0.1 和 0.01）。这就是为何在任何情况下，保证金都不会低于 1000 美元太多的原因，因为有最小手数的限制，即 0.1。所以，为了避免此类“边界效应”，初始保证金要比前一个 1000 美元大 10 倍。

我们发现的现象：尽管在利润有 100 点时会产生精确计算的亏损值（点数），此时几何 MM 会产生正好等于之前盈利的亏损，但实际上还是有一定的交易亏损值范围，在这个范围内，余额的值会稳定地在特定有限范围内循环。我现在还不了解其中的缘由。以下是图示；初始保证金始终是 10000 美元，获利交易 100 个点，几何 MM 的比例为每 1000 美元保证金 0.1 手。

亏损交易 - 91 个点（获利交易大于亏损交易 9 个点）

上图显示了不同 MM 的两个曲线图。以下使用 0.1 手的相同余额曲线被放大，以显示其锯齿状的特征。此外，第二张图不会显示，因为其特征始终与这一个相似。

显示亏损数学期望值等于 91 的图，以说明亏损交易的“阈值”，在这个阈值上，使用“0.1”MM 的正式盈利系统会转变为使用几何 MM 的无盈无亏系统。

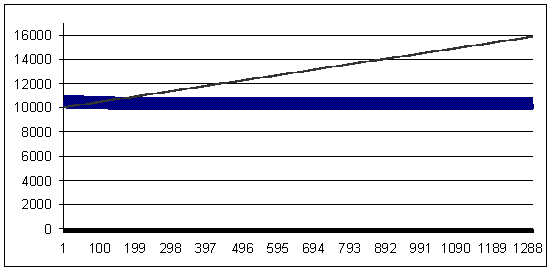
亏损值 91，几何 MM 0.1/$1000

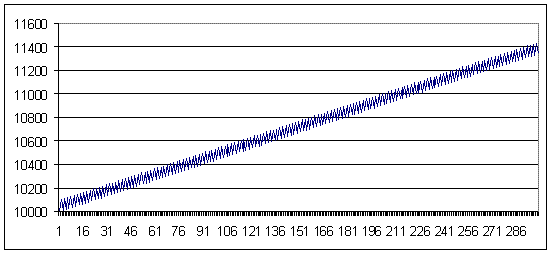
亏损值 91，手数 = 0.1

亏损交易 - 92 个点（获利交易大于亏损交易 8 个点）

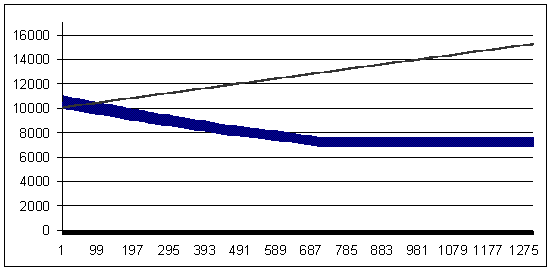
亏损值 92，几何 MM 0.1/$1000

亏损交易 - 93 个点（获利交易大于亏损交易 7 个点）

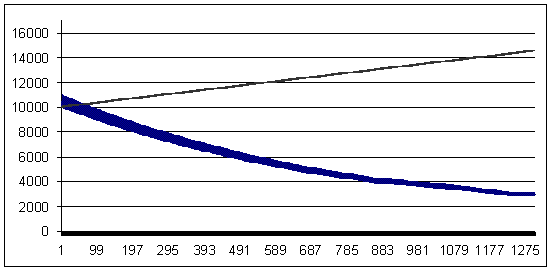
亏损值 93，几何 MM 0.1/$1000

亏损交易 - 94 个点（获利交易大于亏损交易 6 个点）

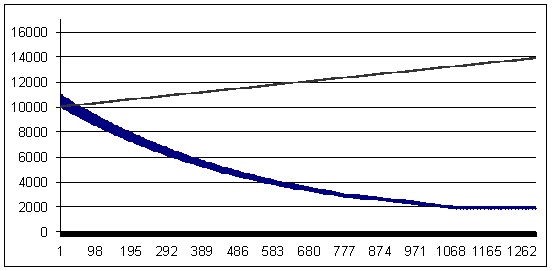
亏损值 94，几何 MM 0.1/$1000

亏损交易 - 96 个点（获利交易大于亏损交易 4 个点）

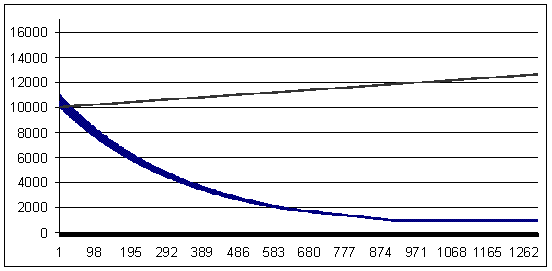
亏损值 96，几何 MM 0.1/$1000

看，曲线外观是相反的。当然，实时系统很少这么“稳定”，但我举这个例子仅仅是为了说明如果我们没有非常慎重地考虑“0.1 手”的测试图表，将会发生什么情况。

现在，让我们看一看，如果我们使几何 MM 更具进取性（例如每 1000 美元保证金 0.2 甚至 0.33 手；你可以在论坛里找到这种案例），将会发生什么情况。之后，你将看到仅属于亏损交易边界值的图表（获利交易仍等于 100 个点）：如果亏损交易超过某个边界值，使用几何 MM 时的曲线特征会变得更糟。

亏损交易 - 84 个点（获利交易大于亏损交易 16 个点）。MM - 几何，0.2 手/1000 美元保证金。

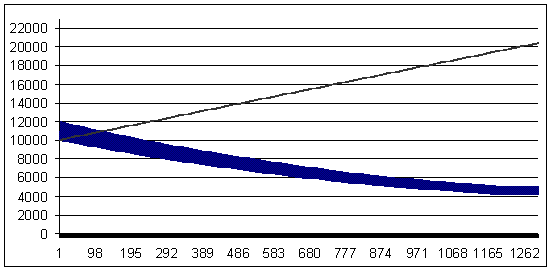
亏损值 84，几何 MM 0.2/$1000

亏损交易 - 75 个点（获利交易大于亏损交易 25 个点）。MM - 几何，0.33 手/1000 美元保证金。

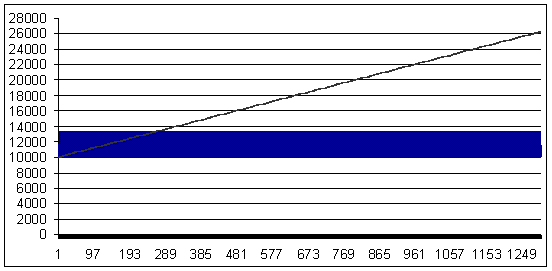
亏损值 75，几何 MM 0.33/$1000

结论：策略的积极性越高，在获利交易的数学期望值不变的情况下，对策略的要求就更高：必须增加交易的数学期望值点数。我们可以确定一个公式，通过以下参数定义亏损交易的阈值点数 (loss)：

- 获利交易的利润（利润），

- 几何 MM 的积极性 (aggr)，即每 10000 美元保证金的仓位手数。

- 1 手证券的 1 点的值 (pointval)。

要证明此公式，我们仅需要打开前两个交易，保证金从 10000 美元开始，然后无论获得了多少保证金都将实现此关联性（稍早前已证明这一点，因为取消了 X 参数）。

1. 第一个交易带来了利润：保证金等于 10000 美元。在达到 aggr 手数时建仓。我们获得的利润为aggr *profit *pointval。平仓。
2. 打开第二个交易，它产生了亏损。截止建仓时，保证金等于 $10000+ aggr*profit*pointval= $101000*(1+aggr*profit*pointval/10000).交易量为 aggr*(1+aggr*profit*pointval/10000)。所需的交易亏损（美元）等于 aggr*(1+aggr*profit*pointval/10000) *loss*pointval。
3. 使这两个获得的表达式等值，并获得亏损公式：

loss = profit / (1+ aggr*profit*pointval /10000)

让我们根据 EURUSD 检查此公式的正确性 (pointval=$10)：

- 如果 profit=100，aggr=1，我们获得 loss = 100/(1+1*100*10/10000) = 100/1.1 ~ 90.91 pips。如之前所述，这种情况下的阈值等于 91 个点（参见第一个图表）；

- 如果 profit=100，aggr=2，我们获得 loss = 100/1.2 ~ 83.33.之前在实验中获得的阈值等于 84 个点；

- 如果 profit=100，aggr=3.33，我们获得 loss = 100/1.33 ~ 75.19.之前在实验中获得的阈值等于 75 个点。

与实验数据的符合程度还不错。但是，实际余额图不会是这样的：获利交易和亏损交易的比例通常是不相等的。我们不会尝试将此模型应用于更复杂的案例，因为人工余额曲线构造的一般原理已经很清楚了。让我们用第三种名为“温和”的 MM 来测试 EA，从而完成我们的研究。

测试 3：手数与保证金的平方根成比例。

策略测试程序报告 20_200 expert_v4.2_AntS

Alpari-Demo (Build 215)

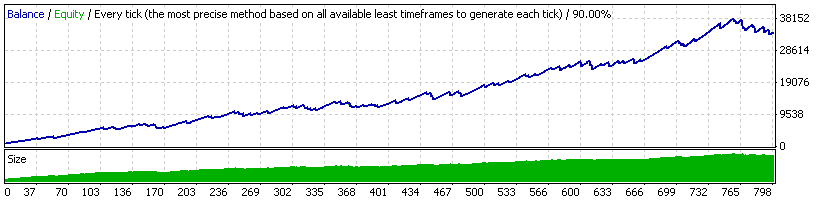
Expert Advisor 20_200 expert_v4.2_AntS，温和 MM

RF= 32764.09 / 5632.51 =5.82

在这种情况下，初始保证金等于1000 美元，初始手数为 0.1。

此 MM 采用上述分析过的两种情况的中间仓位。最大亏损并不很大，但相对亏损仍然相当大，尽管比使用几何 MM 的方法小得多。尽管如此，此曲线仍然相当不错，比第二种（EA "20_200" 的曲线）好得多。此外，它也比第二种稳定得多。

这种方法有多种不同的变化。例如，如果取初始保证金值为 10000 美元，并将初始手数设为 1.0 （注释前一个代码类型）：

case 2: size = 1. * MathSqrt( AccountBalance() / 10000 );

之前显示的将近 8 年的利润增加了 10 倍，当相对亏损并未发生变化。

总结

这部分得出的大多数结论都专门用于几何 MM。作者正在计划发表“谬误”系列的第二篇文章，以说明在某些“有趣的”策略的交易结果序列分析过程中出现的一些统计规律性。说明材料的级别略高于本文，但不会太过令人费解。

现在我对文章标题进行最终的注释：是的，资金管理是第二位的，因为很显然，资金管理很难帮助你挽救一个在 0.1 手时亏损的策略并将其转变为可盈利的强大策略。但是，第二句才真正部分反驳了谚语“物极必反”：任何允许使用不同资金管理类型的策略，即便它盈利能力强而且稳定，仍可能被积极性不足的 MM 所扼杀。