Series temporales de previsión financiera
Introducción
Este artículo trata sobre una de las aplicaciones prácticas más populares de redes neuronales, la previsión de las series temporales del mercado. En este campo, la previsión está relacionada más estrechamente con la rentabilidad y se puede considerar como una de las actividades de los negocios.
Las series temporales de previsión financiera son un elemento imprescindible para cualquier actividad de inversión. El concepto de invertir , poner dinero ahora para ganar beneficios en el futuro, se basa en el concepto de predecir el futuro. Por lo tanto, las series temporales de previsión financiera forman la base de las actividades de toda la industria de la inversión; todos los intercambios organizados y otros sistemas de trading de instrumentos financieros.
Vamos a dar algunas cifras que ilustren la escala de esta industria de previsión (Sharp, 1997). El volumen diario del mercado de valores de Estados Unidos supera los 10 billones de dólares. La Depositary Trust Company de Estados Unidos, donde se registran los valores en la cantidad de 11 trillones de dólares (del volumen total de 18 trillones de dólares), marca aproximadamente 250 billones de dólares diarios. El trading en el FOREX a nivel mundial es incluso más activo. Sus rendimientos diarios superan los 1000 billones de dólares. Es aproximadamente 1/50 del capital global acumulado.
El 99% de todas las transacciones se conocen por ser especulativas, es decir, no están destinadas a la circulación de bienes básicos, pero se llevan a cabo para obtener beneficios de la estrategia: "comprar barato y vender más caro". Todos se basan en las previsiones de los negociadores sobre los cambios de las tasas. Al mismo tiempo, y esto es muy importante, las previsiones hechas por las partes en cada transacción son opuestas. Por lo que el volumen de las transacciones especulativas caracteriza la medida de las discrepancias en el mercado de las previsiones de las partes, que es en realidad la medida de imprevisibilidad de las series temporales financieras.
Esta importante propiedad de las series temporales del mercado forma la base de la hipótesis del mercado eficiente presentada por Louis Bachelier en su tesis en 1900. De acuerdo con esta doctrina, un inversor puede esperar solamente la rentabilidad promedia estimada del mercado mediante tales índices como Dow Jones o S&P500 (para la bolsa de Nueva York). Sin embargo, cada beneficio especulativo se produce aleatoriamente y es parecido a un juego de azar. La imprevisibilidad de las curvas del mercado se determina por la misma razón por la que apenas se encuentra el dinero tirado por el suelo de calles concurridas: hay demasiados voluntarios para recogerlo.
La teoría de los mercados eficientes no se sostiene, como es natural, por los propios participantes en el mercado (porque están exactamente en la búsqueda de este dinero que se "cae"). La mayoría de ellos están seguros de que las series temporales del mercado, aunque parecen ser estocásticas, están llenas de regularidades ocultas, es decir, son al menos parcialmente predecibles. Fue Ralph Elliott, el fundador del análisis técnico, quien intentó descubrir tales regularidades empíricas ocultas en los años 30.
En la década de los 80, este punto de vista encontró un sorprendente apoyo en las dinámicas de la teoría del caos que habían ocurrido poco antes. La teoría se basa en la oposición del estado de caos y la estocasticidad (aleatoriedad). Las series caóticas sólo aparecen aleatoriamente, pero al ser un proceso dinámico determinado, dejan bastante espacio para un pronóstico a corto plazo. La zona de posibles pronósticos está limitada en el tiempo por el horizonte de previsión, pero que puede ser suficiente para obtener auténticos beneficios gracias a las previsiones (Chorafas, 1994). Entonces, aquellos que tienen mejores métodos matemáticos para extraer las regularidades de las series ruidosas caóticas pueden aspirar a un mayor beneficio; a expensas de sus compañeros peor equipados.
En este artículo, vamos a proporcionar datos concretos confirmando la previsibilidad parcial de las series temporales financieras e incluso evaluar numéricamente esta previsibilidad.
Análisis técnico y redes neuronales
En las últimas décadas, el análisis técnico; un conjunto de reglas empíricas basadas en varios indicadores de comportamiento del mercado; llegó a ser más y más popular. El análisis técnico se centra en el comportamiento individual de un instrumento financiero determinado, en relación a otros instrumentos financieros (Pring,1991).
Este enfoque se basa psicológicamente en la concentración de los brókers exactamente en el instrumento financiero con el que están trabajando en un momento concreto. Según Alexander Elder, un conocido analista técnico (se formó inicialmente como psicoterapeuta), el comportamiento de la comunidad del mercado es muy similar a la conducta de la multitud caracterizada por leyes especiales de la psicología de masas. El efecto de la multitud simplifica el pensamiento, allana las peculiaridades individuales y produce las formas del colectivo, el comportamiento gregario que es más primitivo que el individual. En particular, el instinto social realza el papel de un líder, un macho/hembra alfa. La curva de los precios, según Elder, es exactamente este líder que enfoca la conciencia colectiva del mercado sobre sí mismo. Esta interpretación psicológica del comportamiento de los precios en el mercado demuestra esa aplicación de la teoría del caos dinámica.. La previsibilidad parcial del mercado está determinada por un comportamiento colectivo relativamente primitivo de participantes que forman un único sistema dinámico caótico, con una cantidad relativamente pequeña de grados internos de libertad.
Según esta doctrina, tenemos que "romper las ataduras" de la multitud, elevarse por encima de ella y llegar a ser más inteligentes que la multitud para ser capaces de predecir las curvas del mercado. Para este propósito, se supone que debemos desarrollar un sistema de apuestas basado en el comportamiento anterior de una serie temporal y seguir este sistema de manera estricta; sin vernos afectados por las emociones y los rumores que circulan alrededor del mercado. En otras palabras, las previsiones deben basarse en un algoritmo, es decir, que pueden e incluso deben ser entregadas a un ordenador (LeBeau, 1992). Las personas deben simplemente crear este algoritmo, ya que disponen de diversos programas que facilitan el desarrollo y el soporte posterior de las estrategias basadas en las herramientas de análisis técnico.
Según esta lógica, por qué no usar un ordenador en la etapa del desarrollo de la estrategia para encontrar indicadores óptimos y estrategias óptimas para los indicadores encontrados y no como un asistente para calcular los conocidos indicadores del mercado y probar sus estrategias. Este enfoque apoyado por el uso de las tecnologías de redes neuronales ha ido ganando más y más adeptos desde principios de los años 90 (1995, Baestaens Beltratti, 1997), ya que tiene unas ventajas indiscutibles.
En primer lugar, el análisis de redes neuronales, a diferencia del técnico, no supone ninguna limitación en la naturaleza de los datos de entrada. Pueden ser tanto los indicadores de las series temporales dadas y como las informaciones sobre el comportamiento de otros valores del mercado. No sin razón, son los inversores institucionales (por ejemplo, grandes fondos de pensiones) que utilizan activamente las redes neuronales. Esos inversores trabajan con grandes carteras, por lo que las correlaciones entre los distintos mercados son de primordial importancia.
En segundo lugar, a diferencia del análisis técnico basado en recomendaciones generales, las redes neuronales pueden encontrar los indicadores óptimos para un instrumento financiero determinado y en base a ellos pronosticar las estrategias óptimas, de nuevo, para las series temporales determinadas. Además, estas estrategias pueden ser adaptables, cambiar con el mercado, que es de primordial importancia para los nuevos mercados, particularmente para el ruso.
El diseño de la red neuronal se basa únicamente en los datos sin implicar ninguna consideración previa. Allí reside su fuerza y al mismo tiempo su talón de Aquiles. Los datos disponibles pueden ser insuficientes para el aprendizaje, la dimensionalidad de los posibles aportes puede ser demasiado alta. Más adelante en este artículo, vamos a demostrar cómo nos puede ayudar la experiencia adquirida mediante el análisis técnico a superar estas dificultades típicas en el campo de las previsiones financieras.
Técnica de previsión de las series temporales
Como primer paso, vamos a describir el esquema general de la previsión de las series temporales mediante las redes neuronales (Fig. 1).
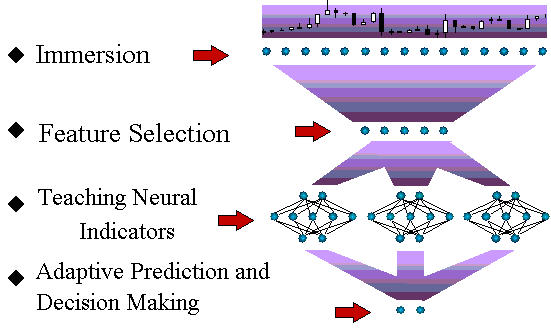
Fig. 1. El esquema del ciclo tecnológico de previsión de las series temporales.
Más adelante en este artículo, explicaremos brevemente todas las etapas de este proceso. Aunque los principios generales de los modelos de redes neuronales son íntegramente aplicables a esta tarea, la previsión de las series temporales financieras tiene sus propias características. Son estas características específicas las que serán descritas en este artículo, en la mayor medida posible.
Técnica de inmersión. Teorema de Tackens
Vamos a empezar con la etapa de inmersión. Como vamos a ver ahora, para todos los pronósticos que parecen ser la extrapolación de datos, las redes neuronales resuelven el problema de la interpolación que aumenta considerablemente la validez de la solución. La previsión de las series temporales se resuelve por sí sola en el problema de la rutina del análisis neuronal; aproximación de una función multivariable para un determinado conjunto de ejemplos; mediante el método de inmersión de las series temporales en un espacio multidimensional (Weigend, 1994). Por ejemplo, un espacio de retraso -dimensional de series temporales ![]() se compone de los valores de las series temporales en instantes sucesivos en el tiempo:
se compone de los valores de las series temporales en instantes sucesivos en el tiempo:
![]() .
.
El siguiente teorema de Tackens se ha demostrado con los sistemas dinámicos: Si las series temporales se generan por un sistema dinámico, es decir, los valores de ![]() son una función arbitraria del estado de un sistema de este tipo, existe tal profundidad de inmersión (aproximadamente igual al número efectivo de los grados de libertad de este sistema dinámico) que proporciona una previsión inequívoca del siguiente valor de las series temporales (Sauer, 1991). Así, la elección de un valor suficientemente grande puede garantizar una clara relación entre el valor futuro de las series temporales y sus valores anteriores:
son una función arbitraria del estado de un sistema de este tipo, existe tal profundidad de inmersión (aproximadamente igual al número efectivo de los grados de libertad de este sistema dinámico) que proporciona una previsión inequívoca del siguiente valor de las series temporales (Sauer, 1991). Así, la elección de un valor suficientemente grande puede garantizar una clara relación entre el valor futuro de las series temporales y sus valores anteriores:![]() es decir que la previsión de unas series temporales se resuelve en el problema de la interpolación de la función multivariable. A continuación, puede usar la red neuronal para restaurar esta función desconocida sobre la base de un conjunto de ejemplos definidos por el historial de estas series temporales.
es decir que la previsión de unas series temporales se resuelve en el problema de la interpolación de la función multivariable. A continuación, puede usar la red neuronal para restaurar esta función desconocida sobre la base de un conjunto de ejemplos definidos por el historial de estas series temporales.
Por el contrario, en cuanto a series temporales aleatorias, el conocimiento del pasado no proporciona ninguna pista útil para predecir el futuro. Así, de acuerdo con la teoría de mercado eficiente, la dispersión de los valores predictivos de las series temporales no cambiará cuando se sumerjan en el espacio retardado.
La diferencia entre una dinámica caótica y un estocástico (aleatorio) detectado durante la inmersión se muestra en la Fig. 2.
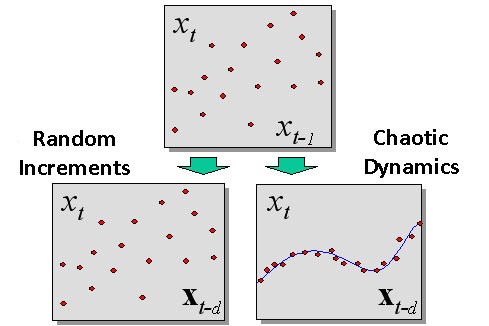
Fig. 2. La diferencia entre un proceso aleatorio y una dinámica caótica detectada durante la inmersión.
Confirmación empírica de la previsibilidad de las series temporales
El método de inmersión nos permite cuantificar la previsibilidad de los instrumentos financieros reales, es decir, probar o refutar la hipótesis del mercado eficiente. De acuerdo con el último, la dispersión de los puntos en todas las coordenadas del espacio retardado es idéntica (si los puntos son valores aleatorios independientes distribuidos idénticamente). Por el contrario, la dinámica caótica que proporciona la previsibilidad debe conducir a que las observaciones estarán agrupadas alrededor de una determinada hipersuperficie 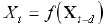 , es decir, la muestra experimental forma un conjunto con una dimensión inferior a la dimensión de todo el espacio retardado.
, es decir, la muestra experimental forma un conjunto con una dimensión inferior a la dimensión de todo el espacio retardado.
Para medir las dimensiones, puede usar la siguiente propiedad intuitiva: Si un conjunto tiene la dimensión D, entonces, siempre y cuando se divide en superficies cúbicas más pequeñas con un lado de ![]() , el número de tales cubos crecerá como
, el número de tales cubos crecerá como![]() . Este hecho se basa en la detección de la dimensión de conjuntos por el método de conteo de recuadros que conocemos de las consideraciones anteriores. La dimensión de un conjunto de puntos se detecta por la tasa de crecimiento del número de recuadros que contienen todos los puntos del conjunto. Para acelerar el algoritmo, tomamos las dimensiones de
. Este hecho se basa en la detección de la dimensión de conjuntos por el método de conteo de recuadros que conocemos de las consideraciones anteriores. La dimensión de un conjunto de puntos se detecta por la tasa de crecimiento del número de recuadros que contienen todos los puntos del conjunto. Para acelerar el algoritmo, tomamos las dimensiones de 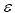 como múltiplos de 2, es decir, la escala de resolución se mide en bits.
como múltiplos de 2, es decir, la escala de resolución se mide en bits.
Como ejemplo de series temporales del mercado, tomaremos herramientas financiera muy conocidas como el índice S&P500 que refleja la dinámica del precio medio en la bolsa de Nueva York La Fig. 3 muestra el índice dinámico para el período de 679 meses. En la figura 4 se muestra la dimensión (dimensión de la información) de incrementos de estas series temporales calculada por el método de conteo de recuadros.
| Fig. 3. Series temporales de 679 valores de S&P500, se usa en este artículo como un ejemplo. | |
Fig. 4. Dimensión de la información de los incrementos de las series temporales de S&P500. |
|---|
Como se deduce de la Fig. 4, los puntos experimentales forman un conjunto de dimensión aproximada 4 en un espacio de inmersión dimensional 15. Esto es muy inferior a los 15 que obtendríamos en base a la teoría del mercado eficiente que considera las series temporales de incrementos como valores aleatorios independientes.
Así, los datos empíricos proporcionan una evidencia de la presencia de un cierto componente previsible en la series temporales financieras, aunque no podemos exponer que aquí hay una completa dinámica caótica determinada. Entonces los intentos para aplicar los análisis de redes neuronales para la previsión de mercado están basados en razones de peso.
Sin embargo, debería señalarse que la previsibilidad teórica no garantiza la posibilidad de alcanzar un nivel de previsión importante en la práctica. Se puede obtener una estimación cuantitativa de la previsibilidad de series temporales concretas midiendo la entropía cruzada, que también es posible mediante la técnica de conteo de recuadros. Por ejemplo, mediremos la previsibilidad de los incrementos de S&P500 en relación con la profundidad de inmersión. Entropía cruzada
![]() ,
,
cuyo gráfico se muestra a continuación (Fig. 5), mide la información adicional en el siguiente valor de las series temporales, en base a los valores anteriores de estas series temporales.
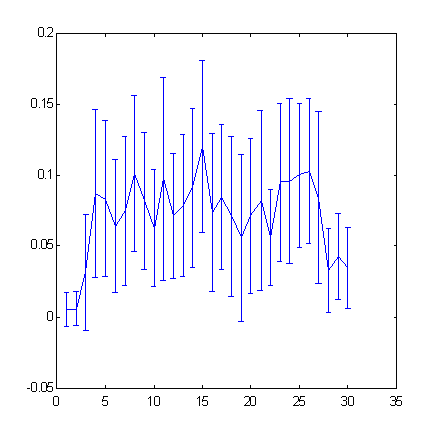
Fig. 5. La previsibilidad de las series temporales S&P500 en función de la profundidad de inmersión (el ancho de la "ventana").
El aumento de la profundidad de inmersión por encima de 25 estará acompañado por una previsibilidad decreciente.
Más adelante evaluaremos el beneficio que es prácticamente alcanzable en tal nivel de previsibilidad.
Formar un espacio de entrada de atributos
En la figura 5 puede ver que el aumento de la anchura de la ventana de inmersión de las series temporales resulta finalmente en la previsibilidad de la disminución; cuando ya no se compensan las dimensiones crecientes de entrada por sus valores de información. En este caso, si la dimensión del espacio retardado es demasiado larga para el número de ejemplos, tenemos que usar métodos especiales para formar un espacio de atributos con dimensiones más pequeñas. Los métodos que usan las series temporales financieras para seleccionar los atributos y/o aumentar la cantidad de los ejemplos disponibles se describirán más abajo.
Elección del error funcional
Para hacer un aprendizaje de la red neuronal, no es suficiente formar conjuntos para el aprendizaje de las entradas/salidas. Se debe determinar también el error de previsión de la red. El error cuadrático medio usado por defecto en la mayoría de las aplicaciones de redes neuronal no tiene mucho "sentido financiero" para las series temporales del mercado. Por esto vamos a abordar los errores específicos para las series temporales financieras y demostrar cómo están relacionados a la posible tasa de beneficio en una sección especial el artículo.
Por ejemplo, para elegir una posición del mercado, una detección fiable de la señal de cambios de la tasa es mucho más importante que la disminución de la desviación elevada al cuadrado. Aunque estas indicaciones no están relacionadas entre sí, las redes optimizadas para una de ellas proporcionarán peores previsiones para la otra. Elegir una función de error adecuada, como lo vamos a demostrar más adelante en este artículo, debe basarse en una cierta estrategia ideal y dictada, por ejemplo, por el deseo de maximizar los beneficios (o minimizar posibles pérdidas).
Aprendizaje de las redes neuronales
Las principales características específicas de previsión de las series temporales están en el campo de datos de pre-procesamiento. El proceso de aprendizaje para las redes neuronales separadas es un estándar. Como de costumbre, los parámetros disponibles están divididos en tres muestras: aprender, validar y probar. El primero se usa para el aprendizaje de la red, el segundo es para seleccionar la arquitectura de la red óptima y/o para seleccionar el momento para detener el aprendizaje de la red. Finalmente, el tercero que no ha sido utilizado para el aprendizaje en absoluto sirve para el control de la calidad de la previsión de la red neuronal "entrenada".
Sin embargo, para las series temporales financieras muy ruidosas, el uso de círculos de redes neuronales puede resultar en la obtención de una significativa fiabilidad de previsión. Terminaremos este artículo con una discusión de esta técnica.
En algunas investigaciones, hay evidencias de la mejora de la calidad de la previsión gracias al uso de las redes neuronales de retroalimentación. Dichas redes pueden tener una memoria local que guarda los datos de de fechas anteriores a las fechas de las entradas. Sin embargo, considerar tales arquitecturas nos apartaría del tema principal, ya que existen otros métodos eficientes de expansión del "horizonte" de la red gracias a las técnicas de inmersión de las series temporales especiales que se describen a continuación.
Formar un espacio de atributos
La codificación eficiente de las entradas es clave para mejorar la calidad de la previsión. Es particularmente importante para las series temporales financieras difícilmente predecibles. Todas las recomendaciones estándar sobre el pre-procesamiento de datos son aplicables aquí también. Sin embargo, existen métodos de series temporales financieras específicas de pre-procesamiento de datos que vamos a examinar en más detalle en esta sección.
Métodos de inmersión de series temporales
En primer lugar, debemos tener en cuenta que no deberíamos usar los valores de las propias cotizaciones, que designamos como ![]() , como entradas o salidas de una red neuronal. Estos son cambios de cotización que son realmente significativos para la previsión. Dado que estos cambios se encuentran, por regla general, dentro de un rango mucho menor que las propias cotizaciones, existe una fuerte correlación entre los valores de las tasas; el siguiente valor más probable de la tasa es igual a su valor anterior:
, como entradas o salidas de una red neuronal. Estos son cambios de cotización que son realmente significativos para la previsión. Dado que estos cambios se encuentran, por regla general, dentro de un rango mucho menor que las propias cotizaciones, existe una fuerte correlación entre los valores de las tasas; el siguiente valor más probable de la tasa es igual a su valor anterior: ![]() . Al mismo tiempo, como se subrayó en repetidas ocasiones, para aumentar la calidad del aprendizaje, deberíamos trabajar para la independencia estadística de las entradas, es decir, para la ausencia de dichas correlaciones.
. Al mismo tiempo, como se subrayó en repetidas ocasiones, para aumentar la calidad del aprendizaje, deberíamos trabajar para la independencia estadística de las entradas, es decir, para la ausencia de dichas correlaciones.
Por eso, es lógico seleccionar los valores más independientes estadísticamente como entradas, por ejemplo, los cambios de cotización ![]() o el logaritmo del incremento relativo
o el logaritmo del incremento relativo ![]() . La última opción es buena para las series temporales de larga duración, donde la inflación influye al llegar a ser bastante notable. En este caso, las simples diferencias en diferentes partes de la serie recaerán en diferentes rangos ya que en realidad se miden en unidades diferentes. Por el contrario, las proporciones entre comillas consecutivas no dependen de las unidades de medición y serán de la misma escala, aunque las unidades de medida cambian debido a la inflación. En consecuencia, una mayor estacionalidad de las series temporales nos va a permitir usar un historial mayor y ofrecer un mejor aprendizaje.
. La última opción es buena para las series temporales de larga duración, donde la inflación influye al llegar a ser bastante notable. En este caso, las simples diferencias en diferentes partes de la serie recaerán en diferentes rangos ya que en realidad se miden en unidades diferentes. Por el contrario, las proporciones entre comillas consecutivas no dependen de las unidades de medición y serán de la misma escala, aunque las unidades de medida cambian debido a la inflación. En consecuencia, una mayor estacionalidad de las series temporales nos va a permitir usar un historial mayor y ofrecer un mejor aprendizaje.
Una de las desventajas de la inmersión en un espacio retardado es la limitación de "horizontes" de la red. Por el contrario, el análisis técnico no soluciona la ventana en el pasado y a veces usa valores muy alejados de las series temporales. Por ejemplo, los valores máximos y mínimos de una serie temporal, incluso tomados de un pasado relativamente remoto, influyen más fuertemente en la psicología de los traders y por lo tanto estos valores deben seguir siendo importantes para la previsión. Una ventana suficientemente amplia para sumergirse en el espacio retardado no puede proporcionar dicha información, lo cual, evidentemente, disminuye la eficiencia de la previsión. Por otra parte, ampliar la ventana a estos valores que cubren los valores distantes y los valores extremos de las series temporales aumentarán las dimensiones de la red. Esto, a su vez, tendrá como resultado la disminución de la exactitud de las previsiones de la red neuronal; ahora debido al crecimiento de la red.
Una manera de salir de este aparente estancamiento de la situación pueden ser los métodos alternativos de codificación del comportamiento pasado de las series temporales. Es obvio que más amplio es el historial de las series temporales, menos influencia tendrá su comportamiento en los resultados de la previsión. Esto está determinado por la percepción subjetiva del pasado por los traders que, estrictamente hablando, forman el futuro. Por lo tanto, deberíamos encontrar esa representación de las series temporales dinámicas, que tendrían una precisión selectiva: cuanto más al pasado, menos detalles. Al mismo tiempo, el aspecto general de la curva debe permanecer intacto. La denominada descomposición ondícula puede ser muy prometedora. Es equivalente en su valor de información a la inmersión retardada, pero hace que sea más sencillo comprimir los datos de modo que el pasado se describe con una precisión selectiva.
Disminución de las dimensiones de las entradas: Atributos
Esta compresión de datos es un ejemplo de cómo extraer los atributos más significativos para la previsión de un número demasiado grande de variables de entrada. Los métodos de extracción sistemática de atributos ya han sido descritos anteriormente. También pueden (y deben) ser sucesivamente aplicados a la previsión de series temporales.
Es importante que la representación de las entradas facilite la extracción de los datos. La representación ondícula es un ejemplo de un bien (desde el punto de vista de la extracción de atributos) que codifica (Kaiser, 1995). Por ejemplo, el siguiente gráfico (Fig. 6) muestra una sección de 50 valores de la serie temporal con su reconstrucción por 10 coeficientes ondícula especialmente seleccionados. Tenga en cuenta que, a pesar de que necesita cinco veces menos datos, el pasado inmediato de las series temporales se reconstruye con precisión, mientras que el pasado remoto se restaura en el esquema general, los altibajos se reflejan correctamente. Por lo tanto, es posible describir una ventana de 50-dimensional con un vector de entrada de sólo 10-dimensional con una precisión aceptable.
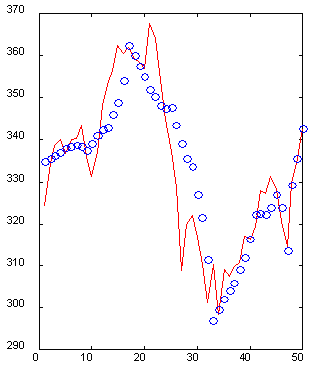
Fig. 6. Un ejemplo de una ventana de 50-dimensional (línea continua) y su reconstrucción por 10 coeficientes de ondícula (o).
Otro posible enfoque está usar diversos indicadores técnicos que se calculan automáticamente en los respectivos paquetes de software (como MetaStock o Windows On Wall Street) como posibles candidatos para el espacio de atributos. El gran número de estos atributos empíricos (Colby, 1988) hace difícil su uso, aunque cada uno de ellos puede resultar útil si se aplica a una determinada serie temporal. Los métodos descritos anteriormente le permitirán seleccionar la combinación más significativa de los indicadores técnicos para usarlos como entradas en la red neuronal.
Método de Sugerencias (hints)
Uno de los puntos más delicados de las previsiones financieras es la falta de ejemplos para el aprendizaje de las redes neuronales. En general, los mercados financieros (especialmente el Ruso) no son estables. Aparecen nuevos índices que aún no se ha acumulado su historial, sin embargo, la naturaleza del trading en los mercados antiguos cambia con el tiempo. En estas condiciones, la duración de la serie temporal disponible para el aprendizaje de redes neuronales es bastante limitada.
Sin embargo, podemos aumentar el número de ejemplos usando algunas consideraciones a priori acerca de las invariantes de la dinámica de series temporales. Este es otro término físico-matemático que puede mejorar considerablemente la calidad de las previsiones financieras. La cuestión es la generación de ejemplos artificiales (consejos) obtenidos a partir de los existentes a través de las distintas transformaciones aplicadas a ellos.
Vamos a explicar la idea principal con un ejemplo. La siguiente premisa es psicológicamente razonable: los traders prestan su atención principalmente a la forma de la curva de precios, no a determinados valores en los ejes. Por lo tanto, si queremos estirar todas las series temporales un poco a lo largo del eje de las cotizaciones, podremos utilizar las series temporales resultantes de dicha transformación (junto con la inicial) para el aprendizaje de las redes neuronales. Así que hemos duplicado el número de ejemplos a priori debido al uso de la información obtenida a partir de las características psicológicas de cómo perciben los traders las series temporales. Además, junto con el aumento del número de ejemplos, nos hemos limitado a la clase de funciones entre las cuales buscamos la solución, lo que también aumenta la calidad de previsión (si, por supuesto, la invariante usada es cierta).
Los resultados del cálculo de la previsibilidad de S&P500 por el método de conteo de recuadros que se muestra a continuación (ver Fig. 7 y 8) ilustran el papel de las sugerencias (hints). En este caso, el espacio de los atributos estaba formado mediante la técnica de ortogonalización. Se utilizaron 30 componentes principales como variables de entrada en el espacio de retardo 100-dimensional. A continuación, hemos seleccionado 7 atributos de estas componentes principales; las combinaciones lineales ortogonales más relevantes. Como se puede ver en las siguientes figuras, en este caso, sólo dio resultado la aplicación de las sugerencias para poder proporcionar una previsibilidad satisfactoria.
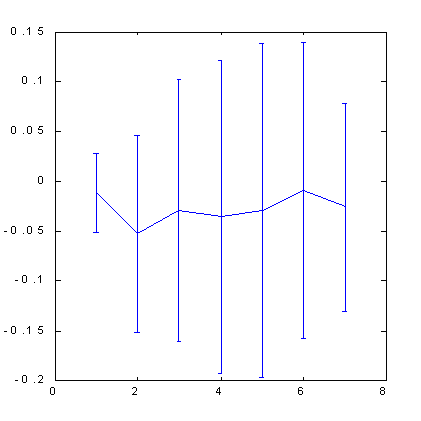
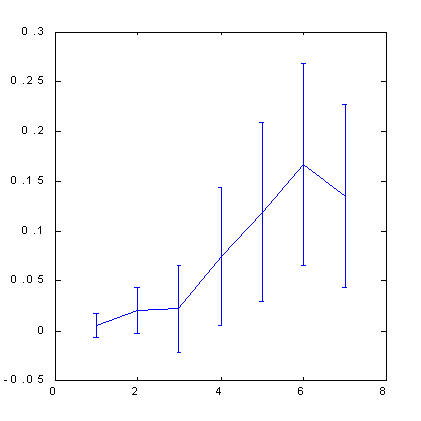
| Fig. 7. Previsibilidad de la señal de cambio de cotizaciones para S&P500. | Fig. 8. La previsibilidad de la señal de cambio de cotizaciones para S&P500 después de la serie de ejemplos ha sido cuadruplicada estirando el eje de los precios. |
Tenga en cuenta que el uso del espacio ortogonal dio lugar a cierto aumento de la previsibilidad, en comparación con el método de inmersión estándar: de 0.12 bits (Fig. 5) a 0.17 bits (Fig. 8). Un poco más tarde, cuando comencemos a discutir la influencia de previsibilidad sobre los beneficios vamos a demostrar que debido a esto la tasa de beneficio puede aumentar de nuevo casi la mitad.
Otro ejemplo menos trivial de un uso satisfactorio utilizando estas sugerencias para que una red neuronal sepa en qué dirección buscar una solución es el uso de la simetría oculta en el trading Forex. El sentido de esta simetría es que las cotizaciones de Forex puedan tenerse en cuenta desde dos puntos de vista ", por ejemplo, como una serie de DM/$ o como una serie de $/DM. El aumento de uno de ellos se corresponde con la disminución del otro. Se puede utilizar esta propiedad para duplicar el número de ejemplos: añadir a cada ejemplo del tipo ![]() su análogo simétrico
su análogo simétrico ![]() . Los experimentos de previsiones de la red neuronal básica mostraron que en el caso de mercados Forex, tener en cuenta la simetría aumenta en beneficio casi el doble, concretamente: entre 5% y 10% al año, considerando los costes actuales de las transacciones (Abu-Mostafa, 1995).
. Los experimentos de previsiones de la red neuronal básica mostraron que en el caso de mercados Forex, tener en cuenta la simetría aumenta en beneficio casi el doble, concretamente: entre 5% y 10% al año, considerando los costes actuales de las transacciones (Abu-Mostafa, 1995).
Medición de la calidad de previsión
Aunque la previsión de las series temporales financieras se resuelve en el problema de aproximación de la función multidimensional, tiene sus propias características especiales tanto formando entradas y seleccionando salidas para una red neuronal. Ya hemos considerado las entradas anteriores. Así que ahora vamos a estudiar las características especiales de la selección de variables de salida. Aunque en primer lugar, debemos responder a la pregunta principal: ¿Cómo puede medirse la calidad de la previsión financiera? Esto nos ayudará a encontrar la mejor estrategia de aprendizaje de redes neuronales.
Relación entre la previsibilidad y la tasa de beneficio
Una característica especial en la previsión de las series temporales financieras es el trabajo para obtener el máximo beneficio, no para minimizar la desviación elevada al cuadrado, como es habitual en el caso de la aproximación de funciones.
En un caso más simple de intercambio diario, los beneficios dependen de la correcta previsión de la señal del cambio de cotización. Esta es la razón por la que la red neuronal debe estar encaminada a una previsión precisa de la señal, no al valor en sí. Ahora veamos cómo se relaciona la tasa de beneficio con la precisión de detección de la señal en el funcionamiento más sencillo para entrar en el mercado diario (Fig. 9).
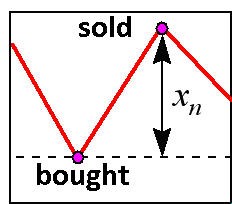
Fig. 9. Entrar en el mercado diario.
Vamos a suponer, que en el momento![]() : el total del capital del trader es
: el total del capital del trader es ![]() , el cambio de cotización relativo es
, el cambio de cotización relativo es ![]() , y como salida de red vamos a tomar su nivel de confianza para la señal de este cambio:
, y como salida de red vamos a tomar su nivel de confianza para la señal de este cambio: ![]() . Esta red con el tipo de salida de no linealidad de
. Esta red con el tipo de salida de no linealidad de ![]() aprende a predecir la señal de cambio y las previsiones de las señal con el rango proporcional a su probabilidad. A continuación, se registran las ganancias de capital en la operación
aprende a predecir la señal de cambio y las previsiones de las señal con el rango proporcional a su probabilidad. A continuación, se registran las ganancias de capital en la operación  del siguiente modo:
del siguiente modo:
![]()
![]()
donde ![]() es la participación del capital "en juego". Es el beneficio para todo el período de trading:
es la participación del capital "en juego". Es el beneficio para todo el período de trading:
que nos permitirá maximizar eligiendo el tamaño óptimo de la tasa 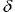 . Deje que el trader pronostique correctamente
. Deje que el trader pronostique correctamente ![]() con las señales y por consiguiente que pronostique erróneamente con la probabilidad de
con las señales y por consiguiente que pronostique erróneamente con la probabilidad de ![]() . A continuación, tenemos el logaritmo de la tasa de beneficio,
. A continuación, tenemos el logaritmo de la tasa de beneficio,
![]() ,
,
y el beneficio en sí será el valor máximo de ![]() y la media:
y la media:
![]() .
.
Aquí hemos introducido el coeficiente de ![]() . Por ejemplo, para la distribución Gaussiana,
. Por ejemplo, para la distribución Gaussiana,![]() . El nivel de la previsibilidad de la señal está directamente relacionado con la entropía cruzada que puede calcularse a priori por el método de recuento de recuadros. Para la salida binaria (véase Fig. 10):
. El nivel de la previsibilidad de la señal está directamente relacionado con la entropía cruzada que puede calcularse a priori por el método de recuento de recuadros. Para la salida binaria (véase Fig. 10):
![]()
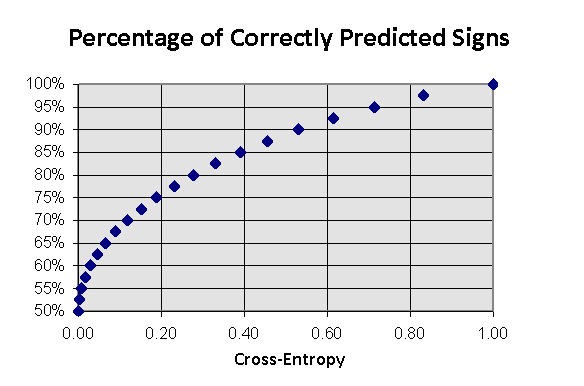
Fig. 10. Fracción de direcciones pronosticadas correctamente de las variaciones de series temporales como una función de entropía cruzada de la señal de salida con entradas conocidas.
Finalmente, obtenemos la siguiente estimación de la tasa de beneficio para el valor de previsibilidad I de la señal expresado en bits:
![]() .
.
Esto significa que, para las series temporales con la previsibilidad I, en principio es posible duplicar el capital dentro de ![]() entradas en el mercado. Así, por ejemplo, la previsibilidad de las series temporales de S&P500 calculada previamente igual a I= 0.17 (véase la Fig. 8) supone duplicar el capital en promedio para
entradas en el mercado. Así, por ejemplo, la previsibilidad de las series temporales de S&P500 calculada previamente igual a I= 0.17 (véase la Fig. 8) supone duplicar el capital en promedio para ![]() entradas al mercado. Por lo tanto, incluso una señal de previsibilidad de un pequeño cambio de cotización puede proporcionar una tasa de beneficio satisfactoria.
entradas al mercado. Por lo tanto, incluso una señal de previsibilidad de un pequeño cambio de cotización puede proporcionar una tasa de beneficio satisfactoria.
Aquí debemos destacar que la tasa de beneficio óptimo requiere más bien un juego cuidadoso, en cada entrada al mercado el jugador arriesga una parte estrictamente definida del capital:
![]() ,
,
donde ![]() es el típico tamaño de beneficio/pérdida para esta volatilidad del mercado
es el típico tamaño de beneficio/pérdida para esta volatilidad del mercado ![]() . Tanto los valores de tasas pequeñas como grandes disminuirán los beneficios, un mercado demasiado arriesgado siendo es capaz de generar pérdidas con cualquier previsibilidad. Se ilustra este hecho en la Fig. 11.
. Tanto los valores de tasas pequeñas como grandes disminuirán los beneficios, un mercado demasiado arriesgado siendo es capaz de generar pérdidas con cualquier previsibilidad. Se ilustra este hecho en la Fig. 11.
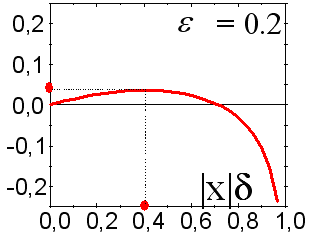
Fig. 11. Dependencia de la tasa de beneficio media de la parte seleccionada del capital "en juego".
Esto se debe a que las estimaciones por arriba dan una idea solamente del límite superior de la tasa de beneficio. Un estudio más cuidadoso, que tenga en cuenta el efecto de la fluctuaciones, no está dentro del alcance de este artículo. Sin embargo, está cualitativamente claro que la elección óptima de los tamaños de los contratos requiere la evaluación de la exactitud de la previsión en cada paso.
Elección del error funcional
Si nos proponemos pronosticar las series temporales financieras para que se maximicen los beneficios, es lógico ajustar la red neuronal a este resultado final. Por ejemplo, si opera de acuerdo al esquema de arriba, puede elegir para el aprendizaje de la red neuronal la siguiente función de error de aprendizaje promediada por todos los ejemplos de la muestra de aprendizaje:
![]() .
.
Aquí, la parte del capital en juego se introduce como una salida de red adicional para ajustarse durante el aprendizaje. Para este enfoque, la primera neurona, ![]() , con función de activación
, con función de activación ![]() nos dará la probabilidad de aumento o disminución de la tasa, mientras que la segunda salida de la red,
nos dará la probabilidad de aumento o disminución de la tasa, mientras que la segunda salida de la red,![]() , proporcionará la parte recomendada del capital para invertir en esta etapa.
, proporcionará la parte recomendada del capital para invertir en esta etapa.
Sin embargo, ya que esta acción, de acuerdo al análisis anterior, debe ser proporcional al nivel de confianza de la previsión, puede reemplazar las dos salidas de red con una sola colocando ![]() y limitándose a la optimización de un sólo parámetro global,
y limitándose a la optimización de un sólo parámetro global,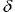 , que minimizará el error:
, que minimizará el error:
![]()
Esto genera la posibilidad de regular la tasa de acuerdo al nivel de riesgo pronosticado por la red. Jugar con tasas variables produce más beneficios que jugar con tasas fijas. Además, si fija la tasa habiéndola definido por su previsibilidad media , entonces la tasa de crecimiento del capital será proporcional a ![]() , mientras que si selecciona la tasa óptima en cada etapa, será proporcional a
, mientras que si selecciona la tasa óptima en cada etapa, será proporcional a ![]() .
.
Usar redes de círculos
Generalmente hablando, las previsiones hechas por diferentes redes entrenadas en la misma muestra serán diferentes debido a la naturaleza aleatoria de elegir los valores iniciales de pesos sinápticos. Esta desventaja (un elemento de indecisión) puede convertirse en una ventaja mediante la creación de un experto neuronal de círculo que está formado por diferentes redes neuronales. La dispersión de las previsiones de los expertos dará una idea del nivel de fiabilidad de estas previsiones que pueden servir para elegir una estrategia de mercado adecuada.
Es fácil probar que la previsión de la media de los valores del círculo debe producir un mejor resultado que la de un experto medio del mismo círculo. Vamos a dejar que el error del i-èsimo experto para el valor de la entrada de![]() sea igual a
sea igual a![]() . Un error medio de un círculo es siempre inferior al error elevado al cuadrado de los expertos individuales desde el punto de vista de la desigualdad de Cauchy:
. Un error medio de un círculo es siempre inferior al error elevado al cuadrado de los expertos individuales desde el punto de vista de la desigualdad de Cauchy:
![]() .
.
Hay que tener en cuenta que la reducción del error puede ser esencial. Si los errores de los expertos individuales no se correlacionan entre sí, es decir,![]() , el error elevado al cuadrado de un círculo formado por L expertos es
, el error elevado al cuadrado de un círculo formado por L expertos es![]() veces más pequeño que el error individual medio de un experto!
veces más pequeño que el error individual medio de un experto!
![]()
Por esto sería mejor basar la previsión en los valores medios de todo el círculo. Este hecho se ilustra en la Fig. 12.
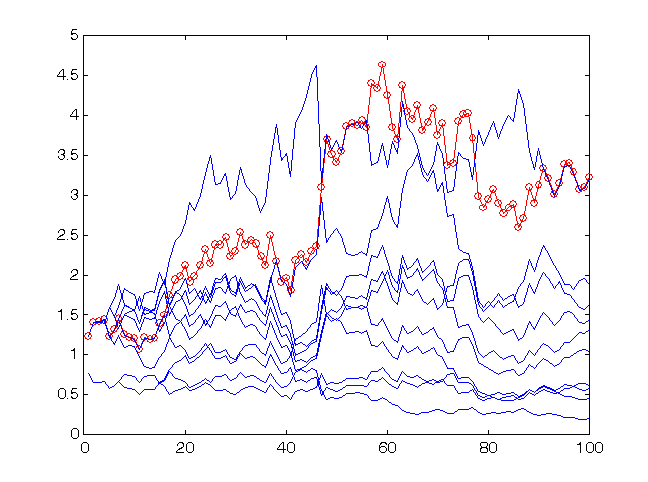
Fig. 12. La tasa de beneficio para los 100 últimos valores de las series temporales sp500 siendo la previsión con un círculo de 10 redes.
El beneficio del círculo (círculos) es superior al de un experto medio. La puntuación de las señales pronosticadas para el círculo es 59:41.
Como puede observar en la Fig. 12, en este caso, el beneficio del círculo es incluso más alto que el de cada experto. Así, el método del círculo puede mejorar esencialmente la calidad de la previsión. Tenga en cuenta el valor absoluto de la tasa del beneficio: El capital del círculo se incrementó 3,25 veces en las 100 entradas al mercado (esta tasa será, por supuesto, más baja si se consideran los costes de las transacciones).
Las previsiones se obtuvieron con el aprendizaje de la red en los 30 promedios móviles exponenciales consecutivos (EMA 1 … EMA 30) de las series temporales de incremento del índice. La señal de incremento en la siguiente etapa fue pronosticada.
En este experimento, la tasa se fijó en el nivel![]() cerca del óptimo para la precisión de esta previsión (59 señales correctamente pronosticadas contra 41 señales erróneamente pronosticadas), es decir,
cerca del óptimo para la precisión de esta previsión (59 señales correctamente pronosticadas contra 41 señales erróneamente pronosticadas), es decir,![]() . En la Fig. 13, puede ver los resultados de un mercado de más riesgo en las mismas previsiones, es decir con
. En la Fig. 13, puede ver los resultados de un mercado de más riesgo en las mismas previsiones, es decir con![]() .
.
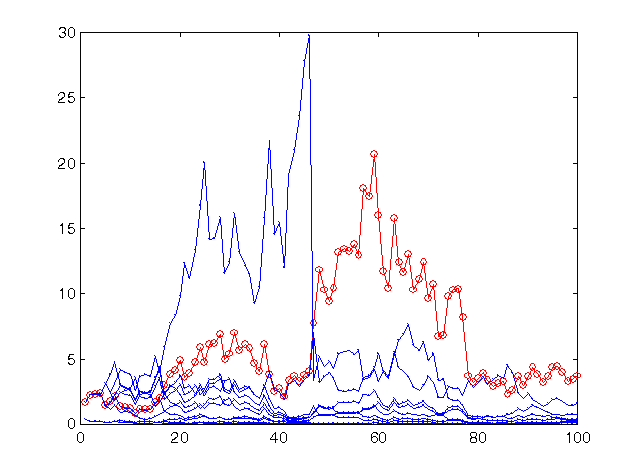
Fig. 13. La tasa de beneficio para los 100 últimos valores de las series temporales sp500 siendo la previsión con el mismo círculo de 10 redes, pero con una estrategia más arriesgada.
El beneficio del círculo permanece en el mismo nivel (un poco incrementado) ya que el valor del riesgo está tan cerca del óptimo como el anterior. Sin embargo, para la mayoría de las redes las previsiones son menos exactas que las de todo el círculo, estas tasas resultan demasiado arriesgadas, lo que dio lugar a su completa ruina.
Los ejemplos anteriores demuestran la importancia de ser capaces de evaluar correctamente la calidad de la previsión y como poder utilizar esta estimación para incrementar la rentabilidad de las mismas previsiones.
Podemos ir incluso más allá y usar las opiniones ponderadas de las redes de expertos en lugar de las medias . Las opiniones ponderadas deberían ser elegidas de forma adaptable para maximizar la capacidad de previsión del círculo en la muestra de aprendizaje. Como resultado, las redes peor entrenadas de un círculo hacen una contribución más pequeña y no estropean la previsión.
Las posibilidades de este método se ilustran con la comparación siguiente de previsiones hechas por dos tipos de redes de círculos que consisten en 25 expertos (vea las Fig. 14 y 15). Las previsiones se hicieron de acuerdo al mismo esquema: como entradas, se usaron los promedios móviles exponenciales de las series temporales con períodos iguales a los 10 primeros números de Fibonacci. De acuerdo con los resultados obtenidos de los 100 experimentos, la previsión de peso proporciona un exceso de media de señales pronosticadas correctamente sobre las predichas incorrectamente, aproximadamente igual a 15, mientras que para la previsión media este factor vale alrededor de 12. Debería tenerse en cuenta que el volumen total de precio aumenta en comparación con las tasas de descenso dentro del plazo que es exactamente igual a 12. Por lo tanto, considerando que la tendencia principal va a aumentar como una previsión constante trivial de la señal "+" da el mismo resultado para el porcentaje de las señales pronosticadas correctamente como la opinión ponderada de 25 expertos.
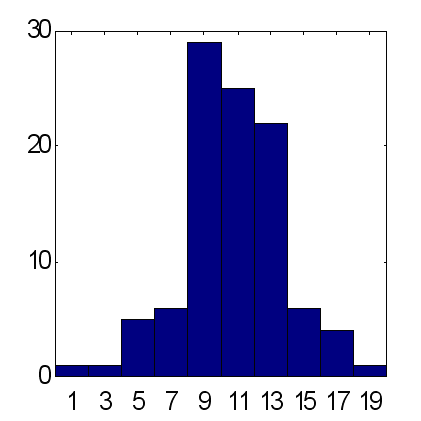
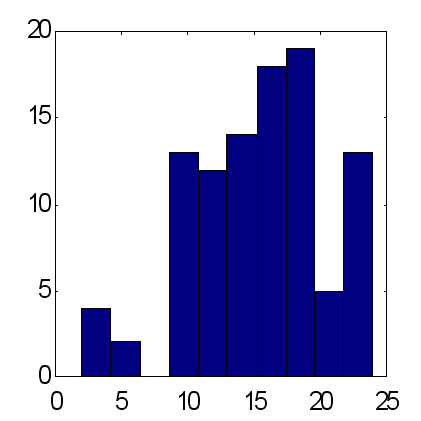
| Fig. 14. Histograma de las sumas de señales pronosticadas correctamente con previsiones medias de 25 expertos. Una media para 100 círculos = 11.7 con la desviación estándar de 3.2. | Fig. 15. Histograma de sumas de señales pronosticadas correctamente con previsiones ponderadas de los mismos de 25 expertos. Una media para 100 círculos = 15.2 con la desviación estándar de 4.9. |
Posible tasa de beneficio de las previsiones de un red neuronal
Hasta ahora, hemos formulado los resultados de los experimentos numéricos como el porcentaje de señales pronosticadas correctamente. Averigüemos ahora la tasa de beneficio realmente alcanzable cuando se lleva a cabo el trading con redes neuronales. Los límites superiores de la tasa de beneficio obtenidos anteriormente sin considerar las fluctuaciones son difícilmente alcanzables en la práctica, sobre todo cuando no se han tenido en cuenta los costes de las transacciones que puedan anular el nivel de previsibilidad alcanzado.
En efecto, tener en cuenta los costes de las comisiones se traduce en la aparición de un término negativo en la exponencial:
![]() .
.
Además, a diferencia del nivel de previsibilidad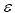 , la comisión
, la comisión ![]() entra linealmente, no cuadráticamente. Por lo tanto, en el ejemplo anterior, los valores típicos de previsibilidad
entra linealmente, no cuadráticamente. Por lo tanto, en el ejemplo anterior, los valores típicos de previsibilidad![]() no pueden superar la comisión
no pueden superar la comisión ![]() .
.
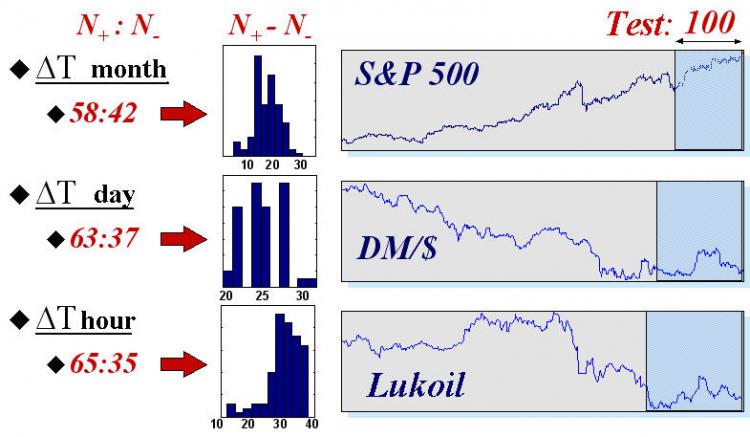
Para dar una idea de las posibilidades reales de las redes neuronales en este campo, daremos los resultados del mercado automatizado usando redes neuronales en tres índices con tiempos típicos diferentes: los valores del índice S&P500 con intervalos mensuales entre lecturas, ofertas diarias de DM/$, y lecturas cada hora de futuras acciones de la Bolsa Rusa. Las estadísticas de previsión se recogieron en 50 sistemas de redes neuronales distintas (conteniendo círculos de 50 redes neuronales cada uno). En la figura 16 de muestran las propias series temporales y los resultados de las previsiones de un prueba de los 100 últimos valores de cada serie temporal.
Fig. 16. Los valores medios y los histogramas del número de señales pronosticadas correctamente (![]() ) e erróneamente (
) e erróneamente (![]() ) en la prueba de muestras de 100 valores de tres índices financieros reales.
) en la prueba de muestras de 100 valores de tres índices financieros reales.
Esos resultados confirman la regularidad intuitivamente obvia: las series temporales son más predecibles cuando transcurre menos tiempo entre las lecturas. En efecto, cuanto más tiempo pasas entre los valores consecutivos de una serie temporal, de la más externa hacia la dinámica, más información hay disponible para los participantes en el mercado y, por lo tanto, menos información sobre el futuro en las propias series temporales.
Entonces las previsiones obtenidas anteriormente se usaron para el mercado en una prueba de conjunto. Al mismo tiempo, el tamaño del contrato en cada etapa se eligió en proporción al grado de confianza de la previsión, mientras que el valor del parámetro global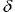 se optimizó en la muestra de aprendizaje. Además, de acuerdo a este éxito, cada red en el círculo tuvo su propia tasa de calificación variable. En cada etapa de la previsión, usamos solamente "mejor" parte real de las redes. Se muestran los resultados de estos traders neuronales "neuronales" en la Fig. 17.
se optimizó en la muestra de aprendizaje. Además, de acuerdo a este éxito, cada red en el círculo tuvo su propia tasa de calificación variable. En cada etapa de la previsión, usamos solamente "mejor" parte real de las redes. Se muestran los resultados de estos traders neuronales "neuronales" en la Fig. 17.
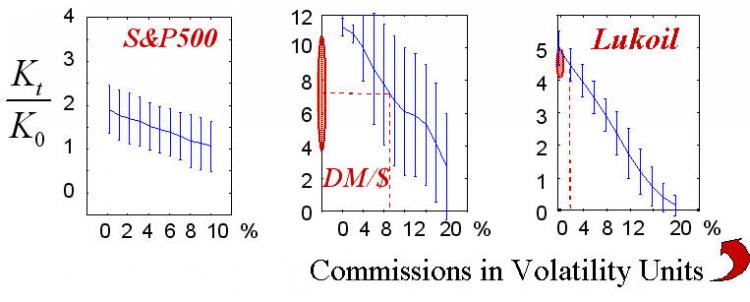
Fig. 17. Las estadísticas ganadoras de 50 implementaciones de acuerdo con la cantidad de comisiones.
Los valores reales de las comisiones dibujados en las líneas discontinuas muestran el área de las tasas de beneficio realmente alcanzables.
La victoria final (como el juego mismo de estrategia), por supuesto, depende del tamaño de la comisión. Los diagramas anteriores muestran esta dependencia. Los valores reales de las comisiones en las unidades de medida elegidas que conoce el autor están marcados en la figura. Hay que mencionar que la naturaleza "cuantificada" del trading real no se tuvo en cuenta en estos experimentos, es decir, no tuvimos en cuenta el hecho de que el tamaño de los mercados debe ser igual al número entero contratos típicos. Este caso se corresponde con el trading con grandes capitales donde las operaciones típicas contienen muchos contratos. Además, el trading garantizado estaba implícito, es decir, la tasa de beneficio se calculó como una relación del capital del instrumento financiero que es mucho más pequeño que la escala de los propios contratos.
Los resultados anteriores muestran que el trading basado en las redes neuronales tiene realmente buenas perspectivas, al menos a corto plazo. Por otra parte, en virtud de la auto-similitud de las series temporales financieras (Peters, 1994), más alta será la tasa de beneficio por unidad de tiempo, menor será el tiempo típico del trading. Por lo tanto, los traders automatizados que usan redes neuronales resultan ser más eficientes con el trading en tiempo real donde sus ventajas frente a los brókers convencionales son más visibles: prueba de fatiga, sin susceptibilidad a las emociones, velocidad de respuesta mucho más alta. Una red neuronal bien entrenada conectada a un sistema de trading automatizado puede tomar decisiones mucho antes que un bróker humano detecte el cambio del precio en los gráficos de su terminal.
Conclusión
Hemos visto que las series temporales (al menos algunas) del mercado eran parcialmente predecibles. Como otra clase de análisis neuronal, las series temporales de previsiones requieren un procesamiento de datos más complicado y más cuidadoso. Sin embargo, trabajar con series temporales tiene sus propias características que se pueden usar para incrementar los beneficios. Esto se refiere tanto a la selección de entradas (usando métodos especiales de representación de datos) como a la selección de salidas y al uso de errores funcionales específicos. Por último, hemos demostrado lo beneficioso que resulta usar los expertos neuronales de círculo en comparación con las redes neuronales separadas y hemos proporcionado datos de tasas de beneficio reales en varios instrumentos financieros reales.
Referencias:
- Sharpe, W.F., Alexander, G.J., Bailey, J.W. (1997). "Investments" (Inversiones). - 6ª edición, Prentice Hall, Inc., 1998.
- Abu-Mostafa, Y.S. (1995). "Financial market applications of learning from hints" (Aplicaciones de aprendizaje a partir de las sugerencias para los mercados financieros). "In Neural Networks in Capital Markets" (En las redes neuronales en los mercados de capital). Apostolos-Paul Refenes (Ed.), Wiley, 221-232.
- Beltratti, A., Margarita, S., y Terna, P. (1995). "Neural Networks for Economic and Financial Modeling" (Redes neuronales para modelos económicos y financieros). ITCP.
- Chorafas, D.N. (1994). "Chaos Theory in the Financial Markets" (Teoría del Caos en los Mercados Financieros). Probus Publishing.
- Colby, R.W., Meyers, T.A. (1988). "The Encyclopedia of Technical Market Indicators" (La enciclopedia de los indicadores de técnicos de los mercados). IRWIN Professional Publishing.
- Ehlers, J.F. (1992). "MESA and Trading Market Cycles" (MESA y ciclos de mercados de trading). Wiley.
- Kaiser, G. (1995). "A Friendly Guide to Wavelets" (Una guía fácil para ondículas). Birk.
- LeBeau, C., y Lucas, D.W. (1992). "Technical traders guide to computer analysis of futures market" (Guía de traders técnicos para el análisis informático del mercado de futuros). Business One Irwin.
- Peters, E.E. (1994). "Fractal Market Analysis" (Análisis fractal del mercado). Wiley.
- Pring, M.G. (1991). "Technical Analysis Explained" (Análisis técnico explicado). McGraw Hill.
- Plummer, T. (1989). "Forecasting Financial Markets" (Previsión de los mercados financieros). Kogan Page.
- Sauer, T., Yorke, J.A., y Casdagli, M. (1991). "Embedology". "Journal of Statistical Physics2 (Revista de física estadística). 65, 579-616.
- Vemuri, V.R., y Rogers, R.D., eds. (1993). "Artificial Neural Networks" (Redes neuronales artificiales). "Forecasting Time Series" (Previsión de las series temporales). IEEE Comp.Soc.Press.
- Weigend, A y Gershenfield, eds. (1994). "Times series prediction: Forecasting the future and understanding the past." (Predicción de series temporales: Predecir el futuro y entender el pasado). Addison-Wesley.
- Baestaens, D.-E., Van Den Bergh, W.-M., Wood, D. "Neural Network Solutions for Trading in Financial Markets" (Soluciones de red neuronal para el trading en los mercados financieros). "Financial Times Management" (Gestión de Tiempos Financieros) (Julio 1994).
El artículo se publica con el consentimiento del autor.
Cursos del autor: Cómputo neuronal y sus aplicaciones en economía y negocios
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/1506
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
 MetaTrader 4 en Linux
MetaTrader 4 en Linux
 El modelado de la apuestas como medio para desarrollar la "intuición del mercado"
El modelado de la apuestas como medio para desarrollar la "intuición del mercado"
 La sandbox aleatoria
La sandbox aleatoria
 Una nueva mirada al gráfico Equivolume
Una nueva mirada al gráfico Equivolume
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso