Prognose von Finanzzeitreihen
Einführung
Dieser Artikel beschäftigt sich mit einer der beliebtesten praktischen Anwendungen von neuronalen Netzen, der Prognose von Marktzeitreihen. In diesem Bereich ist die Prognose am engsten verbunden mit der Rentabilität und kann als eine der Geschäftsaktivitäten betrachtet werden.
Die Prognose der Finanzzeitreihen ist ein erforderliches Element jeder Investitionstätigkeit. Das Konzept der Investition selbst - Geld jetzt einzusetzen, um in der Zukunft Gewinne zu erzielen -basiert auf dem Konzept der Vorhersage der Zukunft. Deshalb unterliegt die Prognose von Finanzzeitreihen den Aktivitäten der gesamten Anlageindustrie - alle organisierten Börsen und andere Handelssysteme.
Nennen wir ein paar Zahlen, die den Umfang dieser Prognose-Industrie illustrieren (Sharp, 1997). Der Tagesumsatz an der US-Aktienbörse beträgt mehr als 10 Mrd. US-Dollar. Die Depositary Trust Company in den USA, bei der Aktien im Wert von mehr als 11 Billionen US-Dollar (des Gesamtvolumens von 18 Billionen US-Dollar) notiert sind, markiert etwa 250 Mrd. US-Dollar täglich. Die Handelswelt FOREX (Devisenhandel) ist sogar noch aktiver. Ihr täglicher Umsatz übersteigt 1.000 Milliarden US-Dollar. Es ist in etwa 1/50 des globalen Gesamtkapitals.
99% aller Transaktionen sind als spekulativ bekannt, das heißt, sie sind nicht darauf ausgerichtet der realen Warenzirkulation zu dienen, sondern sie werden durchgeführt um Gewinne aus dem System zu erzielen: "billig gekauft, besser verkauft". Sie basieren alle auf den Prognosen der Marktteilnehmer über vorgenommene Kursänderungen. Gleichzeitig, und das ist sehr wichtig, sind die von den Teilnehmern bei jeder Transaktion gemachten Prognosen polar. Also kennzeichnet das Volumen spekulativer Transaktionen das Maß an Diskrepanzen in der Prognose der Marktteilnehmer, das heißt, in der Realität, das Maß der Unvorhersehbarkeit der Finanzzeitreihen.
Diese wichtigste Eigenschaft der Marktzeitreihen unterliegt der effizienten Markthypothese, herausgegeben von Louis Bachelier in seiner Dissertation im Jahr 1900. Nach dieser Lehre, kann ein Anleger nur auf die durchschnittliche Marktrentabilität hoffen, geschätzt unter Verwendung solcher Indizes wie Dow Jones oder S&P500 (für die New Yorker Börse). Allerdings tritt jeder spekulative Gewinn zufällig auf und ist dem Glücksspiel ähnlich. Die Unvorhersehbarkeit der Marktkurven wird aus dem gleichen Grund bestimmt, wegen dem kaum Geld auf einer belebten Einkaufsstraße gefunden wird: es gibt zu viele Beteiligte, die es aufheben.
Die effiziente Markttheorie wird nicht (ganz natürlich) von den Marktteilnehmern selbst unterstützt (weil sie genau auf der Suche nach dem "herumliegenden" Geld sind). Die meisten von ihnen sind sicher, dass Marktzeitreihen, obwohl sie stochastisch zu sein scheinen, voll mit versteckten Regelmäßigkeiten sind, das heißt, sie sind zumindest teilweise prognostizierbar. Es war Ralph Elliot, der Gründer der technischen Analyse, der in den 30er Jahren versuchte solche versteckten empirischen Regelmäßigkeiten zu entdecken.
In den 80er Jahren fand dieser Gesichtspunkt überraschende Unterstützung in der dynamischen Chaos Theorie, die kurz vorher auftrat. Die Theorie basiert auf der Gegenseite von Chaoszustand und Stochastizität (Zufälligkeit). Chaotische Reihen erscheinen nur zufällig, jedoch, als ein bestimmter dynamischer Prozess, lassen sie etwas Raum für eine kurzfristige Prognose. Der Bereich der zulässigen Prognose ist durch den Prognosehorizont begrenzt, aber das kann ausreichend sein um echte Profite durch Prognose zu erzielen (Chorafas, 1994). Dann können diejenigen mit besseren mathematischen Methoden zum Extrahieren von Regelmäßigkeiten aus rauschenden chaotischen Reihen auf eine bessere Gewinnquote hoffen - auf Kosten ihrer schlechter ausgestatteten Genossen.
In diesem Artikel werden wir bestimmte Tatsachen angeben, welche die teilweise Vorhersehbarkeit von Finanzzeitreihen bestätigen und diese Vorhersehbarkeit auch numerisch bewerten.
Technische Analyse und Neuronale Netze
In den letzten Jahrzehnten, wurde die technische Analyse - eine Reihe empirischer Regeln, basierend auf verschiedenen Indikatoren des Marktverhaltens - mehr und mehr beliebt. Die technische Analyse konzentriert sich auf individuelles Verhalten eines gegebenen Finanzinstruments, ohne Bezug zu anderen Finanzinstrumenten (Pring, 1991).
Dieser Ansatz basiert psychologisch mit der Konzentration von Brokern auf genau die Sicherheit, mit der sie zu einem bestimmten Zeitpunkt arbeiten. Nach Alexander Elder, einem bekannten technischen Analysten (der ursprünglich als Psychotherapeut arbeitete), ist das Verhalten der Marktgemeinde sehr ähnlich dem Verhalten der Masse, charakterisiert durch besondere Gesetze der Massenpsychologie. Der Masseneffekt vereinfacht das Denken, stuft individuelle Besonderheiten niedriger ein und produziert die Formen kollektiven, geselligen Verhaltens, das einfacher als das individuelle ist. Insbesondere der soziale Instinkt fördert die Rolle eines Anführers, einem/einer Alpha Mann/Frau. Die Kurskurve ist, nach Elder, ist genau diese Führer, das das kollektive Marktbewusstsein auf sich selbst fokussiert. Diese psychologische Interpretation des Marktpreis-Verhaltens von Spielern, die ein einzelnes chaotisch dynamisches System bilden, mit einer relativ kleinen Menge innerer Freiheit.
Nach dieser Lehre, müssen Sie sich "von den Fesseln der Menge befreien", über sie steigen und intelligenter zu werden, als die Masse, um in der Lage zu sein die Marktkurven vorherzusagen. Zu diesem Zweck sollte Sie ein Spielsystem entwickeln, bewertet nach dem vorherigen Verhalten einer Zeitreihe und diesem System streng folgen, unbeeinflusst von Emotionen und kreisenden Gerüchten des gegebenen Marktes. Mit anderen Worten, Vorhersagen müssen auf einem Algorithmus basieren, das heißt, sie können und müssen sogar an einen Computer übergeben werden (LeBeau, 1992). Ein Man sollte nur den Algorithmus erstellen, für dessen Zweck er verschiedene Software-Produkte hat, die die Entwicklung und weitere Unterstützung von auf technischer Analysewerkzeugen basierten programmierten Strategien erleichtern.
Nach dieser Logik, warum nicht einen Computer in der Entwicklungsphase der Strategie nutzen, nicht als Assistenten zum Berechnen der bekannten Marktindikatoren und zum Testen gegebener Strategien, sondern zum Ermitteln der optimalen Indikatoren und optimalen Strategien für die ermittelten Indikatoren. Dieser Ansatz, unterstützt durch die Anwendung neuronaler Netze Technologien, findet seit den frühen 90er Jahren immer mehr Anhänger (Beltratti, 1995, Baestaens, 1997), weil er eine Reihe unbestreitbarer Vorteile hat.
Zuerst, neuronale Netze Analyse, im Gegensatz zur technischen Analyse, unterstellt keine Beschränkungen hinsichtlich der Art der Eingabedaten. Es kann beides sein, die Indikatoren der gegebenen Zeitreihe und die Information über das Verhalten anderer Finanzinstrumente des Marktes. Nicht ohne Grund sind es institutionelle Anleger, (Zum Beispiel große Pensionsfonds), die aktiv neuronale Netze verwenden. Solche Investoren arbeiten mit großen Portfolios, für die Korrelationen zwischen den verschiedenen Märkten von zentraler Bedeutung sind.
Zweitens, im Gegensatz zu auf allgemeinen Empfehlungen basierender technischer Analyse, ermitten neuronale Netze Indikatoren optimal für das gegebene Finanzinstrument und gründen auf diese eine Prognosestrategie, optimal, noch einmal, für die gegebenen Zeitreihen. Darüber hinaus können diese Strategien angepasst werden, sich mit dem Markt verändern, was von zentraler Bedeutung ist für junge, dynamisch entwickelnde Märkte, insbesondere für den russischen.
Neuronale Netze Modellierung ist alleine auf Daten basiert, ohne Einbeziehung irgendwelcher a priori Überlegungen. Dari liegt ihre Stärke und, zur gleichen Zeit, ihre Achillesferse. Die verfügbaren Daten können unzureichend sein zum Lernen, die Dimensionalität potentieller Eingabedaten kann sich als zu hoch herausstellen. Später in diesem Artikel werden wir zeigen, wie die bei der technischen Analyse gesammelten Erfahrungen, helfen können diese im Bereich der Finanzprognose typischen Schwierigkeiten zu überwinden.
Zeitreihen Prognose Technik
Lassen Sie uns als ersten Schritt das allgemeine System der Prognose von Zeitreihen mit neuronalen Netzen beschreiben (Abb. 1).
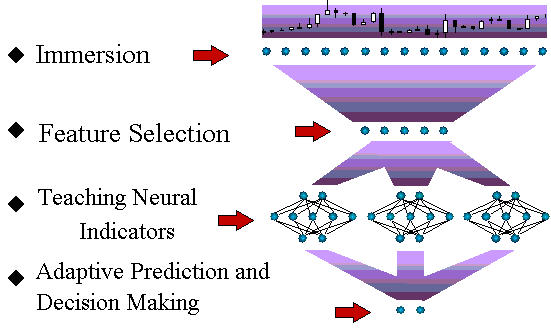
Abb. 1. Das Technologische Zyklus-System der Zeitreihen-Prognose.
Im weiteren Verlauf dieses Artikels werden wir alles Phasen dieses Prozessablaufs besprechen. Obwohl die allgemeinen Prinzipien der Neuronale-Netze-Modellierung in vollem Umfang für diese Aufgabe anwendbar sind, hat die Prognose von Finanzzeitreihen ihren eigenen spezifischen Charakter. Es gibt diese spezifischen Merkmale, die in diesem Artikel so weit wie möglich beschrieben werden.
Immersion Verfahren. Tackens Theorem
Beginnen wir mit dem Immersion-Verfahren. Wie wir jetzt sehen werden, scheint für alle diese Prognosen die Extrapolation von Daten, neuronale Netze, tatsächlich, das Problem der Interpolation zu lösen, was die Geltung der Lösung beträchtlich erhöht. Die Prognose einer Zeitreihe erklärt sich im alltäglichen Problem der neuronalen Analyse - Näherung einer multivariablen Funktion für einen gegebenen Satz an Beispielen - mit dem Verfahren der Immersion der Zeitreihen in einen multidimensionalen Raum (Weigend, 1994). Zum Beispiel, ein dimensionaler Verzögerungs-Raum aus Zeitreihen besteht aus Werten der Zeitreihen bei aufeinanderfolgenden Momenten der Zeit:
![]() .
.
Das folgende Tackens Theorem ist für dynamische Systeme bewiesen: Wenn eine Zeitreihe durch ein dynamisches System erzeugt wird, d.h. sind die Werte von ![]() eine beliebige Funktion des Zustands eines solchen Systems, gibt es eine solche Immersionstiefe (ungefähr gleich zu der effektiven Anzahl der Freiheitsgrade dieses dynamischen Systems) die eine eindeutige Prognose des Wertes der nächsten Zeitreihe bereitstellt (Sauer, 1991). Demnach, wurde eine eher große gewählt, können Sie eine eindeutige Abhängigkeit zwischen dem zukünftigen Wert der Zeitreihe und deren vorhergehenden Werten gewährleisten:
eine beliebige Funktion des Zustands eines solchen Systems, gibt es eine solche Immersionstiefe (ungefähr gleich zu der effektiven Anzahl der Freiheitsgrade dieses dynamischen Systems) die eine eindeutige Prognose des Wertes der nächsten Zeitreihe bereitstellt (Sauer, 1991). Demnach, wurde eine eher große gewählt, können Sie eine eindeutige Abhängigkeit zwischen dem zukünftigen Wert der Zeitreihe und deren vorhergehenden Werten gewährleisten:![]() , das heißt, die Prognose einer Zeitreihe erklärt sich in dem Problem von multivariabler Funktionserweiterung. Dann können Sie neuronale Netze nutzen, um diese unbekannte Funktion auf der Basis einer durch die Historie dieser Zeitreihe bestimmten Reihe von Beispielen wiederherzustellen.
, das heißt, die Prognose einer Zeitreihe erklärt sich in dem Problem von multivariabler Funktionserweiterung. Dann können Sie neuronale Netze nutzen, um diese unbekannte Funktion auf der Basis einer durch die Historie dieser Zeitreihe bestimmten Reihe von Beispielen wiederherzustellen.
Im Gegensatz dazu, wie zu einer zufälligen Zeitreihe, bietet die Kenntnis der Vergangenheit keine nützlichen Hinweise für die Prognose der Zukunft. Also, nach der effinzienten Markt-Theorie, wird sich die Streuung der prognostizierten Werte nicht ändern, wenn sie in den Verzögerungsraum eintauchen.
Der während der Immersion erkannte Unterschied einer chaotischen Dynamik und einer stochastischen (zufälligen), wird in Abb. 2 gezeigt.
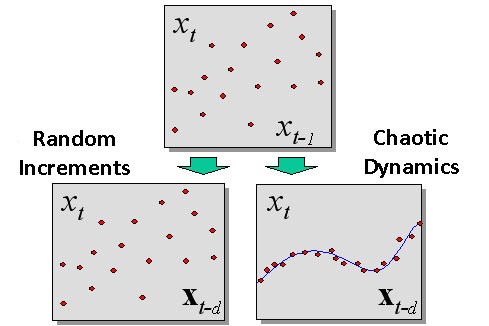
Abb. 2. Der Unterschied zwischen einem zufälligen Prozess und einer chaotischen Dynamik, erkannt während der Immersion.
Empirische Bestätigung der Berechenbarkeit von Zeitreihen
Das Immersionsverfahren ermöglicht uns die Berechenbarkeit von realen Finanzinstrumenten zu quantitativ zu messen, das heißt, die Hypothese effizienter Märkte zu beweisen oder zu widerlegen. Nach Letzterem, ist die Streuung der Punkte in allen Verzögerungsraum-Koordinaten identisch (wenn die Punkte identisch verteilte unabhängige zufällige Werte sind). Im Gegensatz dazu, müssen chaotische Dynamiken, die eine bestimmte Vorhersehbarkeit bieten, dazu führen, dass Beobachtungen um eine bestimmte Hyperfläche gruppiert sind 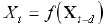 , d.h., experimentelle Muster bilden eine Reihe mit der Dimension, kleiner, als die Dimension des gesamten Verzögerungsraums.
, d.h., experimentelle Muster bilden eine Reihe mit der Dimension, kleiner, als die Dimension des gesamten Verzögerungsraums.
Um die Dimension zu messen, können Sie die folgende intuitive Eigenschaft verwenden: Wenn eine Reihe die Dimension von D hat, dann, sofern sie in immer kleinere kubische Flächen mit einer Seite von ![]() unterteilt ist, wird die Anzahl solcher Würfel wachsen, wie
unterteilt ist, wird die Anzahl solcher Würfel wachsen, wie![]() . Diese Tatsache unterliegt dem Erkennen der Dimension von Reihen mit der Box-Zählmethode, die wir von vorherigen Überlegungen her kennen. Die Dimension einer Reihe von Punkten wird erkannt durch die Wachstumsquote der Anzahl an Boxen, die alle Punkte der Reihe enthalten. Um den Algorithmus zu beschleunigen, nehmen wir Dimensionen von
. Diese Tatsache unterliegt dem Erkennen der Dimension von Reihen mit der Box-Zählmethode, die wir von vorherigen Überlegungen her kennen. Die Dimension einer Reihe von Punkten wird erkannt durch die Wachstumsquote der Anzahl an Boxen, die alle Punkte der Reihe enthalten. Um den Algorithmus zu beschleunigen, nehmen wir Dimensionen von 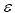 als ein Vielfaches von 2, d.h., die Auflösungsskala wird in Bit gemessen.
als ein Vielfaches von 2, d.h., die Auflösungsskala wird in Bit gemessen.
Als Beispiel einer typischen Marktzeitreihe, nehmen wir ein bekanntes Finanzinstrument wie den S&P500 Index, der die durchschnittliche Kursdynamik an der New Yorker Börse widerspiegelt. Abb. 3 zeigt die Index-Dynamik für den Zeitraum von 679 Monaten. Die Dimension (Informationsdimension ist gemeint) von Schritten dieser Zeitreihe, berechnet mit der Box-Zählmethode, wird i Abb. 4 gezeigt.
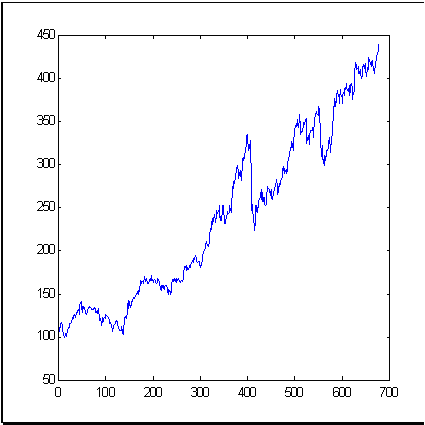
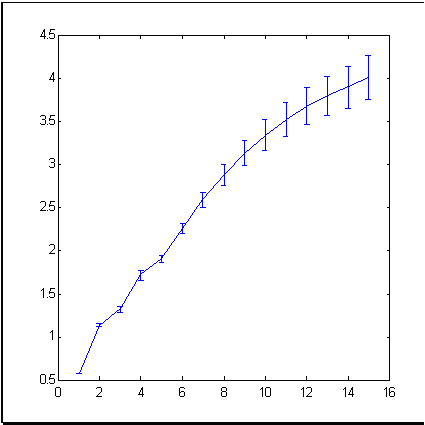
| Abb. 3. Eine Zeitreihe mit 679 Werten des S&P500, verwendet als Beispiel in diesem Artikel. | Abb. 4. Informationsdimension von Schritten der S&P500 Zeitreihe. |
Wie aus Abb. 4 folgt, bilden die experimentellen Punkte eine Reihe der Dimension von ungefähr 4 in einem 15-dimensionalen Immersionsraum. Das ist viel weniger als 15, die wir auf der Theorie effizienter Märkte basierend erhalten würden, welche die Zeitreihe von Schritten als unabhängige Zufallswerte betrachtet.
Somit bieten die empirischen Daten einen überzeugenden Beweis des Vorhandenseins einer bestimmten prognostizierbaren Komponente in Finanzzeitreihen, obwohl wir nicht sagen können, dass es hier eine vollständig bestimmte chaotische Dynamik gibt. Dann basieren die Versuche neuronale-Netze-Analyse für die Markt-Prognose anzuwenden auf starken Gründen.
Es sollte allerdings beachtet werden, dass theoretische Berechenbarkeit die Erreichbarkeit eines praktisch bedeutungsvollen Maß an Prognose nicht garantiert. Eine quantitative Einschätzung der Vorhersehbarkeit von bestimmten Zeitreihen kann durch Messen der Kreuz-Entropie erhalten werden, die mithilfe der Box-Zählung möglich ist. Zum Beispiel werden wir die Berechenbarkeit von S&P500 Schritten in Bezug auf die Immersionstiefe messen. Kreuz-Entropie
![]() ,
,
das Diagramm, das unten dargestellt ist (Abb. 5) misst die zusätzlichen Informationen über den nächsten Wert der Zeitreihe, unterstützt durch bekannte vorherige Werte dieser Zeitreihe.
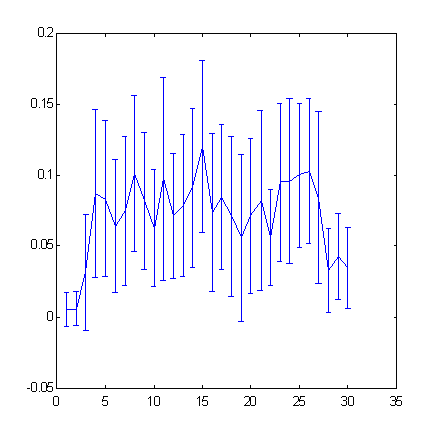
Abb. 5. Vorhersehbarkeit der Schrittzeichen für S&P500 Zeitreihen in Bezug auf die Immersionstiefe (der "Fenster"-Breite).
Eine Zunahme der Immersionstiefe wird von einer Abnahme der Vorhersehbarkeit begleitet werden.
Im Weiteren werden wir den Gewinn bewerten, der mit einem solchen Niveau der Berechenbarkeit praktisch erreichbar ist.
Bildung eines Eingaberaums von Attributen
In Abb. 5 sehen Sie, dass die zunehmende Breite des Immersion-Fensters der Zeitreihe schließlich zur Abnahme der Vorhersehbarkeit führt - wenn die steigenden Eingabedimensionen nicht mehr durch ihre Informationswerte kompensiert werden. In diesen Fall, wenn die Verzögerungsraum-Dimension zu groß ist für die gegebene Anzahl an Beispielen, müssen wir spezielle Verfahren zum Bilden eines Raums an Attributen mit kleineren Dimensionen anwenden. Die Finanzzeitreihen-spezifischen Wege zum auswählen von Attributen und/oder dem Erhhöhen der Anzahl verfügbarer Beispiele, wird im Folgenden beschrieben.
Fehler-Funktional Auswählen
Um ein neuronales Netz lernen zu lassen, ist es nicht ausreichend Lernsätze von Eingaben/Ausgaben zu bilden. Die Netz-Prognoseabweichung muss auch bestimmt werden. Die in den meisten neuronale Netze Anwendungen verwendete Wurzel aus der mittleren quadratischen Abweichung hat nicht viel "finanziellen Sinn" für Marktzeitreihen. Deshalb werden wir in einem speziellen Abschnitt des Artikels die die Abweichung spezifisch für Finanzzeitreihen betrachten, und zeige wie sie im Zusammenhang mit der möglichen Gewinnquote stehen.
Zum Beispiel, für die Auswahl einer Marktposition ist eine zuverlässige Erkennung der Zeichen von Kursänderungen viel wichtiger, als die Verringerung der mittleren qudratischen Abweichung. Obwohl diese Angaben miteinander in Beziehung stehen, werden die für eine von ihnen optimierten Netze schlechte Prognosen für die andere machen. Die Auswahl einer adäquaten Fehlerfunktion, wie wir es später im Artikel beweisen, muss auf einer bestimmten idealen Strategie basieren und bestimmt sein, zum Beispiel, durch den Wunsch Gewinne zu maximieren (oder mögliche Verluste zu minimieren).
Lernen Neuronaler Netze
Die wichtigsten Besonderheiten bei der Prognose von Zeitreihen, liegen im Bereich der Datenvorverarbeitung. Das Lernverfahren für einzelne neuronale Netze ist Standard. In der Regel werden verfügbare Parameter in drei Muster aufgeteilt: Lernen, Validierung und Testen. Das erste wird zum Lernen des Netzes verwendet, das zweite zur Auswahl optimalerNetzarchitektur und/oder zur Auswahl des Zeitpunkts das Lernen des Netzes zu stoppen. Schließlich, die dritte, die beim Lehren nicht verwendet wurde, dient zur Kontrolle der Prognosequalität des "trainierten" neuralen Netzes.
Für sehr verrauschte Finanzzeitreihen jedoch, kann die Verwendung geschlossener neuronaler Netze in einem erheblichen Zuwachs an Prognosesicherheit resultieren. Wir werden diesen Artikel mit einer Besprechung dieser Technik beenden.
In einigen Untersuchungen finden wir den Beweis über bessere Prognosequalität durch den Einsatz von Rückkoppelung neuronaler Netze. Solche Netze können einen lokalen Speicher besitzen, der die Daten entfernterer Vergangenheit speichert, als die der explizit in Eingaben verfügbaren. Die Berücksichtigung solcher Architekturen würde uns jedoch zu weit vom Hauptthema abschweifen lassen, umso mehr, weil es einige alternative Verfahren der effektive Erweiterung des Netz-"Horizont" gibt, durch weiter unten beschriebene spezielle Zeitreihen-Immersionstechniken.
Bilden eines Raums für Attribute
Die effiziente Codierung von Eingaben ist der Schlüssel zu einer besseren Prognosequalität. Es ist von besonderer Bedeutung für schwer vorhersehbare Finanzzeitreihen. Alle Standard-Empfehlungen über Datenvorverarbeitung sind hier auch anwendbar. Allerdings gibt es Finanzzeitreihen-spezifische Verfahren der Datenvorverarbeitung, die wir in diesem Abschnitt detaillierter betrachten werden.
Zeitreihen Eintauchverfahren
Zunächst einmal müssen wir beachten, dass wir die Werte der Kurse selbst nicht verwenden, die wir als ![]() bezeichnen, als Eingaben oder Ausgaben neuronaler Netze. Dies sind Kursänderungen, die für die Prognose von wirklich entscheidender Bedeutung sind. Da diese Änderungen, in der Regel, innerhalb eines viel kleineren Bereichs liegen, als die Kurse selbst, gibt es eine starke Korrelation zwischen den Werten von Kursen - der wahrscheinlichste Wert des Kurses ist gleich zu seinem vorhergehenden Wert:
bezeichnen, als Eingaben oder Ausgaben neuronaler Netze. Dies sind Kursänderungen, die für die Prognose von wirklich entscheidender Bedeutung sind. Da diese Änderungen, in der Regel, innerhalb eines viel kleineren Bereichs liegen, als die Kurse selbst, gibt es eine starke Korrelation zwischen den Werten von Kursen - der wahrscheinlichste Wert des Kurses ist gleich zu seinem vorhergehenden Wert: ![]() . Gleichzeitig müssen wir, wie es wiederholt betont wurde, um die Lernqualität zu erhöhen, für statistische Unabhängigkeit der Eingabedaten arbeiten, das heißt, für das Ausbleiben solcher Korrelationen.
. Gleichzeitig müssen wir, wie es wiederholt betont wurde, um die Lernqualität zu erhöhen, für statistische Unabhängigkeit der Eingabedaten arbeiten, das heißt, für das Ausbleiben solcher Korrelationen.
Von daher ist es logisch, die statistisch unabhängigsten Werte als Eingaben zu wählen, zum Beispiel, Kursänderungen ![]() oder relativen Inkrement-Logarithmus
oder relativen Inkrement-Logarithmus ![]() . Die Letztere Wahl ist gut für langanhaltende Zeitreihen, in denen der Einfluss der Inflation deutlich spürbar geworden ist. In diesem Fall liegen einfache Unterschiede in verschiedenen Teilen der Reihe in unterschiedlichen Bereichen, da sie, in der Tat, in verschiedenen Einheiten gemessen werden. Im Gegensatz dazu, hängen die Verhältnisse aufeinanderfolgender Kurse nicht von Maßeinheiten ab und sie werden auf der gleichen Skala sein, obwohl die Maßeinheiten sich durch die Inflation verändern. Im Ergebnis wird uns eine größere Stationarität der Zeitreihe ermöglichen eine größere Historie zum Lernen zu verwenden und ein besseres Lernen bieten.
. Die Letztere Wahl ist gut für langanhaltende Zeitreihen, in denen der Einfluss der Inflation deutlich spürbar geworden ist. In diesem Fall liegen einfache Unterschiede in verschiedenen Teilen der Reihe in unterschiedlichen Bereichen, da sie, in der Tat, in verschiedenen Einheiten gemessen werden. Im Gegensatz dazu, hängen die Verhältnisse aufeinanderfolgender Kurse nicht von Maßeinheiten ab und sie werden auf der gleichen Skala sein, obwohl die Maßeinheiten sich durch die Inflation verändern. Im Ergebnis wird uns eine größere Stationarität der Zeitreihe ermöglichen eine größere Historie zum Lernen zu verwenden und ein besseres Lernen bieten.
Ein Nachteil des Eintauchens in den Verzögerungsraum sind die begrenzten "Horizonte" des Netzes. Im Gegensatz dazu legt die technische Analyse das Fenster in die Vergangenheit nicht fest und verwendet manchmal sehr entfernte Werte der Zeitreihe. Zum Beispiel die maximal und minimal Werte einer Zeitreihe, sogar von aus relativ weit zurückliegender Vergangenheit genommenen wird behauptet, dass sie die Trader-Psychologie stark beeinflussen, weshalb diese Werte weiterhin wesentlich für die Prognose sind. Ein unzureichend breites Fenster für das Eintauchen in den Verzögerungsraum kann solche Informationen nicht liefern, die, natürlich, die Effizienz der Prognose verringern. Auf der anderen Seite, wird das Fenster bis zu solchen Werten, welche die entfernten Extremwerte abdecken erweitert, wird dies die Netz-Dimensionen erhöhen. Dies seinerseits, wird zu einer verringerten Genauigkeit der neuronalen Netz Prognose führen - jetzt durch das Wachstum des Netzes.
Ein Ausweg aus dieser scheinbaren Pattsituation kann in alternativen Methoden der Codierung des vergangenen Verhaltens einer Zeitreihe gefunden werden. Es ist intuitiv offensichtlich, dass je weiter die Historiendaten einer Zeitreihe zurückreichen, desto weniger Verhaltensdetails beeinflussen die Prognoseergebnisse. Dies wird durch die subjektive Wahrnehmung der Vergangenheit durch die Trader bestimmt, die, streng genommen, die Zukunft bilden. Deshalb müssen wir eine solche Darstellung der Zeitreihen-Dynamik finden, die eine selektive Genauigkeit hätte: je weiter in die Vergangenheit, desto weniger Details. Gleichzeitig muss das allgemeine Erscheinungsbild der Kurve erhalten bleiben. Die sogenannte Wellenzerlegung, oder Wavelet-Zerlegung, kann hier sehr vielversprechend sein. Sie entspricht in ihrem Informationswert der Verzögerungsimmersion, macht es jedoch einfacher die Daten so zu komprimieren, dass die Vergangenheit mit der selektiven Genauigkeit beschrieben wird.
Verringern der Dimensionen von Eingaben: Attribute
Diese Datenkompression ist ein Beispiel für das Extrahieren der wesentlichsten Attribute für die Prognose, aus einer übermäßig großen Anzahl von Eingabevariablen. Die Methoden der systematischen Extraktion von Attributen wurden weiter oben bereits beschrieben. Sie können (und müssen) auch nacheinander auf der Zeitreihen-Prognose angewandt werden.
Es ist wichtig, dass die Darstellung der Eingaben die Datenextraktion möglicherweise erleichtert. Die Wavelet-Darstellung ist ein Beispiel für eine gute (aus Sicht der Attribute-Extraktion) Codierung (Kaiser, 1995). Zum Beispiel das nächste Diagramm (Abb. 6) zeigt einen Abschnitt von 50 Werten einer Zeitreihe mit ihrer Rekonstruktion durch 10 speziell ausgewählten Wavelet Koeffizienten. Bitte beachten Sie, obwohl es fünfmal weniger Daten benötigt, die unmittelbare Vergangenheit der Zeitreihe wird genau rekonstruiert, während die entferntere Vergangeheit im allgemeinen Umriss wiederhergestellt wird, Hochs und Tiefs werden korrekt wiedergegeben. Deshalb ist es möglich ein 50-dimensionalen Fenster mit nur 10-dimensionalem Eingabevektor mit einer akzeptablen Genauigkeit zu beschreiben.
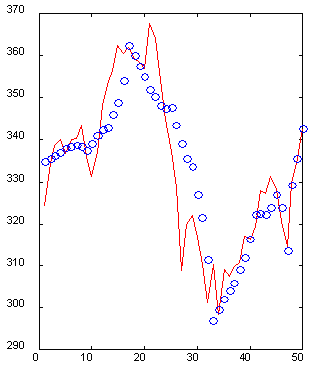
Abb. 6. Ein 50-dimensionales Fenster (durchgehende Linie) und seine Rekonstruktion durch 10 Wavelet Koeffizienten (o).
Ein weiterer möglicher Ansatz verwendet, als mögliche Kandidaten für den Raum von Attributen, die technischen Indikatoren, die automatisch in den richtigen Software-Pakete (wie MetaStock oder Windows On Wall Street) berechnet werden. Die große Anzahl solcher empirischer Attribute (Colby, 1988) macht deren Verwendung schwierig, obwohl sich jeder von ihnen als nützlich herausstellen kann, wenn er zu einer gegebenen Zeitreihe angewendet wird. Die oben beschriebenen Verfahren ermöglichen Ihnen die bedeutendste Kombination technischer Indikatoren zu wählen, als Eingabe in dem neuronalen Netz.
Verfahren von Hinweisen
Einer der schwächsten Punkte in der Finanzprognose, ist das Fehlen an Beispielen für das Lernen von neuronalen Netzen. Allgemein gesagt, Finanzmärkte (speziell der russische) sind nicht stationär. Dort erscheinen neue Indizes, für die noch keine Historie gesammelt wurde, die Art des Handels an den alten Märkten ändert sich mit der Zeit. Unter diesen Umständen ist die Länge der verfügbaren Zeitreihen für das Lernen von neuronalen Netzen eher begrenzt.
Allerdings können wir die Anzahl an Beispielen mit einigen a Priori Überlegungen über Invarianten der Zeitreihen-Dynamik erhöhen. Dies ist ein weiterer physikalisch-mathematischer Begriff, der die Qualität der Finanzprognose erheblich verbessern kann. Es handelt sich um die Erzeugung künstlicher Beispiele (Hinweise), die aus den bestehenden erhalten werden, durch verschiedene auf sie angewandte Transformationen.
Erklären wir den Grundgedanken mit einem Beispiel. Die folgende Annahme ist psychologisch sinnvoll: Trader legen ihre Aufmerksamkeit meist auf die Preiskurve, nicht auf bestimmte Werte auf den Achsen. Also, wenn wir die gesamte Zeitreihe entlang der Kursachse ein wenig strecken, sind wir in der Lage die aus einer solchen Transformation entstehende Zeitreihe für das Lernen des neuronalen Netzes zu verwenden (zusammen mit der ursprünglichen). Somit haben wir die Anzahl der Beispiele durch die Verwendung von a priori Informationen, die aus den psychologischen Eigenschaften wie ein Trader Zeitreihen wahrnimmt resultieren, verdoppelt. Darüber hinaus, zusammen mit der Steigerung der Anzahl an Beispielen, haben wie die Klasse der Funktionen eingegrenzt, unter denen wir die Lösung suchen, was auch die Prognosequalität erhöht (wenn, natürlich, die Invariante zu der Tatsache wahr ist).
Die unten gezeigten Ergebnisse von Berechnungen der Prognostizierbarkeit des S&P500 mit der Box-Zählmethode (siehe Abb. 7,8), verdeutlichen die Rolle von Hinweisen. Der Raum von Attributen, in diesem Fall, wurde durch die Orthologonasierungstechnik gebildet. Wir haben 30 Hauptkomponenten als Eingabevariablen in den 100-dimensionalen Verzögerungsraum verwendet. Dann haben wir 7 Attribute von diesen Hauptkomponenten ausgewählt - die wichtigsten orthogonal linearen Kombinationen. Wie sie in den Abbildungen unten sehen, stellte es sich hereuas, in diesem Fall, dass nur die Anwendung von Hinweisen in der Lage war eine merkliche Prognostizierbarkeit zu bieten.
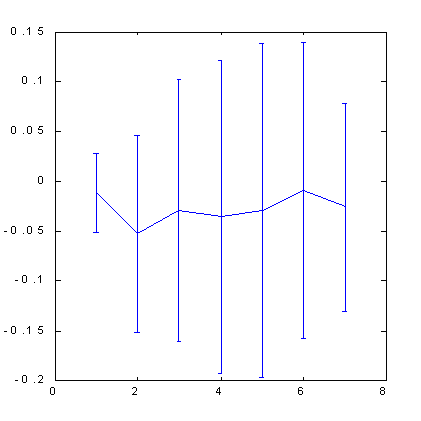
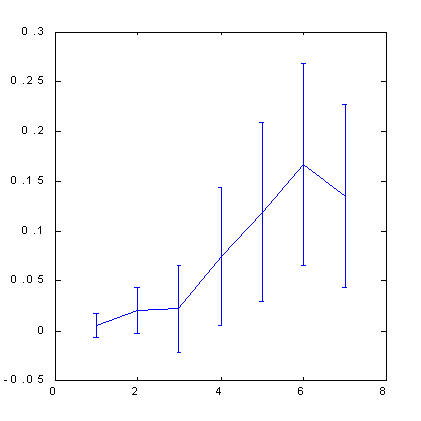
| Abb. 7. Berechenbarkeit von Kursänderungen für S&P500. | Abb. 8. Berechenbarkeit von Kursänderungszeichen für S&P500 nachdem die Anzahl der Beispiel drch Strecken der Kursachse vervierfacht wurde. |
Bitte beachten Sie, dass die Verwendung von orthogonalem Raum in einer bestimmten Steigerung der Prognostizierbarkeit resultiert, verglichen mit dem Immersionsverfahren: von 0.12 Bits (Abb.5) bis 0.17 Bits (Abb.8). Ein wenig später, wenn wir beginnen den Einfluss von Prognostizierbarkeit auf Gewinne zu besprechen, werden wir belegen, dass hierdurch die Gewinnquote um die Hälfte größer werden kann.
Ein anderes, weniger belangloses Beispiel der erfolgreichen Verwendung solcher Hinweise für neuronale Netze, in welche Richtung eine Lösung zu suchen ist, ist die Verwendung versteckter Symmetrie in Forex-Trading. Der Sinn dieser Symmetrie ist, dass Devisenkurse aus zwei "Blickwinkeln" betrachtet werden können, zum Beispiel, als eine Reihe von EUR/$ oder eine Reihe von $/EUR. Eine Steigerung von einem von ihnen, entspricht einer Abnahme des anderen. Diese Eigenschaft kann zum Verdoppeln der Anzahl der Beispiele genutzt werden: Fügen Sie zu jedem Beispiel wie ![]() sein symmetrisches Analog
sein symmetrisches Analog ![]() hinzu. Experimente in der neuronalen-Netz-Prognose zeigten, dass für den grundlegenden Devisenmarkt, die Berücksichtigung der Symmetrie die Gewinnquote um fast das Doppelte erhöht, insbesondere: von 5% bis 10% pro Jahr, unter Berücksichtigung der realen Transaktionskosten (Abu-Mostafa, 1995).
hinzu. Experimente in der neuronalen-Netz-Prognose zeigten, dass für den grundlegenden Devisenmarkt, die Berücksichtigung der Symmetrie die Gewinnquote um fast das Doppelte erhöht, insbesondere: von 5% bis 10% pro Jahr, unter Berücksichtigung der realen Transaktionskosten (Abu-Mostafa, 1995).
Messen der Prognosequalität
Obwohl die Prognose von Finanzzeitreihen sich in dem multidimensionalen Funktion Approximationsproblem erklärt, hat sie ihre eigenen besonderen Eigenschaften, sowohl im Bilden von Eingaben als auch bei der Auswahl von Ausgaben für ein neuronales Netz. Wir haben oben bereits die Eingaben betrachtet. Also untersuchen wir nun die Besonderheiten bei der Auswahl von Ausgabevariablen. Zuerst müssen wir jedoch die wichtigste Frage beantworten: Wie kann die Qualität der Finanzprognose gemessen werden? Dies wird uns helfen die beste neuronales-Netz-Lernstrategie zu ermitteln.
Beziehung zwischen Prognostizierbarkeit und Profitquote
Eine besondere Eigenschaft der Prognose von Finanzzeitreihen ist die Arbeit zum erzielen maximaler Gewinne, nicht zum Minimieren der mittleren quadratischen Abweichung, wie es die Konvention in der Approximation von Funktionen ist.
Im einfachsten Fall des täglichen Trading, sind Gewinne abhängig von richtig vorhergesagten Zeichen der Kursänderung. Aus diesem Grund muss das neuronale Netz auf eine genaue Vorhersage des Zeichens ausgerichtet sein, nicht auf den Wert selbst. Ermitteln wir nun, wie die Profitquote mit der Genauigkeit der Zeichenerkennung verbunden ist, in der einfachsten Performance des täglichen Einstiegs in den Markt (Abb.9).
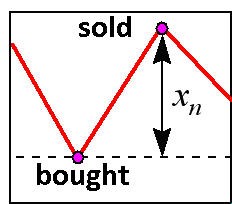
Abb. 9. Täglicher Einstieg in den Markt.
Bestimmen wir ab dem Zeitpunkt von![]() : das gesamte Kapital des Traders ist
: das gesamte Kapital des Traders ist ![]() , die relative Kursänderung ist
, die relative Kursänderung ist ![]() , und lassen Sie uns als Ausgabe des Netzes sein Konfidenzniveau für das Zeichen dieser Änderung nehmen:
, und lassen Sie uns als Ausgabe des Netzes sein Konfidenzniveau für das Zeichen dieser Änderung nehmen: ![]() . Dieses Netz mit der Ausgabe-nicht-Linearität der
. Dieses Netz mit der Ausgabe-nicht-Linearität der ![]() Form, lernt das Änderungszeichen vorherzusagen und prognostiziert das Zeichen mi dem Bereich, proportional zu seiner Wahrscheinlichkeit. Dann wird der Kapitalertrag bei Schritt
Form, lernt das Änderungszeichen vorherzusagen und prognostiziert das Zeichen mi dem Bereich, proportional zu seiner Wahrscheinlichkeit. Dann wird der Kapitalertrag bei Schritt 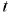 wie folgt notiert:
wie folgt notiert:
![]()
wobei ![]() der Kapitalanteil "im Spiel" ist. Es ist der Gewinn für den gesamten Handelszeitraum:
der Kapitalanteil "im Spiel" ist. Es ist der Gewinn für den gesamten Handelszeitraum:
der durch die Auswahl der optimalen Anteilsgröße 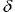 maximiert wird. Lassen wir den Trader
maximiert wird. Lassen wir den Trader ![]() der Zeichen korrekt vorhersagen, dementsprechend, sagt er falsch voraus mit einer Wahrscheinlichkeit von
der Zeichen korrekt vorhersagen, dementsprechend, sagt er falsch voraus mit einer Wahrscheinlichkeit von ![]() . Dann wird der Protitquote Logarithmus,
. Dann wird der Protitquote Logarithmus,
![]() ,
,
und der Profit selbst wird am höchsten Wert von ![]() sein, und durchschnittlich:
sein, und durchschnittlich:
![]() .
.
Hier haben wir den Koeffizienten von ![]() eingeführt. Zum Beispiel für Gaußsche Verteilung,
eingeführt. Zum Beispiel für Gaußsche Verteilung, ![]() . Das Niveau der Prognostizierbarkeit von Zeichen ist direkt verbunden mit der Kreuz-Entropie, die a priori mit dem Box-Zählverfahren eingeschätzt werden kann. Für die binäre Ausgabe (siehe Abb. 10):
. Das Niveau der Prognostizierbarkeit von Zeichen ist direkt verbunden mit der Kreuz-Entropie, die a priori mit dem Box-Zählverfahren eingeschätzt werden kann. Für die binäre Ausgabe (siehe Abb. 10):
![]()
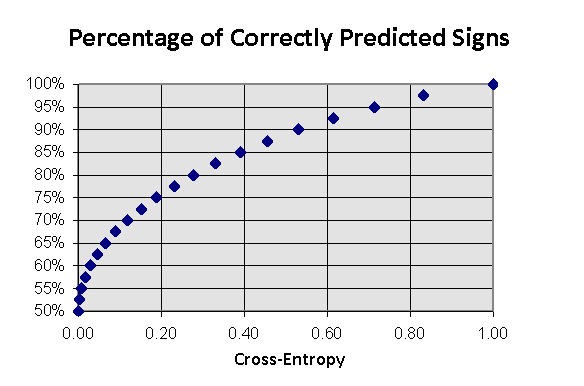
Abb. 10. Anteil der korrekt prognostizierten Richtungen von Zeitreihen-Variationen als eine Kreuz-Entropie Funktion von Ausgabezeichen für bekannte Eingaben.
Schließlich erhalten wir die folgende Einschätzung der Profitquote für den gegebenen Zeichen-Prognostizierbarkeitswert von I, ausgedrückt in Bits:
![]() .
.
Es bedeutet, dass für die Zeitreihen mit der Prognostizierbarkeit von I, es im Prinzip möglich ist das Kapitel innerhalb von ![]() Einstiegen in den Markt zu verdoppeln. So lässt beispielsweise die vorher berechnete S&P500 Zeitreihe Prognostizierbarkeit von gleich I=0.17 (siehe Abb. 8)annehmen, das Kapital im Durchschnitt durch
Einstiegen in den Markt zu verdoppeln. So lässt beispielsweise die vorher berechnete S&P500 Zeitreihe Prognostizierbarkeit von gleich I=0.17 (siehe Abb. 8)annehmen, das Kapital im Durchschnitt durch ![]() Einstiege in den Markt zu verdoppeln. Somit kann auch die Prognostizierbarkeit eines kleinen Änderungszeichens eine sehr bemerkenswert Profitquote bieten.
Einstiege in den Markt zu verdoppeln. Somit kann auch die Prognostizierbarkeit eines kleinen Änderungszeichens eine sehr bemerkenswert Profitquote bieten.
Hier müssen wir betonen, dass die optimale Profitquote ein eher vorsichtiges Vorgehen erfordert, wenn, bei jedem Einstieg in den Markt, der Teilnehmer einen streng bestimmten Anteil des Kapitals riskiert:
![]() ,
,
wo ![]() die typische Gewinn/Verlust Größe für diese Marktvolatilität
die typische Gewinn/Verlust Größe für diese Marktvolatilität ![]() ist. Kleinere und größere Werte von Kursen werden den Profit senken, ein zu riskantes Handeln kann bei jeder Prognostizierbarkeit zum Verlust von Geld führen. Both smaller and larger values of rates will decrease the profit, a too risky trading being able to result in losing money at any predictability. Dieses Tatsache ist in Abb. 11 dargestellt.
ist. Kleinere und größere Werte von Kursen werden den Profit senken, ein zu riskantes Handeln kann bei jeder Prognostizierbarkeit zum Verlust von Geld führen. Both smaller and larger values of rates will decrease the profit, a too risky trading being able to result in losing money at any predictability. Dieses Tatsache ist in Abb. 11 dargestellt.
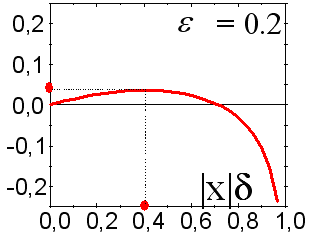
Abb. 11. Abhängigkeit der durchschnittlichen Gewinnrate eines gewählten Anteils des Kapitals "in der Kasse".
Aus diesem Grund geben die oben genannten Einschätzungen nur eine Einsicht in die oberen Grenzen der Profitquote. Eine sorgfältige Untersuchung unter Berücksichtigung des Schwankungseffekts würde den Rahmen dieses Artikels sprengen. As ist jedoch qualitativ klar, dass die Auswahl der optimalen Kontraktgröße die Einschätzung der Prognosegenauigkeit bei jedem Schritt benötigt.
Auswahl der Fehler-Funktion
Wenn wir die Prognose von Finanzzeitreihen zum Zweck der Gewinnmaximierung nehmen, ist es logisch das neuronale Netz zu diesem endgültigen abschließenden Ergebnis anzupassen. Zum Beispiel, wenn Sie nach dem obigen System handeln, können Sie für das Lernen des Neuronalen Netzes die folgende Lern-Fehlerfunktion auswählen, gemittelt durch alle Beispiele aus dem Lernmuster:
![]() .
.
Hier ist der Anteil am Kapital im Spiel als eine zusätzlicher Netz-Ausgabe eingeführt, um während des Lernens angepasst zu werden. Für diesen Ansatz, wird das erste Neuron , ![]() , mit der Aktivierungsfunktion
, mit der Aktivierungsfunktion ![]() uns die Wahrscheinlichkeit eines steigenden oder fallenden Kurses geben, während die zweite Netz-Ausgabe,
uns die Wahrscheinlichkeit eines steigenden oder fallenden Kurses geben, während die zweite Netz-Ausgabe, ![]() , den empfohlenen Anteil am Kapital, der in der gegebenen Phase zu investieren ist, hervorbringt.
, den empfohlenen Anteil am Kapital, der in der gegebenen Phase zu investieren ist, hervorbringt.
Da dieser Anteil jedoch, nach der vorherigen Analyse, proportional zu dem Prognose-Konfidenzniveau sein muss, können Sie zwei Netz-Ausgaben durch nur eine ersetzen, durch Platzieren und sich selbst begrenzen auf die Optimierung nur eines globalen Parameters, der die Fehler minieren wird:
![]()
Dies schafft die Möglichkeit die Quote nach dem durch das Netz prognostizierten Risikoniveau zu regulieren. Das Spielen mit variablen Quoten schafft mehr Gewinn, als mit festen Quoten zu arbeiten. In der Tat, wenn Sie die durch ihre mittlere Prognostizierbarkeit bestimmte Quote festlegen, wird die Wachstumsrate des Kapitals proportional zu ![]() sein, während sie, wenn Sie die optimale Quote bei jedem Schritt wählen, proportional zu
sein, während sie, wenn Sie die optimale Quote bei jedem Schritt wählen, proportional zu ![]() sein wird..
sein wird..
Verwendung Verbundener Netze
Allgemein gesprochen, werden die von verschiedenen auf dem gleichen Muster trainierten Netzen gemachten Prognosen unterschiedlich sein, durch die zufällige Natur der Auswahl der Anfangswerte von synaptischem Gewicht. Dieser Nachtteil (ein Element der Unsicherheit) kann zu einem Vorteil gedreht werden, mit einem verbundenen Neuronal Experten, bestehend aus mehreren neuronalen Netzen. Die Dispersion der Prognosen von Experten wird eine Vorstellung des Konfidenzniveaus dieser Prognosen geben, die zur Auswahl der richtigen Handelsstrategie verwendet werden können.
Es ist leicht zu belegen, dass der Durchschnitt der der verbundenen Werte bessere Prognosen hervorbringen muss, als ein durchschnittlicher Experte des gleichen Verbunds. Lassen wir den Fehler des ith Experten für die Eingabedaten von ![]() gleich sei zu
gleich sei zu ![]() . Ein durchschnittlicher Fehler eines Verbunds ist immer weniger als die mittlere quadratische Abweichung eines einzelnen Experten, im Hinblick auf die Cauchysche Ungleichheit:
. Ein durchschnittlicher Fehler eines Verbunds ist immer weniger als die mittlere quadratische Abweichung eines einzelnen Experten, im Hinblick auf die Cauchysche Ungleichheit:
![]() .
.
Es muss beachtet werden, dass die Reduktion von Fehlern eher wesentlich sind. Wenn die Fehler einzelner Experten nicht miteinander korrelieren, d.h., ![]() , ist die mittlere quadratische Verschiebung eines Verbunds bestehend aus L Experten
, ist die mittlere quadratische Verschiebung eines Verbunds bestehend aus L Experten ![]() Mal kleiner als der mittlere einzelne Fehler eines Experten!
Mal kleiner als der mittlere einzelne Fehler eines Experten!
![]()
Aus diesem Grund wäre es besser die Prognose vo einem, auf die Mittelwerte des ganzen Verbunds zu stützen. Diese Tatsache wird in Abb. 12 dargestellt.
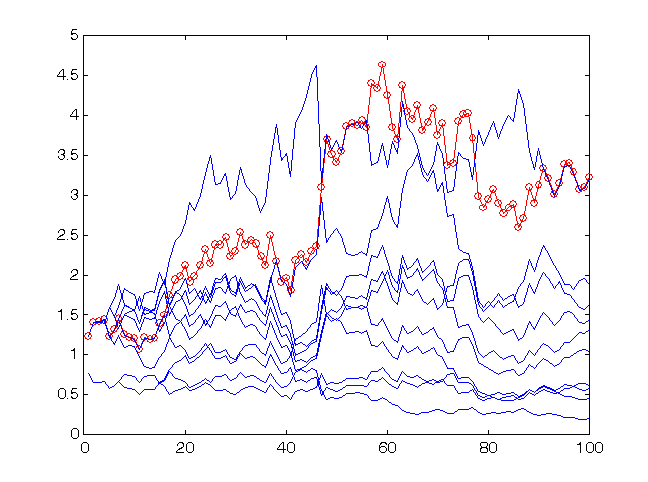
Abb. 12. Profitrate für die letzten 100 Werte der Zeitreihe sp500 beim prognostizieren mit 10 Netzen.
Der Gewinn des Verbunds (Kreise) ist höher als bei einem durchschnittlichen Experten. Der Wert der richtig prognostizierten Zeichen für den Verbund beträgt 59:41.
Wie sie in Abb. 12 sehen können, in diesem Fall, ist der Gewinn des Verbunds sogar höher als die der einzelnen Experten. Somit kann die Verbund-Methode die Prognosequalität deutlich verbessern. Bitte beachten Sie den absoluten Wert der Gewinnrate: Das Kapital des Verbunds stieg um das 3,25-fache bei 100 Einstiegen in den Markt (diese Quote wird, natürlich, niedriger sein, wenn die Transaktionskosten berücksichtigt werden).
Diese Prognosen wurden bei der Ausbildung des Netzes auf den 30 aufeinanderfolgenden Exponential Moving Averages (EMA 1 … EMA 30) der Indexinkrement Zeitreihe erhalten. Das Inkrement-Zeichen des nächsten Schrittes wurde prognostiziert
In diesem Experiment wurde die Rate festgelegt bei dem Niveau von ![]() nah zu dem optimalen für die gegebene Prognosegenauigkeit (59 richtig prognostizierte Zeichen, gegenüber 41 falsch prognostizierten Zeichen), d.h.,
nah zu dem optimalen für die gegebene Prognosegenauigkeit (59 richtig prognostizierte Zeichen, gegenüber 41 falsch prognostizierten Zeichen), d.h., ![]() . In Abb. 13 können Sie die Ergebnisse eines riskanteren Trading auf die gleichen Prognosen sehen, und zwar mit
. In Abb. 13 können Sie die Ergebnisse eines riskanteren Trading auf die gleichen Prognosen sehen, und zwar mit ![]() .
.
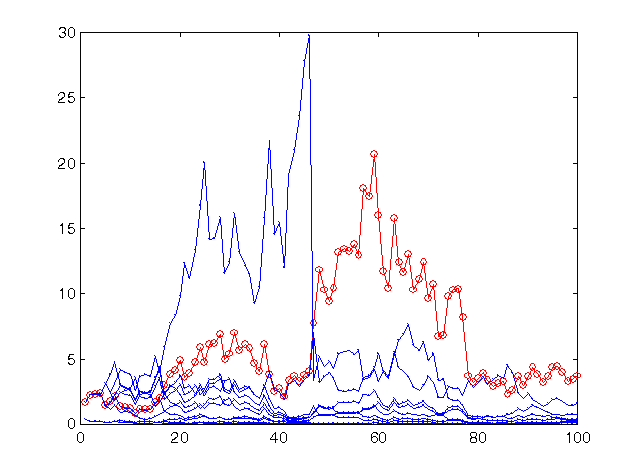
Abb. 13. Gewinnrate für die letzten 100 Werte der Zeitreihe sp500, prognostiziert mit dem glichen Verbund aus 10 Netzen, aber mit riskanterer Strategie.
Der Gewinn des Verbunds bleibt auf dem gleichen Niveau (ein wenig gestiegen), da der Risikowert so nah am Optimum ist wie der vorherige. Jedoch für die meisten Netze, deren Prognosen weniger genau sind, als des Verbunds als Ganzes, stellten sich solche Quoten als riskant heraus, was praktisch zu deren vollständigem Ruin führte.
Die obigen Beispiele zeigen wie wichtig es ist, in der Lage zu sein die Prognosequalität richtig einzuschätzen und wie diese Einschätzung zur Steigerung der Rentabilität mit der gleichen Prognose verwendet werden kann.
Wir können zu noch größeren Extremen gehen und die gewichteten Ansichten von Experten-Netzen nutzen, anstatt den durchschnittlichen. Die Gewichte sollten die vorausschauende Fähigkeit des Verbunds auf dem Lernmuster anpassungsfähig maximieren. Als Ergebnis machen schlechter ausgebildete Netze einen kleineren Beitrag und verderben nicht die Prognose.
Die Möglichkeiten dieser Methode sind unten in dem Vergleich von Prognosen aus 2 Arten von Verbund-Netzen, bestehend aus 25 Experten (siehe Abb. 14 und 15), dargestellt. Die Prognosen wurden nach dem gleichen System gemacht: als Eingabe wurde der Exponential Moving Average der Zeitreihe verwendet, mit Perioden gleich zu den ersten 10 Fibonacci-Zahlen. Entsprechend den Ergebnissen aus 100 Experimenten, bietet die gewichtete Prognose einen durchschnittlichen Überschuss von richtig prognostizierten ungefähr gleich zu 15, während der Faktor für die mittlere Prognose ungefähr 12 ist. Es sollte beachtet werden, dass das die gesamte Anzahl der Kurssteigerungen, verglichen mit fallenden innerhalb der gegebenen Periode, genau gleich 12 ist. Deshalb ergibt die Berücksichtigung der Haupttendenz zum Erhöhen als triviale Prognose des Zeichen "+" das gleiche Ergebnis für den Prozentsatz an richtig prognostizierten Zeichen, wie die gewichtete Ansicht von 25 Experten.
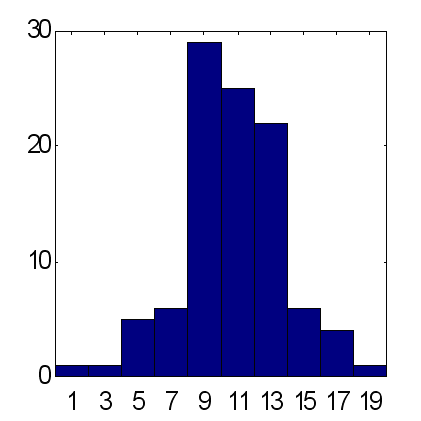
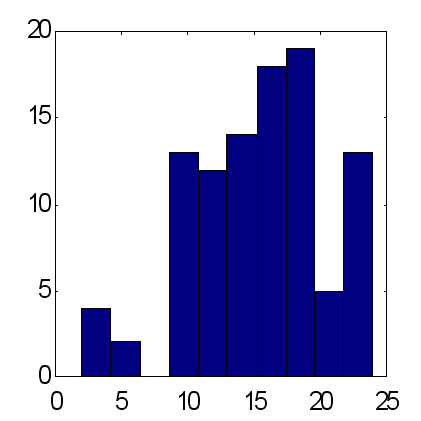
| Abb. 14. Histogramm von Summen prognostizierter Zeichen bei durchschnittlicher Prognose von 25 Experten. Ein Durchschnitt für 100 Verbundene = 11.7 bei Standard-Abweichung von 3.2. | Abb. 15. Histogramm von Summen richtig prognostizierter Zeichen bei gewichteter Prognose der gleichen 25 Experten. Ein Durchschnitt für 100 Verbundene = 15.2 bei Standard-Abweichung von 4.9. |
Mögliche Gewinnrate bei Prognosen mit Neuronalen Netzen
Bisher haben wir die Ergebnisse von nummerischen Experimenten als Prozentsatz der richtig prognostizierten Zeichen formuliert. Nun wollen wir die wirklich erreichbare Gewinnrate für das Trading mit neuronalen Netzen herausfinden. Die oberen Grenzen der Gewinnrate, oben erhalten ohne Berücksichtigung der Schwankungen, sind in der Praxis kaum zu erreichen, umso mehr, weil wir keine Transaktionskosten vorher berücksichtigt haben, die aus dem erreichten Prognose-Niveau gestrichen werden können.
Tatsächlich resultiert die Berücksichtigung der Provisionen im Erscheinen einer Zerfallskonstante:
![]() .
.
Darüber hinaus, im Gegensatz zum Prognostizierbarkeitsniveau 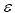 , tritt Provision
, tritt Provision ![]() linear, nicht quadratisch auf. Somit können in dem obigen Beispiel die typischen Werte der Prognostizierbarkeit
linear, nicht quadratisch auf. Somit können in dem obigen Beispiel die typischen Werte der Prognostizierbarkeit ![]() die Provision
die Provision ![]() nicht überschreiten.
nicht überschreiten.
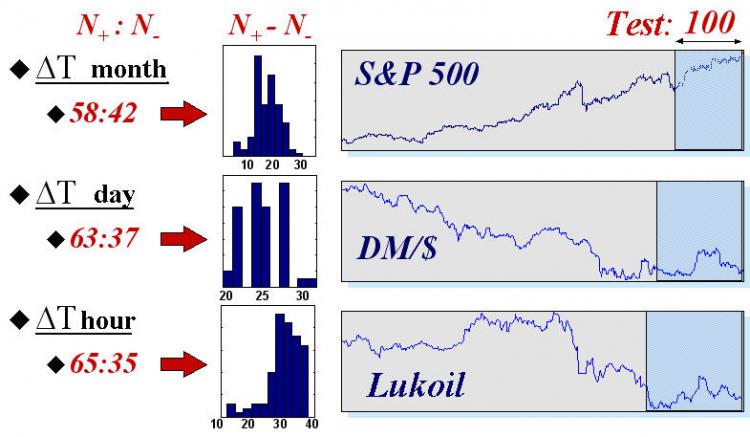
Um eine Vorstellung der realen Möglichkeiten von neuronalen Netzen in diesem Bereich zu geben, werden wir die Ergebnisse von automatisiertem Trading mit neuronalen Netzen an drei Indizes mit typischen Zeiten übergeben: den Wert des Index S&P500 mit monatlichen Abständen zwischen den Lesungen, tägliche Kurse DM/$ und stündliche Lesungen von Futures von Lukoil Aktien an der russischen Börse. Die Statistiken der Prognose wurden auf 50 neuronales Netz Systemen (mit Verbünden von 50 neuronalen Netzen jedes) gesammelt. Die Zeitreihen selbst und die Prognoseergebnisse der Zeichen auf einen Test-Satz der letzten 100 Werte jeder Zeitreihe werden in Abb. 16 gezeigt.
Abb. 16. Mittelwerte und Histogramm der Anzahl richtig (![]() ) und falsch (
) und falsch (![]() ) prognostizierter Zeichen auf Testmustern mit 100 Werten von drei realen Finanz-Indizes.
) prognostizierter Zeichen auf Testmustern mit 100 Werten von drei realen Finanz-Indizes.
Diese Ergebnisse bestätigen die intuitiv offensichtliche Regelmäßigkeit: Die Zeitreihen sind umso berechenbarer, je weniger Zeit zwischen den Lesungen vergeht. In der Tat, je mehr Zeit zwischen den aufeinanderfolgenden Werten einer Zeitreihe vergeht, desto mehr Informationen, externe gegenüber ihrer Dynamik, sind für die Marktteilnehmer verfügbar, und deswegen, ist umso weniger Information über die Zukunft in den Zeitreihen selbst.
Dann wurden die oben erhaltenen Prognosen für Trading auf einer Test-Einstellung verwendet. Gleichzeitig wurde die Größe des Kontrakts in jedem Schritt proportional zu dem Konfidenzgrad der Prognose gewählt, während der Wert des globalen Parameters 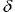 auf das Lernmuster optimiert wurde. Außerdem, seinem Erfolg entsprechend, hatte jedes Netz in dem Verbund seine eigene Bewertung. Während der Prognose bei jedem Schritt, verwendeten wir nur den tatsächlich "besten" Teil von Netzen. Die Ergebnisse von solchen "neuronalen" Tradern werden in Abb. 17 gezeigt.
auf das Lernmuster optimiert wurde. Außerdem, seinem Erfolg entsprechend, hatte jedes Netz in dem Verbund seine eigene Bewertung. Während der Prognose bei jedem Schritt, verwendeten wir nur den tatsächlich "besten" Teil von Netzen. Die Ergebnisse von solchen "neuronalen" Tradern werden in Abb. 17 gezeigt.
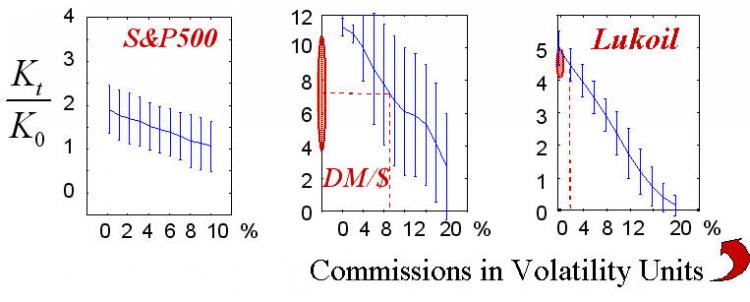
Abb. 17. Gewinnstatistiken von 50 Realisierungen entsprechend der Höhe der Provisionen.
Reale Werte der in gestrichelten Linien eingezeichneten Provisionen zeigen den Bereich wirklich erreichbarer Gewinnraten.
Der endgültige Gewinn (wie die Spielstrategie selbst), natürlich, hängt ab von der Provisionsgröße. Es ist diese Abhängigkeit, die in den obigen Diagrammen dargestellt wird. Die realistischen Werte von Provisionen in dem Autor bekannten Maßeinheiten sind in der Abbildung markiert. Es muss präzisiert werden, dass die "quantifizierte" Natur des realen Trading nicht in diesen Experimenten berücksichtigt wurde, d.h., wir haben nicht die Tatsache berücksichtigt, das die Größe der Trades gleich zu der Ganzzahl (integer) typischer Kontrakte sein muss. Dieser Fall entspricht dem Handel mit großem Kapital, bei dem das typische Trading viele Kontrakte umfasst. Außerdem wurde der garantierte Handel impliziert, d.h., die Gewinnrate wurde als Verhältnis zu dem Sicherheitskapital berechnet, das viel kleiner ist als die Skalierung der Kontrakte selbst.
Die obigen Ergebnisse zeigen, dass Trading mit neuronalen Netzen wirklich vielversprechend ist, zumindest für kurze Laufzeiten. Darüber hinaus, in Anbetracht der Selbstähnlichkeit von Finanzzeitreihen (Peters, 1994), wird die Gewinnrate pro Zeiteinheit umso höher sein, je geringer die typische Handelszeit ist. daher stellen sich automatisierte Trader mit neuronalen Netzen als die effektivsten heraus, wenn sie im Echtzeitmodus handeln, wo ihre Vorteile über typische Broker am deutlichsten sind: müdigkeitsfrei, keine Anfälligkeit für Emotionen, potentiell viel höhere Rücklaufquote. Ein gut trainiertes neuronales Netz, verbunden mit einem automatisierten Handelssystem, kann Entscheidungen viel früher treffen, als ein menschlischer Bediener Kursänderungen im Chart von seinem oder ihrem Terminal bemerkt.
Fazit
Wir haben gezeigt, dass (zumindest einige) Marktzeitreihen zumindest teilweise psognostizierbar sind. Wie jede andere Art neuronaler Analyse, erfordert die Prognose von Zeitreihen eine komplzierte und sorgfältige Datenvorverarbeitung. Die Arbeit mit Zeitreihen hat jedoch ihren eigenen spezifischen Charakter, der genutzt werden kann um die Gewinne in einigen Fällen zu steigern. Dies betrifft sowohl die Auswahl der Eingaben Verwendung besonderer Methoden der Datendarstellung), als auch die Auswahl der Ausgaben, und die verwendung bestimmter Fehlerfunktionen. Schließlich haben wir gezeigt, wie viel rentabler es ist verbundene neuronale Experten zu vewrwenden, im Vergleich zu einzelnen neuronalen Netzen, und bietet außerdem die reae Gewinnrate auf mehrere echte Finanzinstrumente.
Referenzen:
- Sharpe, W.F., Alexander, G.J., Bailey, J.W. (1997). Investments. - 6th edition, Prentice Hall, Inc., 1998.
- Abu-Mostafa, Y.S. (1995). "Financial market applications of learning from hints”. In Neural Networks in Capital Markets. Apostolos-Paul Refenes (Ed.), Wiley, 221-232.
- Beltratti, A., Margarita, S., and Terna, P. (1995). Neural Networks for Economic and Financial Modeling. ITCP.
- Chorafas, D.N. (1994). Chaos Theory in the Financial Markets. Probus Publishing.
- Colby, R.W., Meyers, T.A. (1988). The Encyclopedia of Technical Market Indicators. IRWIN Professional Publishing.
- Ehlers, J.F. (1992). MESA and Trading Market Cycles. Wiley.
- Kaiser, G. (1995). A Friendly Guide to Wavelets. Birk.
- LeBeau, C., and Lucas, D.W. (1992). Technical traders guide to computer analysis of futures market. Business One Irwin.
- Peters, E.E. (1994). Fractal Market Analysis. Wiley.
- Pring, M.G. (1991). Technical Analysis Explained. McGraw Hill.
- Plummer, T. (1989). Forecasting Financial Markets. Kogan Page.
- Sauer, T., Yorke, J.A., and Casdagli, M. (1991). "Embedology". Journal of Statistical Physics. 65, 579-616.
- Vemuri, V.R., and Rogers, R.D., eds. (1993). Artificial Neural Networks. Forecasting Time Series. IEEE Comp.Soc.Press.
- Weigend, A and Gershenfield, eds. (1994). Times series prediction: Forecasting the future and understanding the past. Addison-Wesley.
- Baestaens, D.-E., Van Den Bergh, W.-M., Wood, D. Neural Network Solutions for Trading in Financial Markets. Financial Times Management (July 1994).
Der Artikel ist mit Zustimmung des Autors veröffentlicht.
Über den Autor: Sergey Shumskiy ist der leitende wissenschaftliche Mitarbeiter am Institut für Physik der Russischen Akademie der Wissenschaften, Cand. Sc.(Physik und Mathematik), maschinelles Lernen und Techniker künstlicher Intelligenz, Präsidiumsmitglied der russischen Neuronale-Netze-Gesellschaft, CEO der IQMen Corp., die experten Systeme für Unternehmen entwickelt, mit maschinellen Lerntechnologien. Herr Shumskiy ist ei Co-Autor von mehr als 50 wissenschaftlichen Publikationen.
Die Kurse des Autors: Neuronales Computing und seine Anwendung in Economics and Business
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/1506
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
 Orders.Erstellen aktiver MQL5-Bedienfelder für den Handel
Orders.Erstellen aktiver MQL5-Bedienfelder für den Handel
 Zeichnen Horizontaler Durchbruch-Ebenen mit Fractals
Zeichnen Horizontaler Durchbruch-Ebenen mit Fractals
 Verbindung eines Expert-Systems mit ICQ in MQL5
Verbindung eines Expert-Systems mit ICQ in MQL5
 Grafische Kontrolle der Externen Parameter von Indikatoren
Grafische Kontrolle der Externen Parameter von Indikatoren
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.