Prevendo séries temporais financeiras

Introdução

Esse artigo lida com uma das mais populares práticas de aplicações de redes neurais, a previsão de séries temporais de mercados. Nesse campo a previsão é mais relacionada à rentabilidade e pode ser considerada como uma das atividades de negócios.

A previsão de séries temporais financeiras é um elemento necessário de qualquer atividade investigativa. O conceito de investigação por si - investir dinheiro agora para ganhar lucros no futuro - é baseado no conceito de prever o futuro. Portanto, prever séries temporais financeiras delineiam as atividades de toda a indústria de investimento - todas as trocas organizadas e outros sistemas de negociação de segurança.

Vamos dar alguns números que ilustram a escala dessa indústria de previsão (Sharp, 1997). O giro diário do mercado de ações dos EUA excede os 10 bilhões de dólares. A Depositary Trust Company nos EUA, onde segurados no montante de 11 trilhões de dólares (do volume total de 18 trilhões de dólares) estão registrados, marca aproximadamente um movimento de 250 bilhões de dólares diariamente. O mundo dos negócios FOREX é ainda mais ativo. Seu giro diário excede os 1000 bilhões de dólares. É aproximadamente 1/50 do capital agregado global.

99% de todas as transações são conhecidas como especulativas, isto é, não são focadas em serviços para circulação de bens reais, e sim realizadas para ganhar lucros do esquema: "comprei barato e vendi melhor". Todos eles são baseados nas previsões dos negociadores sobre as mudanças feitas nas taxas. Ao mesmo tempo, e é muito importante, as previsões feitas pelos participantes de cada transação são polares. Então o volume de transações especulativas caracteriza a medida de discrepâncias nas previsões dos participantes do mercado, isto é, na realidade, a medida de imprevisibilidade das séries temporais financeiras.

Essa propriedade mais importante das séries temporais financeiras delineia a hipótese de mercado eficiente apresentada por Louis Bachelier em sua tese em 1900. De acordo com essa doutrina, um investidor pode somente esperar pela rentabilidade média do mercado estimada usando tais índices como Dow Jones ou S&P500 (para a bolsa de valores de Nova York). Entretanto, cada lucro especulativo ocorre aleatoriamente e é similar a uma aposta. A imprevisibilidade das curvas do mercado são determinadas pela mesma razão da qual o dinheiro pode ser dificilmente encontrado perdido no chão em ruas muito movimentadas: existem muitos voluntários para o recolher.

A teoria de mercado eficiente não é suportada, naturalmente, pelos participantes do mercado em si (porque eles estão exatamente em busca desse dinheiro "mentiroso"). A maioria deles tem certeza de que as séries temporais financeiras, embora sejam estocásticas, são cheias de regularidades escondidas, isto é, elas são pelo menos parcialmente previsíveis. Foi Ralph Elliott, o fundador da análise técnica, que tentou descobrir tais regularidades empíricas escondidas no século 30.

Nos anos 80 esse ponto de vista encontrou um suporte surpreendente na teoria do caos dinâmica que ocorreu pouco tempo antes. A teoria é baseada na oposição do estado de caos e estocasticidade (aleatoriedade). Séries caóticas somente parecem aleatórias, mas como um processo dinâmico determinado, elas deixam um bom espaço para uma previsão a curto prazo. A área de previsões possíveis é limitada em tempo pelo horizonte de previsões, mas isso pode ser suficiente para ganhar lucros reais com a previsão (Chorafas, 1994). Então estes com os melhores métodos matemáticos para extrair as regularidades de séries caóticas ruidosas podem esperar uma melhor margem de lucros - ao custo dos seus colegas não tão bem equipados.

Nesse artigo daremos fatos específicos confirmando a previsibilidade parcial de séries temporais financeiras e mesmo uma avaliação numérica dessa previsibilidade.

Análise Técnica e Redes Neurais

Nas décadas recentes, a análise técnica - um conjunto de regras empíricas baseadas em vários indicadores de comportamento de mercado - se tornaram mais e mais populares. A análise técnica se concentra no comportamento individual de uma dada segurança, irrelativa a outras seguranças (Pring, 1911).

Essa abordagem é psicologicamente baseada na concentração de um investidor sobre exatamente a segurança que estão trabalhando em um determinado momento. De acordo com Alexander Elder, um reconhecido analista técnico (anteriormente graduado como psicoterapeuta), o comportamento da comunidade do mercado financeiro é muito parecida com o comportamento de multidão caracterizado pelas leis especiais de psicologia de massas. O efeito da multidão simplifica o pensamento, nivela por baixo as peculiaridades individuais e produz as formas de comportamento coletivo e gregário que são mais primitivas do que as individuais. Particularmente, o instinto social aprimora o papel de um líder, um alfa macho/fêmea. A curva de preços, de acordo com Elder, é exatamente esse líder, focando a consciência coletiva do mercado em si mesma. Essa interpretação psicológica do comportamento do preço do mercado prova aquela aplicação da teoria do caos dinâmico. A previsibilidade parcial do mercado é determinada por um comportamento coletivo relativamente primitivo de jogadores que formam um único sistema dinâmico caótico com uma quantidade relativamente pequena de graus internos de liberdade.

De acordo com essa doutrina, você tem que "quebrar das correntes" da multidão, ascender sobre ela e se tornar mais esperto do que a multidão para ser capaz de prever as curvas do mercado. Para esse propósito, você supostamente tem que desenvolver um sistema de jogo de azar avaliado no comportamento anterior de uma série temporal e seguir esse sistema estritamente, sendo não afetado pelas emoções e rumores circulando ao redor do determinado mercado. Em outras palavras, as previsões precisam ser baseadas em um algoritmo, isto é, elas podem e devem ser entregues a um computador (LeBeau, 1992). Um homem poderia simplesmente criar esse algoritmo, para a finalidade de que ele tenha vários produtos de software que facilitem o desenvolvimento e o posterior suporte das estratégias programadas com base nas ferramentas de análises técnicas.

De acordo com essa lógica, porque não usar um computador no estágio de desenvolvimento da estratégia, com seu foco não sendo um assistente calculando os indicadores conhecidos do mercado e testando as estratégias dadas, mas sim para descobrir indicadores otimizados e estratégias otimizadas para os indicadores encontrados. Essa abordagem suportada pela aplicação de tecnologias de redes neurais está ganhando mais e mais adeptos desde o início dos anos 90 (Beltratti, 1995, Baestaens, 1997) já que tem um número de vantagens incontestáveis.

Primeiramente, análises de redes neurais, ao contrário da técnica, não assume nenhuma limitação da natureza da entrada de dados. Ela pode ser ambos os indicadores das séries temporais dadas e a informação sobre o comportamento de outras seguranças de mercado. Não sem razão, estes são investidores institucionais (por exemplo, grandes fundos de pensão) que ativamente usam redes neurais. Tais investidores trabalham com grandes portfólios, para a qual as correlações entre os mercados diferentes são de importância primordial.

Segundo, diferente de análises técnicas com base em recomendações gerais, redes neurais podem encontrar indicadores otimizados para a segurança dada e baseá-las em uma estratégia otimizada de previsão, novamente, para a série temporal dada . Além disso, essas estratégias podem ser adaptáveis, mudando com o mercado, que é de importância primordial para mercados novos, se desenvolvendo dinamicamente, particularmente para o mercado russo.

O modelamento de redes neurais por si é baseado somente em dados sem envolver qualquer considerações a priori. Ai está sua força e, ao mesmo tempo, seu tendão de Aquiles. Os dados disponíveis podem ser insuficientes para o aprendizado, a dimensionalidade de entradas potenciais pode de fato ser muito alta. Mais adiante neste artigo vamos demonstrar como a experiência acumulada pela análise técnica pode ajudar a superar essas dificuldades, típicas no campo de previsões financeiras.

Técnica de previsão de séries temporais

Como um primeiro passo, vamos descrever o esquema geral das previsões de séries temporais usando redes neurais (fig. 1).

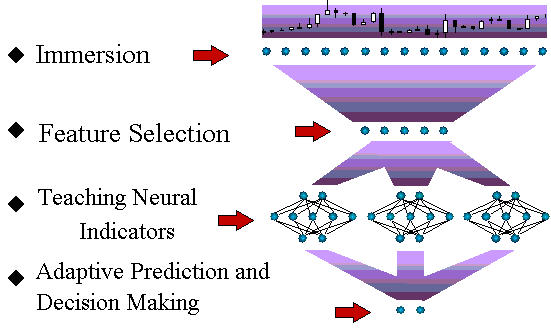
Fig. 1. O esquema do ciclo tecnológico das previsões de séries temporais.

Mais adiante neste artigo vamos discutir brevemente todos estágios desse fluxo de processos. Embora os princípios gerais da modelagem de redes neurais sejam totalmente aplicáveis a essa tarefa, a previsão de séries temporais financeiras tem suas próprias peculiaridades. Esses são os recursos específicos que serão descritos neste artigo ao máximo possível.

Técnica de imersão. Teorema de Tackens

Vamos começar com o estágio de imersão. Como vemos agora, para todas as previsões que parecem ser os dados de extrapolação , redes neurais, certamente, resolvem o problema da interpolação, que aumenta consideravelmente a validade da solução. Prever uma série temporal se resume no problema de rotina da análise neural - aproximação de uma função multivariável para um dado conjunto de exemplos - usando o procedimento de imersão das séries temporais em um espaço multidimensional (Weigend, 1994). Por exemplo um espaço dimensional atrasado de séries temporais consiste de valores das séries temporais em instantes consecutivos de tempo:

.

O seguinte Teorema de Tackens é comprovado para sistemas dinâmicos: Se uma série temporal é gerada por um sistema dinâmico, isso é, os valores de são uma função arbitrária do estado de tal sistema, há uma profundidade de imersão (aproximadamente igual ao número efetivo de graus de liberdade desse sistema dinâmico) que fornece uma previsão inequívocado próximo valor das séries temporais (Sauer, 1991). Assim, tendo escolhido uma série um tanto grande, você pode garantir uma dependência inequívoca entre o valor futuro das séries temporais e seus valores anteriores:, isto é, a previsão de uma série temporal se resolve no problema da interpolação de funções multivariáveis. Assim você pode usar a rede neural para restaurar essa função desconhecida com base em um conjunto de exemplos definidos pelo histórico das séries temporais.

Ao contrário, como em uma série temporal aleatória, o conhecimento do passado não fornece nenhuma ajuda útil para prever o futuro. Então, de acordo com a teoria de mercado eficiente, a dispersão dos valores previstos das séries temporais não mudará quando ser imersa no espaço atrasado.

A diferença entre uma dinâmica caótica e uma estocástica (aleatória) detectada durante a imersão é mostrada na figura 2.

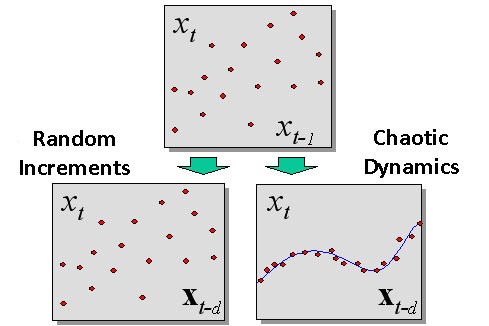
Fig. 2. A diferença entre um processo aleatório e uma dinâmica caótica detectada durante a imersão.

Confirmação empírica da previsibilidade das séries temporais

O método de imersão nos permite quantitativamente medir a previsibilidade de seguranças reais, isto é, provar ou recusar a hipótese de mercado eficiente. De acordo com a última, a dispersão de pontos em todas as coordenadas do espaço atrasado é idêntica (se os pontos forem distribuídos com valores aleatórios independentes). Ao contrário, as dinâmicas caóticas que fornecem uma certa previsibilidade devem levar a observações serão agrupadas ao redor de uma certa hipersuperfície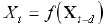, isto é, a amostra experimental forma um conjunto com a dimensão menor do que a dimensão de todo o espaço atrasado.

Para medir as dimensões, você pode usar a seguinte propriedade intuitiva: Se um conjunto tem a dimensão de D, então, desde que esteja dividido em superfícies cúbicas menores e menores com um lado de , o número de tais cubos crescerá como. Esse fato delineia a detecção da dimensão de conjuntos pelo método de contagem de caixas que conhecemos de considerações anteriores. A dimensão de um conjunto de pontos é detectada pela taxa de crescimento do número de caixas que contém todos os pontos do conjunto. Para acelerar o algoritmo, tomamos as dimensões do 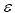como múltiplos de 2, isto é, a escala da resolução é medida em bits.

Como um exemplo de uma série temporal típica, vamos olhar a ferramenta financeira bem conhecida como índice S&P500 que reflete a dinâmica de preço médio na bolsa de valores de Nova York. A fig. 3 mostra a dinâmica de índice para o período de 679 meses. A dimensão (quer dizer, a dimensão de informação) de incrementos dessa série temporal, calculada pelo método de contagem de caixas, é mostrado na figura 4.

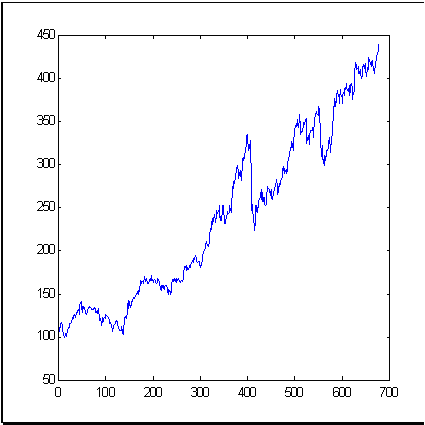
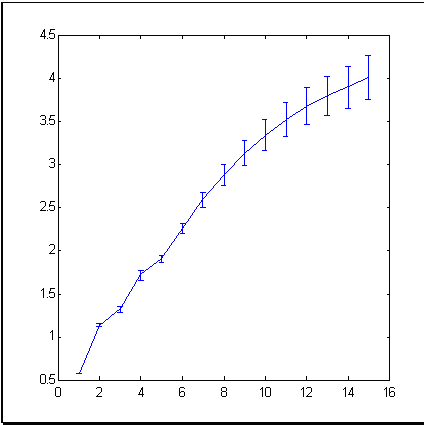
Fig. 3. Uma série temporal de 679 valores de S&P500, usada como um exemplo neste artigo.

4. A informação de dimensão em incrementos da série temporal S&P500.

Como segue a partir da figura 4, os pontos experimentais formam um conjunto da dimensão de aproximadamente 4 em um espaço de imersão de 15 dimensões. Isso é muito menor do que 15 que gostaríamos de obter com base na teoria de mercado eficiente que considera as séries temporais de incrementos como valores aleatóriosindependentes.

Assim, os dados empíricos fornecem uma evidência convincente da presença de um determinado componente previsível em uma série temporal financeira, embora não podemos dizer que há uma dinâmica caótica totalmente determinada aqui. Então as tentativas de aplicar a análise neural para a previsão de mercado são baseadas em fortes razões.

Entretanto, deve ser notado que a previsibilidade teórica não garante a obtenção de um nível praticamente significativo de previsões. Uma estimativa quantitativa da previsibilidade de séries temporais específicas pode ser obtida ao medir a entropia cruzada, que é também possível ao usar a técnica de contagem de caixas. Por exemplo, mediremos a previsibilidade de incrementos S&P500 com relação à profundidade de imersão. Entropia cruzada

,

A tabela dada abaixo (fig. 5) mede a informação adicional sobre o próximo valor das séries temporais, suportado pelos valores anteriormente conhecidos dessa série temporal.

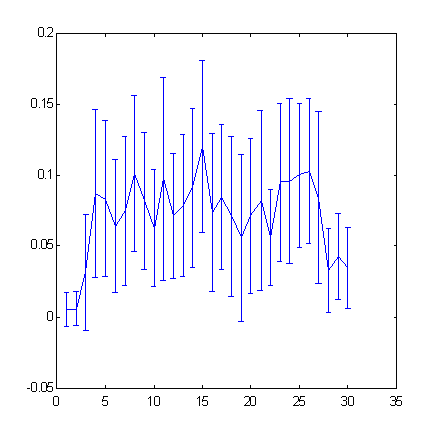
Fig. 5. A previsibilidade dos sinais de incremento para a série temporal S&P500 relacionada à profundidade de imersão (a largura da "janela").

Aumentar a profundidade de imersão além de 25 acompanhará uma diminuição da previsibilidade.

Iremos avaliar posteriormente o lucro que é praticamente alcançável em tais níveis de previsibilidade.

Formando um espaço de entrada de atributos

Na figura 5 você pode ver que aumentar a largura da janela de imersão da série temporal eventualmente resulta na diminuição da previsibilidade - quando as dimensões de entrada aumentadas não são mais compensados por seus valores de informação. Nesse caso, se a dimensão de espaço de atraso for muito grande para o dado número de exemplos, teremos que suar métodos especiais para formar um espaço de atributos com dimensões menores. As maneiras específicas para selecionar atributos em séries temporais financeiras e/ou aumentar a quantidade de exemplos será descrita abaixo.

Escolhendo a funcional de erro

Para fazer o aprendizado de uma rede neural, não é suficiente formar conjuntos de ensino de entradas/saídas. A previsão de erros da rede também deve ser determinada. O erro quadrático médio usado na maioria das aplicações de redes neurais por padrão não possui muito "senso financeiro" para as séries temporais de mercado. É por isso que consideramos em uma seção especial do artigo os erros específicos para séries temporais financeiras e demonstramos como são relacionadas à possível taxa de lucro.

Por exemplo, ao escolher uma posição de mercado, uma detecção confiável do sinal para as mudanças de taxa é muito mais importante do que a diminuição do desvio quadrático médio. Embora essas indicações sejam relacionadas um ao outro, as redes otimizadas para um deles fornecerá previsões piores para o outro. A escolha de uma função de erro adequada, como provamos adiante nesse artigo, deve se basear em uma certa estratégia ideal e ditada, por exemplo, pelo desejo de maximizar lucros (ou minimizar possíveis perdas).

Aprendizado de redes neurais

As características específicas principais de previsões de séries temporais está no campo de pré-processamento de dados. O procedimento de ensino para redes neurais separadas é padrão. Como sempre, os parâmetros disponíveis são divididos em três amostras: aprendizado, validação e testes. O primeiro é usado para aprendizado de rede, o segundo para selecionar a arquitetura de rede otimizada e/ou selecionar o momento para parar de ensinar a rede. Finalmente, o terceiro que não foi usado para ensinar serve para controlar a qualidade das previsões das redes neurais "treinadas".

Entretanto, para séries temporais com muito ruído, o uso de redes neurais em grupo pode resultar em um ganho significativo na confiabilidade de previsões. Terminaremos esse artigo com uma discussão sobre essa técnica.

Em algumas pesquisas, podemos encontrar a evidência de melhores qualidades de previsões devido ao uso de redes neurais de retorno. Tais redes podem ter uma memória local que salva os dados do passado mais distante dos que explicitamente disponíveis nas entradas. Entretanto, considerar tal arquitetura nos desviará do assunto principal, ainda mais porque existem alguns métodos alternativos para expandir eficientemente o "horizonte" da rede devido a técnicas de imersão especiais para séries temporais descritas abaixo.

Formando um espaço de atributos

A programação eficaz de entradas é uma chave para a qualidade aprimorada de previsões. É de especial importância para séries temporais financeiras de previsões difíceis. Todas as recomendações em processamentos de dados são aplicáveis aqui também. Entretanto, existem métodos específicos de pré-processamento de dados de séries temporais financeiras que vamos considerar com mais detalhes nesta seção.

Métodos de imersão de séries temporais

Primeiro, devemos ter em mente que não devemos usar os valores das cotações, que designamos como , como entradas ou saídas de uma rede neural. Essas são mudanças de cotação que são realmente significativas para previsões. Já que esses valores mentem, como regra, dentro de uma faixa muito menor do que as cotações em si, há uma forte correlação entre os valores das taxas - o próximo valor mais provável da taxa é igual a seu valor anterior: . Ao mesmo tempo, como foi enfaticamente repetido, para aumentar a qualidade de aprendizado, devemos trabalhar para a independência estatística de entradas, isto é, a ausência de tais correlações.

É por isso que é lógico selecionar os valores estatisticamente mais independentes como entradas, por exemplo, mudanças de cotações ou logaritmo de incremento relativo . A última escolha é boa para séries temporais de longa duração, onde o efeito da inflação se torna bem notável. Nesse caso, diferenças simples em partes diferentes das séries estarão em faixas diferentes, já que, de fato, são medidas em unidades diferentes. De modo contrário, as razões entre as cotações consecutivas não dependem de unidades de medidas e estarão na mesma escala, embora as unidades de medição mudem devido à inflação. Como resultado, uma estacionariedade das séries temporais nos permitirá usar históricos maiores para ensinar e fornecer um aprendizado melhor.

Uma desvantagem da imersão em um espaço atrasado é o "horizonte" limitado da rede. De modo contrário, análises técnicas não corrigem a janela no passado e algumas vezes usam os valores bem distantes das séries temporais. Por exemplo, os valores máximo e mínimo de uma série temporal, mesmo quando tomados de um passado relativamente remoto, são garantidos para afetar fortemente a psicologia do investidor e, portanto, estes valores devem ainda ser significantes para as previsões. Uma janela insuficientemente ampla para imersão no espaço atrasado não pode fornecer tal informação, que, naturalmente, diminui a eficácia para as previsões. Por outro lado, a janela de tais valores que cobrem os valores distantes e extremos das séries temporais aumentará as dimensões da rede. Isso, por sua vez, resultará na eficácia reduzida das previsões das redes neurais - agora devido ao crescimento da rede.

Uma maneira para sair dessa situação aparentemente sem saída pode ser encontrada nos métodos alternativos de programar o comportamento anterior das séries temporais. É intuitivamente óbvio que quanto mais as datas voltam no histórico das séries temporais, menos os detalhes de comportamento afetam os resultados das previsões. Isso é determinado pela percepção subjetiva do passado por investidores que, estritamente falando, formam o futuro. Portanto, devemos encontrar tal representação das dinâmicas de séries temporais que então terão uma precisão seletiva: quanto mais indo ao passado, menores os detalhes. Ao mesmo tempo, a aparência geral da curva deve permanecer intacta. A chamada decomposição do wavelet (onduleta) pode ser um tanto promissora aqui. Ela é equivalente em seu valor de informação com a imersão de atraso, mas ela torna mais fácil comprimir os dados de modo que o passado seja descrito com a precisão seletiva.

Diminuindo a dimensão das entradas: Atributos

Essa compressão de dados é um exemplo de extração de atributos mais significativos para previsões de um número excessivamente grande de variáveis de entrada. Os métodos de extração sistemática de atributos já foram descritos acima. Eles podem (e devem) ser aplicados sucessivamente para a previsão de séries temporais também.

É importante que a representação de entradas possivelmente facilite a extração de dados. A representação de wavelet é um exemplo de uma boa (do ponto de vista da extração de atributos) programação (Kaiser, 1995). Por exemplo, o próximo gráfico (fig. 6) mostra uma seção de 50 valores de uma série temporal com sua reconstrução por 10 coeficientes wavelet especialmente selecionados. Note que, embora precise de cinco vezes menos dados, o passado imediato da série temporal é reconstruído de modo preciso, enquanto o passado mais remoto é restaurado de modo geral, altos e baixos sendo refletidos corretamente. Portanto, é possível descrever uma janela com 50 dimensões com somente um vetor de entrada de 10 dimensões com uma precisão aceitável.

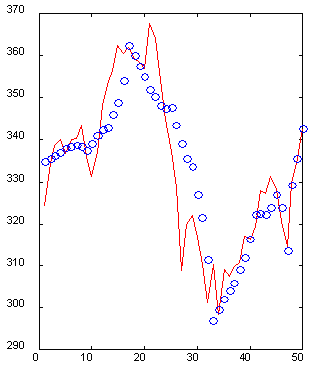
Fig. 6. Um exemplo de uma janela de 50 dimensões (linha sólida) e sua reconstrução por 10 coeficientes wavelet (o).

Outra abordagem possível é usar como possíveis candidatos para o espaço de atributos vários indicadores técnicos que são automaticamente calculados em pacotes de software adequados (como o MetaStock ou Windows on Wall Street). O grande número de tais atributos empíricos (Colby, 1988) torna seu uso difícil, embora cada um deles possa ser útil se aplicado a uma dada série temporal. Os métodos descritos acima permitirão que você selecione a combinação mais significativa de indicadores técnicos a serem usados como entradas na rede neural.

Método de dicas

Um dos pontos mais fracos na previsão financeira é a falta de exemplos para aprendizado de redes neurais. Geralmente falando, os mercados financeiros (especialmente os russos), não são estacionários. Aparecem novos índices lá nos quais não foram acumulados históricos ainda, a natureza dos negócios de velhos mercados muda com o tempo. Nestas condições, o comprimento das séries temporais disponíveis para o aprendizado da rede neural é um pouco limitado.

Entretanto, podemos aumentar o número de exemplos usando algumas considerações a priori sobre as invariantes das dinâmicas das séries temporais. Esse é outro termo físico-matemático que pode consideravelmente melhorar a qualidade das previsões financeiras. O problema é a geração de exemplos artificiais (dicas) obtidas das existentes através de várias transformações aplicadas a eles.

Vamos explicar a ideia principal com um exemplo. A seguinte presunção é psicologicamente razoável: os investidores em sua maioria prestam atenção ao formato da curva de preço, não a valores específicos em eixos. Então, se esticarmos toda série temporal um pouco mais ao longo do eixo das cotações, seremos capazes de usar as séries temporais resultantes de tal transformação (junto da inicial) para o aprendizado da rede neural. Assim, dobramos o número de exemplos devido ao uso de informação a priori resultando de características psicológicas de como investidores percebem as séries temporais. Adicionalmente, junto d aumento do número de exemplos, limitamos a classe de funções para pesquisar a solução junto, que aumenta também a qualidade da previsão (se, naturalmente, a invariante usada é verdadeira a esse fato).

Os resultados dos cálculos da previsibilidade do S&P500 pelo método de contagem de caixas mostrado abaixo (veja a figura 7, 8) ilustra o papel das dicas. O espaço de atributos, neste caso, foi formado pela técnica de ortogonalização. Usamos 30 componentes principais como variáveis de entrada no espaço de atraso com 100 dimensões. Então selecionamos 7 atributos destes componentes principais - as mais significativas combinações lineares ortogonais. Como você pode ver pelas imagens abaixo, somente a aplicação de dicas ajudou, nesse caso, para ser capaz de fornecer uma previsibilidade notável.

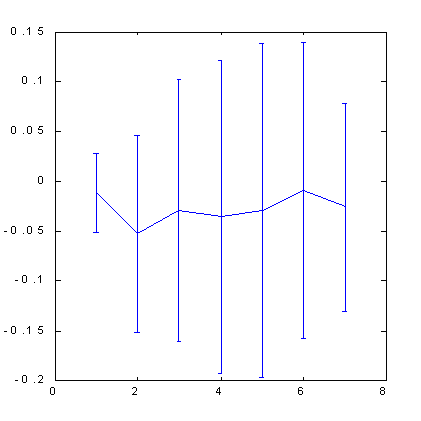
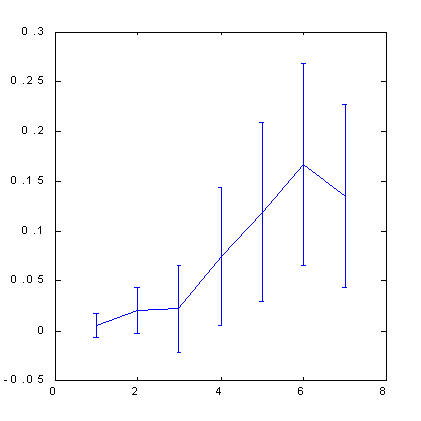
Fig. 7. Previsibilidade do sinal de mudança de cotações para S&P500.

Fig. 8. A previsibilidade do sinal de mudança de cotações para S&P500 após o número de exemplos foi quadruplicada ao esticar o eixo do preço.

Note que o uso de espaço ortogonal resultou em um certo aumento na previsibilidade quando comparado ao método de imersão padrão: de 0.12 bits (fig. 5) para 0.17 bits (fig. 8). Um pouco depois, quando começaremos a discutir a influência da previsibilidade em lucros, provaremos que, devido a isso, a taxa de lucro pode aumentar novamente por mais uma metade.

Outro exemplo menos trivial de sucesso utilizando tais dicas para uma rede neural para qual direção pesquisar uma solução é o uso de simetria escondida em negociações forex. O sentido dessa simetria é de que as cotações forex podem ser consideradas dois "pontos de vista", por exemplo, como uma série de DM/$ ou como uma série de $/DM. Aumentar um deles corresponde a diminuir o outro. Essa propriedade pode ser usada para dobrar o número de exemplos: adicionar a cada exemplo seu análogo simétrico . Experimentos nas previsões de redes neurais mostraram que, para mercados forex básicos, a consideração de simetria aumenta a taxa de lucro quase em dobro, especificamente: de 5% a 10% por ano, considerando custos reais das transações (Abu-Mostafa, 1995).

Medindo a qualidade das previsões

Embora a previsão das séries temporais financeiras se resolva dentro do problema de aproximação da função multidimensional, ela tem suas próprias características especiais ambos ao formar entradas e selecionar saídas para uma rede neural. Já consideramos as entradas acima. Agora vamos estudar as características especiais para selecionar as variáveis de entrada. Entretanto, antes de tudo, devemos responder a pergunta principal: Como pode ser medida a qualidade das previsões financeiras? Isso nos ajudará a encontrar a melhor estratégia de aprendizado de uma rede neural.

Relação entre a previsibilidade e taxa de lucro

Uma função especial da previsão de séries temporais financeiras é a de trabalhar para obter lucros máximos, não minimizando o desvio quadrático médio, como é a convenção de aproximação de funções.

Em um caso mais simples de negociações diárias, lucros dependem dos sinais corretamente previstos das mudanças das cotações. É por isso que a rede neural deve ter como objetivo a previsão exata do sinal, não do valor em si. Agora vamos descobrir como a taxa de lucro se relaciona à exatidão de detecção do sinal com o desempenho mais simples de entrar diariamente no mercado (fig. 9).

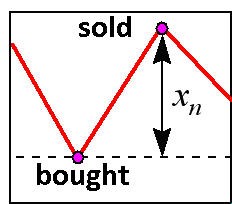
Fig. 9. Entrada diária no mercado.

Vamos designar, no momento do : o capital total do investidor é , a mudança de cotação relativa é , e como a saída de rede vamos usar seu nível de confiança para o sinal desta mudança: . Essa rede com a não linearidade de saída de forma aprende como prever a mudança do sinal e prevê o sinal dentro da faixa proporcional a sua probabilidade. Então o ganho de capital na etapa 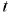será gravado da seguinte forma:

onde é a ação capital "em jogo". É o lucro para todo o período de negociação:

que iremos maximizar ao escolher o tamanho de taxa otimizado 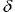. Deixe o investidor prever corretamente prever dos sinais e, correspondentemente, incorretamente prever com a probabilidade de . Então o logaritmo da taxa de lucro,

,

e o lucro em si será o maior no valor de e a média:

.

Aqui introduzimos o coeficiente de . Por exemplo, para distribuição Gaussiana,. O nível de previsibilidade do sinal é diretamente relacionado à entropia cruzada que pode ser estimada a priori pelo método de contagem de caixa. Para saída binária (veja a figura 10):

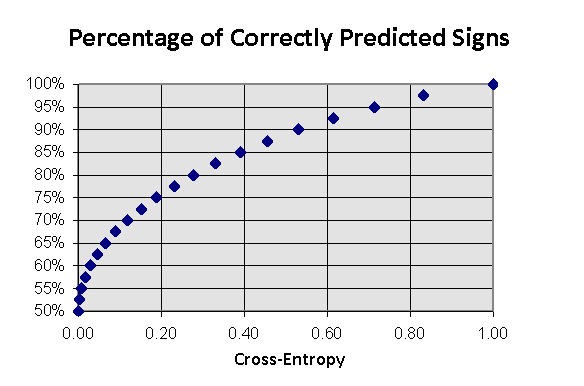
Fig. 10. Frações de direções corretamente previstas de variações de séries temporais como uma função de entropia cruzada de sinais de saída para entradas conhecidas.

Eventualmente, obtemos a seguinte previsão da taxa de lucro para o valor de previsibilidade de um dado sinal de I expressado em bits:

.
Significa que, para a série temporal com a previsibilidade de I, é em princípio possível dobrar o capital dentro de entradas no mercado. Assim, por exemplo, a previsibilidade da série temporal anteriormente calculada S&P500 igual a I=0,17 (consulte a figura 8) assume o capital em uma média para entradas no mercado. Assim, mesmo uma pequena previsibilidade no sinal de mudança de uma cotação pode fornecer uma taxa de lucro muito interessante.

Aqui vamos enfatizar que a taxa de lucro otimizada requer uma jogada bem cautelosa quando, em cada entrada no mercado, o investidor arrisca um parte estritamente definida do capital:

,

onde é o tamanho do lucro/perda típico para avolatilidade desse mercado. . Ambos valores menores e maiores das taxas diminuirão o lucro, uma negociação muito arriscada que é capaz de resultar na perda de dinheiro em qualquer previsibilidade. Esse fato é ilustrado na figura 11.

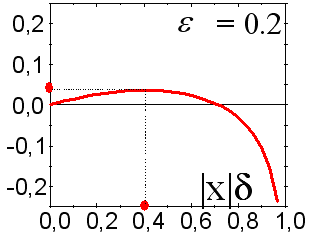
Fig. 11. A dependência da taxa de lucro média do estoque (ação) selecionada do capital "no lixo".

É por isso que as estimativas acima dão uma visão somente sobre o limite superior da taxa de lucro. Um estudo mais cuidadoso considerando o efeito de flutuação está além do escopo desse artigo. Entretanto, está qualitativamente claro que a escolha de um tamanho otimizado de contrato exige a estimativa da precisão da previsão em cada etapa.

Escolhendo a funcional de erro

Se seguirmos o propósito de previsões de séries de tempo financeiras para maximizar os lucros, é lógico ajustar a rede neural a este resultado final. Por exemplo, se você negociar de acordo com o esquema acima, você pode escolher para o aprendizado da rede neural a seguinte função de aprendizado de erro com uma média de todos os exemplos da amostra de aprendizado.

.

Aqui, o compartilhamento do capital em jogo é introduzido como uma saída de rede adicional para ser ajustada durante o aprendizado. Para essa abordagem, o primeiro neurônio, , com a função de ativação nos dará a probabilidade de aumentar ou diminuir a taxa, enquanto a segunda saída de rede,, produzirá a divisão recomendada do capital a ser investido naquele determinado momento.

Entretanto, já que essa divisão, de acordo com a análise anterior, deve ser proporcional ao nível de confiança de previsão, você pode substituir duas saídas de rede com somente uma ao colocar e então se limitar à otimização de somente um parâmetro global,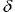, que irá minimizar o erro:

Isso produz uma oportunidade para regular a taxa de acordo com o nível de risco previsto pela rede. Jogar com as taxas variáveis retorna mais lucros do que jogar com as taxas fixas. De fato, se você corrigir a taxa que tem definida por sua previsibilidade média, então a taxa de crescimento do capital será proporcional ao , enquanto, se você selecionar a taxa otimizada em cada etapa, será proporcional ao .

Usando redes de grupos

Falando de modo geral, as previsões feitas por diferentes redes treinadas na mesma amostra serão diferentes devido à natureza aleatória de escolher os valores iniciais de pesos sinápticos. Essa desvantagem (um elemento de incerteza), pode se tornar uma vantagem tendo organizado um grupo neural expert que consiste de diferentes redes neurais. A dispersão de previsões de experts dará uma ideia do nível de confiança dessas previsões, que será usada para escolher uma estratégia de negociação correta.

É fácil provar que a média dos valores do grupo precisa produzir melhor previsão do que um expert de média do mesmo grupo. Deixe o erro do ith expert para o valor de entrada deser igual a. Um erro médio de um grupo é sempre menor do que o erro médio quadrático de experts individuais na visão de desigualdade de Cauchy:

.

Deve ser notado que a redução do erro pode ser um tanto essencial. Se os erros de experts individuais não são correlacionados um com o outro, isto é,, o erro quadrático médio de um grupo consistindo de L experts évezes menor do que o erro individual médio de um expert!

É por isso que é melhor se basear na previsão de valores de uma média do grupo total. Esse fato é ilustrado pela figura 12.

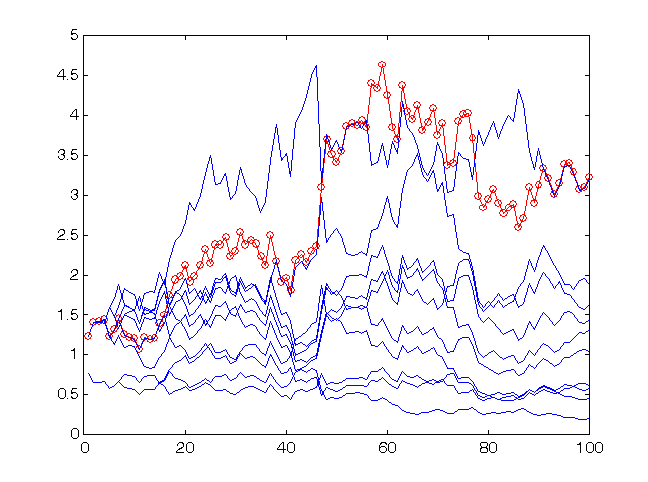
Fig. 12. A taxa de lucro para os últimos 100 valores de séries temporais sp500 ao prever com um grupo de 10 redes.

O lucro do grupo (círculos) é maior do que a média de um expert. A pontuação de sinais corretamente previstos para o grupo é de 59:41.

Como você pode ver na figura 12, nesse caso, o lucro do grupo é ainda maior do que o de cada expert. Assim, o método de grupo pode essencialmente aprimorar a qualidade das previsões. Note o valor absoluto da taxa de lucro: O capital de um grupo aumentou por 3,25 vezes em 100 entradas no mercado (essa taxa irá, naturalmente, ser menor se os custos de transação são considerados).

As previsões foram obtidas em aprendizado de rede nas 30 médias móveis exponenciais consecutivas (EMA 1 … EMA 30) do índice de incremento da série temporal. O sinal de incremento na próxima etapa foi previsto.

Neste experimento, a taxa foi fixada no nível de próximo ao otimizado para a precisão de previsão dada (59 sinais previstos corretamente vs. 41 sinais previstos incorretamente), i.e.,. Na figura 13 você pode ver os resultados de uma negociação mais arriscada nas mesmas previsões, nomeadamente with.

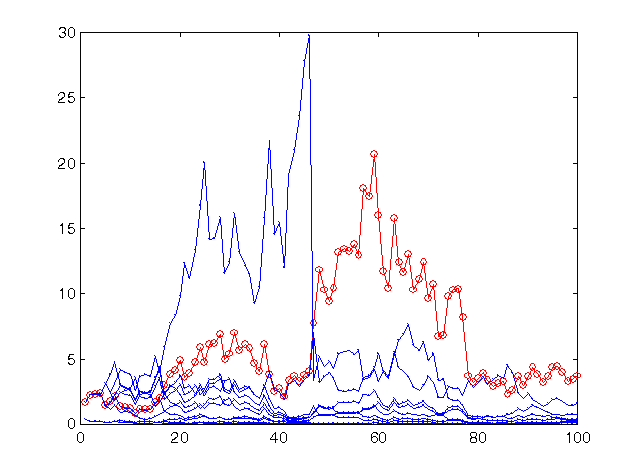
Fig. 13. A taxa de lucro para os últimos 100 valores de séries temporais sp500 ao prever com o mesmo grupo de 10 redes, mas com uma estratégia mais arriscada.

O lucro do grupo permanece o mesmo nível (um pouco aumentado) já que esse valor de risco está tão próximo ao otimizado quanto o anterior. Entretanto, para a maioria das redes, as previsões que são menos precisas do que estas dos grupos como um todo, tais taxas se revelam muito arriscadas, que resultaram em praticamente sua ruína total.

Os exemplos acima demonstram o quão importante é a capacidade de estimar corretamente a qualidade da previsão e como isso é estimado pode ser usado para aumentar a rentabilidade das mesmas previsões.

Podemos ir ainda a mais extremos e usar as opiniões ponderadas das redes experientes ao invés das redes medianas. Os pesos devem ser escolhidos adaptativamente, maximizando a capacidade de previsão do grupo na amostra de aprendizado. Como resultado, redes mal treinadas de um grupo retornam uma menor contribuição e não estragam a previsão.

As possibilidades desse método são ilustradas abaixo pela comparação das previsões feitas por dois tipos de grupos de redes consistindo de 25 experts (veja a figura 14 e 15). As previsões foram feitas de acordo com o mesmo esquema: como entradas, as médias móveis exponenciais das séries temporais foram usadas com períodos iguais aos primeiros 10 números de Fibonacci. De acordo com os resultados obtidos de 100 experimentos, a previsão ponderada fornece uma média de excesso de sinais corretamente previstos sobre os incorretamente previstos, aproximadamente igual a 15, enquanto que para a previsão média esse fator é de cerca de 12. Deve ser notado que a quantidade total de preço aumenta quando comparada a taxas em declínio dentro do mesmo período é exatamente igual a 12. Portanto, considerando a tendência principal de aumento como uma previsão trivial constante do sinal de "+" dá o mesmo resultado para a porcentagem de sinais corretamente previstos como a opinião ponderada de 25 experts.

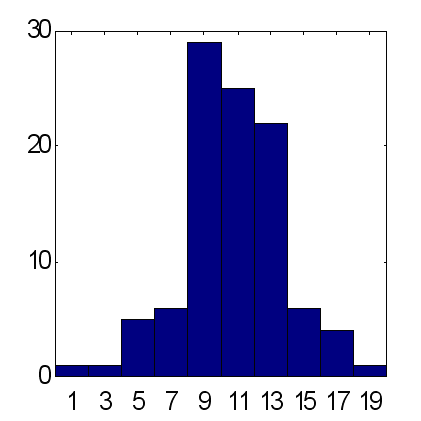
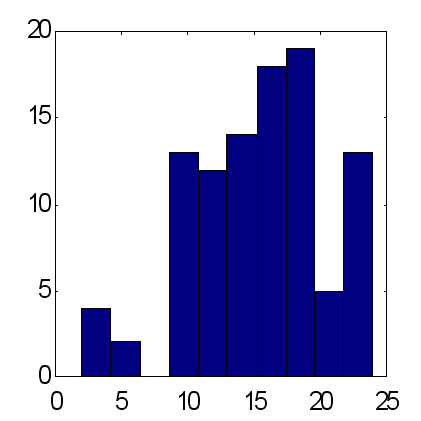
Fig. 14. Histograma das somas de sinais corretamente previstos em previsões médias de 25 experts. Uma média para 100 grupos = 11,7 com desvio padrão de 3,2.

Fig. 15. Histograma das somas de sinais corretamente previstos em previsões ponderadas de 25 experts. Uma média para 100 grupos = 15,2 com desvio padrão de 4,9.

Taxa de lucro possível de previsões de redes neurais

Até agora formulamos os resultados dos experimentos numéricos como uma porcentagem de sinais previstos corretamente. Agora vamos descobrir sobre a taxa de lucro realmente alcançável ao negociar usando as redes neurais. Os limites superiores da taxa de lucro, obtidos acima sem considerar as flutuações, são dificilmente alcançáveis na prática, tanto que não consideramos os custos das transações antes que podem cancelar o nível de previsibilidade alcançado.

Certamente, considerando os resultados das comissões no aparecimento de uma constante de queda:

.
Adicionalmente, diferente do nível de previsibilidade,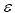, acomissão entra de modo linear, não quadraticamente. Assim, no exemplo acima, os valores típicos de previsibilidade não podem exceder a comissão .

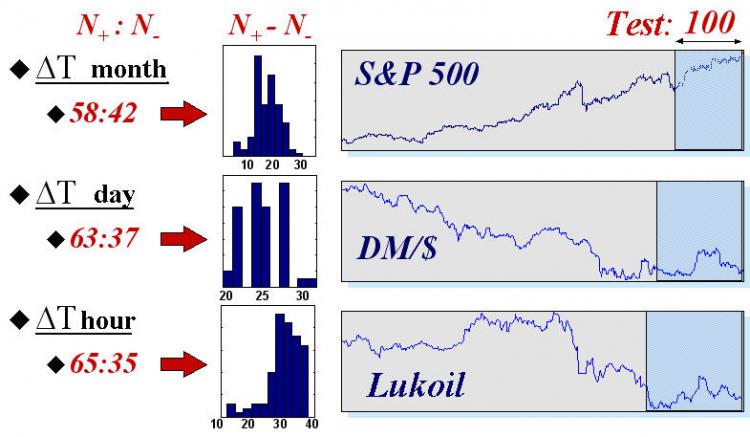
Para dar uma ideia das possibilidades reais de redes neurais nesse campo, daremos os resultados das negociações automatizadas usando redes neurais em três índices com tempos típicos diferentes: os valores do índice S$P500 com intervalos mensais entre as leituras, cotações diárias de DM/$, e leituras a cada hora de futuros para ações Lukoil na bolsa de valores russa. As estatísticas de previsão foram coletadas em 50 sistemas de redes neurais diferentes (contendo grupos de 50 redes neurais cada). As séries temporais por si e os resultados das previsões dos sinais em um conjunto de testes dos últimos 100 valores de cada série temporal são mostrados na figura 16.

Fig. 16. Valores médios e histogramas do número de sinais previstos corretamente ( ) e incorretamente ( ) nas amostras de testes de 100 valores de três índices financeiros reais.

Estes resultados confirmam a regularidade intuitivamente óbvia: as séries temporais são as mais previsíveis, conforme menos tempo se passava entre as leituras. De fato, quanto mais tempo passava entre os valores consecutivos de séries temporais, maior a informação, externa em direção as suas dinâmicas, estava disponível para os participantes do mercado e, portanto, menos informação sobre o futuro está nas séries temporais.

Então as previsões obtidas acima foram usadas para negociar em um conjunto de testes. Ao mesmo tempo, o tamanho do contrato em cada etapa era escolhido proporcionalmente ao grau de confiança da previsão, enquanto o valor do parâmetro global 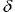foi otimizado na amostra de aprendizado. Além do mais, de acordo com seu sucesso, cada rede no grupo tinha sua própria taxa flutuante. Na previsão em cada etapa usamos somente realmente a "melhor" parte das redes. Os resultados de tais negociadores "neurais" são mostrados na fig. 17.

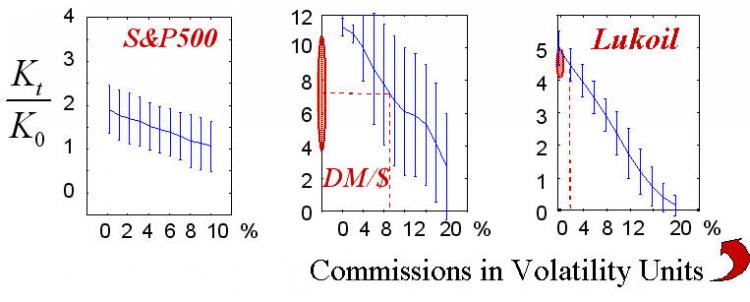
Fig. 17. As estatísticas de ganhos de 50 negociações de acordo com a quantidade de comissões.

Valores reais das comissões desenhados em linhas pontilhadas mostram a área de taxas de lucro realmente alcançáveis.

O ganho final (como no jogo de estratégia), naturalmente, depende do tamanho da comissão. É essa dependência que é mostrada acima nos diagramas. Os valores realísticos de comissões nas unidades escolhidas de medidas conhecidas do autor são marcadas na imagem. Deve ser refinada o fato de que a natureza "quantificada" da negociação real não foi considerada nesses experimentos, isto é, não consideramos que o fato do tamanho das negociações deveria ser igual ao número inteiro de contratos típicos. Esse caso corresponde com o de negociar grandes capitais onde as negociações típicas contém muitos contratos. Além disso, a negociação garantida foi implícita, isto é, a taxa de lucro foi calculada como uma razão do capital de segurança que é muito menor do que o escalamento dos contratos propriamente ditos.

Os resultados acima mostram que as negociações baseadas em redes neurais é realmente promissora, pelo menos em curtos prazos. Adicionalmente, em vista da auto-similaridade das séries temporais financeiras (Peters, 1994), a taxa de lucro por unidade de tempo será maior, quanto menor for o tempo de leitura típico. Assim, negociadores automatizados usando redes neurais acabam sendo mais eficientes ao negociar no modo de tempo real onde suas vantagens sobre investidores típicos são mais notáveis: à prova de cansaço, não suscetíveis a emoções, taxa de resposta potencialmente muito maior. Uma rede neural bem treinada conectada a um sistema de negociação automatizado pode fazer decisões muito antes que um investidor humano reconheça as mudanças de preço nas tabelas do seu terminal.

Conclusão

Demonstramos que as séries temporais de mercado (pelo menos alguma parte) foi particularmente previsível. Como qualquer outro tipo de análise neural, a previsão de séries temporais requer um pré-processamento de dados cuidadoso e complicado. Entretanto, trabalhar com séries temporais tem seu próprio caráter específico que pode ser usado para aumentar lucros. Isso se relaciona tanto para a seleção de entradas (usando métodos especiais de representação de dados) e a seleção de saídas, e o uso de funcionais de erros específicos. Por último, demonstramos como é mais rentável usar experts neurais em grupo quando comparado a redes neurais separadas, e também fornecemos dados de taxas de lucros reais em várias seguranças reais.

Referências:

• Sharpe, W.F., Alexander, G.J., Bailey, J.W. (1997). Investments. - 6º edição, Prentice Hall, Inc., 1998.
• Abu-Mostafa, Y.S. (1995). "Financial market applications of learning from hints”. Em Neural Networks in Capital Markets. Apostolos-Paul Refenes (Ed.), Wiley, 221-232.
• Beltratti, A., Margarita, S., e Terna, P. (1995). Neural Networks for Economic and Financial Modeling. ITCP.
• Chorafas, D.N. (1994). Chaos Theory in the Financial Markets. Probus Publishing.
• Colby, R.W., Meyers, T.A. (1988). The Encyclopedia of Technical Market Indicators. IRWIN Professional Publishing.
• Ehlers, J.F. (1992). MESA and Trading Market Cycles. Wiley.
• Kaiser, G. (1995). A Friendly Guide to Wavelets. Birk.
• LeBeau, C., and Lucas, D.W. (1992). Technical traders guide to computer analysis of futures market. Business One Irwin.
• Peters, E.E. (1994). Fractal Market Analysis. Wiley.
• Pring, M.G. (1991). Technical Analysis Explained. McGraw Hill.
• Plummer, T. (1989). Forecasting Financial Markets. Kogan Page.
• Sauer, T., Yorke, J.A., and Casdagli, M. (1991). "Embedology". Journal of Statistical Physics. 65, 579-616.
• Vemuri, V.R., e Rogers, R.D., eds. (1993). Artificial Neural Networks. Forecasting Time Series. IEEE Comp.Soc.Press.
• Weigend, A e Gershenfield, eds. (1994). Times series prediction: Forecasting the future and understanding the past. Addison-Wesley.
• Baestaens, D.-E., Van Den Bergh, W.-M., Wood, D. Neural Network Solutions for Trading in Financial Markets. Financial Times Management (July 1994).

Esse artigo é publicado com o consentimento do autor.

Sobre o autor: Sergey Shumskiy é o associado de pesquisa sênior no Physics Institute of the Russian Academy of Sciences, Cand. Sc. (Física e Matemática), aprendizado de máquina e técnica de inteligência artificial, membro integrante da Russian Neural Networks Society, CEO da IQMen Corp. que desenvolve sistemas experts empresariais usando tecnologias de aprendizado de máquina. Mr. Shumskiy é o coautor de mais de 50 publicações científicas.
Os cursos do autor: Neural Computing and Its Applications in Economics and Business