Características del Wizard MQL5 que debe conocer (Parte 27): Medias móviles y el ángulo de ataque

Introducción

Continuamos con la serie sobre configuraciones e ideas comerciales que se pueden probar rápidamente y a prueba de tontos gracias al Asistente MQL5 considerando el ángulo de ataque. En términos generales, la expresión «ángulo de ataque» se asocia al ángulo ideal con el que debe despegar un avión de combate, cuando se optimiza para obtener la máxima sustentación y el mínimo consumo de combustible.

Para los operadores, sin embargo, esta expresión suele referirse a la trayectoria del precio de un valor en medio de una tendencia, y el consenso general es que un ángulo pronunciado indica una tendencia fuerte. Por lo tanto, comenzamos este artículo explorando no sólo este punto de vista, sino, lo que es más importante, adoptando también los medios por los que podría medirse el indicador o el ángulo del precio. A continuación, criticamos este enfoque tratando de señalar algunos de sus problemas, proponemos una alternativa posiblemente mejor y concluimos, como siempre, con resultados de pruebas e informes. 

Como siempre, utilizamos una instancia de una clase de señal personalizada para probar nuestras hipótesis sobre cómo medir el ángulo de ataque, y medimos este ángulo no a partir del precio bruto, sino de una media móvil. Utilizamos la media móvil decreciente como indicador para medir y seguir la importancia del ángulo de ataque. Los precios brutos también pueden utilizarse para supervisar los ángulos de ataque, pero como están destinados a tener valores más volátiles que un tampón indicador, adoptamos los primeros. También se podría haber utilizado cualquier media móvil, pero adoptamos la media móvil decreciente porque es un poco novedosa y puede que no resulte familiar a la mayoría de los operadores.

Enfoques actuales de la utilización del ángulo de ataque

El enfoque básico para calcular el ángulo de ataque comienza identificando dos puntos de precio dentro de un margen de precios o de un indicador, desde los cuales se medirá el ángulo. Este búfer pueden ser los precios brutos de los valores, pero éstos tienden a ser muy volátiles, por lo que es más habitual utilizar un búfer suavizado, como un búfer de media móvil. Por lo tanto, si estamos realizando esto en el marco de tiempo diario, obtendríamos la media móvil de hoy y la media móvil de hace N días.

Lo que seguiría a esto es determinar el cambio en la media móvil por periodo, que en nuestro caso son los N periodos a través de los cuales se obtienen los dos valores de la media móvil. Lo primero que se suele determinar es la pendiente, m, que puede calcularse utilizando la fórmula que se presenta a continuación:

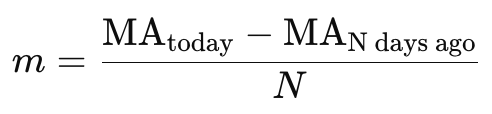
Donde:

• MA (today) es el valor de la media móvil de hoy.
• MA (N days ago) es el valor de la media móvil de hace N días.
• N es el número de días entre los dos puntos.

El valor devuelto de m de nuestra fórmula anterior sí representa la pendiente y es proporcional al ángulo de ataque de la media móvil. Puede utilizarse en su formato actual como indicador de la pendiente y, por tanto, del impulso de los precios. Sin embargo, para mucha gente, la noción de un ángulo se refiere a algo sobre el papel que para los propósitos de esta acción del precio estaría en el rango de 0 - 90 grados.

Si quieres representar esta pendiente por tanto como un ángulo, utilizarías la función arco-tangente (tangente inversa) para convertir la pendiente a grados:

El valor devuelto θ es el ángulo en radianes. Para convertirlo a grados, habría que multiplicarlo por:

Para verlo en acción, veamos un ejemplo de aplicación muy sencillo. Supongamos que dispone de los siguientes datos para un período de 10 días:

• Hace 10 días, la MA era: 100
• Hoy la MA es: 110

A partir de nuestra sencilla fórmula anterior, la pendiente, m, sería:

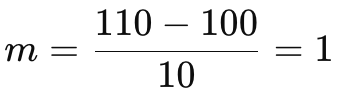
De aquí, el ángulo θ (theta) en radianes sería:

Y si convertimos esto a grados:

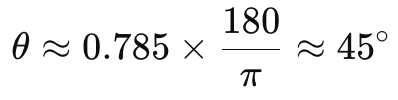
Acabaríamos con un valor que, en opinión de muchos, está a punto de ser muy elevado. 45 grados. Si el valor en cuestión fuera un par de divisas en yenes, podría justificar o entender la idea de los 45 grados. Sin embargo, consideremos una situación en la que el precio es de una empresa tecnológica, y sube la misma cantidad pero en un día. Si hacemos los mismos cálculos que hemos hecho anteriormente, nuestro ángulo es de 84 grados, ¡lo que se aproxima a 90! Sin embargo, la interpretación básica de «ángulo de ataque» con este enfoque, que no es un término estándar en el análisis financiero, lleva a interpretar que la pendiente de una media móvil proporciona información sobre la fuerza y la dirección de la tendencia. Cuanto mayor sea el ángulo (o la pendiente), más fuerte será la tendencia.

Problemas con el enfoque y los métodos actuales

Como se ha mencionado anteriormente en la aplicación de las mediciones actuales del ángulo de ataque, existen una serie de problemas, derivados principalmente de la excesiva sensibilidad a la escala de precios y de los resultados incoherentes del ángulo en distintos marcos temporales. Para ilustrarlos, empecemos con el problema de la sensibilidad a los precios.

Si nuestro valor negociado fuera un par de divisas distinto del yen, como el GBPUSD, entonces una variación de precios comparable de 10 días, que para este par sería de aproximadamente 0,10 más o menos, daría un valor m de 0,01. Si lo multiplicamos por 180 y dividimos el resultado por PI, obtenemos un ángulo de 0,57 grados. Todos sabemos por nuestras observaciones que 45 grados y 0,57 grados están a kilómetros de distancia en magnitud y, sin embargo, ¡ambas divisas, el par del yen y el GBPUSD tuvieron movimientos de 10000 puntos! Se podría argumentar que esta diferencia de ángulos se debe a que los pares de yenes son más volátiles, pero la relación de los dos ángulos es 90x. La mayoría de los operadores estarán de acuerdo en que el yen no es 90 veces más volátil que otros pares como el GBPUSD. Obviamente, esto se debe a que, para evaluar correctamente el cambio en los precios de los pares de divisas, es necesario tener en cuenta el valor del tick del movimiento puntual. Y para ello, según forex.com, ¡los pares más volátiles están encabezados por el AUDUSD y el NZDUSD en 2023!

El par del yen más volátil aparece en el número 3 y esto a pesar de que tanto el AUDUSD como el NZDUSD cotizan con decimales de 5 dígitos, lo que implica que nuestro movimiento de 0,10 puntos anterior produciría el mismo ángulo de 0,57 grados.

Según la lista de forex.com, el AUDUSD es el que presenta mayor volatilidad debido a una variación diaria media del 1,04%. Con un precio aproximado de 0,68150, un movimiento de 10 días con un 1,04% diario equivaldría a 0,070876. Esto nos daría una m, o pendiente de 0,0070876, y un ángulo, a lo largo de los 10 días, de 0,406 grados. Menos que el 0,507 que habíamos estimado con el GBPUSD más arriba, pero más concretamente, el GBPJPY, que ocupaba el 7º puesto de la lista, registró una variación media del precio del 0,81%. Este cambio de precio en 10 días similares, con un precio base de 147,679, daría un ángulo de 50,1 grados.

Por supuesto, el ángulo de ataque no pretende medir la volatilidad per se, pero creo que la mayoría de los lectores y operadores esperarían que la magnitud de un ángulo de ataque estimado fuera una medida, de alguna manera, del tamaño del movimiento eventual del precio del valor. El hecho de que claramente no sea así pone en entredicho este enfoque a la hora de medir este ángulo. Además de estas incoherencias de la sensibilidad al precio, los cambios en el marco temporal de un gráfico/análisis pueden influir enormemente en el tamaño del ángulo de ataque.

Considere, por ejemplo, en nuestros casos anteriores si tuviéramos que cambiar del marco de tiempo diario a, digamos, el marco de tiempo de 4 horas. En la primera ilustración, en la que teníamos el ángulo de 45 grados, ¡ese valor cambiaría a 0,95 grados! Lo que nos lleva a preguntarnos por qué al «detallar» simplemente el periodo en el que medimos el ángulo, sin hacer ningún cambio en la escala de precios, obtenemos de repente un ángulo muy plano inferior a un grado. La respuesta bruta a esto es que tenemos una base alargada y por lo tanto el ángulo se eleva menos cuando se compara con la misma altura, pero como la longitud de la base es realmente la misma cuando se mide en tiempo y no en sus unidades, esta distorsión no debería estar presente.

Introducción de un método alternativo

Sin embargo, un examen más detenido de los problemas derivados de los cambios en el marco temporal presenta una posible solución. En cualquier triángulo, siempre que estemos buscando el tamaño del ángulo, y se nos presenten tanto una altura como una base para este triángulo rectángulo, la arctangente de la base dividida por la altura debería darnos uno de los ángulos en grados.

Fuente

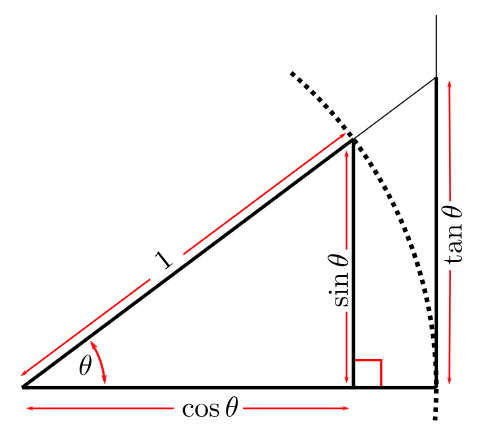
Así, a partir de nuestra imagen de arriba, la base del triángulo rectángulo más grande es en realidad 1, (es más que cosθ), por lo que nuestro lado opuesto tiene una altura de tanθ. El punto clave a tener en cuenta aquí es que las unidades del lado adyacente (la base) son similares a las unidades del lado opuesto (la altura). Cuando este es el caso, se obtienen valores de grados significativos para theta cuando se encuentra el arco-tangente o arco-coseno, cualquiera que sea el caso, del ángulo theta.

El diagrama compartido anteriormente, aunque proporciona «demasiada información», hace hincapié en la definición de la tangente como cociente. De seno a coseno. O comparando elementos equivalentes. Es necesario que el eje horizontal esté en las mismas unidades que el eje vertical para que el ángulo theta tenga sentido. Entonces, cabe preguntarse cómo se pueden armonizar los dos ejes de precio y tiempo para que tengan las mismas unidades.

Las opciones que se plantean en esta normalización son que tanto el eje temporal como el eje de precios se conviertan en unidades de tiempo, o que ambos se conviertan en unidades de precio. Esta noción de conversión puede parecer radical al principio, pero una vez que empecemos a ver y comparar los resultados, todo cobrará sentido. Dado que el precio es lo fundamental y un movimiento de precio en la dirección equivocada genera pérdidas, marcaremos tanto los ejes ‘vertical’ como ‘horizontal’ de nuestra acción del precio en unidades de precio. Así pues, cabe preguntarse cómo reescalar un eje temporal en precio.

Hay varios enfoques que pueden adoptarse al respecto, y nuestro propósito con este artículo no es enumerarlos todos ni utilizar necesariamente el «mejor». Sin embargo, utilizaremos una escala variable. Cuando se presentan dos puntos de precio cualesquiera que están a una distancia D en el tiempo, la distancia D se convertirá en las unidades de precio del rango en precio sobre la distancia anterior D antes de ella. Parece muy simple, pero produce resultados relativamente consistentes para el tamaño del ángulo de ataque. En MQL5, implementaríamos esto de la siguiente manera:

//+------------------------------------------------------------------+
//| Get Angle function
//+------------------------------------------------------------------+
double CSignalAA::Angle(int Index)
{  double _angle = 0.0;
   double _price = DM(Index) - DM(Index+m_length_period);
   double _max = DM(Index+m_length_period+1);
   double _min = DM(Index+m_length_period+1);
   for(int i=Index+m_length_period+2;i<Index+(2*m_length_period);i++)
   {  double _dm = DM(i);
      _max = fmax(_max, _dm);
      _min = fmin(_min, _dm);
   }
   double _time = fmax(m_symbol.Point(), _max - _min);
   _angle = (180.0 / M_PI) * MathArctan(fabs(_price) / _time);
   if(_price < 0.0)
   {  _angle *= -1.0;
   }
   return(_angle);
}

Nuestra función simplemente toma dos marcadores de posición de índice y los utiliza para determinar desde dónde medir el ángulo de ataque y también, como se mencionó anteriormente, qué tan atrás en la historia ir en busca del rango de precios que sirve como nuestra medida de tiempo o valor del eje horizontal. El rango de precios en el historial recogido podría ser cero, por eso tenemos un punto determinado por el tamaño del punto de precio mínimo del valor negociado, que sirve como rango mínimo. Los lectores pueden cambiar este valor para que sea el diferencial en ese momento, o cualquier valor, siempre que se eviten las divisiones por cero. Nos referimos a la función de media móvil decreciente (DM), que se presenta a continuación.

Media móvil decreciente (Decaying Moving Average, DMA)

Esta media móvil proporciona ponderaciones con decaimiento exponencial, que caen más rápidamente que en las medias móviles exponenciales tradicionales. Se define mediante la fórmula que se presenta a continuación:

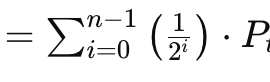
Donde:

• n : Es el tamaño de la muestra promediada.
• i : Es un índice de posición dentro de la muestra.
• P : Es el precio en el momento 'i'.

Al igual que algunas de las medias móviles novedosas que hemos analizado en artículos recientes, dentro de esta serie, ésta puede implementarse como una función o un indicador personalizado si desea operar manualmente con ella. Indicadores personalizados son buenos en el almacenamiento en búfer que puede traer esa eficiencia adicional, incluso a un Asesor Experto. Sin embargo, nos quedamos con el enfoque de la función para nuestros propósitos de prueba como un indicador personalizado implica nuestro Asesor Experto compilado tendrá requisitos adicionales.

Hay un montón de medias exponenciales que dan más peso a los precios recientes, creo que la media móvil decreciente hace esto con esteroides. Podemos implementarlo en MQL5 de la siguiente manera:

//+------------------------------------------------------------------+
//| Decaying Mean                                                   |
//+------------------------------------------------------------------+
double CSignalAA::DM(int Index, int Mask = 8)
{  double _dm = 0.0;
   vector _r;
   if(_r.CopyRates(m_symbol.Name(), m_period, Mask, Index, m_length_period))
   {  //vectors are not series
      double _weight = 0.0;
      for(int i = 0; i < m_length_period; i++)
      {  _dm += (1.0/pow(2.0, m_length_period-i))*_r[i];
         _weight += (1.0/pow(2.0, m_length_period-i));
      }
      if(_weight != 0.0)
      {  _dm /= _weight;
      }
   }
   return(_dm);
}

Simplemente estamos aplicando un peso a cada precio dentro de la muestra que se está promediando, con la principal precaución aquí de que los vectores no copian los tipos como series. Esto significa que debemos tener en cuenta que el precio más alto del índice es el último precio o el precio más cercano al índice a partir del cual comenzamos nuestra copia. Esto implica que nuestra ponderación (exponente dado al denominador 2) se invertirá a medida que vayamos contando en un bucle for.

Clase de señal

Para poner todo esto junto en una clase, añadimos las funciones media de decaimiento y ángulo a una instancia de una clase de señal y, por supuesto, hacemos cambios en las condiciones largas y cortas como se muestra a continuación:

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalAA::LongCondition(void)
{  int result = 0;
   double _angle = Angle(StartIndex());
   if(_angle >= m_threshold)
   {  result = int(round(100.0 * ((_angle) / (90.0))));
   }
   return(result);
}
//+------------------------------------------------------------------+
//| "Voting" that price will fall.                                   |
//+------------------------------------------------------------------+
int CSignalAA::ShortCondition(void)
{  int result = 0;
   double _angle = Angle(StartIndex());
   if(_angle <= -m_threshold)
   {  result = int(round(100.0 * (fabs(_angle) / (90.0))));
   }
   return(result);
}

Nuestras condiciones son realmente sencillas y lo único que comprueban es si el ángulo, medido desde una distancia de entrada, supera o es igual a un umbral de entrada en magnitud. Esto significa que nuestras condiciones siguen intrínsecamente las tendencias. La función «Angle» devuelve un valor positivo o negativo, por lo que las condiciones larga y corta lo comprueban antes de abrir una posición. El enfoque de seguimiento de la tendencia podría invertirse en situaciones en las que el ángulo es demasiado pronunciado. Esto es algo que no hemos explorado en este artículo, sino que se deja al lector para que lo investigue y vea si podría tener algún mérito. Otro punto de interés podría ser cómo hemos dimensionado el valor 'result' en las condiciones. Dado que nuestra función Angle devuelve ahora valores más «coherentes» que los del enfoque ortodoxo, podemos estar seguros de que no obtendremos un ángulo superior o incluso cercano a 90 grados de magnitud.

Por eso normalizamos el valor absoluto del ángulo dividiéndolo por 90 y reescalándolo para que esté en el rango 0 - 100 requerido para que sirva como resultado. De nuevo, se pueden explorar enfoques alternativos para normalizar esto, pero este es el que tiende a dar más peso al valor del ángulo de ataque que es el tema principal de este artículo.

Pruebas de estrategia e informes para ambos enfoques

Si realizamos pruebas en el marco temporal de 4 horas para el par GBPCHF durante el año 2023 (del 2023.01.01 al 2024.01.01) obtendremos los siguientes resultados:

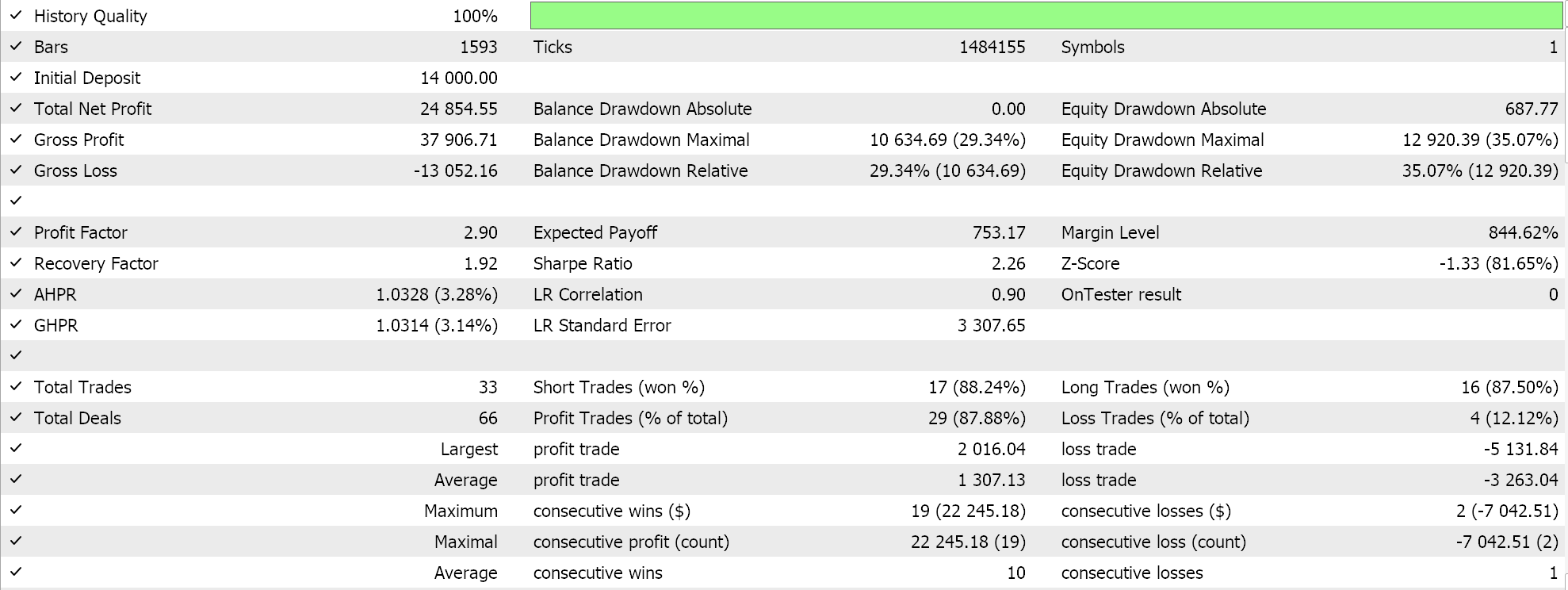
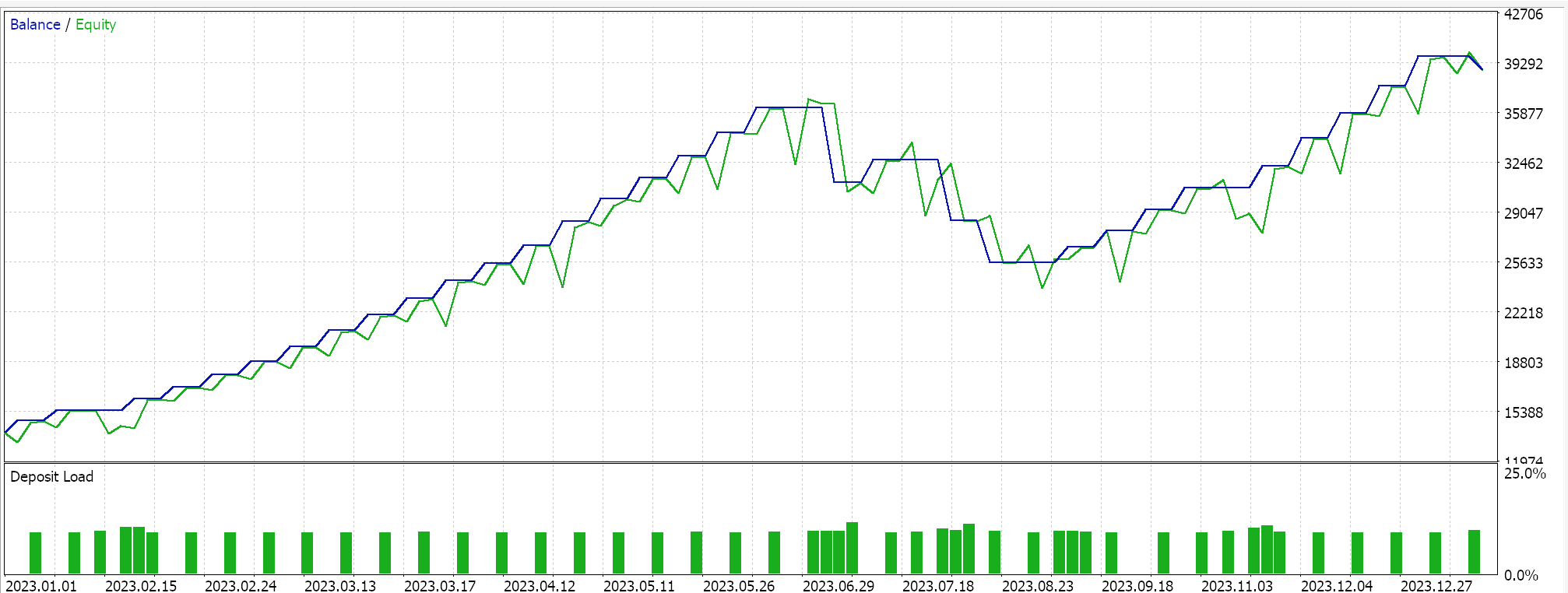
Aunque indican cierto potencial, se podría argumentar que no se están realizando suficientes operaciones. Y por supuesto, estas ejecuciones, además de estar limitadas a solo un año, no utilizan la función de avanzar en el Probador de estrategias, que puede servir como un filtro rápido de lo que funcionará y lo que no. Sin embargo, hemos utilizado la pendiente del promedio móvil decreciente como nuestro indicador de pendiente de precio y debido a que este promedio en particular está fuertemente sesgado hacia los precios más recientes, es probable que obtengamos muchos cambios bruscos en las señales.

Ángulo de ataque crítico

El ángulo de ataque crítico es un concepto que tomaremos prestado de la aerodinámica. Hasta ahora, nuestra configuración ha estado buscando condiciones largas o cortas basándose únicamente en la magnitud del ángulo de la media móvil decreciente. El ángulo crítico de ataque introduce la noción de que este ángulo, en el que basamos nuestras decisiones de apertura, en lugar de estar definido por un valor umbral único, en realidad está mejor definido para estar dentro de una banda o rango específico. Para probarlo y aprovecharlo, modificamos nuestra clase de señal personalizada introduciendo un parámetro adicional.

El parámetro que añadimos a nuestra clase de señal es el valor de tipo doble 'm_band' que ayuda a establecer el rango exterior del ángulo de disparo, puesto que ya tenemos el valor del umbral. Esta modificación se reflejaría del siguiente modo en las funciones de condición larga y corta:

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalAA::LongCondition(void)
{  int result = 0;
   double _angle = Angle(StartIndex());
   if(_angle >= m_threshold && _angle <= m_threshold+m_band)
   {  result = int(round(100.0 * ((_angle) / (90.0))));
   }
   return(result);
}
//+------------------------------------------------------------------+
//| "Voting" that price will fall.                                   |
//+------------------------------------------------------------------+
int CSignalAA::ShortCondition(void)
{  int result = 0;
   double _angle = Angle(StartIndex());
   if(_angle <= -m_threshold && _angle >= -(m_threshold+m_band))
   {  result = int(round(100.0 * (fabs(_angle) / (90.0))));
   }
   return(result);
}

El principal cambio es la comprobación de que el ángulo es superior al umbral, como había ocurrido con nuestra primera señal, pero también que está por debajo de un límite superior que viene definido por el parámetro de banda. Si realizamos pruebas con este fichero de señales, una vez ensamblado en un Asesor Experto (las guías al respecto para los novatos se pueden encontrar aquí y aquí), sí que obtenemos los siguientes resultados de una ejecución de pruebas similar a la que teníamos anteriormente:

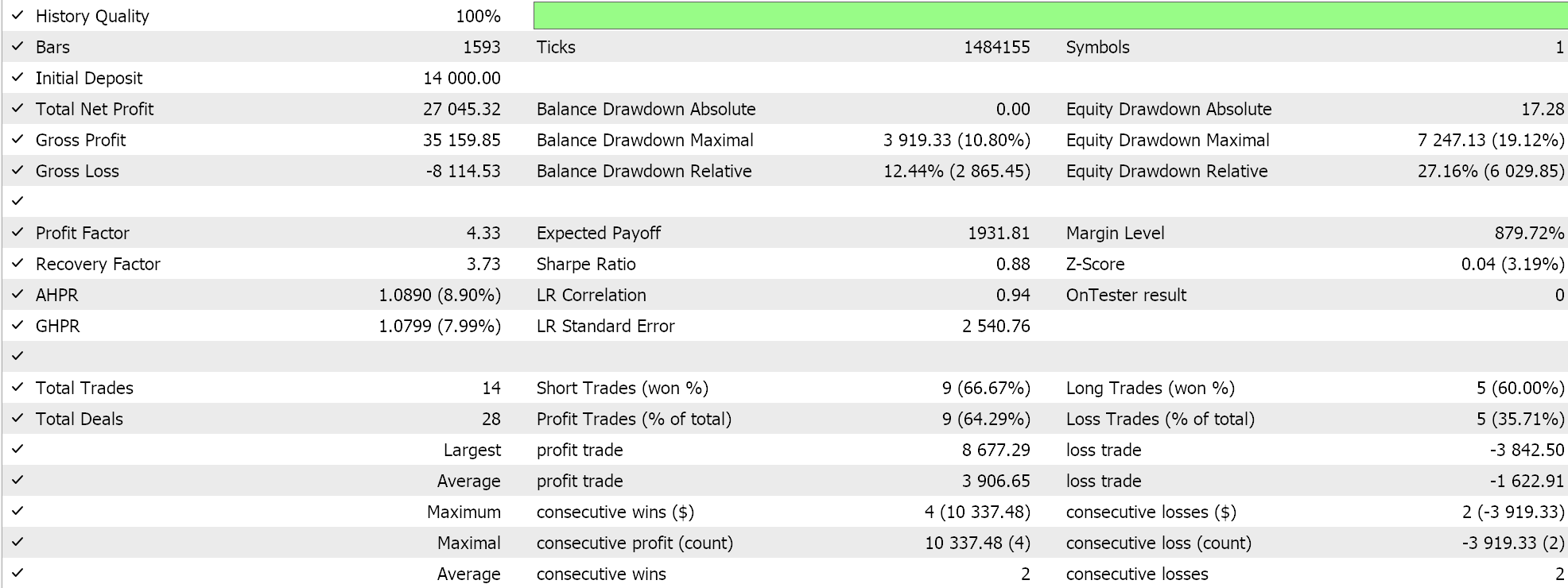
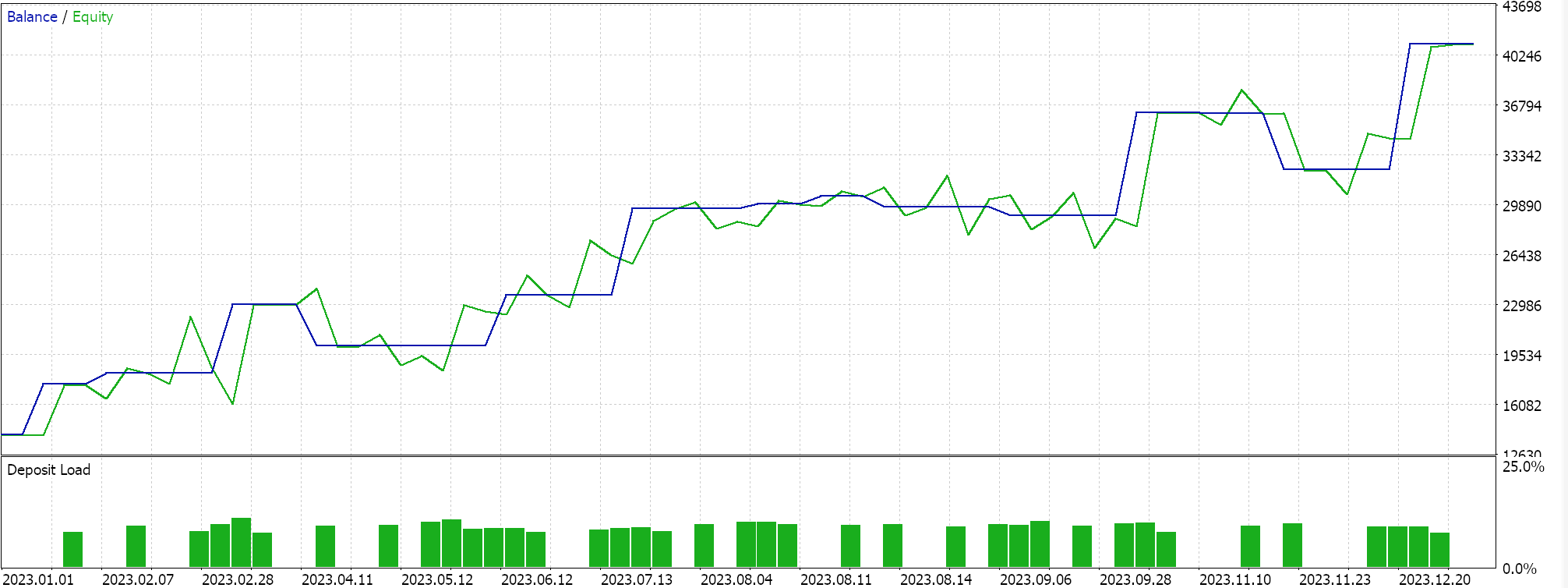
Una rápida comparación con nuestros resultados anteriores muestra claramente que no estamos negociando con tanta frecuencia, y quizá esto sea de esperar porque ahora exigimos que el ángulo no sólo supere el umbral, sino que además se mantenga dentro de una banda determinada. El rendimiento global fue mejor en la mayoría de los parámetros, como el factor de beneficio, el factor de recuperación, el porcentaje de detracciones, etc. Por lo tanto, es algo que podría estudiarse más a fondo mediante pruebas durante periodos más largos y con datos de ticks, antes de sacar conclusiones sobre su eficacia.

Conclusión

En resumen, hemos examinado el ángulo de ataque como métrica para las series temporales financieras, tanto desde el punto de vista tradicional, que consiste simplemente en tomar el ángulo basándose en el precio y los cambios temporales brutos, como desde un enfoque novedoso, que consiste en convertir el eje temporal de las series temporales en unidades de precio. En este artículo no se han realizado pruebas con el enfoque anterior porque hemos detectado tantas incoherencias en la forma de medir el ángulo de ataque que nos ha parecido inútil y un derroche de recursos informáticos intentar realizar pruebas de estrategia.

Sin embargo, las pruebas realizadas con nuestro novedoso planteamiento, consistente en delimitar el eje horizontal o temporal en unidades de tiempo antes de calcular el ángulo de ataque, han arrojado algunos resultados prometedores. Realizamos pruebas con este enfoque en dos modos. En primer lugar, simplemente utilizamos un umbral de ángulo para cribar qué posiciones debíamos abrir y, en segundo lugar, aplicamos el concepto de ángulo crítico, según el cual, para abrir una posición, el ángulo de ataque no sólo tenía que superar el umbral, sino también estar lo suficientemente cerca del umbral al encontrarse dentro de una banda determinada.