MetaTrader 5 / Trading
English Русский 中文 Deutsch 日本語 Português
Cálculo del coeficiente de Hurst

Cálculo del coeficiente de Hurst

MetaTrader 5 — Trading | 18 abril 2017, 11:01
4 443 0
Dmitriy Piskarev
Dmitriy Piskarev

Introducción

Para el trader, una de las tareas principales consiste en definir la dinámica del mercado. A menudo, resulta muy complicado resolver eso a través de las herramientas estándar del análisis técnico. Por ejemplo, МА o MACD pueden indicar en la presencia de una tendencia, pero sin herramientas adicionales no podemos evaluar el grado de su fuerza, estabilidad y si es una tendencia de verdad o no, ya que es muy posible que se trate de un salto de breve duración que se apagará en un futuro cercano. 

Vamos a recordar el siguiente axioma: para operar con éxito en el Forex, siempre es importante saber un poco más que otros participantes del mercado. En este caso, Usted estará a un paso por delante, podrá elegir los momentos de entrada más apropiados y estar seguro de la rentabilidad de la operación. El trading de éxito es una combinación de varias ventajas a la vez: la colocación de órdenes de compra y venta en el momento preciso del cambio de la tendencia, el análisis adecuado a base de los datos fundamentales y técnicos, y desde luego, una absoluta falta de emociones y sentimientos. Todo eso representa las claves para una carrera de éxito del trader.

El análisis fractal puede convertirse en una solución vasta de muchos problemas en el campo de valoración del estado del mercado. Los traders e inversores a menudo desatienden injustamente esta herramienta, pero el análisis fractal de las series temporales ayuda a evaluar con eficacia la presencia y la estabilidad de la tendencia en el mercado.El coeficiente de Hurst es uno de los valores base del análisis fractal.

Antes de pasar directamente a los cálculos, consideraremos brevemente las disposiciones fundamentales del análisis fractal y conoceremos mejor el coeficiente de Hurst.


1. Teoría del mercado fractal (FMT). Análisis fractal

El fractal es un conjunto matemático que posee la propiedad de autosimilaridad. En otras palabras, es un objeto en el que el todo es exacta o aproximadamente similar a una parte de sí mismo: es decir, el todo tiene la misma forma que una o varias de sus partes. El ejemplo más ilustrativo de una estructura fractal es el «árbol fractal»:

Árbol fractal 

Al concepto de la autosimilaridad se le puede dar una definición más profunda: un objeto que posee esta «cualidad» es estatísticamente semejante en diferentes escalas, sean espaciales o temporales.

En contexto del mercado, la palabra «fractal» significa «repetitivo» o «cíclico».

La dimensión fractal es una característica que define de qué manera un objeto o un proceso llena el espacio. Ella describe cómo se altera la estructura del objeto al ser redimensionado. Al proyectar esta definición en los mercados financieros (en nuestro caso, de divisas), se puede postular que la dimensionalidad fractal determina el grado de la «irregularidad» o de la variabilidad de una serie temporal.  Por consiguiente, la línea recta tiene la dimensión d igual a uno, el paseo aleatorio — d=1.5, y para la serie temporal de fractales 1<d<1.5 o 1.5<d<1.

«El propósito de la hipótesis del mercado fractal consiste en proveer el modelo de comportamiento del inversor y movimientos del precio de mercado que corresponden a nuestras observaciones… En un determinado momento de tiempo, los precios no pueden reflejar toda la información disponible, ellos pueden reflejar sólo la información que es importante para un horizonte inversionista específico» — «Análisis fractal de mercados financieros», E. Peters.

En el presente artículo, no vamos a discutir detalladamente el concepto de fractalidad, ya que contamos con el hecho de que el lector ya tenga una idea de este método del análisis. Una descripción exhaustiva de su aplicación en los mercados financieros se puede encontrar en los trabajos de Benoit Mandelbrot y Richard L. Hudson «The Misbehavior of Markets: A Fractal View of Financial Turbulence», Edgar E. Peters «Fractal Market Analysis: Applying Chaos Theory to Investment and Economics», «Chaos and Order in the Capital Markets. A New View of Cycles, Prices and Market Volatility».


2. Análisis R/S y coeficiente de Hurst

2.1. Aparición del análisis R/S


El parámetro clave del análisis fractal es el exponente de Hurst. Es la medida que se utiliza durante el análisis de las series temporales. Cuanto más grande sea el retardo entre dos pares idénticos de valores en una serie temporal, menor será el coeficiente de Hurst.

Este importante exponente fue introducido por Harold Edwin Hurst, un famoso hidrólogo británico que se encargaba del proyecto de la presa en el Nilo, en Egipto. Para la construcción, era necesario estimar el aflujo de agua y, por consiguiente, la necesidad del reflujo. Inicialmente, se consideraba que el aflujo de agua era una variable aleatoria, un proceso estocástico. Sin embargo, Hurst estudió los registros sobre los desbordamientos del Nilo durante nueve siglos y encontró ciertas regularidades en este proceso. Eso fue el punto de partida en su investigación. Se descubrió que los desbordamientos mayores a la media se sustituían por los desbordamientos aún más grandes. Después de eso, el proceso cambiaba de dirección, y los desbordamientos del nivel más bajo a la media se sustituían por otros aún más pequeños. La presencia de los ciclos con una duración no periódica era evidente.

El modelo estadístico de Hurst fue basado en el trabajo de Albert Einstein sobre el movimiento browniano, que era básicamente el modelo del paseo aleatorio de la partícula. La esencia de la teoría consiste en que la distancia recorrida por la partícula R se aumenta proporcionalmente a la raíz cuadrada del tiempo T:


Parafraseamos la fórmula: la amplitud de la variación, R, al hacer muchas pruebas, es igual a la raíz cuadrada del número de las pruebas, T. Precisamente esta fórmula fue tomada por Hurst como base para probar que los desbordamientos del Nilo no eran casuales.

Para formar su método, el hidrólogo utilizaba la serie temporal X1..Xn de los valores del desbordamiento del río. Luego, se aplicaba el siguiente algoritmo, llamado más tarde como el método del rango re-escalado o análisis R/S

  1. Cálculo del valor medio, Xm, de la serie X1..Xn
  2. Cálculo de la desviación estándar de la serie, S
  3. Normalización de la serie mediante la sustracción del valor medio, Zr, donde r=1..n
  4. Creación de la serie temporal acumulativa Y1=Z1+Zr, donde r=2..n
  5. Cálculo de la amplitud de la serie temporal acumulativa R=max(Y1..Yn)-min(Y1..Yn)
  6. División de la amplitud de la serie temporal acumulativa por la desviación estándar S.

Hurst expandió la ecuación de Einstein y la llevó a una forma más general:

 

donde c es una constante.

En general, el valor R/S altera la escala según vaya aumentando el incremento del tiempo, de acuerdo con el valor del grado de dependencia igual a H, que normalmente es llamado el exponente de Hurst. 

El hidrólogo tomó el indicador H por 0,5 si el proceso del desbordamiento fuese accidental. ¡En el proceso de observaciones, él descubrió que H era igual a 0,91! Resulta que la amplitud normalizada se cambia más rápido que la raíz cuadrada del tiempo, es decir el sistema recorre una distancia más grande que el proceso probabilista. Este hecho es una premisa para el momento cuando se puede afirmar que los acontecimientos del pasado tienen un impacto significativo en el presente y el futuro.

2.2. Aplicación de la teoría a los mercados


Posteriormente, fue desarrollada una técnica del cálculo del coeficiente de Hurst en aplicación a los mercados financieros y de valores. Esta característica incluye la normalización de los datos a la media cero y desviación estándar unitaria con el fin de compensar el componente de inflación.En otras palabras, nos vemos de nuevo con el análisis R/S.

¿Cómo se interpreta el coeficiente de Hurst en los mercados?

1. Si el exponente de Hurst se encuentra entre 0,5 y 1 y se diferencia del valor esperado a dos o más desviaciones estándar, el proceso se caracteriza con la memoria de a largo plaza. En otras palabras, existe la persistencia.

Eso quiere decir que dentro de un determinado período de tiempo, las siguientes indicaciones dependen fuertemente de las anteriores. Como ejemplos ilustrativos de una serie temporal persistente tenemos los gráficos de cotizaciones de las empresas más estables e influyentes, por ejemplo, Apple, GE, Boeng, Rosneft, Aeroflot y VTB. Puede estudiar los gráficos de cotizaciones de estas empresas a continuación. Creo que cada inversor practicante ha reconocido en estas imágenes una situación familiar «cada nuevo pico y valle es mayor que el anterior».

Cotizaciones de las acciones de Aeroflot:

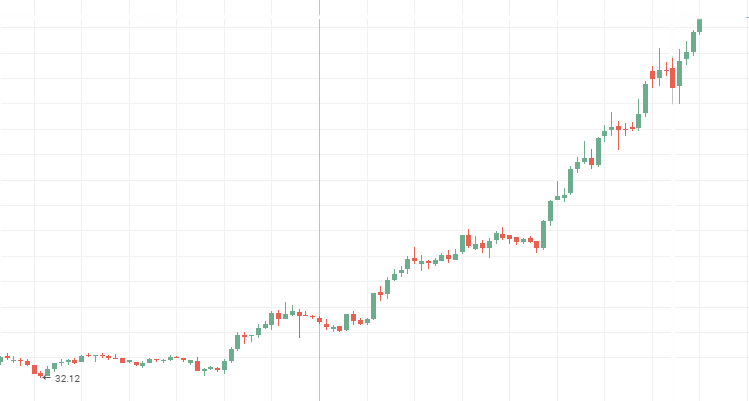
 Cotizaciones de las acciones de Rosneft:

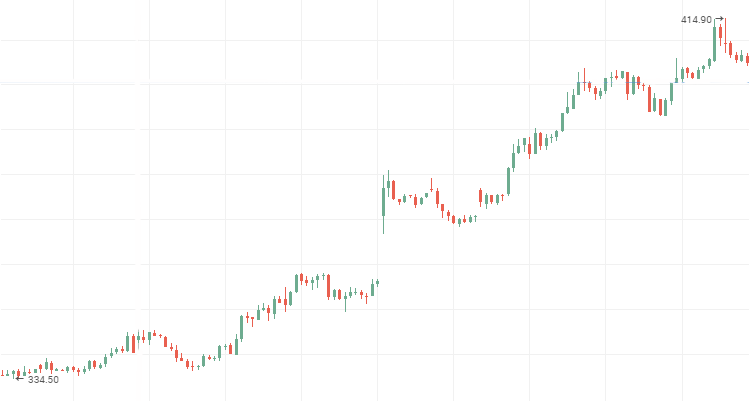
Cotizaciones de las acciones de VTB, serie temporal persistente descendiente


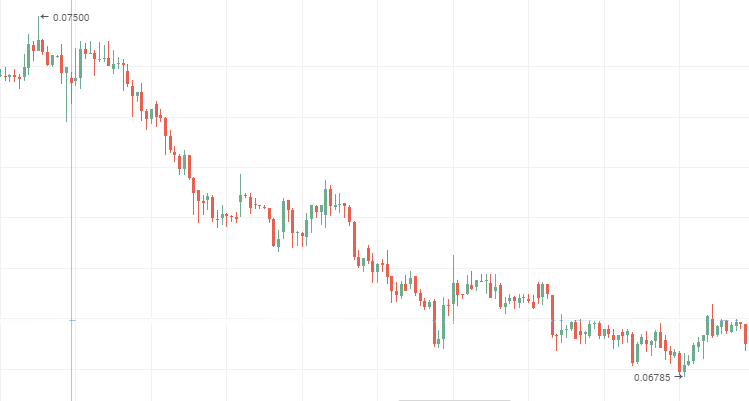
2. El exponente de Hurst que se diferencia del valor esperado en el valor absoluto a dos y más desviaciones estándar, y que recibe un valor desde el intervalo de 0 a 0,5, caracteriza una serie temporal antipersistente.

El sistema se cambia más rápido que un sistema aleatorio, o sea, tiene los cambios frecuentes pero pequeños. Los gráficos de cotizaciones del segundo escalón representan un proceso antipersistente. Durante el período del estancamiento de precios, estos gráficos demuestran las «Blue chips». Abajo, se muestran los gráficos de precios para las acciones de «Mechel», «AvtoVAZ», «Lenenergo», son unos ejemplos claros de las series temporales antipersistentes.

Acciones privilegiadas de «Mechel»:

 

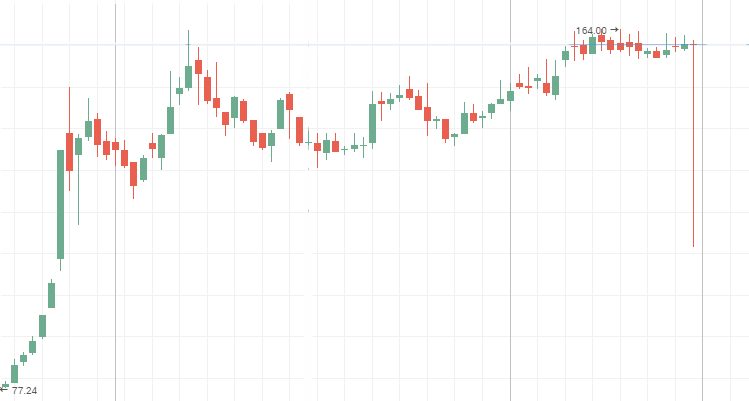
 Movimiento lateral de acciones comunes de AvtoVAZ:

 

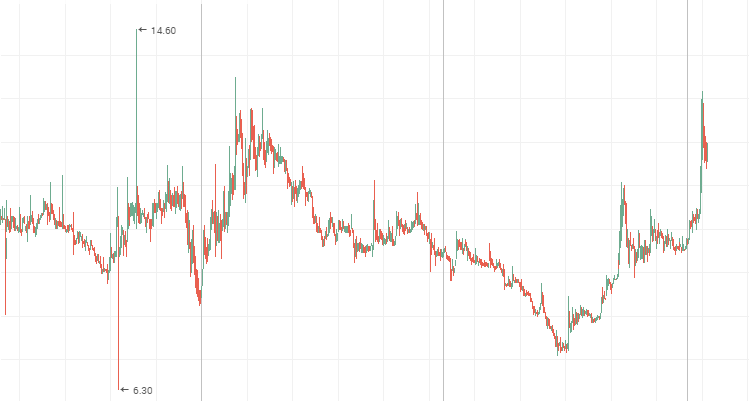
«Lenenergo»:

 

 

3. Si el exponente de Hurst es igual a 0,5 o su valor se diferencia del valor esperado a menos de dos desviaciones estándar, este proceso se considera como un paseo aleatorio y la probabilidad de una dependencia cíclica de a corto o a largo plazo es mínima. Prácticamente, eso significa que durante la negociación no merece la pena atenerse al análisis técnico, ya que los valores del pasado tienen poco efecto sobre el presente. Aquí, la mejor solución es usar el análisis fundamental.

La tabla de abajo contiene los ejemplos de los valores del exponente de Hurst para los instrumentos del mercado de acciones: títulos de varias corporaciones, empresas industriales, mercancías. El cálculo fue realizado para los últimos 7 años. Obsérvese que los valores bajos del coeficiente para las «Blue chips» indican que hay muchas compañías en fase de consolidación durante la crisis financiera. Es curioso que muchos títulos desde el Índice de acciones del segundo nivel muestran un proceso persistente, lo que dice sobre su resistencia a la crisis.

Nombre Exponente de Hurst, H
Gazprom
 0,552
VTB
 0,577
Magnit
 0,554
MMTC
 0,543
Rosneft
 0,648
Aeroflot 0,624
Apple 0,525
GE 0,533
Boeing 0,548
 Rosseti
 0,650
 Raspadskaya
 0,656
 TGC-1
 0,641
 Tattelecom
 0,582
 Linergo
 0,642
 Mechel
 0,635
 AvtoVAZ
 0,574
Gasolina 0,586
Estaño 0,565
Paladio 0,564
Gas natural 0,560
Níquel 0,580


3. Determinación de ciclos y memoria en el análisis fractal

Surge la pregunta, ¿por qué tenemos que estar seguros de que nuestros resultados no son aleatorios (triviales)? Para dar la respuesta, primero, estudiaremos los resultados del análisis RS suponiendo que el sistema analizado no es aleatorio. Es decir, verificamos la validez de la hipótesis nula sobre que el proceso es un paseo aleatorio y su estructura es independiente y está normalmente distribuida.

3.1. Cálculo del valor esperado del análisis R/S

Introducimos el concepto del valor esperado del análisis R/S.

En 1976 Anis y Lloyd hicieron una ecuación que expresaba el valor esperado que necesitamos:


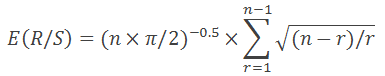
Donde n es el número de observaciones y r representa los enteros de uno a n-1.

Como se observa en el libro «Análisis fractal de los mercados financieros», la formula de arriba es válida solamente para los valores n>20. Para n<20 se debe usar la fórmula siguiente:




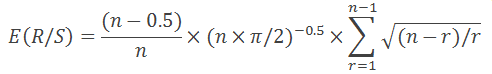
Todo es muy símple:

  1. para cada número de observaciones, calculamos el valor esperado y trazamos el gráfico resultante Log(E(R/S)) de Log(N) juntamente con Log(R/S) de Log(N);
  2. calculamos la dispersión esperada del exponente de Hurst de acuerdo con la fórmula conocida desde la teoría estadística

 

                     donde       H – exponente de Hurst;

                                 N – número de observaciones en el muestreo;

    3. comprobamos la importancia del coeficiente de Hurst obtenido a través de la evaluación del número de desviaciones estándar en los cuales H supera a E(H). El resultado se se considera significativo cuando el indicador de importancia es superior a 2.


3.2. Definición de ciclos

Para no hablar por hablar, estudiaremos un ejemplo. Construimos dos gráficos: uno para la estadística RS y otro para el valor esperado E(R/S), y luego comparamos con la dinámica del mercado. ¿Se concuerdan los resultados de los cálculos con el movimiento de cotizaciones?

Recordemos que Peters apuntaba en sus trabajos que la mejor manera de comprender si había un ciclo, era construir el gráfico de la estadística V en la escala logarítmica a partir del logaritmo del número de observaciones en el subgrupo.  

Es muy fácil evaluar el resultado de la construcción:

  1. si el gráfico en la escala logarítmica, en ambos ejes, es una línea horizontal, entonces se trata de un proceso aleatorio independiente;
  2. si el gráfico tiene un ángulo de inclinación positivo ascendiente, se trata de un proceso persistente que indica, como hemos dicho antes, en que los cambios de la escala R/S se realizan más rápido que la raíz cuadrada del tiempo;
  3. y finalmente, si el gráfico muestra una tendencia descendiente, se trata de un proceso antipersistente.

3.3. Memoria en el análisis fractal y determinación de su profundidad


Para comprender mejor la esencia del análisis fractal, vamos a introducir el concepto de la memoria.

Ya han sido mencionadas las construcciones verbales como las memorias de larga y corta duración. En el análisis fractal, la memoria se refiere a un período durante el cual el mercado recuerda el pasado y toma en cuenta su influencia en los acontecimientos presentes y futuros. Este intervalo de tiempo se llama la memoria de profundidad. En cierto modo, este concepto abarca toda la fuerza y la específica del análisis fractal. La información de este tipo es clave para el análisis técnico, que pone en duda la importancia de cualquier figura técnica en el pasado.

Para determinar la profundidad de la memoria, no se requiere ninguna potencia computacional especial. Para eso, será suficiente un análisis visual simple del gráfico del logaritmo de la estadística V.

  1. Trazamos la línea de la tendencia a lo largo de todos los puntos necesarios del gráfico.
  2. Aseguramos de que la curva no es horizontal.
  3. Determinamos los picos de la curva o las áreas donde la función ha alcanzado sus máximos. Precisamente, en estos máximos la primera «bandera roja» avisa sobre la presencia del ciclo en el gráfico con mayor probabilidad.
  4. Determinamos la coordenada X del gráfico en la escala logarítmica y convertimos el número en una forma más clara: duración del período = exp^ (duración del período en la escala logarítmica). Así, si hemos analizado 12 000 datos horarios del par GBPUSD y hemos obtenido el número 8,2 en la escala logarítmica, entonces el ciclo tiene exp^8,2=3772 horas o 157 días.
  5. Todos los ciclos verdaderos deben guardarse en el mismo intervalo de tiempo, pero con timeframe diferente como base. Por ejemplo, en el punto 4 hemos analizado 12 000 datos horarios del par GBPUSD y hemos supuesto que es un ciclo de 157 días. Cambiamos al timeframe de cuatro horas y analizamos 12000/4=3000 datos. Si el ciclo de 157 días va a tener lugar, es muy probable que haya acertado. En caso contrario, no se desespere: probablemente Usted podrá encontrar los ciclos de memoria más cortos.

3.4. Valores reales del exponente de Hurst para los pares de divisas

Hemos terminado con la descripción de los principios básicos de la teoría del análisis fractal. Antes de proceder a la implementación del análisis R/S por medio de los recursos del lenguaje de programación MQL5, he considerado conveniente mostrar algunos ejemplos más.

La tabla de abajo contiene los valores del exponente de Hurst para 11 pares de divisas del mercado FOREX en los timeframes y número de barras diferentes. Los coeficientes han sido calculados a través de la solución de la regresión usando el método de los cuadrados mínimos (MCM). Como podemos ver, la mayoría de los pares de divisas soportan formalmente el proceso persistente, aunque hay antipersistentes. ¿Pero qué valor tiene este resultado? ¿Podemos confiar en estos números? Hablaremos más tarde de eso.

Tabla 1. Estudio del exponente de Hurst para 2 000 barras

Símbolo H (D1) H (H4) H (H1) H(15M) H (5M) E (H)
EURUSD 0.545 0,497 0.559 0.513 0.567 0.577
EURCHF 0.520 0.468 0.457 0.463 0.522 0.577
EURJPY 0.574 0.501 0.527 0.511 0.546 0.577
EURGBP 0.553 0.571 0.540 0.562 0.550 0.577
EURRUB barras insuficientes 0.536 0.521 0.543 0.476 0.577
USDJPY 0.591 0.563 0.583 0.519 0.565 0.577
USDCHF barras insuficientes 0.509 0.564 0.517 0.545 0.577
USDCAD 0.549 0.569 0.540 0.519 0.565 0.577
USDRUB 0.582 0.509 0.564 0.527 0.540 0.577
AUDCHF 0.522 0.478c 0.504 0.506 0.509 0.577
GBPCHF 0.554 0.559 0.542 0.565 0.559 0,577

Tabla 2. Estudio del exponente de Hurst para 400 barras

Símbolo H (D1) H (H4) H (H1) H(15M) H (5M) E (H)
EURUSD 0.545 0,497 0.513 0.604 0.617 0.578
EURCHF 0.471 0.460 0.522 0.603 0,533 0.578
EURJPY 0.545 0.494 0.562 0.556 0.570 0.578
EURGBP 0.620 0.589 0.601 0.597 0,635 0.578
EURRUB 0,580 0.551 0.478 0.526 0.542 0.578
USDJPY 0.601 0.610 0.568 0.583 0.593 0.578
USDCHF 0.505 0.555 0.501 0.585 0.650 0.578
USDCAD 0.590 0.537 0.590 0.587 0.631 0.578
USDRUB 0.563 0.483 0.465 0.531 0.502 0.578
AUDCHF 0.443 0.472 0.505 0.530 0.539 0.578
GBPCHF 0.568 0,582 0.616 0.615 0.636 0.578

Tabla 3. Resultados de los cálculos del exponente Hurst para los timeframes 15M y 5M

Símbolo H (15M) Importancia  H (5M)  Importancia E (H)
EURUSD 0,543  no significativo 0.542 no significativo  0.544
EURCHF 0.484  significativo 0.480 significativo  0.544
EURJPY 0.513  no significativo 0.513 no significativo  0.544
EURGBP 0.542  no significativo 0.528 no significativo  0.544
EURRUB 0.469  significativo 0.495 significativo  0.544
USDJPY 0.550  no significativo 0,525 no significativo  0.544
USDCHF 0.551  no significativo 0,525 no significativo  0.544
USDCAD 0.519  no significativo 0.550 no significativo  0.544
USDRUB 0.436  significativo 0.485 significativo  0.544
AUDCHF 0.518  no significativo 0.499 significativo  0.544
GBPCHF 0,533  no significativo 0.520 no significativo  0.544

En los estudios de E. Peters, se recomienda analizar algún timeframe básico y buscar en él una serie temporal con dependencias cíclicas. Luego, se recomienda dividir el intervalo analizado en un número de barras menor a través del cambio del tiemeframe y el «ajuste» de la profundidad del historial. De aquí se desprende lo siguiente:

Si el ciclo está presente en el timeframe base, su autenticidad seguramente será confirmada en caso de que el mismo ciclo sea encontrado en una división diferente. 

Usando diferentes combinaciones de las barras disponibles para el estudio, se puede encontrar los ciclos no periódicos cuya longitud será muy útil para cualquier trader que duda de la utilidad del uso de las señales anteriores de los indicadores técnicos.


4. De la teoría a la práctica

Pues bien, hemos obtenido los conocimientos elementales sobre el análisis fractal, hemos conocido qué representa el coeficiente de Hurst y cómo interpretar sus valores. Ahora, nos dedicaremos a la cuestión de la implementación informática de la idea usando los recursos del lenguaje MQL5.

La tarea técnica será la siguiente: es necesario desarrollar un programa que calcule el coeficiente de Hurst para 1000 barras del historial en un determinado par de divisas.

Paso 1. Creamos nuevo script


Como resultado, obtenemos una plantilla que vamos a rellenar con la información. Añadimos inmediatamente la propiedad #property script_show_inputs, porque tendremos que seleccionar un par de divisas al abrir la posición.

//+------------------------------------------------------------------+
//|                                                          New.mq5 |
//|                                    Copyright 2016, Piskarev D.M. |
//|                                      piskarev.dmitry25@gmail.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2016, Piskarev D.M."
#property link      "piskarev.dmitry25@gmail.com"
#property version   "1.00"
#property script_show_inputs
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
  
  }
//+------------------------------------------------------------------+

Paso 2. Definimos un array de los precios del cierre, y al mismo tiempo comprobamos si en este momento están disponibles 1001 barras del historial para el par seleccionado.

¿Por qué 1001, mientras que en la tarea técnica se indican 1000 barras? La respuesta es la siguiente: porque será creado el array de retornos logarítmicos, para la formación del cual hacen falta los datos del valor anterior. 

   double close[];                                              // Declaramos el array dinámico de los precios del cierre
   int copied=CopyClose(symbol,timeframe,0,barscount1+1,close); // copiamos los precios del cierre del par seleccionado a 
                                                                //al array close[] 
   ArrayResize(close,1001);                                     //definimos el tamaño del array
   ArraySetAsSeries(close,true);
   if(bars<1001)                                                //creamos la condición de la presencia de la barra 1001 del historial
     {
      Comment("Too few bars are available! Try another timeframe.");
      Sleep(10000);                                             //retardo del registro durante 10 segundos
      Comment("");
      return;
     }

 Paso 3. Creamos el array de retornos logarítmicos.

Se supone que el array LogReturns ya ha sido declarado y existe la cadena ArrayResize(LogReturns,1001)

for(int i=1;i<=1000;i++)
        LogReturns[i]=MathLog(close[i-1]/close[i]);

Paso 4. Calculamos el coeficiente de Hurst.

Pues bien, para un análisis correcto, es necesario dividir el número de las barras analizado en subgrupos, para que el número de elementos en cada uno de ellos sea por lo menos de 10. Es decir, nuestra tarea es encontrar los divisores de 1000 cuyo valor supera a diez. Esos divisores son 11:

//--- Establecemos el número de elemento en cada subgrupo
      num1=10;
      num2=20;
      num3=25;
      num4=40;
      num5=50;
      num6=100;
      num7=125;
      num8=200;
      num9=250;
      num10=500;
      num11=1000;

Como vamos a calcular los datos para la estadística RS 11 veces, sería conveniente escribir una función personalizada para ello. Los parámetros de la función serán el índice inicial y final del subgrupo para el que se calcula la estadística RS, así como el número de las barras a analizar. El algoritmo dado es completamente idéntico al que ha sido descrito al principio del artículo.

//+----------------------------------------------------------------------+
//|  Función del cálculo de R/S                                          |       
//+----------------------------------------------------------------------+
double RSculc(int bottom,int top,int barscount)
  {
   Sum=0.0;                                      //El valor inicial de la suma es igual a cero
   DevSum=0.0;                                  //El valor inicial de la suma de
                                                 //desviaciones acumuladas es igual a cero  
//--- Cálculo de la suma de retornos
   for(int i=bottom; i<=top; i++)
      Sum=Sum+LogReturns[i];                     //Acumulación de la suma
//--- Cálculo de la media
   M=Sum/barscount;
//--- Cálculo de desviaciones acumuladas
   for(int i=bottom; i<=top; i++)
     {
      DevAccum[i]=LogReturns[i]-M+DevAccum[i-1];
      StdDevMas[i]=MathPow((LogReturns[i]-M),2);
      DevSum=DevSum+StdDevMas[i];               //Componente para el cálculo de la desviación
      if(DevAccum[i]>MaxValue)                  //Si el valor en el array es inferior a un cierto 
         MaxValue=DevAccum[i];                  //máximo, le atribuimos al valor máximo
                                                //el valor del elemento del arrya DevAccum 
      if(DevAccum[i]<MinValue)                  //Lógica idéntica
         MinValue=DevAccum[i];
     }
//--- Cálculo de la amplitud R y desviación S
   R=MaxValue-MinValue;                         //La amplitud es igual a la diferencia del valor máximo 
   MaxValue=0.0; MinValue=1000;                 //y el valor mínimo
   S1=MathSqrt(DevSum/barscount);               //Cálculo de la desviación estándar
//--- Cálculo del exponente R/S
   if(S1!=0)RS=R/S1;                            //Excluimos el error de la división por «cero»
// else Alert("Zero divide!");
   return(RS);                                  //Devolvemos el valor de la estadística RS
  }

Realizamos el cálculo usando el par switch-case.

   //--- Cálculo de componentes Log(R/S)
      for(int A=1; A<=11; A++)                        //el ciclo permite hacer un código bastante compacto
        {                                             //además, tomamos en cuenta todos los divisores posibles
         switch(A)
           {
            case 1:                                   // 100 grupos por 10 elementos en cada uno 
              {
               ArrayResize(rs1,101);
               RSsum=0.0;
               for(int j=1; j<=100; j++)
                 {
                  rs1[j]=RSculc(10*j-9,10*j,10);      //llamamos a la función personalizada RScuclc
                  RSsum=RSsum+rs1[j];
                 }
               RS1=RSsum/100;
               LogRS1=MathLog(RS1);
              }
            break;
            case 2:                                   // 50 grupos por 20 elementos en cada uno 
              {
               ArrayResize(rs2,51);
               RSsum=0.0;
               for(int j=1; j<=50; j++)
                 {
                  rs2[j]=RSculc(20*j-19,20*j,20);     //llamamos a la función personalizada RScuclc
                  RSsum=RSsum+rs2[j];
                 }
               RS2=RSsum/50;
               LogRS2=MathLog(RS2);
              }
            break;
...
...
...
            case 9: // 125 and 16 groups
              {
               ArrayResize(rs9,5);
               RSsum=0.0;
               for(int j=1; j<=4; j++)
                 {
                  rs9[j]=RSculc(250*j-249,250*j,250);
                  RSsum=RSsum+rs9[j];
                 }
               RS9=RSsum/4;
               LogRS9=MathLog(RS9);
              }
            break;
            case 10: // 125 and 16 groups
              {
               ArrayResize(rs10,3);
               RSsum=0.0;
               for(int j=1; j<=2; j++)
                 {
                  rs10[j]=RSculc(500*j-499,500*j,500);
                  RSsum=RSsum+rs10[j];
                 }
               RS10=RSsum/2;
               LogRS10=MathLog(RS10);
              }
            break;
            case 11: //200 and 10 groups
              {
               RS11=RSculc(1,1000,1000);
               LogRS11=MathLog(RS11);
              }
            break;
           }
        }

Paso 5. Función personalizada para calcular la regresión usando el método de los cuadrados mínimos (MCM).

Los parámetros de entrada son los valores de los componentes calculados de la estadística RS.

double RegCulc1000(double Y1,double Y2,double Y3,double Y4,double Y5,double Y6,
                   double Y7,double Y8,double Y9,double Y10,double Y11)
  {
   double SumY=0.0;
   double SumX=0.0;
   double SumYX=0.0;
   double SumXX=0.0;
   double b=0.0; 
   double N[];                                                    //array en el que estarán ubicados los logaritmos de los divisores
   double n={10,20,25,40,50,100,125,200,250,500,1000}             //array de divisores
//--- Cálculo de coeficientes N
   for (int i=0; i<=10; i++)
     {
       N[i]=MathLog(n[i]);
       SumX=SumX+N[i];
       SumXX=SumXX+N[i]*N[i];
     }
   SumY=Y1+Y2+Y3+Y4+Y5+Y6+Y7+Y8+Y9+Y10+Y11;
   SumYX=Y1*N1+Y2*N2+Y3*N3+Y4*N4+Y5*N5+Y6*N6+Y7*N7+Y8*N8+Y9*N9+Y10*N10+Y11*N11;
//--- Cálculo del coeficiente Beta de la regresión o del coeficiente de Hurst que se busca 

   b=(11*SumYX-SumY*SumX)/(11*SumXX-SumX*SumX);
   return(b);
  }

Paso 6. Función personalizada para calcular los valores esperados de la estadística RS. La lógica del cálculo se explica en la parte teórica.

//+----------------------------------------------------------------------+
//|  Función para calcular los valores esperados E(R/S)                  |       
//+----------------------------------------------------------------------+
double ERSculc(double m)                 //m - divisores de 1000
  {
   double e;
   double nSum=0.0;
   double part=0.0;
   for(int i=1; i<=m-1; i++)
     {
      part=MathPow(((m-i)/i), 0.5);
      nSum=nSum+part;
     }
   e=MathPow((m*pi/2),-0.5)*nSum;
   return(e);
  }

Al fin y al cabo, el código completo del programa puede ser el siguiente:

//+------------------------------------------------------------------+
//|                                               hurst_exponent.mq5 |
//|                                    Copyright 2016, Piskarev D.M. |
//|                                      piskarev.dmitry25@gmail.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2016, Piskarev D.M."
#property link      "piskarev.dmitry25@gmail.com"
#property version   "1.00"
#property script_show_inputs
#property strict
input    string  symbol="EURUSD";  // Symbol
input    ENUM_TIMEFRAMES timeframe=PERIOD_D1; // Timeframe
double   LogReturns[],N[],
         R,S1,DevAccum[],StdDevMas[];
int      num1,num2,num3,num4,num5,num6,num7,num8,num9,num10,num11;
double   pi=3.14159265358979323846264338;
double   MaxValue=0.0,MinValue=1000.0;
double   DevSum,Sum,M,RS,RSsum,Dconv;
double   RS1,RS2,RS3,RS4,RS5,RS6,RS7,RS8,RS9,RS10,RS11,
         LogRS1,LogRS2,LogRS3,LogRS4,LogRS5,LogRS6,LogRS7,LogRS8,LogRS9,
         LogRS10,LogRS11;
double   rs1[],rs2[],rs3[],rs4[],rs5[],rs6[],rs7[],rs8[],rs9[],rs10[],rs11[];
double   E1,E2,E3,E4,E5,E6,E7,E8,E9,E10,E11;
double   H,betaE;
int      bars=Bars(symbol,timeframe);
double   D,StandDev;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   double close[];                                              // Declaramos el array dinámico de los precios del cierre
   int copied=CopyClose(symbol,timeframe,0,1001,close);         //Copiamos los precios del cierre del par seleccionado 
                                                                //al array close[] 
   ArrayResize(close,1001);                                     //Establecemos el tamaño del array
   ArraySetAsSeries(close,true);
   if(bars<1001)                                                //Creamos la condición de la presencia de la barra 1001 del historial
     {
         Comment("Too few bars are available! Try another timeframe.");
        Sleep(10000);                                           //Retardo del registro durante 10 segundos
         Comment("");
         return;
     }
//+------------------------------------------------------------------+
//| Preparación de los arrays                                        |
//+------------------------------------------------------------------+        
   ArrayResize(LogReturns,1001);
   ArrayResize(DevAccum,1001);
   ArrayResize(StdDevMas,1001);
//+------------------------------------------------------------------+
//| Array de retornos logarítmicos                                   |
//+------------------------------------------------------------------+
   for(int i=1;i<=1000;i++)
      LogReturns[i]=MathLog(close[i-1]/close[i]);
//+------------------------------------------------------------------+
//|                                                                  |
//|                          análisis R/S                            |
//|                                                                  |
//+------------------------------------------------------------------+
//--- Establecemos el número de elemento en cada subgrupo
   num1=10;
   num2=20;
   num3=25;
   num4=40;
   num5=50;
   num6=100;
   num7=125;
   num8=200;
   num9=250;
   num10=500;
   num11=1000;
//--- Cálculo de componentes Log(R/S)
   for(int A=1; A<=11; A++)
     {
      switch(A)
        {
         case 1:
           {
            ArrayResize(rs1,101);
            RSsum=0.0;
            for(int j=1; j<=100; j++)
              {
               rs1[j]=RSculc(10*j-9,10*j,10);
               RSsum=RSsum+rs1[j];
              }
            RS1=RSsum/100;
            LogRS1=MathLog(RS1);
           }
         break;
         case 2:
           {
            ArrayResize(rs2,51);
            RSsum=0.0;
            for(int j=1; j<=50; j++)
              {
               rs2[j]=RSculc(20*j-19,20*j,20);
               RSsum=RSsum+rs2[j];
              }
            RS2=RSsum/50;
            LogRS2=MathLog(RS2);
           }
         break;
         case 3:
           {
            ArrayResize(rs3,41);
            RSsum=0.0;
            for(int j=1; j<=40; j++)
              {
               rs3[j]=RSculc(25*j-24,25*j,25);
               RSsum=RSsum+rs3[j];
              }
            RS3=RSsum/40;
            LogRS3=MathLog(RS3);
           }
         break;
         case 4:
           {
            ArrayResize(rs4,26);
            RSsum=0.0;
            for(int j=1; j<=25; j++)
              {
               rs4[j]=RSculc(40*j-39,40*j,40);
               RSsum=RSsum+rs4[j];
              }
            RS4=RSsum/25;
            LogRS4=MathLog(RS4);
           }
         break;
         case 5:
           {
            ArrayResize(rs5,21);
            RSsum=0.0;
            for(int j=1; j<=20; j++)
              {
               rs5[j]=RSculc(50*j-49,50*j,50);
               RSsum=RSsum+rs5[j];
              }
            RS5=RSsum/20;
            LogRS5=MathLog(RS5);
           }
         break;
         case 6:
           {
            ArrayResize(rs6,11);
            RSsum=0.0;
            for(int j=1; j<=10; j++)
              {
               rs6[j]=RSculc(100*j-99,100*j,100);
               RSsum=RSsum+rs6[j];
              }
            RS6=RSsum/10;
            LogRS6=MathLog(RS6);
           }
         break;
         case 7:
           {
            ArrayResize(rs7,9);
            RSsum=0.0;
            for(int j=1; j<=8; j++)
              {
               rs7[j]=RSculc(125*j-124,125*j,125);
               RSsum=RSsum+rs7[j];
              }
            RS7=RSsum/8;
            LogRS7=MathLog(RS7);
           }
         break;
         case 8:
           {
            ArrayResize(rs8,6);
            RSsum=0.0;
            for(int j=1; j<=5; j++)
              {
               rs8[j]=RSculc(200*j-199,200*j,200);
               RSsum=RSsum+rs8[j];
              }
            RS8=RSsum/5;
            LogRS8=MathLog(RS8);
           }
         break;
         case 9:
           {
            ArrayResize(rs9,5);
            RSsum=0.0;
            for(int j=1; j<=4; j++)
              {
               rs9[j]=RSculc(250*j-249,250*j,250);
               RSsum=RSsum+rs9[j];
              }
            RS9=RSsum/4;
            LogRS9=MathLog(RS9);
           }
         break;
         case 10:
           {
            ArrayResize(rs10,3);
            RSsum=0.0;
            for(int j=1; j<=2; j++)
              {
               rs10[j]=RSculc(500*j-499,500*j,500);
               RSsum=RSsum+rs10[j];
              }
            RS10=RSsum/2;
            LogRS10=MathLog(RS10);
           }
         break;
         case 11:
           {
            RS11=RSculc(1,1000,1000);
            LogRS11=MathLog(RS11);
           }
         break;
        }
     }
//+----------------------------------------------------------------------+
//|  Cálculo del coeficiente de Hurst                                    |       
//+----------------------------------------------------------------------+
   H=RegCulc1000(LogRS1,LogRS2,LogRS3,LogRS4,LogRS5,LogRS6,LogRS7,LogRS8,
                 LogRS9,LogRS10,LogRS11);
//+----------------------------------------------------------------------+
//|          Cálculo de valores esperados log(E(R/S))                    |       
//+----------------------------------------------------------------------+
   E1=MathLog(ERSculc(num1));
   E2=MathLog(ERSculc(num2));
   E3=MathLog(ERSculc(num3));
   E4=MathLog(ERSculc(num4));
   E5=MathLog(ERSculc(num5));
   E6=MathLog(ERSculc(num6));
   E7=MathLog(ERSculc(num7));
   E8=MathLog(ERSculc(num8));
   E9=MathLog(ERSculc(num9));
   E10=MathLog(ERSculc(num10));
   E11=MathLog(ERSculc(num11));
//+----------------------------------------------------------------------+
//|          Cálculo de Beta de valores esperados log(E(R/S))            |       
//+----------------------------------------------------------------------+  
   betaE=RegCulc1000(E1,E2,E3,E4,E5,E6,E7,E8,E9,E10,E11);
   Alert("H= ", DoubleToString(H,3), " , E= ",DoubleToString(betaE,3));
   Comment("H= ", DoubleToString(H,3), " , E= ",DoubleToString(betaE,3));
}
//+----------------------------------------------------------------------+
//|  Función del cálculo de R/S                                          |       
//+----------------------------------------------------------------------+
double RSculc(int bottom,int top,int barscount)
  {
   Sum=0.0;                                      //El valor inicial de la suma es igual a cero
   DevSum=0.0;                                  //El valor inicial de la suma de
                                                 //desviaciones acumuladas es igual a cero  
//--- Cálculo de la suma de retornos
   for(int i=bottom; i<=top; i++)
      Sum=Sum+LogReturns[i];                     //Acumulación de la suma
//--- Cálculo de la media
   M=Sum/barscount;
//--- Cálculo de desviaciones acumuladas
   for(int i=bottom; i<=top; i++)
     {
      DevAccum[i]=LogReturns[i]-M+DevAccum[i-1];
      StdDevMas[i]=MathPow((LogReturns[i]-M),2);
      DevSum=DevSum+StdDevMas[i];               //Componente para el cálculo de la desviación
      if(DevAccum[i]>MaxValue)                  //Si el valor en el array es inferior a un cierto 
         MaxValue=DevAccum[i];                  //máximo, le atribuimos al valor máximo
                                                //el valor del elemento del arrya DevAccum 
      if(DevAccum[i]<MinValue)                  //Lógica idéntica
         MinValue=DevAccum[i];
     }
//--- Cálculo de la amplitud R y desviación S
   R=MaxValue-MinValue;                         //La amplitud es igual a la diferencia del valor máximo 
   MaxValue=0.0; MinValue=1000;                 //y el valor mínimo
   S1=MathSqrt(DevSum/barscount);               //Cálculo de la desviación estándar
//--- Cálculo del exponente R/S
   if(S1!=0)RS=R/S1;                            //Excluimos el error de la división por «cero»
// else Alert("Zero divide!");
   return(RS);                                  //Devolvemos el valor de la estadística RS
  }
//+----------------------------------------------------------------------+
//|  Calculador de regresión                                             |       
//+----------------------------------------------------------------------+  
double RegCulc1000(double Y1,double Y2,double Y3,double Y4,double Y5,double Y6,
                   double Y7,double Y8,double Y9,double Y10,double Y11)
  {
   double SumY=0.0;
   double SumX=0.0;
   double SumYX=0.0;
   double SumXX=0.0;
   double b=0.0;                                                  //array en el que estarán ubicados los logaritmos de los divisores
   double n[]={10,20,25,40,50,100,125,200,250,500,1000};          //array de divisores
//--- Cálculo de coeficientes N
   ArrayResize(N,11);
   for (int i=0; i<=10; i++)
     {
       N[i]=MathLog(n[i]);
       SumX=SumX+N[i];
       SumXX=SumXX+N[i]*N[i];
     }
   SumY=Y1+Y2+Y3+Y4+Y5+Y6+Y7+Y8+Y9+Y10+Y11;
   SumYX=Y1*N[0]+Y2*N[1]+Y3*N[2]+Y4*N[3]+Y5*N[4]+Y6*N[5]+Y7*N[6]+Y8*N[7]+Y9*N[8]+Y10*N[9]+Y11*N[10];
//--- Cálculo del coeficiente Beta de la regresión o del coeficiente de Hurst que se busca 
   b=(11*SumYX-SumY*SumX)/(11*SumXX-SumX*SumX);
   return(b);
  }
//+----------------------------------------------------------------------+
//|  Función para calcular los valores esperados E(R/S)                  |       
//+----------------------------------------------------------------------+
double ERSculc(double m)                 //m - divisores de 1000
  {
   double e;
   double nSum=0.0;
   double part=0.0;
   for(int i=1; i<=m-1; i++)
     {
      part=MathPow(((m-i)/i), 0.5);
      nSum=nSum+part;
     }
   e=MathPow((m*pi/2),-0.5)*nSum;
   return(e);
  }

Claro que si Usted quiere, puede modernizar el código por sí mismo, implementar una gama más amplia de características a calcular y crear una interfaz gráfica a su medida. 

En el capítulo final, hablaremos sobre las soluciones de software existentes.


5. Soluciones de software

Hay muchos recursos informáticos en los cuales el algoritmo del análisis R/S ya está implementado. Sin embargo, normalmente la implementación de este algoritmo está comprimida y deja la mayor parte del trabajo analítico al usuario. El paquete Matlab es un ejemplo. 

Existe también una utilidad para el terminal MetaTrader 5, que está disponible en el Market con el nombre Fractal Analysis, a través de la cual el usuario puede realizar el análisis fractal de los mercados financieros. Vamos a ver cómo se maneja este analizador.

5.1. Parámetros de entrada

La verdad es que entre la gran variedad de los parámetros de entrada nos van a interesar solamente los tres primeros, a saber: Symbol, Number of bars y Timeframe. 

Como se puede observar en la captura de pantalla de abajo, Fractal Analysis permite seleccionar un par de divisas, incluso no importa en absoluto en la ventana de qué instrumento ha sido iniciada la utilidad: lo más importante es indicar el símbolo en la ventana de inicialización. 

Seleccionamos el número necesario de las barras en un determinado timeframe que se especifica en el siguiente punto.  


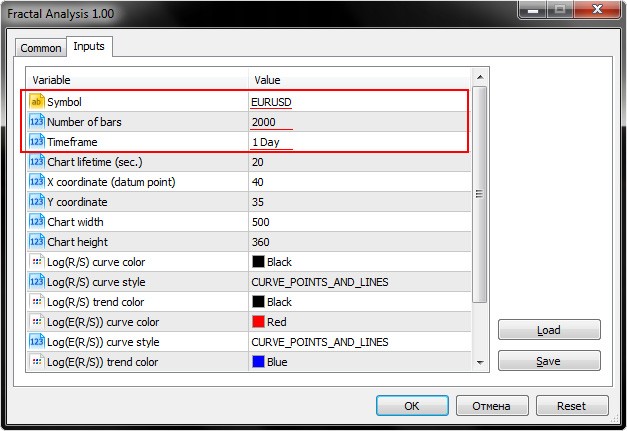
Además, fíjense en el parámetro Chart lifetime que establece el número de segundos durante los cuales Usted podrá trabajar con esta utilidad. Como resultado, después de hacer clic en el botón «OK», el analizador aparecerá en la esquina superior izquierda de la ventana principal del terminal MetaTrader 5. En la captura de pantalla de abajo se muestra un ejemplo:

 

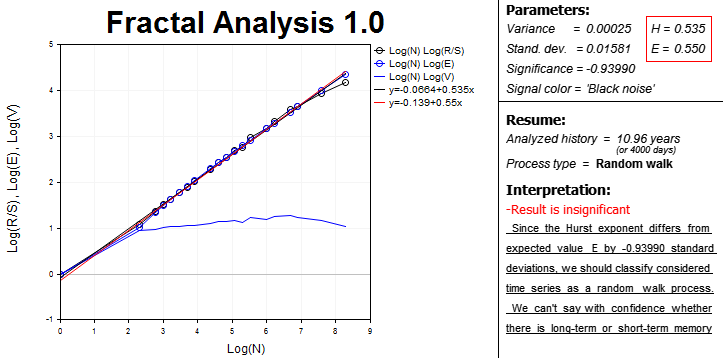
En resumidas cuentas, en la pantalla aparecen todos los datos y resultados necesarios para el análisis fractal, reunidos en bloques.

En la parte izquierda, se encuentra el área con dependencias gráficas en la escala logarítmica:

  • estadística R/S según el número de observaciones en el muestreo;
  • valor esperado de la estadística R/S de E(R/S) según el número de observaciones;
  • estadística V según el número de observaciones.

Ésta es un área interactiva que supone el uso de las herramientas de MetaTrader 5 para el análisis de los gráficos, ya que a veces resulta bastante difícil encontrar la longitud del ciclo «a ojo». 

También están presentes las ecuaciones de las curvas y las líneas de la tendencia, la inclinación de las cuales permite determinar los exponentes numéricos de Hurst (H). Además, se calcula el valor esperado del exponente de Hurst (E). Estas ecuaciones se encuentran en el bloque derecho adyacente, ahí mismo se calcula la dispersión y la importancia del análisis, el color del espectro de la señal. 

Para la conveniencia del usuario, el programa calcula la longitud del período analizado en días. Eso es necesario comprender para evaluar la importancia de los datos históricos.

En la línea Process type, se muestra la característica de la serie temporal:

  • persistente;
  • antipersistente;
  • paseo aleatorio.

Y finalmente, en el bloque «Interpretation», se muestra el resumen breve que será útil para un analista que sólo empieza a familiarizarse con el análisis fractal. 

5.2. Ejemplo de trabajo

Definimos qué instrumento y en qué intervalo temporal vamos a analizar.  Vamos a analizar el par «dólar neocelandés y franco suizo» (NZDCHF), y veremos las últimas cotizaciones en la escala horaria (H1).

 

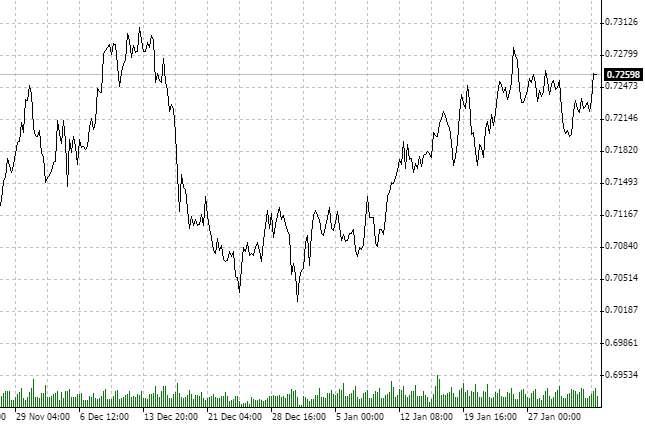
Notamos que durante aproximadamente los últimos dos meses, el mercado se encuentra en modo de consolidación. Una vez más, NO estamos interesados en otros horizontes inversionistas. Es bien posible que el gráfico del timeframe diario muestre la tendencia alcista o bajista. Hemos seleccionado H1 y un determinado número de datos históricos.

Aparentemente, el proceso es antipersistente. Vamos a comprobarlo a través de Fractal Analysis.

De 21.11 a 3.02 tenemos el historial de 75 días. Convertimos 75 días en horas. Obtenemos 1800 datos horarios. Como en la entrada de la utilidad no hay esta cantidad de barras, definimos el valor próximo, es decir, 2 000 períodos horarios analizados.

Al final, obtenemos la siguiente imagen:


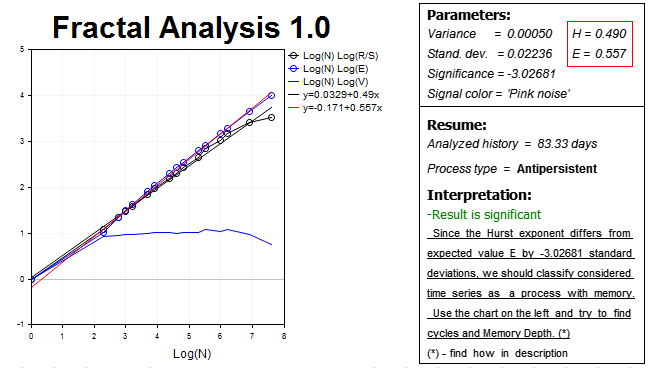
Como se puede observar, nuestra hipótesis se ha confirmado, y en este horizonte el mercado demuestra un proceso antipersistente, que además es bastante significativo: el valor del exponente de Hurst H=0.490, eso está prácticamente a tres desviaciones estándar por debajo del valor esperado E=0.557.

Vamos a consolidar el resultado y cogeremos el timeframe un poco más grande, H2, y por siguiente, la mitad del número de las barras del historial, 1000 valores. El resultado será el siguiente:

 

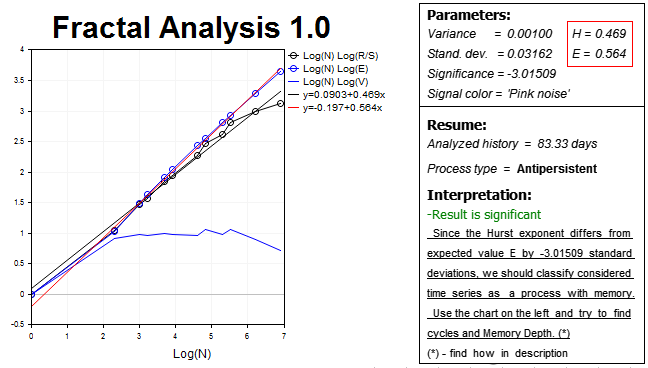
Vemos de nuevo la antipersistencia. El exponente de Hurst H=0.469 atrasa a más de tres desviaciones estándar del valor esperado E=0.564.

Ahora intentaremos encontrar los ciclos.

Volvemos al gráfico para H1, e intentaremos captar el momento cuando la curva R/S se separa de E(R/S). Este momento se caracteriza por la formación de un pico en el gráfico de la estadística V. De esta manera, ahora podemos determinar el valor aproximado del ciclo.

 

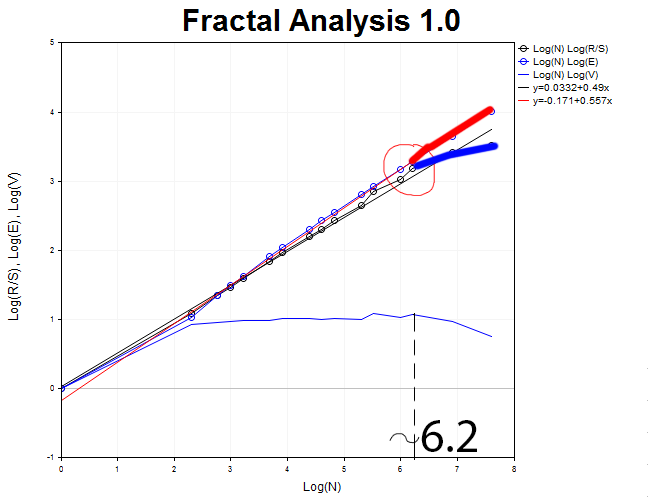
Es igual aproximadamente a N1 = 2.71828^6.2 = 493 horas, lo que equivales a veintiún días.

Desde luego no se puede hablar con seguridad sobre la certeza del resultado, basándose en los resultados de un solo experimento. Como ya se ha dicho antes, es necesario «jugar» con los timeframes y tratar de escoger todas las combinaciones posibles «timeframe — número de barras» con el fin de asegurarse de la certeza del resultado obtenido.

Vamos a realizar el análisis gráfico de 1000 barras en el timeframe H2. 

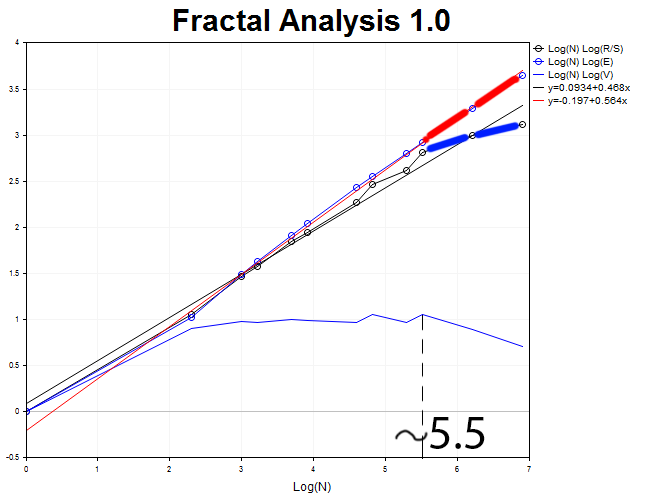
La longitud del ciclo es igual a N2 = 2.71828^5.5 = 245 períodos de dos horas, lo que equivale aproximadamente a veinte días.

Ahora analizaremos el timeframe de 30 minutos y 4 000 valores. Obtenemos el proceso antipersistente con el exponente de Hurst H = 0.492 y el valor esperado E=0.55, que supera H en 3,6 desviaciones estándar.

 

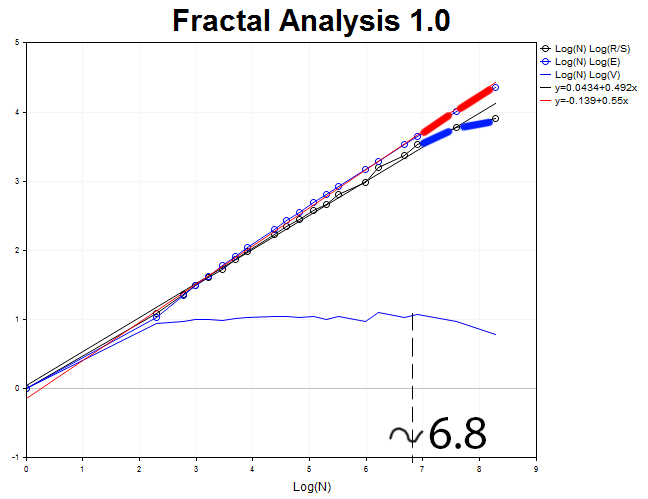
La longitud del ciclo es igual a N3 =  2.71828^6.8 = 898 segmentos de treinta minutos o 18,7 días. 

Como un ejemplo de aprendizaje, tres pruebas serán suficientes. Encontraremos el valor medio de las longitudes obtenidas del período M= (N1 + N2 + N3)/3 = (21 + 20 + 18.7)/3 = 19.9 o 20 días.

Como resultado, obtenemos un período dentro del que realmente se puede confiar en los datos técnicos y construir la estrategia comercial basándose en ellos. Volveré a repetir que este cálculo y el análisis se muestran aquí para el horizonte inversionista con longitud de dos meses. Eso significa que el análisis pierde su relevancia al cambiar al trading de intradía, porque ahí probablemente pasan sus procesos cíclicos de muy corta duración, cuya presencia o ausencia debe ser confirmada. Si los ciclos no se detectan, eso significa que el análisis técnico perderá su relevancia y eficacia, y la solución razonable será pasar al trading usando las noticias y al «trading basado en sentimientos» (sentimientos del mercado).

Conclusión 

El análisis fractal es una especie de sinergia del enfoque técnico, fundamental y estadístico sobre la previsión de la dinámica del mercado. Es una manera universal de procesar la información: el análisis R/S y el exponente de Hurst se han acreditado con éxito en las áreas de ciencia como la geografía, la biología, la física, la economía. El análisis fractal puede aplicarse para construir los modelos de scoring y evaluación utilizados por las entidades de crédito para analizar la solvencia del prestatario.

Y para concluir, me gustaría repetir la idea expresada al principio del artículo: para operar con éxito en los mercados financieros, es importante saber siempre un poco más que los demás inversores. Saboreando la comprensión errónea de la información expuesta, me gustaría advertir al lector de que el mercado tiende a «engañar» al analista. Por eso, siempre compruebe la existencia de un ciclo no periódico en los timeframes mayores y menores. Si no va a aparecer en otros timeframes, es muy probable que el ciclo represente solamente un ruido del mercado.

Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/2930

Archivos adjuntos |
Descargar ZIP
hurst_exponent.mq5 (23.53 KB)
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Pasar a la discusión en el foro de los operadores
Tendencia universal con interfaz gráfica Tendencia universal con interfaz gráfica
En este artículo, a base de una serie de indicadores estándar, se crea el indicador universal de tendencia. Se desarrolla la interfaz gráfica para seleccionar el tipo del indicador y configurar sus parámetros. El indicador se visualiza en una ventana separada con las series de iconos de diferentes colores.
Interfaces gráficas X: Algoritmo del traslado de palabras en el campo de edición multilínea (build 12) Interfaces gráficas X: Algoritmo del traslado de palabras en el campo de edición multilínea (build 12)
Sigamos desarrollando el control «Campo de edición multilínea». Esta vez, nuestra tarea consiste en configurar el traslado automático de palabras a la siguiente línea si no encajan en el campo de edición, o el traslado inverso a la línea anterior si aparece esta posibilidad.
Recetas MQL5 - Señales comerciales de pivotes Recetas MQL5 - Señales comerciales de pivotes
En este artículo se demuestra el proceso del desarrollo e implementación de la clase de señales a base de los pivote, niveles de reversa. A base de esta clase, se construye la estrategia con el uso de la librería estándar. Se consideran las posibilidades del desarrollo de la estrategia de pivotes mediante la adición de los filtros.
Interfaces gráficas X: Ordenamiento, reconstrucción de la tabla y controles en las celdas (build 11) Interfaces gráficas X: Ordenamiento, reconstrucción de la tabla y controles en las celdas (build 11)
Seguimos añadiendo nuevas posibilidades a la tabla dibujada que nos permitirán hacer lo siguiente: ordenar los datos, controlar el número de columnas y filas, establecer el tipo de las celdas para adjuntar los controles.