Red neuronal en la práctica: Mínimos cuadrados

Introducción

Hola a todos, y bienvenidos a un nuevo artículo sobre Redes Neuronales.

En el artículo anterior "Red neuronal en la práctica: Reta secante", comenzamos a ver la cuestión de las matemáticas aplicadas en la práctica. Sin embargo, aquello fue solo una leve y breve introducción al tema. Vimos que la principal operación matemática a utilizar es una función trigonométrica. Y, diferente de lo que muchos imaginan, no es la función tangente, sino la función secante. A pesar de que todo eso puede parecer bastante confuso al principio, pronto verás que es mucho más simple de lo que parece. Y diferente de lo que muchos hacen, que es precisamente generar una gran confusión respecto a la parte matemática, todo se desarrolla de manera bastante natural.

Algo extraño que no entendí

Sin embargo, hay un pequeño fallo, si se puede decir así, que no logré entender, ya que no tiene sentido. Al menos no para mí. No obstante, como podría servir de advertencia para otras personas que puedan intentar hacer lo mismo, dejé las cosas tal como estaban. Pero aquí corregiremos el problema. Esto se debe a que, si no lo corregimos, tendremos muchos otros problemas en la parte matemática.

En el artículo anterior, tenemos el siguiente fragmento, que se muestra a continuación:

19. //+------------------------------------------------------------------+
20. void Func_01(void)
21. {
22.     int A[] {
23.                 -100,  150,
24.                  -80,   50,
25.                   30,  -80,
26.                  100, -120
27.             };
28. 
29.     canvas.LineVertical(global.x, global.y - _SizeLine, global.y + _SizeLine, ColorToARGB(clrRoyalBlue, 255));
30.     canvas.LineHorizontal(global.x - _SizeLine, global.x + _SizeLine, global.y, ColorToARGB(clrRoyalBlue, 255));
31. 
32.     for (uint c0 = 0, c1 = 0; c1 < A.Size(); c0++)
33.         canvas.FillCircle(global.x + A[c1++], global.y + A[c1++], 5, ColorToARGB(clrRed, 255));
34. }
35. //+------------------------------------------------------------------+

Este fragmento tiene como objetivo graficar pequeños círculos cuya posición está en el array A, presente en la línea 22. Hasta aquí nada fuera de lo común. Esa es justamente la idea. Sin embargo, al graficar los puntos, verás la siguiente imagen:

Estos puntos están ubicados en las posiciones incorrectas. Están invertidos en relación al eje X y Y. ¿Pero por qué?!? Bueno, sinceramente no sé explicarlo. Esto se debe a que en la línea 33 del fragmento capturamos los valores presentes en el array, y luego sumamos una posición. Haciendo esto, el compilador debería entender que estamos apuntando al siguiente valor en el array. De hecho, esto sucede, y si no fuera así, se generaría un error de acceso no autorizado a la memoria, lo que se vería como un error de rango, y la aplicación se cerraría.

Sin embargo, los valores que se están sumando a global.x no son los valores de índice par, sino los de índice impar. Y los valores sumados a global.y son los de índice par, cuando lo esperado sería que fueran los de índice impar.

Solo me di cuenta de esto cuando comencé a escribir la parte matemática para este artículo, ya que los cálculos no coincidían con los resultados presentados por la aplicación. Así que decidí verificar la causa. Puedes hacer lo mismo modificando ligeramente el fragmento como se muestra a continuación.

19. //+------------------------------------------------------------------+
20. void Func_01(void)
21. {
22.     int A[]={
23.                 -100,  150,
24.                  -80,   50,
25.                   30,  -80,
26.                  100, -120
27.             };
28. 
29.     int vx, vy;
30.     string s = "";
31. 
32.     canvas.LineVertical(global.x, global.y - _SizeLine, global.y + _SizeLine, ColorToARGB(clrRoyalBlue, 255));
33.     canvas.LineHorizontal(global.x - _SizeLine, global.x + _SizeLine, global.y, ColorToARGB(clrRoyalBlue, 255));
34. 
35.     for (uint c0 = 0, c1 = 0; c1 < A.Size(); c0++)
36.     {
37.         canvas.FillCircle(global.x + (vx = A[c1++]), global.y + (vy = A[c1++]), 5, ColorToARGB(clrRed, 255));
38.         s += StringFormat("[ %d <> %d ] ", vx, vy);
39.     }
40.     canvas.TextOut(global.x - 200, global.y + _SizeLine + 70, s, ColorToARGB(clrBlack));
41. }
42. //+------------------------------------------------------------------+

Esta modificación nos permite ver lo que está sucediendo. El resultado se muestra en la imagen a continuación:

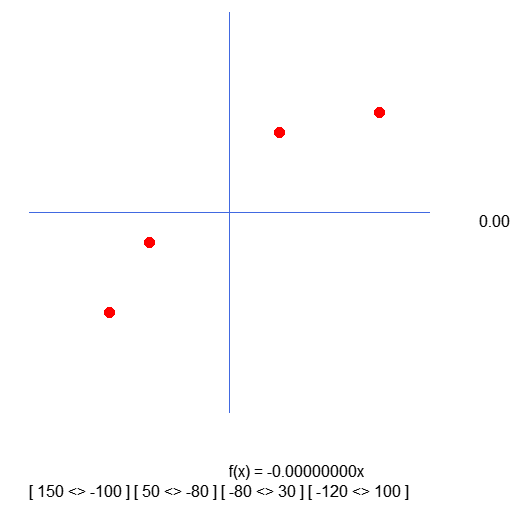
Observa los valores dentro de los corchetes. Estos son el resultado de la captura realizada en la línea 37. Es decir, estamos capturando los valores que se utilizan para posicionar los círculos en el gráfico. Sin embargo, nota que están invertidos en comparación con lo que se declara en el array. Lo cual es bastante extraño. Por este motivo, necesitamos modificar el código como se muestra en el siguiente fragmento.

19. //+------------------------------------------------------------------+
20. void Func_01(void)
21. {
22.     int A[]={
23.                 -100,  150,
24.                  -80,   50,
25.                   30,  -80,
26.                  100, -120
27.             };
28. 
29.     int vx, vy;
30.     string s = "";
31. 
32.     canvas.LineVertical(global.x, global.y - _SizeLine, global.y + _SizeLine, ColorToARGB(clrRoyalBlue, 255));
33.     canvas.LineHorizontal(global.x - _SizeLine, global.x + _SizeLine, global.y, ColorToARGB(clrRoyalBlue, 255));
34. 
35.     for (uint c0 = 0, c1 = 0; c1 < A.Size(); c0++)
36.     {
37.         vx = A[c1++];
38.         vy = A[c1++];
39.         canvas.FillCircle(global.x + vx, global.y + vy, 5, ColorToARGB(clrRed, 255));
40.         s += StringFormat("[ %d <> %d ] ", vx, vy);
41.     }
42.     canvas.TextOut(global.x - 200, global.y + _SizeLine + 70, s, ColorToARGB(clrBlack));
43. }
44. //+------------------------------------------------------------------+

Ahora, el hecho de que utilicemos este nuevo fragmento de código hace que el resultado obtenido sea el que se ve en la imagen justo abajo:

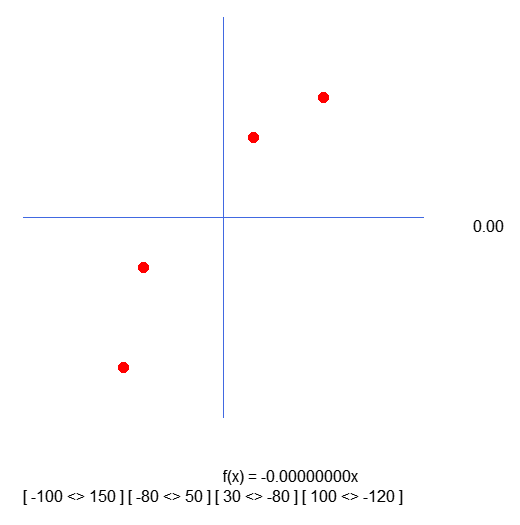
Ahora puedes notar que los valores dentro de los corchetes corresponden a lo que está declarado en el array. Pido disculpas a todos por no haber notado este fallo antes. Pero que esto sirva de advertencia para todos aquellos que deseen hacer las cosas de una manera particular. Como no entendí por qué los índices estaban invertidos, no sé cómo explicar por qué ocurre el fallo. Bien, hecha esta corrección, que es realmente necesaria, podemos continuar con lo próximo a implementar y mostrar.

Preparándonos para hacer cálculos y más cálculos

Muy bien, lo que haremos a partir de este momento puede ser bastante confuso si simplemente te lanzara el código sin más. Como quiero que tú, mi estimado lector, comprendas exactamente qué y por qué estaremos haciendo ciertas cosas, voy a explicar todo con calma. Así que lee con tranquilidad lo que será explicado. Modifica el código conforme se vaya mostrando. Pruébalo y trata de entender lo que está sucediendo. Cuando lo entiendas, pasa a la siguiente etapa. No intentes saltarte pasos, porque si lo haces, puede que no logres entender absolutamente nada de lo que estará ocurriendo.

La primera cosa que haremos es modificar ligeramente el código como se muestra en el fragmento a continuación.

19. //+------------------------------------------------------------------+
20. void Func_01(void)
21. {
22.     int A[]={
23.                 -100,  150,
24.                  -80,   50,
25.                   30,  -80,
26.                  100, -120
27.             };
28. 
29.     int vx, vy;
30.     string s = "";
31.     double ly;
32. 
33.     canvas.LineVertical(global.x, global.y - _SizeLine, global.y + _SizeLine, ColorToARGB(clrRoyalBlue, 255));
34.     canvas.LineHorizontal(global.x - _SizeLine, global.x + _SizeLine, global.y, ColorToARGB(clrRoyalBlue, 255));
35. 
36.     for (uint c0 = 0, c1 = 0; c1 < A.Size(); c0++)
37.     {
38.         vx = A[c1++];
39.         vy = A[c1++];
40.         canvas.FillCircle(global.x + vx, global.y + vy, 5, ColorToARGB(clrRed, 255));
41.         ly = (vx * MathTan(_ToRadians(global.Angle))) - vy;
42.         canvas.LineVertical(global.x + vx, global.y + vy, global.y + (int)(ly + vy), ColorToARGB(clrPurple));
43.         s += StringFormat("sy%d = %.4f  | ", c0, ly);
44.     }
45.     canvas.TextOut(global.x - 200, global.y + _SizeLine + 50, s, ColorToARGB(clrBlack));
46. }
47. //+------------------------------------------------------------------+
48. void NewAngle(const char direct, const double step = 0.2)
49. {
50.     canvas.Erase(ColorToARGB(clrWhite, 255));
51. 
52.     global.Angle = (MathAbs(global.Angle + (step * direct)) < 90 ? global.Angle + (step * direct) : global.Angle);
53.     canvas.TextOut(global.x + _SizeLine + 50, global.y, StringFormat("%.2f", MathAbs(global.Angle)), ColorToARGB(clrBlack));
54.     canvas.TextOut(global.x, global.y + _SizeLine + 20, StringFormat("f(x) = %.8fx", -MathTan(_ToRadians(global.Angle))), ColorToARGB(clrBlack));
55.     canvas.Line(
56.                 global.x - (int)(_SizeLine * cos(_ToRadians(global.Angle))), 
57.                 global.y - (int)(_SizeLine * sin(_ToRadians(global.Angle))), 
58.                 global.x + (int)(_SizeLine * cos(_ToRadians(global.Angle))), 
59.                 global.y + (int)(_SizeLine * sin(_ToRadians(global.Angle))), 
60.                 ColorToARGB(clrForestGreen)
61.             );
62.        
63.     Func_01();
64. 
65.     canvas.Update(true);
66. }
67. //+------------------------------------------------------------------+

A pesar de que las cosas no se están haciendo de la mejor manera, el resultado que se muestra en la animación de abajo presenta exactamente lo que queremos visualizar:

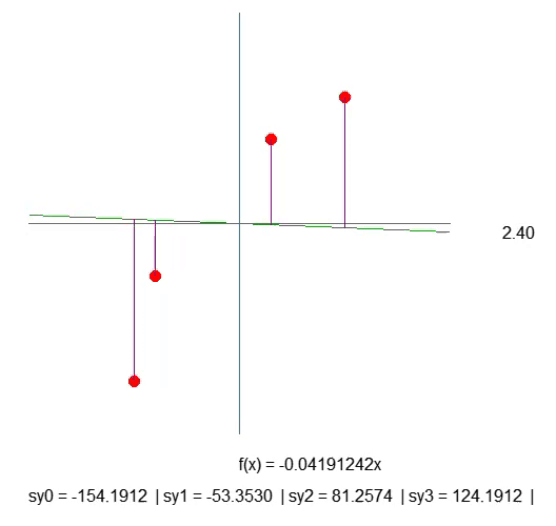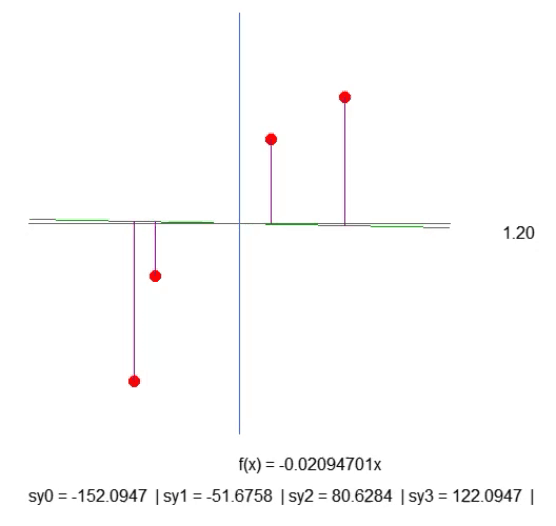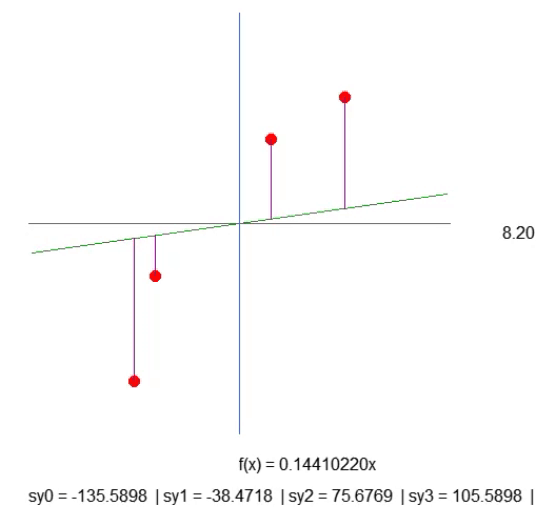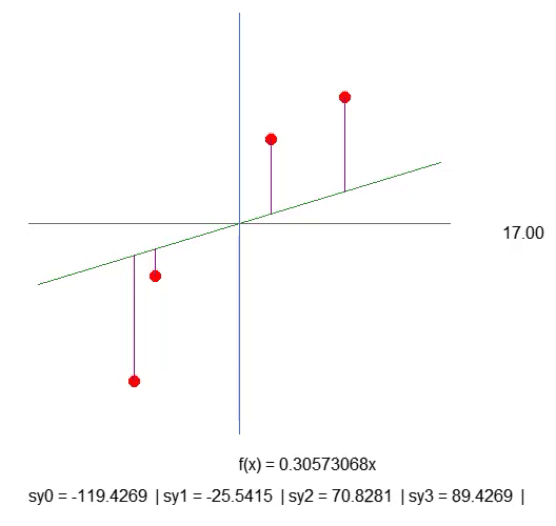
Lo que estamos haciendo es simplemente creando una línea púrpura. Esta nos indica la distancia entre la recta y el punto. Presta atención a esto. La longitud de la línea se obtiene en la línea 41 del fragmento. Aunque el cálculo no es exactamente como debería ser, funciona. Así que vamos con calma, ya que necesitaremos cambiar este cálculo más adelante. En la línea 43, creamos una cadena de texto que nos permite saber cuál es la longitud de esta línea púrpura. Al ver la animación, notarás que existen longitudes negativas, lo cual no tiene sentido. Pero no te preocupes por esto por ahora. Primero quiero que entiendas lo que estamos haciendo.

Ahora quiero que pienses un poco, querido lector. La función de la recta se calcula con base en el coeficiente de inclinación. Este coeficiente se obtiene del ángulo que estamos modificando al presionar las flechas derecha o izquierda. Y el paso con el que esta inclinación cambia está dado por el valor de `step`, presente en la línea 52.

Bien, entonces, observando la longitud de cada una de las líneas púrpuras. Con un poco de paciencia, puedes lograr que la inclinación de la recta sea la mejor posible,haciendo que la longitud de cada una de las líneas púrpuras deje de crecer.Puede disminuir, pero no debería aumentar. Cuando logres que ninguna de las longitudes crezca, habrás encontrado el coeficiente de inclinación ideal.

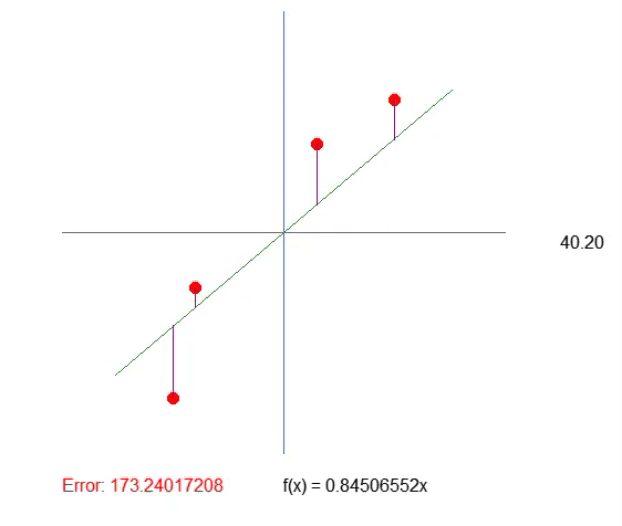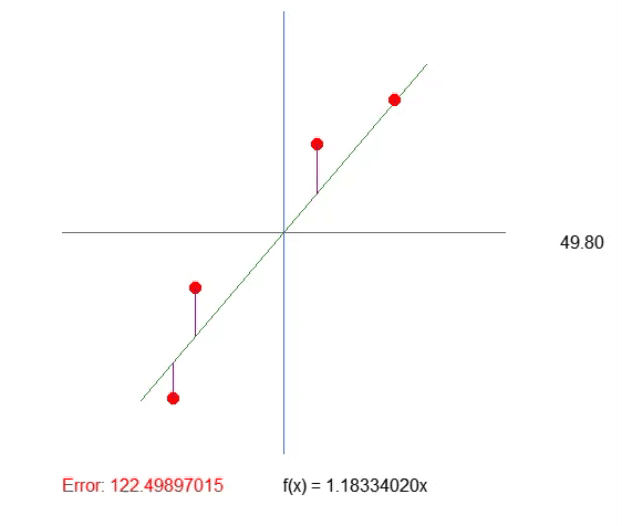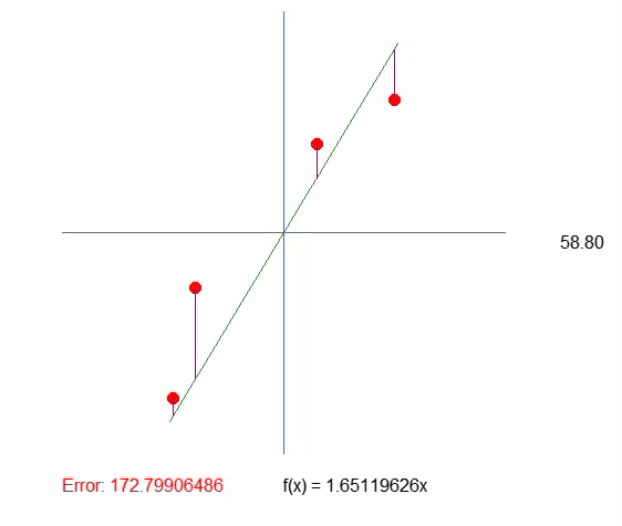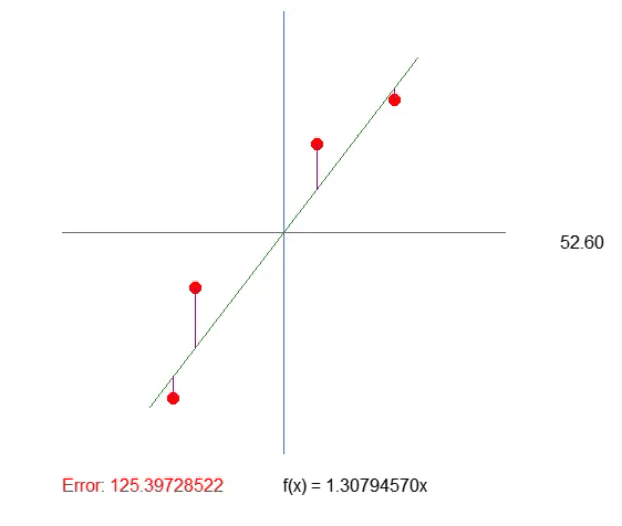
Pero fíjate en lo siguiente: En este caso, solo necesitamos observar cuatro elementos, lo cual es relativamente simple.En este caso, solo necesitamos observar cuatro elementos, lo cual es relativamente simple. Sin embargo, si tuviéramos cientos o miles de puntos en el array, ajustar los valores para que no crezcan más sería algo extremadamente complicado de hacer manualmente.Podemos usar un truco matemático para simplificar este proceso. El truco consiste en lo siguiente: Si sumamos los valores de la longitud de cada una de las líneas púrpuras, solo necesitaríamos observar un único valor.Si este valor comienza a crecer, sabremos que hemos pasado del punto óptimo del coeficiente de inclinación. Sencillo, ¿verdad? Así que modificamos una vez más el fragmento de código, como se muestra a continuación.

19. //+------------------------------------------------------------------+
20. void Func_01(void)
21. {
22.     int A[]={
23.                 -100,  150,
24.                  -80,   50,
25.                   30,  -80,
26.                  100, -120
27.             };
28. 
29.     int vx, vy;
30.     double ly, err;
31. 
32.     canvas.LineVertical(global.x, global.y - _SizeLine, global.y + _SizeLine, ColorToARGB(clrRoyalBlue, 255));
33.     canvas.LineHorizontal(global.x - _SizeLine, global.x + _SizeLine, global.y, ColorToARGB(clrRoyalBlue, 255));
34. 
35.     err = 0;
36.     for (uint c0 = 0, c1 = 0; c1 < A.Size(); c0++)
37.     {
38.         vx = A[c1++];
39.         vy = A[c1++];
40.         canvas.FillCircle(global.x + vx, global.y + vy, 5, ColorToARGB(clrRed, 255));
41.         ly = (vx * MathTan(_ToRadians(global.Angle))) - vy;
42.         canvas.LineVertical(global.x + vx, global.y + vy, global.y + (int)(ly + vy), ColorToARGB(clrPurple));
43.         err += MathAbs(ly);
44.     }
45.     canvas.TextOut(global.x - 200, global.y + _SizeLine + 20, StringFormat("Error: %.8f", err), ColorToARGB(clrRed));
46. }
47. //+------------------------------------------------------------------+

El resultado puede verse en la animación adjunta. Y notarás que ajustar las cosas es mucho más sencillo de esta manera.

Ajustando el cuadrante

Antes de sumergirnos completamente en la parte matemática de la cosa, necesitamos hacer una pequeña modificación.Aunque esta modificación no influirá directamente en lo que estamos por hacer, sí será relevante si decides aplicar lo explicado en otros programas o realizar experimentos manualmente. Muchas veces, comenzamos probando las cosas manualmente, haciendo los cálculos a mano. Hacer esto te ayuda a evitar cometer el error de confiar ciegamente en los cálculos del programa,

incluso cuando están completamente equivocados. No es raro que los programadores principiantes cometan este error, y puede costar mucho tiempo y esfuerzo. Acaban enfocándose en resolver el problema de manera incorrecta. Todo buen programador es también una persona extremadamente desconfiada de los cálculos que se están realizando. Siempre busca probar las cosas de diferentes maneras antes de concluir que puede confiar en los resultados.

Te cuento esto porque, aunque muchos lo ignoran (y yo mismo a veces lo hago), cuando creamos una representación gráfica, siempre estamos trabajando en el cuarto cuadrante del plano cartesiano. Esto afecta todo. No a los cálculos en sí, pero sí a quienes deseen hacer los mismos cálculos manualmente o en algún otro programa. Como MatLab, SCILab o incluso el buen y viejo Excel. En Excel, por ejemplo, tenemos la posibilidad de crear una representación gráfica de los valores y fórmulas que usamos aquí.

Muy bien, pero ¿qué tiene que ver todo esto con lo que estamos por hacer? Bien, estimado lector, si observas la matriz de datos que está en el programa, notarás que es un poco extraña en comparación con lo que se presenta en el gráfico. Si graficas los mismos valores en otro programa de gráficos, verás que el eje Y está invertido. ¿Pero cómo es eso? ¡No entendí. Tranquilo, observa las imágenes a continuación para entender mejor.

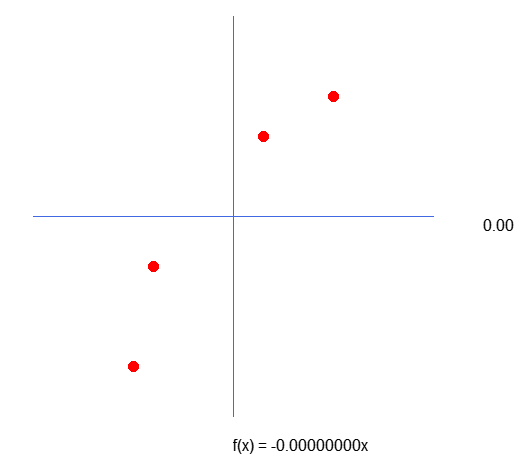
La imagen anterior se muestra cuando graficamos en MetaTrader 5. Sin embargo, al graficar los mismos valores en Excel, por ejemplo, el gráfico presentado se verá así:

Este tipo de inconsistencia puede hacer que la mayoría de los tests que alguien quiera realizar se vuelvan bastante confusos. Especialmente si se desea comprobar que los cálculos se están haciendo de forma correcta.

Ya que hemos corregido cómo presentar los datos correctamente en el tema anterior. Ahora necesitamos corregir este pequeño problema. El hecho de que el eje Y esté invertido o espejado, como prefieras llamarlo.

¿Por qué ocurre este fallo en la presentación?!?! El motivo es simple, y ya lo mencioné al comienzo del tema. La pantalla en la que graficamos los datos está en el cuarto cuadrante. Esto se debe a que su origen, es decir, el punto (0, 0), se encuentra en la esquina superior izquierda. Ahora presta atención. Aunque cambies este punto de origen al centro de la pantalla, esta transferencia es solo virtual. Esto significa que, en realidad, no cambias el punto de origen físico. Solo mueves la presentación de los cálculos a otro punto de referencia. Por esta razón, en el programa sumamos los valores del punto de la matriz a otro conjunto de puntos. Esto nos permite transferir virtualmente el origen de la esquina superior izquierda a cualquier otra ubicación en la pantalla.

Pero como habrás notado en la imagen anterior, hay un problema con la forma en que estoy haciendo esta virtualización. El eje Y está invertido o espejado. Para corregir esto necesitamos cambiar un poco algunas pequeñas cosas en el código. Algo sencillo, pero que hará que todo quede mucho más claro.

En el código, hacemos las siguientes modificaciones, que puedes ver en el siguiente fragmento:

19. //+------------------------------------------------------------------+
20. void Func_01(void)
21. {
22.     int A[]={
23.                 -100, -150,
24.                  -80,  -50,
25.                   30,   80,
26.                  100,  120
27.             };
28. 
29.     int vx, vy;
30.     double ly, err;
31. 
32.     canvas.LineVertical(global.x, global.y - _SizeLine, global.y + _SizeLine, ColorToARGB(clrRoyalBlue, 255));
33.     canvas.LineHorizontal(global.x - _SizeLine, global.x + _SizeLine, global.y, ColorToARGB(clrRoyalBlue, 255));
34. 
35.     err = 0;
36.     for (uint c0 = 0, c1 = 0; c1 < A.Size(); c0++)
37.     {
38.         vx = A[c1++];
39.         vy = A[c1++];
40.         canvas.FillCircle(global.x + vx, global.y - vy, 5, ColorToARGB(clrRed, 255));
41.         ly = vy - (vx * -MathTan(_ToRadians(global.Angle)));
42.         canvas.LineVertical(global.x + vx, global.y - vy, global.y - (int)(ly + vy), ColorToARGB(clrPurple));
43.         err += MathAbs(ly);
44.     }
45.     canvas.TextOut(global.x - 200, global.y + _SizeLine + 20, StringFormat("Error: %.8f", err), ColorToARGB(clrRed));
46. }
47. //+------------------------------------------------------------------+

Observa que el cambio es extremadamente sutil. Primero, modificamos los valores en la matriz. Luego, cambiamos el cálculo en la línea 40 para posicionar correctamente los puntos. También fue necesario modificar las líneas 41 y 42, que son donde se realizan los cálculos para conectar correctamente las líneas púrpuras con los puntos. Este tipo de correcciones, aunque sean básicamente estéticas. Brindan tranquilidad a quienes desean realizar un estudio más profundo sobre el tema que estamos tratando. Porque ahora podrán comparar los gráficos generados sin correr el riesgo de pensar que algo está mal calculado, ya sea en un programa u otro. El proceso se vuelve más simple.

Ahora la tarea es mucho más fácil de realizar. Ya que si el valor del error aumenta, significa que vamos en la dirección equivocada. Y si disminuye, estamos en la dirección correcta.

Bien, pero ahora surge una pregunta, y desde este momento comenzaremos a adentrarnos en lo que rige el tema de las redes neuronales. Ajustar la inclinación de la recta tangente, o el coeficiente de inclinación, es bastante simple cuando observamos el valor de error. Pero, ¿existe una forma de ajustarlo de manera automática? O mejor dicho, crear algún mecanismo que permita que la máquina busque el mejor valor para el coeficiente. Recordando que en este momento estamos usando solo una única variable en el sistema. Dado que la recta tangente pasa exactamente por el punto (0, 0), que es el origen de los planos cartesianos. Sin embargo, no siempre es así. Pero resolvamos primero esta cuestión más simple. Que es precisamente donde tenemos solo una única variable para ajustar.

Si entendiste el artículo anterior, habrás notado que mencioné cómo calcular la recta secante para que se convierta en la recta tangente. Bien, pero aunque eso funcione, vamos a pensar en otra hipótesis un poco más simple. Donde no necesitaremos hacer un bucle para encontrar el valor del coeficiente angular. Intentemos encontrar una fórmula para que el coeficiente se calcule de manera más rápida y sencilla.

Para hacer esto, necesitamos usar algunas artimañas matemáticas. Y para separar mejor las cosas, veremos esto en un nuevo tema.

Buscando el área más pequeña posible

Si tú, mi estimado lector, has investigado sobre el tema de la inteligencia artificial, deberías haber notado algo bastante recurrente que se menciona. Pero no confundas inteligencia artificial con redes neuronales. Aunque ambas están correlacionadas, no se abordan de la misma manera. Esto desde el punto de vista de la programación. Existen algunas pequeñas diferencias. Pero aquí, lo que pretendo hacer es crear una red neuronal que logre encontrar la ecuación que represente de la mejor manera posible los valores en la base de datos. Este tipo de cálculo lo realiza una red neuronal. La inteligencia artificial busca en la base. La red neuronal crea la base.

En este caso, ya podríamos comenzar a usar neuronas para esto. Pero, en mi opinión, todavía es un poco temprano. Podemos nosotros mismos crear un cálculo para tal cosa. Lo que ahorraría un inmenso tiempo de procesamiento.

Para poder calcular, o generar un cálculo que encuentre el coeficiente angular, utilizaremos derivadas. Podríamos hacerlo de otra forma, pero usaremos derivadas aquí. Esto es porque es el camino más rápido. Pero para entender lo que se hará, asumiré que comprendiste lo que se explicó en el tema anterior. Así que ahora pasemos a la parte matemática de la cuestión.

Para calcular el error, estamos realizando el siguiente cálculo matemático, que se muestra a continuación.

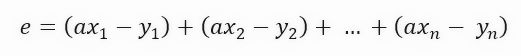
El valor de la constante < a >, que se observa en la fórmula, es precisamente el coeficiente angular de la recta. Es decir, es el valor de la tangente de la recta que se está creando. Muy bien, pero esta fórmula no es lo suficientemente compacta. Podemos simplificarla, haciendo que la fórmula sea un poco más compacta, como se muestra a continuación.

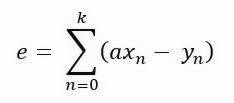
Aunque parezcan fórmulas diferentes, representan lo mismo. Solo se ha cambiado la notación a una más compacta. Al ser más compacta, hará más sencillo escribir las fórmulas que desarrollaremos a continuación. Muy bien, nota que en cada paso tenemos la suma del valor que es la longitud de la línea púrpura en el gráfico mostrado en el tema anterior. Este tipo de cosa no nos permite hacer uso de derivadas. Ya que, si intentamos derivar tal formulación, el resultado sería la constante cero. Pero lo que queremos precisamente es obtener el siguiente resultado, mostrado en la fórmula a continuación.

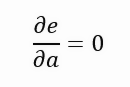
Es decir, queremos derivar el error con respecto al coeficiente angular de la recta. Y a medida que este valor tiende a igualarse a cero, el coeficiente angular se aproxima cada vez más al valor perfecto. Bien, esa es la idea. Sin embargo, difícilmente este valor encontrado será cero. Puede aproximarse a cero, y cuanto más cercano, mejor. No obstante, como mencioné hace un momento, no podemos derivar la función que genera la longitud de la línea púrpura. Pero, sin embargo, con todo y aunque, existe una manera. Y esta es convertir la línea púrpura en una figura cuadrada. Al hacer esto, ya no buscamos la longitud mínima de la línea, sino que buscamos el área más pequeña posible del cuadrado generado por cada una de las líneas. Con esto, llegamos a una nueva formulación que se muestra a continuación.

Observa que ahora, aunque no lo parezca, estamos calculando el mismo coeficiente. Solo que esta vez, usando el área del cuadrado generado por cada una de las líneas púrpuras en el gráfico. Ok, esto empezó a ponerse interesante. Si desarrollamos esta ecuación, llegaremos a la ecuación que se muestra justo abajo.

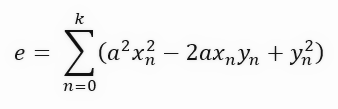
Quizá no te estés dando cuenta de lo que acabamos de hacer. Pero esta ecuación, que surgió simplemente por cambiar el cálculo de la longitud de una línea al área de un cuadrado, es de hecho una ecuación muy, pero muy interesante. ¿Puedes ver esto, estimado lector?!?! ¿Sabes decirme qué ecuación es esta?!?! ¡¿Sí?!?! ¡¿No?!?! ¡¿Tal vez?!?! ¿O quién sabe?!?!

Bueno, si no logras ver qué ecuación es esta, no te preocupes, no hace falta que te sientas mal o deprimido. Esta ecuación no es otra que la ecuación cuadrática. Así es, es la misma ecuación que genera una parábola. Y, por lo tanto, es una ecuación que nos permite crear una derivada de primer orden. Recuerda que queremos derivar con respecto al coeficiente angular. Pero antes de hacer esto, añadiré un paso extra, que normalmente no hacemos. Pero quiero mostrarte por qué la fórmula final tiene un aspecto determinado. Este paso extra consiste en agrupar los términos y separarlos adecuadamente, como se muestra a continuación.

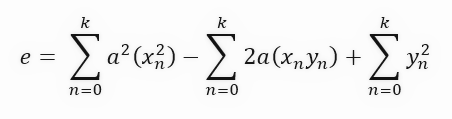
Lo que estoy haciendo aquí, estimado lector, es simplificar la ecuación para que sea más fácil de entender cuando hagamos la derivación. Este paso extra, normalmente no se hace; vamos directamente a la fórmula final, que se ve a continuación.

¡Madre de Dios! Que Dios tenga misericordia de todos nosotros. Ahora se complicó de verdad, porque no estoy entendiendo absolutamente nada. ¿Cómo es posible? ¿Qué cálculo tan loco es este? ¡¿Cómo voy a poder crear esto en términos de código?! Calma, estimado lector. Tranquilo. Normalmente, no me gusta mostrar fórmulas, precisamente para evitar que pienses que la vida es complicada. Cuando en realidad las cosas son bastante simples. Este cálculo es precisamente la derivada que necesitamos calcular. Al hacer esto, tendremos un valor aproximado del que necesitaremos para el coeficiente angular de la recta.

Muy bien, entonces pongamos esto en formato de código para ver qué obtenemos. Esto se ve en el fragmento justo a continuación.

19. //+------------------------------------------------------------------+
20. void Func_01(void)
21. {
22.     int A[]={
23.                 -100, -150,
24.                  -80,  -50,
25.                   30,   80,
26.                  100,  120
27.             };
28. 
29.     int vx, vy;
30.     double ly, err, d0, d1;
31. 
32.     canvas.LineVertical(global.x, global.y - _SizeLine, global.y + _SizeLine, ColorToARGB(clrRoyalBlue, 255));
33.     canvas.LineHorizontal(global.x - _SizeLine, global.x + _SizeLine, global.y, ColorToARGB(clrRoyalBlue, 255));
34. 
35.     err = d0 = d1 = 0;
36.     for (uint c0 = 0, c1 = 0; c1 < A.Size(); c0++)
37.     {
38.         vx = A[c1++];
39.         vy = A[c1++];
40.         d0 += (vx * vy);
41.         d1 += MathPow(vx, 2);
42.         canvas.FillCircle(global.x + vx, global.y - vy, 5, ColorToARGB(clrRed, 255));
43.         ly = vy - (vx * -MathTan(_ToRadians(global.Angle)));
44.         canvas.LineVertical(global.x + vx, global.y - vy, global.y - (int)(ly + vy), ColorToARGB(clrPurple));
45.         err += MathAbs(ly);
46.     }
47.     canvas.TextOut(global.x - 200, global.y + _SizeLine + 20, StringFormat("Error: %.8f", err), ColorToARGB(clrRed));
48.     canvas.TextOut(global.x - 200, global.y + _SizeLine + 40, StringFormat("(de/da) : %.8f", d0 / d1), ColorToARGB(clrForestGreen));
49. }
50. //+------------------------------------------------------------------+

Observa que, a diferencia de lo que podría imaginarse al ver todas esas fórmulas, hacer el cálculo en sí, es decir, en el código, es algo bastante simple y directo. En la línea 40, calculamos la suma de los puntos. Ya en la línea 41, calculamos el cuadrado de los puntos en X. Así de simple. En la línea 48, imprimimos el valor del gráfico. Ahora presta mucha atención a lo que voy a decir: Este valor que encontramos es el ideal cuando tomamos solo una única variable en la ecuación de la recta. Para que puedas entender realmente lo que estoy tratando de explicar, mira la fórmula de la ecuación de la recta. Se puede ver justo abajo.

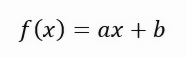
En esta ecuación, el valor de < a > es precisamente el coeficiente angular. El valor de < b > indica el punto donde tenemos la raíz de la ecuación. Para quienes no lo sepan, la raíz de una ecuación son los puntos donde la curva o recta, en este caso, toca el eje Y, cuando el valor de X es igual a cero. Entonces, dado que el valor de < b > en esta solución es igual a cero, el valor devuelto como ideal solo muestra cuál debería ser el coeficiente angular más cercano al ideal. Esto no significa que sea realmente el correcto. Ya que estamos diciendo que la raíz de la ecuación está exactamente en el origen de los planos. Es decir, X e Y iguales a cero. Y esto rara vez ocurrirá en la realidad. Tanto es así que, al ejecutar esta aplicación, obtendremos como resultado la animación que se ve justo abajo.

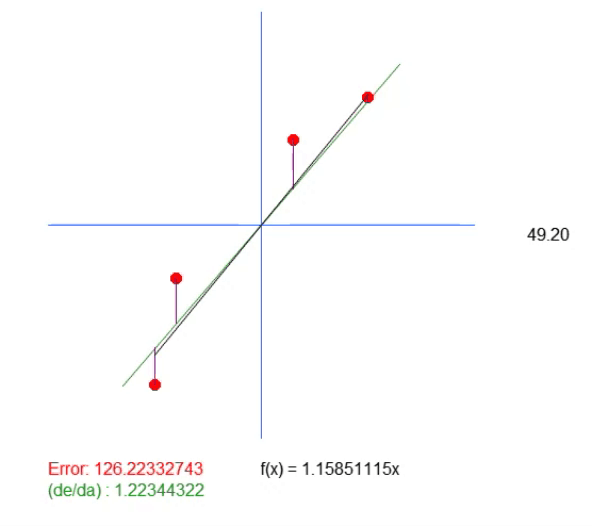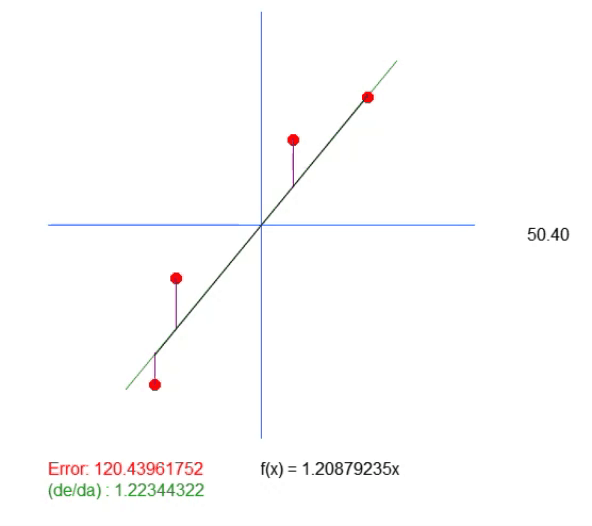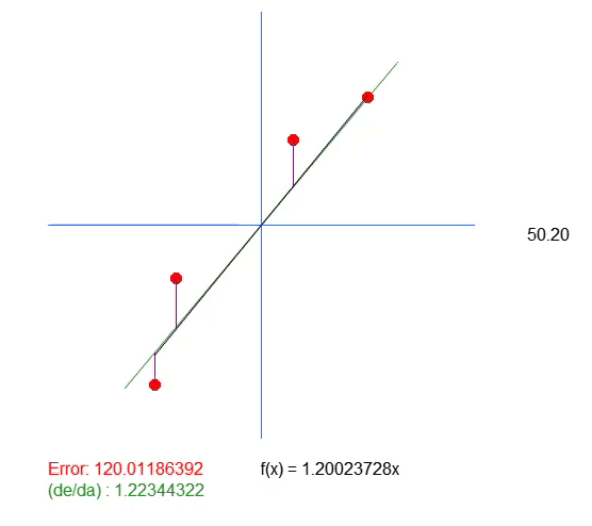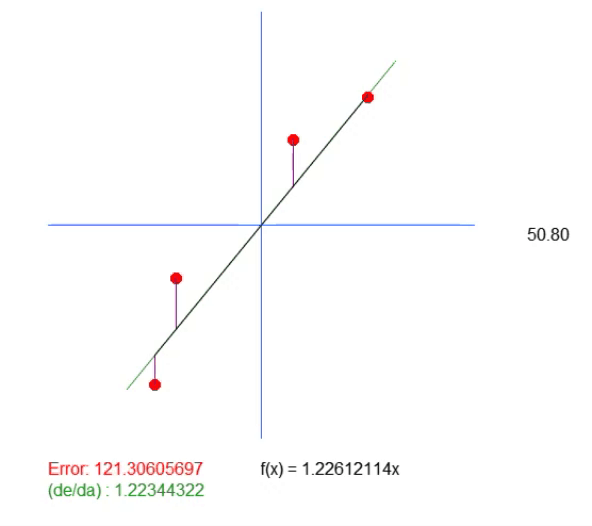
Observa que en esta animación hay una línea de fondo. Está ahí solo para mostrar dónde estaría el valor ideal calculado. Pero presta atención al valor del error y observa que el coeficiente en la ecuación es ligeramente diferente al mostrado en verde.

Este valor en verde es precisamente el valor que calculamos con base en la ecuación desarrollada. Puedes notar claramente que solo calcular el valor del coeficiente angular no es suficiente. Necesitamos que la ecuación de la recta se cree, y para eso, además del valor de < a >, también necesitamos el valor de < b >. Esto para que podamos tener una solución más general y no quedemos atados al punto (0, 0).

Este punto (0, 0), que en realidad no forma parte de la base de datos, genera una influencia implícita en los resultados de los cálculos del coeficiente angular. Sin embargo, para eliminar este punto adecuadamente, necesitamos modificar algunas cosas en la aplicación. De manera que tú, estimado lector, puedas salir de este punto de origen, que es precisamente el (0, 0).Desplazando la raíz de la función de la recta

Como necesitamos preparar la aplicación para lo que haremos a continuación, y que será visto en el próximo artículo, crearemos un mecanismo bastante curioso en el resto de este artículo. Luego, en el próximo, podremos centrarnos en la parte matemática.

Añadir este mecanismo requiere cambiar muy poco en el código. Sin embargo, los efectos serán bastante grandes, ya que nos permitirá buscar una ecuación de la recta donde obtengamos el área más pequeña posible en cualquier situación. Creando así un mecanismo genérico para encontrar el valor de las constantes más adecuadas posibles. Esto es para que la regresión lineal que se representará en el gráfico pueda reflejar de manera más adecuada la base de datos.

Hacer estos cambios es algo muy simple. Todo lo que necesitamos hacer es desplazar la raíz de la función de la recta. Parece algo complicado cuando se escuchan esas palabras, pero cuando lo implementamos en el código, se vuelve bastante simple, como se puede ver a continuación.

001. //+------------------------------------------------------------------+
002. #property copyright "Daniel Jose"
003. #property indicator_chart_window
004. #property indicator_plots 0
005. //+------------------------------------------------------------------+
006. #include <Canvas\Canvas.mqh>
007. //+------------------------------------------------------------------+
008. #define _ToRadians(A) (A * (M_PI / 180.0))
009. #define _SizeLine 200
010. //+------------------------------------------------------------------+
011. CCanvas canvas;
012. //+------------------------------------------------------------------+
013. struct st_00
014. {
015.     int     x,
016.             y;
017.     double  Angle,
018.             Const_B;
019. }global;
020. //+------------------------------------------------------------------+
021. void PlotText(const uchar line, const string sz0)
022. {
023.     uint w, h;
024. 
025.     TextGetSize(sz0, w, h);
026.     canvas.TextOut(global.x - (w / 2), global.y + _SizeLine + (line * h) + 5, sz0, ColorToARGB(clrBlack));   
027. }
028. //+------------------------------------------------------------------+
029. void Func_01(void)
030. {
031.     int A[]={
032.                 -100, -150,
033.                  -80,  -50,
034.                   30,   80,
035.                  100,  120
036.             };
037. 
038.     int vx, vy;
039.     double ly, err;
040.     string s0 = "";
041. 
042.     canvas.LineVertical(global.x, global.y - _SizeLine, global.y + _SizeLine, ColorToARGB(clrRoyalBlue, 255));
043.     canvas.LineHorizontal(global.x - _SizeLine, global.x + _SizeLine, global.y, ColorToARGB(clrRoyalBlue, 255));
044. 
045.     err = 0;
046.     for (uint c0 = 0, c1 = 0; c1 < A.Size(); c0++)
047.     {
048.         vx = A[c1++];
049.         vy = A[c1++];
050.         canvas.FillCircle(global.x + vx, global.y - vy, 5, ColorToARGB(clrRed, 255));
051.         ly = vy - (vx * -MathTan(_ToRadians(global.Angle))) - global.Const_B;
052.         s0 += StringFormat("%.4f || ", MathAbs(ly));
053.         canvas.LineVertical(global.x + vx, global.y - vy, global.y + (int)(ly - vy), ColorToARGB(clrPurple));
054.         err += MathPow(ly, 2);
055.     }
056.     PlotText(3, StringFormat("Error: %.8f", err));
057.     PlotText(4, s0);
058. }
059. //+------------------------------------------------------------------+
060. void NewAngle(const char direct, const char updow, const double step = 0.1)
061. {
062.     canvas.Erase(ColorToARGB(clrWhite, 255));
063. 
064.     global.Angle = (MathAbs(global.Angle + (step * direct)) < 90 ? global.Angle + (step * direct) : global.Angle);
065.     global.Const_B += (step * updow);  
066.     PlotText(1, StringFormat("Angle in graus => %.2f", MathAbs(global.Angle)));
067.     PlotText(2, StringFormat("f(x) = %.4fx %c %.4f", -MathTan(_ToRadians(global.Angle)), (global.Const_B < 0 ? '-' : '+'), MathAbs(global.Const_B)));
068.     canvas.LineAA(
069.                 global.x - (int)(_SizeLine * cos(_ToRadians(global.Angle))), 
070.                 (global.y - (int)global.Const_B) - (int)(_SizeLine * sin(_ToRadians(global.Angle))), 
071.                 global.x + (int)(_SizeLine * cos(_ToRadians(global.Angle))), 
072.                 (global.y - (int)global.Const_B) + (int)(_SizeLine * sin(_ToRadians(global.Angle))), 
073.                 ColorToARGB(clrForestGreen)
074.             );
075.        
076.     Func_01();
077. 
078.     canvas.Update(true);
079. }
080. //+------------------------------------------------------------------+
081. int OnInit()
082. {    
083.     global.Angle = 0;
084.     global.x = (int)ChartGetInteger(0, CHART_WIDTH_IN_PIXELS, 0);
085.     global.y = (int)ChartGetInteger(0, CHART_HEIGHT_IN_PIXELS, 0);
086. 
087.     canvas.CreateBitmapLabel("BL", 0, 0, global.x, global.y, COLOR_FORMAT_ARGB_NORMALIZE);
088.     global.x /= 2;
089.     global.y /= 2;
090.         
091.     NewAngle(0, 0);
092. 
093.     canvas.Update(true);
094.     
095.     return INIT_SUCCEEDED;
096. }
097. //+------------------------------------------------------------------+
098. int OnCalculate(const int rates_total, const int prev_calculated, const int begin, const double &price[])
099. {
100.     return rates_total;
101. }
102. //+------------------------------------------------------------------+
103. void OnChartEvent(const int id, const long &lparam, const double &dparam, const string &sparam)
104. {
105.     switch (id)
106.     {
107.         case CHARTEVENT_KEYDOWN:
108.             if (TerminalInfoInteger(TERMINAL_KEYSTATE_LEFT))
109.                 NewAngle(-1, 0);
110.             if (TerminalInfoInteger(TERMINAL_KEYSTATE_RIGHT))
111.                 NewAngle(1, 0);
112.             if (TerminalInfoInteger(TERMINAL_KEYSTATE_UP))
113.                 NewAngle(0, 1);
114.             if (TerminalInfoInteger(TERMINAL_KEYSTATE_DOWN))
115.                 NewAngle(0, -1);
116.             break;
117.     }
118. }
119. //+------------------------------------------------------------------+
120. void OnDeinit(const int reason)
121. {
122.     canvas.Destroy();
123. }
124. //+------------------------------------------------------------------+

El resultado se muestra en la animación de abajo:

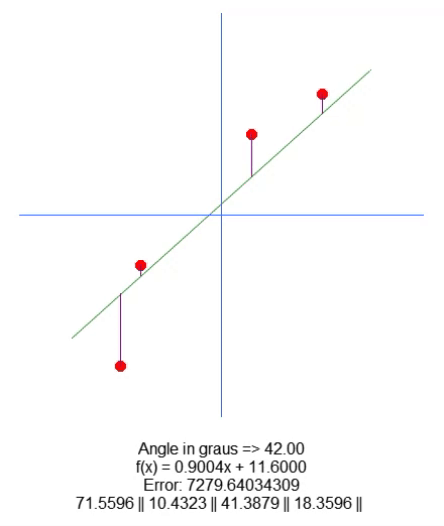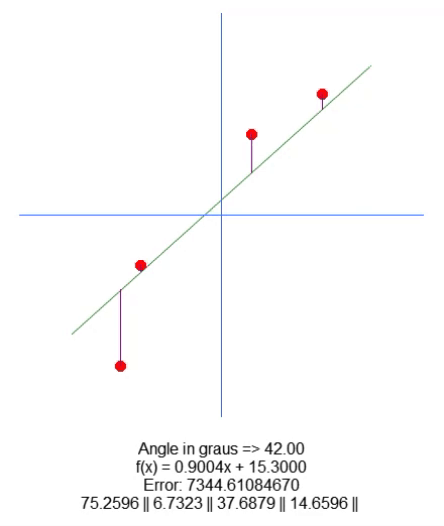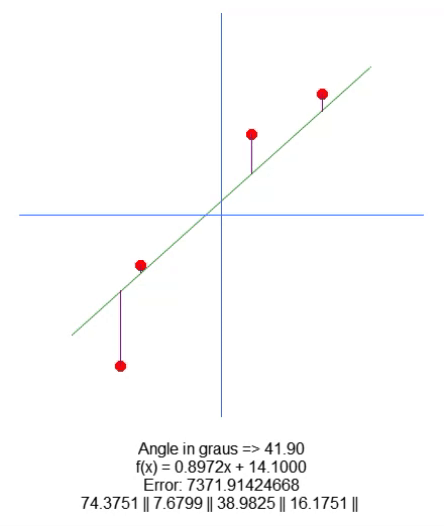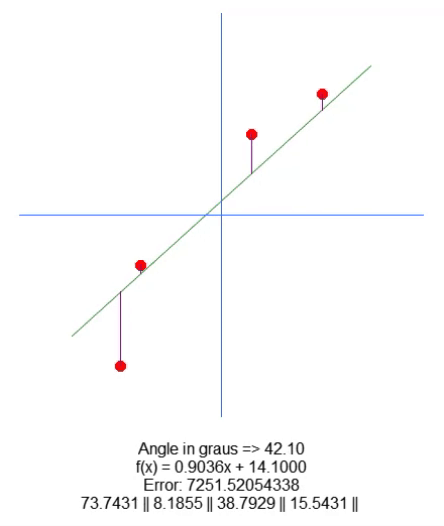
Básicamente, todo lo que fue necesario para desplazar la raíz fue agregar la variable en la línea 18. Y usando las flechas hacia arriba y hacia abajo, cambiamos el valor de esta variable en la línea 65. Todo lo demás es bastante simple. Solo necesitamos corregir el valor de la longitud de la línea púrpura, basado en el valor de esta nueva variable presente en el código. Tengo plena confianza de que no será necesario explicar cómo se está haciendo esto, ya que es algo muy sencillo.

Consideraciones finales

En este artículo, mostré cómo muchas veces las fórmulas matemáticas parecen mucho más complicadas cuando las vemos, que cuando las implementamos en código. Mucha gente piensa que hacer este tipo de cosas es difícil. Pero aquí quedó demostrado que es mucho más simple de lo que parece. Sin embargo, no hemos hecho todo el trabajo. Solo hemos realizado una parte de él. Ahora necesitamos encontrar una forma de crear la ecuación de la recta de manera más adecuada. Y para ello, utilizaremos el último código visto en este artículo. A diferencia de lo que tú, estimado lector, podrías haber imaginado al comienzo de este tema, encontrar la función de la recta a través de un bucle no es algo tan simple como parecía. Y esto es porque solo agregamos una variable más a buscar. Solo piensa en el trabajo que tomaría encontrar la ecuación si tuviéramos un millón de variables. Hacerlo mediante fuerza bruta sería completamente impracticable. Pero usando la matemática de forma adecuada, encontrar la ecuación es algo mucho más sencillo.

Un último detalle: antes de ver el próximo artículo, usa el código visto al final, que genera la última animación, para intentar encontrar la ecuación. Verás que es una tarea bastante desafiante. Así que nos vemos en el próximo artículo.