神经网络实践：最小二乘法

概述

大家好，欢迎阅读关于神经网络的新文章。

在上一篇文章神经网络实践：割线中，我们开始讨论实践中的应用数学。不过，这只是对这个主题的一个简短而快速的介绍。我们已经看到，要使用的基本数学运算是三角函数。而且，与许多人的想法相反，这不是一个正切函数，而是一个正割函数。虽然一开始可能会感到相当困惑，但您很快就会发现，一切都比想象的要简单得多。与许多人在数学环境中只会制造很多混乱不同，这里的一切都是完全自然发展的。

奇怪和不可理解的东西

然而，有一个小缺陷，我无法理解。这没有意义，至少对我来说是这样。因为这可能对任何试图做同样事情的人都有用，所以我保持原样。我们将在这里解决这个问题，因为如果我们不解决它，我们将在数学方面遇到许多其他问题。

上面提到文章的代码如下：

19. //+------------------------------------------------------------------+
20. void Func_01(void)
21. {
22.     int A[] {
23.                 -100,  150,
24.                  -80,   50,
25.                   30,  -80,
26.                  100, -120
27.             };
28. 
29.     canvas.LineVertical(global.x, global.y - _SizeLine, global.y + _SizeLine, ColorToARGB(clrRoyalBlue, 255));
30.     canvas.LineHorizontal(global.x - _SizeLine, global.x + _SizeLine, global.y, ColorToARGB(clrRoyalBlue, 255));
31. 
32.     for (uint c0 = 0, c1 = 0; c1 < A.Size(); c0++)
33.         canvas.FillCircle(global.x + A[c1++], global.y + A[c1++], 5, ColorToARGB(clrRed, 255));
34. }
35. //+------------------------------------------------------------------+

这段代码构建了小圆圈，其位置在第 22 行所示的数组 A 中。还没什么特别的，这正是它的本意。然而，在绘制这些点时，我们会得到以下结果：

这些点放错地方了。它们相对于 X 和 Y 轴是颠倒的。为什么呢？说实话，我不知道该如何解释。出现这种情况是因为在第 33 行代码中，我们获取了数组中的值，然后添加了位置。这样，编译器就会明白我们指向的是数组中的下一个值。事情就是这样发生的，如果情况不同，就会产生未经授权的内存访问错误。这将被视为范围错误，应用程序将终止。

但是，在 global.x 中，添加的是奇数索引值，而不是偶数索引值。因此，global.y 中添加的值是偶数索引，而这些值本应该是奇数索引。

我是在开始写这篇文章的数学计算时才意识到这一点的，因为计算结果与应用程序提供的结果不符。于是我决定找出原因。您可以通过稍微修改代码来完成同样的操作，如下所示。

19. //+------------------------------------------------------------------+
20. void Func_01(void)
21. {
22.     int A[]={
23.                 -100,  150,
24.                  -80,   50,
25.                   30,  -80,
26.                  100, -120
27.             };
28. 
29.     int vx, vy;
30.     string s = "";
31. 
32.     canvas.LineVertical(global.x, global.y - _SizeLine, global.y + _SizeLine, ColorToARGB(clrRoyalBlue, 255));
33.     canvas.LineHorizontal(global.x - _SizeLine, global.x + _SizeLine, global.y, ColorToARGB(clrRoyalBlue, 255));
34. 
35.     for (uint c0 = 0, c1 = 0; c1 < A.Size(); c0++)
36.     {
37.         canvas.FillCircle(global.x + (vx = A[c1++]), global.y + (vy = A[c1++]), 5, ColorToARGB(clrRed, 255));
38.         s += StringFormat("[ %d <> %d ] ", vx, vy);
39.     }
40.     canvas.TextOut(global.x - 200, global.y + _SizeLine + 70, s, ColorToARGB(clrBlack));
41. }
42. //+------------------------------------------------------------------+

这种修改可以让我们看到正在发生的事情。结果显示如下:

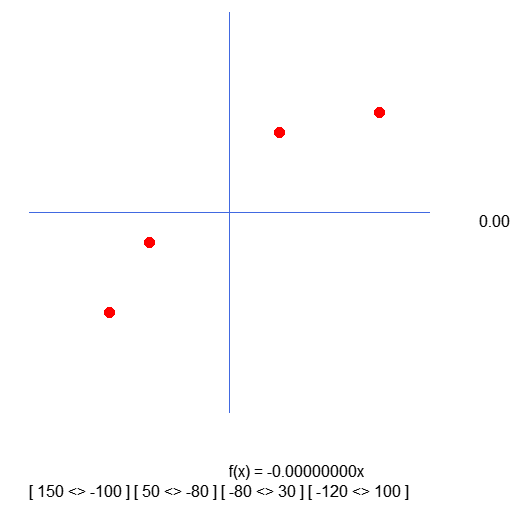
注意括号内的数值。它们是第 37 行获取的结果。也就是说，我们修正了用于在图形上定位圆圈的值。不过，请注意，与数组中声明的内容相比，它们是颠倒的。而这是很奇怪的。因此，我们需要按如下所示修改代码。

19. //+------------------------------------------------------------------+
20. void Func_01(void)
21. {
22.     int A[]={
23.                 -100,  150,
24.                  -80,   50,
25.                   30,  -80,
26.                  100, -120
27.             };
28. 
29.     int vx, vy;
30.     string s = "";
31. 
32.     canvas.LineVertical(global.x, global.y - _SizeLine, global.y + _SizeLine, ColorToARGB(clrRoyalBlue, 255));
33.     canvas.LineHorizontal(global.x - _SizeLine, global.x + _SizeLine, global.y, ColorToARGB(clrRoyalBlue, 255));
34. 
35.     for (uint c0 = 0, c1 = 0; c1 < A.Size(); c0++)
36.     {
37.         vx = A[c1++];
38.         vy = A[c1++];
39.         canvas.FillCircle(global.x + vx, global.y + vy, 5, ColorToARGB(clrRed, 255));
40.         s += StringFormat("[ %d <> %d ] ", vx, vy);
41.     }
42.     canvas.TextOut(global.x - 200, global.y + _SizeLine + 70, s, ColorToARGB(clrBlack));
43. }
44. //+------------------------------------------------------------------+

现在，当我们使用这段新代码时，结果将如下所示：

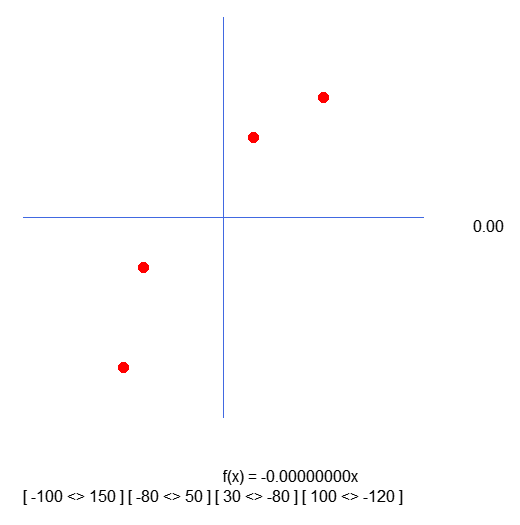
可以看到，方括号内的值与数组中声明的值一致了。我很抱歉之前没有注意到这个错误。但是，让我们以此警示所有那些想按自己的方式行事的人。因为我不明白为什么索引会颠倒，所以也不知道该如何解释。在完成了这项必要的修正工作后，我们就可以继续开展下一步工作了。

准备做数学和更多的数学

如果只是深入研究代码，我们从这里开始做的事情可能会让人很困惑。我想让你明白我们到底要做什么，为什么要这么做，所以我会心平气和地向你解释一切。因此，我建议大家仔细阅读，按原样修改代码，试着了解发生了什么。只有当你明白了一切，才能继续下一步。不要试图跳过某些步骤，因为你可能还完全没有明白。

我们要做的第一件事就是稍微修改一下代码。

19. //+------------------------------------------------------------------+
20. void Func_01(void)
21. {
22.     int A[]={
23.                 -100,  150,
24.                  -80,   50,
25.                   30,  -80,
26.                  100, -120
27.             };
28. 
29.     int vx, vy;
30.     string s = "";
31.     double ly;
32. 
33.     canvas.LineVertical(global.x, global.y - _SizeLine, global.y + _SizeLine, ColorToARGB(clrRoyalBlue, 255));
34.     canvas.LineHorizontal(global.x - _SizeLine, global.x + _SizeLine, global.y, ColorToARGB(clrRoyalBlue, 255));
35. 
36.     for (uint c0 = 0, c1 = 0; c1 < A.Size(); c0++)
37.     {
38.         vx = A[c1++];
39.         vy = A[c1++];
40.         canvas.FillCircle(global.x + vx, global.y + vy, 5, ColorToARGB(clrRed, 255));
41.         ly = (vx * MathTan(_ToRadians(global.Angle))) - vy;
42.         canvas.LineVertical(global.x + vx, global.y + vy, global.y + (int)(ly + vy), ColorToARGB(clrPurple));
43.         s += StringFormat("sy%d = %.4f  | ", c0, ly);
44.     }
45.     canvas.TextOut(global.x - 200, global.y + _SizeLine + 50, s, ColorToARGB(clrBlack));
46. }
47. //+------------------------------------------------------------------+
48. void NewAngle(const char direct, const double step = 0.2)
49. {
50.     canvas.Erase(ColorToARGB(clrWhite, 255));
51. 
52.     global.Angle = (MathAbs(global.Angle + (step * direct)) < 90 ? global.Angle + (step * direct) : global.Angle);
53.     canvas.TextOut(global.x + _SizeLine + 50, global.y, StringFormat("%.2f", MathAbs(global.Angle)), ColorToARGB(clrBlack));
54.     canvas.TextOut(global.x, global.y + _SizeLine + 20, StringFormat("f(x) = %.8fx", -MathTan(_ToRadians(global.Angle))), ColorToARGB(clrBlack));
55.     canvas.Line(
56.                 global.x - (int)(_SizeLine * cos(_ToRadians(global.Angle))), 
57.                 global.y - (int)(_SizeLine * sin(_ToRadians(global.Angle))), 
58.                 global.x + (int)(_SizeLine * cos(_ToRadians(global.Angle))), 
59.                 global.y + (int)(_SizeLine * sin(_ToRadians(global.Angle))), 
60.                 ColorToARGB(clrForestGreen)
61.             );
62.        
63.     Func_01();
64. 
65.     canvas.Update(true);
66. }
67. //+------------------------------------------------------------------+

虽然这不是最理想的方法，但下面动画中显示的结果正是我们想要的可视化效果：

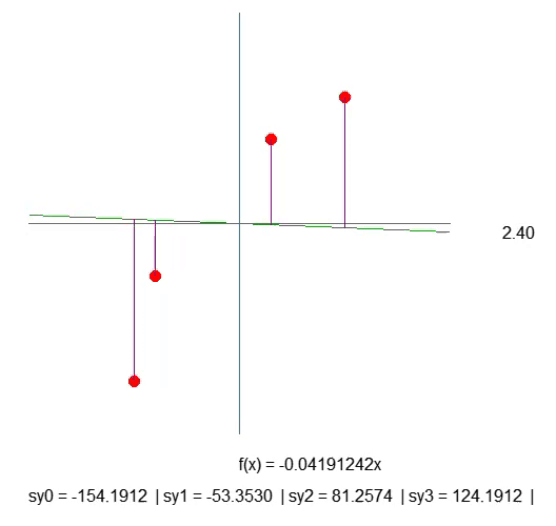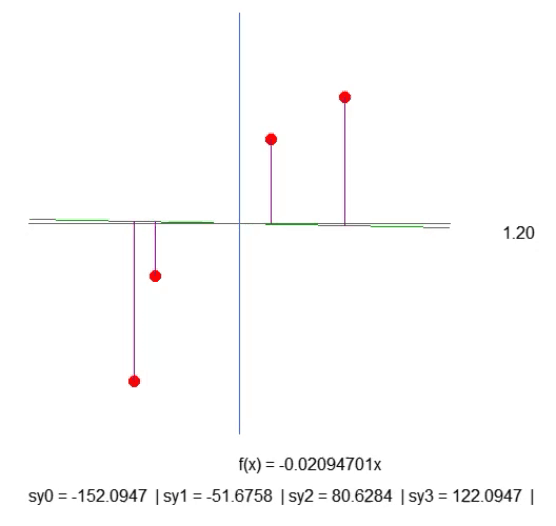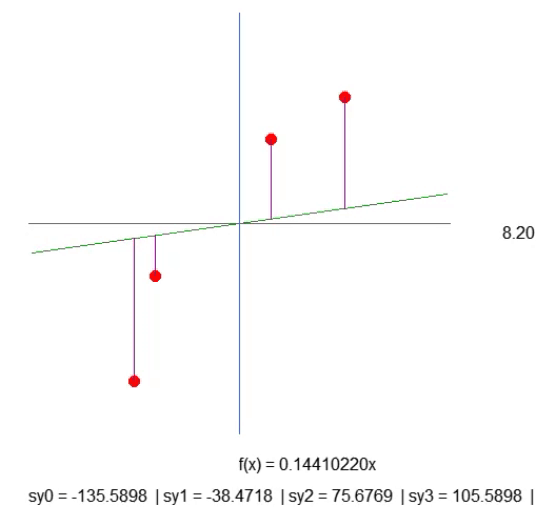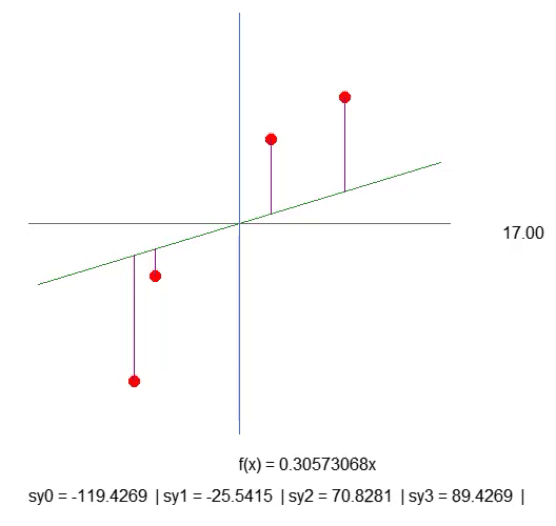
我们只是创建一条紫色的线，它表示了线和点之间的距离。请注意这一点。线的长度由代码段第 41 行的代码决定。虽然计算结果不尽如人意，但还是能用的。所以我们不要着急，因为稍后我们将需要修改这一计算方法。在第 43 行中，我们创建了一个文本字符串，通过它我们可以找出所给紫色线的长度。看看动画，你会发现出现了负值的长度，这是不合理的。但是现在担心还为时过早。首先，我希望你们了解我们工作的本质。

现在，亲爱的读者，我希望你稍微思考一下。直线函数是根据斜率系数计算出来的。这个系数可以从角度获得，我们可以通过点击向右或向左的箭头来改变角度。斜率的变化率由第 52 行中的 "step" 值确定。

然后看看每条紫色线的长度。只要稍有耐心，我们就能使直线的斜率尽可能陡峭，从而使每条紫色线的长度不再增加（可以减少，但不应增加）。当长度都不增长时，我们就找到了理想的斜率。

但请注意以下几点：在这种情况下，我们只需考虑四个要素，非常简单。但是，如果数组中有成百上千个点，要手动调整数值使其不增加就会非常困难。我们可以用数学技巧来简化这一过程。技巧就在于此：如果我们把每条紫色线的长度加起来，我们只需要观察一个值，如果它开始上升，我们就知道我们已经通过了最佳斜率点。很简单，不是吗？就这样，让我们对代码进行如下修改。

19. //+------------------------------------------------------------------+
20. void Func_01(void)
21. {
22.     int A[]={
23.                 -100,  150,
24.                  -80,   50,
25.                   30,  -80,
26.                  100, -120
27.             };
28. 
29.     int vx, vy;
30.     double ly, err;
31. 
32.     canvas.LineVertical(global.x, global.y - _SizeLine, global.y + _SizeLine, ColorToARGB(clrRoyalBlue, 255));
33.     canvas.LineHorizontal(global.x - _SizeLine, global.x + _SizeLine, global.y, ColorToARGB(clrRoyalBlue, 255));
34. 
35.     err = 0;
36.     for (uint c0 = 0, c1 = 0; c1 < A.Size(); c0++)
37.     {
38.         vx = A[c1++];
39.         vy = A[c1++];
40.         canvas.FillCircle(global.x + vx, global.y + vy, 5, ColorToARGB(clrRed, 255));
41.         ly = (vx * MathTan(_ToRadians(global.Angle))) - vy;
42.         canvas.LineVertical(global.x + vx, global.y + vy, global.y + (int)(ly + vy), ColorToARGB(clrPurple));
43.         err += MathAbs(ly);
44.     }
45.     canvas.TextOut(global.x - 200, global.y + _SizeLine + 20, StringFormat("Error: %.8f", err), ColorToARGB(clrRed));
46. }
47. //+------------------------------------------------------------------+

结果如下图所示。这样调整数值就容易多了。

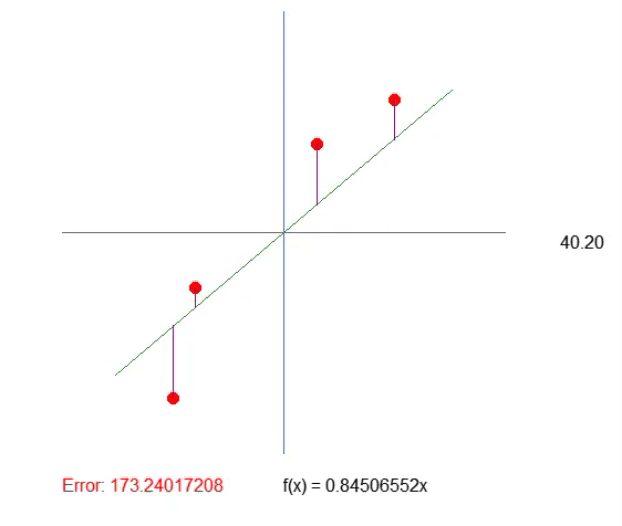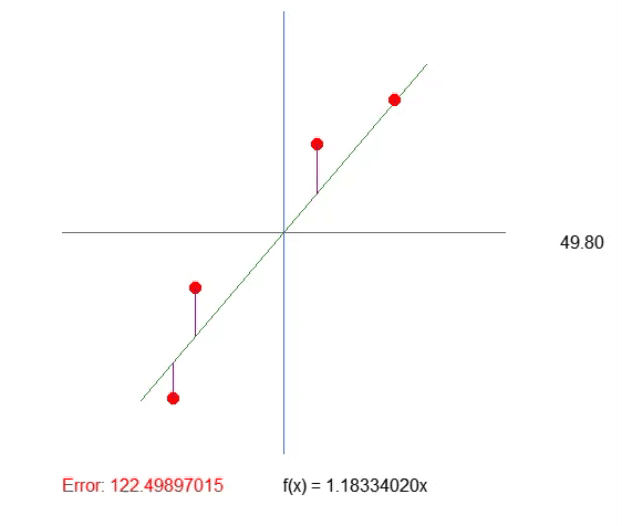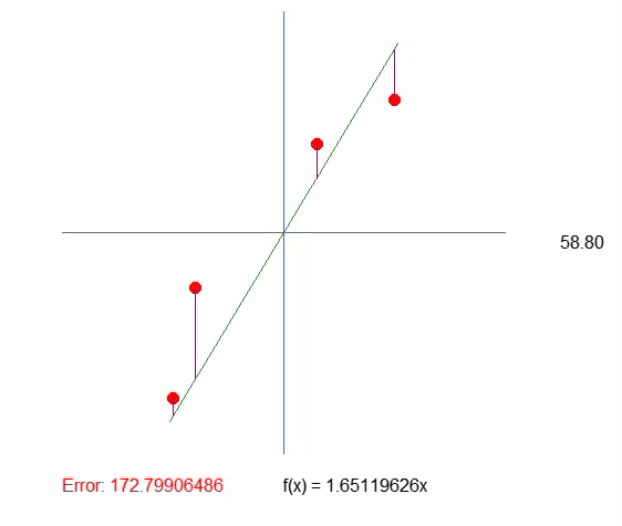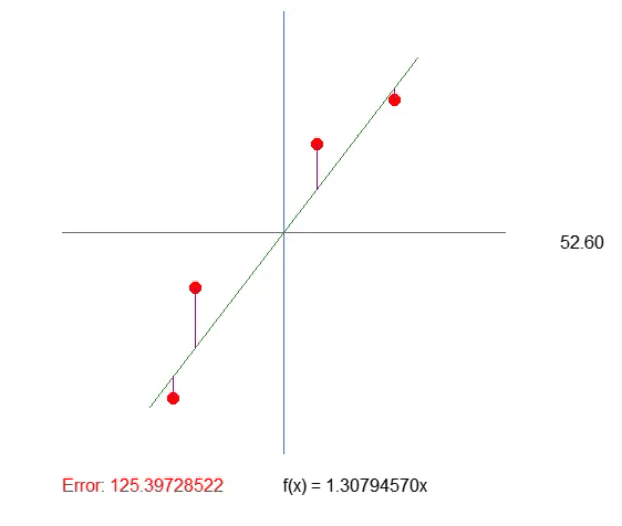
调整象限

在完全深入研究数学问题之前，我们需要做一个小小的修改。虽然它不会直接影响我们要做的事情，但如果我们决定应用其他程序中解释的内容，或者在手动实验时，它将是相关的。通常情况下，我们一开始都是手动尝试，用同样的方法进行计算。以下内容将帮助您避免盲目依赖程序计算时的错误。

即使他们完全错了,初学者程序员经常犯这个错误，这可能会花费大量的时间和精力。因此，他们专注于以错误的方式解决问题。每一个优秀的程序员也是一个对正在进行的计算非常怀疑的人。程序员在最终相信结果之前，总是试图以多种不同的方式测试不同的东西。

我告诉你这一点是因为，尽管许多人忽略了这一点，但当我们创建图形图像时，我们总是在笛卡尔平面的第四象限工作。这影响了一切。不是计算本身，而是那些想手动或在另一个程序中执行相同计算的人。例如，MatLab、SCILab，甚至是老式的 Excel。例如，在 Excel 中，我们可以创建我们在这里使用的值和公式的图形表示。

这很好，但这一切与我们要做的事情有什么关系？好吧，亲爱的读者，如果你看看程序中的数据矩阵，你会发现它与图上显示的相比有点奇怪。如果我们在另一个绘图程序中绘制相同的值，我们会看到 Y 轴是颠倒的。但我还是不明白这是怎么发生的。请慢慢看下面的图片，以便更好地理解。

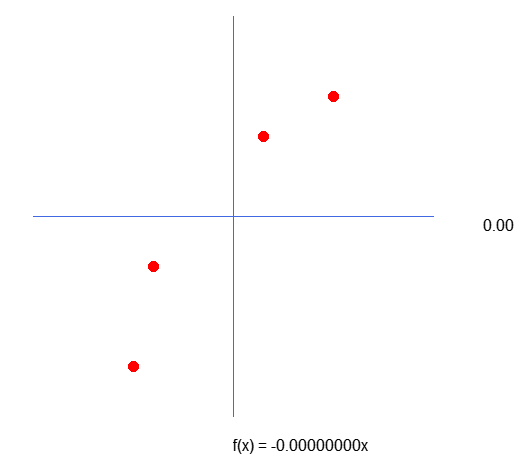
在 MetaTrader 5 中绘制图表时可以看到上图。但是，当在 Excel 中绘制相同的值时，图形将如下所示：

这种不匹配可能导致需要执行的大多数测试完全无法理解，特别是如果您需要检查计算是否正确执行。

在前面的主题中，我们已经弄清楚了如何正确地呈现数据。现在，我们需要解决这个问题。问题是 Y 轴被反转（或镜像）。

为什么会发生这种代表性的失败？！原因很简单，我们在主题一开始就提到了。我们绘制数据的屏幕位于第四象限。这是因为原点，即点（0，0）位于左上角。现在请注意以下几点。即使我们将参考点更改为屏幕的中心，这种转换也只是虚拟的。这意味着我们不会改变物理参考点，我们只是将计算的表示移到了一个不同的起点。因此，在程序中，我们将矩阵中一个点的值添加到另一组点上。这允许我们将虚拟原点从左上角移动到屏幕上的任何其他位置。

但您可能已经注意到，在上图中，我们如何实现这种虚拟化存在问题。Y 轴被倒置或镜像。要解决这个问题，我们需要修改代码中的一些内容。这很简单，但它会让一切变得更加清晰。

在代码中，我们将做出以下更改：

19. //+------------------------------------------------------------------+
20. void Func_01(void)
21. {
22.     int A[]={
23.                 -100, -150,
24.                  -80,  -50,
25.                   30,   80,
26.                  100,  120
27.             };
28. 
29.     int vx, vy;
30.     double ly, err;
31. 
32.     canvas.LineVertical(global.x, global.y - _SizeLine, global.y + _SizeLine, ColorToARGB(clrRoyalBlue, 255));
33.     canvas.LineHorizontal(global.x - _SizeLine, global.x + _SizeLine, global.y, ColorToARGB(clrRoyalBlue, 255));
34. 
35.     err = 0;
36.     for (uint c0 = 0, c1 = 0; c1 < A.Size(); c0++)
37.     {
38.         vx = A[c1++];
39.         vy = A[c1++];
40.         canvas.FillCircle(global.x + vx, global.y - vy, 5, ColorToARGB(clrRed, 255));
41.         ly = vy - (vx * -MathTan(_ToRadians(global.Angle)));
42.         canvas.LineVertical(global.x + vx, global.y - vy, global.y - (int)(ly + vy), ColorToARGB(clrPurple));
43.         err += MathAbs(ly);
44.     }
45.     canvas.TextOut(global.x - 200, global.y + _SizeLine + 20, StringFormat("Error: %.8f", err), ColorToARGB(clrRed));
46. }
47. //+------------------------------------------------------------------+

请注意，这些变化非常微妙。首先，我们改变矩阵中的数值。然后，我们更改第 40 行的计算，以便正确定位这些点。还需要修改第 41 和 42 行，这两行进行计算，以正确连接紫色线和点。这种类型的修复，即使主要是美学性质的，也给那些想对这个问题进行更深入研究的人带来了信心。现在，我们可以比较生成的图形，而不必认为某个程序中的计算结果很差。这个过程变得更加容易。

就这样，现在执行任务也容易得多。因为如果误差值增大，就意味着我们前进的方向是错误的。如果减少，那么我们的方向就是正确的。

但现在又出现了另一个问题，从这一点上，我们将开始深入研究神经网络的驱动因素。如果查看误差值，调整切线的斜率或斜率因子相当简单。但有没有自动设置的方法？是否有可能建立一种机制，让机器搜索系数的最佳值。重要的是要记住，我们现在在系统中只使用一个变量，因为切线正好穿过笛卡尔平面的起点（0,0）。但情况并非总是如此。不过，让我们先来解决这个比较简单的问题。这种情况下，我们只需要调整一个变量。

如果你阅读了上一篇文章，你就会知道我提到了如何计算割线，使其成为切线。即使这有效，让我们考虑另一个更简单的假设，在这个假设中，我们不必经历那么多麻烦来找到斜率的值。让我们试着找到一个公式，以便更快、更容易地计算系数。

为此，我们需要运用一些数学技巧。为了使演示更加清晰，我们将在一个新的主题中探讨这一点。

寻找尽可能小的区域

如果你曾经尝试过研究人工智能的话题，你可能会注意到有一些东西一直在出现。但不要把人工智能与神经网络混为一谈。虽然这两个概念相互关联，但需要以不同的方式加以处理。这是从编程的角度来看的。有一些小的差异，但在这里我打算创建一个神经网络，它可以找到一个最能代表数据库中值的方程。这类计算由神经网络完成。人工智能在基础上进行搜索。而神经网络创建此基础。

在这种情况下，我们可以开始使用神经元来实现这一点，但在我看来，这还为时过早。我们可以自己为此创建计算，这将节省大量的处理时间。

为了计算或创建计算来找到斜率，我们将使用导数。我们可以用另一种方法来实现，但这里我们将使用导数，这是最快的方法。我假设你已经理解了上一个主题中解释的所有内容，这样我们就可以继续了。现在让我们转到问题的数学部分。

为了找到误差，我们将执行以下数学计算。

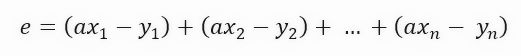
公式中常数 <a> 的值正是直线的角系数，即创建的切线的值。但这个公式不够紧凑。我们可以通过使公式更紧凑来简化它，如下所示。

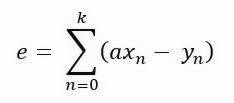
虽然它们看起来像不同的公式，但它们代表的是同一件事，只是符号被修改得更简洁。由于它更紧凑，编写我们将在下面开发的公式将更容易。请注意，在每一步中，我们都有一个值的总和，即上一主题所示图表中紫色线的长度。这些因素阻碍了我们使用导数，因为如果我们试图推导出这样的公式，我们最终会得到一个零常数。我们希望得到下式所示的结果。

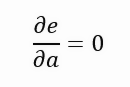
因此，我们希望输出相对于直线斜率的误差，当该值趋近于零时，斜率会越来越接近理想值。这就是思路，但这一数值很难为零。它可以接近零，而且越接近零越好，但正如我所说，我们无法推导出一个决定紫色线长度的函数。不过，还是有办法的。我们需要将紫色线转换为正方形图形，在这种情况下，我们不是在寻找线的最小长度，而是寻找每条线形成的正方形的最小可能面积。这样，我们就得到了下面的新表示。

请注意，现在（虽然看起来不像）我们计算的是相同的系数，只是这次使用的是图形上每条紫色线所构成的正方形的面积。事情变得越来越有趣了。如果我们进一步发展这个公式，就会得到下图所示的结果。

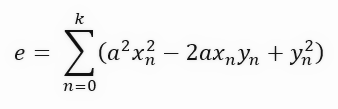
你可能不明白我们刚才做了什么。这个公式的出现，仅仅是将直线长度的计算方法改为正方形面积的计算方法，实际上是一个非常有趣的公式。你看到了吗？你能告诉我这个等式是什么吗？

如果你不知道这个公式是什么，不用担心。这只不过是一个二次方程式。这是生成抛物线的同一个方程，因此它允许我们创建一阶导数。我们要得到斜率的导数。但在此之前，我将添加一个我们通常不会采取的步骤。我想告诉你为什么最终的公式是这样的。这一额外步骤涉及对术语进行分组并相应地将其分离，如下所示。

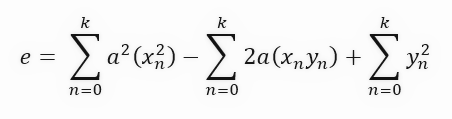
我们简化了公式，以便在推导时更容易理解。通常情况下，我们不执行这一额外步骤，而是直接使用下图所示的最终公式。

亲爱的圣母玛利亚！现在，一切都变得非常复杂。我完全不明白，这怎么可能？这是什么疯狂的计算？如何用代码实现这些功能？一切都在掌控之中，保持冷静。我通常不喜欢展示公式，以免读者感到困惑。同时，一切都非常简单：这正是我们需要计算的导数。这样，我们就得到了直线角系数的近似值。

现在让我们将其转换为代码格式，看看会发生什么。代码如下。

19. //+------------------------------------------------------------------+
20. void Func_01(void)
21. {
22.     int A[]={
23.                 -100, -150,
24.                  -80,  -50,
25.                   30,   80,
26.                  100,  120
27.             };
28. 
29.     int vx, vy;
30.     double ly, err, d0, d1;
31. 
32.     canvas.LineVertical(global.x, global.y - _SizeLine, global.y + _SizeLine, ColorToARGB(clrRoyalBlue, 255));
33.     canvas.LineHorizontal(global.x - _SizeLine, global.x + _SizeLine, global.y, ColorToARGB(clrRoyalBlue, 255));
34. 
35.     err = d0 = d1 = 0;
36.     for (uint c0 = 0, c1 = 0; c1 < A.Size(); c0++)
37.     {
38.         vx = A[c1++];
39.         vy = A[c1++];
40.         d0 += (vx * vy);
41.         d1 += MathPow(vx, 2);
42.         canvas.FillCircle(global.x + vx, global.y - vy, 5, ColorToARGB(clrRed, 255));
43.         ly = vy - (vx * -MathTan(_ToRadians(global.Angle)));
44.         canvas.LineVertical(global.x + vx, global.y - vy, global.y - (int)(ly + vy), ColorToARGB(clrPurple));
45.         err += MathAbs(ly);
46.     }
47.     canvas.TextOut(global.x - 200, global.y + _SizeLine + 20, StringFormat("Error: %.8f", err), ColorToARGB(clrRed));
48.     canvas.TextOut(global.x - 200, global.y + _SizeLine + 40, StringFormat("(de/da) : %.8f", d0 / d1), ColorToARGB(clrForestGreen));
49. }
50. //+------------------------------------------------------------------+

请注意，与您通过查看所有这些公式所想象的不同，在代码中进行实际计算非常简单明了。在第 40 行，我们计算各点的总和。在第 41 行，我们计算 X 点的平方。这一切都很简单。在第 48 行，我们打印出图形的值。现在仔细听我说：当我们只取直线方程中的一个变量时，我们发现这个值是理想的。看下面这条线的方程式。

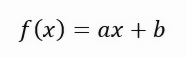
在这个等式中，< a > 的值正是角度系数。< b > 的值表示方程根所在的点。对于那些不知道的人来说，方程的根是当 X 值为零时，曲线或直线（在本例中）与 Y 轴相交的点。然后，由于该解中 < b > 的值为零，因此作为理想值返回的值仅显示了最接近理想值的斜率。但这并不意味着它实际上是正确的，因为我们是说方程的根正好在原点，也就是说 X 和 Y 都为零。实际上，这种情况很少发生，以至于当我们运行这个应用程序时，我们得到了下面显示的动画。

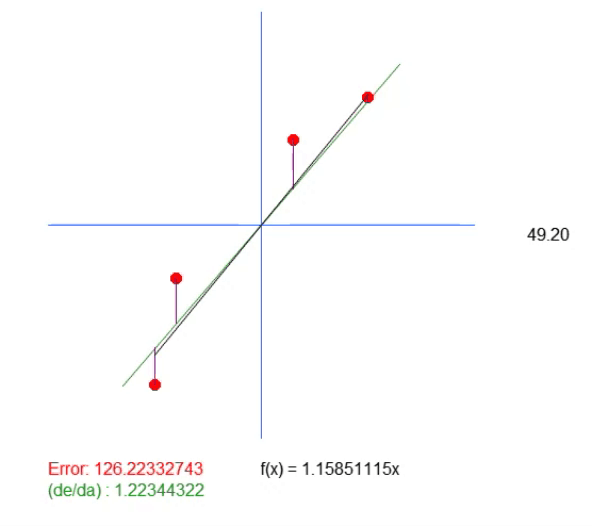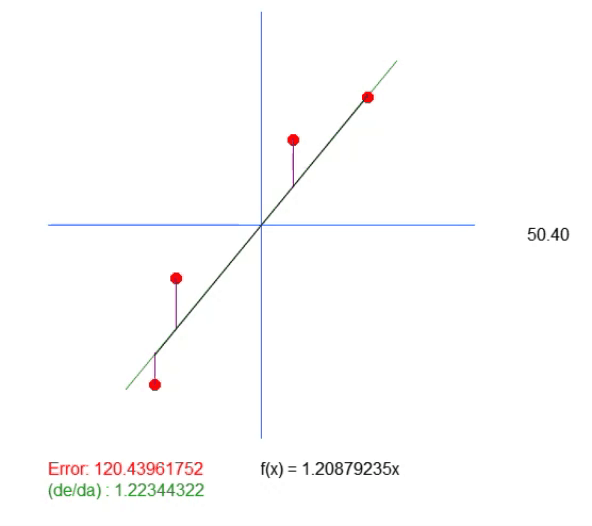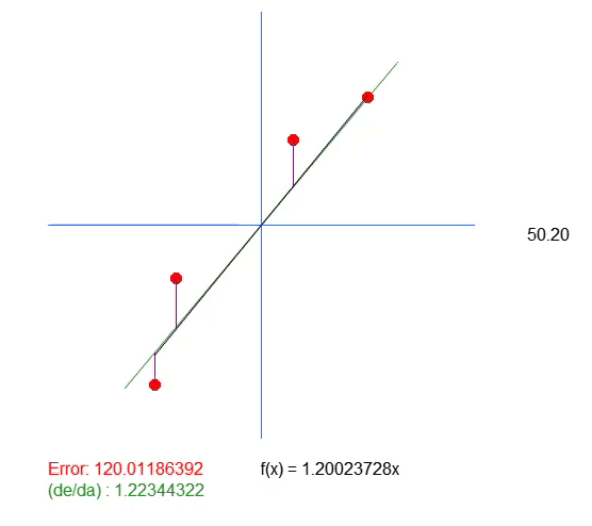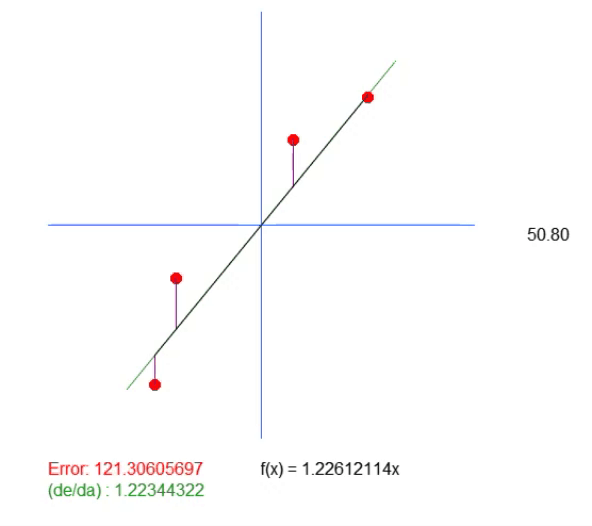
请注意，这段动画中还有另外一条线。只需要显示计算出的理想值在哪里。但如果查看误差值，就会发现等式中的系数与绿色显示的系数略有不同。

这个绿色值与我们根据公式计算出的值完全一致。可见，在此仅仅计算斜率值是不够的。我们需要创建直线的方程，为此，除了 < a > 的值之外，我们还需要得到 < b > 的值。这是必要的，以便有一个更通用的解决方案，而不是与点（0,0）挂钩。

该点（0,0）实际上不是数据库的一部分，对角系数的计算结果有隐含影响。为了正确删除此点，我们需要更改应用程序中的一些内容，以便您可以在（0,0）处远离此参考点。

移动直线函数的根

由于我们需要为进一步的工作准备应用程序（将在下一篇文章中讨论），我们将在本文的其余部分创建一个相当有趣的机制。然后，我们就可以把重点放在数学方面了。

添加这一机制无需对代码进行任何特殊修改。然而，这种影响将非常显著，因为它将使我们能够找到在任何情况下都能给我们最小可能面积的直线方程。这将是找到最合适常数的一般机制。通过这种机制，将在图上绘制的线性回归将更充分地反映数据库。

进行这些更改非常简单，我们需要做的就是移动直线函数的根。这些词看起来有点复杂，但当我们在代码中实现更改时，一切都变得非常简单，如下图所示。

001. //+------------------------------------------------------------------+
002. #property copyright "Daniel Jose"
003. #property indicator_chart_window
004. #property indicator_plots 0
005. //+------------------------------------------------------------------+
006. #include <Canvas\Canvas.mqh>
007. //+------------------------------------------------------------------+
008. #define _ToRadians(A) (A * (M_PI / 180.0))
009. #define _SizeLine 200
010. //+------------------------------------------------------------------+
011. CCanvas canvas;
012. //+------------------------------------------------------------------+
013. struct st_00
014. {
015.     int     x,
016.             y;
017.     double  Angle,
018.             Const_B;
019. }global;
020. //+------------------------------------------------------------------+
021. void PlotText(const uchar line, const string sz0)
022. {
023.     uint w, h;
024. 
025.     TextGetSize(sz0, w, h);
026.     canvas.TextOut(global.x - (w / 2), global.y + _SizeLine + (line * h) + 5, sz0, ColorToARGB(clrBlack));   
027. }
028. //+------------------------------------------------------------------+
029. void Func_01(void)
030. {
031.     int A[]={
032.                 -100, -150,
033.                  -80,  -50,
034.                   30,   80,
035.                  100,  120
036.             };
037. 
038.     int vx, vy;
039.     double ly, err;
040.     string s0 = "";
041. 
042.     canvas.LineVertical(global.x, global.y - _SizeLine, global.y + _SizeLine, ColorToARGB(clrRoyalBlue, 255));
043.     canvas.LineHorizontal(global.x - _SizeLine, global.x + _SizeLine, global.y, ColorToARGB(clrRoyalBlue, 255));
044. 
045.     err = 0;
046.     for (uint c0 = 0, c1 = 0; c1 < A.Size(); c0++)
047.     {
048.         vx = A[c1++];
049.         vy = A[c1++];
050.         canvas.FillCircle(global.x + vx, global.y - vy, 5, ColorToARGB(clrRed, 255));
051.         ly = vy - (vx * -MathTan(_ToRadians(global.Angle))) - global.Const_B;
052.         s0 += StringFormat("%.4f || ", MathAbs(ly));
053.         canvas.LineVertical(global.x + vx, global.y - vy, global.y + (int)(ly - vy), ColorToARGB(clrPurple));
054.         err += MathPow(ly, 2);
055.     }
056.     PlotText(3, StringFormat("Error: %.8f", err));
057.     PlotText(4, s0);
058. }
059. //+------------------------------------------------------------------+
060. void NewAngle(const char direct, const char updow, const double step = 0.1)
061. {
062.     canvas.Erase(ColorToARGB(clrWhite, 255));
063. 
064.     global.Angle = (MathAbs(global.Angle + (step * direct)) < 90 ? global.Angle + (step * direct) : global.Angle);
065.     global.Const_B += (step * updow);  
066.     PlotText(1, StringFormat("Angle in graus => %.2f", MathAbs(global.Angle)));
067.     PlotText(2, StringFormat("f(x) = %.4fx %c %.4f", -MathTan(_ToRadians(global.Angle)), (global.Const_B < 0 ? '-' : '+'), MathAbs(global.Const_B)));
068.     canvas.LineAA(
069.                 global.x - (int)(_SizeLine * cos(_ToRadians(global.Angle))), 
070.                 (global.y - (int)global.Const_B) - (int)(_SizeLine * sin(_ToRadians(global.Angle))), 
071.                 global.x + (int)(_SizeLine * cos(_ToRadians(global.Angle))), 
072.                 (global.y - (int)global.Const_B) + (int)(_SizeLine * sin(_ToRadians(global.Angle))), 
073.                 ColorToARGB(clrForestGreen)
074.             );
075.        
076.     Func_01();
077. 
078.     canvas.Update(true);
079. }
080. //+------------------------------------------------------------------+
081. int OnInit()
082. {    
083.     global.Angle = 0;
084.     global.x = (int)ChartGetInteger(0, CHART_WIDTH_IN_PIXELS, 0);
085.     global.y = (int)ChartGetInteger(0, CHART_HEIGHT_IN_PIXELS, 0);
086. 
087.     canvas.CreateBitmapLabel("BL", 0, 0, global.x, global.y, COLOR_FORMAT_ARGB_NORMALIZE);
088.     global.x /= 2;
089.     global.y /= 2;
090.         
091.     NewAngle(0, 0);
092. 
093.     canvas.Update(true);
094.     
095.     return INIT_SUCCEEDED;
096. }
097. //+------------------------------------------------------------------+
098. int OnCalculate(const int rates_total, const int prev_calculated, const int begin, const double &price[])
099. {
100.     return rates_total;
101. }
102. //+------------------------------------------------------------------+
103. void OnChartEvent(const int id, const long &lparam, const double &dparam, const string &sparam)
104. {
105.     switch (id)
106.     {
107.         case CHARTEVENT_KEYDOWN:
108.             if (TerminalInfoInteger(TERMINAL_KEYSTATE_LEFT))
109.                 NewAngle(-1, 0);
110.             if (TerminalInfoInteger(TERMINAL_KEYSTATE_RIGHT))
111.                 NewAngle(1, 0);
112.             if (TerminalInfoInteger(TERMINAL_KEYSTATE_UP))
113.                 NewAngle(0, 1);
114.             if (TerminalInfoInteger(TERMINAL_KEYSTATE_DOWN))
115.                 NewAngle(0, -1);
116.             break;
117.     }
118. }
119. //+------------------------------------------------------------------+
120. void OnDeinit(const int reason)
121. {
122.     canvas.Destroy();
123. }
124. //+------------------------------------------------------------------+

结果如下：

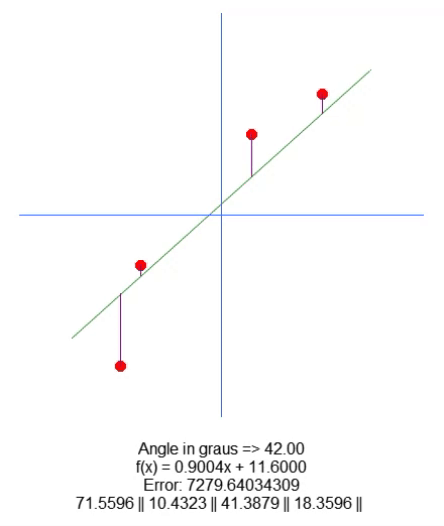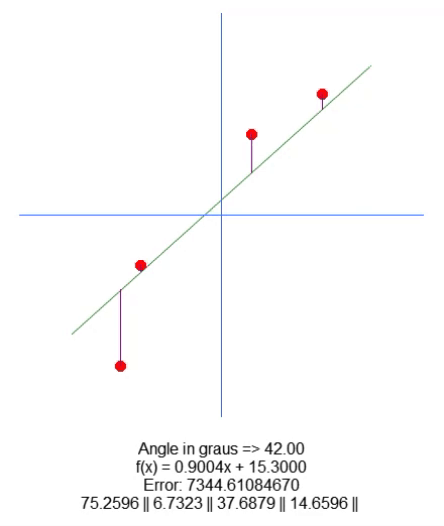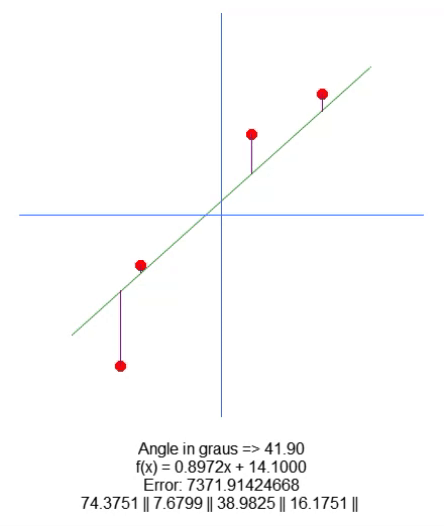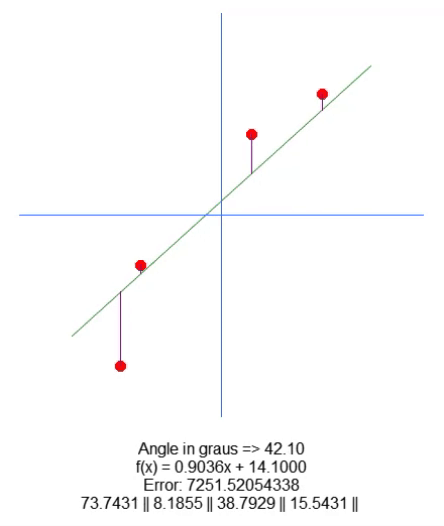
本质上，为了移动根，我们在第18行添加了一个变量。使用上下箭头，我们可以更改第 65 行中此变量的值。其他一切都很简单。我们只需要根据代码中存在的这个新变量的值调整紫线长度值。我确信我不需要解释如何做到这一点，因为这很简单。

最后的探讨

在本文中，我们看到数学公式通常看起来比它们在代码中的实现复杂得多。许多人认为做这些事情很难，但在这里我们已经证明，一切都比看起来简单得多。但我们还没有完成所有的工作。我们只实现了其中的一部分。现在我们需要找到一种更合适的方法来写直线方程。为此，我们将使用本文中的最后一段代码。与您在本主题开始时的想象相反，通过循环找到直线函数并不像看起来那么容易。这是因为我们添加了另一个变量进行搜索。试想，如果我们有一百万个变量，找到一个方程需要多少工作。用蛮力做这件事是完全不可能的，但通过正确使用数学，找到方程要容易得多。

最后一件事：在继续阅读下一篇文章之前，请使用末尾提供的代码，该代码会生成上图所示的内容，以尝试找到方程式。你会发现这是一项相当艰巨的任务。下一篇文章见。