MetaTrader 5 / 機械学習
English Русский 中文 Español Deutsch Português
preview
ニューラルネットワークの実践：最小二乗法

ニューラルネットワークの実践：最小二乗法

MetaTrader 5 — 機械学習 | 4 11月 2024, 13:00
156 0
Daniel Jose
Daniel Jose

はじめに

みなさんこんにちは。ニューラルネットワークに関する新しい記事へようこそ。

前の「ニューラルネットワークの実践：割線」稿では、応用数学の実践についての説明を始めましたが、これはトピックの簡潔で手短な紹介にすぎませんでした。使用する基本的な数学演算は三角関数であることがわかりました。そして、多くの人が考えるのとは異なり、これは正接関数ではなく割線関数です。最初はすべてが非常に混乱しているように見えるかもしれませんが、実際にはすぐにすべてが見た目ほど複雑ではないと理解できるでしょう。数学の分野で混乱を招きがちな多くの要素とは異なり、ここではすべてが自然な流れで展開されます。


奇妙で理解できないもの

ただ、私には理解できない小さな欠陥が1つあります。少なくとも私には意味が通じませんが、同じことに取り組もうとする人には役立つかもしれないので、そのままにしておきます。この問題を解決する理由は、解決しないと数学的な観点から他にも多くの問題が発生するためです。

上記の記事には次のコードがあります。

19. //+------------------------------------------------------------------+
20. void Func_01(void)
21. {
22.     int A[] {
23.                 -100,  150,
24.                  -80,   50,
25.                   30,  -80,
26.                  100, -120
27.             };
28. 
29.     canvas.LineVertical(global.x, global.y - _SizeLine, global.y + _SizeLine, ColorToARGB(clrRoyalBlue, 255));
30.     canvas.LineHorizontal(global.x - _SizeLine, global.x + _SizeLine, global.y, ColorToARGB(clrRoyalBlue, 255));
31. 
32.     for (uint c0 = 0, c1 = 0; c1 < A.Size(); c0++)
33.         canvas.FillCircle(global.x + A[c1++], global.y + A[c1++], 5, ColorToARGB(clrRed, 255));
34. }
35. //+------------------------------------------------------------------+

このコードは、22行目に示されている配列Aにある位置に小さな円を作成します。特別な処理はまだ何もしておらず、まさに意図したとおりの動作です。ただし、点をプロットすると、次のようになります。


これらの点は、予期しない場所にプロットされています。X軸とY軸が反転しているのです。その理由は何でしょうか。正直に言って、うまく説明できる自信はありません。これは、コードの33行目で配列内の値を取得して位置を追加する処理が原因です。この方法では、コンパイラが配列内の次の値を指し示していると認識する必要があり、異なる場合には不正なメモリアクセスエラーが発生します。このエラーは範囲エラーとして扱われ、アプリケーションは終了します。

しかし、ここで問題なのは、global.xには奇数ではなく偶数インデックスの値が追加されていることです。したがって、global.yに追加された値は偶数インデックスにあるべきなのに、実際には奇数インデックスに位置しています。

この記事の計算を書き始めたときに、初めてこの問題に気付きました。計算結果がアプリの提供する結果と一致しなかったため、原因を特定する必要がありました。以下に示すように、コードを少し変更することで、同じ操作を正しく実行できます。

19. //+------------------------------------------------------------------+
20. void Func_01(void)
21. {
22.     int A[]={
23.                 -100,  150,
24.                  -80,   50,
25.                   30,  -80,
26.                  100, -120
27.             };
28. 
29.     int vx, vy;
30.     string s = "";
31. 
32.     canvas.LineVertical(global.x, global.y - _SizeLine, global.y + _SizeLine, ColorToARGB(clrRoyalBlue, 255));
33.     canvas.LineHorizontal(global.x - _SizeLine, global.x + _SizeLine, global.y, ColorToARGB(clrRoyalBlue, 255));
34. 
35.     for (uint c0 = 0, c1 = 0; c1 < A.Size(); c0++)
36.     {
37.         canvas.FillCircle(global.x + (vx = A[c1++]), global.y + (vy = A[c1++]), 5, ColorToARGB(clrRed, 255));
38.         s += StringFormat("[ %d <> %d ] ", vx, vy);
39.     }
40.     canvas.TextOut(global.x - 200, global.y + _SizeLine + 70, s, ColorToARGB(clrBlack));
41. }
42. //+------------------------------------------------------------------+

この変更により、何が起こっているのかがわかります。結果は以下のとおりです。


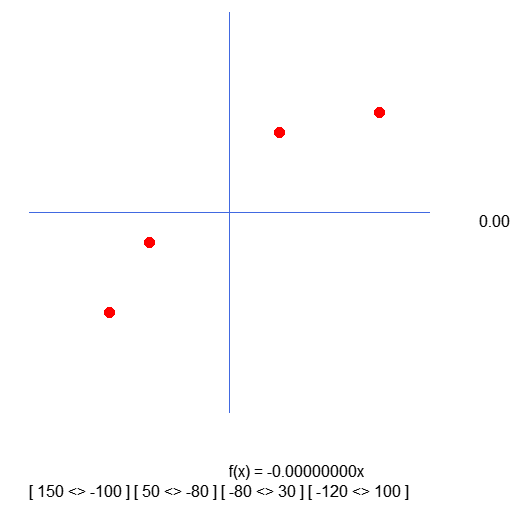
括弧内の値に注意してください。これらの値は、37行目でおこなわれたキャプチャの結果です。つまり、グラフ上の円の位置を決定するために使用される値を固定しています。ただし、配列で宣言された値とは逆の順序になっている点に注意が必要です。これは非常に奇妙であり、コードを次のように修正する必要があります。

19. //+------------------------------------------------------------------+
20. void Func_01(void)
21. {
22.     int A[]={
23.                 -100,  150,
24.                  -80,   50,
25.                   30,  -80,
26.                  100, -120
27.             };
28. 
29.     int vx, vy;
30.     string s = "";
31. 
32.     canvas.LineVertical(global.x, global.y - _SizeLine, global.y + _SizeLine, ColorToARGB(clrRoyalBlue, 255));
33.     canvas.LineHorizontal(global.x - _SizeLine, global.x + _SizeLine, global.y, ColorToARGB(clrRoyalBlue, 255));
34. 
35.     for (uint c0 = 0, c1 = 0; c1 < A.Size(); c0++)
36.     {
37.         vx = A[c1++];
38.         vy = A[c1++];
39.         canvas.FillCircle(global.x + vx, global.y + vy, 5, ColorToARGB(clrRed, 255));
40.         s += StringFormat("[ %d <> %d ] ", vx, vy);
41.     }
42.     canvas.TextOut(global.x - 200, global.y + _SizeLine + 70, s, ColorToARGB(clrBlack));
43. }
44. //+------------------------------------------------------------------+

この新しいコードを使用すると、結果は次のようになります。


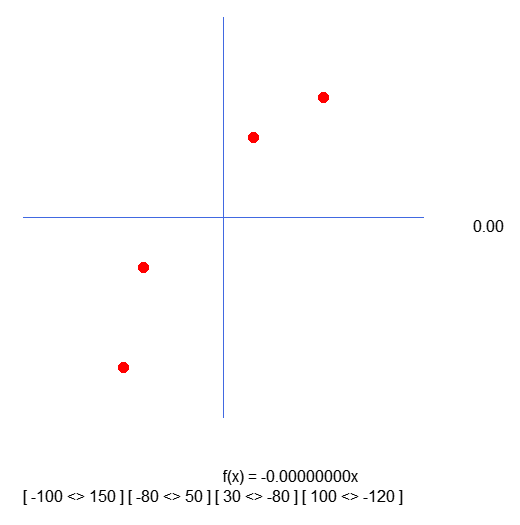
角括弧内の値は、配列で宣言されている値と一致していることがわかります。このエラーに早く気付かなかったことをお詫びしますが、これは独自の方法で作業しようとするすべての方への警告として役立つかもしれません。インデックスが逆になっている理由が不明のため、うまく説明することはできませんが、必要な修正は済ませたので、次のステップに進めます。


数学と数学の準備

ここから先は、ただコードに飛び込むだけでは混乱が生じるかもしれません。これからおこなう内容と、その理由を正確に理解していただきたいので、すべてを丁寧に説明します。注意深く読むことをお勧めします。表示されているとおりにコードを変更し、何が起こっているのかを理解するようにしてください。すべてを理解してから次のステップに進むことを強くお勧めします。理解できていないままステップを飛ばすと、予期しない問題が生じる可能性があります。

まず最初におこなうことは、コードの一部を少し変更することです。

19. //+------------------------------------------------------------------+
20. void Func_01(void)
21. {
22.     int A[]={
23.                 -100,  150,
24.                  -80,   50,
25.                   30,  -80,
26.                  100, -120
27.             };
28. 
29.     int vx, vy;
30.     string s = "";
31.     double ly;
32. 
33.     canvas.LineVertical(global.x, global.y - _SizeLine, global.y + _SizeLine, ColorToARGB(clrRoyalBlue, 255));
34.     canvas.LineHorizontal(global.x - _SizeLine, global.x + _SizeLine, global.y, ColorToARGB(clrRoyalBlue, 255));
35. 
36.     for (uint c0 = 0, c1 = 0; c1 < A.Size(); c0++)
37.     {
38.         vx = A[c1++];
39.         vy = A[c1++];
40.         canvas.FillCircle(global.x + vx, global.y + vy, 5, ColorToARGB(clrRed, 255));
41.         ly = (vx * MathTan(_ToRadians(global.Angle))) - vy;
42.         canvas.LineVertical(global.x + vx, global.y + vy, global.y + (int)(ly + vy), ColorToARGB(clrPurple));
43.         s += StringFormat("sy%d = %.4f  | ", c0, ly);
44.     }
45.     canvas.TextOut(global.x - 200, global.y + _SizeLine + 50, s, ColorToARGB(clrBlack));
46. }
47. //+------------------------------------------------------------------+
48. void NewAngle(const char direct, const double step = 0.2)
49. {
50.     canvas.Erase(ColorToARGB(clrWhite, 255));
51. 
52.     global.Angle = (MathAbs(global.Angle + (step * direct)) < 90 ? global.Angle + (step * direct) : global.Angle);
53.     canvas.TextOut(global.x + _SizeLine + 50, global.y, StringFormat("%.2f", MathAbs(global.Angle)), ColorToARGB(clrBlack));
54.     canvas.TextOut(global.x, global.y + _SizeLine + 20, StringFormat("f(x) = %.8fx", -MathTan(_ToRadians(global.Angle))), ColorToARGB(clrBlack));
55.     canvas.Line(
56.                 global.x - (int)(_SizeLine * cos(_ToRadians(global.Angle))), 
57.                 global.y - (int)(_SizeLine * sin(_ToRadians(global.Angle))), 
58.                 global.x + (int)(_SizeLine * cos(_ToRadians(global.Angle))), 
59.                 global.y + (int)(_SizeLine * sin(_ToRadians(global.Angle))), 
60.                 ColorToARGB(clrForestGreen)
61.             );
62.        
63.     Func_01();
64. 
65.     canvas.Update(true);
66. }
67. //+------------------------------------------------------------------+

これは最適な方法ではありませんが、下のアニメーションに示されている結果はまさに私たちが可視化したいものです。


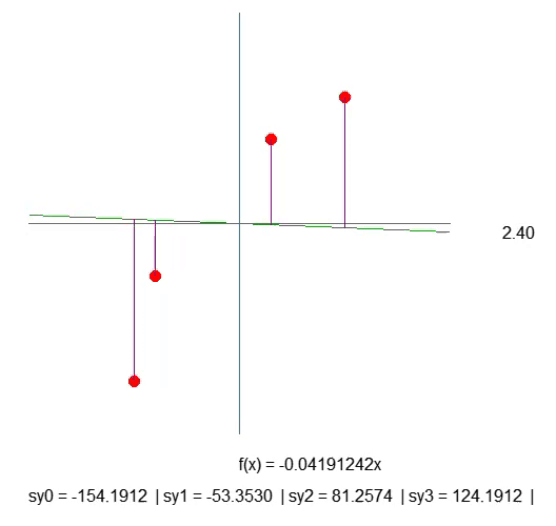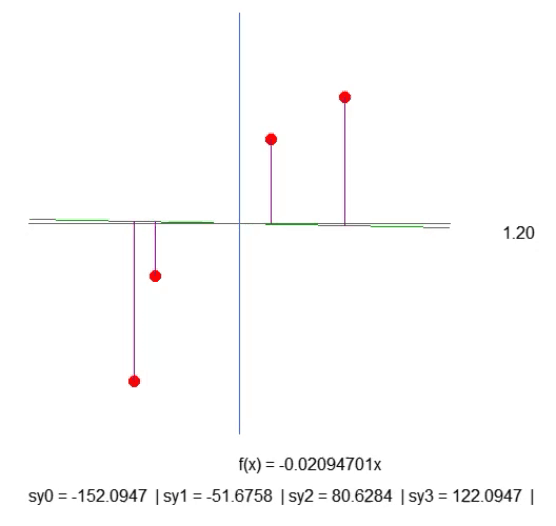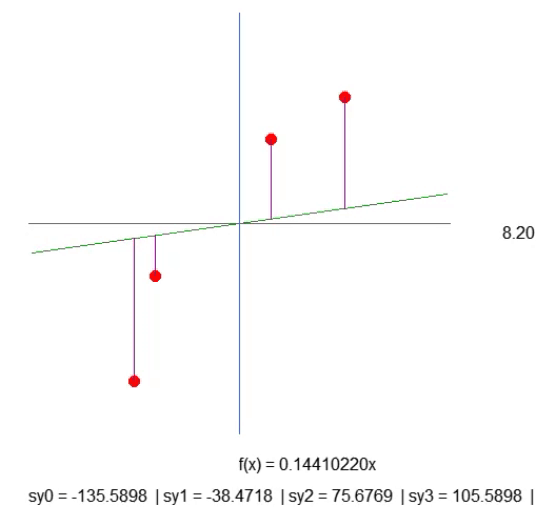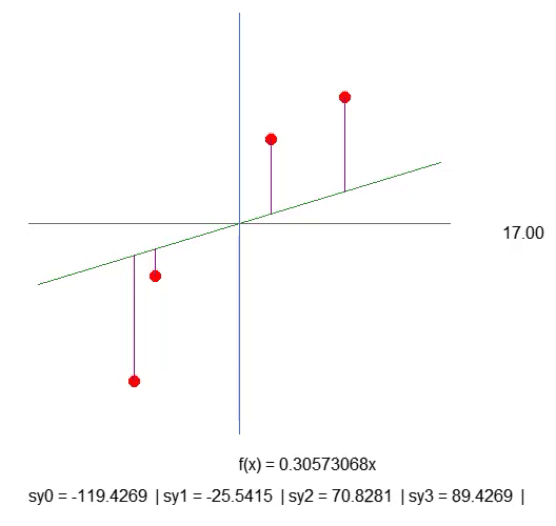
紫色の線を作成します。これは、線と点との距離を示すものですので、注意深く確認してください。線の長さはフラグメントの41行目のコードによって決まります。この計算は期待通りではないものの、意図通りに機能します。ただし、後でこの計算を修正する必要があるため、ここで急ぐべきではありません。43行目では、指定された紫色の線の長さを表示するテキスト文字列を作成します。アニメーションを確認すると、負の長さが表示されることがありますが、これは意味をなさないものですので、今の段階では気にする必要はありません。まず、全体の作業の本質を理解していただければと思います。

さて、ここで少し考えてみてください。直線関数は傾斜係数に基づいて計算されます。この係数は、右または左の矢印をクリックすることで変更される角度から取得できます。また、この傾斜の変化速度は、52行目にあるstep値によって決定されます。

次に、紫色の線の長さに注目してください。少しの忍耐をもって、傾斜を可能な限り急にして、紫色の線の長さが増加しないように設定できます（減少することはあっても、増加しない状態にすることが重要です）。長さがまったく増加しなくなる地点に到達したら、それが理想的な傾斜です。

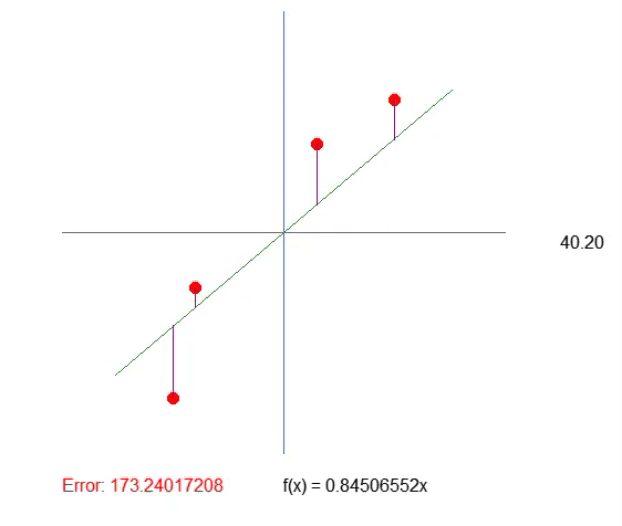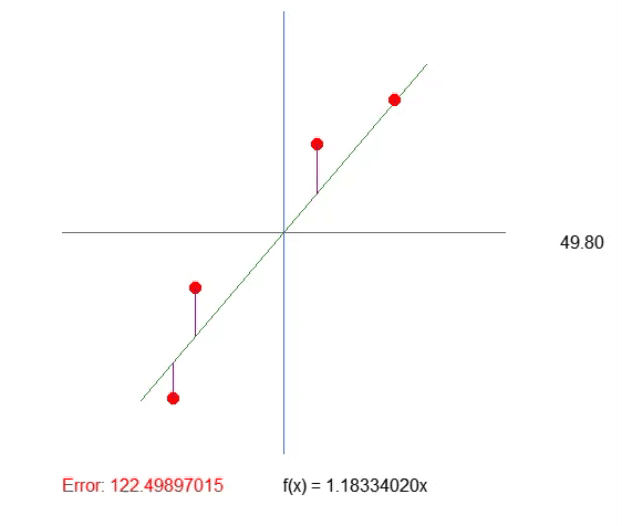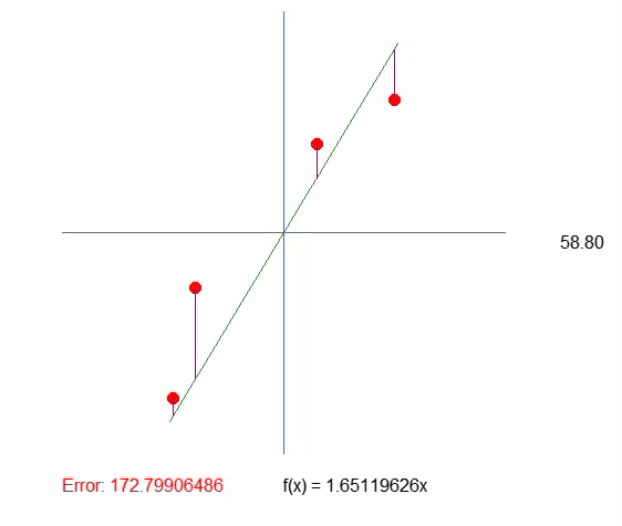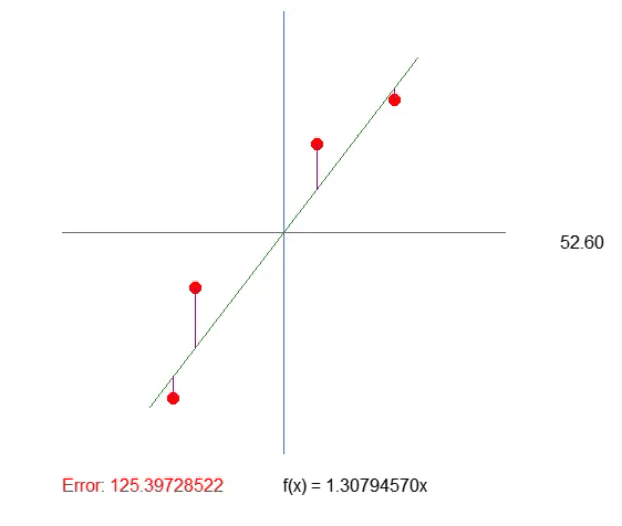
ただし、次の点にも注意が必要です。この場合、考慮すべき要素は4つだけなので簡単ですが、もし配列に数百、数千もの点がある場合、長さが増加しないよう手動で調整するのは非常に困難です。この調整を簡単にするためには数学的な工夫を活用できます。工夫の内容は次の通りです。紫色の線の長さをすべて合計し、1つの値だけを監視します。その値が上昇し始めたら、最適な傾斜点を過ぎたと判断できるのです。簡単ですよね。では、コードを以下のように修正しましょう。

19. //+------------------------------------------------------------------+
20. void Func_01(void)
21. {
22.     int A[]={
23.                 -100,  150,
24.                  -80,   50,
25.                   30,  -80,
26.                  100, -120
27.             };
28. 
29.     int vx, vy;
30.     double ly, err;
31. 
32.     canvas.LineVertical(global.x, global.y - _SizeLine, global.y + _SizeLine, ColorToARGB(clrRoyalBlue, 255));
33.     canvas.LineHorizontal(global.x - _SizeLine, global.x + _SizeLine, global.y, ColorToARGB(clrRoyalBlue, 255));
34. 
35.     err = 0;
36.     for (uint c0 = 0, c1 = 0; c1 < A.Size(); c0++)
37.     {
38.         vx = A[c1++];
39.         vy = A[c1++];
40.         canvas.FillCircle(global.x + vx, global.y + vy, 5, ColorToARGB(clrRed, 255));
41.         ly = (vx * MathTan(_ToRadians(global.Angle))) - vy;
42.         canvas.LineVertical(global.x + vx, global.y + vy, global.y + (int)(ly + vy), ColorToARGB(clrPurple));
43.         err += MathAbs(ly);
44.     }
45.     canvas.TextOut(global.x - 200, global.y + _SizeLine + 20, StringFormat("Error: %.8f", err), ColorToARGB(clrRed));
46. }
47. //+------------------------------------------------------------------+

結果は下の GIF で確認できます。この方法で値を調整する方がはるかに簡単です。


象限の調整

数学的な内容に完全に入る前に、まず小さな変更を加える必要があります。この変更は、これからおこなう内容に直接影響を与えるわけではありませんが、他のプログラムで説明されていることを実践する際や、手動で検証をおこなう際に役立ちます。多くの場合、私たちは最初にすべてを手動で試して、同じ方法で計算が正しいかどうかを確認します。この方法を理解しておけば、プログラムの計算結果を盲目的に信頼してしまうことで陥りがちな誤りを避けることができます。

たとえその計算が完全に間違っていたとしても、初心者のプログラマーはこうした誤りを犯しやすく、結果として多くの時間と労力を費やしてしまいます。その結果、誤った方法で問題を解決しようとすることに集中してしまいます。優秀なプログラマーは、計算結果に対して常に懐疑的な目を向けており、最終的に結果を信頼する前に、複数の方法で検証を試みるものです。

私がこれを強調する理由は、多くの人が見落としがちな点として、グラフィックイメージを作成する際には常に直交平面の第4象限で作業していることが挙げられるからです。これは、計算そのものではなく、同じ計算を手動で実行したり、異なるプログラムで実行したりする場合に影響を及ぼします。たとえば、MatLab、SCILab、またはExcelなどでは、ここで使用する数値や数式を使ってグラフィック表示を作成することができます。

では、これが今回の内容とどう関係するのでしょうか。読者の皆さん、プログラム内でデータマトリックスを確認すると、グラフ上に表示されているものと少し異なることに気付かれるでしょう。別のグラフ作成プログラムで同じ値をプロットしてみると、Y軸が反転していることがわかるはずです。しかし、この現象がどのようにして起こるのかはまだ明らかではありません。少し時間をかけて、下に示す画像を見て、より理解を深めてください。


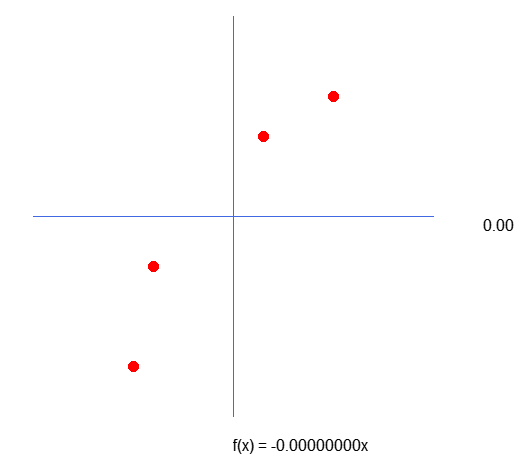
上記の画像は、MetaTrader 5でチャートをプロットしたときに表示されます。ただし、たとえばExcelで同じ値をプロットすると、グラフは次のようになります。


この不一致のために、テストの大半が完全に理解できなくなる可能性があります。特に、計算が正しく実行されているか確認する必要がある場合に問題となります。

前のセクションで、データを正しく表示する方法を理解しました。次は、このY軸の反転（またはミラー化）に関する問題を修正する必要があります。

なぜこのような表示の不具合が発生するのでしょうか。理由は単純で、冒頭で触れたように、データをプロットする画面が第4象限に位置しているためです。この場合、原点、つまり点(0, 0)は画面の左上隅に位置します。ここで重要なのは、参照点を画面の中央に変更しても、この移動は仮想的なものに過ぎないということです。物理的な参照点そのものは変更されず、単に計算上の原点が異なる場所に設定されているだけです。このため、プログラムはマトリックス内の点の値を別の点のセットとして追加し、仮想原点を左上隅から画面上の別の場所に移動できるようにしています。

しかし、先ほどの画像を見ると、仮想化の実装方法に問題があることに気づくかもしれません。具体的には、Y軸が反転またはミラー化されています。この問題を解決するには、コードをいくつか変更する必要があります。この変更は単純ですが、画面表示が格段に明確になります。

次に、コードで加えるべき変更について説明します。

19. //+------------------------------------------------------------------+
20. void Func_01(void)
21. {
22.     int A[]={
23.                 -100, -150,
24.                  -80,  -50,
25.                   30,   80,
26.                  100,  120
27.             };
28. 
29.     int vx, vy;
30.     double ly, err;
31. 
32.     canvas.LineVertical(global.x, global.y - _SizeLine, global.y + _SizeLine, ColorToARGB(clrRoyalBlue, 255));
33.     canvas.LineHorizontal(global.x - _SizeLine, global.x + _SizeLine, global.y, ColorToARGB(clrRoyalBlue, 255));
34. 
35.     err = 0;
36.     for (uint c0 = 0, c1 = 0; c1 < A.Size(); c0++)
37.     {
38.         vx = A[c1++];
39.         vy = A[c1++];
40.         canvas.FillCircle(global.x + vx, global.y - vy, 5, ColorToARGB(clrRed, 255));
41.         ly = vy - (vx * -MathTan(_ToRadians(global.Angle)));
42.         canvas.LineVertical(global.x + vx, global.y - vy, global.y - (int)(ly + vy), ColorToARGB(clrPurple));
43.         err += MathAbs(ly);
44.     }
45.     canvas.TextOut(global.x - 200, global.y + _SizeLine + 20, StringFormat("Error: %.8f", err), ColorToARGB(clrRed));
46. }
47. //+------------------------------------------------------------------+

この変更は非常に微細ですが、重要です。まず、行列内の値を調整し、点が正しい位置に配置されるように40行目の計算を修正します。また、紫色の線が各点に正しく接続されるように、41行目と42行目で実行される計算も修正する必要があります。こうした変更は見た目の改善が主な目的ですが、問題をさらに詳しく調査したい人にとっても、データの信頼性を高めることにつながります。この修正により、別のプログラムとの計算結果を比較する際も、どちらかのプログラムが不正確に計算されているのではないかと疑わずに済むようになります。プロセスがこれまでよりはるかに簡単で直感的になりました。

この結果、タスクの実行も大幅に効率化されました。誤差値が増加している場合は、計算が誤った方向に向かっていることを意味し、逆に誤差値が減少している場合は正しい方向に進んでいることを示します。

しかし、ここで新たな疑問が生じます。これをきっかけに、ニューラルネットワークのさらなる応用に関して探求を深めていきます。誤差値を観察すれば、接線の傾きや傾き係数を手動で調整することは比較的簡単にできますが、これを自動化する方法はあるでしょうか。つまり、機械が自律的に最適な係数を見つけ出せるようなメカニズムを構築できるかどうか、という問いです。現在のシステムでは、接線が直交平面の原点 (0, 0) を通過するため、単一の変数だけが使用されていますが、これが今後も続くとは限りません。まずはこの単純な疑問に焦点を当て、単一の変数だけを調整する場合を考えます。

前回の記事を読んでいれば、割線が接線となるための計算方法について触れたことをご存知かと思います。これが正しく機能した場合でも、さらに単純化した仮説を考えてみましょう。傾斜値を容易に見つけ出せるように、係数を高速かつ簡単に計算する式を見つけ出すことができるかもしれません。

このためには、いくつかの数学的な工夫を適用する必要があります。この内容については、よりわかりやすく説明するために、新しいトピックで取り上げることにします。


可能な限り小さな面積を探す

人工知能に関する学習を進める中で、よく目にするのが「最適化」というテーマです。人工知能とニューラルネットワークは異なる概念ですが、これらは密接に関連しており、異なるアプローチが必要です。これはプログラミングの観点からのものです。いくつか小さな違いはありますが、ここでは、データベース内の値を最もよく表す方程式を見つけるためにニューラルネットワークを利用する予定です。この種の計算は、ニューラルネットワークが得意とするところです。人工知能は基盤となるパターンを探すものであり、ニューラルネットワークはそのパターンを実際に構築します。

ただし、この段階ではニューロンを使い始めるのは早すぎるかもしれません。自分で計算をおこなえば、処理時間を大幅に節約できるからです。

傾斜を求める計算式には導関数を使用します。別の方法で実装することも可能ですが、ここでは最も迅速な方法である導関数を選択します。前のトピックで説明した内容を理解した上で、次のステップに進みましょう。では、質問の数学的な部分に進みます。

誤差を見つけるためには、次の数学的な計算をおこないます。


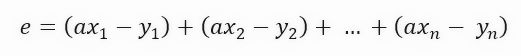
ここで、式中の定数「a」の値は直線の傾き、つまり接線の傾きの値を示します。しかし、この式はもう少し簡潔に表現できる余地があります。以下のように、式を簡略化することが可能です。


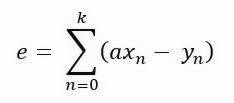
一見異なるように見えるこれらの式は、実際には同じ内容を表しています。単に表記を簡潔にしただけです。簡潔になったことで、以下で示す式の展開が容易になります。各ステップで値の合計、つまり紫色の線の長さを考慮することが重要です。この段階で導関数を直接使用することはできません。このように定義を導出しようとすると、定数がゼロになってしまうからです。次の式の結果を得たいと考えています。


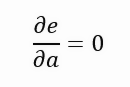
理想的には、傾きに対する誤差を出力したいのですが、その値がゼロに近づくことで、傾きが理想的な値に近づいていくという考え方です。もちろん、この値が完全にゼロになることは稀ですが、近づくことは可能です。しかし、紫色の線の長さを決定する関数を導出することは容易ではありません。それでも、方法はあります。紫色の線を正方形に変換する必要がありますが、今回は線の最小の長さではなく、各線によって形成される正方形の最小の面積を求めることにします。そこで、新しい定式が得られます。


ここで注目すべきは、この式でも同じ係数を計算しているということです。ただし、今回は紫色の線によって形成される正方形の面積を考慮しています。このアプローチはより興味深いものになっています。方程式をさらに展開すると、次のような結果が得られます。


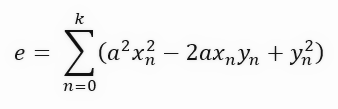
おそらく、ここで何をしたのか理解できていないかもしれません。この方程式は線の長さの計算を正方形の面積に変換したもので、非常に興味深いものです。おわかりでしょうか。この方程式は何を示しているのでしょうか。

わからなくても、心配しないでください。この方程式は単なる二次方程式です。放物線を生成する方程式であり、したがって、1次導関数を生成できるものです。傾きに関する導関数を取得することができます。しかし、その前に、通常はおこなわないもう1つの手順を追加する必要があります。最終的な式がこのようになる理由を説明したいと思います。以下のように、この手順では、項をグループ化し、分離します。


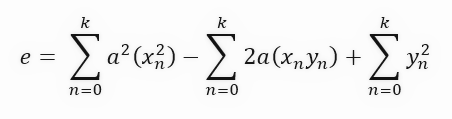
この手順は導出を分かりやすくするためにおこなわれます。通常、この手順はスキップされ、直接以下の最終式に進むことが多いです。


さて、これでかなり複雑に思えるかもしれません。どうしてこんなことが可能なのでしょうか。これは一体どういう計算なのでしょうか。これをコードで実装するにはどうすればよいのでしょうか。すべては理解可能です。落ち着いてください。通常、私は読者を混乱させないように数式を示すことを好まないのですが、実際にはこの計算は非常に単純です。これが計算する必要のある導関数です。したがって、直線の角度係数の近似値を得ることができます。

この理論をコードに変換して、何が起こるか見てみましょう。以下がそのコードです。

19. //+------------------------------------------------------------------+
20. void Func_01(void)
21. {
22.     int A[]={
23.                 -100, -150,
24.                  -80,  -50,
25.                   30,   80,
26.                  100,  120
27.             };
28. 
29.     int vx, vy;
30.     double ly, err, d0, d1;
31. 
32.     canvas.LineVertical(global.x, global.y - _SizeLine, global.y + _SizeLine, ColorToARGB(clrRoyalBlue, 255));
33.     canvas.LineHorizontal(global.x - _SizeLine, global.x + _SizeLine, global.y, ColorToARGB(clrRoyalBlue, 255));
34. 
35.     err = d0 = d1 = 0;
36.     for (uint c0 = 0, c1 = 0; c1 < A.Size(); c0++)
37.     {
38.         vx = A[c1++];
39.         vy = A[c1++];
40.         d0 += (vx * vy);
41.         d1 += MathPow(vx, 2);
42.         canvas.FillCircle(global.x + vx, global.y - vy, 5, ColorToARGB(clrRed, 255));
43.         ly = vy - (vx * -MathTan(_ToRadians(global.Angle)));
44.         canvas.LineVertical(global.x + vx, global.y - vy, global.y - (int)(ly + vy), ColorToARGB(clrPurple));
45.         err += MathAbs(ly);
46.     }
47.     canvas.TextOut(global.x - 200, global.y + _SizeLine + 20, StringFormat("Error: %.8f", err), ColorToARGB(clrRed));
48.     canvas.TextOut(global.x - 200, global.y + _SizeLine + 40, StringFormat("(de/da) : %.8f", d0 / d1), ColorToARGB(clrForestGreen));
49. }
50. //+------------------------------------------------------------------+

これらすべての数式を見て想像するのとは異なり、コード内で実際に計算をおこなうのは非常に単純でわかりやすいことに注意してください。40 行目では点の合計を計算します。41行目では、X内の点の2乗を計算します。すべて非常に簡単です。48行目ではグラフの値を出力します。ここで私が言っていることに注意を払ってください。この値は、直線の方程式で1つの変数だけを取る場合に理想的です。下の直線の方程式の式を見てください。


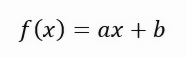
この方程式では、値<a>は角度係数そのものです。値<b>は方程式の根が位置する点を示します。知らない人のために説明すると、方程式の根とは、X値が0のときに曲線または直線（この場合は）がY軸に接する点です。この解の<b>の値は0なので、理想値として返される値は、理想に最も近い傾きを示すだけです。ただし、これは実際に正しいということではありません。方程式の根が正確に原点にある、つまりXとYが0であるという意味だからです。実際には、このようなことはめったに起こりません。めったに起こらないので、このアプリケーションを実行すると、以下に示すアニメーションが表示されます。


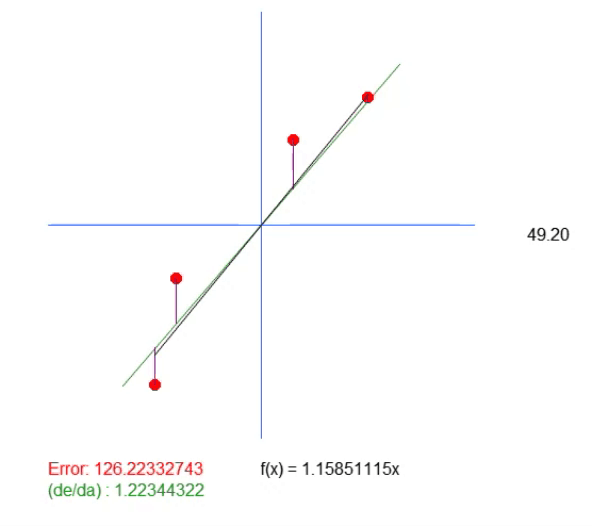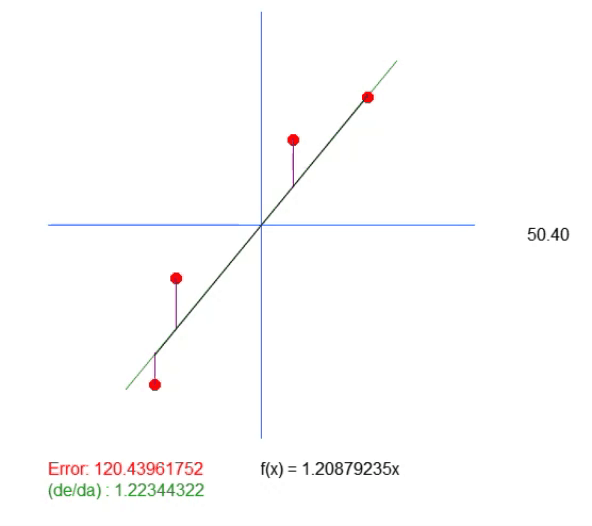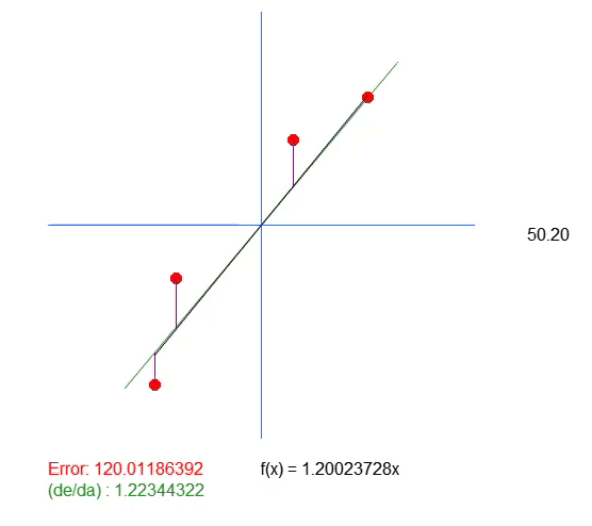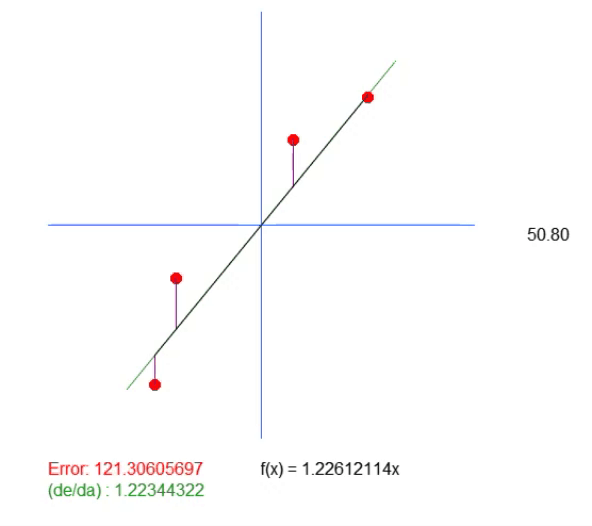
このアニメーションには別の線があることに注目してください。これは、計算された理想値がどこにあるかを示すためだけに必要です。ただし、誤差値を見ると、方程式の係数が緑色で示されているものとわずかに異なることがわかります。

この緑の値は、方程式に基づいて計算した値と正確に一致しています。ここでは、傾斜の値を計算するだけでは不十分であることがわかります。作成する線の方程式が必要であり、そのためには、値<a>に加えて、値<b>も取得する必要があります。これは、より一般的解を得て、点(0, 0)に縛られないために必要です。

この点(0, 0)は実際にはデータベースの一部ではありませんが、角度係数の計算結果に暗黙的な影響を及ぼします。この点を適切に削除するには、アプリケーションでいくつかの変更をおこない、この参照点(0, 0)から離れられるようにする必要があります。

直線関数の根を移動する

今後の作業のためにアプリケーションを準備する必要があるため（次の記事で説明します）、この記事の残りの部分では、かなり興味深いメカニズムを作成します。その後、数学的な側面に焦点を当てます。

このメカニズムを追加するために、コードに特別な変更を加える必要はありません。ただし、どのような状況でも可能な限り最小の面積を与える直線方程式を見つけることができるため、効果は非常に大きくなります。これは、最も適切な定数を見つけるための一般的なメカニズムになります。このメカニズムにより、グラフにプロットされる線形回帰は、データベースをより適切に反映するようになります。

これらの変更は非常に簡単です。直線関数の根を移動するだけです。言葉で言うと少し複雑に思えますが、コードで変更を実装すると、以下に示すようにすべてが非常に簡単になります。

001. //+------------------------------------------------------------------+
002. #property copyright "Daniel Jose"
003. #property indicator_chart_window
004. #property indicator_plots 0
005. //+------------------------------------------------------------------+
006. #include <Canvas\Canvas.mqh>
007. //+------------------------------------------------------------------+
008. #define _ToRadians(A) (A * (M_PI / 180.0))
009. #define _SizeLine 200
010. //+------------------------------------------------------------------+
011. CCanvas canvas;
012. //+------------------------------------------------------------------+
013. struct st_00
014. {
015.     int     x,
016.             y;
017.     double  Angle,
018.             Const_B;
019. }global;
020. //+------------------------------------------------------------------+
021. void PlotText(const uchar line, const string sz0)
022. {
023.     uint w, h;
024. 
025.     TextGetSize(sz0, w, h);
026.     canvas.TextOut(global.x - (w / 2), global.y + _SizeLine + (line * h) + 5, sz0, ColorToARGB(clrBlack));   
027. }
028. //+------------------------------------------------------------------+
029. void Func_01(void)
030. {
031.     int A[]={
032.                 -100, -150,
033.                  -80,  -50,
034.                   30,   80,
035.                  100,  120
036.             };
037. 
038.     int vx, vy;
039.     double ly, err;
040.     string s0 = "";
041. 
042.     canvas.LineVertical(global.x, global.y - _SizeLine, global.y + _SizeLine, ColorToARGB(clrRoyalBlue, 255));
043.     canvas.LineHorizontal(global.x - _SizeLine, global.x + _SizeLine, global.y, ColorToARGB(clrRoyalBlue, 255));
044. 
045.     err = 0;
046.     for (uint c0 = 0, c1 = 0; c1 < A.Size(); c0++)
047.     {
048.         vx = A[c1++];
049.         vy = A[c1++];
050.         canvas.FillCircle(global.x + vx, global.y - vy, 5, ColorToARGB(clrRed, 255));
051.         ly = vy - (vx * -MathTan(_ToRadians(global.Angle))) - global.Const_B;
052.         s0 += StringFormat("%.4f || ", MathAbs(ly));
053.         canvas.LineVertical(global.x + vx, global.y - vy, global.y + (int)(ly - vy), ColorToARGB(clrPurple));
054.         err += MathPow(ly, 2);
055.     }
056.     PlotText(3, StringFormat("Error: %.8f", err));
057.     PlotText(4, s0);
058. }
059. //+------------------------------------------------------------------+
060. void NewAngle(const char direct, const char updow, const double step = 0.1)
061. {
062.     canvas.Erase(ColorToARGB(clrWhite, 255));
063. 
064.     global.Angle = (MathAbs(global.Angle + (step * direct)) < 90 ? global.Angle + (step * direct) : global.Angle);
065.     global.Const_B += (step * updow);  
066.     PlotText(1, StringFormat("Angle in graus => %.2f", MathAbs(global.Angle)));
067.     PlotText(2, StringFormat("f(x) = %.4fx %c %.4f", -MathTan(_ToRadians(global.Angle)), (global.Const_B < 0 ? '-' : '+'), MathAbs(global.Const_B)));
068.     canvas.LineAA(
069.                 global.x - (int)(_SizeLine * cos(_ToRadians(global.Angle))), 
070.                 (global.y - (int)global.Const_B) - (int)(_SizeLine * sin(_ToRadians(global.Angle))), 
071.                 global.x + (int)(_SizeLine * cos(_ToRadians(global.Angle))), 
072.                 (global.y - (int)global.Const_B) + (int)(_SizeLine * sin(_ToRadians(global.Angle))), 
073.                 ColorToARGB(clrForestGreen)
074.             );
075.        
076.     Func_01();
077. 
078.     canvas.Update(true);
079. }
080. //+------------------------------------------------------------------+
081. int OnInit()
082. {    
083.     global.Angle = 0;
084.     global.x = (int)ChartGetInteger(0, CHART_WIDTH_IN_PIXELS, 0);
085.     global.y = (int)ChartGetInteger(0, CHART_HEIGHT_IN_PIXELS, 0);
086. 
087.     canvas.CreateBitmapLabel("BL", 0, 0, global.x, global.y, COLOR_FORMAT_ARGB_NORMALIZE);
088.     global.x /= 2;
089.     global.y /= 2;
090.         
091.     NewAngle(0, 0);
092. 
093.     canvas.Update(true);
094.     
095.     return INIT_SUCCEEDED;
096. }
097. //+------------------------------------------------------------------+
098. int OnCalculate(const int rates_total, const int prev_calculated, const int begin, const double &price[])
099. {
100.     return rates_total;
101. }
102. //+------------------------------------------------------------------+
103. void OnChartEvent(const int id, const long &lparam, const double &dparam, const string &sparam)
104. {
105.     switch (id)
106.     {
107.         case CHARTEVENT_KEYDOWN:
108.             if (TerminalInfoInteger(TERMINAL_KEYSTATE_LEFT))
109.                 NewAngle(-1, 0);
110.             if (TerminalInfoInteger(TERMINAL_KEYSTATE_RIGHT))
111.                 NewAngle(1, 0);
112.             if (TerminalInfoInteger(TERMINAL_KEYSTATE_UP))
113.                 NewAngle(0, 1);
114.             if (TerminalInfoInteger(TERMINAL_KEYSTATE_DOWN))
115.                 NewAngle(0, -1);
116.             break;
117.     }
118. }
119. //+------------------------------------------------------------------+
120. void OnDeinit(const int reason)
121. {
122.     canvas.Destroy();
123. }
124. //+------------------------------------------------------------------+

結果は次のとおりです。


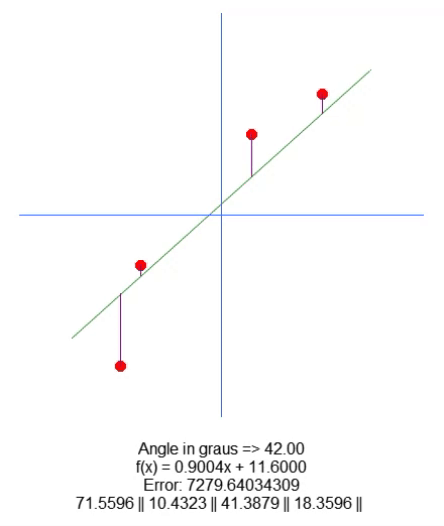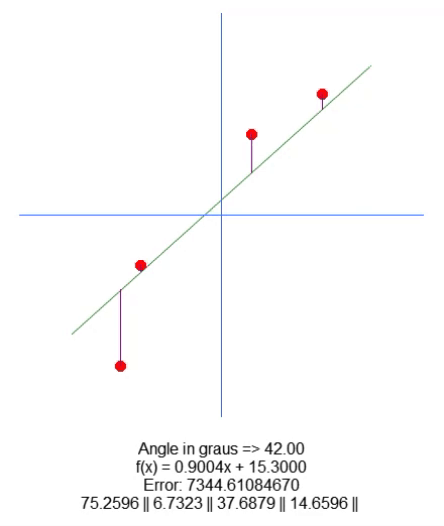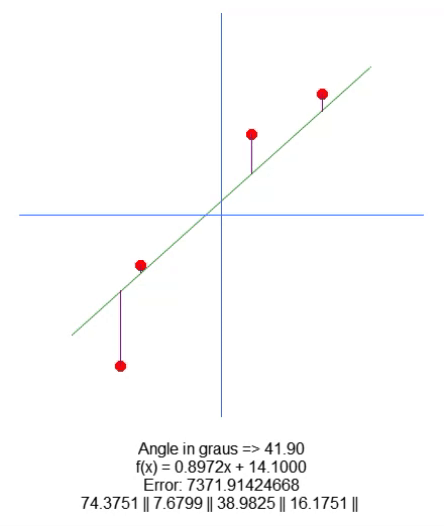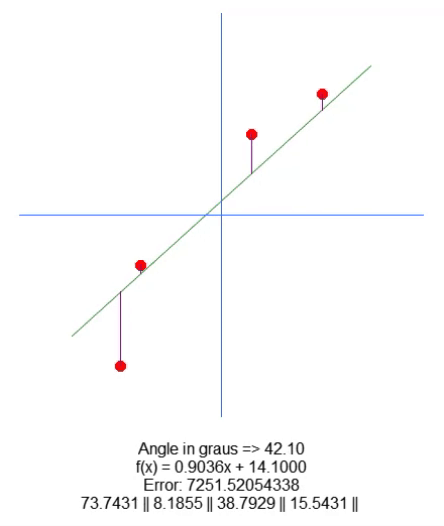
基本的に、根を移動するために、18行目に変数を追加しました。上矢印と下矢印を使用して、65行目のこの変数の値を変更できます。他のすべては非常に簡単です。コード内にあるこの新しい変数の値に基づいて、紫色の線の長さの値を調整するだけです。非常に簡単なので、その方法を説明する必要はないと思います。


最終的な考察

この記事では、数式がコードでの実装よりもはるかに複雑に見えることが多いことを説明しました。多くの人は、そのようなことをおこなうのは難しいと考えていますが、ここではすべてが見た目よりもはるかに簡単であることを示しました。しかし、すべての作業が完了したわけではありません。実装したのはその一部だけです。次に、直線の方程式をより適切な方法で記述する方法を見つける必要があります。これには、この記事の最後のコードを使用します。このトピックの冒頭で想像していたこととは反対に、ループを介して直線関数を見つけることは、思ったほど簡単ではありません。これは、探索する別の変数を追加するためです。100万の変数がある場合、方程式を見つけるのにどれだけの作業が必要になるか考えてみてください。これを力ずくでおこなうことは完全に不可能ですが、数学を適切に使用すれば、方程式を見つけるのははるかに簡単になります。

最後にもう1つ。次の記事に進む前に、最後に提供されているコード（上の画像に示すものを生成する）を使用して方程式を見つけてみてください。これは非常に難しい作業であることがわかるでしょう。それでは、次の記事でお会いしましょう。



MetaQuotes Ltdによりポルトガル語から翻訳されました。
元の記事: https://www.mql5.com/pt/articles/13670

添付されたファイル |
ZIPをダウンロード
Anexo.mq5 (4.53 KB)
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動
リプレイシステムの開発（第49回）：物事は複雑になる(I) リプレイシステムの開発（第49回）：物事は複雑になる(I)
この記事では、物事は少し複雑になります。前回の記事で紹介した内容を使用して、ユーザーが独自のテンプレートを使用できるようにテンプレート ファイルを開きます。ただし、MetaTrader 5の負荷を軽減するために指標を改良していく予定なので、変更は徐々におこなっていく予定です。
リプレイシステムの開発（第48回）：サービスの概念を理解する リプレイシステムの開発（第48回）：サービスの概念を理解する
何か新しいことを学んでみませんか。この記事では、スクリプトをサービスに変換する方法と、それがなぜ便利なのかについて説明します。
リプレイシステムの開発（第50回）：物事は複雑になる(II) リプレイシステムの開発（第50回）：物事は複雑になる(II)
チャートIDの問題を解決すると同時に、ユーザーが希望する資産の分析とシミュレーションに個人用テンプレートを使用できるようにする機能を提供し始めます。ここで提示される資料は教育目的のみであり、提示される概念の学習および習得以外の目的には決して適用されないものとします。
行列分解：より実用的なモデリング 行列分解：より実用的なモデリング
行と列ではなく列のみが指定されているため、行列モデリングが少し奇妙であることに気付かなかったかもしれません。行列分解を実行するコードを読むと、これは非常に奇妙に見えます。行と列がリストされていることを期待していた場合、因数分解しようとしたときに混乱する可能性があります。さらに、この行列モデリング方法は最適ではありません。これは、この方法で行列をモデル化すると、いくつかの制限に遭遇し、より適切な方法でモデル化がおこなわれていれば必要のない他の方法や関数を使用せざるを得なくなるためです。