
El modelo de movimiento de precios y sus principales disposiciones (Parte 1): La versión del modelo más simple y sus aplicaciones
Introducción
Hasta el día de hoy, aún no se había creado una teoría matemática rigurosa del movimiento de precios: solo había una serie de suposiciones, sin respaldo estadístico o teoría alguna, que afirmaban que después de tales patrones, el precio se mueve de tal o cual manera. Este artículo presenta los conceptos y fundamentos del aparato matemático de una teoría rigurosa del movimiento de precios.
Conceptos y representaciones básicas del modelo
El modelo analítico desarrollado del movimiento de precios se basa en 6 nociones principales que veremos a continuación
1. El mercado financiero es un sistema altamente complejo, sujeto a la acción de una gran variedad de factores aleatorios externos que lo modifican (noticias políticas o económicas importantes, la entrada de grandes jugadores al mercado y un largo etcétera). Debido a la dinámica de los factores que actúan sobre dicho sistema, este debe caracterizarse por un estado variable en el tiempo o fundamentalmente dinámico (no estacionario). Asumiremos que el estado actual del mercado está descrito por las cotizaciones actuales ![]() , sus herramientas clave
, sus herramientas clave ![]() y sus velocidades
y sus velocidades ![]() . Estos últimos, sin embargo, solo se estiman aproximadamente a partir de la historia reciente.
. Estos últimos, sin embargo, solo se estiman aproximadamente a partir de la historia reciente. ![]() , donde:
, donde:
-
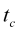 es el momento actual del tiempo,
es el momento actual del tiempo, -
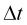 es el intervalo de la historia seleccionado para evaluar la tasa de cambio de las cotizaciones
es el intervalo de la historia seleccionado para evaluar la tasa de cambio de las cotizaciones 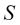 .
.
Para recoger estadísticas más o menos significativas que nos permitan establecer estas tasas (determinadas, por ejemplo, por la inclinación de las rectas de regresión) con un error que resulte mínimo, deberemos aumentar ![]() , lo cual creará incertidumbre respecto al momento actual al que se refieren los parámetros calculados. Por ello, siempre existirá una incertidumbre fundamental al identificar el estado del mercado.
, lo cual creará incertidumbre respecto al momento actual al que se refieren los parámetros calculados. Por ello, siempre existirá una incertidumbre fundamental al identificar el estado del mercado.
Además, a diferencia de, por ejemplo, la mecánica cuántica, para cada cotización tenemos solo una historia y ningún conjunto ![]() de historias similares que podrían haber aumentado significativamente las estadísticas, haciendo que la descripción del mercado ya resulte muy incierta. También está claro que todas las cotizaciones del mercado están interconectadas, por lo tanto
de historias similares que podrían haber aumentado significativamente las estadísticas, haciendo que la descripción del mercado ya resulte muy incierta. También está claro que todas las cotizaciones del mercado están interconectadas, por lo tanto ![]() y
y ![]() , que describen el mercado, son sus coordenadas y velocidades generalizadas, es decir, parámetros cuyo número se puede reducir debido a sus conexiones.
, que describen el mercado, son sus coordenadas y velocidades generalizadas, es decir, parámetros cuyo número se puede reducir debido a sus conexiones.
2. Los factores y eventos importantes, en sí mismos, no influyen en el mercado. Hay una gran variedad de participantes en el mercado: bancos centrales y comerciales, agentes interbancarios, casas de cambio, fondos de inversión, brókeres, tráders, analistas, etc. Los participantes del mercado, tras recibir información sobre eventos importantes, influyen en el estado del mercado en el contexto de su comprensión de estos eventos según la situación que ya se ha desarrollado en el mercado y, por supuesto, según sus intereses.
En general, el mercado afecta a sus participantes y sus participantes influyen en él; por consiguiente, en el mercado se dan numerosas retroalimentaciones. Las retroalimentaciones positivas permiten que pequeños impactos produzcan una fuerte respuesta similar a una avalancha, mientras que las negativas, por el contrario, resisten la aparición de respuestas tan fuertes, manteniendo la estabilidad de la dinámica del mercado o la inercia de su desarrollo.
3. La retroalimentación positiva del mercado ocurre, por lo general, justo después de la acción de factores aleatorios externos y fuertes sobre el mismo, causando revuelo entre sus participantes. Este cambia abruptamente su estado y, en consecuencia, los valores de las cotizaciones que lo caracterizan. Los tiempos característicos ![]() de tales saltos son muy pequeños y, en la práctica, resulta difícil identificar el comienzo de la aparición de movimientos tan fuertes, cuyas direcciones también tengan un grado suficiente de fiabilidad y, lo más importante, no tengan demoras (para el mismo
de tales saltos son muy pequeños y, en la práctica, resulta difícil identificar el comienzo de la aparición de movimientos tan fuertes, cuyas direcciones también tengan un grado suficiente de fiabilidad y, lo más importante, no tengan demoras (para el mismo ![]() ) no establecidas según la historia previa más próxima. Más concretamente, no están modelados en la aproximación de la teoría del mercado ahora presentada. Pero en el mercado, como en la realidad física, funciona el principio universal de Le Chatelier, según el cual, cualquier impacto sobre un sistema que se encuentre en un estado de equilibrio estable (en este caso, cuasi-estable, es decir, que pasa por estados de equilibrio cercano) provocará procesos de fortalecimiento encaminados a contrarrestar los cambios generados por dicho impacto.
) no establecidas según la historia previa más próxima. Más concretamente, no están modelados en la aproximación de la teoría del mercado ahora presentada. Pero en el mercado, como en la realidad física, funciona el principio universal de Le Chatelier, según el cual, cualquier impacto sobre un sistema que se encuentre en un estado de equilibrio estable (en este caso, cuasi-estable, es decir, que pasa por estados de equilibrio cercano) provocará procesos de fortalecimiento encaminados a contrarrestar los cambios generados por dicho impacto.
En apariencia, existen muchos mecanismos que buscan devolver el mercado a su estado original, por ejemplo, el enfrentamiento entre “toros” y “osos”, el deseo de los bancos de mantener los tipos de cambio en ciertos niveles, la opinión expresada por distintos analistas en artículos personalizados pagados por ciertos intereses contrapuestos de grupos, etcétera, que son precisamente en lo que consisten las retroalimentaciones negativas, que comienzan a actuar inmediatamente después de fuertes saltos provocados por eventos importantes u otras razones -ya internas-, de las que hablaremos un poco más adelante.
Al mismo tiempo, cuando una de las fuerzas inclina el mercado más allá de cierto límite en la dirección que necesitan, estas se "calman", pero las fuerzas antagónicas se vuelven más activas. Por lo tanto, estas contraposiciones a cambios abruptos dan lugar a fluctuaciones en las cotizaciones que suceden después de que el mercado haya sido sacado de su estado de equilibrio dinámico por alguna fuerte influencia de terceros (o propia, como analizaremos más adelante). Obviamente, según la presencia de toda una variedad de mecanismos diferentes para volver al estado inicial, también surgirá todo un espectro de frecuencias de fluctuación de las cotizaciones.
Por lo tanto, después de fuertes eventos que perturban el equilibrio del mercado, surgen diversas fluctuaciones de cotizaciones que, además, se amortiguan, ya que la relevancia de los eventos que han causado su salto se pierde con el tiempo, y un número creciente de participantes del mercado transfieren gradualmente su actividad a otros eventos -sucedidos más tarde-, formando respuestas ya para ellos. Por lo tanto, las cotizaciones tienen muchos modos de ![]() oscilaciones, que se caracterizan por frecuencias
oscilaciones, que se caracterizan por frecuencias ![]() y atenuación
y atenuación ![]() , así como el momento de su aparición
, así como el momento de su aparición ![]() .
.
4. La confrontación de fuerzas opuestas (como la “lucha de toros y osos”) que provoca fluctuaciones en las cotizaciones no siempre es totalmente compensada, y, con frecuencia, una de estas fuerzas, en un grado u otro, prevalece sobre su antagonista, generando un deriva media del precio, más precisamente, entonces tiene lugar una deriva estadística promedio de la moda de fluctuación de precios correspondiente que viene junto con sus fluctuaciones basadas en el tiempo ![]() . Es esta ruptura del equilibrio de acción de la mayoría de las fuerzas polares lo que genera la velocidad de fase
. Es esta ruptura del equilibrio de acción de la mayoría de las fuerzas polares lo que genera la velocidad de fase![]() correspondiente a la moda de oscilación, que resulta diferente para diferentes modas de oscilación y es proporcional al grado de desequilibrio de las fuerzas que generan cada moda. Obviamente, esta velocidad de fase puede tomar valores tanto positivos como negativos, lo cual nos permite hablar del vector de onda de la
correspondiente a la moda de oscilación, que resulta diferente para diferentes modas de oscilación y es proporcional al grado de desequilibrio de las fuerzas que generan cada moda. Obviamente, esta velocidad de fase puede tomar valores tanto positivos como negativos, lo cual nos permite hablar del vector de onda de la ![]() moda correspondiente
moda correspondiente ![]() . La presencia de frecuencias y velocidades de fase hace legítimo analizar ondas de fluctuaciones que de alguna manera se propagan por la medición del precio, que para cada precio forman un paquete con su conjunto completo, cuya velocidad de grupo caracterizará el movimiento promedio del precio dado.
. La presencia de frecuencias y velocidades de fase hace legítimo analizar ondas de fluctuaciones que de alguna manera se propagan por la medición del precio, que para cada precio forman un paquete con su conjunto completo, cuya velocidad de grupo caracterizará el movimiento promedio del precio dado.
5. En la teoría del mercado también hay que considerar, por supuesto, que el precio no es un único número en cada momento, ya que, en primer lugar, hay dos precios separados por un spread: el de compra y el de venta, que, además, forman una profundidad de mercado para muchas órdenes pendientes de los precios reales del mercado financiero, donde cada punto de la escala de precios se caracteriza por el volumen de órdenes colocadas en él, es decir, podemos hablar de una determinada distribución de las probabilidades de las solicitudes por medida de precio.
La profundidad de mercado expresa el equilibrio natural de la oferta y la demanda, y precisamente este equilibrio determina en gran medida hacia dónde irá el precio promedio. Después de todo, si el número de órdenes límite de compra excede el número de órdenes límite de venta, será más fácil vender a un precio de mercado (sin deslizamiento), mientras que el precio promedio bajará. Por el contrario, cuanto más superen los volúmenes de venta a los de compra, más fácil será comprar a precio de mercado, mientras que el precio subirá, es decir, el precio tenderá a moverse en contra de la asimetría de su distribución en la profundidad del mercado tratando de igualarlo.
Pero debido a muchos otros factores (salvo el equilibrio de la oferta y la demanda, que, por cierto, también es probable) que actúan sobre el precio, su proceso de movimiento es probabilístico, en el sentido de que no determina claramente el precio futuro, sino que establece la subsiguiente distribución de sus probabilidades, lo cual, en la práctica, es característico de los precios de mercado en cada momento, tanto para el pasado como para el presente, y no solo para el futuro.
El hecho es que los precios actuales (demanda u oferta) que vemos en los gráficos son simplemente expresiones abstractas simplificadas de estos precios, que en realidad están descritos por funciones mucho menos definidas (que los gráficos de precios). Después de todo, en realidad, el precio para un participante particular del mercado, que, estrictamente hablando, tiene el significado de un acuerdo entre el vendedor y el comprador, puede adquirir un valor exacto para este participante solo después de que se haya completado la transacción (venta, compra o cierre de una posición en el mercado)
Esto es similar a la reducción mecánica cuántica: un estado inicialmente vago, en este caso, el valor del precio, expandido en el mercado real (y, además, en un centro de negociación) por el aumento del spread, el deslizamiento, los retrasos en la ejecución de las órdenes, que son solo reflejos visibles del precio inicialmente distribuido, y que en su forma verdadera está latente y no se muestra en los gráficos. Por lo tanto, de forma objetiva, el precio está descrito por la distribución de la probabilidad, y el grupo de ondas que describe el movimiento del precio en forma de modelo, describe el movimiento de su distribución.
6. Y, finalmente, si tratamos de desvelar exhaustivamente la ontología del funcionamiento del mercado, empezaremos a detectar patrones internos o propios, que van más allá del alcance de todo lo anteriormente mencionado. Por supuesto, los precios de los instrumentos de mercado son fijados prácticamente por los participantes del mercado, que, por cierto, no pueden evitar introducir elementos subjetivos en los precios. Sin embargo, resulta que el orden de cambio del precio puede describirse formalmente como una descomposición en cambios surgidos caóticamente, diferentes en magnitud, los saltos de precios y las numerosas ondas causadas por ellos, que se propagan por la dimensión del precio, lo cual ya expresa un modelo teórico para describir el movimiento de precios.
Entonces, se hace posible tal modelización y, además, esta adquiere un carácter objetivo, debido a la presencia de un gran número de participantes del mercado y su estrecha interconexión en un único sistema que expresa este mercado, en el que, por tanto, surgen patrones estadísticos derivados de su acción acumulativa. Y, aunque la interacción y las acciones de los participantes individuales del mercado de ninguna forma son caracterizadas por las ondas en la dimensión del precio, no obstante, si echamos una mirada analítica a lo que está sucediendo en él, las ondas de precios podrán ser identificadas y se percibirá su existencia, como sus características emergentes, formalmente separadas de la actividad de los numerosos participantes del mercado, y adquiriendo su propia realidad.
Como resultado, estas ondas de precios se convertirán en elementos constitutivos de la formación de una dinámica macroscópica propia del mercado, que, como algo integral (surgido según el tipo de formación de patrones estadísticos), ya no dependerá de las influencias aleatorias, externas e individuales ni de las reacciones de los participantes del mercado a dichas influencias. El funcionamiento correcto de sistemas complejos, no estacionarios e inestables, tales como el mercado, se describe usando ecuaciones no lineales que permiten muchas soluciones (a veces incluso muy diferentes), cuyos cambios aleatorios (en los llamados “puntos de bifurcación”) producen instantáneamente su reordenamiento, expresado para el mercado en la aparición de grandes saltos de las cotizaciones que lo describen, lo que en este caso se debe puramente a procesos propios del mercado, y no a influencias externas individuales.
Análisis del modelo más simple
Entonces, las numerosas modas de onda de las fluctuaciones amortiguadas en las cotizaciones de un determinado instrumento ![]() causadas por eventos diferentes, ocurridos en distintos puntos en el tiempo
causadas por eventos diferentes, ocurridos en distintos puntos en el tiempo ![]() y diferentes en fuerza y génesis, se superpondrán unas a otras, dando lugar a una oscilación compleja
y diferentes en fuerza y génesis, se superpondrán unas a otras, dando lugar a una oscilación compleja
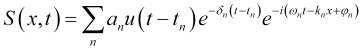 , (1)
, (1)
dónde
-
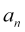 es la amplitud real inicial de la oscilación de la moda
es la amplitud real inicial de la oscilación de la moda 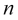
-
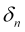 es su coeficiente de atenuación,
es su coeficiente de atenuación, -
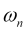 es la frecuencia de oscilación de esta moda,
es la frecuencia de oscilación de esta moda, -
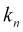 es el vector de onda de su distribución por la escala de precios
es el vector de onda de su distribución por la escala de precios 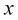 ,
, -
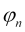 es la fase inicial de esta oscilación,
es la fase inicial de esta oscilación, - y
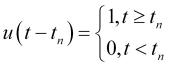 es la función unitaria que expresa el momento de inicio de la oscilación
es la función unitaria que expresa el momento de inicio de la oscilación 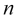 .
.
Introducimos una amplitud compleja
![]() , (2)
, (2)
que, obviamente, es una función de módulo decreciente. Entonces, podemos describir la expresión para la oscilación multimodal (1) de forma más simple
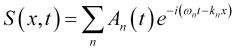 , (3)
, (3)
Teniendo en cuenta que la velocidad de fase de propagación de la moda de oscilación es igual a ![]() , la relación (3) toma la forma
, la relación (3) toma la forma
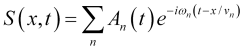 (4)
(4)
Es obvio que la densidad de la probabilidad del precio es el cuadrado del módulo de la amplitud de su paquete de ondas (4)
![]() . (5)
. (5)
Tenga en cuenta que en el modelo más simple presentado aquí, los momentos ![]() de la aparición de nuevos eventos fuertes de terceros y propios, y las amplitudes iniciales
de la aparición de nuevos eventos fuertes de terceros y propios, y las amplitudes iniciales ![]() de las fluctuaciones que provocan se consideran fundamentalmente aleatorias (aunque, tal vez, puedan predecirse con cierto grado de certeza basándose en un análisis de la historia de cotizaciones anterior). Por lo tanto, en este modelo, el intervalo de desarrollo predecible del mercado comienza desde el último evento fuerte y continúa hasta que ocurre el próximo evento de este tipo.
de las fluctuaciones que provocan se consideran fundamentalmente aleatorias (aunque, tal vez, puedan predecirse con cierto grado de certeza basándose en un análisis de la historia de cotizaciones anterior). Por lo tanto, en este modelo, el intervalo de desarrollo predecible del mercado comienza desde el último evento fuerte y continúa hasta que ocurre el próximo evento de este tipo.
Vamos a intentar, desarrollando de forma teórica el modelo establecido anteriormente, obtener conclusiones útiles en la práctica. El grupo de ondas (3) describe la distribución de la amplitud de la probabilidad del precio. El precio, como se ha mostrado en el punto 5, posee incertidumbres fundamentales tanto en su valor como en su velocidad (punto 1), que se corresponde totalmente con su descripción usando un paquete de ondas (4), el cual contiene las incertidumbres en coordenadas de tiempo y frecuencias, o de posición espacial y vector de onda, a partir de lo cual también podemos encontrar la incertidumbre de su velocidad. Vamos a establecer las relaciones para las incertidumbres de precio que surgen en este caso ![]() y el vector de onda
y el vector de onda ![]() .
.
Los valores ![]() del parámetro
del parámetro ![]() multidimensional en sus modos básicos (ortonormales)
multidimensional en sus modos básicos (ortonormales) ![]() de las oscilaciones, el sistema oscilante lineal (las oscilaciones de modos simples interfieren)
de las oscilaciones, el sistema oscilante lineal (las oscilaciones de modos simples interfieren)
![]() (6)
(6)
se encuentran de la forma estándar para sistemas oscilantes a partir de ecuaciones (características) para los valores propios de tales parámetros
![]() , (7)
, (7)
dónde ![]() son los operadores de las cantidades correspondientes.
son los operadores de las cantidades correspondientes.
Así que si ![]() y describe el modo de las fluctuaciones de precios, entonces los operadores de precio y el vector de onda se podrán especificar como
y describe el modo de las fluctuaciones de precios, entonces los operadores de precio y el vector de onda se podrán especificar como ![]() y
y 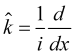 , que cumplirán sus ecuaciones (7). La incertidumbre de los parámetros
, que cumplirán sus ecuaciones (7). La incertidumbre de los parámetros ![]() viene dada por sus fluctuaciones de la raíz cuadrada media
viene dada por sus fluctuaciones de la raíz cuadrada media
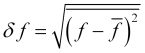 . (8)
. (8)
Dado que![]() de la amplitud de probabilidad del estado
de la amplitud de probabilidad del estado ![]() y los valores
y los valores ![]() del parámetro
del parámetro ![]() , entonces tendremos que el valor promedio de este parámetro
, entonces tendremos que el valor promedio de este parámetro
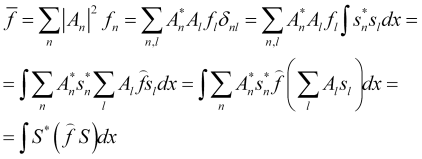 . (9)
. (9)
Está claro que (9) es verdadera bajo la condición de normalización
![]() . (10)
. (10)
Obviamente, para cualquier ![]() real
real
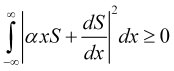 (11)
(11)
Expandiendo el integrando, obtenemos
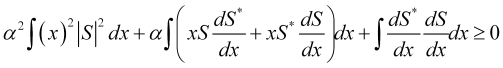 . (12)
. (12)
La primera integral en esta expresión es el cuadrado de la incertidumbre del valor del precio ![]() . La segunda integral, debido a la normalización de la amplitud de la probabilidad del precio, resultará ser una constante
. La segunda integral, debido a la normalización de la amplitud de la probabilidad del precio, resultará ser una constante
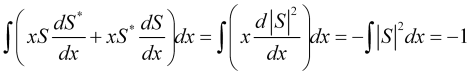 . (13)
. (13)
Y la tercera expresa el cuadrado de la incertidumbre del número de onda
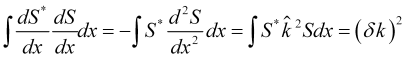 . (14)
. (14)
Las relaciones (12-14) y la incertidumbre del precio al cuadrado, juntas, dan la desigualdad
![]() . (15)
. (15)
La desigualdad (15) se cumple para cualquier ![]() real, cuando el discriminante de la ecuación cuadrática correspondiente es negativo, lo cual nos da una expresión para las incertidumbres del precio y su vector de onda. Escribiendo la expresión para el discriminante, obtenemos la relación entre la incertidumbre del valor del precio y su vector de onda
real, cuando el discriminante de la ecuación cuadrática correspondiente es negativo, lo cual nos da una expresión para las incertidumbres del precio y su vector de onda. Escribiendo la expresión para el discriminante, obtenemos la relación entre la incertidumbre del valor del precio y su vector de onda
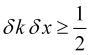 . (16)
. (16)
Minimiza la relación (16) de la sinusoide modulada gaussiana
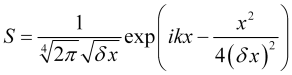 . (17)
. (17)
La relación (17) es importante para la práctica, ya que nos dará una expresión para la función wavelet (llamada wavelet de Morlet), según la cual la serie de precios puede descomponerse de manera óptima o con el menor error para su extrapolación.
Aplicaciones prácticas del modelo más simple
Pronosticar el movimiento del precio usando la ecuación (4) resulta problemático y poco fiable, debido a la dificultad que implica identificar los parámetros presentes en ella, la presencia de incertidumbres fundamentalmente inamovibles en los parámetros y, lo que es más importante, debido a los saltos aleatorios frecuentes e impredecibles (según el modelo más simple) que se presentan. Sin embargo, hay una serie de indicadores que resultan útiles a la hora de comerciar: los osciladores, que simplemente filtran estos grandes saltos impredecibles y tienen un poder predictivo por sí mismos, teniendo solo un inconveniente, pero extremadamente significativo, el retraso, cosa inherente a todas las medias móviles en los que se basan. Por lo tanto, junto con el pronóstico directo de los precios, resulta prometedor, o incluso quizás más prometedor, predecir las lecturas de dichos indicadores, lo cual nivelará su retraso.
El paquete de oscilaciones (4) está clasificado por osciladores para evitar saltos fuertes y presenta el mismo desvanecimiento rápido de sus componentes espectrales, por lo que las lecturas de dichos indicadores se extrapolan mejor usando ciertas funciones wavelet que también disminuyen rápidamente. Al mismo tiempo, para la descomposición más adecuada de los procesos de mercado en un espectro, necesitamos funciones wavelet que expresen los rasgos característicos de estos procesos, revelados a partir del siguiente.
El precio en el mercado, en términos generales, siempre se mueve a saltos, que, más precisamente, forman su movimiento principal, cuyos aspectos se presentan en el blog "True and illusory currency market trends". Con toda claridad, los saltos de precio son revelados visualmente por el indicador de densidad de la probabilidad del precio Probabilities distribution of price .
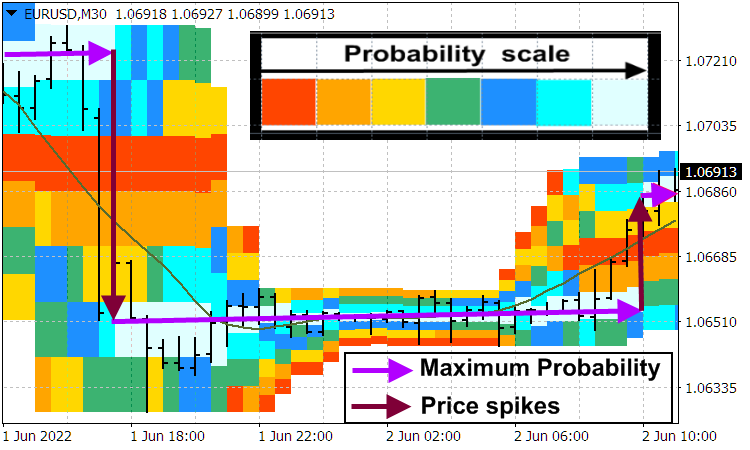
Supongamos, por ejemplo, que el precio ha saltado desde el nivel ![]() hasta la magnitud
hasta la magnitud ![]() . Después de una avalancha de saltos de precio ascendentes y el comienzo de su desaceleración, muchos tráders que han logrado abrir en esa tendencia cierran sus posiciones, lo cual provoca un retroceso brusco en la dirección opuesta hasta un nuevo mínimo de precios.
. Después de una avalancha de saltos de precio ascendentes y el comienzo de su desaceleración, muchos tráders que han logrado abrir en esa tendencia cierran sus posiciones, lo cual provoca un retroceso brusco en la dirección opuesta hasta un nuevo mínimo de precios. ![]() . Luego, las fluctuaciones de los precios se relajan gradualmente y el precio promedio se establece aproximadamente en el área
. Luego, las fluctuaciones de los precios se relajan gradualmente y el precio promedio se establece aproximadamente en el área ![]() , que, de hecho, cruza muy rápidamente después de su valor atípico negativo (retroceso). El indicador de oscilador filtra el salto
, que, de hecho, cruza muy rápidamente después de su valor atípico negativo (retroceso). El indicador de oscilador filtra el salto ![]() y refleja la fluctuación de precios amortiguada con la amplitud inicial
y refleja la fluctuación de precios amortiguada con la amplitud inicial ![]() sobre el nivel
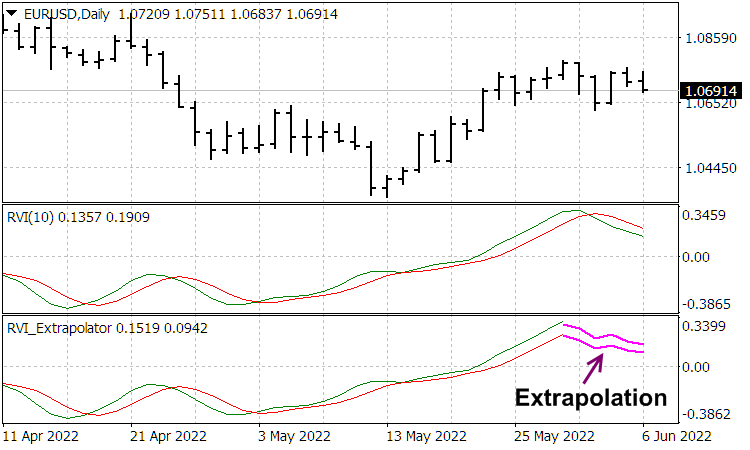
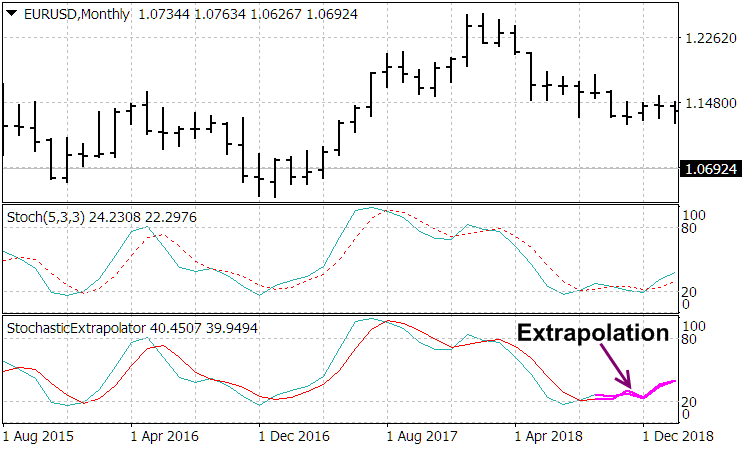
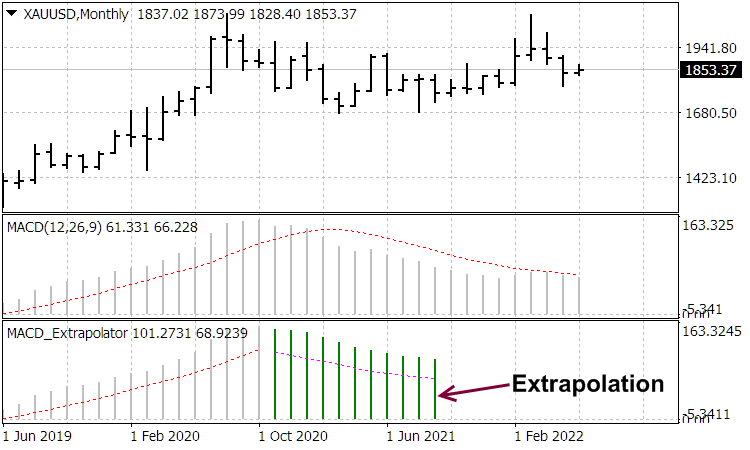
sobre el nivel ![]() , en relación con el cual, al principio, se produce un fuerte aumento positivo; luego sigue un rebote negativo, generando una función antisimétrica a partir de dos picos agudos dirigidos de manera opuesta; al mismo tiempo, la constante de tiempo del indicador que funciona como filtro expande dichos picos, un par de los cuales, junto con las posteriores fluctuaciones relajadas de precio, forman funciones de ondículas antisimétricas, según las cuales las lecturas del indicador de oscilador correspondiente son bien descompuestas. Los indicadores-extrapoladores correspondientes son presentados por el autor en el artículo del blog "Wavelet extrapolation of oscillator indicators".
, en relación con el cual, al principio, se produce un fuerte aumento positivo; luego sigue un rebote negativo, generando una función antisimétrica a partir de dos picos agudos dirigidos de manera opuesta; al mismo tiempo, la constante de tiempo del indicador que funciona como filtro expande dichos picos, un par de los cuales, junto con las posteriores fluctuaciones relajadas de precio, forman funciones de ondículas antisimétricas, según las cuales las lecturas del indicador de oscilador correspondiente son bien descompuestas. Los indicadores-extrapoladores correspondientes son presentados por el autor en el artículo del blog "Wavelet extrapolation of oscillator indicators".
Podemos juzgar las lecturas de estos indicadores a partir de las siguientes capturas de pantalla
Conclusión
Hoy hemos presentado los principios básicos de la formación de precios y el funcionamiento del mercado. También hemos mostrado que el precio puede formarse no solo por la interacción de los participantes del mercado, sino también debido a procesos de mercado emergentes internos similares a ondas que aparecen debido a la gran cantidad de estos participantes. Asimismo, hemos presentado parcialmente los conceptos básicos de análisis para describir estos procesos emergentes y un enfoque para su pronóstico. Además, en el próximo artículo, mostraremos el aparato matemático del comercio óptimo, desarrollado sobre la base de este análisis.
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/10955
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Aprendiendo a diseñar un sistema de trading con MFI
Aprendiendo a diseñar un sistema de trading con MFI
 Aprendizaje automático y data science (Parte 03): Regresión matricial
Aprendizaje automático y data science (Parte 03): Regresión matricial
 Vídeo: Configuramos MetaTrader 5 y MQL5 para el comercio automatizado sencillo
Vídeo: Configuramos MetaTrader 5 y MQL5 para el comercio automatizado sencillo
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso
Respecto a la primera imagen. Estoy de acuerdo. Las distribuciones de probabilidad, como los paquetes de ondas, se extenderán, por supuesto, con el tiempo, aumentando su semiancho.
Esto se codifica en el exponente, donde el exponente es el tiempo multiplicado por el factor de amortiguación.
En cuanto a los otros dos gráficos (uno muestra el impulso y el retroceso, el otro muestra la ruptura y la inversión).
Los conceptos (ideas) que se dan en mi artículo son simplemente la base ideológica del modelo matemático del movimiento del precio desarrollado por mí. Por sí mismos, estos conceptos no pueden ser confirmados ni refutados por ningún gráfico de precios. Pero, si el modelo matemático en sí ya es capaz de explicar los movimientos de precios mostrados por usted en los gráficos (y mi modelo matemático lo explica), entonces estos gráficos servirán como confirmación de este modelo. Tales cuestiones son consideradas por mí en el tercer artículo, que pronto será publicado.
Sí, el modelo de Markov de conmutación de modos, el enlace a la que usted proporciona, con el fin, tal como yo lo entiendo, para explicar la inversión en el segundo gráfico, por supuesto, es interesante, pero esto es un modelo puramente técnico de cambio de las características de la serie de tiempo y nada más. Mi modelo es mucho más fundamental y va a los fundamentos mismos de la fijación de precios y de los procesos propios del mercado.
Idea principal 5: "... Sin embargo, debido a otros muchos factores que afectan al precio (aparte del equilibrio de la oferta y la demanda, que también tiene carácter probabilístico), su movimiento también es probabilístico en el sentido de que no determina claramente el precio futuro, sino que establece la distribución posterior de sus probabilidades, que es característica de los precios de mercado en todo momento: pasado, presente y futuro."
"...el precio queda objetivamentedescritopor la distribución de probabilidades,y el conjunto de ondas, que describe el movimiento del precio en forma de modelo, describe el movimiento de su distribución."
===========================================================================================================
Idea principal 6:
"... Tal modelización se hace posible. Además, se hace más objetiva debido a la presencia de un enorme número de participantes en el mercado y su estrecha interconexión en un único sistema, en el que, por tanto, surgen patrones estadísticos de su acción acumulativa. ... Sin embargo, en el caso del enfoque analítico, las ondas de precios resultan ser detectables y existentes..."
".. . , al igual que sus parámetrosemergentes que se desprenden formalmente de la actividad de los numerosos participantes en el mercado que las crean conjuntamente, adquiriendo realidad propia."
En principio, tus gráficos pueden servir como buenas ilustraciones de las ideas que expongo. Gracias.
En principio, sus gráficos pueden servir para ilustrar bien las ideas que expongo. Gracias.
Gracias a usted.
Estoy estudiando las ecuaciones.