As was previously shown in the blog " True and illusory currency market trends" the price in the market always moves in jumps, which, more precisely, form its main movement.
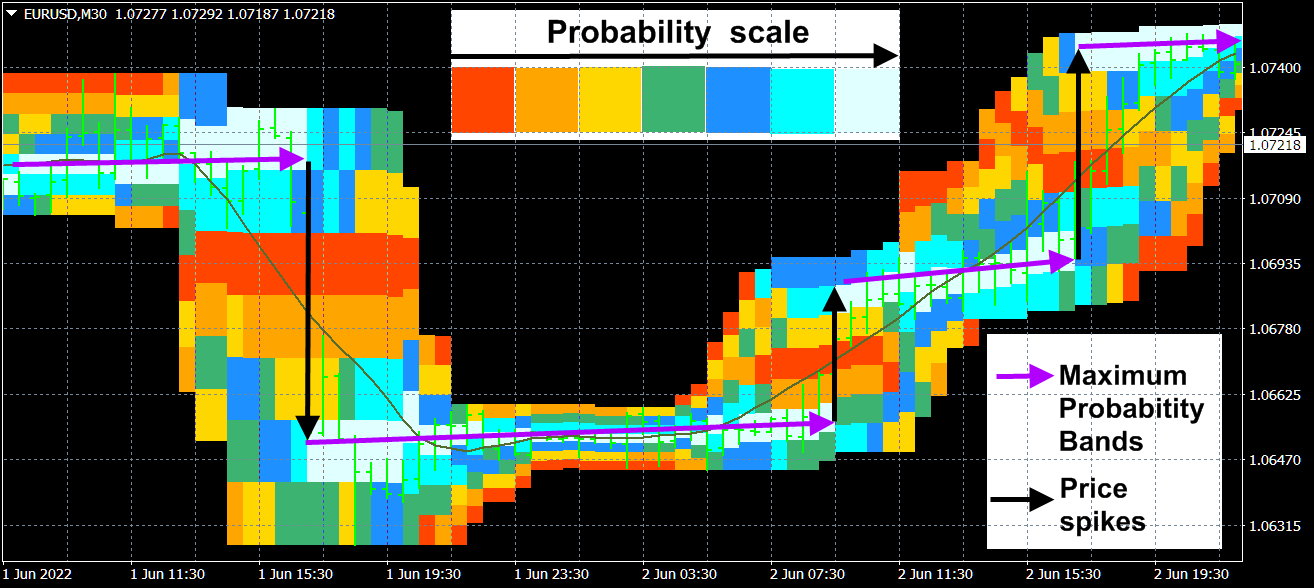
Probabilities distribution of price
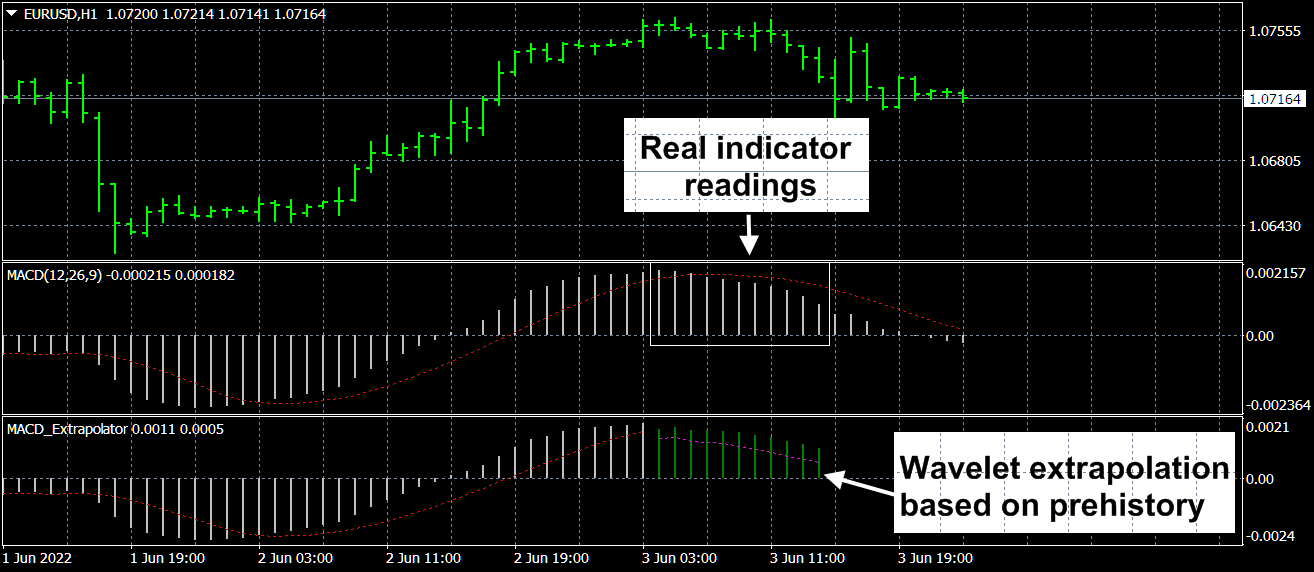
These jumps are caused both by external strong events - such as important news, and by own processes in the market, which, as a most complex system, has its own dynamics and, due to sharply different solutions of the equations describing it, can make sharp changes in its state at bifurcation points. The moments of such jumps and their magnitudes are practically unpredictable, in any case, if they are predictable, then with a low confidence level. Because of what, the movement of the price itself is very problematic to predict. However, there are a number of indicators that are useful for trading - oscillators, which, in fact, filter out these large unpredictable jumps and have predictive power themselves. But these oscillator indicators have one extremely significant drawback - lagging, which is inherent in all moving averages on which they are based. Therefore, it is promising to predict the readings of such indicators, which levels their lag. The author bases his approach to predicting the readings of oscillator indicators on the following.
The market has a very short memory, in any case, the information formally describing it quickly becomes obsolete and loses its weight in the formation of the current prices of its instruments. Therefore, from a mathematical point of view, to predict the future parameters of the market, the most promising is the expansion of its parameters over the spectrum of rapidly decreasing wavelet functions with further extrapolation of such expressions towards future values. Moreover, for the most adequate decomposition of processes into a spectrum, functions are needed that express the characteristic features of these processes, which for market processes are contained in wavelet functions. The very correspondence of wavelet functions to the readings of oscillator indicators is due to the following or similar things.
Suppose, for example, the price jumped up from the level 
to the value 
. After an avalanche of increasing price jump and the beginning of its slowdown, many traders who managed to open on such a trend close their positions, which leads to a sharp rollback in the opposite direction to a new price low 
. Then the price fluctuations gradually relax and the average price is set approximately at the level of 
, which it, in fact, very quickly crosses after its negative surge (rollback). The oscillator indicator filters jump 
and reflects a fading price fluctuation with an initial amplitude of 
around the level of 
, relative to which a sharp positive surge occurs first, and then a negative rebound follows, generating an antisymmetric function from two oppositely directed sharp peaks; at the same time, the time constant of the indicator working as a filter expands such peaks, a pair of which, together with the mediating relaxing price fluctuations, forms antisymmetric wavelet functions, according to which the readings of the corresponding oscillator indicator are well decomposed.
The author uses a number of wavelet functions (including the Morlet wavelet and a slightly modified Gaussian function, which are shown here in Figure 1), the expansion of which more or less reliably allows extrapolating the future values of oscillator indicators.
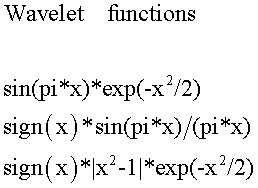
Figure. 1.
However, the most accurate approach for forecasting is to use the Morlet function in the following form
,
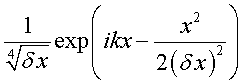where 
is the average wave number of price fluctuations, and 
is its variance, due to a number of mathematical difficulties, the author has not yet implemented.
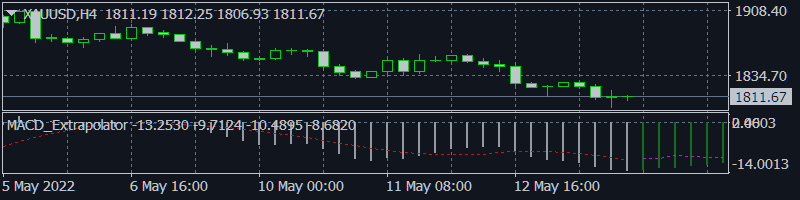
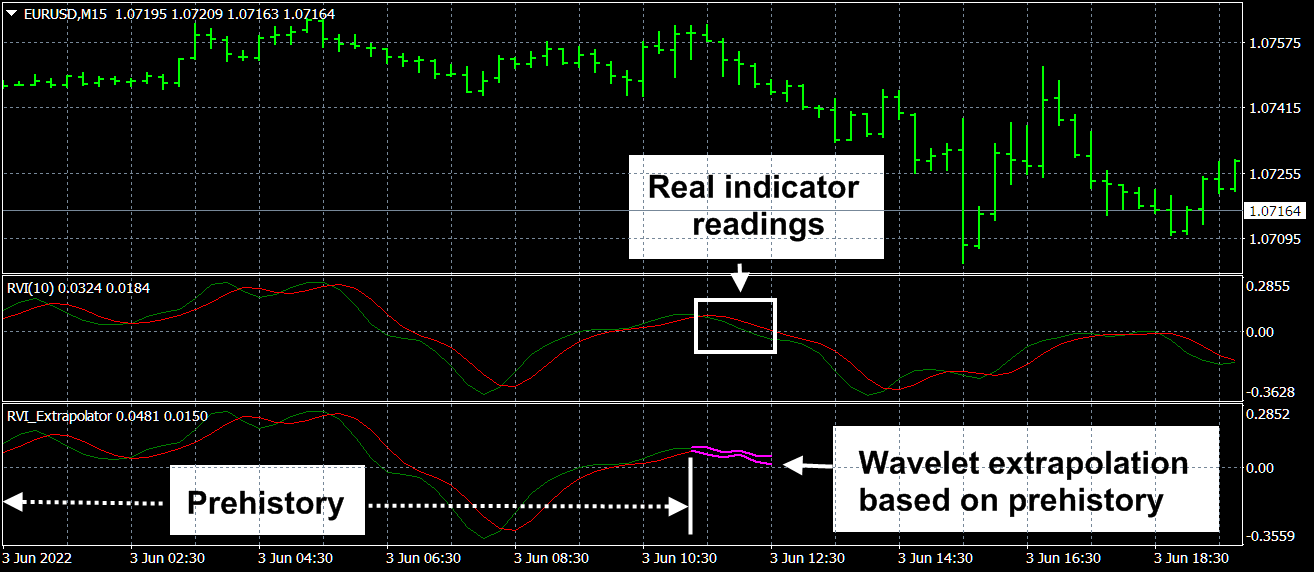
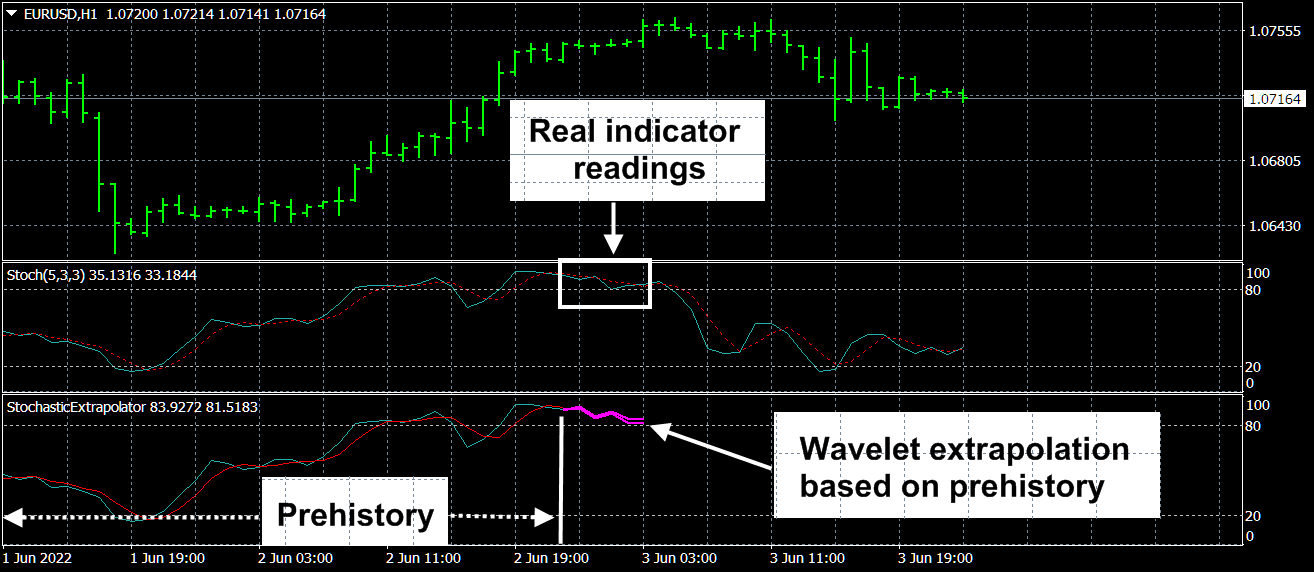
The author presents the following extrapolator indicators:
StochasticExtrapolator
RVI Extrapolator
MACD Extrapolator
