El modelo de movimiento de precios y sus principales disposiciones (Parte 3): Cálculo de parámetros óptimos en el juego bursátil

Introducción

Si en artículos anteriores (Parte 1 y Parte 2) presentamos los principios fundamentales y los mecanismos latentes para generar la dinámica de precios, los cuales tenían un carácter puramente teórico e incluso iban más allá del alcance de lo observado (siendo, sin embargo, la base del mismo) , en este artículo y en los siguientes, en cambio, trataremos de sentar las bases de una nueva disciplina de ingeniería (donde, en consecuencia, muchos cálculos serán de carácter evaluativo), lo que nos permitirá sacar conclusiones útiles en la práctica sobre la dinámica de precios observada, así como aplicar estas directamente en el comercio. En este artículo hablaremos sobre enfoques y algoritmos de ingeniería que, en general, son capaces de ofrecer beneficios sostenibles, y también sobre cálculos probabilísticos de valores óptimos de take profit y stop loss que, en principio, permitirán lograr la ganancia promedio máxima.

1. Modelo.

En el artículo anterior (Parte 2), se obtuvo la fórmula (II.3) para la densidad de flujo de probabilidad de precios (para abreviar, aquí y en adelante, la fórmula (N) del artículo Parte R se numerará como (RN), donde R será un número romano). Este flujo de probabilidad en forma reducida u observable ya se expresa en las probabilidades de que el precio suba o baje; para ser más concretos, genera dichas probabilidades. Vamos a formular un enfoque para evaluar de forma práctica dichas probabilidades.

 

En la representación discreta (basada en el concepto de barra) del tiempo, cuando una sección de la historia del precio (que puede ser el precio de apertura, cierre, máximo o mínimo) se representa como una serie (aquí el orden de numeración será tal que las barras posteriores tengan números mayores que las anteriores), el precio se moverá a saltos, lo cual permitirá a gran escala o en una escala suficientemente grande hablar de las probabilidades de tales saltos, estimadas para la probabilidad de los movimientos de precio hacia arriba, como , dónde será el número de miembros del conjunto , o hacia abajo , donde será el número de miembros .  En este caso, podremos calcular la longitud del salto medio. 

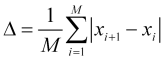                                                                                                    (1.1)

del precio .  En la práctica, podremos establecer que el precio se mueve caóticamente a través de varios saltos durante un periodo debido al paseo aleatorio, alejándose de su posición promedio actual (determinada por dichas probabilidades) en una cantidad del orden de

              , (1.2)

(esto lo confirman las lecturas del indicador "Casual Channel", cuyas líneas de canal son o las desviaciones (1.2) de la media móvil con un periodo ).

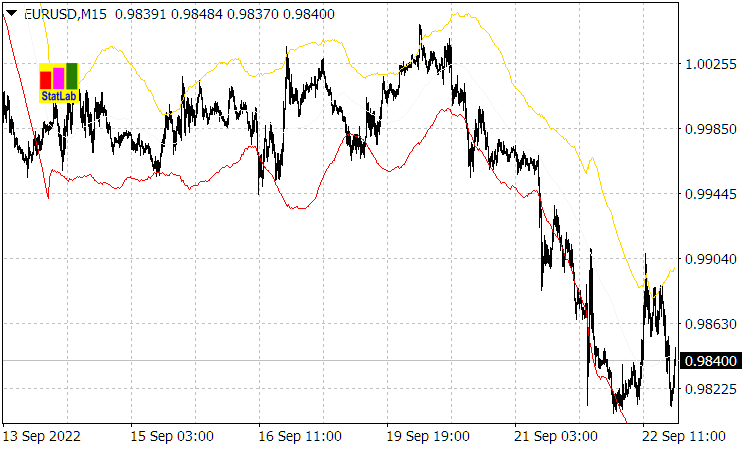
Fig. 1.  Indicador "Casual Channel"

Resulta obvio que el tiempo característico de una desviación aleatoria del precio en la magnitud del orden , donde supondrá la duración de la barra del marco temporal correspondiente.  Se produciría exactamente la misma desviación (1.2) del precio respecto del promedio si se desplazara aleatoriamente a través de saltos idénticos de valores exactamente iguales .    

 

Por consiguiente, en la simplificación del modelo presentada aquí, asumiremos que el precio se moverá en saltos iguales , cuyas direcciones tendrán las probabilidades Y . 

 

Vamos a observar el salto calculado usando los métodos presentados anteriormente y las probabilidades que eran relevantes ya para el intervalo anterior en general, es decir como valores promedio para este intervalo, y no para los movimientos de precios actuales, que se forman bajo la influencia de saltos ligeramente diferentes y, lo más importante, probabilidades y , lo cual aún queda por predecir.

 

También debemos enfatizar de inmediato que, dado que, como dijimos antes (en el artículo Parte 2), los métodos de la estadística clásica ordinaria y su aparato matemático son poco aplicables a la dinámica de precios formada a partir de superposiciones de ondas de probabilidad y funcionan en este caso con grandes errores, el análisis basado en el uso de los datos observados y los correspondientes cálculos probabilístico-estáticos resultarán aproximados.   

2. Determinación práctica de las probabilidades operativas previas y la velocidad de precios normalizada. Principio de uso de dichos parámetros a la hora de calcular la distribución futura de precios.

La velocidad promedio del movimiento de precios durante el intervalo promedio será igual a

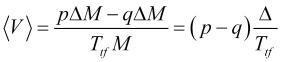                                                                                  (2.1)

y caracterizará la velocidad de cambio de la media móvil (donde será el índice de las barras) con el periodo de promediación correspondiente, y sin ningún tipo de fluctuaciones de velocidad. Por tanto, la velocidad media será una cantidad prácticamente calculable.

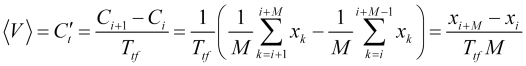                .         (2.2)

Igualando (2.1) a (2.2) obtendremos un parámetro determinado empíricamente

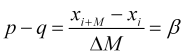               , (2.3)

que llamaremos velocidad de precio normalizada, dado que A . Que resulta fácil de mostrar. En realidad, por ejemplo, de (1.1) se sigue la desigualdad

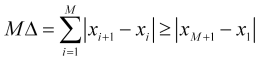              , (2.4)

de donde precisamente (2.3) sigue . También podemos imaginar , y dado que la probabilidad , entonces . Use (2.3) y para encontrar las probabilidades 

                 Y , (2.5)

así como otra expresión para la velocidad normalizada

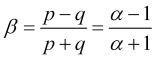                 , (2.6)                               

donde el parámetro

                .                                                                   (2.7)

En cálculos posteriores también necesitaremos el parámetro  

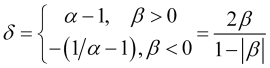               ,                                                            (2.8)

a través del cual la velocidad normalizada en sí se expresa de la forma que sigue

                .                                                                                            (2.9)

 

Las probabilidades (2.5) de saltos calculadas en el intervalo de los precios son las medias durante este intervalo y participan en la formación del precio final, por tanto, si con antelación en el momento actual , cuando se conoce el precio , conocemos estas probabilidades promedio, entonces podremos predecir cuál será el precio en un momento futuro , más precisamente, la distribución de la probabilidad de este precio.  Al comparar gráficos de precios y la velocidad normalizada (a partir de los cuales se calculan y ) podemos rastrear la gran similitud de estos (por la coincidencia de las ubicaciones de sus vértices), lo cual demuestra que ha sido esta velocidad (más precisamente, las probabilidades correspondientes a ella) la que ha formado el precio actual .

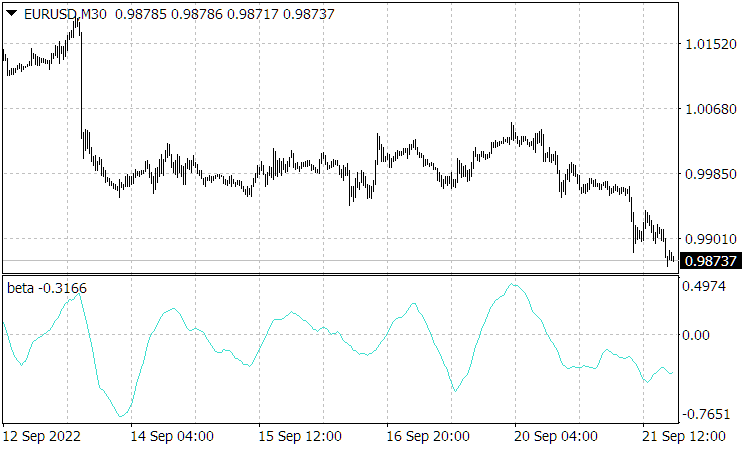
Fig. 2. La figura representa un gráfico de velocidad normalizada.

 

Esto es comprensible. De hecho, de (2.3) se sigue . Entonces el precio se formará a partir del precio el conjunto de velocidades futuras o sus valores promedio durante un intervalo dado

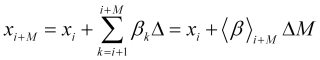  ,                         (2.10)                                                              

donde la velocidad promedio normalizada durante el intervalo futuro, mostrada en su gráfico en el punto 

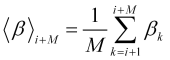            , (2.11)

y la probabilidad promedio en este intervalo Y , se encuentran tras la sustitución en las fórmulas (2.5) (obviamente, si en (2.10) el término orden , entonces aparece la similitud de gráficos Y ). Entonces, habiendo predicho funciones suficientemente suaves en barras más adelante calcularemos las probabilidades requeridas y , que permitirá calcular al momento la distribución de la probabilidad del precio futuro y sus características necesarias para la negociación (dirección de las posiciones de apertura y posiciones de las órdenes stop).

 

La esencia del pronóstico de velocidad normalizada utilizado aquí es la siguiente. Función de tiempo de la velocidad normalizada fluctúa en el rango alrededor de su esperanza matemática igual a cero (o un valor pequeño , expresando la velocidad de la tendencia global, si abarca toda el área considerada). En este caso, por ejemplo, el pronóstico estadístico más simple se basa en la esperanza matemática condicional, que luego toma la forma , acercará la función predictiva a cero o según la ley , es decir, a medida que la función de autocorrelación del proceso correspondiente desciende , lo que solo reducirá drásticamente el número de posiciones abiertas según una condición como y hará que el juego resulte incluso menos rentable que un juego con un pronóstico trivial basado en el último valor . Por otro lado, la dinámica de los precios está bien modelada y predicha usando los procesos oscilatorios cuya esencia hemos revelado en artículos anteriores. En esta etapa del desarrollo de la teoría, el pronóstico de la función (que tiene una naturaleza oscilatoria) en barras por delante se ha realizado usando como base la extrapolación de Fourier calculada sobre la base de datos históricos empíricos , porque el uso de la extrapolación wavelet propuesta en artículos anteriores en este caso aún no ha proporcionado ventajas notables.

3. Factor de calidad de la tendencia. Una aproximación para evaluar el alcance de las tendencias actuales y futuras, horizonte de trabajo adecuado.

Si la tendencia dura más que el tiempo promedio , entonces el aumento natural del precio durante el tiempo de promediación (según (2.1) y (2.3)) será del orden de

               .                                    (3.1)

La incertidumbre de este incremento 

                ,                                                                                               (3.2)

entonces, el rango completo de movimiento de precios (ver. fig. 1), cuando se mueve desde un límite del canal indicador Casual Channel al otro y al mismo tiempo se desplaza en promedio a una velocidad normalizada , se estimará como

                 ,                                                               (3.3)

dónde

                 .                                                                                 (3.4)         

Si jugamos según la tendencia, entonces resultará deseable que el valor del desplazamiento (3.1) sea significativamente superior a la incertidumbre (3.2) de este desplazamiento

               ,                                                                (3.5)

de este, y de (2.6) y (2.9), para el tiempo promedio requerido obtendremos una estimación menor

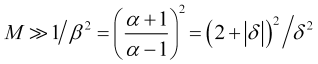              ,                                                   (3.6)

al cumplirse, según (3.4), el tiempo promedio (en barras) se calculará como 

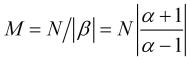              .                                                                                  (3.7)

Si la incertidumbre del incremento del precio no puede despreciarse, entonces el tiempo promedio se calculará como la raíz positiva de la ecuación cuadrática (3.4).

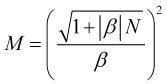               .                                                                                        (3.7.1)

 

Vamos a determinar la calidad de la tendencia

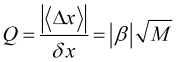               ,                                                                                        (3.8)

como la relación entre su incremento natural respecto a su incertidumbre o ruido. Está bastante claro que para un juego estable y rentable puramente según la tendencia, se requiere una calidad alta . Pero el indicador “Quality Trend” (fig. 3), que calcula la calidad de la tendencia, en el mejor de los casos alcanzará un valor de varias unidades para la divisa. Además, incluso tras identificar una tendencia de calidad, no resulta posible determinar cuándo terminará esta, debido a la imprevisibilidad de la aparición de fuertes eventos externos que pueden perturbar la propia dinámica del mercado y poner fin a una tendencia o incluso revertirla. Por tanto, una estrategia rentable solo podrá comenzar con la obtención de beneficios de fluctuaciones relativamente pequeñas en la dirección de la tendencia.

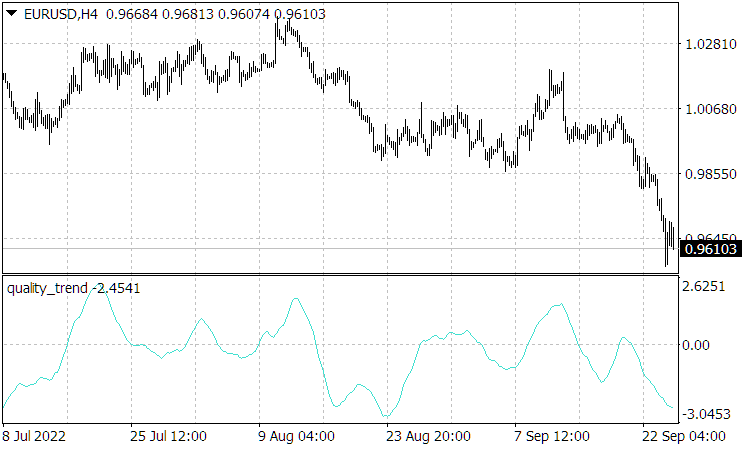
fig. 3. Indicador "Quality Trend", donde el incremento de precio no se toma en módulo, es decir el signo del indicador muestra la dirección de la tendencia.

Tenga en cuenta que las lecturas del indicador " Quality Trend", al ser proporcionales a la velocidad normalizada, como se muestra en la relación (2.10), resultan ser similares en las posiciones de sus picos a la historia de precios y, en consecuencia, las lecturas de “ Quality Trend” no se quedarán atrás. Además, las lecturas de este indicador pueden provocar (y a menudo provocan) movimientos de precio, ya que incluso antes de que cambie la tendencia, la velocidad correspondiente del movimiento de precio (crecimiento en una tendencia alcista o caída en una tendencia bajista) disminuye. No obstante, dicho comportamiento predictivo de este indicador se produce solo en ausencia de fuertes influencias en el mercado que interrumpan su propio movimiento. Y después de tales influencias, durante su tiempo de relajación, las lecturas del indicador “ Quality Trend” se retrasarán de forma “habitual”, con un retardo determinado por su periodo de promediación.

 

Vamos a analizar el comportamiento de la función y en base a esto, evaluaremos el posible alcance de las tendencias, siempre que no existan fuertes influencias de terceros en el mercado. Con un periodo promedio decreciente pueden aumentar los valores de velocidad normalizada calculados durante este periodo (después de todo, sus valores "instantáneos" en un mercado en constante cambio variarán con mayor amplitud que los valores promedio y cuanto mayor sea el promedio, menores serán dichas variaciones), es decir, en la relación para el factor de calidad, cuyos términos y viceversa , lo que hace posible la existencia de máximos en la función . No obstante, en un intervalo muy pequeño, cuando las verdaderas probabilidades y de los saltos que actúan sobre él, debido a pequeños cambios en la situación del mercado, resultan constantes, sus valores calculados estadísticamente y durante este corto periodo de promediación, seguramente diferirán mucho de las probabilidades reales, porque con periodo decreciente de incertidumbre y las probabilidades calculadas sobre él aumentarán. Por lo tanto, para el periodo promedio , que ofrece un cálculo de probabilidades más o menos fiables, se deben cumplir las relaciones del tipo , lo cual determinará su valor mínimo. De lo contrario, cuando (pero esto, observemos, es un caso más amplio que el caso de las grandes fluctuaciones en la velocidad instantánea normalizada en pequeños intervalos promedio, ya que tal relación también puede ocurrir en grandes intervalos con un cambio rápido en la probabilidad real ), no se pueden utilizar valores de probabilidad calculados estadísticamente. Tenga en cuenta que en casos de fuertes fluctuaciones de la velocidad normalizada, la función calculada sobre su base también fluctuará fuertemente cerca de su máximo, por lo que el máximo utilizado para analizar la situación del mercado deberá elegirse de manera que se forme sin problemas, lo cual, como se desprende de lo anterior, se logra con periodos promedio suficientemente grandes. Si se cumple la misma condición que se supone que se cumple en la teoría sucesiva, las probabilidades estimadas y se pueden identificar con las probabilidades efectivas y , que luego también escribiremos como y .

 

Además, precisamente en aquellas áreas donde las probabilidades y son constantes, se forma una tendencia estable y una caída en la probabilidad predominante, que denotaremos (es decir, ), lo que reducirá la tasa de crecimiento del incremento y tal vez incluso (cuando se logra la relación inversa ) se invertirá la tendencia, lo que también provocará un descenso de la calidad calculada. Por el contrario, una alta calidad y su crecimiento indicarán no solo un fuerte predominio de la probabilidad prevalente sobre , sino también su constancia e incluso su aumento. Por tanto, cuanto mayor sea la calidad (3,8) de la tendencia, mayor será la probabilidad de que esté ahí, es decir, durante todo el intervalo , estará realmente presente, mientras que valor pequeño de la calidad caracterizará, por el contrario, un movimiento lateral (flat). También resulta obvio que si aumentamos el periodo promedio , abarcaremos no solo la tendencia (que luego tendrá una extensión ), sino también el flat y, además, un segmento de la historia de precios con una tendencia opuesta, entonces la calidad descenderá bruscamente; por lo tanto la longitud de la tendencia se identificará usando el máximo factor de calidad .

 

Si aumentamos el periodo tanto es así que con ello abarcaremos una tendencia unidireccional de mayor escala , que la escala de una sección de tendencia más pequeña con una longitud ; entonces el factor de calidad de la tendencia, por el contrario, generalmente aumentará, ya que debido a la similitud de los gráficos en diferentes marcos temporales, siempre que , la escala de velocidades normalizadas en (3.8) al aumentar prácticamente no se darán cambios, pero aumentará. Además (y esto requiere una corrección en el cálculo del valor que aparece en la fórmula (3.8) de la calidad), el ruido de la tendencia aumentará considerablemente con esos caóticos saltos de precio grandes y pequeños que van más allá de la distribución estadística formada por los saltos "estándar" (correspondientes al modelo analizado) con probabilidades y . Estos saltos no estándar son los mismos para todas las escalas y crearán ruido "adicional" para la tendencia, por lo que el peso de este ruido adicional disminuirá a medida que aumenten las escalas en las que se identifica la tendencia. Todo lo anterior nos lleva al hecho de que en la función , en presencia de una tendencia unidireccional global, se determinarán una serie de picos de calidad que aumentarán con el incremento o un aumento en la escala de las áreas de tendencia identificadas.

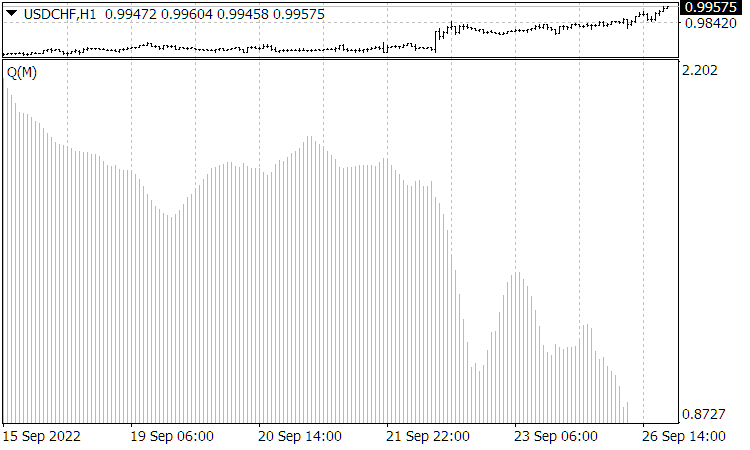
Figura 4. La función en este momento. Aquí en la escala de abscisas no aparece el tiempo, sino el periodo promedio para “Quality Trend” de 10 a 160.

  

Y finalmente, el juego no se basa en una historia ya formada, sino en el tiempo real, por lo que resulta necesario conocer una serie de pronósticos basado en el conjunto de los valores previstos de velocidad normalizada. Por lo tanto, para evaluar el posible alcance de una nueva tendencia emergente, deberemos recorrer todo el espectro de periodos promedio e identificar una serie de máximos de la calidad del pronóstico , cuando su pronóstico avanza por barras de la barra actual, es decir calculando

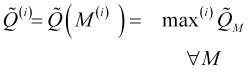               ,                                                                 (3.9)                 

donde será una función de identificación del -mo máximo. En este caso, también será necesario establecer el pico máximo

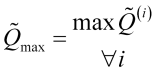                 ,                                                                                    (3.10) 

y su punto correspondiente en la escala promedio.  

 

Resulta obvio que a intervalos promedio más pequeños que se desplacen hasta el pico máximo de la calidad pronosticada, si, por supuesto, en estos intervalos el factor de calidad también es significativo y crece monótonamente o en una secuencia de picos crecientes (también basados ​​en un «colchón» creciente), veremos la tendencia unidireccional correspondiente (con retrocesos después de cada pico de la calidad). Después del pico máximo de calidad, cuando esta comienza a caer en la escala del promedio correspondiente , se producirá una desaceleración de la tendencia, que pronto podría provocar una reversión. Esto último resulta más probable cuando el valor máximo en sí es muy significativo en el sentido de que la calidad del instrumento bursátil considerado rara vez alcanza valores grandes. En cualquier caso, la tendencia creciente continuará hasta la marca , antes de alcanzar la cual, se deberá cerrar la posición abierta según esta tendencia.   

 

Vamos a tratar ahora de estimar el alcance de las áreas de tendencia prometedoras para el comercio, que no necesariamente deben ser iguales a la duración prevista de la tendencia. En primer lugar, el beneficio, debido a la baja fiabilidad del funcionamiento de las propias matemáticas predictivas (que se refiere a todos sus tipos, ya sean varios extrapoladores de frecuencia y otros elementos, o redes neuronales, incluso a ARIMA, etc.), deberá tomarse en áreas relativamente pequeñas y próximas de la futura tendencia identificable en las que resulte más probable que se forme esta tendencia. Por lo tanto, como se desprende del párrafo anterior, la desigualdad deberá cumplirse necesariamente.  En segundo lugar, el modelo presentado utiliza estimaciones de valores de probabilidad futuros y y se presupone la constancia de los saltos promedio del precio, que son previsiones que funcionan cuando el mercado se desarrolla por inercia y según sus propias leyes. Sin embargo, como mostramos en el primer artículo (Parte 1) , el intervalo de desarrollo predecible del mercado comienza desde el último evento externo fuerte y continúa hasta que ocurre el siguiente evento de este tipo. Por tanto, existe un horizonte de trabajo adecuado de todo el aparato matemático desarrollado aquí, donde la cantidad es igual al número de barras desde la barra actual hasta la barra futura del inicio de un evento externo fuerte. Si (y esto resulta extremadamente importante), intentamos utilizar un aparato matemático de este tipo más allá de un horizonte determinado, esto provocará un funcionamiento incorrecto y pérdidas inevitables. Para determinar un posible horizonte para el funcionamiento adecuado de dicho aparato matemático, deberemos basarnos en un análisis fundamental o una investigación de expertos que evalúe la fuerza de la influencia de todos los eventos políticos y económicos actuales y futuros sobre el estado del mercado.  Por lo tanto, la longitud de cualquier sección de tendencia prevista que resulte prometedora para el comercio se estimará desde arriba mediante la relación

              ,                                                                        (3.11)   

desde abajo, la longitud deberá estimarse usando como base la relación previamente establecida entre la pequeñez de la incertidumbre (fluctuaciones) de la probabilidad en comparación con la propia probabilidad

               ,                                                                                    (3.12)

que también se determinará a partir del gráfico de la calidad prevista y se corresponderá con aquellas áreas donde este gráfico cambie con bastante suavidad. El cambio de precio natural esperado en esta sección de la tendencia será

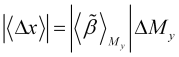               ,                                                                                    (3.13)

que corresponde al orden de beneficio obtenido con una estrategia puramente de tendencia.

 

En tercer lugar, la elección de la duración del segmento de la tendencia del juego también deberá basarse en los cálculos presentados a continuación, que esencialmente permiten establecer el intervalo de las magnitudes , en el que, en principio, en determinadas condiciones de mercado resulta posible obtener un beneficio estadístico medio, es decir . Además de todo esto, el propio tráder elige el marco temporal para el juego, mientras que la calidad verdadera (y no la calidad modelo, calculada según la fórmula (3.8)) caerá con la disminución en el marco temporal debido al ruido del precio en todos los marcos temporales por sus saltos no modelados (idénticos en todos los marcos temporales). Por lo tanto, al tráder se le ofrece o bien una selección de opciones con una alta calidad de tendencia, pero con una larga espera para obtener beneficios, como es el caso de los marcos temporales largos; o bien obtener beneficios rápidamente, pero en tendencias con una calidad más baja (y, en consecuencia, con mayores riesgos de pérdida), lo cual resulta típico de marcos temporales pequeños.

4. Cálculo probabilístico de los valores de take profit y stop loss que ofrezcan el máximo beneficio al darse probabilidades operativas constantes y la expresión de estas últimas.

Formulación del problema. 

El precio se moverá en saltos individuales en la dimensión vertical desde la marca cero. La probabilidad de un salto de precio hacia arriba , la probabilidad de salto del precio hacia abajo , respectivamente, Claro, aquí existen las medias pronosticadas y , lo cual no importa ahora.  En la parte superior, a la distancia "a", se encuentra un take profit, mientras que en la parte inferior, a la distancia "b" de la marca cero se halla un stop loss (cuando miramos en los ejes de coordenadas ).  Encuentre los parámetros del juego bursátil que aseguren el máximo beneficio.

 

Solución del problema.

              El precio puede llegar al punto con la coordenada “n” o desde abajo desde el punto “n-1” o desde arriba desde el punto “n+1”. Por lo tanto, la probabilidad de encontrar el precio en el punto “n” será igual a 

               .                                                                                     (4.1)

De (4.1) obtendremos la ecuación en diferencias finitas 

                                                                                (4.2)

 

Saltos equiprobables. 

              Consideraremos primero el caso de los saltos equiprobables En este caso, además, de (4.2) obtendremos

               ,                                           (4.3)

donde será la constante, de donde encontraremos

               .                                                                                                 (4.4)

              La probabilidad de que el precio se encuentre en cero en el momento inicial de su movimiento , por eso, 

               .                                                                                                      (4.5)

              Vamos a suponer que el stop loss “b” junto con el take profit “a” constituyen la característica estimada aquí (3.4) en los saltos medios del precio del movimiento de precios durante el periodo de su promedio (y movimiento), en el que se basará la constancia de las probabilidades y . La probabilidad de que el precio ya esté en el punto de stop loss, donde , alcanzará un take profit igual a cero , sustituyendo eso en (4.5), obtendremos

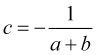                                                                                                                       (4.6)

lo que junto con (4.5) ofrecerá la probabilidad de lograr una take profit igual a

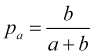                                                                                                                        (4.7)

y la probabilidad de que se active un stop loss

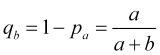               .                                                                                         (4.8)

Por lo tanto, con saltos de precios igualmente probables en diferentes direcciones, el beneficio promedio en el número de saltos

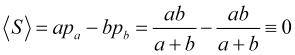                                                                          (4.9)

siempre será cero (el spread, por supuesto, lo hará negativo) independientemente de la posición del take profit y el stop loss, que puede ser cualquier cosa. 

 

Existe una tendencia a avanzar hacia el take profit.

 

Supongamos que (más concretamente ) entonces, multiplicando todas las ecuaciones (4.2), tendremos

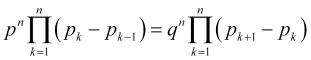               ,                                                      (4.10)

reduciendo factores idénticos en (4.10) usando la notación (2.7) y dado que , obtendremos 

                .                                                                                 (4.11)

Imaginemos que como la suma de las diferencias de los términos adyacentes de la serie de probabilidades, utilizando otras relaciones (4.11) y la fórmula para sumar la progresión geométrica

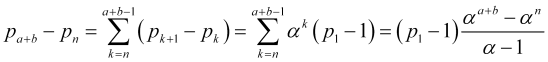 ,             (4.12)

 , por eso,

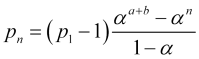                                                                                                   (4.13)

 , por consiguiente,

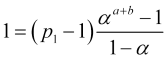              , (4.14)

dividiendo (4.13) por (4.14) encontraremos la probabilidad de lograr el take profit “a”               

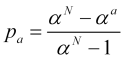              .                                                                                                      (4.15)

La probabilidad de que se active el stop loss será, por tanto, igual a , entonces el beneficio medio por posición en los saltos del precio serán iguales a

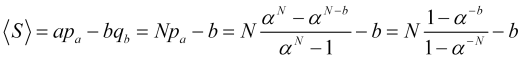               ,         (4.16)

que en la representación (4.16) será una función del valor de stop loss “in”, que en esta representación será simplemente un número de los saltos, pero en realidad tenemos un valor . Tenemos beneficios .  Está claro que con un aumento en la probabilidad del movimiento de precios hacia una posición abierta, el beneficio promedio (4.16) aumentará y, en el límite cuando asuma el valor ; es decir, será una función creciente de .

 

Encontraremos el máximo del beneficio estadístico promedio (4.16) sujeto a los valores dados de Ny , para ello igualaremos su derivada a cero

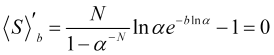                , (4.17)

de donde encontraremos el valor del stop loss deseado en los saltos de precio 

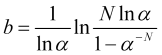               .                                                                                        (4.18)

 

Dado que , entonces el logaritmo será positivo y y, en consecuencia, el valor del logaritmo 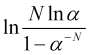deberá ser positivo, cosa que se cumplirá bajo la condición

               ,                                                                                               (4.19)

o   

      ,                                                      (4.20)                                                                                      

donde . La desigualdad (4.20) se cumplirá estrictamente para cualquier , ya que el exponente pasará por encima de la línea recta y solo la tocará en el punto . 

Segunda derivada de la función (4.16)

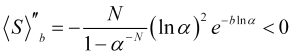                                                                            (4.21)

en estas condiciones siempre será negativo, es decir la curvatura de función estará dirigida hacia abajo y tendremos el máximo en el punto (4.18).  El aspecto de la función (4.16) con N=100 y se muestra en la figura 5. 

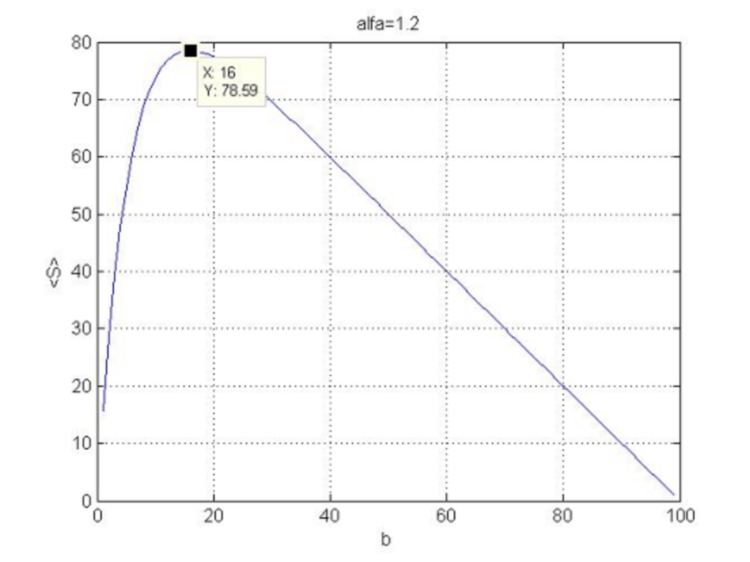
Fig.5. Dependencia de la función de beneficio respecto al stop loss.

Subrayaremos que el beneficio medio era positivo, el coeficiente deberá superar significativamente la unidad. De hecho, si , donde y será posible despreciar el segundo término de la expansión, dejando solo el primer término , entonces el beneficio medio por transacción 

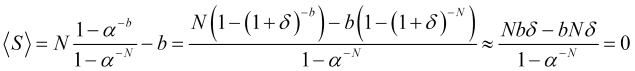    (4.22)

será (como en el caso de las probabilidades iguales de saltos opuestos) igual a cero. Si no podemos despreciar el segundo término de la expansión, entonces, considerando que el número de saltos es lo suficientemente grande o , tendremos

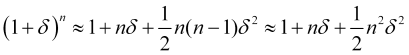               ,                               (4.23)

lo que dará un valor positivo para el beneficio promedio (4.16)

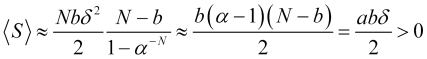               ,                          (4.24)

porque , (y por lo tanto, ).

              El beneficio promedio aproximado (4.24) relativo al argumento será una parábola cuadrática invertida cuyo máximo se alcanzará en (que es la igualdad del stop loss y el take profit), cuando .

 

Ahora viene un punto esencial. En la teoría anteriormente presentada, calculamos el beneficio promedio, que se computaba únicamente usando como base de los valores promedio de los precios, que, de hecho, fluctúan mucho y pueden incluso exceder con creces los desplazamientos promedio correspondientes en el rango de sus fluctuaciones. Las órdenes stop (take profit y stop loss) no se cierran en los valores promedio del precio, sino precisamente en los bordes de la banda de sus fluctuaciones. Por lo tanto, para que el aparato matemático presentado, basado en los valores promedio, funcione más o menos, el stop loss debería ser mucho mayor de la incertidumbre del precio (de modo que su respuesta a la fluctuación diferirá poco de la respuesta del modelo en términos del promedio y estas fluctuaciones podrán despreciarse), es decir, según (1.2), 

                .                                                                                                         (4.25)

Luego, usando las expresiones (3.7.1) para el periodo promedio, obtendremos de (4.25) una función para la cual se deberá cumplir la desigualdad

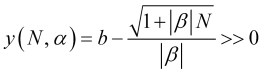               ,                                                                 (4.26)

que será un criterio para determinar la pequeñez de las fluctuaciones de precios, donde se hallará a partir de la relación (2.6). Sustituyendo el stop loss (4.18) en (4.26) construiremos un gráfico (fig. 6) de esta función, de donde se desprende que dicha función no es mucho mayor que cero, sino que, por el contrario, será fundamentalmente negativa, es decir la relación (4.25), con un stop loss óptimo (4.18), nunca se cumplirá.

 

Código MATLAB

>> [N,a]=meshgrid([3:200],[1.01:0.01:3]);
>> b=log(N.*log(a)./(1-a.^(-N)))./log(a);
>> beta=(a-1)./(a+1);
>> s=(N.*beta+1).^(1/2)./beta;
>> y=b-s;
>> plot3(N,a,y)
>> grid on

   

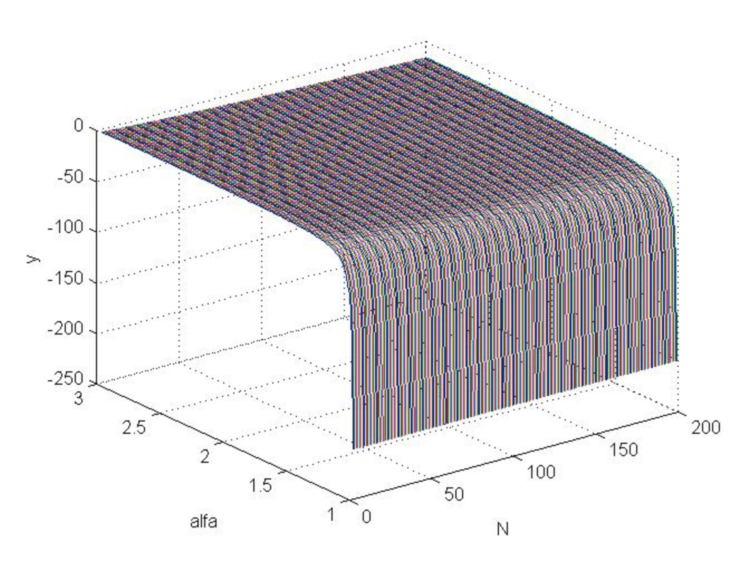
Fig.6. Gráfica de la función “y” cuando Alfa cambia de 1 a 3 y N de 3 a 200.

 

 

Por lo tanto, el uso de los valores de la orden stop calculados anteriormente conducirá a pérdidas estadísticas promedio, ya que las fluctuaciones de precio resultan fundamentalmente superiores a las fluctuaciones óptimas en el modelo de su movimiento promedio de stop loss.

               .                                                                                                              (4.27)

Esto significa que deberemos cambiar el tamaño del stop loss en sí y no buscar un periodo promedio que haga que el stop loss óptimo (4.18) sea relativamente pequeño (4.25) (ya que este problema no tiene solución), lo cual, por supuesto, cambiará también los beneficios.

 

El take profit óptimo para el modelo de movimiento de precio promedio, en términos generales, coincide con el punto del precio promedio móvil previsto, que se encuentra de la barra actual a una distancia de barras por delante. Pero si consideramos las fuertes desviaciones de precio con respecto al promedio en el que se cierran las órdenes stop, entonces, como podemos ver en el gráfico del indicador "Casual Channel" (fig. 1), para garantizar un juego rentable, semejante take profit óptimo deberá reducirse en una magnitud mayor que la desviación promedio.

              ,                                                                                                  (4.28)

donde el coeficiente deberá ser ligeramente mayor que la unidad para las tendencias débiles (para las cuales prácticamente no hay beneficios) y del orden para tendencias fuertes, siendo aquí precisamente el parámetro cuyo valor exacto se debe buscar mediante la optimización, mientras que el stop loss deberá incrementarse en la misma cantidad, es decir 

               .                                                                                                  (4.29)

Así pues, un stop loss, como valor aparte del valor promedio de la posible variación del precio (por barras futuras) del precio contra una posición abierta en , funcionará con mucha menos frecuencia y, además, con una probabilidad menor de , mientras que el take profit funcionará, por el contrario, más a menudo y con mayor probabilidad . En consecuencia, para conseguir el beneficio máximo, obtendremos la estimación

               , (4.30)

donde será el valor de (4.16), o, teniendo en cuenta (3.7.1)

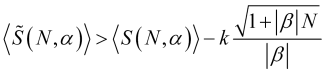                                                                    (4.31)

cuya función (en el caso del óptimo b de (4.18)) se puede construir, de forma que seamos capaces de encontrar el N maximizador, y luego el periodo promedio a partir de él. 

 

Código MATLAB para k=3

>> [N,a]=meshgrid([3:200],[1.01:0.01:3]);
>> b=log(N.*log(a)./(1-a.^(-N)))./log(a);
>> beta=(a-1)./(a+1);
>> s=(N.*beta+1).^(1/2)./beta;
>> s0=N.*(1-a.^(-b))./(1-a.^(-N))-b;
>> Profit=s0-3*s;
>> plot3(N , a, Profit)
>> grid on 

 

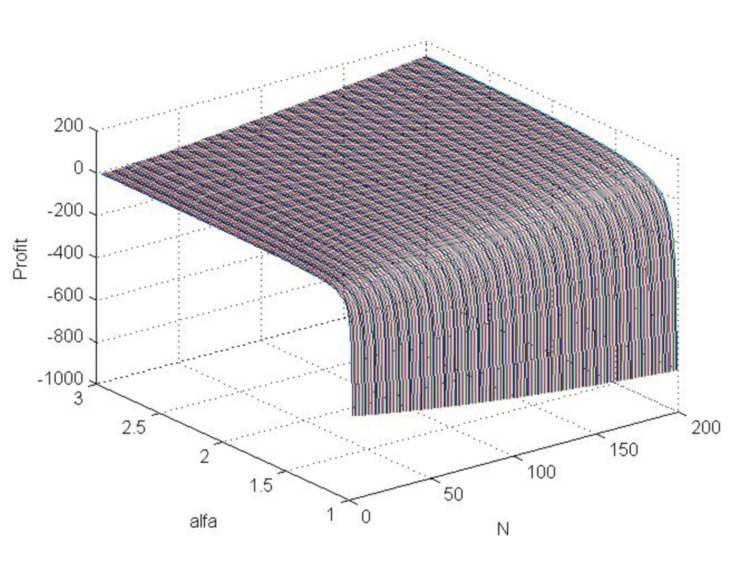
Fig.7. Gráfico de la función de beneficio (en saltos de precio de modelo) cuando Alpha cambia de 1 a 3 y N de 3 a 200.

El gráfico muestra que el beneficio con una esperanza matemática positiva es, en principio, posible, y aumenta con el incremento de Alpha y N. 

 

Para encontrar el mejor periodo de promediación (más prometedor para el trading), deberemos construir una función de calidad predictiva . Para ello hemos desarrollado el script “CalculeScientificTradePeriod”, y determinado este periodo prometedor según dicha posición máxima de la función de calidad, donde , cuando este máximo se alcanza de forma suave (se cumple la relación (3.12)) y no se ubica más allá del horizonte de trabajo adecuado. Y, si el valor encontrado de esta forma proporciona un valor de beneficio positivo (y superior al menos a un par de spreades) (4,31) y una probabilidad suficientemente alta de ganar (4,15), lo cual establecerá el intervalo , entonces, en esta situación, la decisión comercial deberá basarse en ello. Para calcular los take profit y stop loss óptimos (que maximicen el beneficio promedio) y determinar la tendencia futura del movimiento de precios y su futura trayectoria, hemos desarrollado el indicador ScientificTrade, cuyos algoritmos se basan en la teoría completa presentada anteriormente.

 

Tenga en cuenta que el algoritmo del script "CalculateScientificTradePeriod" consume muchos recursos, por lo que usaremos un script y no un indicador que ejecute este algoritmo en cada tick, bloqueando el funcionamiento de la computadora. Para mostrar la información calculada por el script, utilizaremos el indicador "FindScientificTradePeriod".  

 

 

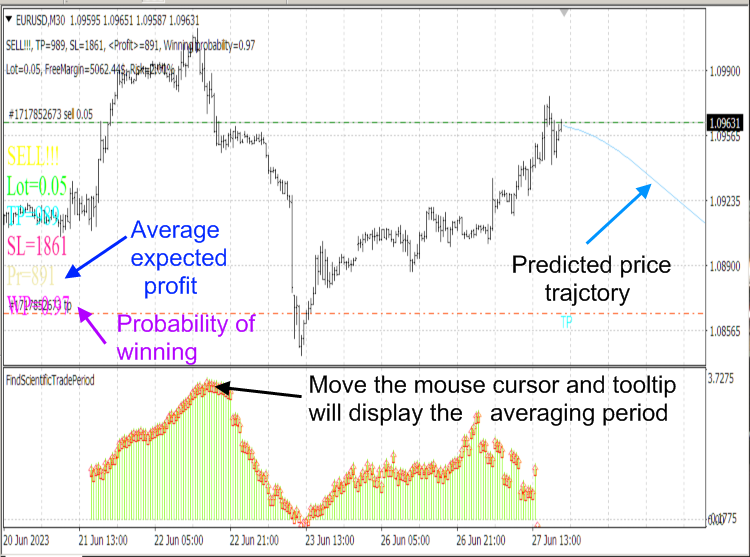
Fig.8.  Indicadores "ScientificTrade" y " FindScientificTradePeriod ". 

 

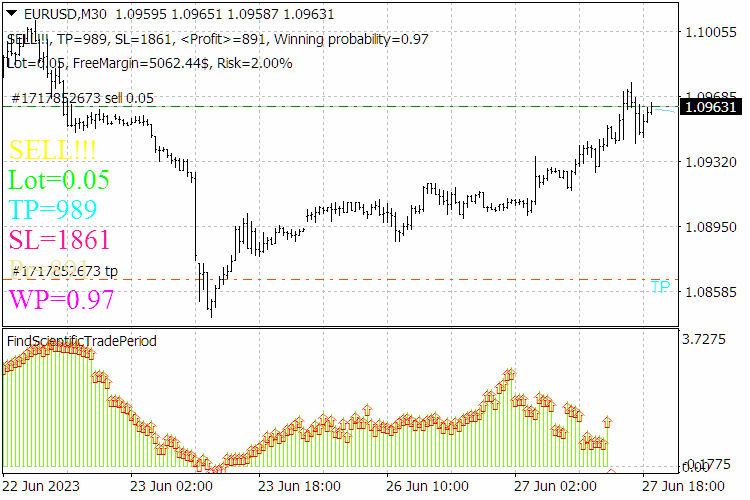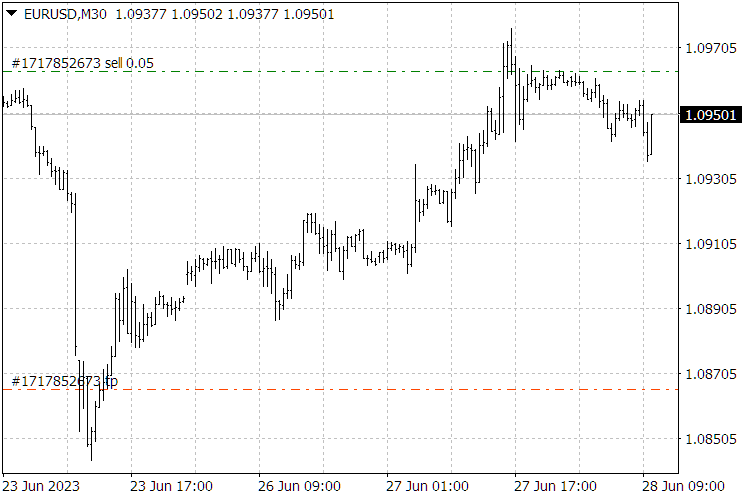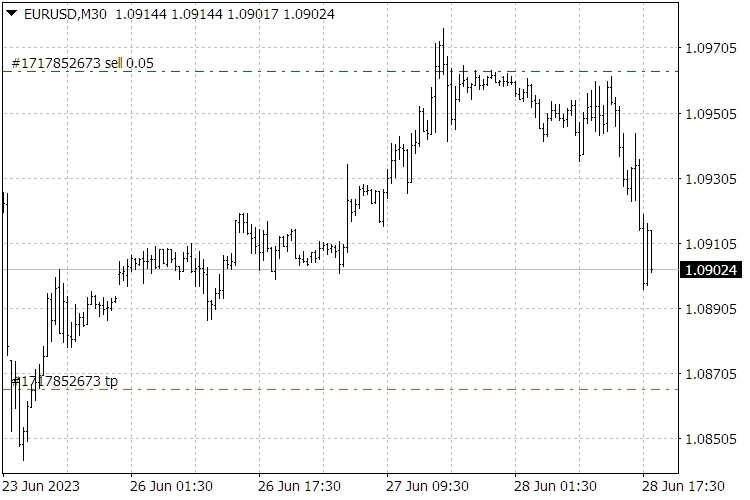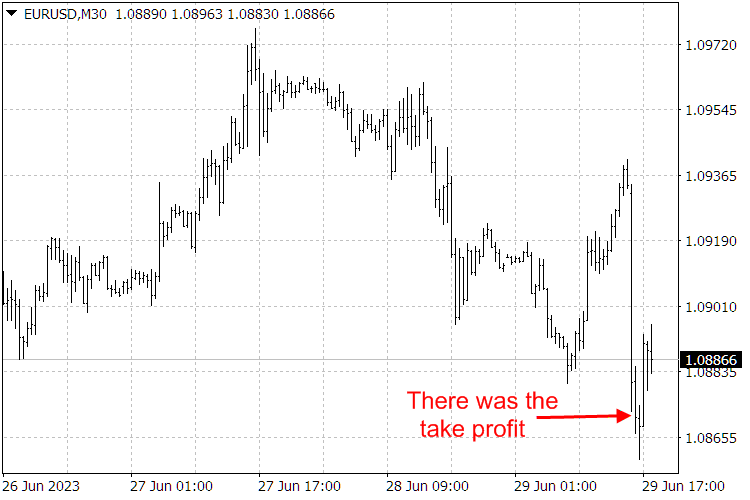
Fig.9.  Resultados del indicadorScientificTrade. 

5. El error en los cálculos usados aquí es inamovible en el marco del propio aparato matemático. Enfoque para identificar los momentos de rebote y las reversiones de precio que ocurren naturalmente.

Como ya hemos dicho antes, las tendencias predichas por el indicadorScientificTrade y las posiciones de stop loss y take profit calculadas por este indicador se basan en los valores previstos y , que pueden resultar erróneos debido a la falta de fiabilidad del propio aparato de pronóstico (en este caso, en el indicador de Fourier extrapolador). Por lo tanto, dichos pronósticos pueden resultar falsos incluso dentro del horizonte de un funcionamiento adecuado de todo el aparato matemático presentado anteriormente.

Para excluir al menos algunos casos de pronósticos matemáticos falsos, las tendencias calculadas por el indicador "ScientificTrade" en el intervalo determinado para él usando el script "CalculeScientificTradePeriod" deben coincidir con las tendencias de pronóstico dadas por expertos autorizados en análisis fundamental en este intervalo. Está claro que si tanto «ScientificTrade» como los asesores expertos ofrecen el mismo pronóstico falso (que no podemos conocer), las pérdidas también resultarán inevitables. Según mis observaciones subjetivas (no dispongo de suficientes datos estadísticos), los expertos son más propensos a cometer errores que el indicador ScientificTrade en combinación con el script CalculateScientificTradePeriod, lo que en mi opinión se debe a que las leyes internas de desarrollo del mercado tienen un impacto más fuerte que la mayoría de los eventos externos que causan cambios en las tendencias, cosa que los expertos no pueden determinar. Además, estas reversiones del mercado, causadas por razones internas, a menudo suceden antes del inicio de fuertes eventos externos y con mayor frecuencia que estos. Discutiremos sus mecanismos más adelante.        

Para expresar la esencia del problema anterior, cabe señalar en primer lugar que el precio, incluso cuando el mercado se desarrolla según sus propias leyes (cuando el precio no es impulsado por fuertes eventos externos), no siempre se mueve en saltos equidistantes; este concepto es el modelo simplificado utilizado aquí, que nos permite al menos entender y calcular algo dentro del caos del mercado. En realidad, el precio realiza ocasionalmente fuertes movimientos a corto plazo (fuera del alcance de la estadística clásica) contrarios a las tendencias estáticas medias, según las cuales se mueve lentamente (con grandes fluctuaciones) en una dirección concreta. Además, si esos fuertes movimientos no están causados por influencias externas al mercado, sino que se originan en sus procesos internos, suelen ir en contra de las tendencias estadísticas. Por consiguiente, estos fuertes movimientos anulan las órdenes stop loss y generan pérdidas máximas para la mayoría de los tráders pequeños.

De hecho (si excluimos la anulación intencionada de las órdenes stop loss por parte de los proveedores de servicios de negociación y cotización), el principio de Le Chatelier funciona aquí en conjunto con la ley dialéctica de la transición de la cantidad a la calidad. Al alcanzar un determinado nivel de crecimiento (o caída) también dependiente del mercado, de un determinado instrumento de mercado, se produce un brusco salto en la calidad, que, según el principio de Le Chatelier (cuya acción se extiende a cualquier sistema complejo en equilibrio, incluida la economía, que la mayor parte del tiempo evoluciona a través de estados de cuasi-equilibrio), tiende a resistir el mencionado aumento de la cantidad, reduciéndola bruscamente (de un salto). En tal situación, dado que el mercado como sistema, con su desarrollo monótono, pasa gradualmente a través de estados cercanos de casi equilibrio, el principio de Le Chatelier no reacciona a sus pequeños cambios, sino que actúa abruptamente cuando ya se han acumulado grandes cambios cuantitativos en un determinado sistema. Desde el punto de vista del modelo de ondas (Parte 1) del mercado, tales saltos pueden explicarse por la proximidad (o igualdad) de las fases de las ondas de probabilidad parcial del instrumento de mercado correspondiente.

En teoría, el enfoque de un salto natural de precios puede identificarse usando la relación (II.17). Sin embargo, en la práctica resulta mucho más sencillo juzgar la aproximación de dicho salto utilizando el gráfico del factor de calidad previsto. Es decir, si el factor de calidad previsto en algún momento futuro (distante de la barra actual en barras) supera o se acerca a un cierto valor crítico para un instrumento de mercado determinado en el marco temporal correspondiente , es decir (si consideramos la situación actual y no la prevista, entonces simplemente ), en este momento será posible un cambio en la tendencia global.

En general, los saltos naturales de precios (de cualquier tipo, tanto globales como pequeños) a nivel de las amplitudes de probabilidad de su distribución se describen mediante ondículas antisimétricas (Parte 1 relación (I.17)), cuando, tras captar la proximidad e incluso la igualdad de las fases de todas las ondas de precios parciales, de las cuales se suma su amplitud de probabilidad total, la fase de esta última, debido a la antisimetría de las ondas correspondientes, se invierte, lo cual conduce a un cambio brusco en las probabilidades reales y , que entonces será fundamentalmente diferente de las probabilidades previstas y .  Está claro que situaciones tan críticas, en las que se producen saltos de calidad debido a las propias leyes del mercado, deberán excluirse del comercio. Notemos, dicho sea de paso, que dicha antisimetría de las ondas parciales de precio asegura su similitud con los fermiones, lo cual viene determinado por la tendencia constante de los niveles de precio y su anchura significativa a cambiar (se interpreta como el resultado de las fluctuaciones de precio). Por lo tanto, resulta más correcto describir la evolución de los instrumentos de mercado no mediante estadísticas ordinarias, sino usando estadísticas de Fermi-Dirac.  

Debido al efecto descrito de la inversión de la onda del precio (Parte 1) en la fase más intensa de su movimiento (el máximo del módulo de la amplitud de su probabilidad), también es curioso observar que, aparentemente, los parámetros comerciales más óptimos basados en la calidad más alta también deben garantizar el máximo beneficio. Sin embargo, los parámetros comerciales identificados por la mayoría de los tráders (intuitiva o matemáticamente) usando como base ideas habituales (características de todo lo observado en el macrocosmos físico) sobre la monotonía de los procesos y su inercia causan en realidad las pérdidas máximas.

Como resultado, la “ley” cotidiana también resulta cierta aquí: el dinero fluye hacia el dinero, la mayor parte del cual está en los bancos, por lo que el mercado retira dinero de los pequeños tráders. Después de todo, el mercado, por las razones mencionadas anteriormente, de repente (lo cual hace regularmente) comienza a desarrollarse de forma opuesta a las tendencias predichas por la mayoría de los tráders que juegan en su contra: este proceso no tiene ninguna intención humana "maligna". El mercado no posee la inercia constante (utilizada por los pequeños tráders para obtener beneficios durante un cierto periodo de tiempo) característica de los macroprocesos físicos, y en determinados momentos (impredecibles para los expertos y los tráders no armados con la teoría adecuada) invierte fácilmente las fases de todas las ondas parciales individuales de precio emitidas por los distintos participantes en el mercado bajo la influencia de leyes internas propias que operan a un nivel emergente (superando la influencia incluso de fuertes acontecimientos externos). 

En general, el caos es quien gobierna en el mercado. Por lo tanto, si algún orden de mercado se identifica al máximo, este deberá ser violado, lo que puede considerarse una ley del mercado bastante observada, sin cuyo conocimiento resulta imposible obtener un beneficio estable.

Conclusión

Este artículo presenta el enfoque de ingeniería que hemos desarrollado para crear una estrategia comercial rentable. El presente enfoque muestra que el mercado deja al tráder un conjunto extremadamente limitado de condiciones para abrir y cerrar posiciones, lo cual podría proporcionarle un juego con una ganancia esperada positiva; este conjunto de condiciones no es identificable mediante métodos clásicos. Pero jugar con una esperanza positiva de beneficios es, en principio, posible, lo cual se confirma hasta cierto punto en mi uso personal (aunque las estadísticas aún son pequeñas) del indicador «ScientificTrade», basado en este enfoque de ingeniería y la previsión con uso de la extrapolación de Fourier. Obviamente, este indicador todavía necesita ser mejorado y en este momento su principal inconveniente es el uso de un aparato de pronóstico matemático insuficientemente preciso.