MQL5 Wizard Techniques you should know (Part 59): Reinforcement Learning (DDPG) with Moving Average and Stochastic Oscillator Patterns

Introduction

In the last article we had introduced DDPG, a reinforcement-learning algorithm and had looked at 3 of its crucial classes as implemented in Python. The replay buffer class, the actor-network class, and the critic-network class. What was not covered was the DDPG-agent class; importing MetaTrader 5 price data to Python; functions for the MA, & Stochastic-Oscillator;  a get-pattern function for bringing together data from the two indicators into a binary input vector for the supervised learning network (implemented in the earlier supervised-learning article via MQL5); and finally an environment simulation loop for training the actor & critic networks.

All these are part of Reinforcement-Learning (RL) which we are looking at as a segue from Supervised-Learning (SL) to Inference-Learning (IL) (or unsupervised learning). Any one of these modes can be used unilaterally to train and use a model, however, these articles are trying to make the case they could be used together to build something more interesting. So we continue our look at RL and by dealing with the very important DDPG-Agent class.

DDPG-Agent

The core architecture and initialization of this class can be defined as follows:

def __init__(self, state_dim, action_dim):

    # Actor networks
    self.actor = Actor(state_dim, action_dim, HIDDEN_DIM).to(device)
    self.actor_target = Actor(state_dim, action_dim, HIDDEN_DIM).to(device)
    self.actor_target.load_state_dict(self.actor.state_dict())
    self.actor_optimizer = optim.Adam(self.actor.parameters(), lr=LR_ACTOR)
   
    # Critic networks  
    self.critic = Critic(state_dim, action_dim, HIDDEN_DIM).to(device)
    self.critic_target = Critic(state_dim, action_dim, HIDDEN_DIM).to(device)
    self.critic_target.load_state_dict(self.critic.state_dict())
    self.critic_optimizer = optim.Adam(self.critic.parameters(), lr=LR_CRITIC)

    self.replay_buffer = ReplayBuffer(BUFFER_SIZE)

The critical components here are the dual network architecture, optimizer setup, and experience management. The dual architecture maintains a separate policy (actor network) and a separate value (critic network) from the two main policy and value networks. These implement target networks for both, which is important for stability when training. The initialization of the respective targets is done with same weights as their main networks.

The optimizer setup features separate Adam optimizers for the actor and critic networks. Also, as is typically the case, we use separate learning rates for the policy and value networks. Finally, for experience management, we ensure that the replay buffer stores transitions for off-policy learning and by fixing buffer size we prevent unbounded memory usage. We select actions by incorporating exploration as follows:

def select_action(self, state, noise_scale=0.1):
    state = torch.FloatTensor(state).unsqueeze(0).to(device)
    action = self.actor(state).cpu().data.numpy().flatten()
    action += noise_scale * np.random.randn(self.action_dim)
    return np.clip(action, -1, 1)

The key mechanisms here are state-processing, exploration-strategy, and device-management. State-processing oversees the conversion of NumPy array to proper tensor format, the addition of a batch dimension (by un squeezing), and finally by ensuring computation is on the correct device.

The exploration-strategy adds Gaussian noise to the deterministic policy output. The noise scale controls exploration magnitude and clipping maintains a valid action range. Device-management ensures an efficient movement between GPU/CPU if applicable. Also, a final output as NumPy array is returned by the function for environment compatibility. The learning update mechanism is as follows:

def update(self):

    if len(self.replay_buffer) < BATCH_SIZE:

        return

This if-clause serves as an update gate where updates are skipped until sufficient experiences, numbering the batch size, are collected. This ensures meaningful batch statistics. Updating of the 2 critic networks is as follows:

# Sample batch

states, actions, rewards, next_states, dones = self.replay_buffer.sample(BATCH_SIZE)

# Target Q calculation
next_actions = self.actor_target(next_states)
target_q = self.critic_target(next_states, next_actions)
target_q = rewards + (1 - dones) * GAMMA * target_q

# Current Q estimation
current_q = self.critic(states, actions)

# Loss computation and backpropagation
critic_loss = nn.MSELoss()(current_q, target_q.detach())
self.critic_optimizer.zero_grad()
critic_loss.backward()
self.critic_optimizer.step()

The key aspects addressed by this code are target value calculation, loss-computation, and gradient-management. The target-value calculation uses target networks to get stable Q-targets. It implements the Bellman equation with termination handling as set by the experience parameter ‘dones’. A discount factor of GAMMA controls future reward importance.

For the loss-computation, mean squared error between the current and target Q-values are determined. The detach() method prevents target gradients from flowing (or being carried by the tensor for transferability). And, the standard temporal-difference learning is applied. Gradient management simply ensures all gradients are reset to zero, and the optimization of the critic network is a separate step. Actor network updates are also performed as follows:

actor_loss = -self.critic(states, self.actor(states)).mean()
self.actor_optimizer.zero_grad()
actor_loss.backward()
self.actor_optimizer.step()

The policy-gradient specifics dealt with here are maximizing Q-values through the minimization of negative Q, differentiating through both the actor and critic networks, as well as applying a pure policy gradient approach with no log probabilities (being deterministic). The target-network updates are as follows:

for target, param in zip(self.actor_target.parameters(), self.actor.parameters()):

    target.data.copy_(TAU * param.data + (1 - TAU) * target.data)

for target, param in zip(self.critic_target.parameters(), self.critic.parameters()):

    target.data.copy_(TAU * param.data + (1 - TAU) * target.data)

This soft update mechanism features polyak-averaging with a TAU value that is typically less than 1. The network weights are tracked slowly, as this provides an alternative to periodic hard updates. This process on the whole maintains stability while allowing learning. Our model needs to be persistent. It should be able to load previously saved network weights and also save them after training. We accomplish this as follows:

def save(self, filename):

    torch.save({
        'actor': self.actor.state_dict(),

        'critic': self.critic.state_dict(),

        'actor_target': self.actor_target.state_dict(),

        'critic_target': self.critic_target.state_dict(),
    }, filename)


def load(self, filename):

    checkpoint = torch.load(filename)
    self.actor.load_state_dict(checkpoint['actor'])
    self.critic.load_state_dict(checkpoint['critic'])
    self.actor_target.load_state_dict(checkpoint['actor_target'])
    self.critic_target.load_state_dict(checkpoint['critic_target'])

Key features with our listing above are: we save/load all network states; we maintain target network consistency; allow training continuation; and support model evaluation. To sum up the agent-class therefore, when implementing a DDPG-agent, there are a few critical design choices that need to be made. These could broadly fall under three categories, namely: Choosing DDPG-specific components, harnessing strengths of the implementation, and making potential enhancements.

The DDPG-components used are mainly the target networks, the deterministic-policy, and separate learning-rates. The target-networks are very important for stable learning of the rewards from actions taken (Q-Learning) when dealing with continuous action spaces. The use of continuous spaces makes this paramount. This deterministic policy does then necessitate external exploration with noise in order to build robustness. The use of separate learning rates is also a typical application where the policy (actor-network) has a slower learning rate than the value network.

Choices made that make this a relatively strong implementation are clear ‘separation of concerns’ where we have well-defined methods for action selection and also updates. Also, there is a device-awareness that ensures consistent handling of GPU/CPU transitions. Batch-processing is also used in order to make the tensor operations more efficient, and finally shape-safety is checked at multiple points to ensure consistent tensor-dimensionality.

Potential-enhancements, though, could be: gradient clipping in order to avert exploding-gradients; using a learning-rate-schedule in order to refine and better control the learning process; using a priority replay for efficient sampling though this ties into the already mentioned replay-buffer in the last article; and finally parallel exploration where multiple instances of the actor can be used for faster data collection.

There are also a few training-dynamics that are noteworthy and these are to do with the update-sequence, and hyperparameter considerations. The update-sequence features the critic networks being updated first. This is because more accurate Q-values do guide the policy improvement. In order to introduce some extra stability, the delaying of policy updates can also be implemented. Finally, frequent target updates are performed to slow-track the parameters (network-weights) that have been learnt.

Hyperparameter considerations should include a focus on TAU, since it controls the target network speed and therefore is a key driver for the stability of the overall learning process. There should be use of a noise scale that allows decay over time. Buffer-sizing is also critical since it affects the learning efficiency and the batch size has an impact on the variance of updates

MA and Stochastic Functions

These two functions are implemented in python for reinforcement-learning (RL) unlike in supervised-learning article where we did this in MQL5 and simply exported the network input data to Python for training. With our implementation here, we are using MetaTrader’s MetaTrader 5 Python-module to connect to a running terminal instance and then retrieve price data. There are guides in the documentation here on how to do this. Our indicator functions below transform raw price data into technical indicator data that served as inputs into our supervised learning model after being converted/ normalized to a binary pattern vector. 

The outputs of the supervised learning model are what we cast as states, since in essence they are forecasting changes in price action. These states are then used as inputs for the DDPG RL agent. Our MA function takes as input a panda data frame of prices from the MetaTrader 5 Python-module. This data frame needs to be validated and prepared as follows:

p = np.asarray(p).flatten()  # Convert to 1D array if not already

if len(p) < window:

    raise ValueError("Window size cannot be larger than the number of prices.")

What we are doing here is standardizing the array to ensure consistent 1D input format regardless of input shape. We also have error handling that averts invalid window sizes that would cause computation errors. Data integrity also maintains clean data flow through the processing pipeline. The calculation mechanism is as follows:

return np.convolve(p, np.ones(window), 'valid') / window

This implementation uses convolution for efficient rolling of the average computation. Use of the ‘valid’ input parameter ensures only fully computed windows are returned. Normalization is also done by window size to produce a true average. The entire operation is vectorized for optimal performance. The financial significance of this is that it smooths price data to help identify trends, and the window size used (aka averaging period) determines the sensitivity to price changes. The stochastic oscillator function validates its inputs as follows:

p = np.asarray(p).flatten()

if len(p) < k_window:
    raise ValueError("Window size for %K cannot be larger than the number of prices.")

Design considerations here are consistent input formatting with the MA function. There needs to be a separate validation for the %K calculation window, with the raising of an error as an early failure for invalid parameters. The %K calculation is as follows:

for i in range(k_window - 1, len(p)):

    current_close = p[i]
    lowest_low = min(p[i - k_window + 1:i + 1])
    highest_high = max(p[i - k_window + 1:i + 1])
    K = ((current_close - lowest_low) / (highest_high - lowest_low)) * 100
    K_values.append(K)

Important components here rolling-window-analysis, market-context, and overall implementation. The rolling window analysis needs to examine price range over a look-back period. This helps identify the relative position of the current close price, with a standard scaling of 0 to 100 being applied. The market context helps us assess the overbought/oversold conditions. Values near 100 suggest potential reversal down, while values near 0 would suggest an upward turn. The overall implementation uses an explicit loop for clarity, uses proper window indexing to handle edge cases, and preserves temporal order of the results. The %D calculation is as follows:

D_values = MA(K_values, d_window)

Essentially, this is a signal refinement where a smoothed version of %K moving average is used. Typical assignment for this averaging period is 3 and that is what we are using. This additional buffer provides confirmation for swings in %K and thus helps reduce false signals from a raw %K.

Get Pattern Function

This function is used to integrate data from our two indicator buffers above into the learning pipeline. It plays a feature engineering role. This is because: it helps in dimensionality-reduction, given that it transforms raw prices into more meaningful signals; it helps with stationary-improvement, since indicators are often more stable than raw prices; and finally, it allows temporal-context-capture given that widowed calculations maintain time dependencies (a generated input vector of say [1,0,0,1] can be associated with the time it is produced just like any indicator value or raw prices are also tagged with the time they are generated).

Primarily, though, it is used for supervised-learning preparation. The features it outputs in a binary vector of 0s and 1s train the model to forecast the next price changes. The MA provides trend information, while the STO function gives us momentum and reversal information. We covered the combined complementary patterns from both indicators in article 57. The forecast price change outputs then serve as RL state representation.

This implies our supervised-learning model predictions become state inputs for DDPG. Our used indicators of MA and STO therefore end up helping the DDPG agent by providing market context to help in understanding a given market regime. This reduces the need for raw history prices when defining the state.

Implementation strengths include robustness from validating inputs to prevent silent failures, dimension handling to ensure consistent array shapes, and error messages for clear messaging in the even of improper usage. Also, pro-performance considerations of using vectorized operations where possible, explicit looping and memory efficiency from streaming-friendly design. It does remain relevant to traders, and not lost in technicalities. This is because industry standard indicators are being used to generate states. The indicators are complementary since they bring together trend and momentum metrics, and the state outputs are in a normalized range, which is important for consistency.

Potential enhancements are computation optimization by using vectorized implementation of %K calculation, using numba acceleration (imported from JIT) to speed up loops in STO function, and caching of intermediate calculations. Extended functionality can be added through additional validation for NaN/inf values can also be added. This code implementing reinforcement learning with DDPG is sizable and whereas it would be appropriate to provide comment on its key sections, I will simply attach the uncovered portions of it at the endo of this article. Chief among will be this get pattern function.

Testing

Of the 10 patterns we tested in the supervised learning article, #57, only 7 were able to walk forward profitably for a year, having been trained on a year prior. Because each pattern amounted to its own network, we have to generate reinforcement-learning networks and environments also for each pattern. We follow a similar methodology in article 57 where we train on the pair EUR USD for the year 2023 on the daily time frame. In this case, we are training our reinforcement-learning networks by simulating the year 2023 as a ‘live-market’ environment. As argued in the last 2 articles, reinforcement-learning is a system in place for supporting and protecting an already established and trained model, which in our case is the network we trained by supervised-learning in article 57. 

This it does by back-propagating when in production or live environments and not on historical data. Because back propagating an ONNX network from MQL5 is not feasible, we are ‘simulating’ a live environment, which in our case is still the year 2023.

Rather than ask we posed in supervised learning, what is price going to do next?, we ask the question given this incoming price changes, what actions should the trader take. We thus perform simulation trainings as outlined above for the year 2023 and then do a forward walk for the year 2024 where our entry conditions get modified slightly.

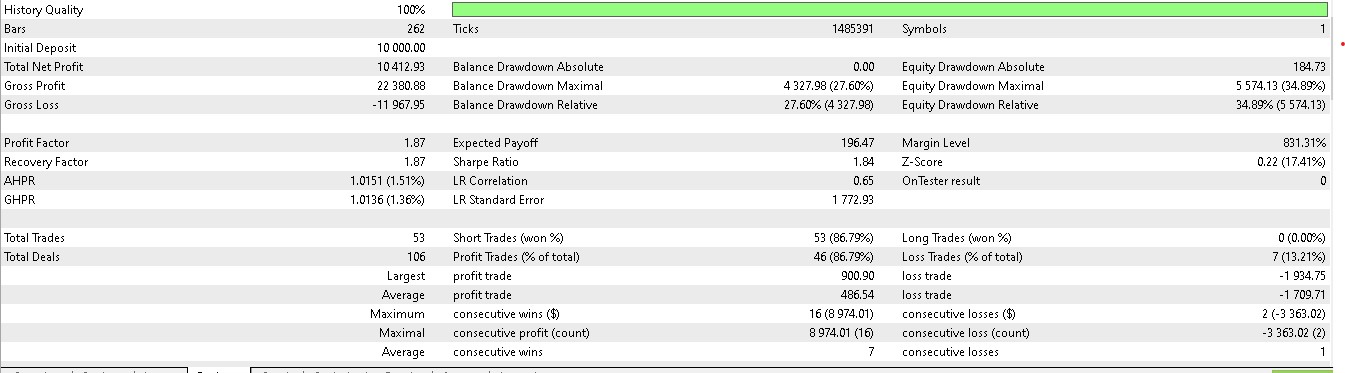
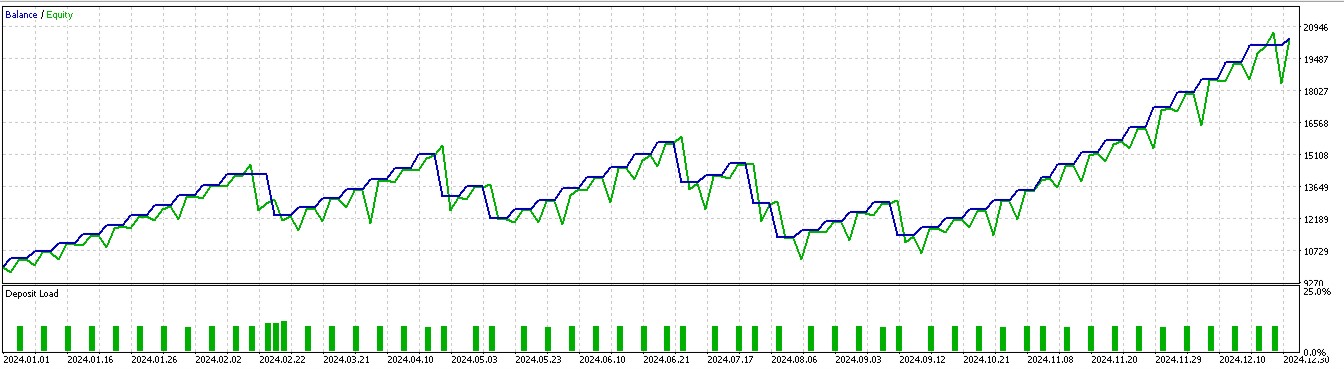
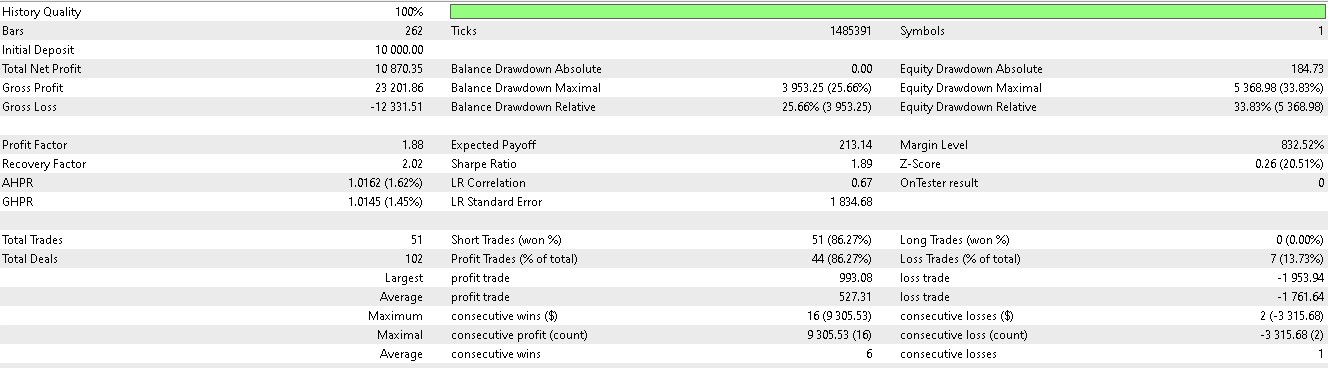
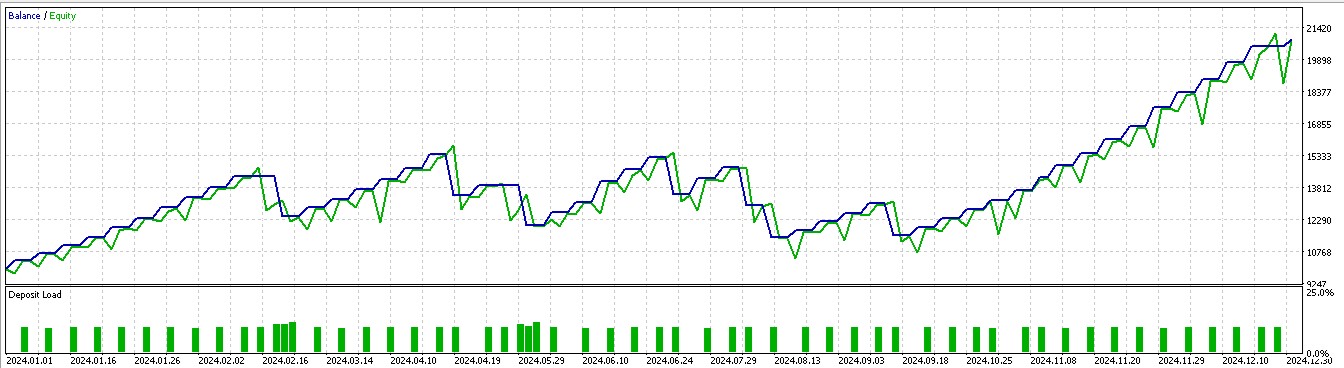
Rather than solely basing our long or short positions on what price is going to do next, we also consider what actions we really need to take in light of what price will do next. We also factor in whether the rewards will be profitable. Of the 7 patterns that walked forward in article 57, only 3 walk forward meaningfully when reinforcement-learning is used. Using our indexing of the 10 that runs from 0 to 9, these patterns are 1, 2, and 5. Their reports are presented below:

For pattern 1:

For pattern 2:

For pattern 5:

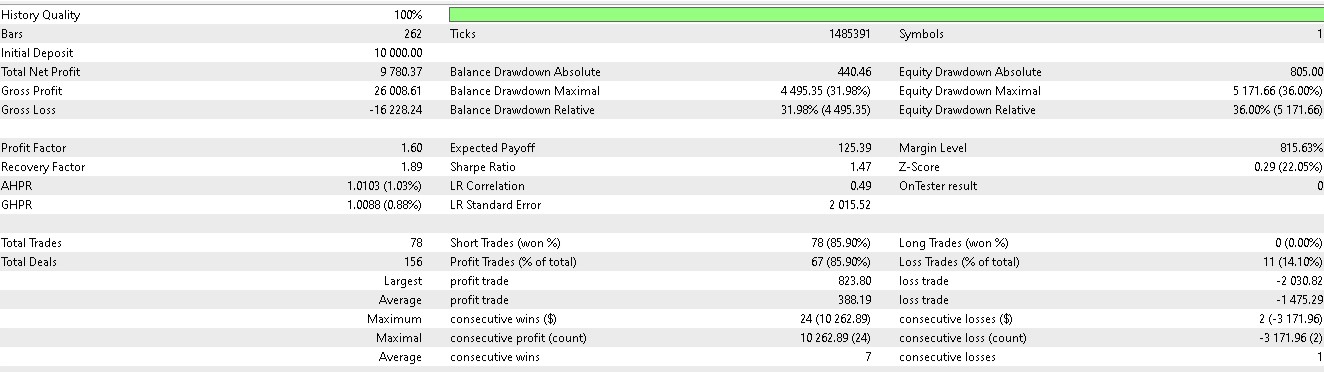
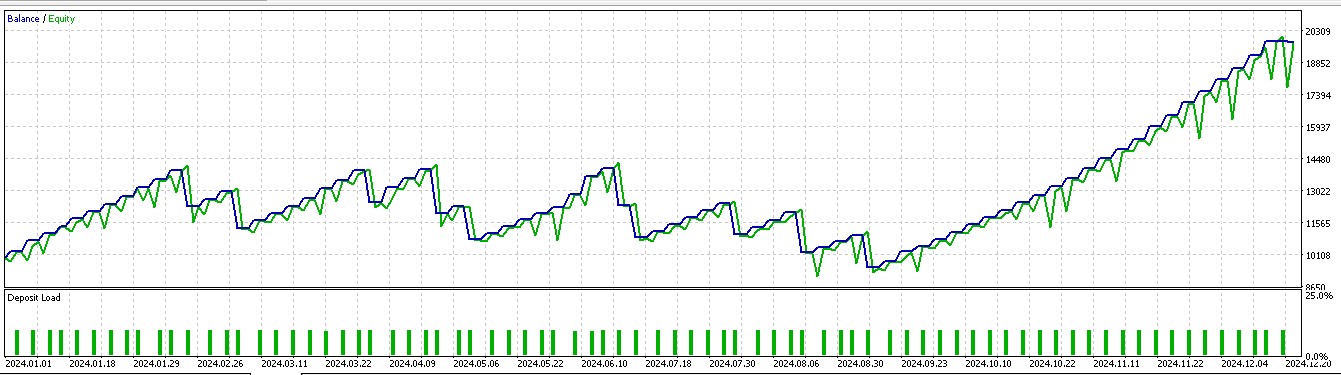
The tested Expert Advisor as always is built with a custom signal class whose code is attached below. We make changes to the signal class file we had in article 57, by renaming the function 'IsPattern' to 'Supervise'. Also, we introduce a new function 'Reinforce'. The code of both of these is shared below:

//+------------------------------------------------------------------+
//| Supervised Learning Model Forward Pass.                          |
//+------------------------------------------------------------------+
double CSignal_DDPG::Supervise(int Index, ENUM_POSITION_TYPE T)
{  vectorf _x = Get(Index, m_time.GetData(X()), m_close, m_ma, m_ma_lag, m_sto);
   vectorf _y(1);
   _y.Fill(0.0);
   int _i=Index;
   if(_i==8)
   {  _i -= 2;
   }
   ResetLastError();
   if(!OnnxRun(m_handles[_i], ONNX_NO_CONVERSION, _x, _y))
   {  printf(__FUNCSIG__ + " failed to get y forecast, err: %i", GetLastError());
      return(double(_y[0]));
   }
   if(T == POSITION_TYPE_BUY && _y[0] > 0.5f)
   {  _y[0] = 2.0f * (_y[0] - 0.5f);
   }
   else if(T == POSITION_TYPE_SELL && _y[0] < 0.5f)
   {  _y[0] = 2.0f * (0.5f - _y[0]);
   }
   return(double(_y[0]));
}
//+------------------------------------------------------------------+
//| Reinforcement Learning Model Forward Pass.                       |
//+------------------------------------------------------------------+
double CSignal_DDPG::Reinforce(int Index, ENUM_POSITION_TYPE T, double State)
{  vectorf _x(1);
   _x.Fill(float(State));
   vectorf _y(1);
   _y.Fill(0.0);
   vectorf _y_state(1);
   _y_state.Fill(float(State));
   vectorf _y_action(1);
   _y_action.Fill(0.0);
   vectorf _z(1);
   _z.Fill(0.0);
   int _i=Index;
   if(_i==8)
   {  _i -= 2;
   }
   ResetLastError();
   if(!OnnxRun(m_handles_a[_i], ONNX_NO_CONVERSION, _x, _y))
   {  printf(__FUNCSIG__ + " failed to get y action forecast, err: %i", GetLastError());
   }
   _y_action[0] = _y[0];
   ResetLastError();
   if(!OnnxRun(m_handles_c[_i], ONNX_NO_CONVERSION, _y_state, _y_action, _z))
   {  printf(__FUNCSIG__ + " failed to get z reward forecast, err: %i", GetLastError()); 
   }
   //normalize action output & check for state-action alignment
   if(T == POSITION_TYPE_BUY && _y[0] > 0.5f)
   {  _y[0] = 2.0f * (_y[0] - 0.5f);
   }
   else if(T == POSITION_TYPE_SELL && _y[0] < 0.5f)
   {  _y[0] = 2.0f * (0.5f - _y[0]);
   }
   else
   {  _y[0] = 0.0f;
   }
   return(double(_y[0]*_z[0]));
}

This custom signal class file is meant to be assembled into an Expert Advisor via the MQL5 wizard and for readers who are new they can find guidance here and here on how to do this.

Conclusion

We have looked at the case for applying reinforcement-learning when models are in deployment/ production. Our reinforcement-learning was using the deep deterministic policy gradient algorithm and this implementation had the classes: replay buffer, actor, critic and agent as covered in this and the last article.  Reinforcement-learning in deployment/production serves as a means of keeping the model focused on what was learnt in the supervised-learning phase (exploitation) while also looking out for new unknown changes in the environment/market-conditions that should be considered when making decisions going forward (exploitation). In doing this correctly, we inherently have to back propagate and train a model while it is being used. 

However, since training an ONNX model in MQL5 is unsupported, we opted for a simulation of live trading conditions on historical data. Post simulation, we tested the trained reinforcement-learning models on the subsequent year from the training year and only 3 of the 7 were able to forward walk, albeit with skewed trade results since positions were mostly held in long only or short only. This as we argued in article 57 is most likely down to a small test-window, meaning extensive training and testing over more data should rectify this. We now look at inference next.

Type	Description
*.*onnx files	ONNX model files in the Python Subfolder within location of custom signal class file
*.*mqh files	Custom signal class file in and file with function for processing input network data (57_X)
*.*mq5 files	Wizard Assembled Expert Advisor whose header shows files used.