Introduction to MQL5 (Part 20): Introduction to Harmonic Patterns

Introduction

Welcome back to Part 20 of the Introduction to MQL5 series! In this part, we'll explore another advanced chart pattern, the harmonic pattern. These patterns rely on precise Fibonacci ratios to map out potential reversal zones and are widely recognized in technical analysis.

If you’ve been trying to understand this concept in depth, this article is for you. This particular article will introduce you to the concept, covering the structure of harmonic patterns along with the essential Fibonacci extension and retracement tools used to define them.

We will explore the essential elements of some of the most well-known harmonic structures, including the Gartley, Bat, Butterfly, and Crab patterns, as well as the precise Fibonacci measurements that define them. Since even a slight divergence can render the setup invalid, it is important to understand these ratios. The next article will concentrate on using this knowledge to programmatically apply it to MQL5, allowing for the automatic identification of both bearish and bullish harmonic patterns.

In this article, you'll learn:

• The fundamentals of harmonic patterns and how they are applied in trading.
• Mathematical concepts behind Fibonacci retracements and why they are important for pattern identification.
• How Fibonacci extensions work and their role in determining potential price targets.
• Implementing harmonic pattern detection in MQL5, including using Fibonacci ratios programmatically.
• The structure of the different harmonic patterns and how to recognize them on a chart

Fibonacci Extension and Retracement

You have to understand Fibonacci extension and Fibonacci retracement before we can discuss the concept of harmonic patterns. The Fibonacci Retracement and Fibonacci Extension objects are probably familiar to you from your MetaTrader 5 toolbox, but have you ever wondered about the mathematical formulas used to determine those levels?

If so, that's fantastic; this section will help you learn more. If not, don't worry; I'll take care of you. You will know exactly how these Fibonacci levels are determined and why they are crucial for recognizing harmonic patterns by the end of this discussion.

Fibonacci Retracement

Both Fibonacci retracement and extension work with percentages. Think of it like measuring how much of a move the market has “given back” or “extended beyond.” Let’s use a simple example. Imagine the market makes a clear swing, first a swing low, then a swing high.

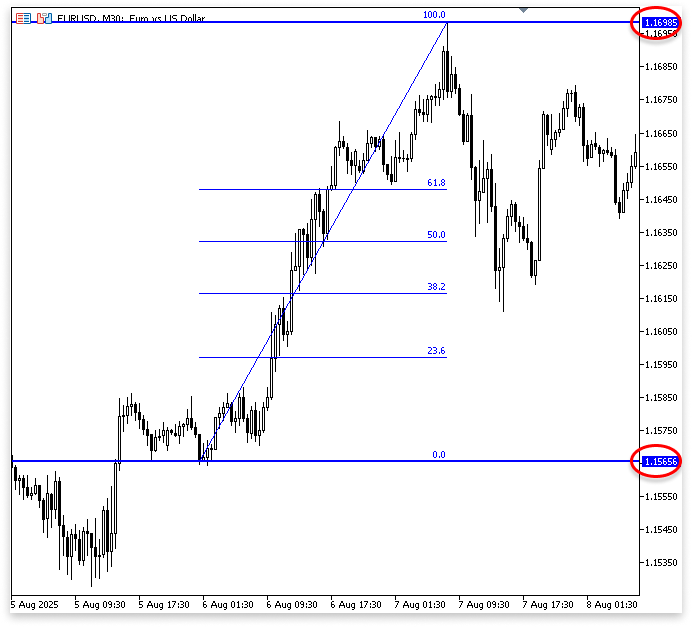
To calculate Fibonacci retracement levels, we take the difference between these two points (the height of the move).

Example:

double price_differecence;
double swing_high;
double swing_low;

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//---

//---
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//---

  }
//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
//---
   swing_high =  1.16985;
   swing_low = 1.15656;

   price_differecence = swing_high - swing_low;

  }

Always subtract swing_low from swing_high to get a positive price difference. Reversing the order gives a negative value. 

What would happen if the market reversed course midway from that peak? A 50% retracement is what that is. It indicates that half of the price's upward movement has been retracted.

Example:

double price_diff_50_percent;

//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
//---

   swing_high =  1.16985;
   swing_low = 1.15656;

   price_differecence = swing_high - swing_low;

   price_diff_50_percent = (50.0/100.0) * price_differecence; // (Fibonacci Retracement level / 100) * Price Difference

  }

50% of the total price difference is calculated on this line, and the calculation is handled as floating-point division because 50.0 and 100.0 are used rather than simple integers. Because floating-point division yields an accurate decimal value, this is significant. Some computer languages would read 50/100 as integer division if we had expressed it in integers.

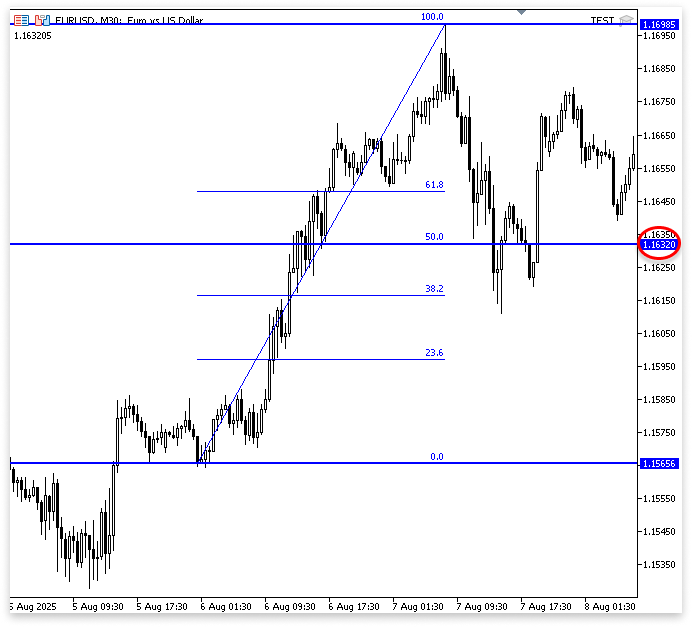
Think of it as going up ten steps on a staircase. You have retraced half of your climb if you take five steps back down. You can look at certain percentage levels in Fibonacci retracement. The price may pause or reverse at these levels, which frequently function as unseen support or resistance zones. According to Fibonacci proportions, the price simply retraced almost two-thirds of the way from the swing high toward the swing low when you hear "the market retraced to the 61.8% level."

Fibonacci Extension

Fibonacci extension focuses on estimating how far the next move could stretch beyond the initial swing, whereas Fibonacci retracement is mostly used to gauge how much the market has pulled back from a prior move. Although both are expressed as percentages, extension levels surpass the original swing by 100 percent.

If you want to measure something in the market, you can use Fibonacci extensions in two different ways.

First Scenario (Standard Use with Retracement):

In the normal application, the Fibonacci extension tool requires the market to retrace before the extension levels are plotted. Here, you will use three anchors:

• The first anchor is placed at point X.
• The second anchor is placed at point A.
• The third anchor is placed at point B, where B is a retracement of the XA move.

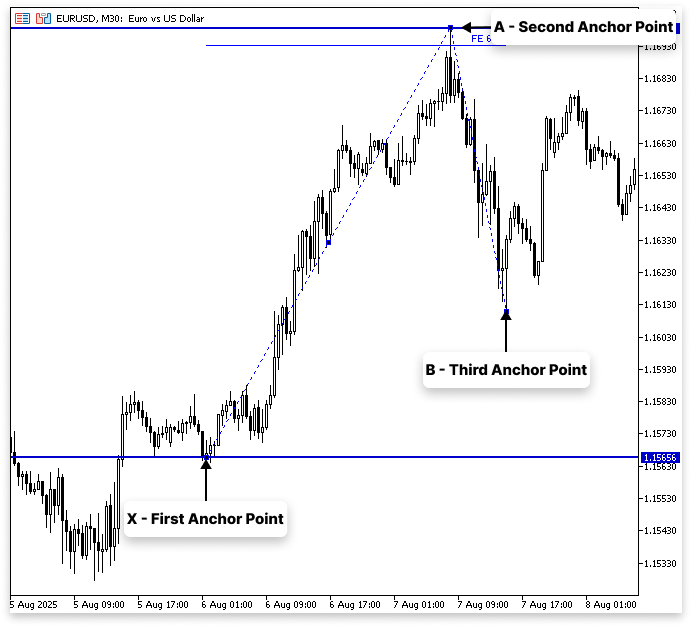
We start with a price swing, which we refer to as XA, in the first scenario of Fibonacci extensions. In this case, X and A stand for the move's beginning and finishing points, respectively. The market typically retraces to point B, which is situated halfway between X and A, following this first price movement. X, A, and B are the three anchors that we employ to compute Fibonacci extensions. The extension tool gives you a sense of where the market might go once the retracement is complete by projecting possible price objectives beyond point A.

Mathematically, we first calculate the price difference between X and A:

price difference=A−X

This gives the total size of the XA move. Next, we take the chosen Fibonacci extension ratio, for example, 61.8%, and express it as a decimal by dividing by 100:

fibo ratio= 61.8/100.0

Now, we multiply this ratio by the price difference to determine how far the extension will go beyond point A:

extension distance = fibo ratio×price difference

Finally, we add this extension distance to point B to get the Fibonacci extension level:

fibo extension = B+extension distance

In actuality, this means that the extension tool predicts where the subsequent bullish leg may end beyond A if XA is a bullish move and B is a retracement of that move. Likewise, in a negative market, the extension tool aids in locating possible downside targets outside of A. Fibonacci extensions are guaranteed to be systematic forecasts based on proportional relationships inside the price swing rather than merely random lines on a chart thanks to this mathematical procedure.

Second Scenario (Direct Use in Harmonic Patterns):

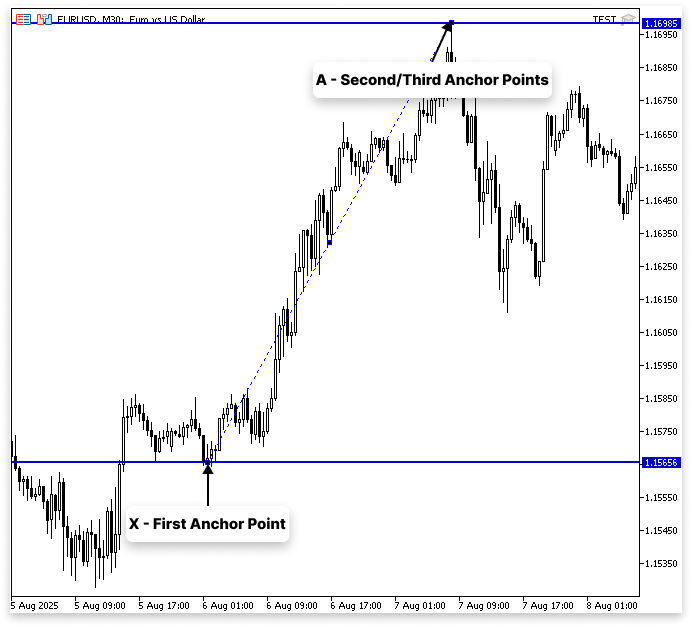
The Fibonacci extension is applied differently from the conventional retracement when working with harmonic patterns. The first anchor is positioned at point X, and the second and third anchors are positioned at point A, rather than using the tool on a pullback. Instead of measuring corrections, this setup focuses on estimating future price targets.

Although the Fibonacci extension and retracement in this case may appear to be comparable, they are not. If point A is a swing high, we often subtract the Fibonacci percentage of the XA leg from it; if it is a swing low, we add it. But with extensions, we add the value rather than deduct it if point A is a swing high; thus it's an extension rather than a retracement.

Example:

double price_differecence;
double swing_high; //A
double swing_low;  //X
double price_diff_161_8_percent;
double fibo_extension_161_8;

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//---

//---
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//---

  }
//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
//---

   swing_high =  1.16985;
   swing_low = 1.15656;

   price_differecence = swing_high - swing_low;

   price_diff_161_8_percent = (61.8/100.0) * price_differecence;
   fibo_extension_161_8 = swing_high + price_diff_161_8_percent;


  }

For instance, X to A is regarded as 100%. The Fibonacci level of XA is 61.8 percent, which provides us with an extension beyond point A. When the value is added to point A rather than subtracted, the resulting level is 161.8. For this reason, extensions such as 127.2 or 161.8 are frequently employed in harmonic patterns; they are not retracements within the initial XA movement, but rather projects beyond it.

This method eliminates the need for an actual retreat from XA and makes it simpler to identify the probable location of the subsequent swing in harmonic patterns. Rather, the price movement from X to A is mathematically stretched, and these forecasts aid in determining crucial points at which the market may reverse or finish the harmonic structure.

Harmonic Pattern

It is much simpler to discuss harmonic patterns after the ideas of Fibonacci retracement and Fibonacci extension have been clarified. This is because Fibonacci ratios are the foundation of all harmonic patterns. In actuality, the degree to which the price legs match particular Fibonacci retracement and extension levels, in addition to the pattern's appearance on the chart, is what distinguishes any harmonic pattern.

Geometric price structures that recur over various time periods are known as harmonic patterns. They consist of successive swings, or legs, like XA, AB, BC, and CD, and to validate the pattern, each leg must satisfy exact Fibonacci requirements. Harmonic patterns are distinct and more objective than simple chart patterns like triangles or flags since they rely significantly on mathematical ratios.

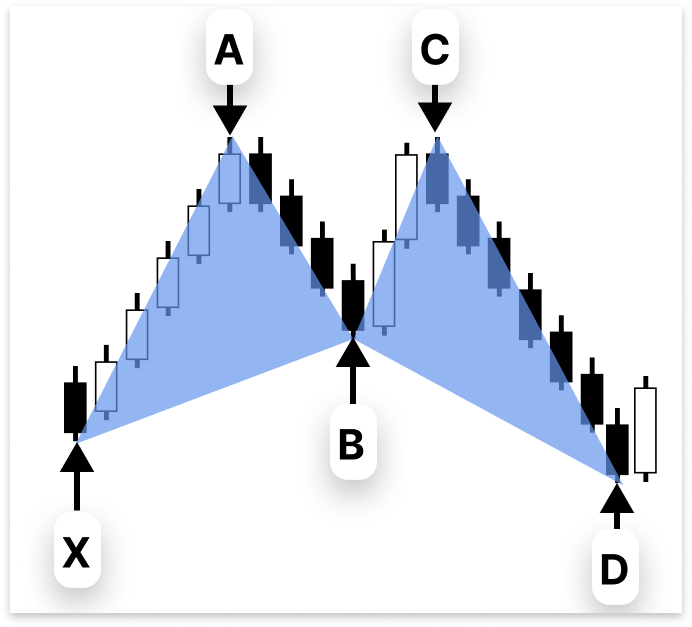
The Gartley, Bat, Butterfly, and Crab patterns are a few of the most popular harmonic patterns. The link between the legs is defined by a unique Fibonacci "recipe" for each of these patterns. For instance, for a pattern to be deemed legitimate, the retracement of AB relative to XA or the extension of CD relative to BC must fall within particular Fibonacci ranges and not be arbitrary.

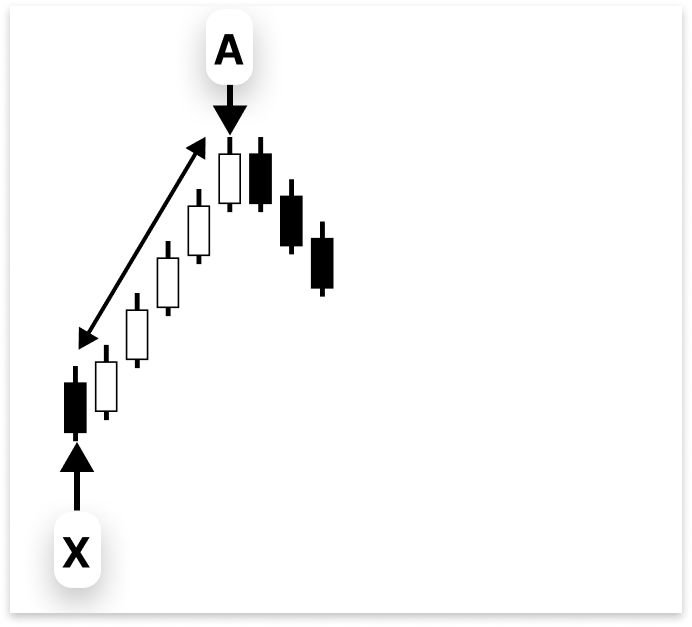
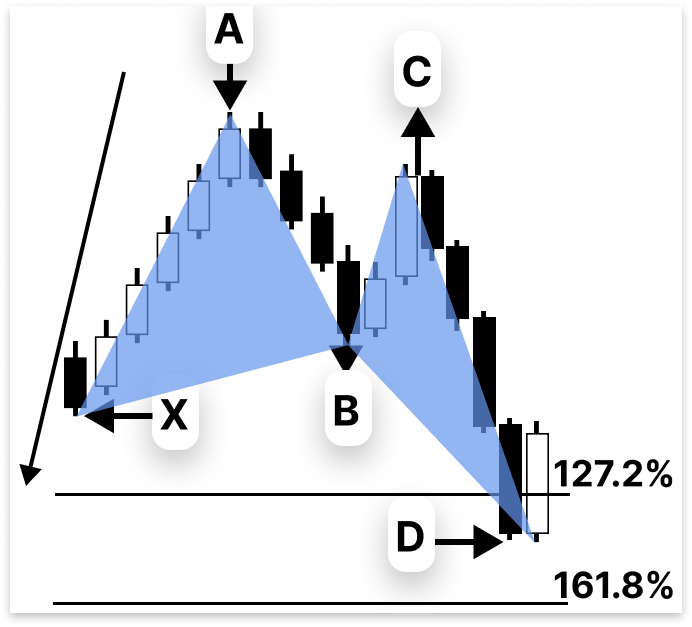
Butterfly Harmonic Pattern

In a typical butterfly pattern, the first leg starts from point X to A, which forms the initial price move.

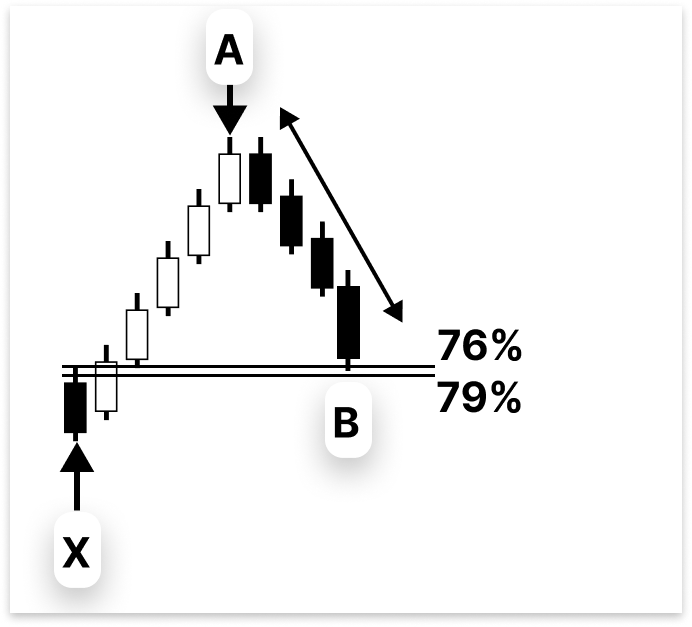
Point B should retrace the A-B leg between 76% and 79% of the X-A leg. Even though 78.6% is frequently mentioned as the "ideal" retracement, the price seldom hits that precise level. For this reason, using a range instead of a fixed point is safer.

Example:

double swing_low_x;  //X
double swing_high_x; //A
double price_differecence;
double fib_ret_79;
double fib_ret_76;

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//---

//---
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//---

  }
//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
//---


   swing_low_x = 1.15656;
   swing_high_x =  1.16985;

   price_differecence = swing_high_a - swing_low_x;

   fib_ret_79 = swing_high_x - ((79.0/100.0) * price_differecence);
   fib_ret_76 = swing_high_x - ((76.0/100.0) * price_differecence);


   /*
      if(B <= fib_ret_76 && B>= fib_ret_79)
      {



      }

    */
  }

Explanation:

This algorithm calculates the Fibonacci retracement levels between swing points X and A, laying the groundwork for locating point B in a Bat harmonic pattern. The price difference is determined, and the 79% and 76% retracement levels are calculated to provide the range within which point B should ideally form.

After calculating the retracement levels, we can compare the B point's price with this range. In the commented block:

if(B <= fib_ret_76 && B >= fib_ret_79) { }

This condition determines if the B point is within the specified XA leg's retracement. The B point fulfills the Bat harmonic pattern rules if the condition is true, in which case we can move on to additional validation for points C and D.

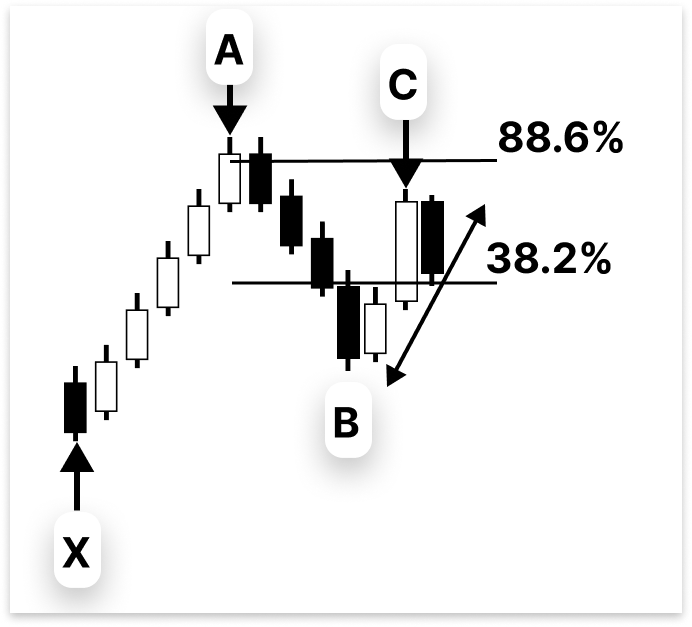
Between roughly 38.2%  and nearly 88.6%  of the previous A-B move is typically pulled back by the B-C segment. There is some flexibility in this segment compared to the others. Until this retreat remains within the anticipated bounds, the whole pattern is deemed proper.

Example:

double swing_low_x;  //X
double swing_high_a; //A
double price_differecence;
double fib_ret_79;
double fib_ret_76;

double swing_low_b;  //B
double price_differecence_ab;
double fib_ret_88_6_ab;
double fib_ret_38_2_ab;

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//---

//---
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//---

  }
//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
//---


   swing_low_x = 1.15656;
   swing_high_a =  1.16985;

   price_differecence = swing_high_a - swing_low_x;
   fib_ret_79 = swing_high_a - ((79.0/100.0) * price_differecence);
   fib_ret_76 = swing_high_a - ((76.0/100.0) * price_differecence);

   price_differecence_ab = swing_high_a - swing_low_b;
   fib_ret_88_6_ab = swing_low_b + ((88.6/100.0) * price_differecence_ab);
   fib_ret_38_2_ab = swing_low_b + ((38.2/100.0) * price_differecence_ab);


   /*
     if(B <= fib_ret_76 && B>= fib_ret_79 && C >= fib_ret_38_2_ab && C <= fib_ret_88_6_ab)
     {



     }

   */

  }

Explanation:

The overall price movement between two significant market points is calculated in this section. It determines particular Fibonacci retracement levels based on this movement, which show possible locations for the price to reverse or find support and resistance. The 38.2% level employs a smaller fraction of the movement added to the same point, while the 88.6% retracement level finds two reference levels for analysis by taking the majority of the entire price movement and adding it to the lower point.

These levels aid in locating potential price reaction zones during a retracement move. Lastly, as part of a pattern confirmation logic, the commented if statement determines whether point B is between two particular retracement levels and whether point C is likewise inside the specified Fibonacci range.

Lastly, the C-D leg, which delineates the potential reversal zone (PRZ), is the most crucial component of the Butterfly pattern. The D point in a valid Butterfly stretches from 127.2% to 161.8% of the original X-A leg. The completion zone, where traders search for possible reversal signs, is formed by this extension. Given that X-A is 100%, D will be approximately 161.8% of X-A after a 61.8% extension.

Example:

double swing_low_x;  //X
double swing_high_a; //A
double price_differecence;
double fib_ret_79;
double fib_ret_76;

double swing_low_b;  //B
double price_differecence_ab;
double fib_ret_88_6_ab;
double fib_ret_38_2_ab;

double xa_price_differecence;
double fib_ext_127_2_xa;
double fib_ext_161_8_xa;

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//---

//---
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//---

  }
//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
//---

   swing_low_x = 1.15656;
   swing_high_a =  1.16985;

   price_differecence_ab = swing_high_a - swing_low_b;
   fib_ret_79 = swing_high_a - ((79.0/100.0) * price_differecence);
   fib_ret_76 = swing_high_a - ((76.0/100.0) * price_differecence);

   fib_ret_88_6_ab = swing_low_b + ((88.6/100.0) * price_differecence_ab);
   fib_ret_38_2_ab = swing_low_b + ((38.2/100.0) * price_differecence_ab);

   xa_price_differecence = swing_high_a - swing_low_x;
   fib_ext_127_2_xa = MathAbs(swing_low_x - ((127.2/100.0) * xa_price_differecence));
   fib_ext_161_8_xa = MathAbs(swing_low_x - ((161.8/100.0) * xa_price_differecence));

   /*
     if(B <= fib_ret_76 && B>= fib_ret_79 && C >= fib_ret_38_2_ab && C <= fib_ret_88_6_ab && D <= fib_ext_127_2_xa && D >= fib_ext_161_8_xa)
     {

     }

   */

  }

Explanation:

This part of the code calculates the separation between two important market pattern swing points. The price movement is then used to determine the Fibonacci extension levels for that pattern segment. By computing the difference between the starting and finishing swing points and using the 127.2% and 161.8% Fibonacci ratios, it essentially forecasts where the price might extend next. To ensure that the computation functions for both upward and downward moves, the code makes use of a function that converts any result into a positive integer. These ratios are then applied to the initial price movement, either adding or deleting them according to the direction of the move, to get the forecast extension levels.

The mathematical underpinnings of Fibonacci extensions and retracements, as well as their application in MQL5, are now well understood. To verify harmonic patterns, we now know how to use Fibonacci ratios, compute the price differentials between swing points, and pinpoint important levels. The same logic we used here may be used for other harmonic patterns since all of them use similar Fibonacci-based calculations to identify potential reversal and continuation zones. Now that we have this framework in place, we can confidently look into more harmonic patterns. These concepts will be applied to identify potential trading opportunities using price action and Fibonacci connections.

Gartley Pattern: The XA, AB, BC, and CD steps are followed by the Gartley pattern. Point D is located inside XA's 127.2%–161.8% extension, Point B retraces around 61.8% of XA, and Point C retraces 38.2%–88.6% of AB. This indicates a possible trading reversal zone.

Bat Pattern: Certain Fibonacci ratios define the harmonic structure known as the Bat pattern. Point D, usually within XA's 88.6% retracement zone, marks the completion of the pattern, with Point B retracing 38.2% to 50% of the XA leg.

Conclusion

The principles of harmonic patterns and their use in trading have been discussed in this article. You now understand how to apply Fibonacci retracements and extensions in MQL5 and the mathematical principles underlying them. By employing harmonic patterns to construct a fully working Expert Advisor (EA), we will go from theory to practice in the upcoming article. Additionally, you will discover how to visually recognize and emphasize these patterns on your trading charts using MQL5's chart elements. You will have the information and resources necessary to successfully automate trading methods based on harmonic patterns by the end of the following article.